Optical Design and Lens Fabrication for Automotive Thermal Imaging Using Chalcogenide Glass
Abstract
1. Introduction
2. Experiments and Discussion
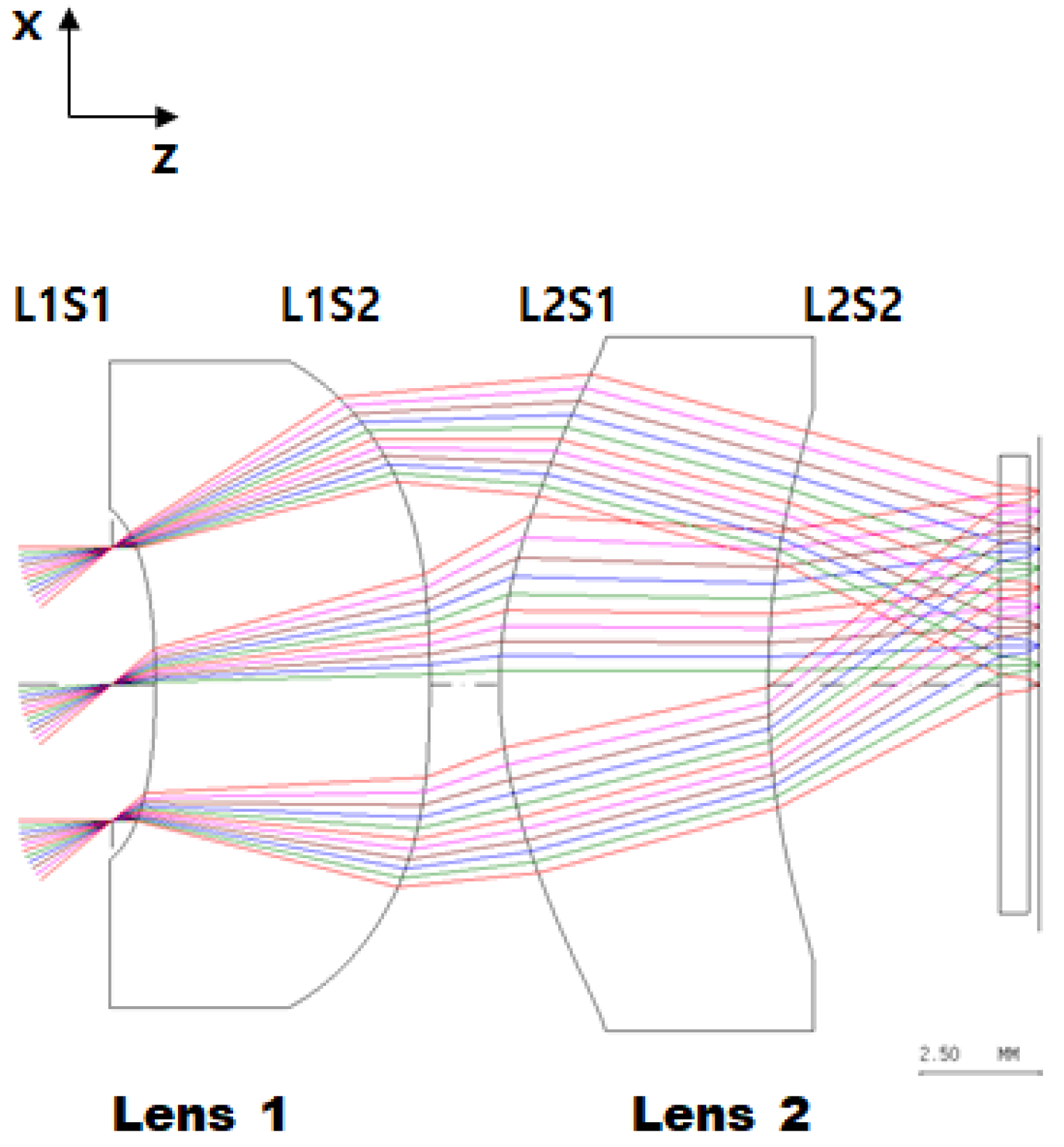
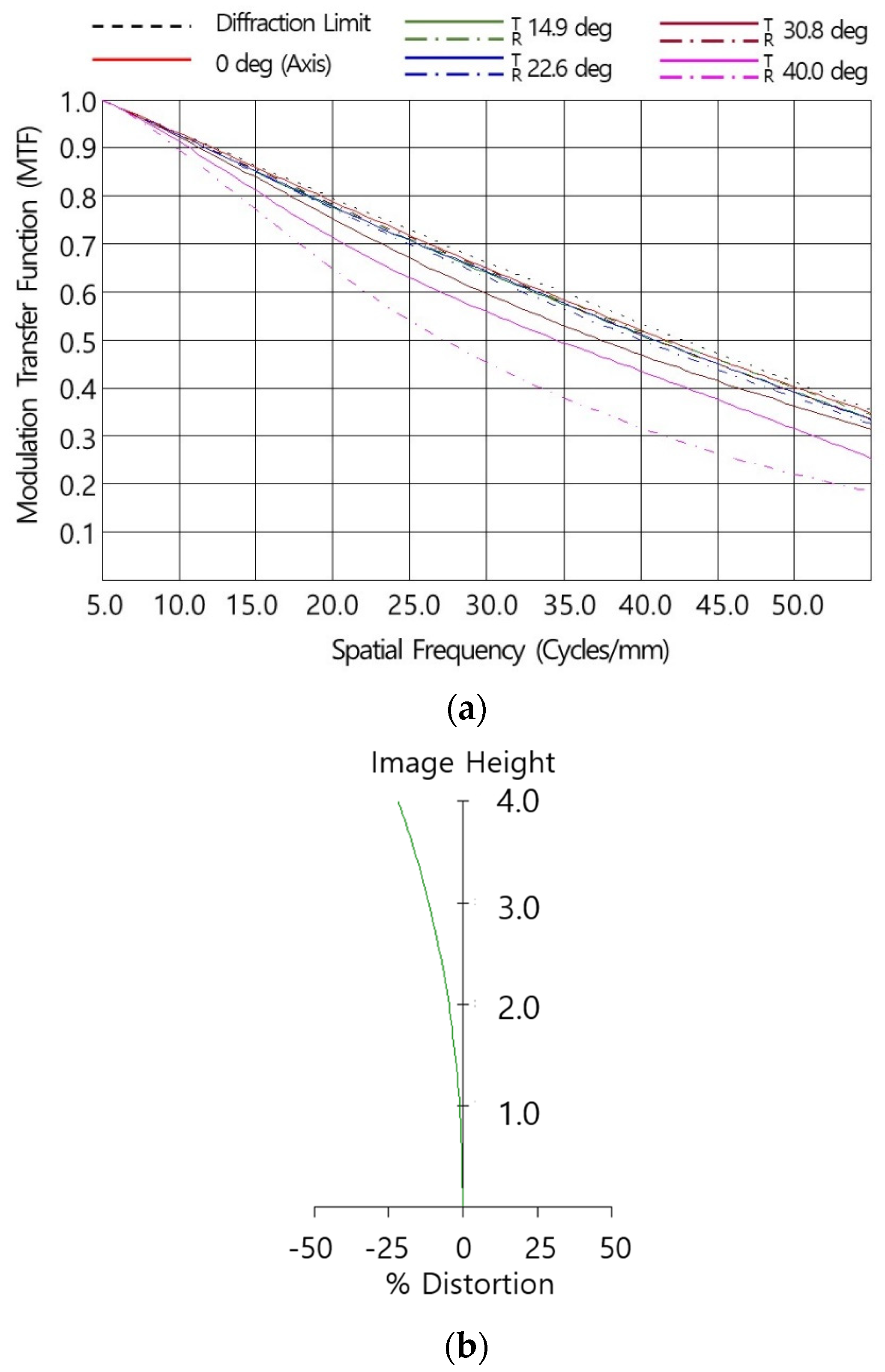
2.1. Optical Design
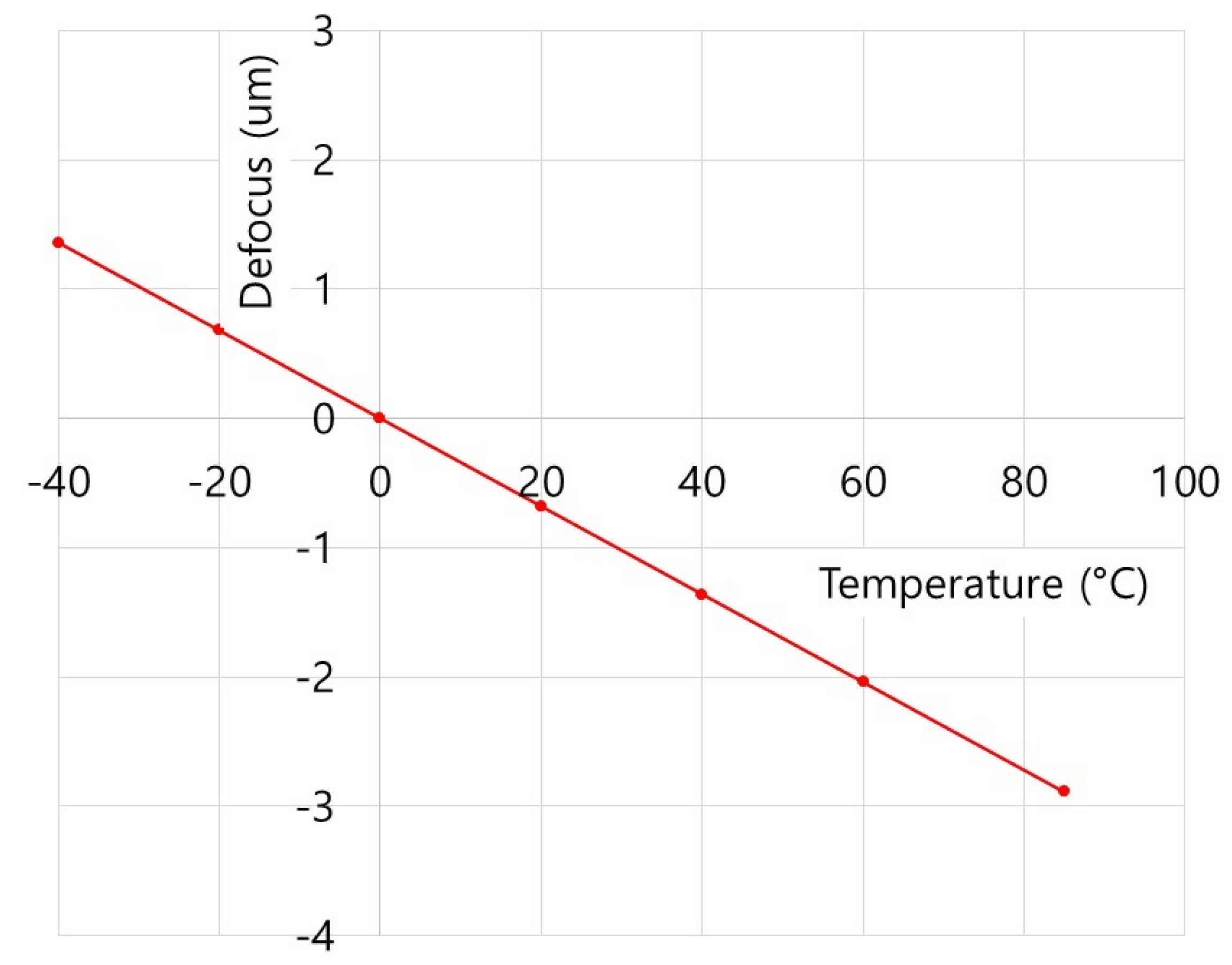
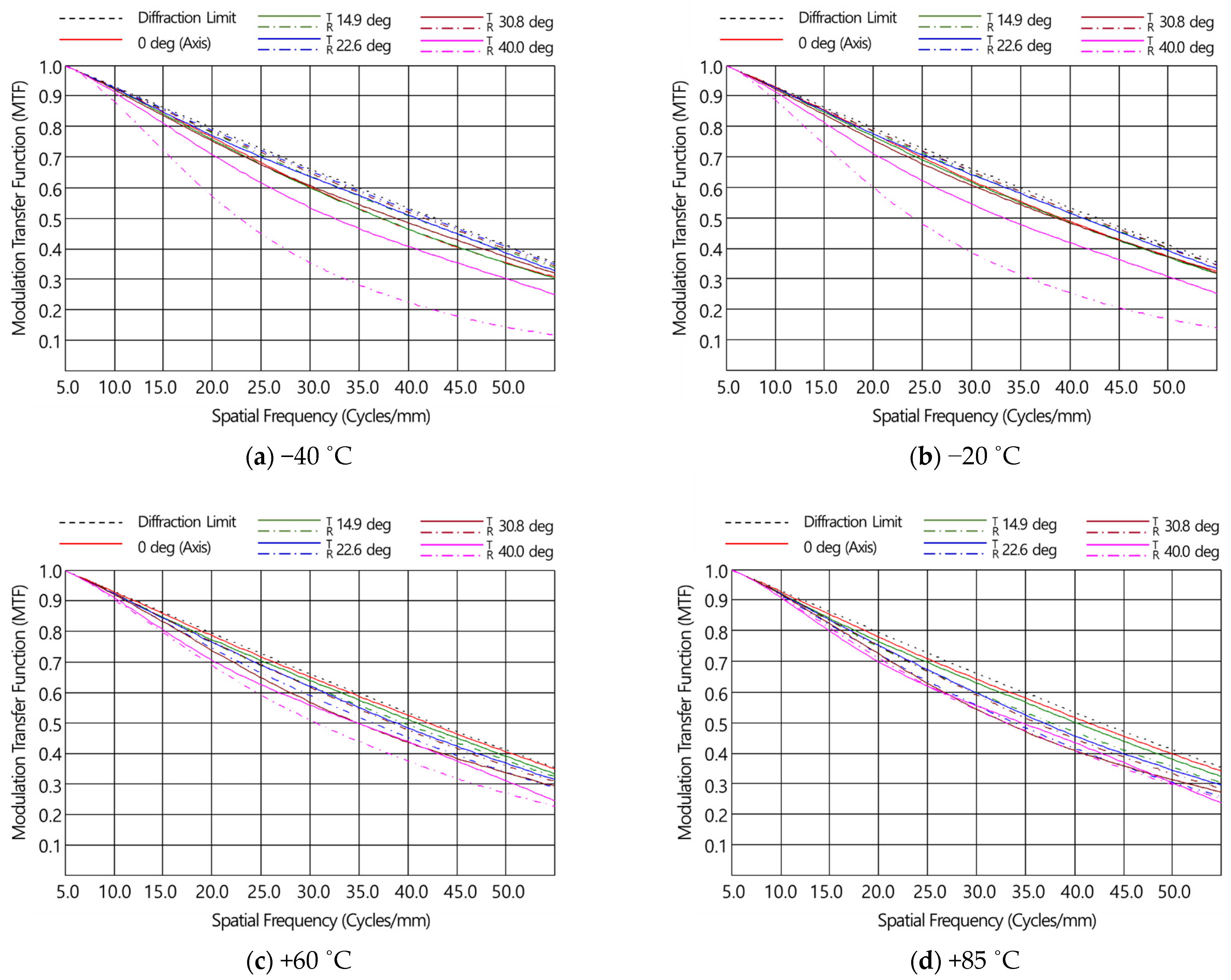
2.2. Athermalization Design of the Infrared Optical System
2.3. Molding of Chalcogenide Glass Lens and Thermal Imaging Evaluation
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farooq, M.A.; Shariff, W.; O’callaghan, D.; Merla, A.; Corcoran, P. On the role of thermal imaging in automotive applications: A critical review. IEEE Access 2023, 11, 25152–25173. [Google Scholar] [CrossRef]
- Bourget, A.; Guimond, Y.; Franks, J.; Vandenbergh, M. Molded infrared optics making night vision for cars within reach. Proc. SPIE 2005, 5663, 182–189. [Google Scholar]
- Wilson, A.N.; Gupta, K.A.; Koduru, B.H.; Kumar, A.; Jha, A.; Cenkeramaddi, L.R. Recent advances in thermal imaging and its applications using machine learning: A review. IEEE Sens. J. 2023, 23, 3395–3407. [Google Scholar] [CrossRef]
- Zhou, T.; Zhu, Z.; Liu, X.; Liang, Z.; Wang, X. A review of the precision glass molding of chalcogenide glass (ChG) for infrared optics. Micromachines 2018, 9, 337. [Google Scholar] [CrossRef] [PubMed]
- Graham, A.; LeBlanc, R.A.; Hilton, R., Sr. Low cost infrared glass for IR imaging applications. Proc. SPIE 2003, 5078, 216–224. [Google Scholar]
- Xu, Z.; Dai, S.; Liu, C.; Wu, Z.; Xu, L. Investigation of the Ga–Sb–S chalcogenide glass with low thermo-optic coefficient as an acousto-optic material. Ceram. Int. 2022, 48, 21663–21670. [Google Scholar] [CrossRef]
- Guillevic, E.; Zhang, X.; Pain, T.; Calvez, L.; Adam, J.-L.; Lucas, J.; Guilloux-Viry, M.; Ollivier, S.; Gadret, G. Optimization of chalcogenide glass in the As–Se–S system for automotive applications. Opt. Mater. 2009, 31, 1688–1692. [Google Scholar] [CrossRef]
- Ok, C.M.; Kong, H.B.; Park, H.W. Design and analysis of an optical system for an uncooled thermal-imaging camera using a hybrid lens. Korean J. Opt. Photonics 2017, 28, 241–249. [Google Scholar]
- Son, B.R.; Kim, K.; Choi, Y.S.; Park, C.S. Transferability of diffractive structure in the compression molding of chalcogenide glass. Micromachines 2023, 14, 273. [Google Scholar] [CrossRef] [PubMed]
- Bigwood, C.R. New infrared optical systems using diffractive optics. In Current Developments in Lens Design and Optical Engineering III; Proceedings Volume 4767; SPIE: Bellingham, WA, USA, 2002. [Google Scholar]
- Cha, D.H.; Kim, H.J.; Park, H.S.; Hwang, Y.; Kim, J.H.; Hong, J.H.; Lee, K.S. Effect of temperature on the molding of chalcogenide glass lenses for infrared imaging applications. Appl. Opt. 2010, 49, 1607–1613. [Google Scholar] [CrossRef] [PubMed]
- Cha, D.H.; Kim, H.J.; Hwang, Y.; Jeong, J.C.; Kim, J.H. Fabrication of molded chalcogenide-glass lens for thermal imaging applications. Appl. Opt. 2012, 51, 5649–5656. [Google Scholar] [CrossRef] [PubMed]
- Cha, D.H.; Kim, J.H.; Kim, H.J. Experimental study of the fabrication of chalcogenide glass lenses by using precision glass molding. J. Korean Phys. Soc. 2014, 65, 1675–1681. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, H.L.; Lucas, J.; Guimond, Y.; Kodjikian, S. Optical fibers and molded optics in infrared transparent glass-ceramic. J. Non-Cryst. Solids 2004, 336, 49–52. [Google Scholar] [CrossRef]
- Katsuki, M. Transferability of glass lens molding. Proc. SPIE 2006, 6149, 61490M1. [Google Scholar]


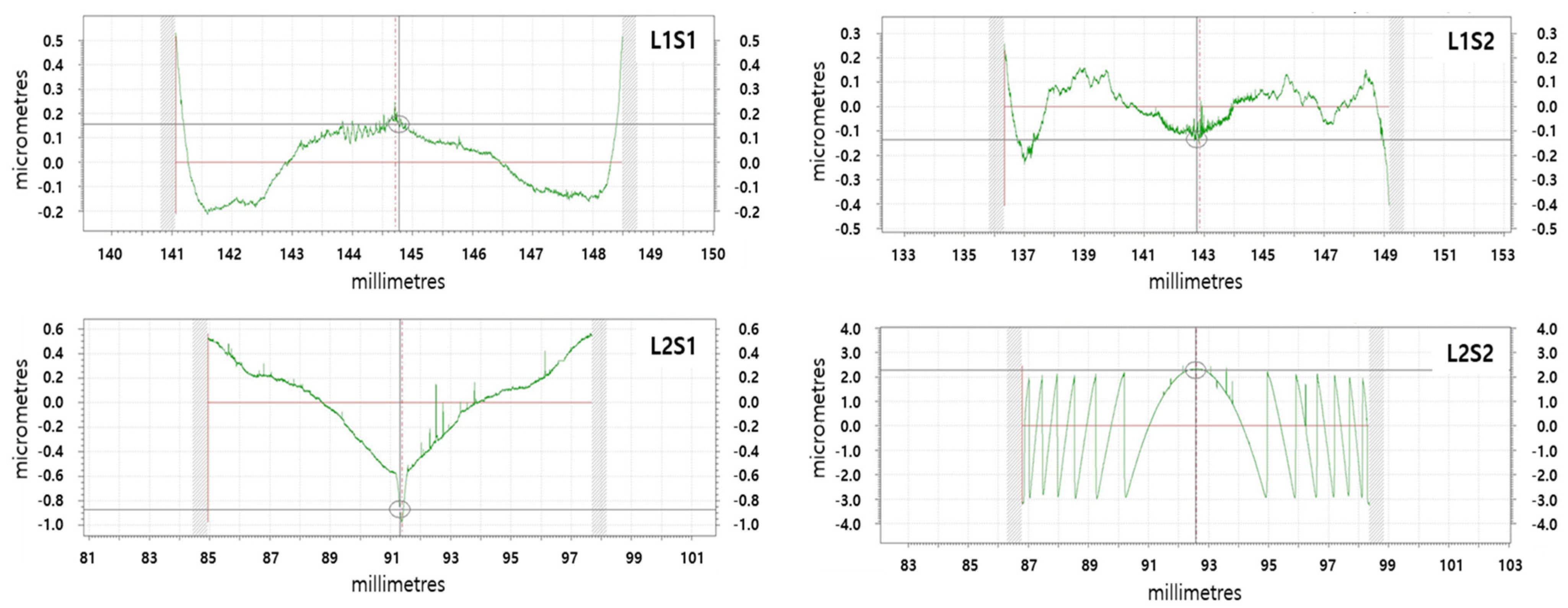
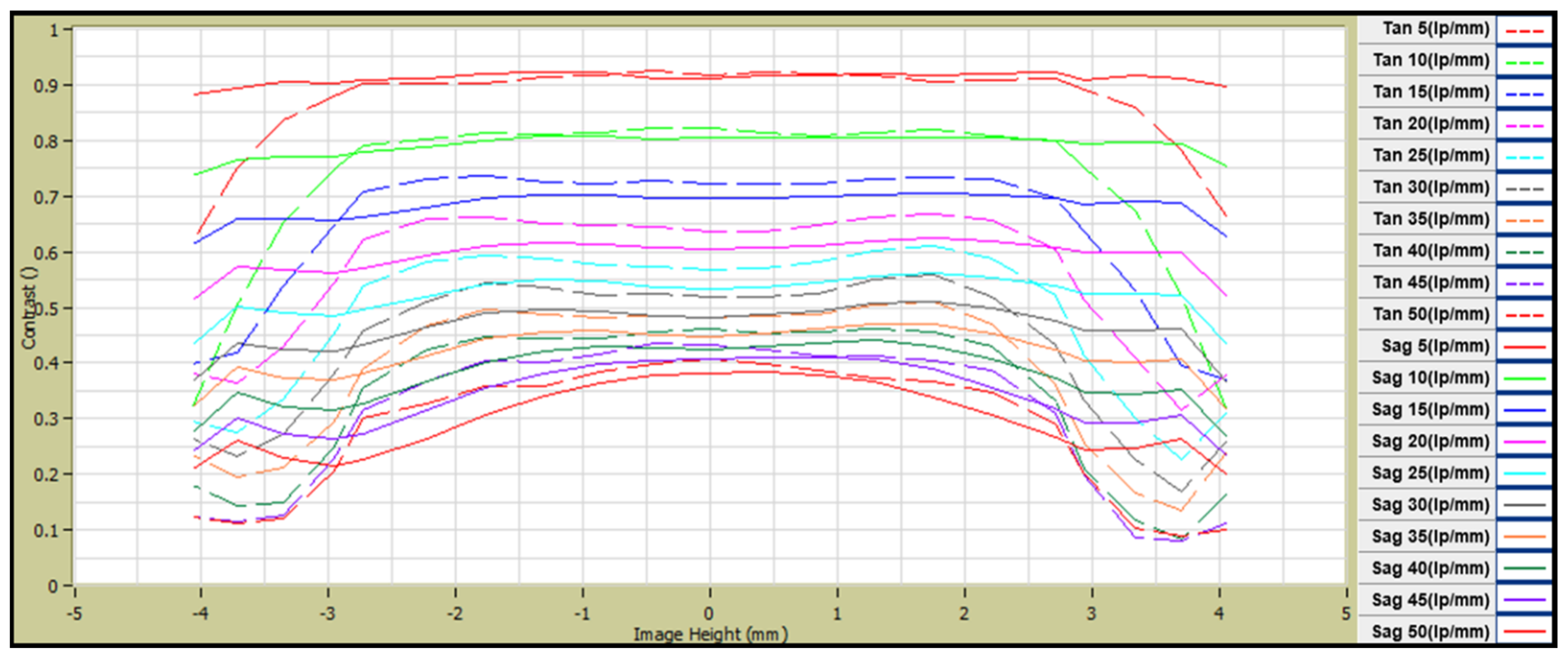

| Parameters | Requirements | |
|---|---|---|
| Detector | 640 × 480, 10 μm | |
| Spectral range | 8.0~12.0 μm | |
| F/number (fno.) | 1.1 | |
| Field of view (Horizontal × Vertical) | 61.6° × 45.5° | |
| MTF @50 lp/mm | (Center) | ≥0.3 |
| (HFOV) | ≥0.25 | |
| Optical distortion | ≤|25|% | |
| Athermalization (−40~+85 °C) | MTF (@ 50 lp/mm; On-axis) ≥ 0.2 | |
| Term | Unit | Value |
|---|---|---|
| Transition temperature (Tg) | °C | 185 |
| Thermal conductivity | W/m·K | 0.24 |
| Thermal expansion coefficient (@20 °C) | 10−6/K | 20.8 |
| Thermal change (dn/dT) (@10.6 μm wavelength) | 10−6/K | 32.2 |
| Softening temperature (Ts) | °C | 236 |
| Scheme | Radius (mm) | Thickness (mm) | Material | ||||
|---|---|---|---|---|---|---|---|
| 1. STO | Infinity | 0.9 | - | ||||
| 2. L1 | −15.1 | 5.7 | IRG26 | ||||
| 3 | −32.3 | 1.45 | - | ||||
| 4. L2 | 8.2 | 5.6 | IRG26 | ||||
| 5 | 19.4 | 4.8 | - | ||||
| 6 | Infinity | 0.6 | Si | ||||
| Surface No. | 2 | 3 | 4 | 5 | |||
| K | 0.0000 | 0.0000 | 0.0000 | 1.1103 | |||
| A4 | −1.9503 × 10−5 | 1.9486 × 10−4 | −3.1136 × 10−4 | −1.8326 × 10−5 | |||
| A6 | −4.9027 × 10−6 | −4.6883 × 10−6 | −1.8813 × 10−5 | −2.1507 × 10−6 | |||
| A8 | 3.8746 × 10−7 | −4.7384 × 10−8 | 2.3311 × 10−6 | 1.0116 × 10−7 | |||
| A10 | −4.8155 × 10−0 | −1.2605 × 10−7 | −2.5402 × 10−7 | −2.7805 × 10−9 | |||
| A12 | 1.6997 × 10−9 | 5.8932 × 10−9 | 1.2779 × 10−8 | 3.6328 × 10−11 | |||
| C1 | - | - | - | −0.9165 × 10−3 | |||
| C2 | - | - | - | 0.2132 × 10−5 | |||
| Refractive Index [n10μm] | Clear Aperture | Depth | Number of Rings |
|---|---|---|---|
| 2.7781 | 10.45 mm | 5.63 μm | 5.4 |
| Element | Material | Refractive Index [n10μm] | Abbe Number [ν8–12μm] | α [×10−6/K] | dn/dT10μm [@−50~75 °C; ×10−6/K] |
|---|---|---|---|---|---|
| Lens | IRG26 | 2.7781 | 161 | 20.8 | 32.2 |
| Housing | Aluminum (AL6061) | - | - | 26.3 | - |
| Lens | Material | EFL(mm) @20 °C | (dn/dT)/(n − 1) [×10−6/K] | dfr/dT [mm/K] |
|---|---|---|---|---|
| L1 | IRG26 | −18.60 | 18.1 | −0.000050 |
| L2 | IRG26 | 5.96 | 18.1 | 0.000016 |
| Preheating | Heating | Pressing | Gradual Cooling | ||
|---|---|---|---|---|---|
| Temp. (°C) | Top plate | - | 245 | 260 | 100 |
| Bottom plate | 180 | 245 | 245 | 100 | |
| Pressure (MPa) | - | - | 0.2 | 0.05 | |
| Unit-processing time (s) | 300 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.-S.; Kim, J.-K. Optical Design and Lens Fabrication for Automotive Thermal Imaging Using Chalcogenide Glass. Micromachines 2025, 16, 901. https://doi.org/10.3390/mi16080901
Choi Y-S, Kim J-K. Optical Design and Lens Fabrication for Automotive Thermal Imaging Using Chalcogenide Glass. Micromachines. 2025; 16(8):901. https://doi.org/10.3390/mi16080901
Chicago/Turabian StyleChoi, Young-Soo, and Ji-Kwan Kim. 2025. "Optical Design and Lens Fabrication for Automotive Thermal Imaging Using Chalcogenide Glass" Micromachines 16, no. 8: 901. https://doi.org/10.3390/mi16080901
APA StyleChoi, Y.-S., & Kim, J.-K. (2025). Optical Design and Lens Fabrication for Automotive Thermal Imaging Using Chalcogenide Glass. Micromachines, 16(8), 901. https://doi.org/10.3390/mi16080901









