Executed Movement Using EEG Signals through a Naive Bayes Classifier
Abstract
:1. Introduction
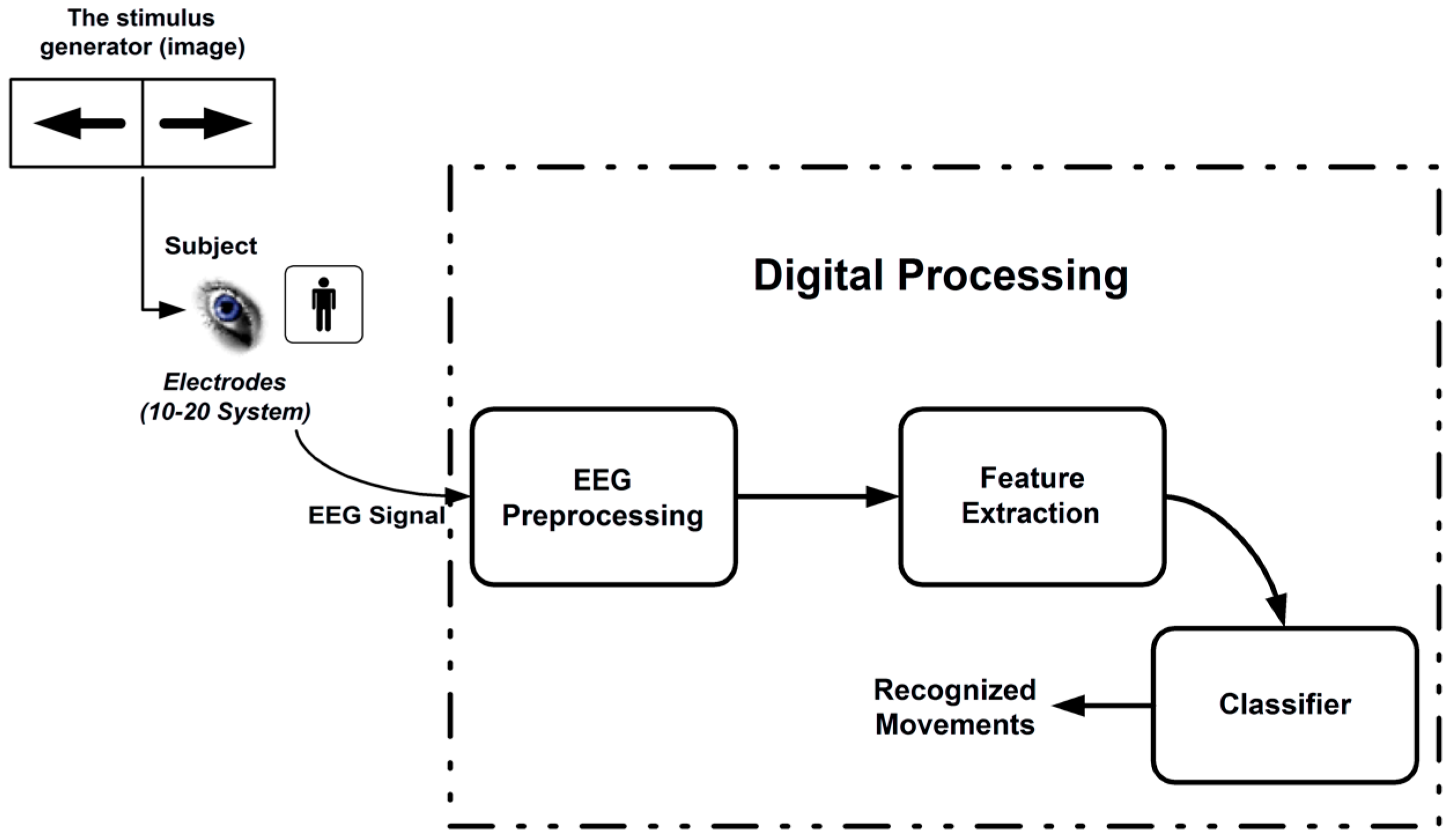
2. Methods
2.1. Pre Processing
2.1.1. Spectral Estimation
2.1.2. Spatial Filter
2.2. Signal Classification
2.2.1. Naive Bayes
2.2.2. Linear Discriminant Analysis
3. Experimental Section
3.1. Materials and Data Synchronization
- (1)
- From 0 to 1.5 s: a white screen appeared establishing the so-called reference period;
- (2)
- From 1.5 to 3 s: a pre-stimulus a cross appeared on the screen;
- (3)
- From 3 to 6 s: the stimulus presentation occurred (a blue arrow pointing to the right or a red arrow pointing to the left);
- (4)
- From 6 to 8 s: a white screen appeared once again establishing the so-called post-stimulus period.


3.2. EEG Signal Processing
CSP Filter
- (1)
- Estimate and (which are the co-variance matrices for the left and right classes, respectively) through the training set;
- (2)
- Find the matrix ;
- (3)
- Perform the “whitening” operation in order to obtain the matrix P;
- (3)
- Decompose and through matrix P to obtain the matrices and , whose eigenvalues and represent the discriminatory activity in the new CSP channel space;
- (5)
- Select both the largest eigenvalues and that will maximize the variance in the left-hand movement condition while minimizing the variance in the right-hand movement condition;
- (6)
- Calculate the spatial filter and select columns of the matrix W, which are related to the largest eigenvalues of and , respectively.
3.3. Features Extraction
3.3.1. Energy of CSP Filtered EEG
3.3.2. Welch’s Periodogram Components

4. Results and Discussion
4.1. Analysis Based on Signal Energy


4.2. Analysis Based on LI
4.3. Analysis Based on the Welch Periodogram



4.4. Analysis Based on the Spatial Filter

| Without CSP Filter, Channel C4 | With CSP Filter, Channel CSP4 |
|---|---|
| = 0.59 | = 0.63 |
4.5. Classification Based on Signal Energy
| Window | Hit rate by session (% average ± standard deviation) | |||
|---|---|---|---|---|
| S1 | S2 | S3 | S4 | |
| W1 | 66.8 ± 10.6 | 68.5 ± 8.72 | 69.0 ± 10.3 | 64.8 ± 9.48 |
| W2 | 66.5 ± 10.7 | 67.0 ± 8.91 | 69.9 ± 10.6 | 64.5 ± 7.95 |
| W3 | 65.2 ± 9.51 | 66.8 ± 8.88 | 70.6 ± 10.1 | 65.1 ± 7.62 |
| W4 | 66.7 ± 9.13 | 66.4 ± 8.45 | 68.5 ± 9.91 | 66.8 ± 8.77 |
| W5 | 64.1 ± 10.6 | 67.8 ± 8.24 | 69.6 ± 9.01 | 65.4 ± 8.71 |
| W6 | 64.9 ± 9.73 | 66.4 ± 8.71 | 68.1 ± 11.2 | 67.4 ± 9.12 |
| Window | Hit rate by session (% average ± standard deviation) | |||
|---|---|---|---|---|
| S1 | S2 | S3 | S4 | |
| W1 | 66.1 ± 10.5 | 66.2 ± 9.32 | 64.3 ± 9.76 | 62.9 ± 9.34 |
| W2 | 64.4 ± 10.7 | 64.6 ± 8.86 | 64.6 ± 10.6 | 62.4 ± 8.15 |
| W3 | 63.6 ± 9.93 | 65.2 ± 8.40 | 65.2 ± 10.6 | 62.1 ± 8.55 |
| W4 | 64.6 ± 11.4 | 63.5 ± 8.50 | 65.0 ± 9.87 | 62.0 ± 9.85 |
| W5 | 62.6 ± 10.5 | 65.1 ± 8.87 | 65.0 ± 10.4 | 59.7 ± 9.32 |
| W6 | 63.1 ± 10.1 | 64.0 ± 8.94 | 62.6 ± 9.55 | 59.5 ± 9.34 |
| Window | Hit rate session S3 (% average ± standard deviation) | |
|---|---|---|
| LDA | Naive Bayes | |
| W1 | 67.8 ± 9.75 | 63.2 ± 10.5 |
| W2 | 68.3 ± 8.85 | 63.3 ± 10.0 |
| W3 | 68.2 ± 10.4 | 63.7 ± 11.5 |
| W4 | 67.1 ± 9.65 | 63.3 ± 8.68 |
| W5 | 68.8 ± 10.2 | 63.1 ± 10.7 |
| W6 | 66.7 ± 9.65 | 61.2 ± 10.1 |
4.6. Classification Based on the Spectral Components as the Input Feature
| Session | Spectral Components | |||||
|---|---|---|---|---|---|---|
| 2 | 4 | 10 | ||||
| LDA | NB | LDA | NB | LDA | NB | |
| S1 | 62.5 ± 16.6 | 62.9 ± 17.5 | 62.5 ± 13.3 | 65.4 ± 15.3 | 61.2 ± 16.6 | 63.5 ± 16.3 |
| S2 | 60.7 ± 14.9 | 52.8 ± 12.4 | 61.6 ± 13.6 | 55.7 ± 13.9 | 61.9 ± 14.5 | 56.1 ± 14.5 |
| S3 | 60.9 ± 16.0 | 57.3 ± 15.9 | 60.6 ± 15.2 | 56.8 ± 15.2 | 60.6 ± 13.5 | 60.3 ± 14.3 |
| S4 | 62.4 ± 14.0 | 59.4 ± 13.1 | 60.9 ± 11.8 | 58.8 ± 11.9 | 68.4 ± 11.8 | 65.4 ± 11.6 |
| Session | Spectral Components | |||||
|---|---|---|---|---|---|---|
| 2 | 4 | 10 | ||||
| LDA | NB | LDA | NB | LDA | NB | |
| S1 | 62.6 ± 16.2 | 64.9 ± 18.4 | 59.6 ± 16.1 | 68.4 ± 17.3 | 54.6 ± 17.2 | 65.8 ± 13.5 |
| S2 | 62.6 ± 13.9 | 50.7 ± 13.4 | 64.3 ± 12.5 | 54.1 ± 14.9 | 59.3 ± 13.6 | 51.7 ± 14.8 |
| S3 | 56.1 ± 15.2 | 55.7 ± 13.3 | 52.7 ± 15.9 | 53.8 ± 16.1 | 45.9 ± 15.6 | 51.1 ± 15.9 |
| S4 | 58.9 ± 12.4 | 51.0 ± 14.1 | 60.1 ± 12.6 | 55.4 ± 13.0 | 60.8 ± 12.7 | 54.7 ± 11.9 |
5. Conclusions
| Classification Method | Accuracy (%) | Reference |
|---|---|---|
| Gaussian Support Vector Machines | 86 | [48] |
| LDA | 61 | |
| Multi-Layer Neural Network | 80.4 | [49] |
| LDA | 80.6 | |
| Hidden Markov Model | 81.4 | [50] |
| Finite Impulse Neural Network | 87.4 | [51] |
| Morlet Wavelet and Bayes Quadratic integrated over time | 89.3 | [52] |
| LDA | 65.6 | [53] |
Author Contributions
Conflicts of Interest
References
- Wolpaw, J.R.; Birbaumer, C.; McFarland, D.J.; Pfurtscheller, G.; Vaughan, T.M. Brain-computer interfaces for communication and control. Clinic. Neurophysiol. 2002, 113, 767–791. [Google Scholar] [CrossRef]
- Neuper, C.; Muller, G.R.; Kubler, A.; Birbaumer, N.; Pfurtscheller, G. Clinical application of an EEG-based brain-computer interface: A case study in a patient with severe motor impairment. Clinic. Neurophysiol. 2003, 114, 399–409. [Google Scholar] [CrossRef]
- Blankertz, B.; Dornhege, G.; Krauledat, M.; Muller, K.R.; Curio, G. The non-invasive Berlin brain-computer interface: Fast acquisition of effective performance in untrained subjects. NeuroImage 2007, 37, 539–550. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Aggarwal, V.; Ramos, A.; Acharya, S.; Thakor, N.V. A brain-computer interface with vibrotactile biofeedback for haptic information. J. Neuroeng. Rehabil. 2007, 4, 4–40. [Google Scholar] [CrossRef] [PubMed]
- Kamousi, B.; Amini, A.N.; He, B. Classification of motor imagery by means of cortical current density estimation and Von Neumann entropy for brain-computer interface applications. J. Neural Eng. 2007, 4, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Brunner, C.; Schlogl, A.; Lopes da Silva, F.H. Mu rhythm (de)synchronization and EEG single-trial classification of different motor imagery tasks. Neuroimage 2006, 31, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Pineda, J.A.; Silverman, D.S.; Vankov, A.; Hestenes, J. Learning to control brain rhythms: Making a brain-computer interface possible. IEEE Trans. Neural Syst. Rehabil. Eng. 2003, 11, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Birbaumer, N.; Ghanayim, N.; Hinterberger, T.; Iversen, I.; Kotchoubey, B.; Kubler, A. A spelling device for the paralysed. Nature 1999, 398, 297–298. [Google Scholar] [CrossRef] [PubMed]
- Bayliss, J.D. Use of the evoked potential P3 component for control in a virtual apartment. IEEE Trans. Neural Syst. Rehabil. Eng. 2003, 11, 113–116. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, U.; Vesin, J.M.; Ebrahimi, T.; Diserens, K. An efficient P300-based brain-computer interface for disabled subjects. J. Neurosci. Methods 2008, 167, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Lalor, E.C.; Kelly, S.P.; Finucane, C.; Burke, R.; Reilly, R.B. Steady-state VEP-based brain-computer interface control in an immersive 3D gaming environment. EURASIP J. Appl. Signal Process. 2005, 2005, 3156–3164. [Google Scholar] [CrossRef]
- Middendorf, M.; McMillan, G.; Calhoun, G.; Jones, K.S. Brain-computer interfaces based on the steady-state visual-evoked response. IEEE Trans. Rehabil. Eng. 2000, 8, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Galan, F.; Nuttin, M.; Lew, E.; Ferrez, P.W.; Vanacker, G.; Philips, E. A brain-actuated wheelchair: Asynchronous and non-invasive brain-computer interfaces for continuous control of robots. Clinic. Neurophysiol. 2008, 119, 2159–2169. [Google Scholar] [CrossRef]
- Pfurtscheller, G. Induced oscillations in the alpha band: Functional meaning. Epilepsia 2003, 44, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Decety, J.; Inqvar, D. Brain structures participating in mental simulation of motor behavior: A neuropsychological interpretation. Acta Psychol. 1990, 73, 13–34. [Google Scholar] [CrossRef]
- Jeannerod, M.; Frak, V. Mental imaging of motor activity in humans. Curr. Opin. Neurobiol. 1999, 9, 735–739. [Google Scholar] [CrossRef] [PubMed]
- McFarland, D.J.; Wolpaw, J.R. Brain-computer interface operation of robotic and prosthetic devices. IEEE Comput. Soc. 2008, 41, 82–86. [Google Scholar] [CrossRef]
- Pfurtscheller, G. Functional topography during sensorimotor activation studied with event-related desynchronization mapping. J. Clinic. Neurophysiol. 1989, 6, 75–84. [Google Scholar] [CrossRef]
- Neuper, C.; Pfurtschelle, G. Event-related negativity and alpha band desynchronization in motor reactions. EEG EMG Z Elektroenzephalogr. Elektromyogr. Verwandte Geb. 1992, 2, 55–61. [Google Scholar]
- Pfurtscheller, G.; Neuper, C. Motor imagery activates primary sensorimotor area in humans. Neurosci. Lett. 1997, 239, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Caldara, R.; Deiber, M.P.; Andrey, C.; Michel, C.; Thut, G.; Hauert, C.A. Actual and mental motor preparation and execution: A spatiotemporal ERP study. Exp. Brain Res. 2004, 159, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Zalaudek, K.; Neuper, C. Event-related beta synchronization after wrist, finger and thumb movement. Electroencephalogr. Clinic. Neurophysiol. 1998, 2, 154–160. [Google Scholar] [CrossRef]
- Neuper, C.; Pfurtscheller, G. Evidence for distinct beta resonance frequencies in human EEG related to specific sensorimotor cortical areas. Clinic. Neurophysiol. 2001, 11, 2084–2097. [Google Scholar] [CrossRef]
- Stancak, A., Jr.; Feige, B.; Lucking, C.H.; Kristeva-Feige, R. Oscillatory cortical activity and movement-related potentials in proximal and distal movements. Clinic. Neurophysiol. 2000, 4, 636–650. [Google Scholar] [CrossRef]
- Cassim, F.; Monaca, C.; Szurhaj, W.; Bourriez, J.L.; Defebvre, L.; Derambure, P.; Guieu, J.D. Does post-movement beta synchronization reflect and idling motor cortex? Neuroreport 2001, 3859–3863. [Google Scholar] [CrossRef]
- Gernot, R.M.P.; Zimmerman, D.; Graimann, B.; Nestinger, K.; Korisek, G.; Pfurtscheller, G. Event-related beta EEG-changes during passive and attempted foot movements in paraplegic patients. Brain Res. 2007, 1137, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Nam, C.S.; Jeon, Y.; Kim, Y.J.; Lee, I.; Park, K. Movement imagery-related lateralization of event-related de(synchronization) (ERD/ERS): Motor-imagery duration effects. Clinic. Neurophysiol. 2011, 3, 567–577. [Google Scholar] [CrossRef]
- BCI Competition II. Available online: http://www.bbci.de/competition/ii/ (accessed on 12 July 2011).
- Herman, P.; Prasad, G.; McGinnity, T.M.; Coyle, D. Comparative analysis of spectral approaches to feature extraction for EEG-based motor imagery classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 4, 317–326. [Google Scholar] [CrossRef]
- Bendat, J.; Piersol, A. Random Data Analysis: Analysis and Measurement Procedures; John Wiley: New York, NY, USA, 1986. [Google Scholar]
- Dornhege, G.; Millán, J.R.; Hinterberger, T.; McFarland, D.; Muller, K.R. Towards Brain-Computer Interfacing; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Oppenheim, A.; Schaefer, R.; Buck, J. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Welch, P.D. The use of Fats Fourier Transform for the estimation of power spectra: A method based on time averaging over shot, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 2, 70–73. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C.; Brunner, C.; Lopes da Silva, F. Beta rebound after different types of motor imagery in man. Neurosci. Lett. 2005, 378, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Ramoser, H.; Müller-Gerking, J.; Pfurtscheller, G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 1998, 8, 441–446. [Google Scholar] [CrossRef]
- Mitchel, T. Machine Learning; McGraw-Hill Science: New York, NY, USA, 1997. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley-Interscience: Toronto, Canada, 2000. [Google Scholar]
- Jasper, H.H. The ten twenty electrode system. Int. Fed. Electroencephalogr. Clinic. Neurophysiol. 1958, 10, 371–375. [Google Scholar]
- Sanei, S.; Chambers, J.A. EEG Signal Processing; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- PfurtschNeller, G.; Lopes da Silva, F.H. Event-related EEG/MEG synchronization and desynchronization: Basic principles. Clinic. Neurophysiol. 1999, 11, 1842–1857. [Google Scholar] [CrossRef]
- Carra, M.; Balbinot, A. Evaluation of sensorimotor rhythms to control a wheelchair. In Proceedings of the 2013 ISSNIP Biosignals and Biorobotics Conference (BRC2013), Rio de Janeiro, Brazil, 18–20 February 2013; pp. 1–4.
- Doyle, L.M.F.; Yarrow, K.; Brown, P. Lateralization of event-related beta desynchronization in the EEG during pre-cued reaction time tasks. Clinic. Neurophysiol. 2005, 116, 1879–1888. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Khasnobish, A.; Amit, K.; Tibarewala, D.N.; Nagar, A.K.; Irvine, D.; Gongora, M. Performance analysis of left/right hand movement classification from EEG signal by intelligent algorithms. In Proceedings of 2011 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind and Brain (CCMB), Paris, France, 11–15 April 2011; pp. 1–8.
- Carra, M.; Balbinot, A. Development of a brain-computer interface system based on sensorimotor rhythms. In Proceedings of the 2012 ISSNIP Biosignals and Biorobotics Conference (BRC2012), Manaus, Brazil, 9–11 January 2012; pp. 21–25.
- Garcia, G.N.; Ebrahimi, T.; Vesin, J.M. Support vector EEG classification in the Fourier and time-frequency correlation domains. In Proceedings of 1st International IEEE EMBS Conference on Neural Engineering, Capri Island, Italy, 20–22 March 2003; pp. 591–594.
- Hoffmann, U.; Garcia, G.; Vesin, J.M.; Diserens, K.; Ebrahimi, T. A boosting approach to p300 detection with application to brain–computer interfaces. In Proceedings of 2nd International IEEE EMBS Conference Neural Engineering, Arligton, TX, USA, 16–19 March 2005; pp. 97–100.
- Boostani, R.; Moradi, M.H. A new approach in the BCI research based on fractal dimension as feature and Adaboost as classifier. J. Neural Eng. 2004, 1, 51–56. [Google Scholar] [CrossRef]
- Obermeier, B.; Guger, C.; Neuper, C.; Pfurtscheller, G. Hidden Markov models for online classification of single trial EEG data. Pattern Recognit. Lett. 2001, 22, 1299–1309. [Google Scholar] [CrossRef]
- Haselsteiner, E.; Pfurtscheller, G. Using time-dependant neural networks for EEG classification. IEEE Trans.Rehabil. Eng. 2000, 8, 457–463. [Google Scholar] [CrossRef] [PubMed]
- Lemm, S.; Schafer, C.; Curio, G. BCI competition 2003–data set III: Probabilistic modeling of sensorimotor mu rhythms for classification of imaginary hand movements. IEEE Trans. Biomed. Eng. 2004, 51, 1077–1080. [Google Scholar] [CrossRef] [PubMed]
- Solhjoo, S.; Moradi, M.H. Mental task recognition: A comparison between some of classification methods. In Proceedings of BIOSIGNAL 2004 17th International EURASIP, Brno, Czech Republic, 23–24 June 2004; pp. 273–277.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, J.; Balbinot, A. Executed Movement Using EEG Signals through a Naive Bayes Classifier. Micromachines 2014, 5, 1082-1105. https://doi.org/10.3390/mi5041082
Machado J, Balbinot A. Executed Movement Using EEG Signals through a Naive Bayes Classifier. Micromachines. 2014; 5(4):1082-1105. https://doi.org/10.3390/mi5041082
Chicago/Turabian StyleMachado, Juliano, and Alexandre Balbinot. 2014. "Executed Movement Using EEG Signals through a Naive Bayes Classifier" Micromachines 5, no. 4: 1082-1105. https://doi.org/10.3390/mi5041082
APA StyleMachado, J., & Balbinot, A. (2014). Executed Movement Using EEG Signals through a Naive Bayes Classifier. Micromachines, 5(4), 1082-1105. https://doi.org/10.3390/mi5041082




