Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Effect of Rastering Pattern on the Specimen Shape
3.2. Effect of Laser Power
3.2.1. Effect of Laser Power on the Dimensions of the Fabricated Product
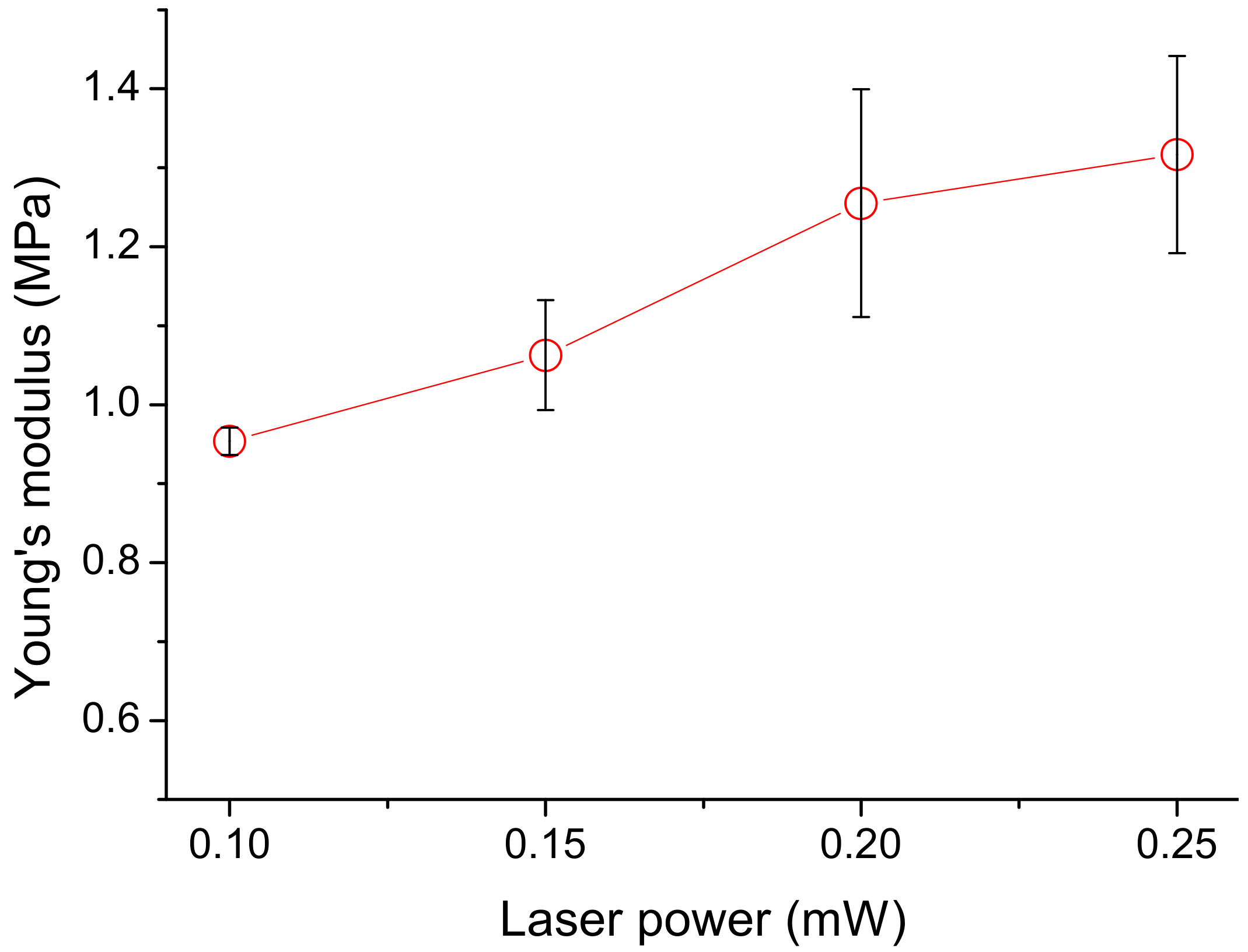
3.2.2. Effect of Laser Power on the Young’s Modulus of the Fabricated Product
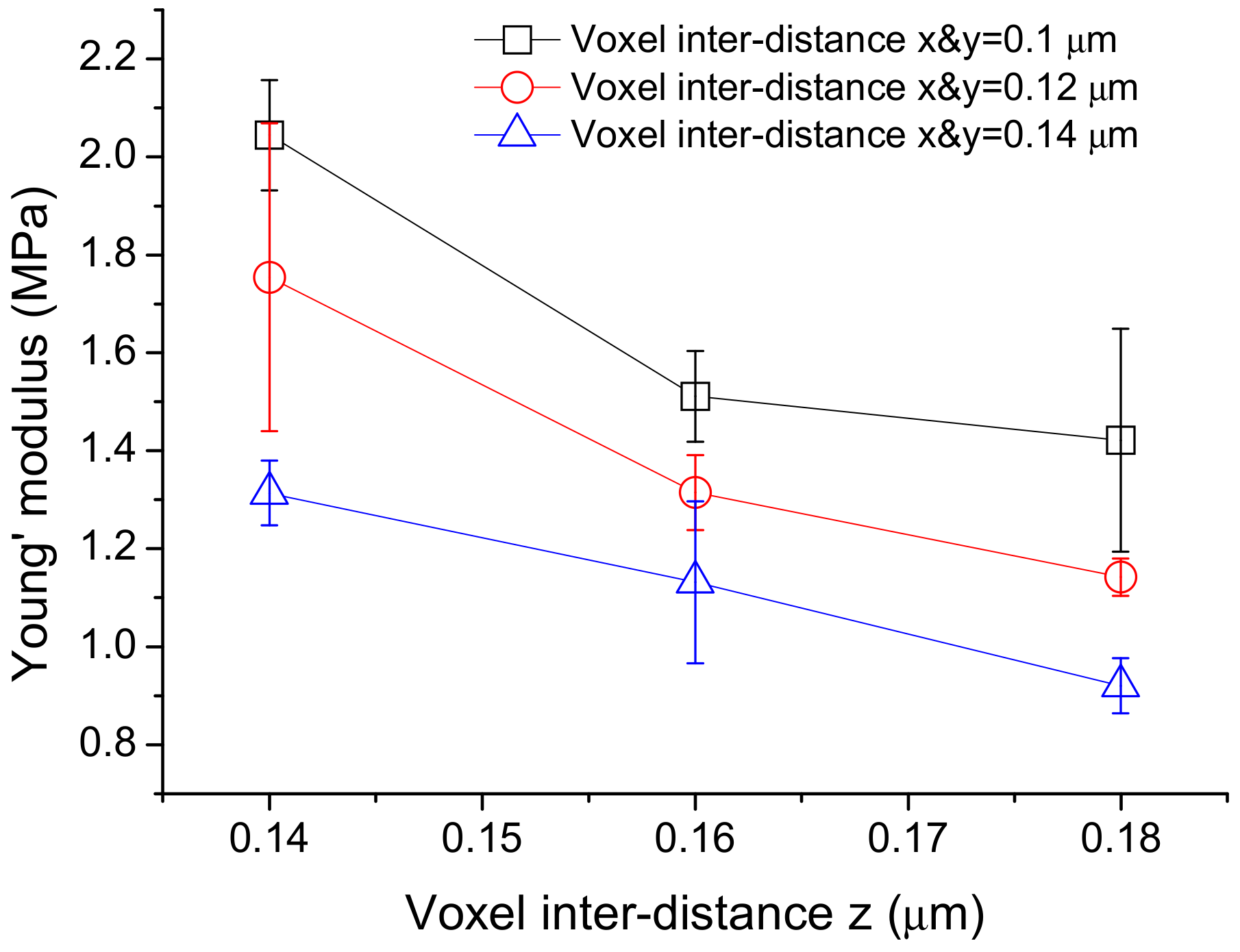
3.3. Effect of Inter-Voxel Distances on the Young’s Modulus of the Fabricated Product
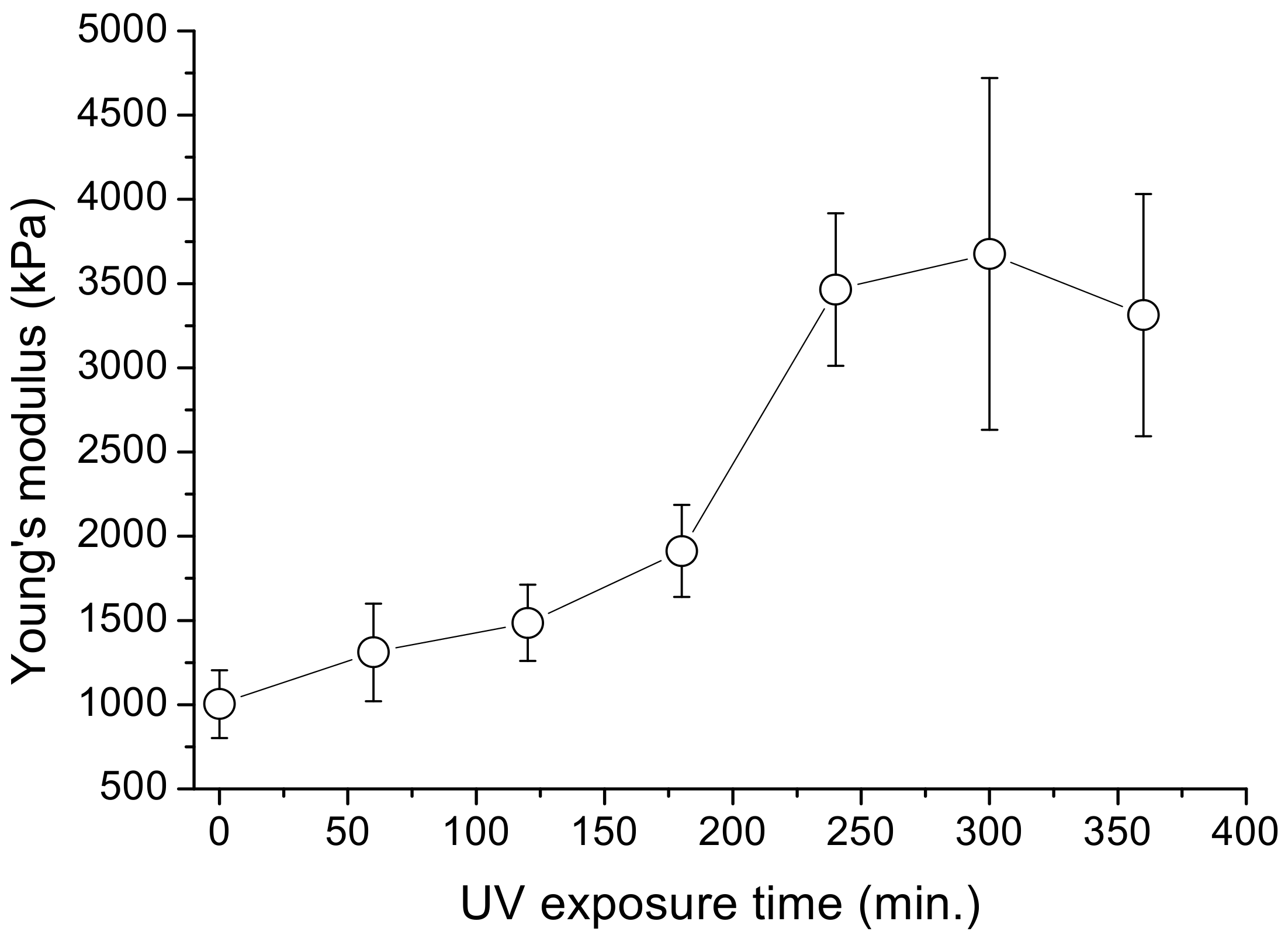
3.4. Effect of Post-Fabricated UV Exposure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tottori, S.; Zhang, L.; Qiu, F.; Krawczyk, K.K.; Franco-Obregón, A.; Nelson, B.J. Magnetic helical micromachines: Fabrication, controlled swimming, and cargo transport. Adv. Mater. 2012, 24, 811–816. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xia, H.; Xu, B.-B.; Niu, L.-G.; Wu, D.; Chen, Q.-D.; Sun, H.-B. Remote manipulation of micronanomachines containing magnetic nanopa. Opt. Lett. 2009, 34, 581–583. [Google Scholar] [CrossRef] [PubMed]
- Yasui, M.; Ikuta, K. 3D general photocurabel model of resin with various kinds of microparticles. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 453–456. [Google Scholar]
- Tribuzi, V.; Corrêa, D.S.; Avansi, W.; Ribeiro, C.; Longo, E.; Mendonça, C.R. Indirect doping of microstructures fabricated by two-photon polymerization with gold nanoparticles. Opt. Express 2012, 20, 21107–21113. [Google Scholar] [CrossRef] [PubMed]
- Bobrinetskiy, I.I.; Emelianov, A.V.; Lin, C.-L.; Otero, N.; Romero, P.M. Ultrafast laser patterning of graphene. Proc. SPIE 2017, 10248, 1024812. [Google Scholar]
- Arul, R.; Oosterbeek, R.N.; Robertson, J.; Xu, G.; Jin, J.; Simpson, M.C. The mechanism of direct laser writing of graphene features into graphene oxide films involves photoreduction and thermally assisted structural rearrangement. Carbon 2016, 99, 423–431. [Google Scholar] [CrossRef]
- Bobrinetskiy, I.I.; Emelianov, A.V.; Otero, N.; Romero, P.M. Patterned graphene ablation and two-photon functionalization by picosecond laser pulses in ambient conditions. Appl. Phys. Lett. 2015, 107, 043104. [Google Scholar] [CrossRef]
- Odian, G. Principles of Polymerization, 3rd ed.; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Maruo, S.; Nakamura, O.; Kawata, S. Three-dimensional microfabrication with two-photon-absorbed photopolymerization. Opt. Lett. 1997, 22, 132–134. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Sun, H.-B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.-B.; Maeda, M.; Takada, K. Scaling laws of voxels in two-photon photopolymerization nanofabrication. Appl. Phys. Lett. 2003, 83, 1104–1106. [Google Scholar] [CrossRef]
- Takada, K.; Sun, H.-B.; Kawata, S. The study on spatial resolution in two-photon induced polymerization. Proc. SPIE 2006, 6110, 61100A. [Google Scholar]
- Zhou, X.; Hou, Y.; Lin, J. A review on the processing accuracy of two-photon polymerization. AIP Adv. 2015, 5, 030701. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.-S.; Kim, R.H.; Yang, D.-Y.; Park, S.H. Advances in 3D nano/microfabrication using two-photon initiated polymerization. Prog. Polym. Sci. 2008, 33, 631–681. [Google Scholar] [CrossRef]
- Mendonca, C.R.; Correa, D.S.; Marlow, F.; Voss, T.; Tayalia, P.; Mazur, E. Three-dimensional fabrication of optically active microstructures containing an electroluminescent polymer. AIP Adv. 2009, 95, 113309. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.-H.; Liu, Y.-J.; Baldeck, P.L.; Lin, C.-L. Fabrication of Periodic 3D Nanostructuration for Optical Surfaces by Holographic Two-Photon-Polymerization. Int. J. Inf. Electron. Eng. 2016, 6, 151–154. [Google Scholar] [CrossRef]
- Lin, C.-L.; Lee, Y.-H.; Lin, C.-T.; Liu, Y.-J.; Hwang, J.-L.; Chung, T.-T.; Baldeck, P.L. Multiplying optical tweezers force using a micro-lever. Opt. Express 2011, 19, 20604–20609. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-L.; Vitrant, G.; Bouriau, M.; Casalegno, R.; Baldeck, P.L. Optically driven Archimedes micro-screws for micropump applications. Opt. Express 2011, 19, 8267–8276. [Google Scholar] [CrossRef] [PubMed]
- Chung, T.-T.; Tseng, C.-L.; Hung, C.-P.; Lin, C.-L.; Baldeck, P.L. Design and two-photon polymerization of complex functional micro-objects for lab-on-a-chip: Rotating micro-valves. J. Neurosci. Neuroeng. 2013, 2, 53–57. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Liu, Y.-J.; Tzou, C.; Bouriau, M.; Baldeck, P.L.; Lin, C.-L. Optically driven gear-based mechanical micro-transducer for lab-on-a-chip. J. Neurosci. Neuroeng. 2013, 2, 58–60. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Lee, Y.-H.; Lin, Y.-S.; Tsou, C.; Baldeck, P.L.; Lin, C.-L. Optically driven mobile integrated micro-tools for lab-on-a-chip. Actuators 2013, 2, 19–26. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Chen, P.-Y.; Yang, J.-Y.; Tsou, C.; Lee, Y.-H.; Baldeck, P.L.; Lin, C.-L. Three-dimensional passive micromixer fabricated by two-photon polymerization for microfluidic mixing. Sens. Mater. 2014, 26, 39–44. [Google Scholar]
- Liu, Y.-J.; Yang, J.-Y.; Nie, Y.-M.; Lu, C.-H.; Huang, E.-D.; Shin, C.-S.; Baldeck, P.L.; Lin, C.-L. A Simple and Direct Reading Flow Meter Fabricated by Two-photon Polymerization for Microfluidic Channel. Microfluid. Nanofluid. 2014, 18, 427–431. [Google Scholar] [CrossRef]
- Xu, B.-B.; Zhang, Y.-L.; Xia, H.; Dong, W.-F.; Ding, H.; Sun, H.-B. Fabrication and multifunction integration of microfluidic chips by femtosecond laser direct writing. Lab Chip 2013, 13, 1677–1690. [Google Scholar] [CrossRef] [PubMed]
- Sima, F.; Sugioka, K.; Vázquez, R.M.; Osellame, R.; Kelemen, L.; Ormos, P. Three-dimensional femtosecond laser processing for lab-on-a-chip applications. Lab Chip 2018, 7, 613–634. [Google Scholar] [CrossRef]
- Sugioka, K.; Xu, J.; Wu, D.; Hanada, Y.; Wang, Z.; Cheng, Y.; Midorikawa, K. Femtosecond laser 3D micromachining: A powerful tool for the fabrication of microfluidic, optofluidic, and electrofluidic devices based on glass. Lab Chip 2014, 18, 3447–3458. [Google Scholar] [CrossRef] [PubMed]
- Marino, A.; Tricinci, O.; Battaglini, M.; Filippeschi, C.; Mattoli, V.; Sinibaldi, E.; Ciofani, G. A 3D real-scale, biomimetic, and biohybrid model of the blood-brain barrier fabricated through two-photon lithography. Small 2018, 14, 1702959. [Google Scholar] [CrossRef] [PubMed]
- Marino, A.; Desii, A.; Pellegrino, M.; Pellegrini, M.; Filippeschi, C.; Mazzolai, B.; Mattoli, V.; Ciofani, G. Nanostructured Brownian surfaces prepared through two-photon polymerization: Investigation of stem cell response. ACS Nano 2014, 8, 11869–11882. [Google Scholar] [CrossRef] [PubMed]
- Koroleva, A.; Deiwick, A.; Nguyen, A.; Schlie-Wolter, S.; Narayan, R.; Timashev, P.; Popov, V.; Bagratashvili, V.; Chichkov, B. Osteogenic differentiation of human mesenchymal stem cells in 3-D Zr-Si organic-inorganic scaffolds produced by two-photon polymerization technique. PLoS ONE 2015, 10, e118164. [Google Scholar] [CrossRef] [PubMed]
- Miwa, M.; Douoka, K.; Yoneyama, S.; Tuchitani, S.; Kosihmoto, Y.; Kaneko, R. Young’s module control of the microcantilever made by micro-stereolithography. Proc. SPIE 2005, 5719, 6–13. [Google Scholar]
- Cicha, K.; Koch, T.; Torgersen, J.; Li, Z.; Liska, R.; Stampfl, J. Young’s modulus measurement of two-photon polymerized micro-cantilevers by using nanoindentation equipment. J. Appl. Phys. 2012, 112, 094906. [Google Scholar] [CrossRef]
- Bayindir, Z.; Sun, Y.; Naughton, M.J.; LaFratta, C.N.; Baldacchini, T.; Fourkas, J.T.; Stewart, J.; Saleh, B.E.A.; Teich, M.C. Polymer microcantilevers fabricated via multiphoton absorption polymerization. Appl. Phys. Lett. 2005, 86, 064105. [Google Scholar] [CrossRef]
- Nakanishi, S.; Shoji, S.; Kawata, S.; Sun, H.-B. Giant elasticity of photopolymer nanowires. Appl. Phys. Lett. 2007, 91, 063112. [Google Scholar] [CrossRef]
- Lemma, E.D.; Rizzi, F.; Dattoma, T.; Spagnolo, B.; Sileo, L.; Qualtieri, A.; Vittorio, M.D.; Pisanello, F. Mechanical properties tunability of three-dimensional polymeric structures in two-photon lithography. IEEE Trans. Nanotechnol. 2017, 16, 23–31. [Google Scholar] [CrossRef]
- Sun, H.-B.; Takada, K.; Kawata, S. Elastic force analysis of functional polymer submicron oscillators. Appl. Phys. Lett. 2001, 79, 3173–3175. [Google Scholar] [CrossRef]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef] [Green Version]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Wright, W.H.; Sonek, G.J.; Berns, M.W. Parametric study of the forces on microspheres held by optical tweezers. Appl. Opt. 1994, 33, 1735–1748. [Google Scholar] [CrossRef] [PubMed]
- Moffitt, J.R.; Chemla, Y.R.; Smith, S.B.; Bustamante, C. Recent advances in optical tweezers. Annu. Rev. Biochem. 2008, 77, 205–228. [Google Scholar] [CrossRef] [PubMed]
- Singer, W.; Bernet, S.; Hecker, N.; Ritsch-Marte, M. Three-dimensional force calibration of optical tweezers. J. Mod. Opt. 2000, 47, 2921–2931. [Google Scholar] [CrossRef]
- Hibbeler, R.C. Engineering Mechanics: Statics; 11th Edition in SI Units; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Hibbeler, R.C. Mechanics of Materials, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Yousif, E.; Haddad, R. Photodegradation and photostabilization of polymers, especially polystyrene: Review. Springerplus 2013, 2, 398. [Google Scholar] [CrossRef] [PubMed]
- UV/EB Radcure Product Guide, IGM Resins. Available online: http://igmresins.com/public/upload/product/brochure/product_brochure_4-2018_digital.pdf (accessed on 25 April 2018).
- Jiang, L.J.; Zhou, Y.S.; Xiong, W.; Gao, Y.; Huang, X.; Jiang, L.; Baldacchini, T.; Silvain, J.-F.; Lu, Y.F. Two-photon polymerization: Investigation of chemical and mechanical properties of resins using Raman microspectroscopy. Opt. Lett. 2014, 39, 3034–3037. [Google Scholar] [CrossRef] [PubMed]

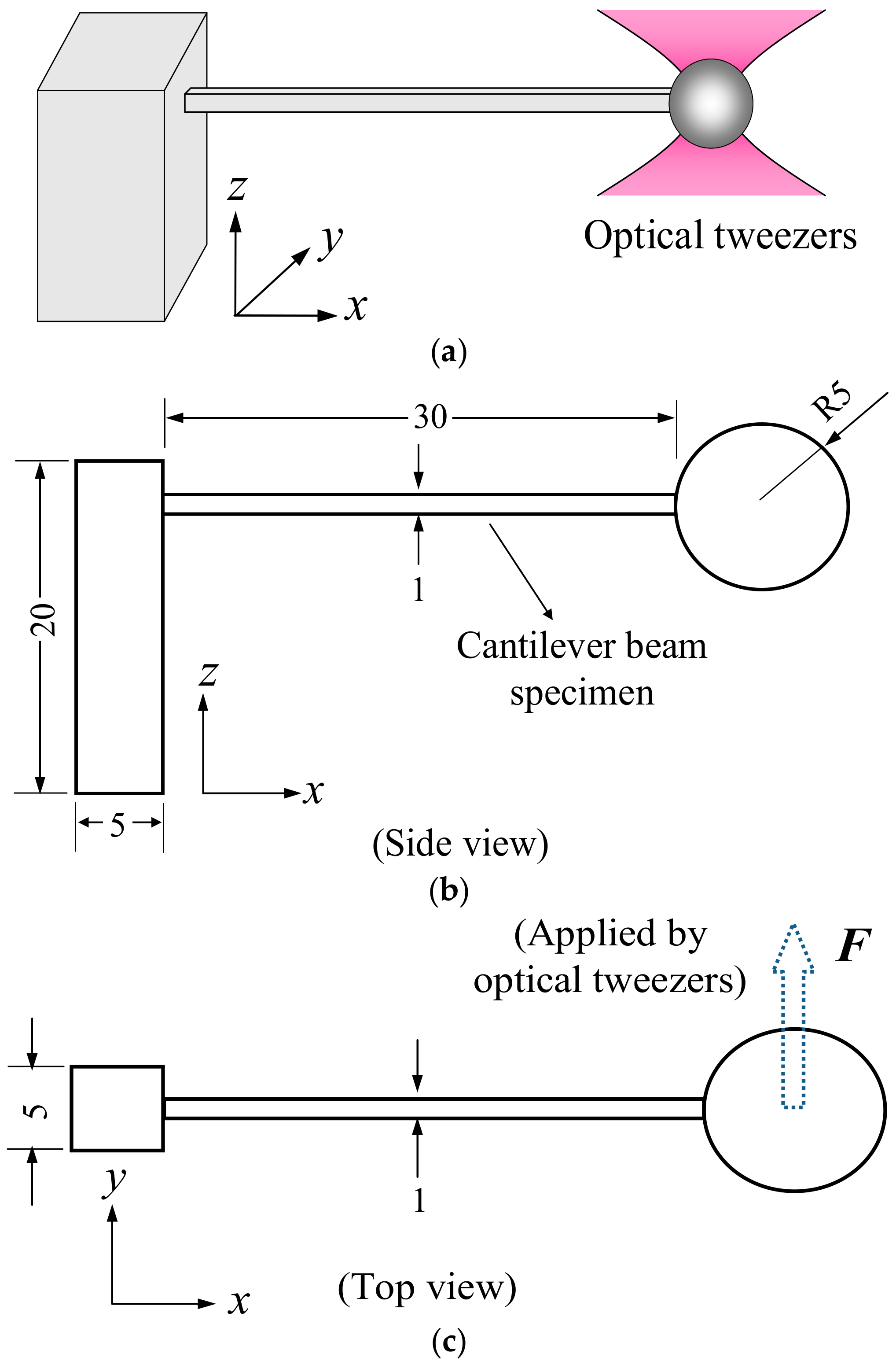
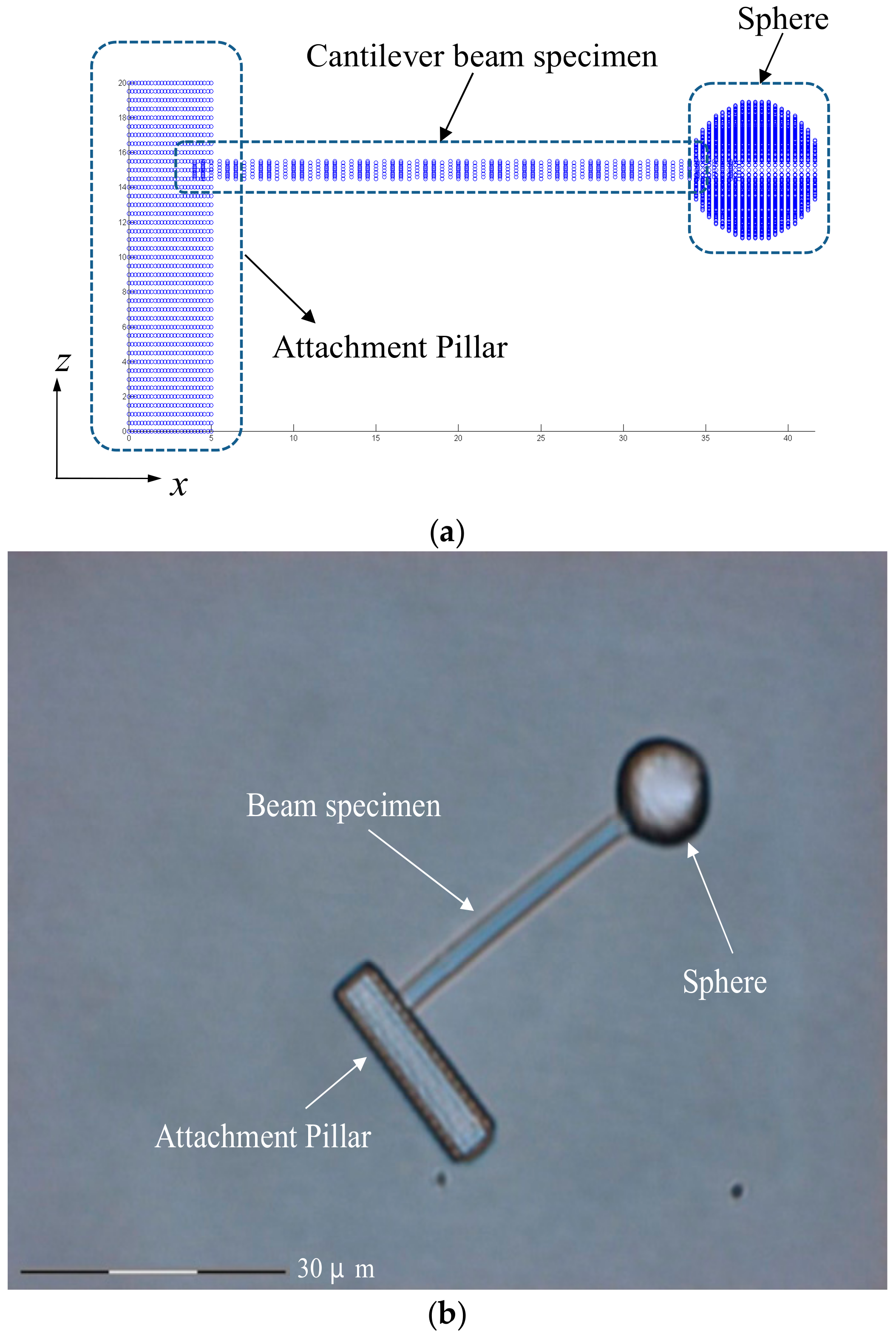




| Cases | Power (mW) | Inter-Voxel x & y Distance (μm) | Inter-Voxel z Distance (μm) |
|---|---|---|---|
| 1-1 | 0.10 | 0.13 | 0.16 |
| 1-2 | 0.15 | 0.13 | 0.16 |
| 1-3 | 0.20 | 0.13 | 0.16 |
| 1-4 | 0.25 | 0.13 | 0.16 |
| Cases | Power (mW) | Inter-Voxel x & y Distance (μm) | Inter-Voxel z Distance (μm) |
|---|---|---|---|
| 2-1 | 0.15 | 0.10 | 0.14 |
| 2-2 | 0.15 | 0.10 | 0.16 |
| 2-3 | 0.15 | 0.10 | 0.18 |
| 2-4 | 0.15 | 0.12 | 0.14 |
| 2-5 | 0.15 | 0.12 | 0.16 |
| 2-6 | 0.15 | 0.12 | 0.18 |
| 2-7 | 0.15 | 0.14 | 0.14 |
| 2-8 | 0.15 | 0.14 | 0.16 |
| 2-9 | 0.15 | 0.14 | 0.18 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, C.-S.; Li, T.-J.; Lin, C.-L. Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications. Micromachines 2018, 9, 615. https://doi.org/10.3390/mi9120615
Shin C-S, Li T-J, Lin C-L. Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications. Micromachines. 2018; 9(12):615. https://doi.org/10.3390/mi9120615
Chicago/Turabian StyleShin, Chow-Shing, Tzu-Jui Li, and Chih-Lang Lin. 2018. "Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications" Micromachines 9, no. 12: 615. https://doi.org/10.3390/mi9120615
APA StyleShin, C. -S., Li, T. -J., & Lin, C. -L. (2018). Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications. Micromachines, 9(12), 615. https://doi.org/10.3390/mi9120615





