Invariant-Based Safety Assessment of FPGA Projects: Conception and Technique

Abstract

This paper describes a proposed method and technology of safety assessment of projects based on field programmable gate arrays (FPGA). Safety assessment is based on special invariants, e.g., properties which remain unchanged when a specified transformation is applied. A classification and examples of FPGA project invariants are provided. In the paper, two types of invariants are described. The first type of invariants used for such assessment are those which are versatile since they reflect the unchanged properties of FPGA projects, hardware description languages, etc. These invariants can be replenished as experience gained in project implementation accumulates. The second type of invariants is formed based on an analysis of the specifics of a particular FPGA project and reflects the features of the tasks to be solved, the algorithms that are implemented, the hardware FPGA chips used, and the computer-aided design tools, etc. The paper contains a description of the overall conception and particular stages of FPGA projects invariant-based safety assessment. As examples for solving some tasks (using of invariants and defect injections), the paper contains several algorithms written in the VHSIC hardware description language (VHDL). The paper summarizes the results obtained during several years of practical and theoretical research. It can be of practical use for engineers and researchers in the field of quality, reliability, and security of embedded systems, software and information management systems for critical and business applications.

1. Introduction

Ensuring the functional safety and reliability of instrumentation and control systems (I&Cs) is highly dependent on the quality of the software (SW) and programmable components. Independent verification and validation (IV&V) is a key test methodology for critical software and programmable logic-based systems (e.g., FPGA) [1,2,3]. As an example, IV&V is performed as a mandatory (regulatory) requirement for the safety-important ICSs used in nuclear power plants (NPP) (regulations are included in IAEA standards), space systems (such regulations are included in ECSS, ESA standards) and other types of critical systems [4,5]. For critical domains like the energy sector (already mentioned NPPs) the operating reliability assessment of FPGA-based I&Cs is always one of the most important activities [6].

Evidence-based measurable implementation of the principle of technological diversity is the basic concept in achieving the required reliability of results and cost-effectiveness in the IV&V. Evidence consists of providing trustworthy quantitative assessments during the verification process of software (SW) or FPGA-based design.

Many publications related to IV&V are based on formal methods, which use algebraic and special notations like B, Z, Event-B, VDM, and temporal logic as well as appropriate methods for verifying the correctness of the description and fulfillment of requirements within the relevant formal systems [7,8,9,10]. Some cases of their use in industrial systems have been successful [1,9].

Recently, methods based on the validation of models built for SW or systems in general, in particular the verification of the fulfillment of a set of invariants—certain statements, analytical or logical relationships that are fulfilled under any circumstances [11,12], have become widespread. Examples of formal verification methodologies for FPGA-based systems are presented in [13,14]. In [15] FPGA is used as a tool to prove that the system can meet the real-time requirement through an obstacle avoidance demonstration in a changing environment. The approach presented here can be applied to different systems’ dynamics, and potentially leveraged for higher dimension systems.

The papers [16,17] contain a description of the functional verification methodology for highly parametrizable, continuously operating FPGA designs in such safety-critical domains as a radiation monitoring system at CERN. The papers [18,19,20] describe methods of model-checking-based verification of FPGA projects for NPP I&Cs. In [21] authors propose a formal verification methodology for checking both functional and timing requirements of real-time digital controllers targeted at FPGA as well.

The authors of [22,23] note that the search for vulnerabilities and faults and formal verification are integral stages of design, especially for the model method for developing FPGA projects, determining their compliance with the requirements. Requirements can be defined in UML [24], or text form, while the FPGA design can be created in VHDL [25] or System Verilog [26] and then embodied in binary code. Systems and tools for formal verification (such as VC Formal [27], Vivado Verification [28], JasperGold [29], and others) have been developed by many industrial companies and implemented in the process of creating and certificating FPGA platforms and platform-based decisions.

The authors of [30,31] develop an algebraic approach, insertion models as generalizations of algebraic modeling for sets of agents and environments, insertional semantics of VHDL language, represented by behavioral algebra [32,33] and can be implemented using algebraic virtual machines. [34]. The method of model verification and abstract interpretation is investigated in [35]. In [36] heuristic methods are used to identify potential places in a race, a review of which is given in [37]. For parallel constructions, it is necessary to perform appropriate verification for the permutability property [38].

There are specific problems for the verification of FPGA projects for safety-critical systems, such as reactor trip systems, based on the application of diversity [39,40,41] and defense-in-depth [39,42] (the so-called D3 principle). These problems are caused by requirements to detect and tolerate design faults (joint and individual) of different versions [43].

The main results of the analysis can be summarized in three points. Firstly, there are severe restrictions on the use of the analyzed formal and semi-formal methods, due to their great complexity and the inability to use automation tools to generate descriptions of requirements (in understandable notation) as well as the complexity of their implementation. Secondly, the application of these methods is limited by the fact that engineers must be skilled in terms of knowledge of mathematical logic methods to provide a formal description and make a formal check. Thirdly, the inability to find models, multiple models, or invariants that provide the necessary completeness and reliability of the estimation. Additionally, for some types of systems, even the use of formal methods requires independent verification and validation.

Due to the task of invariant-based of assessment safety in FPGA projects the following aspects are still challenging: the determination of the main stages of evaluating FPGA projects using invariants, development of the features of invariants for FPGA projects, defining the universal invariants and their means of calibration for VHDL. The attributes of the quality model of invariants for FPGA designs as a measure of invariants need to be determined and the procedure for formation and selection of a set of invariants for evaluating the FPGA project needs to be provided.

Structurally, the paper consists of the following sections. Section 2 is devoted to describing the conception and stages of invariant-based assessment of FPGA projects, including the development of a set of invariants and their calibration. General requirements and attributes for invariants are discussed in Section 3. Classification and different types of invariants are analyzed in Section 4. Principles and stages of FPGA project invariant development are described in Section 5. A case study of safety invariant-based assessment of the FPGA project is presented in Section 6. Section 7 concludes the research results and discusses future steps.

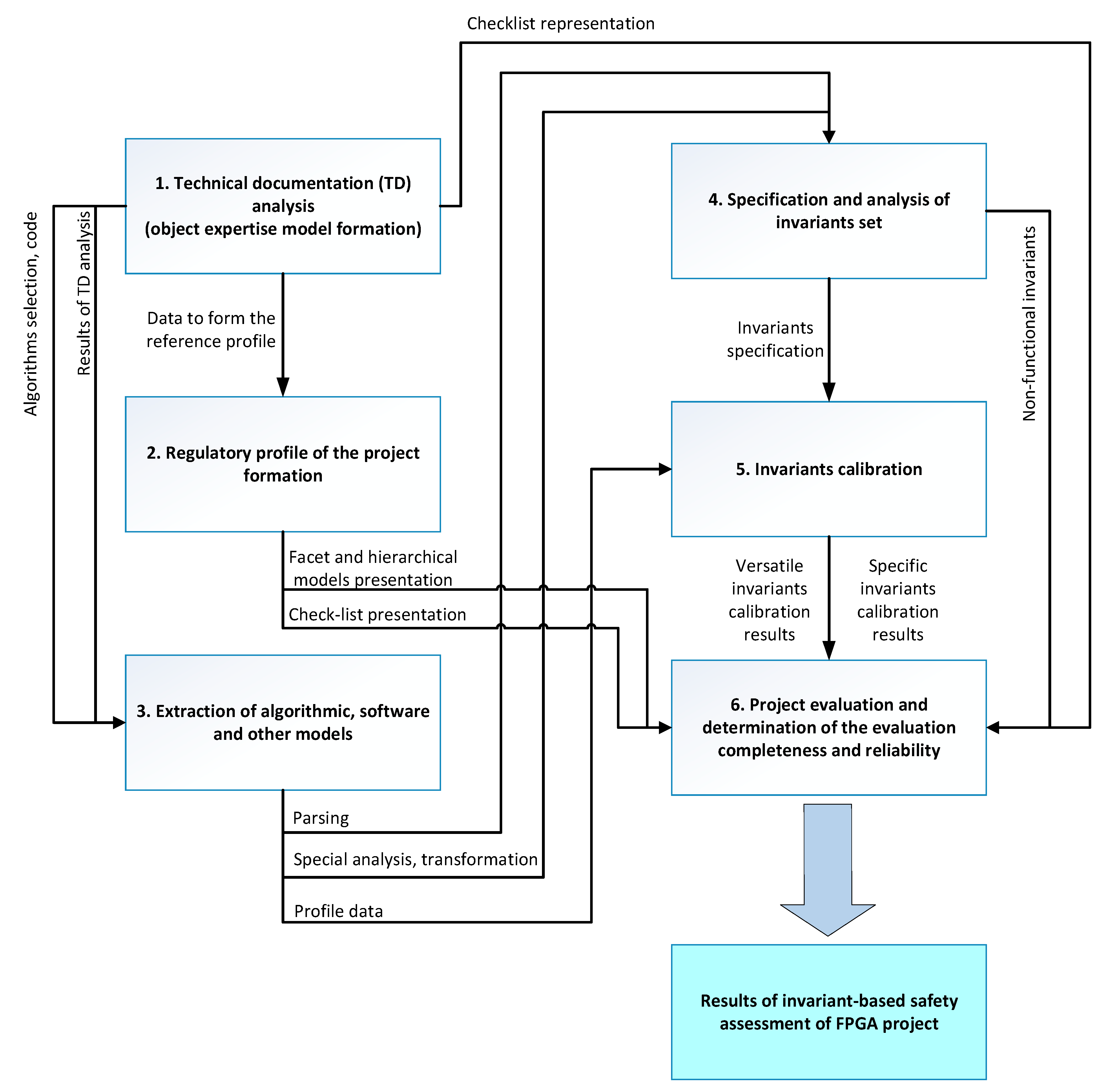
2. Conception and Stages of Invariant-Oriented Assessment of FPGA Projects

2.1. Overall Tasks and Conception Invariant-Oriented Assessment

Safety assessment of FPGA projects following the general principles of invariant-oriented assessment includes six basic interrelated tasks and stages of their solution:

• analysis of technical documentation and development of a model of the object under assessment (SW and technical documentation) in the FPGA project;
• development of the regulatory profile (set of requirements) of the FPGA-based project based on the purpose and type of system where FPGA is used;
• extraction (development) of algorithmic, software, and other models, which is performed during the analysis of FPGA project documentation;
• specification and analysis of a set of invariants;
• invariant calibration;
• determination of FPGA project assessment reliability and completeness.

The overall scheme of an invariant-oriented assessment of FPGA projects following these tasks and steps is presented in Figure 1. The brief description of each of the six stages according to the scheme is as follows: problem statement, concept, solution method, results, requirements for tool development. Several types of lines are used depicting different types of interrelations between six tasks: main connections are marked with a normal line; calibration links are marked with a dashed line and links for nonfunctional requirements are marked with a dash-dotted line.

This section does not consider aspects of evaluating microprocessor-based projects. However, the structure and correlation of the tasks presented in Figure 1 go beyond the evaluation of FPGA projects.

Brief description of all stages will be given below in the Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6 and Section 2.7 using the following structure:

• problem statement and description of goal of the current stage;
• description of the solution and implementation of the obtained results;
• input and output data for the particular stage;
• requirements for tools development.

2.2. Analysis of Technical Documentation and Developing the Model of the FPGA Project Assessment

Problem statement: to analyze the technical documentation and to develop an assessment object model of the FPGA projects.

Concept: presentation of the expertise object model in the form of a checklist of documents that should be considered during the evaluation.

Initial data: a set of documentation for the FPGA project.

Solution: requirements of regulatory documents containing the structure of the technical documentation of the project systems on complex electronic components (i.e., FPGA) analysis and experience in the development and verification of FPGA projects analysis are to be provided.

Results: a model of the FPGA project (e.g., documentation).

Tool development requirements: this task can be implemented in the form of a tool for presenting the project documentation.

2.3. Formation of the Regulatory Profile of the FPGA Project Based on the Purpose and Type of the System

Problem statement: to develop a reference regulatory profile for the FPGA project to compare the reference and real models.

Concept: presentation of the normative profile of the project in the form of a parameterizable facet-hierarchical model and/or checklist.

Initial data: results of solving the first stage (Figure 1) as well as a replenishing profile-forming base of standards.

Solution method: regulatory documents analysis with development and configuration of the profile-forming base, the formation of a project-oriented system profile convenient for comparison.

Results: a detailed structure of the reference regulatory profile of the FPGA project and/or checklist for checking the real profile should be presented. The results of solving the first stage (Figure 1) can be part of a general checklist. The results of the stage are used in the sixth stage (Figure 1).

Tool development requirements: this task can be implemented in the form of a tool for generating a normative project profile, which provides the ability to compare data obtained in this task and the first stage (Figure 1).

2.4. Extraction of Algorithmic, Software and Other Models, Carried out According to the Design Documentation Analysis Results

Problem statement: define a list of extracted software, algorithmic, and other (automatic or set-theoretic) models for FPGA projects similar to software or other formal structures suitable for further software processing.

Concept: software-implemented functions of FPGA project model representation, as well as other project components for invariant-oriented analysis and evaluation.

Input data: results of the first stage (Figure 1), as well as a replenishing set of models for FPGA projects.

The solution method: structure and technical content review of a typical FPGA design documentation and the technologies for its development and verification to identify extractable software models and specify various invariants.

Results: The structure of technical documentation for FPGA project analysis should be presented and extracted from software models (i.e., control algorithm models in languages such as VHDL, PID controllers, and soft processors (IP cores)), as well as other models for checking invariants should be defined.

The results of this step are used in the fourth stage (Figure 1). Additionally, the results of the step can be used in the fifth stage to refine the defect profile.

Tool development requirements: this task can be implemented either in a non-automatic mode or in the form of a tool that implements the function of storing the extracted models.

2.5. Specification and Analysis of Set of Invariants

Problem statement: define a specification of invariants in the form of a list for extractable software and other models for FPGA projects.

Concept: invariants list definition is performed considering the extracted software, algorithmic, and other models for FPGA project specifics and their presentation features at different stages of project development and operation lifecycle after implementation in the chip.

Initial data: results of the third stage (Figure 1) as well as an updated set of invariants for FPGA projects.

Solution method: extractable software models for FPGA projects and features of automatic models of implemented projects analysis, including state graphs, time diagrams, etc. in order to identify sets of versatile and specific invariants.

Results: a preliminary grouped list of invariants should be presented (control algorithm models in languages such as VHDL, PID controllers, soft processors (IP cores)), which can be specified for further work. The results of this stage are used in the fifth and sixth stages (Figure 1).

Tool development requirements: this task can be implemented either in a non-automatic mode or in the form of an information (or information-analytical) type tool that implements the function of generating and storing invariants for extracted models’ groups.

2.6. Invariant Calibration

Problem statement: the development of procedures for assessing the sensitivity of invariants to various types of defects, i.e., determination of a binary value (0 or 1) for invariance or invariant distortion in the presence of appropriate FPGA design defects.

Concept: calibration of invariants is performed based on injection-oriented procedures and reasonable profiles of defect injection.

Initial data: the previous tasks results, as well as replenished defect profiles to increase calibration accuracy.

The solution method: using drop injection of defects of various types and fixing the invariants’ verification results to assess their sensitivity. Calibration of a part of the invariants (the so-called versatile invariants) should be performed in advance. The calibration of specific invariants of the evaluated project can be performed during the verification process. The defect profile needs to be developed considering the FPGA project features.

Results: sensitivity indicators of each invariant should be determined. These results can be represented by the “invariant-defect” matrix of Boolean type; in case the sensitivity metric is not binary but is determined in the range from 0 to 1. The results of the stage are used in the sixth task.

Tool development requirements: it can be implemented as an analytical-type tool that performs the following set of operations: defect selection from versatile or project-oriented invariant profiles, injecting operational defects at a selected point of the program (project), development of test sequences, checking the invariant analysis results, resulting in sensitivity matrix presentation.

2.7. Project and Determination of the Trustworthiness Assessment

Problem statement: to develop a procedure for comparing the normative (reference) profile and the project profile, as well as a general assessment of the FPGA project, considering the results of invariant verification with an indication of its reliability.

Concept: reliability assessment of FPGA project safety assessment based on the invariants verification analysis results, including the reference and real project profile comparison.

Initial data: results of the third, fifth, and sixth stages (Figure 1).

The solution method: processing the obtained invariants checking result, considering their calibration and matrices of sensitivity to defects results and mismatch metric calculation and the common assessment formation based on it.

Results: The results of the evaluation in metric form and a set of reports on interim and final assessments should be obtained.

Tool development requirements: this task can be implemented in the form of an analytical-type tool that provides comparison and analysis of data obtained during the second, fourth, and fifth stages, metric calculation, and convolution, assessment results report generation.

After this step, the requirements to invariants (as a checking procedure) are formulated based on the operation sequences of invariant-based assessment.

3. General Requirements of Invariants

To assess the quality and correctness of individual invariants, as well as systems of invariants, many properties and characteristics can be used. Some of them were previously described by authors concerning invariants for formal methods supported by Event-B notation [7].

Table 1. Invariants’ requirements.

Requirement	Description
Conciseness and formality of description	The invariant must be characterized by a number or a compact mathematical construction: a tuple of numbers, a predicate, an equation or an inequality, an expression of temporal logic, a simple graph containing several vertices and arcs, a fragment of an automaton table that defines the functions of transitions and outputs, etc.
Clarity and physicality	The invariant has a clear physical meaning and purpose (it limits the permissible values range of a certain system variable, determines the compatibility of events, or sets the logic for changing system states). The purpose is determined by the type of invariant, based on the used test feature (e.g., accuracy, logical, functional, semantic, etc.).
Measurability	The invariant should be subject to simple verification, and it should be evaluated using simple metrics within the given scale.
Criticality	Following the criticality characteristic, invariants can form a priority series, which should be considered during evaluations, as well as when forming a system of invariants to ensure the required reliability while minimizing costs. For critical applications, in which development implies using formal methods, the invariants must control the observance of properties associated primarily with safety functions.
Traceability	For each invariant, it should be clearly understood which requirement verification fulfillment it meets, and which violation of this requirement is monitored. The traceability characteristics can be described by the matrix “FPGA design requirements—invariants”. The invariant allows one to verify the performance of one or more system properties and their corresponding requirements.
Globality	The invariant must be true constantly on the whole set of states or only when the system is in a certain state. For invariants, the field of their action must be known (i.e., the entire system and its model or individual components of the system).
Controllability	For an invariant, the following conditions should be met: a subset of controlled requirements (i.e., completeness of control, degree of coverage) is established; the reliability of the control of the requirement(s) is provided; the possible control errors are specified. These characteristics can be determined experimentally by defect injection and evaluating the invariant sensitivity.
Diagnostic ability	The diagnostic ability of an invariant consists of the possibility of determining the cause (defect or another anomaly) by which the invariant violation occurred. This characteristic is not fundamental, since the main purpose of any invariant is to solve the monitoring problem.
Flexibility and scalability	This characteristic consists of varying (i.e., adjusting) the mathematical representation of the invariant possibility depending on the requirements for a controlling or other ability, as well as on the design features.
Non-redundancy	Invariants should not repeat the checks and can be used to control defects detected by standard tools (compiler, supplied tools). The presence of such invariants increases the cost of verification. Simultaneously, excessive invariants can be used within the system, if their use allows increasing the verification trustworthiness

lists the characteristics of the invariants that provide their quality model.

These characteristics are the basis for the introduction of the quality indicators of invariants that evaluate the degree of perfection (i.e., reachability) of the corresponding characteristics. They set the scale and methodology for measuring these characteristics.

As mentioned above, a set or a system of invariants is a consistent set that allows, as mentioned above, controlling the correct behavior of the developed FPGA project on the whole set of its possible states. The quality criteria for a system of invariants are as follows [44,45]: invariant system completeness, minimum sufficiency to control system properties by requirements, sabotage (i.e., permissible redundancy) allowing to check one condition or property in several ways, consistency. Invariants forming a system cannot be based on conflicting rules.

To assess the quality of the invariant system, it is proposed to use the metrics of completeness, minimality, admissible and unacceptable redundancy, which allow one to estimate and choose an invariant system that is optimal by some criteria. The requirements (characteristics) of invariants form a priority series depending on their value and importance. Among the most important are the following: controllability, measurability, traceability, laconicism, and formality of the description.

4. Classification and Analysis of Invariants

4.1. Classification Attributes

As classification attributes for invariants the following are proposed to be used:

• universality degree—determines the possibility or expediency of using the invariant to test different FPGA projects;
• used model type (for which the invariant is being developed)—the model is the primary basis for invariant development;
• controlled attribute—determined by developing and checking the invariant method;
• type of a particular invariant—determined by the model type (a feature concerning a hierarchy with a previous feature, i.e., dependent on it). Each invariant belongs to a group characterized by a controlled trait;
• calibration method—defines the rules, procedures, and software used to evaluate sensitivity;
• scope—sets the project capacity or indicates the set of its components on which the invariant is used;
• source object for which the invariant is synthesized. This feature depends on the previous feature, the scope of the invariant;
• sensitivity values—determines the set of sensitivity values for the invariant (with a general fixed range of values (0–1));
• rigidity degree—allows invariant differentiation based on the mandatory implementation. It may be in a hierarchical relationship with the previous attribute;
• verification sign—specifies the type of invariant based on its verification features and objectives;
• parameterization ability—determined by the adaptability of the invariant to change depending on the type of project and the requirements for sensitivity.
• Figure 2 shows the structured classification scheme of invariants for FPGA projects.

4.2. Grouping the Invariants

By universality degree, the invariants are divided into versatile and specific. The first one can be used to test different FPGA projects, the second are developed to be applied to the individual projects. A key feature of the classification is used model type. Based on it, invariant sets of FPGA projects are divided into the following groups: invariants of nonfunctional (general) requirements models M_NFR; invariants for functional requirements models M_FR; invariants for program models M_P; invariants for algorithmic models M_AD; invariants for time chart models M_TC, etc.

Based on the controlled attribute, the following sets of the invariants are then formed (The types of specific invariants for various models are described below)

• precision invariants—based on the identification and fixing of restrictions on the system variables (i.e., setting the range of permissible changes);
• semantic invariants—based on the system variables physical dimension invariance determination during their transformations in the process of computing or restrictions on an allowable change in dimension, considering the known laws of physics;
• functional invariants—based on the behavior of the system control. Being in a certain state, getting out of it, and transitions between states when performing different functions;
• logical invariants—based on the start and verification of the fulfillment of the necessary pre- and post-conditions for the occurrence of events, calling procedures or functions.

The classification of the possible sets of invariants is described further in the current section.

Invariants can be distinguished by the calibration method. In such cases, the sensitivity of the invariant can be determined as follows: analytically using formal reasoning and rigorous evidence, using fault-oriented procedures and using the expert methods.

Depending on the scope, the invariants can be distinguished in the following way: global invariants valid for the entire FPGA project, local invariants for individual project components or their clearly fixed parts.

According to the source object for which the invariant is synthesized, they can be distinguished as obtained for system requirements, designed to test system properties that can be derived from requirements, synthesized based on the results obtained at individual project stages, developed for individual project architecture components, obtained from a known set of defects or anomalies that may be inherent in the project.

This facet depends on the previous one, since the first, second, and fifth (and, under certain conditions, third) types of invariants of this facet are global invariants, and the third to fifth (and probably the first) are local invariants.

By the sensitivity value, the set of invariants is divided into binary invariants for which the sensitivity metric takes two values (0 and 1), normalized invariants for which the sensitivity metric takes an infinite or fixed set of values in the interval from 0 to 1.

It should be considered that since the sensitivity value of an invariant can have different meanings with respect to different project anomalies, a type of mixed invariant with binary and normalized components is possible.

According to the rigidity degree, invariants can be of two types:

• conditional (i.e., soft) invariants, which fulfillment is not mandatory. (e.g., they may relate to the style of programming in the VHDL language);
• unconditional (i.e., hard) invariants, which the fulfillment is mandatory from the point of view of safety requirements. Invariants of this type are hierarchically related to the previous taxonomic group. Conditional invariants, as a rule, are a subset of normalized invariants and a scale from 0 to 1 is used to estimate them, and unconditional invariants are a subset of, primarily, binary invariants, and two discrete values 0 and 1 are used to estimate them.

By verification sign, these sets of invariants are possible:

• positive invariants that should always be fulfilled for the entire FPGA project or within the specified local zone;
• negative invariants defined by constraints (rules) that should never be violated. In other words, in a binary sensitivity estimation-positive estimation, positive invariants should always be equal to “1”, and negative invariants should never turn to “0”.
• By parameterization ability, the invariants are divided into two groups:
• non-parametrizable which cannot be customized for a specific project and are fixed in their view;
• parameterizable which can be changed (e.g., be configured, adapted) depending on

  ○

  project type—this type of parameterization consists of considering project type features and the corresponding mathematical representation of invariant correction (e.g., variation in “width”);

  ○

  sensitivity requirements—this type of parameterization for sensitivity is also implemented by correcting the mathematical representation (e.g., variation in “depth” and “width”).

A special type of parameterization is the variation of the set of invariants in the chosen system. Here, it is possible to choose not a minimal, but redundant in a sense system based on the requirements for completeness and reliability of the assessment.

The following classification of the invariants used for operational control is used in the FPGA design verification. Most of these invariants can be used during the intended application of the developed system or its components for the implementation of on-line testing schemes. These invariants include, first, the following sets: precision, semantic, functional and logical invariants (classification attribute: “controlled attribute”), global and local invariants (attribute: “scope”), binary invariants (attribute: “sensitivity value”), negative and positive invariants (attribute: “verification sign”), parametrizable and non-parametrizable invariants (attribute: “parameterization ability”).

5. FPGA Project Invariant Development

5.1. Development Principles

The task of generating (i.e., searching, synthesizing) of invariants is not formal. Its solution depends on the experience and qualifications of the developer, expert, or evaluator. This task is heuristic and is close to an art (in the sense of the “art of programming”).

To some extent, it contradicts the essence of formal methods and the model-based approach (i.e., model-checking). Simultaneously, if there is sufficient information to calculate the metrics of the individual invariants, an assessment of the quality of the system of invariants can be a clear and formal (i.e., engineering) procedure.

The synthesis of invariants can be conducted based on several approaches that differ in the use of sources of information, stages and principles of invariant development:

• Based on the system requirements analysis. It is implemented in the early stages of system development and requires minimal specific design results data. This path is general and does not depend on the type of system (e.g., FPGA design, microprocessor or other systems). The specificity of FPGA projects is manifested here through a method for checking invariants.
• Based on the entire system analysis and identification of its properties, which can be represented by invariants. It can be implemented during the verification of a completed project. This approach is also general, and the specificity of the project affects the way of checking the invariant.
• Based on the analysis of the results obtained at each stage of the project development. It is realized during step-by-step detailing and verification of stages, starting from the verbal specification and ending with the generation of program code with a proof of the correctness of the project. Such a path to the greatest extent considers the specifics of the FPGA project.
• Based on the analysis of each system component property identification. It should be implemented during and after completion of the individual components of the system development: software, hardware, or based on FPGAs; in turn, each component can be decomposed into subcomponents to extract invariants.
• Based on the analysis of typical defects characteristic of individual components and the system as a whole or detected at different stages of its development. This approach can be considered a derivative or part of approaches 1–4.

The synthesis results of invariants can be presented in the form of the following local or global matrices: matrices “requirements-invariants” Ω_RI = ||ω_ji||, matrices “properties-invariants” Ω_PI = ||ω_ki||, matrices “stages-invariants” Ω_SI = ||ω_li||, matrices “components-invariants” Ω_CI = ||ω_mi||, matrices “defects-invariants” Ω_DI = ||ω_pi||.

In the matrices the corresponding elements ω_ji indicate that the invariant I_i covers the requirement r_j (property p_k, stage s_l, component c_m, defect f_p).

Note that the synthesis of invariants can be conducted in the general case according to two schemes (strategies):

• “top-down”—when a method synthesizes (generates) an invariant (or system of invariants) and then the defects that are “covered” by this invariant are determined;
• “bottom-top”—when the possible defects of the FPGA design are first determined and invariants are developed for certain types of these defects.

A mixed principle of development is also possible when the development strategy may be different for different anomalies, the design of its components and stages.

In the concept of this work, the principle of developing top-down invariants has been adopted as the main one. However, for some situations the mixed principle may also be applied.

5.2. The Invariants Development Stages

5.2.1. Overall Development Stages Description

The synthesis (i.e., selection) of a system of invariants in the general case includes five stages (their list and content correspond to the conceptual scheme of an invariant-oriented evaluation of FPGA projects, Figure 1):

• Requirements, system design, results of individual steps’ analyses;
• Clarification of the requirements for the estimation reliability (selection of the optimality criteria for a set of invariants);
• Software, algorithmic, automaton and other mathematical models set formation and their corresponding invariants;
• Each of the invariant calibration;
• The choice of a subset of invariants that is optimal by some criteria.

It should be emphasized that problems three and four can be solved by analyzing and selecting invariants from the previously obtained (and replenished from project to project) set of possible invariants, some of which (as noted above in Section 4) are universal and some are specific.

5.2.2. The Invariants Synthesis Algorithm

This approach of the invariant synthesis can be implemented in such a general sequence:

• The requirements set RS = {R_i} to the system is analyzed and normalized (priority ones that need to be verified are selected and specified). Many RSs include both functional and nonfunctional requirements;
• For each requirement R_i or their subset ∆R a “covering” invariant I_j or a “covering” subset of ∆I_r is defined. It is solved in three ways:
  • a degenerate case: each requirement is an invariant, and its verification is carried out by an expert or other ways. The most convenient form for presenting the results is a checklist;
  • each requirement or a subset is associated with an invariant (a subset of invariants) based on the physical meaning of the requirements, the possibility of their semantic compression and compact mathematical representation. An intermediate step here may be to obtain a mathematical model according to the requirements;
  • a combination of methods “a” and “b”. Within this combination method “a” is used to verify nonfunctional requirements and method “b” is used to verify functional requirements;

• The problem of covering requirements is solved with the invariant set IS = {I_j} and the minimal invariants systems ISys belonging to IS are determined;
• The optimal system of invariants ISys_opt is selected according to given criteria, considering the calibration results of each invariant.

Given this sequence, in the case of using formal FPGA project development methods (e.g., BHDL [46,47]), it is unclear how (i.e., architecturally) the system functionality is based on the invariant system ISys_opt.

An alternative to this sequence is the step-by-step detailing procedure accepted for formal methods, when invariants are determined at each step. Then at each step it is possible to develop and solve the local problem of obtaining the minimal subsystem of invariants ISys_h.

5.2.3. Invariant Synthesis Based on the Property Analysis

The second approach is implemented in a similar general sequence as the first. The difference is that the source of information for obtaining the invariants is not the requirements, but the properties of the system, analysis of which reveals some constant relationships. Such relationships (i.e., invariants) may include, e.g., semantic invariants that control the correctness of the variable dimension. This example belongs to the number of versatile invariants that can be applied regardless of the specific application:

• The property set of the system PS = {P_f} is analyzed and formed. Among the elements of the set, priority ones (critical for the system) can also be selected.
• For each property P_f or their subset ∆P the “covering” invariant I_f or the “covering” subset ∆I_f are defined.
• The problem of covering requirements is solved by the invariant set IS = {I_f} and the minimal systems of invariants ISys_w belonging to IS are determined.
• The optimal invariants system IS_opt is selected according to a given criterion considering the calibration results of each invariant.

5.2.4. The of Invariant Synthesis Based on the Stages of Project Development Analysis Results

The peculiarity of this action sequence lies in the fact that operations one and two of the previous methods are repeated here for each stage, and then the resulting set is analyzed in the following way:

• Requirements set RS^z for the development stage S_z are analyzed (and the RS^z properties identified at this stage) and their prioritization and preliminary selection are conducted.
• For each requirement R^z_a belonging to RS^z (properties P^z_b belonging to RS^z) or their subsets ∆R^z the “covering” invariant I^z_{a (b)} or the “covering” subset of the invariants ∆I^z_{a (b)} are defined.
• Operations 1 and 2 are repeated for all stages (z = 1, …, E).
• The problem of covering the requirements of RS or RS^z with invariants sets IS = {IS^z} is solved and the minimal systems of invariants ISys_h, belonging to IS re determined (by stages or/and as a whole).
• The optimal invariants system ISys_opt is selected according to a given criterion, considering the calibration results of each of the invariants.

The optimization task in this case can be solved in two ways, depending on the table used and the coverage problem solving results: as a set of particular tasks for each stage considering local coverages (tables of coverages by stages) and as a general optimization problem, considering general coverage (a common coverage table that considers all the invariants found for all stages).

Obviously, the second method provides a more accurate solution, but it incurs large computational costs. Additionally, when solving the problem in the first way, there are risks that some of the possible defects associated with the step-by-step approach will not be identified.

5.2.5. Invariant Synthesis Based on the System Components’ Properties Analysis and Identification

Here, a component-oriented approach is used to form the invariant set. For each project component, including the FPGA project the approaches described above based on an analysis of requirements or properties, respectively, can be implemented.

The second one is preferable, since the requirements for individual components of the project may not be described in detail and, therefore, for the implementation of the approach based on the requirements, it will be necessary to conduct their detailed elaboration.

Therefore, the synthesis of invariants based on the FPGA project components properties analysis and identification can be performed in the following sequence:

• The system components set CS = {K^d} is formed.
• Component properties are set CPS^d = {CP^d_f} for each component C^d and priorities (critical for the system) are selected.
• For each property CP^d_f or it’s subset ∆CP^d_f a “covering” invariant I_f or a “covering” subset of invariants ∆I_f is defined.
• The problem of covering the component properties with the invariants set IS^d = {I^d_f} and the minimal invariants systems ISys^d_v, belonging to IS^d is determined.
• Minimal invariant systems ISys_x are obtained: to obtain them, the Cartesian product of the sets, ISys^d_v, found for the individual components is performed, and then the groups that meet the criterion of minimality are selected.
• According to a given criterion, the optimal invariants system ISys_opt is selected considering the calibration results of each invariant and the costs associated with their use.

It should be emphasized that for a complete solution to the problem, the invariants set IS_opt must be supplemented by an invariant or invariants subset, allowing us to verify the project configuration problem and solution correctness.

6. Case Study to FPGA Safety Invariant-Based Assessment

The described approach and technique were applied during the implementation of several projects: a fully industrial project on the certification of FPGA platform developed by RadICS [48,49,50], capacity building of higher education and implementation of the joint academia–industry project “Safety-critical software independent verification and latent fault assessment based on diverse measurement of invariants”. Invariant-based safety assessment of FPGA projects also served as a good support for achieving the required reliability of results and cost-effectiveness when assessing of hardware diversity during the IV&V of safety-critical systems [51].

FPGA design (FPGA project) is a set of electronic circuit components that are represented as a set of expressions in the hardware description language (HDL—description) and intended for loading into a microcircuit. The components of the electronic FPGA project are IP cores and IIP infrastructures.

The tools used to develop electronic FPGA projects should be licensed software products. IPs must undergo preliminary verification and certification and are acceptable for use in security-related applications. The syntax of the VHDL language is presented in IEEE 1076–2019 “IEEE Standard for VHDL Language Reference Manual” [52]. The source code of objects written by programmers must comply with this standard and must not contain extensions of the VHDL language. The following invariants were used in these projects:

• usage of the explicit principle of mapping component ports to the signals arriving at them in the port map (=>);
• “sensitivity list” should contain signals that are used in the body of the process;
• the use of conditional operators must be accompanied by a post-condition (full condition);
• not to use a “hard” index when working with a signal vector, etc.
• It should be emphasized that the control of the rules for the use of the VHDL programming language are quality assurance and risk management mechanisms in the development of electronic FPGA projects that implement functions important to safety.

6.1. Explicit Principle of Mapping Components to the Signals in the PORT MAP Section

Using the explicit principle of mapping component ports to the signals arriving at them in the port map (=>). Using this invariant provides an exception: errors in declaring and using components or errors when changing port names in the “entity” (interface) of the component.

A computer-aided design (CAD) tool detects an error for mixed port assignment only when explicit assignment is used at first and implicit lately. Mixed port assignment is allowed in the following sequence: ports are specified first implicitly, and subsequent ports are binding explicitly using “=>”.

The following examples can describe this principle:

• Explicit port assignment

• HKDFF: DFFE port map (d => D_I, clk => CLK_I, q => Q_O, ena => Enable_I, clrn => Clear_I, prn => Set_I);

• Implicit port assignment

• HKDFF: DFFE port map (D_I, CLK_I, Q_O, Enable_I, Clear_I, Set_I);

• Mixed port assignment

• HKDFF: DFFE port map (D_I, CLK_I, q => Q_O, ena => Enable_I, clrn => Clear_I, prn => Set_I);

• Captured CAD

• HKDFF: DFFE port map (q => Q_O, ena => Enable_I, clrn => Clear_I, prn => Set_I, D_I, CLK_I);

To calibrate the invariant, the following operations are performed:

• Searching for the PORT MAP (); construction.
• Reading the contents of the brackets.
• Invariant check: whether it worked or not?
• Injecting the defect: replacing the explicit principle of specifying ports with positional one: replacing each design x => y with y.
• Invariant check: whether it worked or not?
• Injecting the defect: replacing the explicit principle of specifying mixed ports: replacing the first structure (s) x => y with y.
• Invariant check: whether it worked or not?

6.2. Using of the Signals from PROCESS “Sensitivity List” in Its Body

In this case, the exception is provided by either unnecessary triggering of the process, and as a result, frequent changes in the output, or failure of the process at the right time. CAD issues a warning if the sensitivity list does not contain all the input signals of the process but does not respond to the redundancy of its contents.

Table 2. Examples of use of the signals from PROCESS “sensitivity list”.

	Full Sensitivity List	Incomplete Sensitivity List	Excess Sensitivity List
1.	Activation: PROCESS (CLK_I, Data_I) IS	Activation: PROCESS (CLK_I) IS	Activation: PROCESS (CLK_I, Data_I, test) IS
2.	BEGIN	BEGIN	BEGIN
3.	IF RISING_EDGE(CLK_I) THEN	IF RISING_EDGE(CLK_I) THEN	IF RISING_EDGE(CLK_I) THEN
4.	IF Data_I = ‘1’ THEN Data_O <= ‘0’;	IF Data_I = ‘1’ THEN Data_O <= ‘0’;	IF Data_I = ‘1’ THEN Data_O <= ‘0’;
5.	ELSE Data_O <= ‘1′;	ELSE Data_O <= ‘1′;	ELSE Data_O <= ‘1’;
6.	END IF;	END IF;	END IF;
7.	END IF;	END IF;	END IF;
8.	END PROCESS Activation;	END PROCESS Activation;	END PROCESS Activation;

lists the mentioned examples (i.e., full, incomplete and excess sensitivity lists) are provided.

6.3. Calibration of the Invariant

To calibrate the invariant, the following operations are performed:

• Search for the PROCESS (); construction
• Reading the contents of the brackets and searching the process body for all input signals
• Invariant check: whether it worked or not?
• Injecting the defect (if the list contains two or more signals): replacing the complete sensitivity list with an incomplete one: remove the signal that is used in the body of the process from the list.
• Invariant check: whether it worked or not?
• Injecting the defect: redundant sensitivity list formation: supplementing the sensitivity list with an input signal that is not used in the process body.
• Invariant check: whether it worked or not?

Checking of the invariants considering their calibration results allows assessing FPGA project in the process of IV&V.

7. Discussion

The invariant-oriented assessment is part of the model checking. The main idea of model checking is to overcome the dimensionality problems, which take place in the verification. However, simultaneously, a contradiction always arises as to how the completeness of verification is ensured. Since there is a transition from the enumeration of all input sets to building a model and to checking the object against the model the dimension of the problem decreases, but a problem arises with the completeness of the assessment.

Within the framework of the work presented, this contradiction is untied by identifying invariants as some checking entities and then determining the set of invariants that is necessary to ensure the required completeness of coverage. However, it is not enough. Secondly, thanks to the calibration of invariants, the reliability of the control of one or another entity using this invariant is assessed.

For many I&Cs, the risk is that the required number of invariants will not be found to provide completeness of the estimation. In this sense, FPGA systems and the corresponding projects provide several additional opportunities for constructing a set of invariants. When using the described conception (besides, it could be applied not only for FPGA-based projects), two requirements must always be considered: the completeness of the coverage and the reliability of the assessment. This problem is solved with the help of the invariant calibration. The proposed classification of the set of invariants makes it possible to evaluate FPGA projects from different angles in terms of covering requirements, stages, components and possible defects. The difficulty here lies in assessing the compatibility of these invariants and how they complement each other in terms of the completeness and reliability of the assessment. The proposed classification and different types of invariants allow a comprehensive assessment of the project and reduce the risks that the assessment will be incomplete or unreliable.

An important issue that affects the reliability of the safety assessment when using the invariant-based approach is the synthesis (selection) of a system of invariants for a specific FPGA project, which will minimize the risks of undetected failures. For this purpose, a calibration procedure is implemented, which makes it possible to clarify the individual characteristics of the invariants, and the procedure for forming a set of FPGA invariants, which provides the required estimation indicators. Presented results can contribute to the development of hyper-reliable logic and memory elements memory elements, based on FPGAs, their simulation, and reliability and safety assessment as well [53].

The ongoing and future research is devoted to the development of tool-based quantitative assessment of FPGA project safety by use of set of metrics. Besides, an important research direction is searching for specific invariants and development of invariant based verification methods and tools for multi-version FPGA systems [40,41,42].

8. Conclusions

Invariant-based safety assessment is based on a set of invariants that are partly universal and formed in advance, since they reflect the invariable properties of FPGA projects, hardware description languages. This set can be replenished as experience is gained during project implementation. Another part of the invariants is formed on the basis of the specific FPGA project requirements analysis and reflects the features of the tasks to be solved, the algorithms that are implemented, the chips and tools used.

The following results were obtained in the current paper: A conception of invariant-oriented safety assessment of FPGA projects was suggested. The corresponding stages of the conception application were described. A classification of invariants that considers features of FPGA technology was presented. Several invariant-oriented procedures were proposed for the developer, including the development of set of invariants for different approaches and procedures for constructing and choosing invariants.

Requirements for invariants were given and some use-cases related to the application of the suggested invariant-based safety assessment technique were provided for IV&V of FPGA projects.