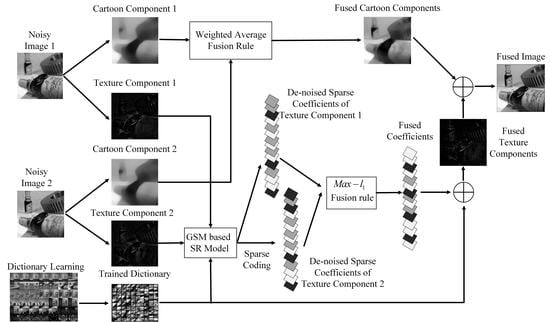
Figure 1.
The Proposed Fusion Framework.
Figure 1.
The Proposed Fusion Framework.
Figure 2.
The Proposed Fusion Framework. (a) a noisy image, (b) cartoon components, and (c) texture components.
Figure 2.
The Proposed Fusion Framework. (a) a noisy image, (b) cartoon components, and (c) texture components.
Figure 3.
Parts of Used Representative source images. (a–l) are selected source images.
Figure 3.
Parts of Used Representative source images. (a–l) are selected source images.
Figure 4.
Simultaneous denoising and fusion results of noisy multi-focus image pairs -1. (a–h) are source multi-focus images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 4.
Simultaneous denoising and fusion results of noisy multi-focus image pairs -1. (a–h) are source multi-focus images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 5.
Simultaneous denoising and fusion results of noisy multi-focus image pairs -2. (a–h) are source multi-focus images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 5.
Simultaneous denoising and fusion results of noisy multi-focus image pairs -2. (a–h) are source multi-focus images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 6.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy multi-modality medical image pairs -1. (a–h) are source multi-modality medical images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 6.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy multi-modality medical image pairs -1. (a–h) are source multi-modality medical images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 7.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy multi-modality medical image pairs -2. (a–h) are source multi-modality medical images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 7.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy multi-modality medical image pairs -2. (a–h) are source multi-modality medical images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 8.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy infrared-visible image pairs. (a–h) are source infrared-visible images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 8.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy infrared-visible image pairs. (a–h) are source infrared-visible images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 9.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy infrared-visible image pairs -2. (a–h) are source infrared-visible images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 9.
Simultaneous denoising and fusion results of FDESD, FDS and the proposed method for noisy infrared-visible image pairs -2. (a–h) are source infrared-visible images with additional noise respectively; (i–t) are simultaneous denoising and fusion results of source images with additional noise by FDESD, FDS and proposed method respectively.
Figure 10.
Comparison of separate and simultaneous image denoising and fusion results. (a–d) and (m–p) are denoising and fusion results of multi-focus image with additional noise by SDF and proposed method respectively. (e–h) and (q–t) are denoising and fusion results of malti-modality medical image with additional noise by SDF and proposed method respectively. (i–l) and (u–x) are denoising and fusion results of infrared-visible image with additional noise by SDF and proposed method respectively.
Figure 10.
Comparison of separate and simultaneous image denoising and fusion results. (a–d) and (m–p) are denoising and fusion results of multi-focus image with additional noise by SDF and proposed method respectively. (e–h) and (q–t) are denoising and fusion results of malti-modality medical image with additional noise by SDF and proposed method respectively. (i–l) and (u–x) are denoising and fusion results of infrared-visible image with additional noise by SDF and proposed method respectively.
Table 1.
Objective evaluations of simultaneous multi-focus image denoising and fusion -1.
Table 1.
Objective evaluations of simultaneous multi-focus image denoising and fusion -1.
| | | | | | | | VIFF |
| FDESD | 0.6685 | 0.8160 | 0.7287 | 0.7539 | 1.7420 | 0.8963 | 0.6444 | 0.6257 |
| FDS | 0.7529 | 0.8190 | 0.7479 | 0.8387 | 1.9337 | 0.9248 | 0.7228 | 0.6770 |
| proposed | 0.9163 | 0.8251 | 0.7305 | 0.8499 | 2.3450 | 0.9657 | 0.7569 | 0.6962 |
| | | | | | | | VIFF |
| FDESD | 0.6056 | 0.8106 | 0.5614 | 0.5689 | 1.5623 | 0.7404 | 0.6132 | 0.6009 |
| FDS | 0.6446 | 0.8152 | 0.5745 | 0.6821 | 1.6617 | 0.7765 | 0.6745 | 0.6346 |
| proposed | 0.6527 | 0.8156 | 0.5857 | 0.6992 | 1.8871 | 0.7825 | 0.6804 | 0.6450 |
| | | | | | | | VIFF |
| FDESD | 0.5563 | 0.8122 | 0.4459 | 0.4078 | 1.4352 | 0.6336 | 0.5728 | 0.5549 |
| FDS | 0.6053 | 0.8140 | 0.4787 | 0.5188 | 1.5570 | 0.6713 | 0.6245 | 0.5578 |
| proposed | 0.6102 | 0.8142 | 0.4873 | 0.5538 | 1.5672 | 0.6933 | 0.6371 | 0.5777 |
| | | | | | | | VIFF |
| FDESD | 0.4511 | 0.8100 | 0.2633 | 0.1726 | 1.1615 | 0.4413 | 0.4928 | 0.4257 |
| FDS | 0.5369 | 0.8119 | 0.2619 | 0.2352 | 1.3656 | 0.4568 | 0.4696 | 0.4268 |
| proposed | 0.5472 | 0.8122 | 0.3014 | 0.3055 | 1.3852 | 0.5030 | 0.5276 | 0.4340 |
Table 2.
Objective evaluations of simultaneous multi-focus image denoising and fusion -2.
Table 2.
Objective evaluations of simultaneous multi-focus image denoising and fusion -2.
| | | | | | | | VIFF |
| FDESD | 0.6752 | 0.8098 | 0.7279 | 0.7692 | 1.7583 | 0.9034 | 0.6579 | 0.6372 |
| FDS | 0.7682 | 0.8197 | 0.7392 | 0.8393 | 1.9872 | 0.9244 | 0.7382 | 0.6804 |
| proposed | 0.9192 | 0.8317 | 0.7408 | 0.8503 | 2.3581 | 0.9694 | 0.7593 | 0.6985 |
| | | | | | | | VIFF |
| FDESD | 0.6193 | 0.8132 | 0.5687 | 0.5793 | 1.5736 | 0.7534 | 0.6328 | 0.6196 |
| FDS | 0.6487 | 0.8157 | 0.5783 | 0.6894 | 1.6689 | 0.7793 | 0.6784 | 0.6372 |
| proposed | 0.6576 | 0.8186 | 0.5873 | 0.6998 | 1.8903 | 0.7896 | 0.6864 | 0.6497 |
| | | | | | | | VIFF |
| FDESD | 0.5604 | 0.8146 | 0.4494 | 0.4184 | 1.4423 | 0.6406 | 0.5804 | 0.5569 |
| FDS | 0.6085 | 0.8195 | 0.4808 | 0.5268 | 1.5596 | 0.6792 | 0.6294 | 0.5608 |
| proposed | 0.6181 | 0.8237 | 0.4906 | 0.5587 | 1.5693 | 0.6987 | 0.6395 | 0.5788 |
| | | | | | | | VIFF |
| FDESD | 0.4595 | 0.8187 | 0.2693 | 0.1774 | 1.1709 | 0.4473 | 0.4989 | 0.4267 |
| FDS | 0.5409 | 0.8121 | 0.2746 | 0.2429 | 1.3726 | 0.4589 | 0.4785 | 0.4326 |
| proposed | 0.5503 | 0.8173 | 0.3068 | 0.3094 | 1.3873 | 0.5096 | 0.5316 | 0.4389 |
Table 3.
Average objective evaluations of simultaneous multi-focus image denoising and fusion.
Table 3.
Average objective evaluations of simultaneous multi-focus image denoising and fusion.
| | | | | | | | VIFF |
| FDESD | 0.6749 | 0.8096 | 0.7277 | 0.7689 | 1.7580 | 0.9031 | 0.6576 | 0.6369 |
| FDS | 0.7678 | 0.8194 | 0.7388 | 0.8392 | 1.9867 | 0.9242 | 0.7380 | 0.6801 |
| proposed | 0.9187 | 0.8314 | 0.7404 | 0.8598 | 2.3579 | 0.9690 | 0.7590 | 0.6981 |
| | | | | | | | VIFF |
| FDESD | 0.6189 | 0.8127 | 0.5684 | 0.5789 | 1.5732 | 0.7531 | 0.6325 | 0.6192 |
| FDS | 0.6482 | 0.8153 | 0.5780 | 0.6889 | 1.6685 | 0.7790 | 0.6781 | 0.6369 |
| proposed | 0.6572 | 0.8183 | 0.5870 | 0.6994 | 1.8900 | 0.7893 | 0.6861 | 0.6493 |
| | | | | | | | VIFF |
| FDESD | 0.5601 | 0.8142 | 0.4490 | 0.4181 | 1.4421 | 0.6402 | 0.5899 | 0.5564 |
| FDS | 0.6081 | 0.8192 | 0.4803 | 0.5264 | 1.5592 | 0.6788 | 0.6291 | 0.5602 |
| proposed | 0.6177 | 0.8233 | 0.4902 | 0.5583 | 1.5689 | 0.6983 | 0.6391 | 0.5782 |
| | | | | | | | VIFF |
| FDESD | 0.4591 | 0.8182 | 0.2690 | 0.1772 | 1.1703 | 0.4470 | 0.4986 | 0.4264 |
| FDS | 0.5407 | 0.8118 | 0.2742 | 0.2426 | 1.3723 | 0.4584 | 0.4781 | 0.4323 |
| proposed | 0.5500 | 0.8171 | 0.3065 | 0.3092 | 1.3869 | 0.5094 | 0.5313 | 0.4386 |
Table 4.
Objective evaluations of simultaneous multi-modality medical image denoising and fusion -1.
Table 4.
Objective evaluations of simultaneous multi-modality medical image denoising and fusion -1.
| | | | | | | | VIFF |
| FDESD | 0.5571 | 0.8071 | 0.4010 | 0.4271 | 0.9989 | 0.4717 | 0.4252 | 0.3337 |
| FDS | 0.5677 | 0.8072 | 0.4837 | 0.5333 | 1.0068 | 0.5626 | 0.4686 | 0.3601 |
| proposed | 0.6537 | 0.8099 | 0.6583 | 0.5371 | 1.2223 | 0.7150 | 0.4698 | 0.4362 |
| | | | | | | | VIFF |
| FDESD | 0.4870 | 0.8064 | 0.3067 | 0.2584 | 0.9256 | 0.3998 | 0.3338 | 0.3075 |
| FDS | 0.5367 | 0.8069 | 0.3355 | 0.3852 | 0.9758 | 0.4635 | 0.3461 | 0.3167 |
| proposed | 0.5600 | 0.8077 | 0.4082 | 0.3938 | 1.0551 | 0.5408 | 0.3778 | 0.3729 |
| | | | | | | | VIFF |
| FDESD | 0.4331 | 0.8057 | 0.2661 | 0.1702 | 0.8386 | 0.3546 | 0.3349 | 0.2880 |
| FDS | 0.5099 | 0.8066 | 0.2815 | 0.2908 | 0.9459 | 0.3891 | 0.3245 | 0.2908 |
| proposed | 0.4871 | 0.8067 | 0.3221 | 0.2989 | 0.9477 | 0.4269 | 0.3594 | 0.3904 |
| | | | | | | | VIFF |
| FDESD | 0.2975 | 0.8041 | 0.1517 | 0.0663 | 0.5883 | 0.2200 | 0.2901 | 0.2360 |
| FDS | 0.4542 | 0.8058 | 0.1852 | 0.1548 | 0.8593 | 0.2744 | 0.2338 | 0.2402 |
| proposed | 0.4875 | 0.8064 | 0.2554 | 0.1903 | 0.9326 | 0.3472 | 0.2994 | 0.3013 |
Table 5.
Objective evaluations of simultaneous multi-modality medical image denoising and fusion -2.
Table 5.
Objective evaluations of simultaneous multi-modality medical image denoising and fusion -2.
| | | | | | | | VIFF |
| FDESD | 0.5582 | 0.8077 | 0.4047 | 0.4306 | 0.9997 | 0.4773 | 0.4302 | 0.3371 |
| FDS | 0.5691 | 0.8085 | 0.4869 | 0.5361 | 1.0103 | 0.5689 | 0.4690 | 0.3634 |
| proposed | 0.6575 | 0.8112 | 0.6599 | 0.5389 | 1.2286 | 0.7183 | 0.4708 | 0.4397 |
| | | | | | | | VIFF |
| FDESD | 0.4887 | 0.8077 | 0.3093 | 0.2604 | 0.9296 | 0.4063 | 0.3359 | 0.3096 |
| FDS | 0.5384 | 0.8098 | 0.3392 | 0.3887 | 0.9791 | 0.4663 | 0.3486 | 0.3191 |
| proposed | 0.5641 | 0.8103 | 0.4094 | 0.3974 | 1.0588 | 0.5437 | 0.3792 | 0.3764 |
| | | | | | | | VIFF |
| FDESD | 0.4362 | 0.8079 | 0.2686 | 0.1747 | 0.8406 | 0.3583 | 0.3385 | 0.2901 |
| FDS | 0.5102 | 0.8081 | 0.2855 | 0.2934 | 0.9481 | 0.3906 | 0.3273 | 0.2975 |
| proposed | 0.5132 | 0.8091 | 0.3234 | 0.2996 | 0.9497 | 0.4284 | 0.3606 | 0.3937 |
| | | | | | | | VIFF |
| FDESD | 0.2994 | 0.8080 | 0.1542 | 0.0676 | 0.5897 | 0.2221 | 0.2932 | 0.2393 |
| FDS | 0.4576 | 0.8087 | 0.1891 | 0.1586 | 0.8612 | 0.2786 | 0.2367 | 0.2435 |
| proposed | 0.4902 | 0.8093 | 0.2577 | 0.1938 | 0.9361 | 0.3496 | 0.3008 | 0.3037 |
Table 6.
Average objective evaluations of simultaneous multi-modality medical image denoising and fusion.
Table 6.
Average objective evaluations of simultaneous multi-modality medical image denoising and fusion.
| | | | | | | | VIFF |
| FDESD | 0.5580 | 0.8075 | 0.4043 | 0.4302 | 0.9994 | 0.4771 | 0.4300 | 0.3369 |
| FDS | 0.5688 | 0.8082 | 0.4866 | 0.5357 | 1.0101 | 0.5685 | 0.4686 | 0.3631 |
| proposed | 0.6572 | 0.8108 | 0.6595 | 0.5386 | 1.2282 | 0.7180 | 0.4702 | 0.4393 |
| | | | | | | | VIFF |
| FDESD | 0.4883 | 0.8074 | 0.3090 | 0.2601 | 0.9293 | 0.4059 | 0.3355 | 0.3092 |
| FDS | 0.5381 | 0.8095 | 0.3388 | 0.3882 | 0.9787 | 0.4660 | 0.3482 | 0.3187 |
| proposed | 0.5635 | 0.8100 | 0.4091 | 0.3971 | 1.0585 | 0.5433 | 0.3786 | 0.3761 |
| | | | | | | | VIFF |
| FDESD | 0.4359 | 0.8076 | 0.2684 | 0.1744 | 0.8404 | 0.3581 | 0.3382 | 0.2987 |
| FDS | 0.5198 | 0.8077 | 0.2851 | 0.2932 | 0.9476 | 0.3902 | 0.3270 | 0.2971 |
| proposed | 0.5129 | 0.8087 | 0.3231 | 0.2992 | 0.9493 | 0.4281 | 0.3602 | 0.3933 |
| | | | | | | | VIFF |
| FDESD | 0.2991 | 0.8078 | 0.1538 | 0.0672 | 0.5893 | 0.2217 | 0.2928 | 0.2390 |
| FDS | 0.4572 | 0.8083 | 0.1887 | 0.1582 | 0.8607 | 0.2782 | 0.2362 | 0.2431 |
| proposed | 0.4897 | 0.8090 | 0.2572 | 0.1934 | 0.9358 | 0.3492 | 0.3005 | 0.3033 |
Table 7.
Objective evaluations of simultaneous infrared-visible image denoising and fusion -1.
Table 7.
Objective evaluations of simultaneous infrared-visible image denoising and fusion -1.
| | | | | | | | VIFF |
| FDESD | 0.2891 | 0.8040 | 0.5818 | 0.3201 | 0.6301 | 0.6924 | 0.4884 | 0.2814 |
| FDS | 0.2989 | 0.8043 | 0.6229 | 0.4378 | 0.6638 | 0.7774 | 0.5425 | 0.3122 |
| proposed | 0.3582 | 0.8059 | 0.6543 | 0.5000 | 0.8173 | 0.8785 | 0.5434 | 0.3975 |
| | | | | | | | VIFF |
| FDESD | 0.2949 | 0.8041 | 0.3473 | 0.1734 | 0.6460 | 0.4862 | 0.4878 | 0.2870 |
| FDS | 0.2948 | 0.8041 | 0.4259 | 0.2773 | 0.6531 | 0.5748 | 0.5085 | 0.3011 |
| proposed | 0.3185 | 0.8048 | 0.4514 | 0.3049 | 0.7232 | 0.6580 | 0.5111 | 0.3727 |
| | | | | | | | VIFF |
| FDESD | 0.2808 | 0.8031 | 0.3204 | 0.1188 | 0.6253 | 0.4873 | 0.4561 | 0.2835 |
| FDS | 0.2928 | 0.8031 | 0.3314 | 0.2081 | 0.6455 | 0.4660 | 0.4624 | 0.2706 |
| proposed | 0.3217 | 0.8050 | 0.3862 | 0.2355 | 0.7309 | 0.5704 | 0.4641 | 0.3429 |
| | | | | | | | VIFF |
| FDESD | 0.2114 | 0.8031 | 0.2259 | 0.0534 | 0.4697 | 0.3914 | 0.4380 | 0.2038 |
| FDS | 0.2606 | 0.8035 | 0.1894 | 0.1079 | 0.5614 | 0.3176 | 0.3946 | 0.2065 |
| proposed | 0.2933 | 0.8041 | 0.2378 | 0.1324 | 0.6522 | 0.3856 | 0.3771 | 0.2356 |
Table 8.
Objective evaluations of simultaneous infrared-visible image denoising and fusion -2.
Table 8.
Objective evaluations of simultaneous infrared-visible image denoising and fusion -2.
| | | | | | | | VIFF |
| FDESD | 0.2906 | 0.8043 | 0.5843 | 0.3236 | 0.6341 | 0.6952 | 0.4897 | 0.2846 |
| FDS | 0.3006 | 0.8049 | 0.6251 | 0.4398 | 0.6658 | 0.7793 | 0.5449 | 0.3141 |
| proposed | 0.3593 | 0.8063 | 0.6561 | 0.5011 | 0.8189 | 0.8793 | 0.5452 | 0.3996 |
| | | | | | | | VIFF |
| FDESD | 0.2961 | 0.8051 | 0.3488 | 0.1749 | 0.6473 | 0.4881 | 0.4890 | 0.2887 |
| FDS | 0.2964 | 0.8059 | 0.4268 | 0.2782 | 0.6562 | 0.5767 | 0.5097 | 0.3038 |
| proposed | 0.3194 | 0.8062 | 0.4539 | 0.3077 | 0.7261 | 0.6595 | 0.5133 | 0.3752 |
| | | | | | | | VIFF |
| FDESD | 0.2821 | 0.8052 | 0.3228 | 0.1201 | 0.6275 | 0.4888 | 0.4579 | 0.2851 |
| FDS | 0.2942 | 0.8050 | 0.3336 | 0.2101 | 0.6473 | 0.4687 | 0.4653 | 0.2728 |
| proposed | 0.3234 | 0.8068 | 0.3879 | 0.2371 | 0.7327 | 0.5721 | 0.4663 | 0.3447 |
| | | | | | | | VIFF |
| FDESD | 0.2135 | 0.8049 | 0.2280 | 0.0553 | 0.4707 | 0.3946 | 0.4399 | 0.2060 |
| FDS | 0.2631 | 0.8051 | 0.1910 | 0.1097 | 0.5633 | 0.3196 | 0.3971 | 0.2082 |
| proposed | 0.2946 | 0.8056 | 0.2391 | 0.1340 | 0.6537 | 0.3872 | 0.3787 | 0.2369 |
Table 9.
Average objective evaluations of simultaneous infrared-visible image denoising and fusion.
Table 9.
Average objective evaluations of simultaneous infrared-visible image denoising and fusion.
| | | | | | | | VIFF |
| FDESD | 0.2903 | 0.8041 | 0.5840 | 0.3234 | 0.6340 | 0.6959 | 0.4892 | 0.2842 |
| FDS | 0.3003 | 0.8045 | 0.6247 | 0.4395 | 0.6654 | 0.7790 | 0.5445 | 0.3137 |
| proposed | 0.3590 | 0.8059 | 0.6558 | 0.5008 | 0.8185 | 0.8790 | 0.5448 | 0.3991 |
| | | | | | | | VIFF |
| FDESD | 0.2957 | 0.8048 | 0.3483 | 0.1745 | 0.6471 | 0.4877 | 0.4886 | 0.2884 |
| FDS | 0.2961 | 0.8054 | 0.4266 | 0.2777 | 0.6557 | 0.5763 | 0.5092 | 0.3034 |
| proposed | 0.3191 | 0.8057 | 0.4535 | 0.3074 | 0.7256 | 0.6591 | 0.5130 | 0.3748 |
| | | | | | | | VIFF |
| FDESD | 0.2818 | 0.8047 | 0.3223 | 0.1197 | 0.6272 | 0.4885 | 0.4577 | 0.2848 |
| FDS | 0.2940 | 0.8046 | 0.3332 | 0.2096 | 0.6470 | 0.4681 | 0.4650 | 0.2722 |
| proposed | 0.3231 | 0.8062 | 0.3877 | 0.2366 | 0.7323 | 0.5717 | 0.4659 | 0.3444 |
| | | | | | | | VIFF |
| FDESD | 0.2131 | 0.8043 | 0.2275 | 0.0548 | 0.4702 | 0.3943 | 0.4395 | 0.2057 |
| FDS | 0.2627 | 0.8047 | 0.1905 | 0.1093 | 0.5630 | 0.3192 | 0.3966 | 0.2078 |
| proposed | 0.2942 | 0.8053 | 0.2386 | 0.1335 | 0.6533 | 0.3868 | 0.3785 | 0.235 |
Table 10.
The Average Computational Efficiency Comparison of Noisy Image Fusion.
Table 10.
The Average Computational Efficiency Comparison of Noisy Image Fusion.
| Resolution | | |
|---|
| FDESD | 36.82 s | 46.53 s |
| FDS | 20.71 s | 24.56 s |
| Proposed | 21.55 s | 26.71 s |
Table 11.
Objective evaluations of separate and simultaneous noisy-multi-focus image denoising and fusion.
Table 11.
Objective evaluations of separate and simultaneous noisy-multi-focus image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.7158 | 0.8189 | 0.6975 | 0.8337 | 1.9508 | 0.8560 | 0.7154 | 0.6665 |
| proposed | 0.9163 | 0.8251 | 0.7305 | 0.8499 | 2.3450 | 0.9657 | 0.7569 | 0.6962 |
| | | | | | | | VIFF |
| SDF | 0.6650 | 0.8171 | 0.4871 | 0.6259 | 1.7849 | 0.7047 | 0.6647 | 0.6326 |
| proposed | 0.6527 | 0.8156 | 0.5857 | 0.6992 | 1.8871 | 0.7825 | 0.6804 | 0.6450 |
| | | | | | | | VIFF |
| SDF | 0.6045 | 0.8134 | 0.3771 | 0.5575 | 1.6920 | 0.6060 | 0.6361 | 0.5696 |
| proposed | 0.6102 | 0.8142 | 0.4873 | 0.5538 | 1.5672 | 0.6933 | 0.6371 | 0.5777 |
| | | | | | | | VIFF |
| SDF | 0.5183 | 0.8150 | 0.2662 | 0.3792 | 1.2276 | 0.4690 | 0.4570 | 0.4154 |
| proposed | 0.5472 | 0.8122 | 0.3014 | 0.3055 | 1.3852 | 0.5030 | 0.5276 | 0.4340 |
Table 12.
Objective evaluations of separate and simultaneous noisy-multi-modality medical image denoising and fusion.
Table 12.
Objective evaluations of separate and simultaneous noisy-multi-modality medical image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.6438 | 0.8092 | 0.4780 | 0.4423 | 1.2116 | 0.7236 | 0.5301 | 0.4440 |
| proposed | 0.6537 | 0.8099 | 0.6583 | 0.5371 | 1.2223 | 0.7150 | 0.4698 | 0.4362 |
| | | | | | | | VIFF |
| SDF | 0.4505 | 0.8055 | 0.2155 | 0.2314 | 0.7749 | 0.3289 | 0.4240 | 0.2797 |
| proposed | 0.5600 | 0.8077 | 0.4082 | 0.3938 | 1.0551 | 0.5408 | 0.3778 | 0.3729 |
| | | | | | | | VIFF |
| SDF | 0.4530 | 0.8055 | 0.1845 | 0.1833 | 0.7530 | 0.3245 | 0.3710 | 0.2725 |
| proposed | 0.4871 | 0.8067 | 0.3221 | 0.2689 | 0.9477 | 0.4269 | 0.3594 | 0.3904 |
| | | | | | | | VIFF |
| SDF | 0.4443 | 0.8055 | 0.1348 | 0.1240 | 0.7440 | 0.2724 | 0.3188 | 0.2510 |
| proposed | 0.4875 | 0.8064 | 0.2554 | 0.1903 | 0.9326 | 0.3472 | 0.2994 | 0.3013 |
Table 13.
Objective evaluations of separate and simultaneous noisy-infrared-visible image denoising and fusion.
Table 13.
Objective evaluations of separate and simultaneous noisy-infrared-visible image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.3867 | 0.8070 | 0.6435 | 0.5897 | 0.7985 | 0.7908 | 0.4808 | 0.3042 |
| proposed | 0.3582 | 0.8059 | 0.6543 | 0.5000 | 0.8173 | 0.8785 | 0.5434 | 0.3975 |
| | | | | | | | VIFF |
| SDF | 0.3383 | 0.8064 | 0.4510 | 0.2406 | 0.7029 | 0.6174 | 0.5279 | 0.2820 |
| proposed | 0.3185 | 0.8048 | 0.4514 | 0.3049 | 0.7232 | 0.6580 | 0.5111 | 0.3727 |
| | | | | | | | VIFF |
| SDF | 0.3095 | 0.8051 | 0.3602 | 0.1283 | 0.6554 | 0.5401 | 0.4515 | 0.2540 |
| proposed | 0.3217 | 0.8050 | 0.3862 | 0.2355 | 0.7309 | 0.5704 | 0.4641 | 0.3429 |
| | | | | | | | VIFF |
| SDF | 0.2744 | 0.8054 | 0.2235 | 0.0909 | 0.6228 | 0.3038 | 0.3233 | 0.1893 |
| proposed | 0.2933 | 0.8041 | 0.2378 | 0.1324 | 0.6522 | 0.3856 | 0.3771 | 0.2356 |
Table 14.
Average objective evaluations of separate and simultaneous noisy-multi-focus image denoising and fusion.
Table 14.
Average objective evaluations of separate and simultaneous noisy-multi-focus image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.7165 | 0.8194 | 0.6979 | 0.8343 | 1.9513 | 0.8564 | 0.7159 | 0.6668 |
| proposed | 0.9166 | 0.8255 | 0.7308 | 0.8503 | 2.3454 | 0.9662 | 0.7574 | 0.6968 |
| | | | | | | | VIFF |
| SDF | 0.6655 | 0.8174 | 0.4876 | 0.6265 | 1.7855 | 0.7050 | 0.6653 | 0.6330 |
| proposed | 0.6532 | 0.8160 | 0.5863 | 0.6999 | 1.8877 | 0.7829 | 0.6808 | 0.6455 |
| | | | | | | | VIFF |
| SDF | 0.6048 | 0.8138 | 0.3776 | 0.5579 | 1.6924 | 0.6063 | 0.6367 | 0.5699 |
| proposed | 0.6106 | 0.8149 | 0.4878 | 0.5542 | 1.5677 | 0.6938 | 0.6375 | 0.5782 |
| | | | | | | | VIFF |
| SDF | 0.5188 | 0.8155 | 0.2668 | 0.3798 | 1.2281 | 0.4696 | 0.4575 | 0.4159 |
| proposed | 0.5477 | 0.8125 | 0.3018 | 0.3059 | 1.3857 | 0.5035 | 0.5280 | 0.4346 |
Table 15.
Average objective evaluations of separate and simultaneous noisy-multi-modality medical image denoising and fusion.
Table 15.
Average objective evaluations of separate and simultaneous noisy-multi-modality medical image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.6443 | 0.8098 | 0.4787 | 0.4428 | 1.2120 | 0.7242 | 0.5307 | 0.4448 |
| proposed | 0.6546 | 0.8105 | 0.6589 | 0.5378 | 1.2227 | 0.7155 | 0.4704 | 0.4370 |
| | | | | | | | VIFF |
| SDF | 0.4511 | 0.8062 | 0.2164 | 0.2319 | 0.7753 | 0.3294 | 0.4248 | 0.2804 |
| proposed | 0.5606 | 0.8083 | 0.4087 | 0.3945 | 1.0558 | 0.5415 | 0.3784 | 0.3735 |
| | | | | | | | VIFF |
| SDF | 0.4534 | 0.8061 | 0.1852 | 0.1838 | 0.7536 | 0.3249 | 0.3716 | 0.2731 |
| proposed | 0.4876 | 0.8072 | 0.3226 | 0.2696 | 0.9484 | 0.4275 | 0.3599 | 0.3911 |
| | | | | | | | VIFF |
| SDF | 0.4448 | 0.8062 | 0.1354 | 0.1248 | 0.7447 | 0.2729 | 0.3193 | 0.2517 |
| proposed | 0.4879 | 0.8068 | 0.2560 | 0.1908 | 0.9333 | 0.3478 | 0.3001 | 0.3019 |
Table 16.
Average objective evaluations of separate and simultaneous noisy-infrared-visible image denoising and fusion.
Table 16.
Average objective evaluations of separate and simultaneous noisy-infrared-visible image denoising and fusion.
| | | | | | | | VIFF |
| SDF | 0.3873 | 0.8076 | 0.6440 | 0.5905 | 0.7992 | 0.7914 | 0.4813 | 0.3048 |
| proposed | 0.3590 | 0.8064 | 0.6547 | 0.5006 | 0.8176 | 0.8791 | 0.5439 | 0.3978 |
| | | | | | | | VIFF |
| SDF | 0.3389 | 0.8067 | 0.4515 | 0.2412 | 0.7036 | 0.6179 | 0.5286 | 0.2827 |
| proposed | 0.3189 | 0.8054 | 0.4519 | 0.3056 | 0.7239 | 0.6586 | 0.5119 | 0.3735 |
| | | | | | | | VIFF |
| SDF | 0.3102 | 0.8058 | 0.3608 | 0.1289 | 0.6562 | 0.5409 | 0.4522 | 0.2546 |
| proposed | 0.3223 | 0.8057 | 0.3868 | 0.2362 | 0.7317 | 0.5710 | 0.4648 | 0.3434 |
| | | | | | | | VIFF |
| SDF | 0.2750 | 0.8059 | 0.2241 | 0.0916 | 0.6234 | 0.3045 | 0.3238 | 0.1899 |
| proposed | 0.2938 | 0.8046 | 0.2383 | 0.1328 | 0.6529 | 0.3860 | 0.3778 | 0.2363 |
Table 17.
Comparison of Average Computational Efficiency.
Table 17.
Comparison of Average Computational Efficiency.
| Noisy Image Fusion Computational Efficiency of Images |
| Processing Time of SDF | Total Processing Time of Proposed Method |
| Image Denoising and Fusion |
| Denoising | Fusion | Total |
| 41.77 s | 28.61 s | 70.38 s | 21.73 s |
| Noisy Image Fusion Computational Efficiency of Images |
| Processing Time of SDF | Total Processing Time of Proposed Method |
| Image Denoising and Fusion |
| Denoising | Fusion | Total |
| 48.72 s | 34.69 s | 83.41 s | 26.83 s |