Solution of the Optimal Reactive Power Flow Problem Using a Discrete-Continuous CBGA Implemented in the DigSILENT Programming Language

Abstract

The problem of the optimal reactive power flow in transmission systems is addressed in this research from the point of view of combinatorial optimization. A discrete-continuous version of the Chu & Beasley genetic algorithm (CBGA) is proposed to model continuous variables such as voltage outputs in generators and reactive power injection in capacitor banks, as well as binary variables such as tap positions in transformers. The minimization of the total power losses is considered as the objective performance indicator. The main contribution in this research corresponds to the implementation of the CBGA in the DigSILENT Programming Language (DPL), which exploits the advantages of the power flow tool at a low computational effort. The solution of the optimal reactive power flow problem in power systems is a key task since the efficiency and secure operation of the whole electrical system depend on the adequate distribution of the reactive power in generators, transformers, shunt compensators, and transmission lines. To provide an efficient optimization tool for academics and power system operators, this paper selects the DigSILENT software, since this is widely used for power systems for industries and researchers. Numerical results in three IEEE test feeders composed of 6, 14, and 39 buses demonstrate the efficiency of the proposed CBGA in the DPL environment from DigSILENT to reduce the total grid power losses (between 21.17% to 37.62% of the benchmark case) considering four simulation scenarios regarding voltage regulation bounds and slack voltage outputs. In addition, the total processing times for the IEEE 6-, 14-, and 39-bus systems were $32.33$ s, $49.45$ s, and $138.88$ s, which confirms the low computational effort of the optimization methods directly implemented in the DPL environment.

1. Introduction

Electric power systems in high-voltage levels are electrical networks with the responsibility of transporting large amounts of energy from generation plants to sub-transmission and distribution substations [1]. These grids are typically composed by transmission lines that cover hundreds of kilometers of territory and these are typically operated at voltage levels larger than 220 kV [2]; to compensate possible voltage swell and overvoltages produced by load variations reactive power compensators are integrated on these grids based on capacitor and reactor banks, which operate in steps of injection as a function of the grid requirements [3,4]. In addition, to control the voltage profiles along the grid the tap changers are also used in transformers and the voltage controllers in the synchronous machines [5]. These devices must be properly coordinated to support voltage and frequency for all possible operative conditions of the network [6]; however, these are not easy tasks as specialized control and optimization methodologies are required [1].

An additional aspect in the operation of the power systems under steady state conditions corresponds to the admissible power losses in the normal operation of the network [7], since the energy losses can be reduced with the adequate operation of the taps in transformers, capacitor and reactive power compensators as well as the voltage controllers in the synchronous machines [5]. To represent the problem of power losses minimization in power systems it is required the formulation of an optimization problem that has a mixed-integer nonlinear programming (i.e., MINLP) structure, where efficient and easily implementable optimization strategies to solve it are needed.

In the specialized literature multiple approaches have been proposed to solve the aforementioned problem which is widely known as the optimal reactive power flow problem based on combinatorial optimization methods. Some of these methodologies are described below.

Authors of [8] have presented a multi-objective model to represent the problem of the optimal reactive power flow in power systems where the energy production costs and the total grid energy losses are considered as conflict objectives. The proposed MINLP formulation is solved through the $ϵ$-constrained method through the General Algebraic Modeling System (i.e., GAMS) software. Numerical results demonstrate the effectiveness of the proposed methodology in IEEE test systems composed of 14 and 30 buses, when compared with metaheuristic optimizers such as particle swarm optimization, and differential evolution algorithm, among others. Authors in [9] proposed a specialized metaheuristic optimization algorithm to deal with the optimal reactive power flow problem in power systems which is named stochastic fractal search method. In the objective function it is considered the minimization of the grid energy losses, the voltage deviation, and the voltage stability index. Londoño et al., in [6] presented the application of the mean-variance mapping optimization algorithm to the optimal reactive power flow problem. The effectiveness and robustness of the proposed algorithm is tested in the IEEE 30-bus system, and compared with multiple metaheurisitic optimizers. These comparisons demonstrated that the proposed algorithm reaches the minimum power losses for this system with the best numerical convergence of 10 comparative methodologies. Authors in [10] presents a comparison of three optimization methods to address the reactive power solution in power systems composed of 6, 14 and 39 bus systems. These algorithms correspond to the particle swarm and genetic algorithms improved with the pattern search optimization algorithm. Numerical results demonstrated the effectiveness of the proposed optimization approaches; however, the authors do not provide enough information to corroborate their results, additionally, the variables were codified using continuous approximations, which can affect the final solution based on the integrity and feasibility of the solution space. Authors in [11] have proposed a novel fuzzy adaptive heterogeneous comprehensive-learning based particle swarm optimization algorithm with enhanced exploration and exploitation processes to solve the optimal reactive power dispatch problem in large-scale transmission systems. Numerical validations were performed in power systems with sizes within 30 to 354 nodes, and their results improved the solutions reached with the classical Particle swarm optimization algorithm. In [12] it is presented a complete revision regarding the optimal reactive power flow problem in transmission systems. In addition, the authors have proposed the application of the sine-cosine algorithm to solve this problem with tests instances of 14, 30 and 57 nodes, respectively. The main contribution of these authors corresponds to the statistical validation of the the proposed sine-cosine algorithm when compared with other metaheuristics such as differential evolution and particle swarm optimization, among others. Zhao et al. in [13] presented an interesting work regarding the optimal power flow problem considering the intrinsic relation between the transmission and the distribution networks. The main contribution of this approach corresponds to the proposition of the a distributed gradient-based optimization algorithm to solve the optimal reactive power flow problem considering dispersed distributed generation in distribution networks.

Some additional optimization techniques applied to reactive power flow problem in power systems are: particle swarm optimization [14,15,16,17,18]; gravitational search algorithm [19,20]; moth-flame optimization technique [21]; differential evolution algorithm [22]; bat optimization algorithm [23]; genetic algorithms [5,8,24]; tabu search algorithms [25,26]; and slime mold algorithm [27], among others

Unlike the previous reported approaches, in this research the purpose is the implementation of a specialized genetic algorithm in the DigSILENT programming language (DPL) to set all the variables associated with the optimal reactive power flow problem. The main advantage of the proposed optimization method corresponds to the usage of the well known power flow tools in the DigSILENT software [28]. In addition, this software allows to model the complete power system as much as possible with synchronous machines, two- and three-winding transformers, capacitive and reactive compensators and models of complete line [29]. The validation of the proposed optimization approach is carried out in three different power systems composed of 6, 14 and 39 nodes, respectively, which present prominent numerical results. An important fact of our proposed optimization approach is that the genetic algorithm that solves the optimization problem combines binary and discrete variables in a unified codification [30]. This codification make possible to solve the integer and continuous part of the exact MINLP model in one step, which reduces the complexity of the optimization tool and decreases the total processing time required in its solution. In addition, to guarantee the repeatability of our results, all the DigSILENT systems with the optimization codes are provided into a free repository to allow future research developments.

It is worth mentioning that the DigSILENT software has been selected for all the numerical implementations based on the following criteria:

✓

It has an embedded programming language that uses the power system interface to evaluate multiple power flows with minimum computational requirements.

✓

The DigSILENT software allows the detailed modeling of the power system components such as transformers, reactors, transmission lines, generators and induction motors, among others. These are easily integrated in power flow studies through the Newton-Raphson approach.

✓

The DPL tool avoids to use external programming interfaces to implement the optimization codes; which reduces the total computational time of the optimization strategy.

In addition, it is important to mention that the main goal with this contribution is to provide an efficient and reliable optimization technique (also classical and well-known as the case of CBGA) that can be easily adapted for power system operators as part of their analysis tools [31,32]. However, due to the recent advances in optimization techniques, it becomes quite interesting to implement the solution strategies based on artificial intelligence for future works [11].

The remainder parts of this document are rearranged as follows: Section 2 presents the general mathematical formulation of the optimal reactive power flow problem in power systems; Section 3 presents the main aspects of the solution methodology based on the implementation of a discrete-continuous version of the CBGA. Section 4 presents a general description of the DPL environment from DigSILENT. Section 5 shows the main features of the IEEE bus systems which are composed of 6, 14 and 39 buses, respectively. Section 6 presents all the computation validations for these test systems, considering four simulation scenarios associated with the voltage output at the slack node and the lower and upper voltage bounds. Finally, Section 7 lists the concluding remarks and possible future works derived from this study.

2. Mathematical Model

The problem of the optimal reactive power dispatch in power systems is a complex MINLP model, where the continuous variables are associated with the voltage magnitudes and angles, and active and reactive power generations, among others; while the integer variables are mainly associated with the tap positions in transformers, and active and reactive power compensators. The complete optimization model considered in this research is described below.

2.1. Objective Function

The typical objective function regarding associated with the problem of the optimal reactive power flow problem corresponds to the minimization of the total grid power losses for a particular load operation scenario. This objective function can be formulated as follows:

$$\begin{array}{c}\hfill min{p}_{\mathrm{loss}}=\sum _{k\in \mathcal{N}}\sum _{m\in \mathcal{N}}{Y}_{km}\left(t_p\right)v_k{v}_{m}cos\left({\theta }_k-{\theta }_m-{\varphi }_{km}\left(t_p\right)\right),\end{array}$$

(1)

where $p_{\mathrm{loss}}$ corresponds to the value of the objective function associated with the grid power losses; $v_k$ and $v_m$ represent the voltage magnitudes in the k and m nodes, respectively, which have angles ${\theta }_k$ and ${\theta }_m$, respectively; $Y_{km}\left(t_a\right)$ is the magnitude of the admittance that relates nodes k and w which is a function of the transformer taps $t_p$. This admittance has an angle ${\varphi }_{km}\left(t_a\right)$. Note that these values are obtained from the nodal admittance matrix. In addition, $\mathcal{N}$ represents the set that contains all the grid nodes.

It is worth mentioning that the admittance matrix that relates all the nodes of the system is a nonlinear function of the tap positions in all the transformers, since these devices modify the operative state of the transformer by adding capacities and inductive effects on it, which produce modifications on the reactance components of the admittance matrix between the nodes when the transformers are connected [33].

2.2. Set of Constraints

The set of constraints of the reactive power flow problem includes the active and reactive power balance equations, tap in reactive power compensators and generation capabilities, among others. The complete list of constraints in the reactive power flow problem is presented below [10].

$$\begin{array}{c}\hfill p_k^g-p_k^d=\sum _{k\in \mathcal{N}}\sum _{m\in \mathcal{N}}{Y}_{km}\left(t_a\right)v_k{v}_{m}cos\left({\theta }_k-{\theta }_m-{\varphi }_{km}\left(t_a\right)\right),\forall k\in \mathcal{N}\end{array}$$

(2)

$$\begin{array}{c}\hfill q_k^g-q_k^d+q_k^c\left(c_j\right)-q_k^l\left(r_l\right)=\sum _{k\in \mathcal{N}}\sum _{m\in \mathcal{N}}{Y}_{km}\left(t_a\right)v_k{v}_{m}sin\left({\theta }_k-{\theta }_m-{\varphi }_{km}\left(t_a\right)\right),\forall k\in \mathcal{N}\end{array}$$

(3)

$$\begin{array}{c}\hfill v_i^{g,min}\le v_i^g\le v_i^{g,max},\forall i\in \mathcal{G}\end{array}$$

(4)

$$\begin{array}{c}\hfill q^{g,min}\le q_k^g\le q_k^{g,max},\forall k\in \mathcal{N}\end{array}$$

(5)

$$\begin{array}{c}\hfill c_j^{min}\le c_j\le c_j^{max},\forall j\in \mathcal{C}\end{array}$$

(6)

$$\begin{array}{c}\hfill r_l^{min}\le r_l\le r_l^{max},\forall l\in \mathcal{L}\end{array}$$

(7)

$$\begin{array}{c}\hfill t_a^{min}\le t_a\le t_a^{max},\forall a\in \mathcal{T}\end{array}$$

(8)

$$\begin{array}{c}\hfill v_k^{min}\le v_k\le v_k^{max},\forall k\in \mathcal{N}\end{array}$$

(9)

where $p_k^g$ and $q_k^g$ represent the active and reactive power injections provided by the generator connected at node k; $p_k^d$ and $p_k^d$ are the active and reactive power consumptions in the node k by the constant power loads; $q_k^c\left(c_j\right)$ represents the reactive power injection by a capacitor bank connected at node k with the tap position $c_j$; $q_k^l\left(r_l\right)$ represents the reactive power absorption by a reactor connected at node k with the tap position $r_l$; $v_i^g$ is the output voltage for a generator i; $c_j$ tap position for the $j\mathrm{th}$ capacitor bank; $r_l$ tap position for the $l\mathrm{th}$ reactor compensator; $v_i^{g,min}$ and $v_i^{g,max}$ represent the lower and upper bounds associated with the voltage variables in the generation nodes; $q_k^{g,min}$ and $q_k^{g,max}$ are the lower and upper reactive power generation bounds for a generator connected at node k; $c_j^{min}$ and $c_j^{max}$ are the minimum and maximum bounds allowed for the tap position in the $j\mathrm{th}$ capacitor bank; $r_l^{min}$ and $r_l^{max}$ are the minimum and maximum bounds allowed for the tap position in the $l\mathrm{th}$ reactor; $t_a^{min}$ and $t_a^{max}$ are the minimum and maximum bounds allowed for the tap position in the $a\mathrm{th}$ transformer; and $v_k^{min}$ and $v_k^{max}$ represents the lower and upper voltage regulation bounds applied to the $k\mathrm{th}$ node.

It is worth mentioning that the reactive power injection in the capacitor banks or the reactive power absorption in the reactors is a function of the tap position in these devices [6,34]. In addition, depending on the nature of the tap modeling, these can be represented as continuous variables (ideal case) or with discrete stages (real case), where the former produces a nonlinear optimization model, and the latter a general MINLP problem [35].

2.3. Interpretation of the Mathematical Model

The interpretation of the mathematical model (1)–(9) is described as follows: Equation (1) defines the objective function of the optimization problem which is related with the total grid power losses for a particular load condition. Equation (2) defines the active power balance in all the nodes of the network, and Equation (3) defines the reactive power balance in all the buses of the system. Inequality constraints (4) and (5) define the voltage and reactive power generation bounds in all the generators connected to the power system. Constraints (6) to (8) guarantees that all the taps in capacitor banks, reactors and power transformers are within their bounds; finally, inequality constraint (9) ensures that the voltage regulation bounds in all the nodes of the network stay within of their maximum and minimum allowed bounds.

The main complication of the optimization problem (1)–(9) is associated with the non-convexity of the solution space mainly caused by the active and reactive power balance constraints and the nonlinear dependence of the admittance matrix with the transformer taps [9,36]. Additional to these complications, the presence of the integer variables that generate disconnections in the solution space, make necessary to propose efficient optimization techniques that ensure adequate solution with low computational requirements, even when these are sub-optimal solutions.

3. Solution Methodology

To solve the problem of the optimal reactive power flow in power systems, represented through the optimization model (1)–(9), in this research, we propose the implementation of the well-known CBGA in the DPL by combining discrete and continuous codifications in a unique solution vector. The main advantage of the proposed approach corresponds to the usage of the additional power system analysis tools in the DigSILENT software as is the case of the power flow solution via the Newton-Raphson method. 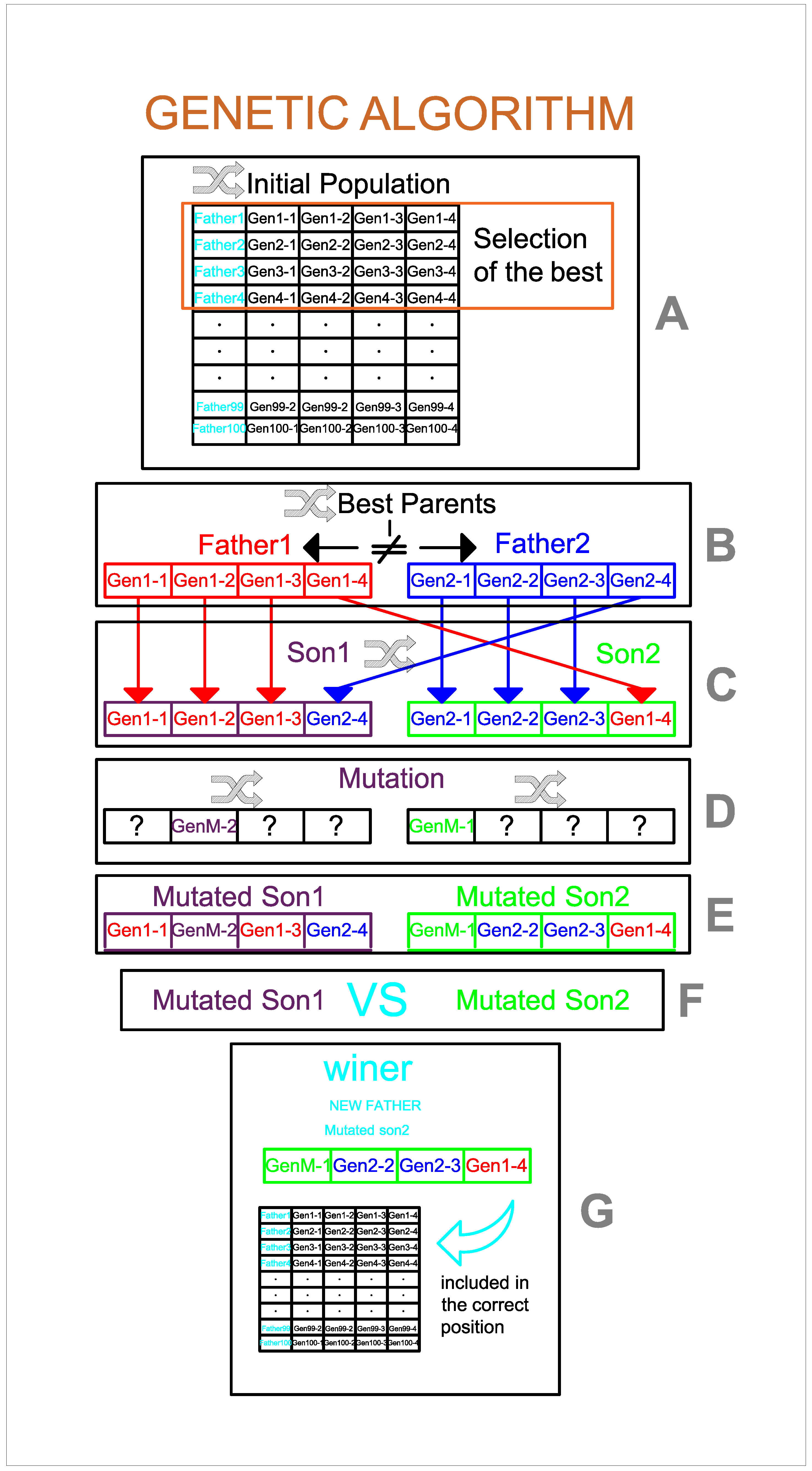Figure 1 presents the main aspects of the implementation of a CBGA to solve optimization problems.

Note that the implementation of the CBGA depicted in Figure 1 is composed of 7 main aspects tagged with A to G letters. Here, we highlight each one of these aspects.

• Section A: In this step it is formed the initial population of the CBGA which corresponds to a generation of multiple random solutions that fulfills the nature and upper and lower bounds of the decision variables. Then, each one of these solutions is evaluated in the power flow tool of the DigSILENT software and ordered in ascending form based on their power losses. Then, the first N individuals are selected as the reduced initial population. Note that this individual in the current population must be different to fulfill the diversity criterion of the CBGA.
• Sections B, C, D and E: In these sections are applied the selection, recombination, and mutation operators of the CBGA, where the main characteristic is that the parents selected must be different. These are randomly selected from the current population. Note that once the mutation operator is applied, to preserve the feasibility of its descending individual, the upper and lower bounds of the decision variables are revised and corrected if necessary.
• Sections F: In this stage, both descending individuals are evaluated in the power flow tool in the DigSILENT software to determine the power losses reached by each one of these configurations.
• Sections G: Finally, in this stage, the best descending is selected (i.e., the winner son) to evaluate the possibility of including it in the current population. To decide whether or not this individual is inserted into the current population, two aspects are revised: (i) the winner individual is different from all the parents in the population; and (ii) the objective function of the winner individual is better than the worst individual in the population. If both criteria are met, then, the current population is updated with the winner individual.

Remark 1.

Note that the evaluative process of the CBGA illustrated in Figure 1 returns from Section G to Section B, while the maximum number of iterations assigned for the exploration and exploitation of the solution space has not been reached.

To illustrate the general structure of a solution individual applied to the problem of the optimal reactive power dispatch in power systems, in (10) the proposed codification is presented.

$$\begin{array}{c}\hfill \left[\begin{array}{c}{v}_1^g{v}_2^g\cdots v_{n_g}^g|t_1{t}_2\cdots t_{n_t}|c_1{c}_2\cdots c_{n_c}|r_1{r}_2\cdots r_{n_l}\end{array}\right],\end{array}$$

(10)

Note that in this codification, the first $n_g$ positions corresponds to the decision variables associated with the voltage output in all the generators, the second part of the vector is composed by $n_t$ positions that are related with the tap positions in all the transformers; the third part of the codification is associated with the $n_c$ positions related with the capacitor taps, and the fourth part of the codification is associated with the $n_l$ positions related with the reactor taps; respectively.

4. DigSILENT Programming Language

The DigSILENT software is a power system analysis tool where static and dynamic analyses can be developed from high- to low-voltage AC networks, including direct current applications [37]. This is a widely recognized software used by power system industries, universities and research facilities to analyze electrical networks, being the main advantage that most of the components of these systems can be modeled with a high-level of precision [38]. In this research is used the DigSILENT software to model the three IEEE power systems under study; in addition, one of its main tool, i.e., the Digsilent Programming Language, is used to implement the proposed CBGA.

The main advantage of using DPLs in the DigSILENT software is that uses its own DigSILENT objects to evaluate the electrical performance of the electrical network with low computational effort [29]. The DPL is, in general, a structured programming language embedded in the DigSILENT software that permits call iteratively its different DigSILENT power system tools, e.g., balance and unbalanced power flow tool or stability analysis tool, to propose efficient algorithms that improve some objective performance indicators such as power and energy losses or stability indexes [39], among others.

In this research, the DPL environment is used to implement the CBGA to solve the reactive power flow problem in transmission systems by using recursively the Newton-Raphson power flow tool available in the DigSILENT software [29]. To illustrate a small DPL implementation, the power flow tool is called in the DPL for the IEEE 6-bus system (this system is presented in detail in the following section) to determine the total power losses of the network and report in the output window as can be seen in Figure 2.

It is worth mentioning that to implement the power flow evaluation presented in Figure 2 it is necessary to know about the DPL syntax and possible embedded functions as the case of the FLUJO.execute(), where the word “FLUJO” is a word define by the programmer that is related with the power flow object in the DigSILENT programming tool selection.

For complete details regarding the usage of the DPL environment from DigSILENT, references [29,40] are recommended.

5. Power Systems under Study

In this section are presented the main characteristics of the power test systems under study, being these composed of 6, 14, and 39 nodes, respectively. Note that the latter two systems can be found directly in the DigSILENT test systems; however, to allow future validation of the proposed approach, here, we describe in detail each one of these test systems.

5.1. IEEE 6-Bus System

The electrical configuration of the IEEE 6-bus system is depicted in Figure 3. This system corresponds to a meshed transmission system composed of 5 transmission lines, 2 power transformers, 2 power generators (including the slack node), and 2 capacitive banks. The main characteristics of these devices is listed in

Table 1. Main parameters for the IEEE 6-bus system.

Line Characteristics
Line	Starting	Ending	Line Impedance’s
#	Busbar	Busbar	R($\Omega$)	X($\Omega$)
1	6	3	4.88187	20.55942
2	6	4	3.17520	14.68530
3	4	3	3.84993	16.15383
4	5	2	11.19258	25.40160
5	2	1	28.69587	41.67450
Transformer Characteristics
Transformer	Starting	Ending	Transformer Tap
#	Busbar	Busbar	Settings
1	4	1	9100
2	3	5	9100
Bus-Bar Characteristics
Bus	Load Consumption		Injection Power
#	${\mathit{P}}_{\mathit{L}}$(MW)	${\mathit{Q}}_{\mathit{L}}$(Mvar)	${\mathit{P}}_{\mathit{G}}$(MW)	${\mathit{Q}}_{\mathit{G}}$(Mvar)
1	55	13	0	0
2	0	0	50	0
3	50	5	0	5
4	0	0	0	5
5	30	18	0	0
6	-	-	Slack node

.

Note that in Table 1 were reported all the nominal parameters of the generators, transformers, capacitor banks and loads associated with the IEEE 6-bus system. Note that in the case of the capacitor banks these are modeled with synchronous compensators (see Figure 3) with nominal capabilities of reactive power generation from 0 to 5 Mvar.

Table 2. Characterization of the transformers in the IEEE 6-bus system.

Transformer	Starting	Ending	Voltage	Voltage	Addition Voltage	Voltage
#	Bus-Bar	Bus-Bar	Minimum	Maximum	Per Tap (%)	Range (%)
1	4	1	9100	11,100	0.001	−0.1 ≤ pT ≤ 0.1
2	3	5	9100	11,100	0.001	−0.1 ≤ pT≤ 0.1

presents the main characteristics of the transformers of the IEEE 6-bus system, where variations from $\pm 10\%$ are the maximum range for a safe operation of these transformers. It is worth mentioning that the information provided in Table 2 is required for the proper parametrization of the transformers in the DigSILENT software.

The electrical characterization of the power generators in the IEEE 6-bus system is reported in

Table 3. Characterization of the generators in the IEEE 6-bus system.

Generator	Terminal	${\mathit{v}}_1^{\mathit{g},min}={\mathit{v}}_6^{\mathit{g},min}$ (pu)	${\mathit{v}}_1^{\mathit{g},max}$ (pu)	${\mathit{v}}_6^{\mathit{g},max}$ (pu)
1	2	0.95	1.1	1.15
Slack	6	0.95	1.05	1.1

. Observe that the slack source is assigned to the bus 6 and the voltage-controlled node is assigned to the bus 1. In addition, their minimum voltages are assigned as $0.95$ pu and their maximum bounds are $1.15$ pu, and $1.00$ pu, respectively.

For validating the proposed CBGA implemented in the DPL environment of the DigSILENT software, we consider four different simulation scenarios regarding the voltage output in the slack source. These scenarios are listed in

Table 4. Different voltage outputs and bounds used for IEEE 6-bus system, IEEE 14-bus system and IEEE 39-bus system.

Scenario	${\mathit{v}}_6^{\mathit{g}}$ (pu)	${\mathit{v}}_6^{\mathit{g},max}$ (pu)
Case A1	1.0500	1.1000
Case A2	1.1000	1.1000
Case B1	1.0500	1.1500
Case B2	1.1000	1.1500

.

Note that the main idea of these scenarios is to observe the effect of the voltage variation at the slack bus in the total power losses of the network.

5.2. IEEE 14-Bus System

This test system is composed of four areas with different voltage levels, which are 1 kV, 11 kV, 33 kV, and 132 kV. Each one of these areas are highlighted with different colors in Figure 4. This system is composed of 5 transformers, 16 transmission lines, 2 generators and 3 capacitor banks. The main characteristics of these devices will be specified below.

The parametric information of the transmission lines is listed in

Table 5. Main parameters for the IEEE 14-bus system.

Lines Characteristic
Line	Starting	Ending	Line Impedance’s		Line	Starting	Ending	Line Impedance’s
#	Busbar	Busbar	R ($\Omega$)	X ($\Omega$)	#	Busbar	Busbar	R ($\Omega$)	X ($\Omega$)
1	1	2	6.753542	20.61956	9	6	11	1.034332	2.16602
2	1	2	6.753542	20.61956	10	6	12	1.33849	2.78577
3	1	5	9.414187	38.86250	11	6	13	0.72037	1.41864
4	2	3	8.187537	34.49428	12	9	10	0.34641	0.92020
5	2	4	10.12509	30.72200	13	9	14	1.38422	2.94443
6	2	5	9.922968	30.29685	14	10	11	0.89352	2.09164
7	3	4	11.67582	29.80027	15	12	13	2.40581	2.17669
8	4	5	2.326104	7.33724	16	13	14	1.86142	3.78993
Transformers Characteristic
Trans.	Starting	Ending	Tap		Trans.	Starting	Ending	Tap
#	Busbar	Busbar	Settings		#	Busbar	Busbar	Settings
1	5	6	11,100		4	8	7	11,100
2	4	9	11,100		5	4	7	11,100
3	9	7	11,100
Bus-Bar Characteristics (All Power Units in MW and Mvar)
Bus	Load		Injection		Bus	Load		Injection
#	${\mathit{P}}_{\mathit{L}}$	${\mathit{Q}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{G}}$	${\mathit{P}}_{\mathit{G}}$	#	${\mathit{P}}_{\mathit{L}}$	${\mathit{Q}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{G}}$	${\mathit{P}}_{\mathit{G}}$
1	-	-	Node Slack		8	0.0	0.0	0.0	30.0
2	21.7	12.7	40.0	42.4	9	29.5	16.6	0.0	0.0
3	94.2	19.0	0.0	20.0	10	9.0	5.8	0.0	0.0
4	47.8	−3.9	0.0	0.0	11	3.5	1.8	0.0	0.0
5	7.6	1.6	0.0	0.0	12	6.1	1.6	0.0	0.0
6	11.2	7.5	0.0	20.0	13	13.5	5.8	0.0	0.0
7	0.0	0.0	0.0	20.0	14	14.9	5.0	0.0	0.0

and the information regarding transformers is reported in

Table 6. Characterization of the transformers in the IEEE 14-bus system.

Transformer	Starting	Ending	Voltage	Voltage	Addition Voltage	Voltage
#	Bus-Bar	Bus-Bar	Minimum	Maximum	Per Tap (%)	Range (%)
1	4	7	9100	11,100	0.0022	−2.2 ≤ pT ≤ 2.2
2	4	9	9100	11,100	0.0031	−3.1 ≤ pT ≤ 3.1
3	5	6	9100	11,100	0.0068	−6.8 ≤ pT ≤ 6.8
4	8	7	9100	11,100	0.0068	−6.8 ≤ pT ≤ 6.8
5	9	7	9100	11,100	0.0068	−6.8 ≤ pT ≤ 6.8

. In this system the slack node is assigned to the bus 1 and the generator at node 2 corresponds to a voltage-controlled node. In addition, three capacitor banks are initially installed into the network which are modeled in the continuous domain by using synchronous compensators. These compensators are located in buses 3, 6, and 8; buses 3 and 6 have nominal power of 20 Mvar and the bus 8 have a nominal power of 30 Mvar.

5.3. 39-Bus System

This test system is composed of four areas with different voltage levels, which are 16.5 kV, 138 kV, 230 kV, and 345 kV. Each one of these areas are highlighted with different colors in Figure 5. This system is composed of 12 transformers, 34 transmission lines, and 10 generators.

The main parameters for this test system are listed in

Table 7. Standard power system 39 Bus-Bar.

Lines Characteristic
Line	Starting	Ending	Line Impedance’s		Line	Starting	Ending	Line Impedance’s
#	Busbar	Busbar	R ($\Omega$)	X ($\Omega$)	#	Busbar	Busbar	R ($\Omega$)	X ($\Omega$)
1	1	2	0.025547	0.30	18	13	14	0.026732	0.30
2	1	39	0.012000	0.30	19	14	15	0.024884	0.30
3	2	3	0.025827	0.30	20	15	16	0.028723	0.30
4	2	25	0.244186	0.30	21	16	17	0.023595	0.30
5	3	4	0.018309	0.30	22	16	19	0.024615	0.30
6	3	18	0.024812	0.30	23	16	21	0.017777	0.30
7	4	5	0.018750	0.30	24	16	24	0.015254	0.30
8	4	14	0.018604	0.30	25	17	18	0.025609	0.30
9	5	6	0.023076	0.30	26	17	27	0.022543	0.30
10	5	8	0.021428	0.30	27	21	22	0.017142	0.30
11	6	7	0.019565	0.30	28	22	23	0.018750	0.30
12	6	11	0.025609	0.30	29	23	24	0.018857	0.30
13	7	8	0.026086	0.30	30	25	26	0.029721	0.30
14	8	9	0.019008	0.30	31	26	27	0.028571	0.30
15	9	39	0.012000	0.30	32	26	28	0.027215	0.30
16	10	11	0.027906	0.30	33	26	29	0.027360	0.30
17	10	13	0.027906	0.30	34	28	29	0.027814	0.30
Transformers characteristic
Trans.	Starting	Ending	Tap		Trans.	Starting	Ending	Tap
#	Busbar	Busbar	Settings		#	Busbar	Busbar	Settings
1	2	30	9100		7	19	33	9100
2	6	31	9100		8	20	34	9100
3	10	32	9100		9	22	35	9100
4	11	12	9100		10	23	36	9100
5	13	12	9100		11	25	37	9100
6	19	20	9100		12	29	38	9100
Bus-Bar Characteristics (All Power Units in MW and Mvar)
Bus	Load		Injection		Bus	Load		Injection
#	${\mathit{P}}_{\mathit{L}}$	${\mathit{Q}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{G}}$	${\mathit{P}}_{\mathit{G}}$	#	${\mathit{P}}_{\mathit{L}}$	${\mathit{Q}}_{\mathit{L}}$	${\mathit{P}}_{\mathit{G}}$	${\mathit{P}}_{\mathit{G}}$
3	322.0	2.4	-	-	27	281.0	75.5	-	-
4	500.0	184.0	-	-	28	206.0	27.6	-	-
7	233.8	84.0	-	-	29	283.5	26.9	-	-
8	522.0	176.0	-	-	30	-	-	250	0.0
12	7.5	88.0	-	-	31	9.2	4.6	Node Slack
15	320.0	153.0	-	-	32	-	-	650	0.0
16	329.0	32.3	-	-	33	-	-	632	0.0
18	158.0	30.0	-	-	34	-	-	254	0.0
20	628.0	103.0	-	-	35	-	-	650	0.0
21	274.0	115	-	-	36	-	-	560	0.0
23	247.5	84.6	-	-	37	-	-	540	0.0
24	308.0	−92.2	-	-	38	-	-	830	0.0
25	224.0	47.2	-	-	39	1104	250	1000	0.0
26	139.0	17.0	-	-

and

Table 8. Characterization of the transformers in the IEEE 39-bus system.

Transformer	Starting	Ending	Voltage	Voltage	Addition Voltage	Voltage
#	Bus-Bar	Bus-Bar	Minimum	Maximum	Per Tap (%)	Range (%)
1	02	30	9100	11,100	0.0025	−2.5 ≤ pT ≤ 2.5
2	25	37	9100	11,100	0.0025	−2.5 ≤ pT ≤ 2.5
3	29	38	9100	11,100	0.0025	−2.5 ≤ pT ≤ 2.5
4	22	35	9100	11,100	0.0025	−2.5 ≤ pT ≤ 2.5
5	23	36	9100	11,100	0.0070	−7.0 ≤ pT ≤ 7.0
6	19	33	9100	11,100	0.0070	−7.0 ≤ pT ≤ 7.0
7	20	34	9100	11,100	0.0009	−0.9 ≤ pT ≤ 0.9
8	19	20	9100	11,100	0.0060	−6.0 ≤ pT ≤ 6.0
9	10	32	9100	11,100	0.0070	−7.0 ≤ pT ≤ 7.0
10	13	12	9100	11,100	0.0006	−0.6 ≤ pT ≤ 0.6
11	11	12	9100	11,100	0.0006	−0.6 ≤ pT ≤ 0.6
12	06	31	9100	11,100	0.0070	−7.0 ≤ pT ≤ 7.0

, respectively.

6. Numerical Validation

In this section it is presented all the computational validations of the proposed CBGA implemented in the DPL environment from the DigSILENT software to solve the optimal reactive power flow problem in power systems. These validations were carried out in a personal computer AMD Ryzen 5 3500U processor 2.10 GHz. RAM 8 Gb, with a Windows 10 operating system, single language, 64 bits.

6.1. IEEE 6-Bus System

Table 9. Numerical results for the CBGA implemented in DPL environment from DigSILENT applied to the IEEE 6-bus system.

Elements	Original Values	Case A1	Case A2	Case B1	Case B2
Generators	Voltage (p.u)	Voltage (p.u)		Voltage (p.u)
G1 Bus06(slack)	1.0000	1.0500	1.1000	1.0500	1.1000
G2 Bus02	1.0000	1.0999	1.0999	1.1331	1.1499
Transformers	Position Tap	Position Tap		Position Tap
Trafo Bus 04-01	9100	11,089	9104	11,095	11,099
Trafo Bus 03-05	9100	11,099	11,096	11,097	11,100
Capacitor Bank	Reactive power (Mvar)	Reactive power (Mvar)		Reactive power (Mvar)
PQ Bus03	0.0000	4.9992	4.9987	4.9951	4.9991
PQ Bus04	0.0000	4.9995	4.9992	4.9995	4.9997
Power Losses (MW)	12.910	10.089	9.262	10.014	8.964
Reduction(%)	-	21.85 (%)	28.26 (%)	22.43 (%)	30.56 (%)

presents the results provided by the CBGA in the IEEE 6-bus system considering that in the scenarios A1 and A2 the maximum output voltage was limited to 1.1 pu, while for scenarions B1 and B2, this limit was increased to 1.15 pu. In the case of the slack bus, its voltage outputs were assigned in 1.05 pu for scenarios A1 and A2, and 1.10 pu for scenarios B1 and B2, respectively.

Numerical results in Table 9 show that: (i) for all the simulation scenarios the power losses vary from $21.85\%$ to $30.56\%$; the improvement in the power losses reduction is mainly attributed to the fact that when compared scenarios A1 and A2 with B1 and B2, the voltage in the slack source is increased and the maximum voltage limits are also increased, which are directly related with the reduction of the current magnitudes through the lines and transformers, i.e., related directly with the reduction of the total power losses; (ii) regarding the reactive power injection in the capacitor banks, it is observed that these are closer to the 5 Mvar, which implies that these are assigned to their maximum limit. This situation occurs mainly due to the high inductive load profiles on the grid added with the inductive losses in lines and transformers; (iii) in the case of transformers, these are inclined to the maximum tap position, i.e., 11,100, where the voltage is incremented $0.1\%$ with respect to the nominal voltage output; which as mentioned below implies that the larger the voltage profiles the fewer power losses are achieved.

Table 10. Line chargeability for the IEEE 6-bus system at each simulation scenario.

Line	Original Values	Case A1	Case A2	Case B1	Case B2
(Start–End)	Loading (%)	Loading (%)		Loading (%)
Line 6-3	48.2314	41.2668	39.8269	40.5615	38.5875
Line 6-4	55.8039	47.4526	46.0645	46.4623	44.3956
Line 4-3	10.9207	9.5843	9.0065	9.5818	8.9407
Line 5-2	33.5334	30.4007	28.8446	30.5282	28.7939
Line 1-2	17.4563	16.1338	15.3570	16.3936	15.3563

presents the line chargeability at each simulation scenario. It is worth mentioning that the progressive increments in the voltage profiles for all nodes of the network, effectively, reduce the amount of current flow though the lines.

Note that there are some transmission lines that reduce their chargeability up to 10%; for example, the line 6-4 that passes from an initial condition of 55.80% to 44.40% in the simulation scenario B2; which is translated into an effective reduction of about 20% with respect to the initial operation scenario.

Figure 6 depicts the amount of power losses in kW for each one of the simulation scenarios and its comparison to the benchmark case. Notice that the simulation scenarios A2 and B2 are the cases where the voltage output at the slack node was set at 1.10 pu. In these scenarios is where the most important reductions in power losses are reached, with improvements of about $30\%$ respect to the benchmark case. In addition, for the simulation cases A1 and B1 where the voltage output at the slack node was set at 1.05 pu, the total reduction of power losses with respect to the benchmark case was about 22%.

On the other hand, Figure 7 reports the behavior of the voltage profile at each simulation case including the benchmark case. Note that in general for all the simulation scenarios it is noted the improvement without violating the imposed maximum and minimum voltage regulation bounds.

Some of the buses of the network present important voltage improvements as the case of the bus 5, where the voltage magnitude is $0.83$ pu for the benchmark case, and for all the simulation scenarios, the improvement is reflected between 15% and 22%, with voltage magnitudes between 0.95 pu and 0.9 pu, respectively.

6.2. IEEE 14-Bus System

Table 11. Numerical results for the CBGA implemented in DPL environment from DigSILENT applied to the IEEE 14-bus system.

Elements	Original Values	Case A1	Case A2	Case B1	Case B2
Generators	Voltage (p.u)	Voltage (p.u)		Voltage (p.u)
G1 Bus01(slack)	1.0000	1.0500	1.1000	1.0500	1.1000
G2 Bus02	1.0000	1.0370	1.0860	1.0372	1.0863
Transformers	Position Tap	Position Tap		Position Tap
Trafo Bus 05-06	11,100	9100	9700	9100	9119
Trafo Bus 04-09	11,100	9100	10172	9102	9102
Trafo Bus 09-07	11,100	11,100	10,784	11,097	11,099
Trafo Bus 08-07	11,100	10,415	9100	11,097	9126
Trafo Bus 04-07	11,100	9100	10545	9103	9102
Capacitor Bank	Reactive power (Mvar)	Reactive power (Mvar)		Reactive power (Mvar)
PQ Bus06	0.0000	19.9936	19.7050	19.9951	19.9787
PQ Bus08	0.0000	19.99025	16.9378	19.9928	14.4969
PQ Bus03	0.0000	26.4670	24.6779	26.4815	24.7687
Power Losses (MW)	17.200	13.558	12.278	13.558	12.229
Reduction (%)	-	21.18	28.61	21.17	28.90

reports the optimal reactive power outputs in shunt compensators, voltage outputs in generators, positions of the taps in transformers and the total power losses for each simulation scenario including the benchmark case. Observe that the amount of power losses vary from $21.18\%$ to $28.90\%$ from the scenario A1 to the scenario B2.

When the capacitor banks are observed (being their nominal rates 20 Mvar for the compensator located at nodes PQBus06, and PQBus08, and 30 Mvar for the capacitor at bus PQB03), these are operated not necessarily in their upper bounds. For example, the scenario A2, after the implemetation of the CBGA in the DPL environment, the reactive power outputs in these capacitor banks were $19.70$ Mvar, $16.90$ Mvar, and $24.60$ Mvar, respectively.

Unlike the previous IEEE 6-bus system, where the tap of the transformers was set closer to their maximum values; in the IEEE 14-bus system, the behavior of these taps was different, being these variations mainly conditioned by the voltage outputs in the power generators, since not a particular tendency is evidenced on the transformers. Note that for the scenario A1, where the minimum and maximum bounds for all the tap positions were 9100 and 11,100, respectively, the mean values for the tap positions in this scenario were about 10415. Regarding the voltage outputs, it was observed that in the scenarios A1 and A2 where the maximum voltage bound was set to $1.10$ pu, the power generators provide voltages of $1.03$ pu and $1.08$ pu, respectively. This situation was repeated for the simulation scenarios B1 and B2 where the movement of the maximum voltage bound to $1.15$ pu is not an important effect of the voltage profiles, keeping these very similar to the simulation scenarios A1 and A2. The behavior of the voltage profiles in the different simulation scenarios is mainly attributable to the fact that the IEEE 14-bus system is a high-meshed network where the movement in one of the voltage output in a generator implies large variations in the total power losses.

In

Table 12. Chargeability of Lines for the IEEE 14-bus system.

Line	Original Values	Case A1	Case A2	Case B1	Case B2
(Start–End)	Loading (%)	Loading (%)		Loading (%)
Line 01-02(1)	36.7485	32.9993	31.2504	33.0088	31.2513
Line 01-02(2)	36.7486	32.9993	31.2504	33.0088	31.2513
Line 01-05	33.3443	31.6365	30.0595	31.6359	30.0780
Line 02-03	35.2074	30.8695	29.3896	30.8649	29.3630
Line 02-04	27.7888	23.7087	22.6042	23.7044	22.5725
Line 02-05	21.1140	17.5080	16.6725	17.5044	16.6900
Line 03-04	11.3021	10.4849	9.9690	10.4840	9.9735
Line 04-05	30.5788	27.1440	25.9479	27.1425	25.7359
Line 06-11	13.1368	11.6951	11.3317	11.7005	11.1870
Line 06-12	15.4418	12.7432	12.7043	12.7440	12.1539
Line 06-13	34.6838	29.6405	29.4780	29.6438	28.2752
Line 09-10	28.5486	13.8137	13.4548	13.7931	13.0189
Line 09-14	28.9935	17.4872	17.4476	17.4768	16.5777
Line 10-11	12.4895	6.1880	5.5545	6.1854	5.8933
Line 12-13	2.3032	2.5620	2.5517	2.5636	2.4511
Line 13-14	9.9979	8.8853	8.6183	8.8881	8.4833

is reported the chargeability percentage at each transmission line. For all the simulation scenarios this percentage is reduced with respect to the benchmark case. Note that there are some cases where transmission lines reduce their chargeability up to higher than $50\%$. Notice that line 09-10 passes from $28.54$% in the benchmark case to $13.81\%$ for the simulation scenario A1, and $13.01\%$ for the simulation scenario B2. In addition, the transmission line 12-13 presents a contrary behavior, where the benchmark case shows a chargearbiltiy of about $2.30\%$ and is increased to about $2.56\%$ for simulation cases A1, A2 and B1, and $2.45\%$ for the simulation scenario B2. However, this increment is associated with the load flow redistribution caused by the injection of reactive power with capacitor banks and active and reactive power outputs in generators. This does not increase significantly the amount of power losses, since most of the lines reduce their chargeability, which implies that in conjunction the total grid power losses is minimized.

Figure 8 presents the amount of power losses in the IEEE 14-bus system in kW for all the simulation scenarios including the benchmark case. Note that the simulation cases A2 and B2 where the slack bus was set with an operative voltage of $1.10$ pu, the reduction of power losses are prominent with reductions of about $28.89\%$ with respect to the benchmark case. In the case of the simulation cases A1 and B1, where the voltage output in the slack node was fixed in $1.05$ pu, the average reduction of the power losses with respect to the benchmark case was about 21%. These results show the importance of the effect that has the voltage output in the reference bus, since this directly conditioned the expected power losses in the whole grid.

Figure 9 reports the voltage profile at each bus for all the simulation scenarios, where is evidenced that the optimal reactive power improves these when compared with the benchmark case without violating the lower and upper voltage bounds assigned at each simulation case.

Note that some of the buses show important improvements in their voltage magnitudes as the cases of the buses 12 and 13, which had magnitudes of $0.83$ pu and $0.82$ pu in the benchmark case; however, for all the four simulation scenarios the improvements were about $30\%$, being both buses with a voltage value of $1.08$ pu in the scenario A1, with $v_k^{max}=1.10$ pu; and in scenario B2 the voltage in buses 12 and 13 were $1.10$ pu and $1.13$ pu, respectively, when $v_k^{max}=1.15$ pu. A general conclusion after implementing the CBGA in the DPL environment for the IEEE 14-bus system is that all the voltage profiles present improvements higher than $20\%$ for all the simulation cases when compared with the benchmark case. This is a result from increasing the voltage output in the slack bus, the injection of reactive power through the capacitor banks and the modification of the tap position in all the transformers.

6.3. 39-Bus System

Table 13. Numerical results for the CBGA implemented in DPL environment from DigSILENT applied to the IEEE 39-bus system.

Elements	Original Values	Case A1	Case A2	Case B1	Case B2
Generators	Voltage (p.u)	Voltage (p.u)		Voltage (p.u)
G1 Bus39	1.0000	1.0776	1.0762	1.1262	1.1258
G2 Bus31(slack)	1.0000	1.0500	1.1000	1.0500	1.1000
G3 Bus32	1.0000	10,810	1.0770	1.1370	1.1476
G4 Bus33	1.0000	1.0985	1.0679	1.1149	1.1401
G5 Bus34	1.0000	1.0414	1.0291	1.1393	1.1179
G6 Bus35	1.0000	1.0970	1.0969	1.1485	1.1283
G7 Bus36	1.0000	1.0761	1.0801	1.1079	1.1471
G8 Bus37	1.0000	1.0792	1.0953	1.1188	1.1282
G9 Bus38	1.0000	1.0982	1.0791	1.1474	1.1215
G10 Bus30	1.0000	1.0652	1.0443	1.1406	1.1052
Transformers	Position Tap	Position Tap		Position Tap
Trafo Bus 02-30	9100	10,440	11,092	9474	10,643
Trafo Bus 25-37	9100	10,830	10,420	11,052	10,864
Trafo Bus 29-38	9100	10,021	10,577	9852	10,560
Trafo Bus 22-35	9100	10,214	10,345	10,439	11,030
Trafo Bus 23-36	9100	11,065	10,913	11,095	10,545
Trafo Bus 19-33	9100	10,562	11,077	10,474	10,399
Trafo Bus 20-34	9100	9648	10,974	11,082	10,424
Trafo Bus 19-20	9100	10,729	10,542	11,087	10,737
Trafo Bus 10-32	9100	11,037	10,864	10,759	10,548
Trafo Bus 13-12	9100	10,725	9663	11,093	10,968
Trafo Bus 11-12	9100	10,085	11,007	9107	10,228
Trafo Bus 06-31	9100	11,058	10,986	11,090	11,086
Power Losses (MW)	38.790	26.476	26.288	24.533	24.197
Reduction(%)	-	31.75(%)	32.23(%)	36.75(%)	37.62(%)

reports the solutions reached by the proposed CBGA in the DPL environment from DigSILENT for the IEEE 39-bus system. Note that for all the simulation cases were obtained reductions in the total grid power losses from $31.75\%$ to $37.62\%$.

An important fact is that this system does not include in their topology reactive power compensators; however, due to the presence of 12 transformers and 9 power sources, with the proposed CBGA is possible to reach an optimal combination of the tap positions and voltage outputs that allows to achieve general power losses reduction higher than $30\%$ when compared to the benchmark case.

Regarding the tap positions in the transformers, there is no evidence of a general tendency towards the upper or lower bounds, and these are distributed in all the operative range. This situation is mainly justified on the high meshed connection of this system where the movement of one voltage magnitude in a particular node produces important effects on the grid. In addition, when the voltage output in the slack bus was set to $1.05$ pu and $1.10$ pu in the scenarios A1 and A2 with a maximum voltage regulation limit of $1.10$ pu, it is possible to observe that all the voltage profiles in the whole grid are between 1.02 pu and 1.098 pu, respectively.

Table 14. Chargeability of the lines for the IEEE 39-bus system.

Lines (Start End)	Original	Cases				Lines	Original	Cases
	Values	A1	A2	B1	B2	(Start	Values	A1	A2	B1	B2
	Loading (%)	Loading (%)		Loading (%)		End)	Loading (%)	Loading (%)		Loading (%)
L 01-02	31.59	21.96	21.67	21.62	21.30	L 13-14	52.33	44.16	43.64	41.63	41.43
L 01-39	24.68	24.10	24.37	23.99	24.28	L 14-15	5.24	8.08	9.85	3.46	7.10
L 02-03	71.58	56.83	57.08	54.51	54.56	L 15-16	62.73	51.76	51.11	51.10	49.73
L 02-25	44.42	37.91	37.73	36.35	36.25	L 16-17	46.88	35.56	35.50	34.00	34.02
L 03-04	30.80	16.90	15.50	19.21	16.36	L 16-19	92.55	77.72	77.49	74.46	74.31
L 03-18	13.07	9.09	8.52	10.33	9.17	L 16-21	60.79	51.61	51.60	49.06	49.29
L 04-05	27.64	22.77	25.46	20.17	21.73	L 16-24	17.58	17.71	17.09	17.57	16.78
L 04-14	50.52	43.94	42.92	42.84	41.74	L 17-18	38.43	32.67	32.33	31.81	31.31
L 05-06	86.27	72.23	73.42	68.19	68.65	L 17-27	13.80	6.22	5.65	6.82	5.87
L 05-08	59.16	50.89	50.62	48.88	48.50	L 21-22	112.76	93.69	93.62	89.76	89.52
L 06-07	79.22	67.63	67.51	64.71	64.42	L 22-23	22.76	11.75	9.69	7.52	8.43
L 06-11	67.12	58.46	56.15	58.76	55.13	L 23-24	64.03	54.10	54.02	51.68	51.66
L 07-08	35.66	29.40	29.55	28.05	27.99	L 25-26	16.42	12.67	12.15	12.92	12.24
L 08-09	37.89	12.25	9.11	15.55	11.51	L 26-27	51.42	41.54	41.21	39.85	39.45
L 09-39	32.02	17.00	20.27	14.84	19.02	L 26-28	25.38	23.51	23.84	22.99	23.50
L 10-11	67.60	59.44	56.78	59.09	55.72	L 26-29	33.93	31.49	31.83	30.81	31.33
L 10-13	54.52	46.93	45.33	44.66	43.85	L 28-29	60.76	53.79	54.01	51.82	52.15

presents the percentage of chargeability of each one of the transmission lines in all the simulation cases for the IEEE 39-bus system. In general, all the lines present a reduction larger than $40\%$ of their chargeability when compared with the benchmark case. Notice the case of the line 03-04 that passes from $30.80\%$ of loadability in the benchmark case to $16.90\%$ for the scenario A1 and $15.50\%$ for the scenario A2, respectively. In addition, observe that the line 14-15 presents an increment in its loadability that passes from $5.24\%$ in the benchmark case to the $9.80\%$ in the scenario A2. This behavior is expected in power systems since the redistribution of the power flow through the lines implies that some of the lines with low loadability increases their power flow; however, these increments do not affect the objective function and in general, this reaches its optimum value.

On the other hand, in Figure 10 it is reported the amount of power losses in kW for the IEEE 39-bus system in the benchmark case and the proposed simulation scenarios. Note that scenarios B1 and B2 present higher reductions with respect to the benchmark case which are about 37%. These results are justified in the fact that for these simulation cases all the maximum voltage limit is $1.15$ pu, while for scenarios A1 and A2 this limit is $1.10$ pu. This implies that without the presence of capacitor banks, the unique form to reduce the total power losses on the whole grid is via increasing the voltage outputs in all the generators.

Finally, Figure 11 reports the voltage profile performance for all the nodes in all the simulation scenarios including the benchmark case. Note that all the voltage profiles remain within their bounds for each scenario; which implies that the proposed CBGA ensures the feasibility of the solution with high-quality regarding the objective function value.

In the IEEE 39-bus system, some of the buses present important improvements in their voltage profiles. See the nodes 10 and 12, which in the benchmark case have voltage values of $0.90$ pu and $0.97$ pu; nevertheless, for all the simulation scenarios these were improved in more than $20\%$ reaching values of 1.09 pu and 1.07 pu in the scenario A1 and, 1.13 pu and 1.11 pu for the scenario B1, respectively. It is worth mentioning that in general the improvement of the voltage profiles of the nodes was about 15% in the four studied scenarios of simulation.

6.4. Processing Times

To demonstrate the effectiveness and robustness of the proposed CBGA implemented in the DPL environment from DigSILENT to resolve the optimal reactive power flow problem in transmission networks, we report in

Table 15. Average processing times for all the IEEE bus systems in the four studied scenarios.

Topology	Case A1 (s)	Case A2 (s)	Case B1 (s)	Case B2 (s)
IEEE 6-bus system	30.4	32.2	33.1	33.6
IEEE 14-bus system	48.2	48.6	48.7	52.3
IEEE 39-bus system	134.6	136.2	142.2	142.5

the average processing times for all the IEEE bus systems.

Note that as is expected, when the number of nodes increases, the total processing times are increased due to computational effort in the power flow evaluation considering that the number of the decision variables is directly related to the size of the power system under study. Note that the average time for all the simulation cases is $32.33$ s for the IEEE 6-bus system, $49.45$ s for the IEEE 14-bus system, and $138.88$ s for the IEEE 39-bus system, respectively. Note that for calculating these processing times, the proposed CBGA was evaluated 100 times per simulation scenario; in addition, the proposed CBGA was set with a random population of 1000 individuals, which is ordered to obtain the best 20 individuals that define the initial population, and 10,000 iterations are considered during the exploration and exploitation of the solution space. It is worth mentioning that all the descending individuals are crossed and mutated.

7. Conclusions

The optimal reactive power flow problem in transmission systems was addressed in this research from the point of view of the combinatorial optimization by implementing a CBGA in DPL environment from DigSILENT software. The main advantage of using the DPL is that all the functionalities of the DigSILENT software for system modeling and power calculations can be easily used with its own programming objects. The computational validations of the proposed solution methodology was carried-out in three IEEE power systems composed of 6, 14 and 39 buses, considering as optimization variables the voltage outputs in generators, tap position in transformers and reactive power injection in capacitor Banks. Four simulation scenarios were considered with the modification on the voltage in the slack bus and the maximum voltage regulation bounds, with the purpose of validating the effectiveness of the proposed CBGA in the DPL environment.

Numerical results in all the three IEEE test systems demonstrated that the percentage of reduction for the power losses was within $21.17\%$ to $37.62\%$ with respect to benchmark case. In the case of the IEEE 6-bus system the minimum and maximum reductions were 21.85% and 30.56% for the scenarios A1 and B2; the IEEE 14-bus system reported 21.17% and 28.90% for the scenarios B1 and B2 (21.18% for the scenario A1) and in the IEEE 39-bus systems these values were $31.65\%$ and $37.62\%$ for scenarios A1 and B2, respectively. It was noted that the voltage magnitude in the slack node strongly conditioned the percentage of power losses reduction, since for scenarios A1 and B1 where the slack was fixed in 1.05 pu, the reduction of power losses were considerably less than the scenarios A2 and B2 where were set in 1.10 pu, respectively.

The loadability of the transmission lines was in general reduced for all the test systems with average values between $10\%$ for the IEEE 6-bus and IEEE 14-bus systems, and $40\%$, with two particular cases in the IEEE 14- and 39-bus systems, where the chargeability in some lines with low loadability <5% increase their values up to $10\%$ at most. This behavior is explained due to the power flow redistribution of the variations in the power injections in generators, tap positions in transformers and reactive power injections in capacitor banks.

As future works it will be possible to develop the following researches: (i) to implement recent developed discrete-continuous algorithms such as the vortex search algorithm and the sine cosine algorithm to solve the problem addressed in this study; and (ii) to implement in the DPL environment from DigSILENT a solution for the problem of the optimal reactive power compensation using STATCOMs and fixed-step capacitor banks.