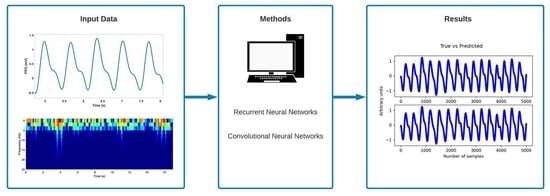
The Application of Deep Learning Algorithms for PPG Signal Processing and Classification
Abstract
:1. Introduction
Related Work
2. Materials and Methods
2.1. Data Acquisition and Pre-Processing
2.2. Feature Extraction Using Time-Frequency Analysis
2.3. Proposed Models
2.4. Evaluated Metrics
3. Results
3.1. LSTM and BiLSTM with PPG Input
Testing and Improvements
3.2. BiLSTM with SSFT Input
3.3. CNN-LSTM with PPG Input
3.4. CNN-LSTM with SSFT Input
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef] [Green Version]
- Elgendi, M. On the Analysis of Fingertip Photoplethysmogram Signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef]
- Ram, M.R.; Madhav, K.V.; Krishna, E.H.; Komalla, N.R.; Reddy, K.A. A Novel Approach for Motion Artifact Reduction in PPG Signals Based on AS-LMS Adaptive Filter. IEEE Trans. Instrum. Meas. 2012, 61, 1445–1457. [Google Scholar] [CrossRef]
- Jang, D.-G.; Park, S.; Hahn, M.; Park, S.-H. A Real-Time Pulse Peak Detection Algorithm for the Photoplethysmogram. Int. J. Electron. Electr. Eng. 2014, 45–49. [Google Scholar] [CrossRef]
- Argüello-Prada, E.J. The mountaineer’s method for peak detection in photoplethysmographic signals. Rev. Fac. Ing. Univ. Antioquia 2019, 90, 42–50. [Google Scholar] [CrossRef] [Green Version]
- Vadrevu, S.; Manikandan, M.S. A Robust Pulse Onset and Peak Detection Method for Automated PPG Signal Analysis System. IEEE Trans. Instrum. Meas. 2019, 68, 807–817. [Google Scholar] [CrossRef]
- Siontis, K.C.; Noseworthy, P.A.; Attia, Z.I.; Friedman, P.A. Artificial intelligence-enhanced electrocardiography in cardiovascular disease management. Nat. Rev. Cardiol. 2021, 18, 465–478. [Google Scholar] [CrossRef] [PubMed]
- Tamura, T. Current progress of photoplethysmography and SPO2 for health monitoring. Biomed. Eng. Lett. 2019, 9, 21–36. [Google Scholar] [CrossRef]
- Cardoso, F.E.; Vassilenko, V.; Batista, A.; Bonifácio, P.; Martin, S.R.; Muñoz-Torrero, J.; Ortigueira, M. Improvements on Signal Processing Algorithm for the VOPITB Equipment. In Proceedings of the DoCEIS: Doctoral Conference on Computing, Electrical and Industrial Systems, Costa de Caparica, Portugal, 7–9 July 2021; pp. 324–330. [Google Scholar] [CrossRef]
- Ribeiro, A.H.; Ribeiro, M.H.; Paixão, G.M.; Oliveira, D.M.; Gomes, P.R.; Canazart, J.A.; Ferreira, M.P.; Andersson, C.R.; Macfarlane, P.W.; Wagner, M., Jr.; et al. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat. Commun. 2020, 11, 1760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Soltane, M.; Ismail, M.; Rashid, Z.A.A. Artificial Neural Networks (ANN) Approach to PPG Signal Classification. Int. J. Comput. Inf. Sci. 2004, 2, 58. [Google Scholar]
- Liu, S.-H.; Li, R.-X.; Wang, J.-J.; Chen, W.; Su, C.-H. Classification of Photoplethysmographic Signal Quality with Deep Convolution Neural Networks for Accurate Measurement of Cardiac Stroke Volume. Appl. Sci. 2020, 10, 4612. [Google Scholar] [CrossRef]
- Yen, C.-T.; Chang, S.-N.; Liao, C.-H. Deep learning algorithm evaluation of hypertension classification in less photoplethysmography signals conditions. Meas. Control 2021, 54, 439–445. [Google Scholar] [CrossRef]
- Song, S.B.; Nam, J.W.; Kim, J.H. NAS-PPG: PPG-Based Heart Rate Estimation Using Neural Architecture Search. IEEE Sens. J. 2021, 21, 14941–14949. [Google Scholar] [CrossRef]
- Alessandrini, M.; Biagetti, G.; Crippa, P.; Falaschetti, L.; Turchetti, C. Recurrent Neural Network for Human Activity Recognition in Embedded Systems Using PPG and Accelerometer Data. Electronics 2021, 10, 1715. [Google Scholar] [CrossRef]
- Li, Y.-H.; Harfiya, L.N.; Purwandari, K.; Lin, Y.-D. Real-Time Cuffless Continuous Blood Pressure Estimation Using Deep Learning Model. Sensors 2020, 20, 5606. [Google Scholar] [CrossRef]
- Laitala, J.; Jiang, M.; Syrjälä, E.; Naeini, E.K.; Airola, A.; Rahmani, A.M.; Dutt, N.D.; Liljeberg, P. Robust ECG R-peak detection using LSTM. In Proceedings of the 35th Annual ACM Symposium on Applied Computing, Brno, Czech Republic, 30 March–3 April 2020; pp. 1104–1111. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.-H.; Pyun, J.-Y. ECG Identification for Personal Authentication Using LSTM-Based Deep Recurrent Neural Networks. Sensors 2020, 20, 3069. [Google Scholar] [CrossRef] [PubMed]
- Malali, A.; Hiriyannaiah, S.; Siddesh, G.M.; Srinivasa, K.G.; Sanjay, N.T. Supervised ECG wave segmentation using convolutional LSTM. ICT Express 2020, 6, 166–169. [Google Scholar] [CrossRef]
- Liang, Y.; Yin, S.; Tang, Q.; Zheng, Z.; Elgendi, M.; Chen, Z. Deep Learning Algorithm Classifies Heartbeat Events Based on Electrocardiogram Signals. Front. Physiol. 2020, 11, 569050. [Google Scholar] [CrossRef]
- Ruffini, G.; Ibañez, D.; Castellano, M.; Dubreuil-Vall, L.; Soria-Frisch, A.; Postuma, R.; Gagnon, J.-F.; Montplaisir, J. Deep Learning with EEG Spectrograms in Rapid Eye Movement Behavior Disorder. Front. Neurol. 2019, 10, 806. [Google Scholar] [CrossRef] [Green Version]
- Boashash, B. Time-Frequency Signal Analysis and Processing; Academic Press: London, UK, 2016. [Google Scholar]
- Alam, M.Z.; Rahman, M.S.; Parvin, N.; Sobhan, M.A. Time-frequency representation of a signal through non-stationary multipath fading channel. In Proceedings of the 2012 International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 18–19 May 2012; pp. 1130–1135. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.; Cao, Z.; Chen, Q.; Xiao, W. Extreme Learning Machine for Heartbeat Classification with Hybrid Time-Domain and Wavelet Time-Frequency Features. J. Healthc. Eng. 2021, 2021, 6674695. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.; Murray, A. Effects of filtering on multi-site photoplethysmography pulse waveform characteristics. In Proceedings of the Computers in Cardiology, Chicago, IL, USA, 19–22 September 2004; pp. 485–488. [Google Scholar] [CrossRef]
- Béres, S.; Hejjel, L. The minimal sampling frequency of the photoplethysmogram for accurate pulse rate variability parameters in healthy volunteers. Biomed. Signal Process. Control 2021, 68, 102589. [Google Scholar] [CrossRef]
- Gasparini, F.; Grossi, A.; Bandini, S. A Deep Learning Approach to Recognize Cognitive Load using PPG Signals. In Proceedings of the 14th PErvasive Technologies Related to Assistive Environments Conference, Corfu, Greece, 29 June–2 July 2021; pp. 489–495. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P.; Lin, Y.-T.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.-T. Time-Frequency Reassignment and Synchrosqueezing: An Overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Salamon, J.; Bello, J.P. Deep Convolutional Neural Networks and Data Augmentation for Environmental Sound Classification. IEEE Signal Process. Lett. 2017, 24, 279–283. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Thakur, G.; Wu, H.-T. Synchrosqueezing-Based Recovery of Instantaneous Frequency from Nonuniform Samples. SIAM J. Math. Anal. 2011, 43, 2078–2095. [Google Scholar] [CrossRef] [Green Version]
- Saadatnejad, S.; Oveisi, M.; Hashemi, M. LSTM-Based ECG Classification for Continuous Monitoring on Personal Wearable Devices. IEEE J. Biomed. Health Inform. 2020, 24, 515–523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Azar, J.; Makhoul, A.; Couturier, R.; Demerjian, J. Deep recurrent neural network-based autoencoder for photoplethysmogram artifacts filtering. Comput. Electr. Eng. 2021, 92, 107065. [Google Scholar] [CrossRef]
- Hu, J.; Wang, X.; Zhang, Y.; Zhang, D.; Zhang, M.; Xue, J. Time Series Prediction Method Based on Variant LSTM Recurrent Neural Network. Neural Process. Lett. 2020, 52, 1485–1500. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Fredriksson, D.; Glandberger, O. Neural Network Regularization for Generalized Heart Arrhythmia Classification. Master’s Thesis, Blekinge Institute of Technology, Karlshamn, Sweden, 2020. [Google Scholar]
- Singh, A.; Saimbhi, A.S.; Singh, N.; Mittal, M. DeepFake Video Detection: A Time-Distributed Approach. SN Comput. Sci. 2020, 1, 212. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Elkan, C.; Naryanaswamy, B. Optimal Thresholding of Classifiers to Maximize F1 Measure. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Nancy, France, 14–18 September 2014; pp. 225–239. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Sun, W.; Zhao, H.; Jin, Z. A facial expression recognition method based on ensemble of 3D convolutional neural networks. Neural Comput. Appl. 2019, 31, 2795–2812. [Google Scholar] [CrossRef]








| Parameters | Value |
|---|---|
| Loss Function | Categorical-cross entropy |
| Optimizer | Adam and SGD 1 |
| Hidden Activation Function | Sigmoid and Tanh |
| Dropout Rate | 0.4 |
| Learning Rate | 10−2, 10−3, 10−4, 10−5 and 10−6 |
| Model | Number of Neurons in Each Layer | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | |
|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | |||||||
| L-D-S | 32 | - | 50 | 10,000 | 0.719 | 0.743 | 0.947 | 0.833 |
| L-TD(D)-S | 50 | - | 50 | 40,000 | 0.709 | 0.759 | 0.897 | 0.822 |
| L-TD(D)-S | 200 | - | 50 | 40,000 | 0.719 | 0.757 | 0.919 | 0.830 |
| L-L-TD(D)-S | 8 | 16 | 50 | 40,000 | 0.724 | 0.755 | 0.934 | 0.835 |
| L-L-TD(D)-S | 16 | 32 | 50 | 40,000 | 0.718 | 0.758 | 0.917 | 0.830 |
| L-L-TD(D)-S | 32 | 64 | 50 | 40,000 | 0.720 | 0.757 | 0.922 | 0.831 |
| L-L-TD(D)-S | 32 | 64 | 50 | 20,000 | 0.712 | 0.766 | 0.886 | 0.822 |
| L-L-TD(D)-S | 256 | 128 | 100 | 70,000 | 0.733 | 0.760 | 0.940 | 0.840 |
| B-TD(D)-S | 50 | - | 50 | 40,000 | 0.744 | 0.751 | 0.982 | 0.851 |
| B-TD(D)-S | 200 | - | 50 | 40,000 | 0.730 | 0.756 | 0.965 | 0.848 |
| B-B-TD(D)-S | 8 | 16 | 50 | 40,000 | 0.744 | 0.750 | 0.986 | 0.852 |
| B-B-TD(D)-S | 16 | 32 | 50 | 40,000 | 0.740 | 0.751 | 0.976 | 0.849 |
| B-B-TD(D)-S | 32 | 64 | 50 | 40,000 | 0.729 | 0.755 | 0.945 | 0.839 |
| B-B-TD(D)-S | 32 | 64 | 50 | 20,000 | 0.739 | 0.752 | 0.973 | 0.848 |
| B-B-TD(D)-S | 256 | 128 | 100 | 70,000 | 0.744 | 0.756 | 0.971 | 0.850 |
| Model | Optimizer | Number of Neurons in Each Layer | Weights | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Opt. | LR | 1st | 2nd | 3rd | ||||||||
| L-L-TD(D)-S | A | 10−3 | 16 | 32 | - | - | 20 | 40,000 | 0.627 | 0.771 | 0.715 | 0.742 |
| L-L-TD(D)-S | A | 10−3 | 16 | 32 | - | SW | 20 | 40,000 | 0.551 | 0.796 | 0.539 | 0.643 |
| L-L-TD(D)-S | A | 10−3 | 16 | 32 | - | SW | 20 | 8000 | 0.574 | 0.796 | 0.581 | 0.672 |
| L-L-TD(D)-S | A | 10−3 | 16 | 32 | - | SW | 200 | 1000 | 0.612 | 0.788 | 0.659 | 0.718 |
| L-L-TD(D)-S | SGD | 10−4 | 32 | 64 | - | SW | 50 | 40,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-TD(D)-S | SGD | 10−5 | 32 | 64 | - | SW | 20 | 40,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-TD(D)-S | SGD | 10−5 | 32 | 64 | - | SW | 50 | 40,000 | 0.614 | 0.741 | 0.745 | 0.743 |
| L-L-TD(D)-S | SGD | 10−6 | 32 | 64 | - | SW | 50 | 40,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-L-TD(D)-S | A | 10−3 | 16 | 32 | 16 | - | 20 | 20,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-L-TD(D)-S | A | 10−3 | 32 | 64 | 32 | - | 20 | 20,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-L-TD(D)-S | A | 10−3 | 64 | 128 | 64 | - | 20 | 20,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| L-L-L-TD(D)-S | SGD | 10−4 | 32 | 64 | 32 | SW | 50 | 40,000 | 0.730 | 0.754 | 0.949 | 0.840 |
| L-L-L-TD(D)-S | SGD | 10−5 | 32 | 64 | 32 | SW | 50 | 20,000 | 0.563 | 0.738 | 0.647 | 0.690 |
| L-L-L-TD(D)-S | SGD | 10−5 | 32 | 64 | 32 | SW | 50 | 40,000 | 0.603 | 0.728 | 0.750 | 0.739 |
| L-L-L-TD(D)-S | SGD | 10−6 | 32 | 64 | 32 | SW | 50 | 40,000 | 0.668 | 0.741 | 0.855 | 0.794 |
| Model | Hidden Activation Function | Number of Neurons in Each Layer | Weights | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | |||||||||
| B-B-TD(D)-S | Sigmoid | 50 | - | - | SW | 100 | 40,000 | 0.737 | 0.753 | 0.966 | 0.846 |
| B-B-TD(D)-S | Sigmoid | 200 | - | - | SW | 100 | 40,000 | 0.691 | 0.762 | 0.854 | 0.805 |
| B-B-TD(D)-S | Sigmoid | 16 | 32 | - | SW | 100 | 40,000 | 0.717 | 0.766 | 0.896 | 0.826 |
| B-B-TD(D)-S | Sigmoid | 16 | 32 | - | - | 10 | 40,000 | 0.683 | 0.744 | 0.881 | 0.807 |
| B-B-TD(D)-S | Tanh | 16 | 32 | - | - | 5 | 40,000 | 0.691 | 0.745 | 0.894 | 0.813 |
| B-B-TD(D)-S | Tanh | 16 | 32 | - | - | 10 | 40,000 | 0.731 | 0.749 | 0.964 | 0.843 |
| B-B-TD(D)-S | Tanh | 16 | 32 | - | SW | 20 | 20,000 | 0.737 | 0.752 | 0.969 | 0.847 |
| B-B-TD(D)-S | Tanh | 16 | 32 | - | SW | 10 | 40,000 | 0.713 | 0.759 | 0.903 | 0.825 |
| B-B-TD(D)-S | Sigmoid | 32 | 64 | - | SW | 100 | 40,000 | 0.730 | 0.761 | 0.931 | 0.837 |
| B-B-TD(D)-S | Sigmoid | 32 | 64 | - | - | 10 | 40,000 | 0.703 | 0.746 | 0.913 | 0.821 |
| B-B-TD(D)-S | Tanh | 32 | 64 | - | - | 10 | 40,000 | 0.599 | 0.765 | 0.671 | 0.715 |
| B-B-TD(D)-S | Tanh | 32 | 64 | - | SW | 40 | 40,000 | 0.727 | 0.756 | 0.939 | 0.838 |
| B-B-TD(D)-S | Tanh | 64 | 128 | - | SW | 100 | 20,000 | 0.739 | 0.758 | 0.957 | 0.846 |
| B-B-B-TD(D)-S | Tanh | 16 | 32 | 16 | SW | 40 | 20,000 | 0.708 | 0.766 | 0.878 | 0.818 |
| B-B-B-TD(D)-S | Tanh | 16 | 32 | 16 | - | 100 | 15,000 | 0.749 | 0.749 | 1.000 | 0.856 |
| B-B-B-TD(D)-S | Tanh | 16 | 32 | 16 | SW | 100 | 15,000 | 0.729 | 0.762 | 0.928 | 0.837 |
| B-B-B-TD(D)-S | Tanh | 64 | 128 | 64 | SW | 100 | 20,000 | 0.745 | 0.757 | 0.965 | 0.848 |
| B-B-B-TD(D)-S | Sigmoid | 64 | 128 | 64 | SW | 100 | 20,000 | 0.733 | 0.754 | 0.955 | 0.843 |
| B-B-B-TD(D)-S | Sigmoid | 64 | 128 | 64 | - | 100 | 20,000 | 0.743 | 0.757 | 0.968 | 0.850 |
| Model | Hidden Activation Function | Number of Neurons in Each Layer | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | ||||||||
| B-B-TD(D)-S | Sigmoid | 16 | 32 | - | 100 | 40,000 | 0.723 | 0.742 | 0.961 | 0.837 |
| B-B-TD(D)-S | Tanh | 16 | 32 | - | 100 | 40,000 | 0.734 | 0.770 | 0.847 | 0.807 |
| B-B-TD(D)-S | Sigmoid | 32 | 64 | - | 100 | 20,000 | 0.713 | 0.791 | 0.762 | 0.776 |
| B-B-TD(D)-S | Tanh | 32 | 64 | - | 100 | 20,000 | 0.713 | 0.791 | 0.763 | 0.777 |
| B-B-TD(D)-S | Tanh | 256 | 512 | - | 10 | 20,000 | 0.735 | 0.767 | 0.855 | 0.809 |
| B-B-B-TD(D)-S | Sigmoid | 16 | 32 | 16 | 100 | 20,000 | 0.724 | 0.784 | 0.798 | 0.791 |
| B-B-B-TD(D)-S | Tanh | 16 | 32 | 16 | 100 | 20,000 | 0.735 | 0.768 | 0.855 | 0.809 |
| B-B-B-TD(D)-S | Sigmoid | 32 | 64 | 32 | 100 | 20,000 | 0.734 | 0.769 | 0.849 | 0.807 |
| B-B-B-TD(D)-S | Tanh | 32 | 64 | 32 | 100 | 20,000 | 0.736 | 0.764 | 0.862 | 0.810 |
| B-B-B-TD(D)-S | Tanh | 256 | 512 | 256 | 10 | 20,000 | 0.732 | 0.772 | 0.846 | 0.807 |
| Model | Loss Function | Number of Neurons in Each Layer | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | ||||||||
| C-MP-B-L-TD(D) | MSE | 16 | 8 | 4 | 10 | 60 | 0.669 | 0.742 | 0.857 | 0.795 |
| C-MP-B-L-TD(D) | MSE | 32 | 16 | 8 | 10 | 60 | 0.646 | 0.740 | 0.813 | 0.775 |
| C-MP-B-L-TD(D) | Categorical | 16 | 8 | 4 | 10 | 60 | 0.619 | 0.741 | 0.756 | 0.748 |
| C-MP-B-L-TD(D) | Categorical | 32 | 16 | 8 | 10 | 60 | 0.670 | 0.742 | 0.856 | 0.795 |
| C-MP-B-L-TD(D) | MSE | 16 | 8 | 4 | 30 | 60 | 0.719 | 0.749 | 0.939 | 0.833 |
| C-MP-B-L-TD(D) | MSE | 32 | 16 | 8 | 30 | 60 | 0.679 | 0.745 | 0.870 | 0.803 |
| C-MP-B-L-TD(D) | Categorical | 16 | 8 | 4 | 30 | 60 | 0.675 | 0.744 | 0.864 | 0.800 |
| C-MP-B-L-TD(D) | Categorical | 32 | 16 | 8 | 30 | 60 | 0.657 | 0.742 | 0.831 | 0.784 |
| Model | Number of Neurons in Each Layer | Weights | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | ||||||||
| C-MP-B-L-TD(D) | 32 | 64 | 32 | - | 20 | 30 | 0.800 | 0.801 | 0.907 | 0.851 |
| C-MP-B-L-TD(D) | 32 | 64 | 32 | SW | 20 | 30 | 0.752 | 0.792 | 0.841 | 0.816 |
| C-MP-B-L-TD(D) | 32 | 64 | 32 | - | 50 | 100 | 0.771 | 0.788 | 0.889 | 0.835 |
| C-MP-B-L-TD(D) | 32 | 64 | 32 | - | 100 | 50 | 0.804 | 0.805 | 0.925 | 0.861 |
| C-MP-B-L-TD(D) | 64 | 128 | 64 | - | 200 | 50 | 0.894 | 0.923 | 0.914 | 0.918 |
| C-MP-B-L-TD(D) | 256 | 64 | 48 | - | 20 | 30 | 0.800 | 0.810 | 0.907 | 0.856 |
| C-MP-B-L-TD(D) | 256 | 128 | 64 | SW | 20 | 30 | 0.787 | 0.813 | 0.877 | 0.844 |
| Model | Number of Neurons in Each Layer | Data Input | Epochs | Batch-Size | Accuracy | Precision | Recall | F1-Score | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | ||||||||
| B-B-B-TD(D)-S | 64 | 128 | 64 | PPG | 100 | 20,000 | 0.745 | 0.757 | 0.965 | 0.848 |
| B-B-B-TD(D)-S | 32 | 64 | 32 | SSFT | 100 | 20,000 | 0.736 | 0.764 | 0.862 | 0.810 |
| C-MP-B-L-TD(D) | 16 | 8 | 4 | PPG | 30 | 60 | 0.719 | 0.749 | 0.939 | 0.833 |
| C-MP-B-L-TD(D) | 64 | 128 | 64 | SSFT | 200 | 50 | 0.894 | 0.923 | 0.914 | 0.918 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esgalhado, F.; Fernandes, B.; Vassilenko, V.; Batista, A.; Russo, S. The Application of Deep Learning Algorithms for PPG Signal Processing and Classification. Computers 2021, 10, 158. https://doi.org/10.3390/computers10120158
Esgalhado F, Fernandes B, Vassilenko V, Batista A, Russo S. The Application of Deep Learning Algorithms for PPG Signal Processing and Classification. Computers. 2021; 10(12):158. https://doi.org/10.3390/computers10120158
Chicago/Turabian StyleEsgalhado, Filipa, Beatriz Fernandes, Valentina Vassilenko, Arnaldo Batista, and Sara Russo. 2021. "The Application of Deep Learning Algorithms for PPG Signal Processing and Classification" Computers 10, no. 12: 158. https://doi.org/10.3390/computers10120158
APA StyleEsgalhado, F., Fernandes, B., Vassilenko, V., Batista, A., & Russo, S. (2021). The Application of Deep Learning Algorithms for PPG Signal Processing and Classification. Computers, 10(12), 158. https://doi.org/10.3390/computers10120158