Approximator: A Software Tool for Automatic Generation of Approximate Arithmetic Circuits
Abstract
:1. Introduction
2. Approximate Adders
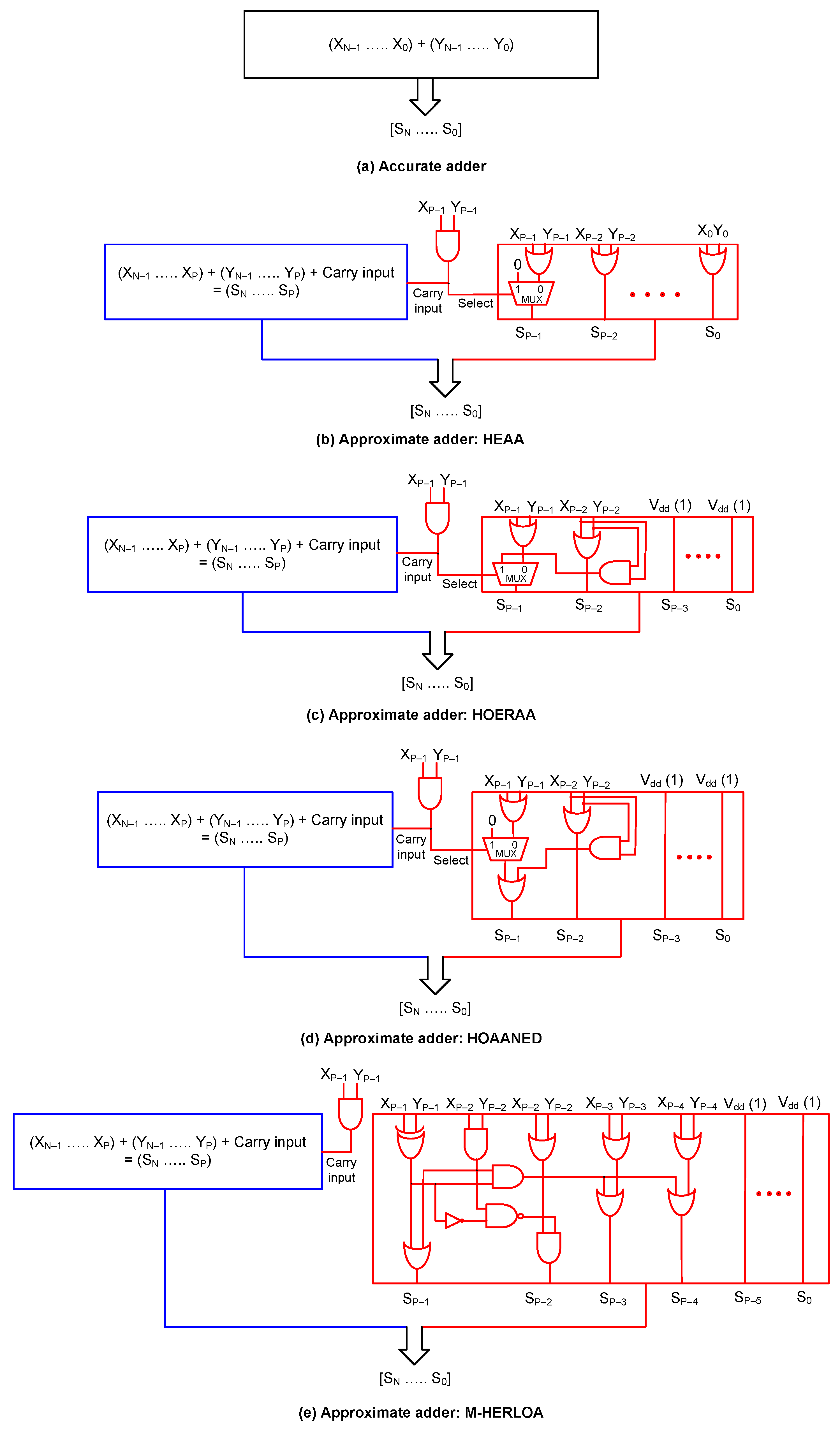
2.1. Approximate Adders—Architectures
2.2. Image Processing Application
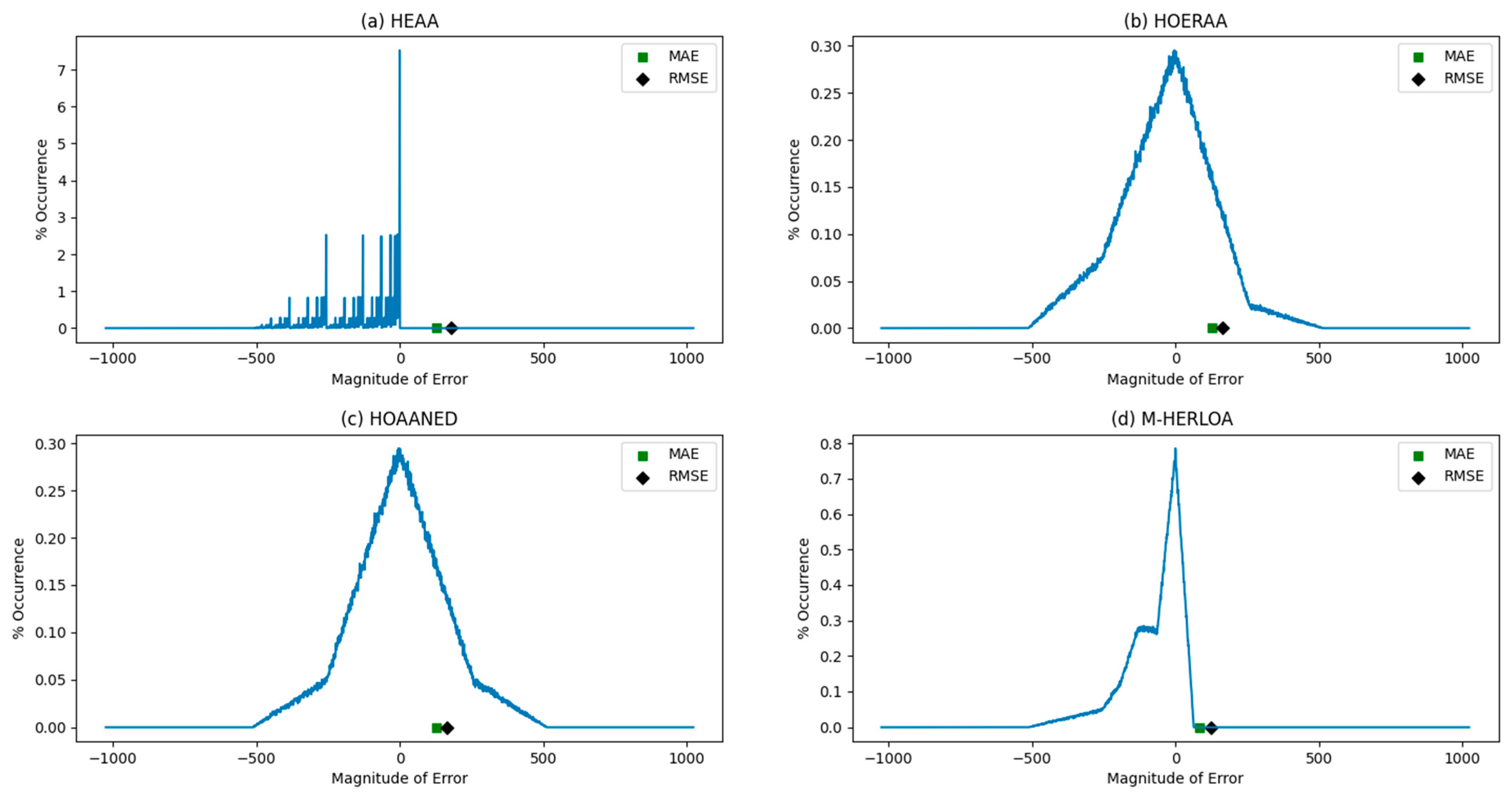
2.3. Error Calculation for Approximate Adders
2.4. Design Metrics of Accurate and Approximate Adders
3. Approximate Multipliers
3.1. Approximate Array Multipliers—Architectures
- AAM00—Binary 0 is assigned to dangling internal inputs and dangling product bits.
- AAM01—Binary 0 is assigned to dangling internal inputs and binary 1 is assigned to dangling product bits.
- AAM10—Binary 1 is assigned to dangling internal inputs and binary 0 is assigned to dangling product bits.
- AAM11—Binary 1 is assigned to dangling internal inputs and dangling product bits.
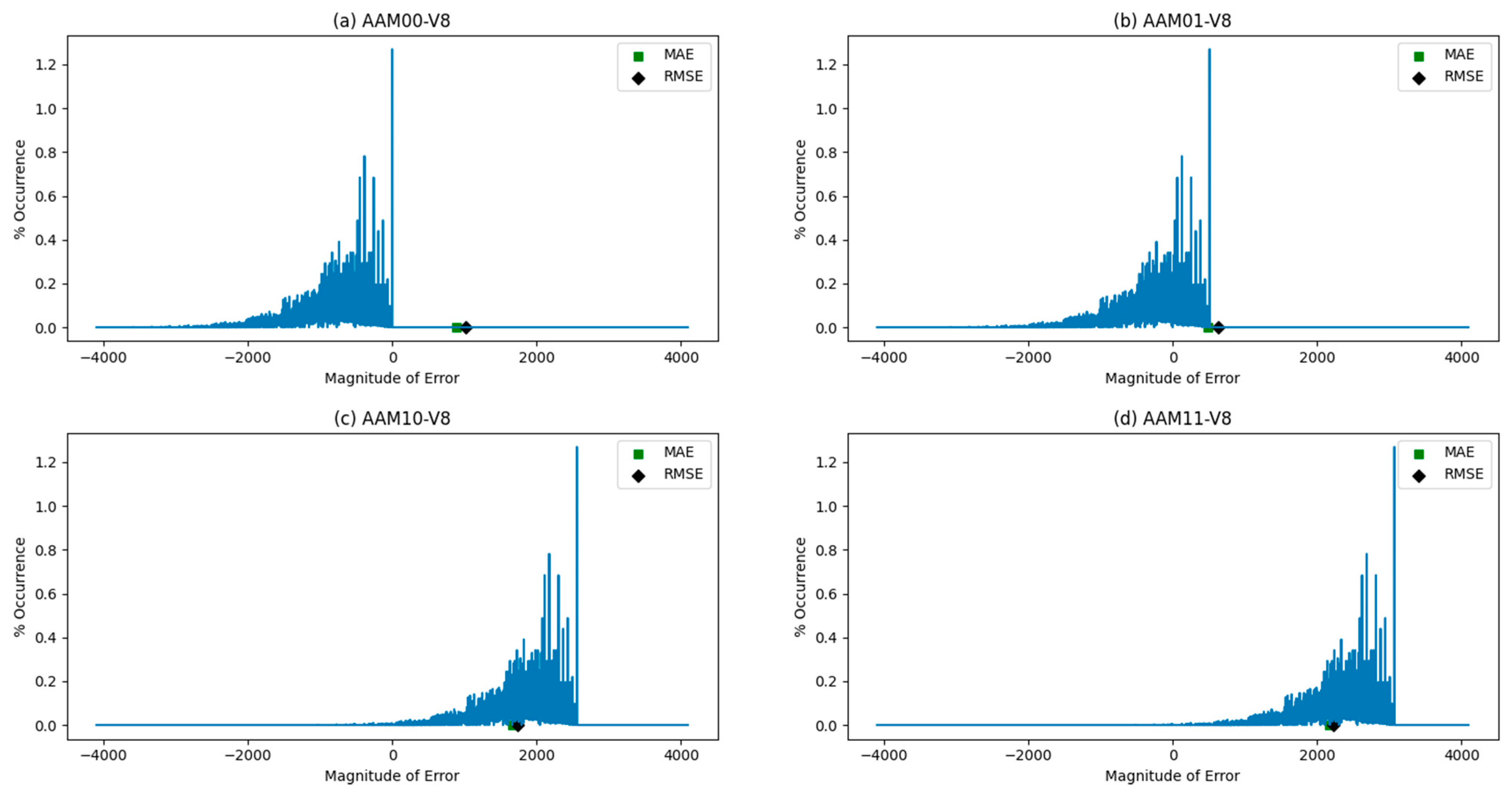
3.2. Error Analysis of Approximate Multipliers
3.3. Image Blending Application
3.4. Design Metrics of Accurate and Approximate Multipliers
4. Automated Generation of Approximate Arithmetic Circuits
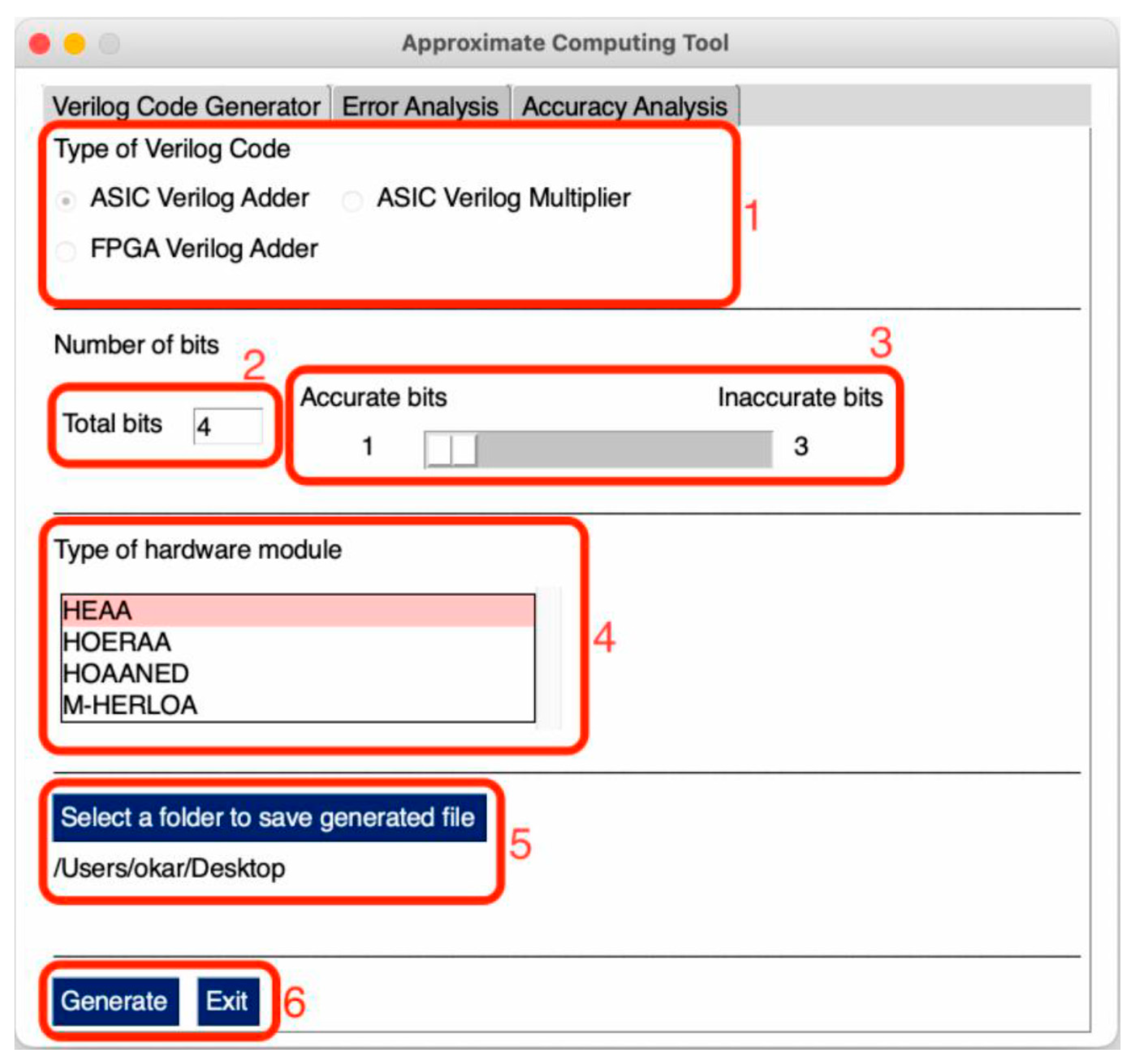
4.1. GUI Version of Approximator
4.2. Developer Perception of Approximator GUI
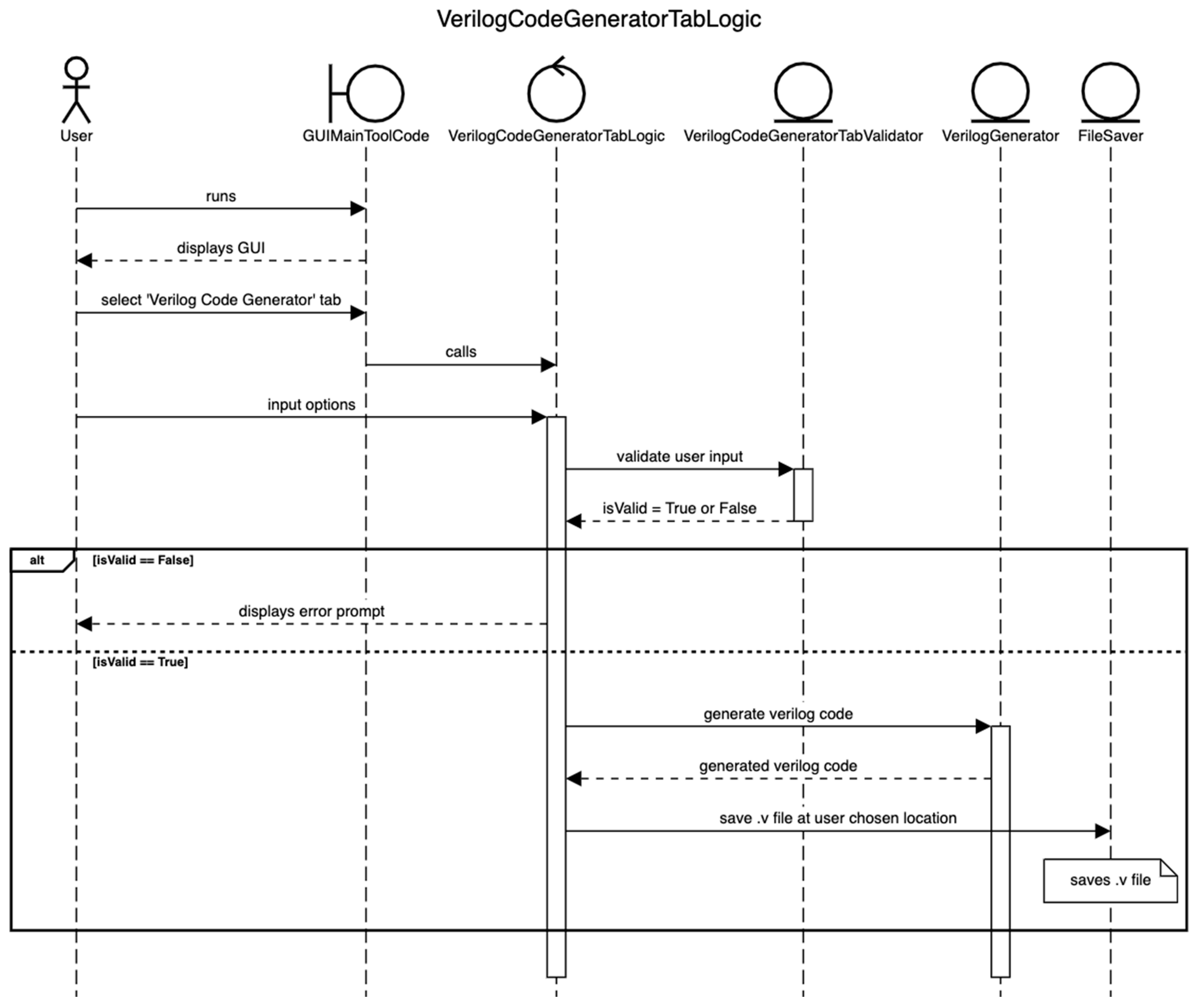
4.2.1. Verilog Code Generation for Approximate Arithmetic Circuits
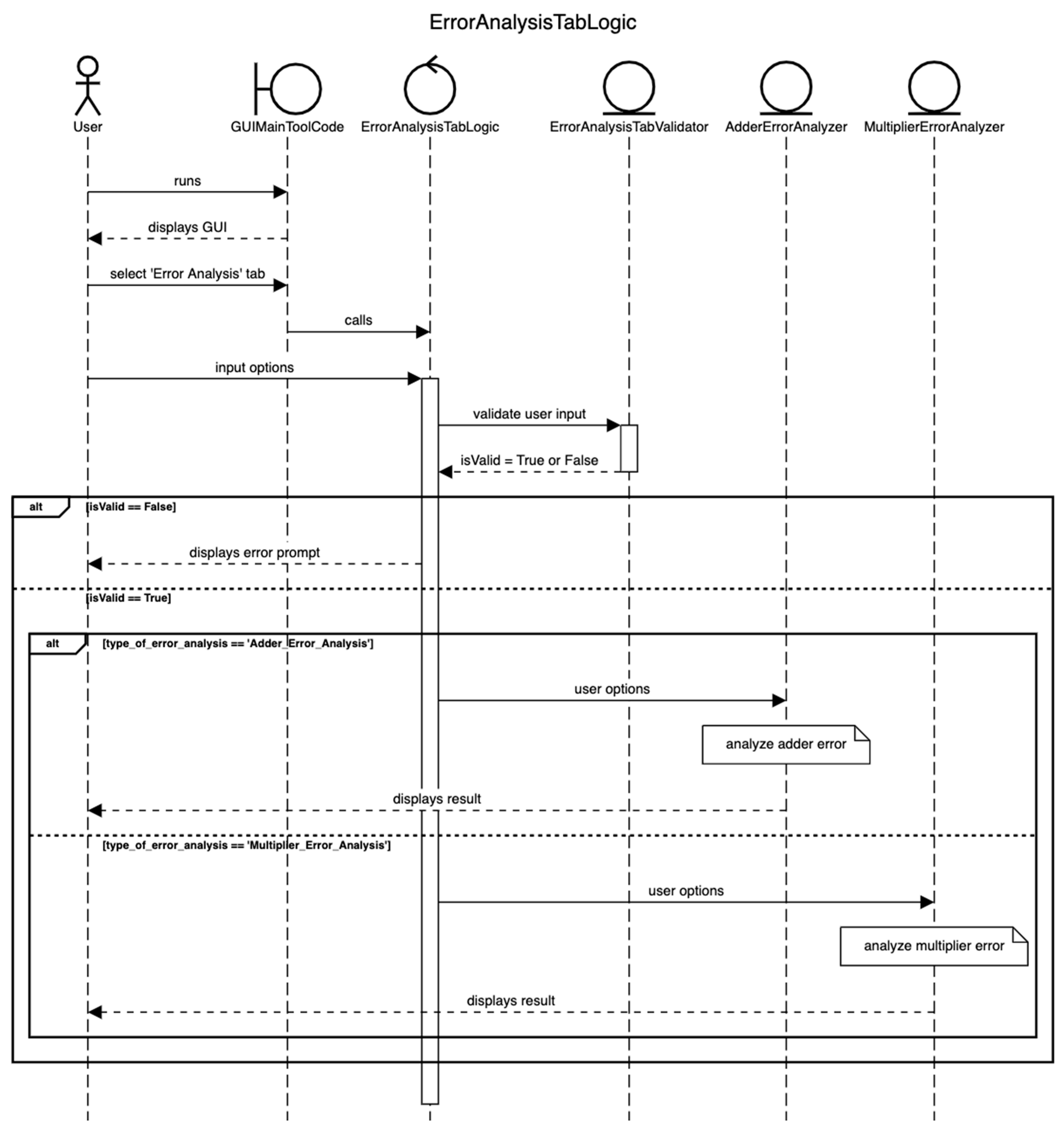
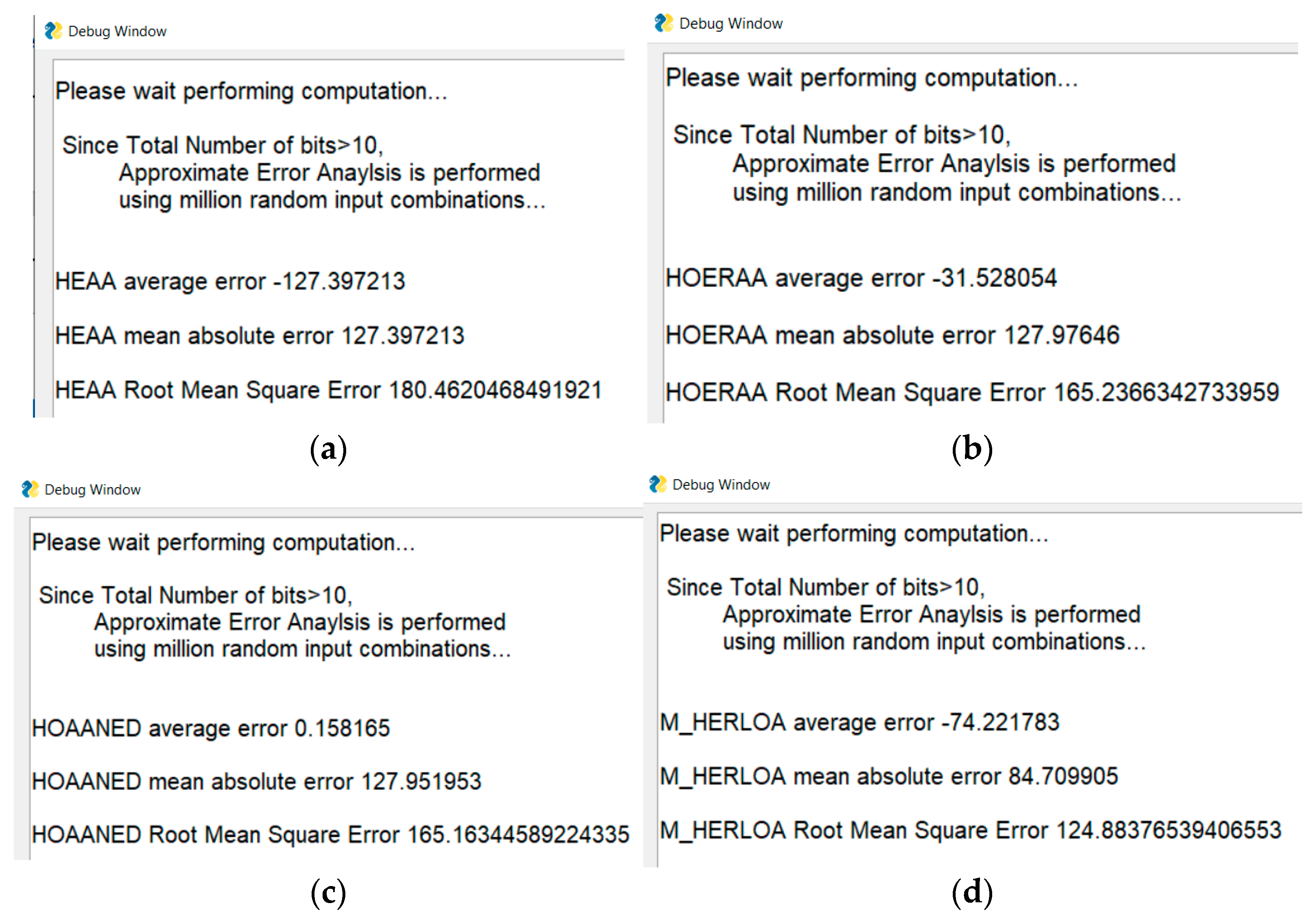
4.2.2. Error Analysis of Approximate Arithmetic Circuits
4.2.3. Accuracy Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Venkataramani, S.; Chakradhar, S.T.; Roy, K.; Raghunathan, A. Approximate computing and the quest for computing efficiency. In Proceedings of the 52nd Design Automation Conference, San Francisco, CA, USA, 8–12 June 2015. [Google Scholar]
- Breuer, M.A. Multi-media applications and imprecise computation. In Proceedings of the 8th Euromicro Conference on Digital System Design, Porto, Portugal, 30 August–3 September 2005. [Google Scholar]
- Zhang, H.; Putic, M.; Lach, J. Low power GPGPU computation with imprecise hardware. In Proceedings of the 51st Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014. [Google Scholar]
- Shoushtari, M.; Rahmani, A.M.; Dutt, N. Quality-configurable memory hierarchy through approximation. In Proceedings of the 14th International Conference on Compilers, Architecture, and Synthesis for Embedded Systems, Taipei, Taiwan, 9–14 October 2011. [Google Scholar]
- Sarwar, S.S.; Srinivasan, G.; Han, B.; Wijesinghe, P.; Jaiswal, A.; Panda, P.; Raghunathan, A.; Roy, K. Energy efficient neural computing: A study of cross-layer approximations. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 796–809. [Google Scholar] [CrossRef]
- Sampson, A.; Deitl, W.; Fortuna, E.; Gnanapragasam, D.; Ceze, L.; Grossman, D. EnerJ: Approximate data types for safe and general low-power computation. In Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, San Jose, CA, USA, 4–8 June 2011. [Google Scholar]
- Sampson, A.; Nelson, J.; Strauss, K.; Ceze, L. Approximate storage in solid-state memories. In Proceedings of the 46th Annual IEEE/ACM International Symposium on Microarchitecture, Davis, CA, USA, 7–11 December 2013. [Google Scholar]
- Nair, R. Big data needs approximate computing: Technical Perspective. Commun. ACM 2015, 58, 104. [Google Scholar] [CrossRef]
- Panda, P.; Sengupta, A.; Sarwar, S.S.; Srinivasan, G.; Venkataramani, S.; Raghunathan, A.; Roy, K. Cross-layer approximations for neuromorphic computing: From devices to circuits and systems. In Proceedings of the 53rd Annual Design Automation Conference, Austin, TX, USA, 5–9 June 2016. [Google Scholar]
- Jiang, H.; Santiago, F.J.H.; Mo, H.; Liu, L.; Han, J. Approximate arithmetic circuits: A survey, characterization, and recent applications. Proc. IEEE 2020, 108, 2108–2135. [Google Scholar] [CrossRef]
- Scarabottolo, I.; Ansaloni, G.; Constantinides, G.A.; Pozzi, L.; Reda, S. Approximate logic synthesis: A survey. Proc. IEEE 2020, 108, 2195–2213. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, C.; Liu, L.; Lombardi, F.; Han, J. A review, classification, and comparative evaluation of approximate arithmetic circuits. ACM J. Emerg. Technol. Comput. Syst. 2017, 13, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Garside, J.D. A CMOS VLSI implementation of an asynchronous ALU. In Proceedings of the IFIP Working Conference on Asynchronous Design Methodologies, Manchester, UK, 31 March–2 April 1993. [Google Scholar]
- Wanhammar, L. DSP Integrated Circuits, 1st ed.; Academic Press: Cambridge, MA, USA, 1999; ISBN 9780127345307. [Google Scholar]
- Raha, A.; Jayakumar, H.; Raghunathan, V. Input-based dynamic reconfiguration of approximate arithmetic circuits for video encoding. IEEE Trans. VLSI Syst. 2016, 24, 846–857. [Google Scholar] [CrossRef]
- Ercegovac, M.D.; Lang, T. Digital Arithmetic; Morgan Kaufmann: Burlington, MA, USA, 2003; ISBN 978-1558607989. [Google Scholar]
- Jiang, H.; Liu, C.; Maheshwari, N.; Lombardi, F.; Han, J. A comparative evaluation of approximate multipliers. In Proceedings of the IEEE/ACM International Symposium on Nanoscale Architectures, Beijing, China, 18–20 July 2016. [Google Scholar]
- Vai, M.M. VLSI Design; CRC Press: Boca Raton, FL, USA, 2000; ISBN 978-0849318764. [Google Scholar]
- Mahdiani, H.R.; Ahmadi, A.; Fakhraie, S.M.; Lucas, C. Bio-inspired computational blocks for efficient VLSI implementation of soft-computing applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 850–862. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Maskell, D.L. Hardware efficient approximate adder design. In Proceedings of the IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018. [Google Scholar]
- Balasubramanian, P.; Maskell, D.L. Hardware optimized and error reduced approximate adder. Electronics 2019, 8, 1212. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, P.; Nayar, R.; Maskell, D.L.; Mastorakis, N.E. An approximate adder with a near-normal error distribution: Design, error analysis and practical application. IEEE Access 2021, 9, 4518–4530. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Nayar, R.; Maskell, D.L. An approximate adder with reduced error and optimized design metrics. Accepted for publication. In Proceedings of the 17th IEEE Asia Pacific Conference on Circuits and Systems, Penang, Malaysia, 22–26 November 2021. [Google Scholar]
- Balasubramanian, P.; Nayar, R.; Maskell, D.L. Approximate array multipliers. Electronics 2021, 10, 630. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Nayar, R.; Min, O.; Maskell, D.L. Image blending using approximate multiplication. In Proceedings of the IEEE 32nd International Conference on Microelectronics, Nis, Serbia, 12–14 September 2021. [Google Scholar]
- Approximator. Available online: https://github.com/OkkarMin/approximator-tool (accessed on 7 November 2021).
- Approximator Tool Documentation. Available online: https://tool-documentation.vercel.app (accessed on 7 November 2021).
- Zhu, N.; Goh, W.L.; Zhang, W.; Yeo, K.S.; Kong, Z.H. Design of low-power high-speed truncation-error-tolerant adder and its application in digital signal processing. IEEE Trans. VLSI Syst. 2010, 18, 1225–1229. [Google Scholar]
- Albicocco, P.; Cardarilli, G.C.; Nannarelli, A.; Petricca, M.; Re, M. Imprecise arithmetic for low power image processing. In Proceedings of the 46th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2012. [Google Scholar]
- Gupta, V.; Mohapatra, D.; Raghunathan, A.; Roy, K. Low-power digital signal processing using approximate adders. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 124–137. [Google Scholar] [CrossRef]
- Dalloo, A.; Najafi, A.; Garcia-Ortiz, A. Systematic design of an approximate adder: The optimized lower part constant-OR adder. IEEE Trans. VLSI Syst. 2018, 26, 1595–1599. [Google Scholar] [CrossRef]
- Seo, H.; Yang, Y.S.; Kim, Y. Design and analysis of an approximate adder with hybrid error reduction. Electronics 2020, 9, 471. [Google Scholar] [CrossRef] [Green Version]
- Bovik, A. Handbook of Image and Video Processing, 2nd ed.; Academic Press: Orlando, FL, USA, 2005; ISBN 978-0080533612. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Processing 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, W.-T.J.; Kahng, A.B.; Kang, S.; Kumar, R.; Sartori, J. Statistical analysis and modeling for error composition in approximate computation circuits. In Proceedings of the 31st IEEE International Conference on Computer Design, Asheville, NC, USA, 6–9 October 2013. [Google Scholar]
- Balasubramanian, P.; Maskell, D.L. Factorized carry lookahead adders. In Proceedings of the IEEE 14th International Symposium on Signals, Circuits and Systems, Iasi, Romania, 11–12 July 2019. [Google Scholar]
- Synopsys SAED_EDK32/28_CORE Databook. Revision 1.0.0, January 2012. Available online: https://www.synopsys.com/community/university-program/teaching-resources.html (accessed on 27 September 2021).
- Yamamoto, T.; Taniguchi, I.; Tomiyama, H.; Yamashita, S.; Hara-Azumi, Y. A systematic methodology for design and analysis of approximate array multipliers. In Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems, Jeju, Korea, 25–28 October 2016. [Google Scholar]
- Gamma, E.; Helm, R.; Johnson, R.; Vlissides, J.; Booch, G. Design Patterns: Elements of Reusable Object-Oriented Software, 1st ed.; Addison-Wesley: Boston, MA, USA, 1994; ISBN 978-0201633610. [Google Scholar]
- Shinya, T. Pyverilog: A Python-based hardware design processing toolkit for Verilog HDL. In Proceedings of the 11th International Symposium on Applied Reconfigurable Computing, Bochum, Germany, 14–17 April 2015. [Google Scholar]
- NumPy. Available online: https://numpy.org (accessed on 10 June 2021).
- PySimpleGUI. Available online: https://pysimplegui.readthedocs.io/en/latest (accessed on 19 June 2021).

















| Approximate Adder | MAE | RMSE |
|---|---|---|
| LOA | 191.96 | 256.10 |
| LOAWA | 255.70 | 361.74 |
| APPROX5 | 256.22 | 295.71 |
| HEAA | 127.71 | 180.80 |
| OLOCA | 208.07 | 276.63 |
| HOERAA | 127.96 | 165.18 |
| HOAANED | 128.00 | 165.24 |
| HERLOA | 87.71 | 129.15 |
| M-HERLOA | 84.46 | 124.56 |
| Adder | Clock Period (ns) | LUTs | FFs | Power (W) |
|---|---|---|---|---|
| Accurate FPGA Adder | 2.10 | 32 | 97 | 0.209 |
| LOA | 1.89 | 27 | 97 | 0.198 |
| LOAWA | 1.86 | 27 | 97 | 0.198 |
| APPROX5 | 1.84 | 22 | 88 | 0.200 |
| HEAA | 1.89 | 27 | 97 | 0.199 |
| OLOCA | 1.87 | 23 | 73 | 0.187 |
| HOERAA | 1.87 | 23 | 73 | 0.188 |
| HOAANED | 1.87 | 23 | 73 | 0.188 |
| HERLOA | 1.89 | 28 | 97 | 0.199 |
| M-HERLOA | 1.90 | 25 | 79 | 0.190 |
| Adder | Critical Path Delay (ns) | Area (µm²) | Power (µW) |
|---|---|---|---|
| Accurate CLA | 1.17 | 564.60 | 94.33 |
| LOA | 0.96 | 428.36 | 71.77 |
| LOAWA | 0.96 | 413.37 | 68.86 |
| APPROX5 | 0.96 | 424.58 | 73.54 |
| HEAA | 0.96 | 430.65 | 71.49 |
| OLOCA | 0.96 | 420.03 | 66.11 |
| HOERAA | 0.96 | 430.38 | 68.82 |
| HOAANED | 0.96 | 425.36 | 67.73 |
| HERLOA | 0.96 | 443.28 | 74.01 |
| M-HERLOA | 0.96 | 433.94 | 69.11 |
| Approximate Array Multiplier | MAE | RMSE |
|---|---|---|
| AAM00-V8 | 896.25 | 1024.76 |
| AAM01-V8 | 484.25 | 628.71 |
| AAM10-V8 | 1664.76 | 1736.35 |
| AAM11-V8 | 2174.80 | 2230.78 |
| Multiplier | Critical Path Delay (ns) | Area (µm²) | Power (µW) |
|---|---|---|---|
| Accurate Multiplier (Using multiplication operator) | 1.75 | 474.39 | 144.20 |
| Accurate Array Multiplier | 2.00 | 509.47 | 183.80 |
| AAM00-V8 and AAM01-V8 | 1.58 | 187.11 | 50.90 |
| AAM10-V8 and AAM11-V8 | 1.53 | 179.99 | 57.68 |
| Tool Feature | Adder/Multiplier | Name of Approximate Arithmetic Circuit |
|---|---|---|
| Verilog code generation | ASIC-based adder | HEAA |
| HOERAA | ||
| HOAANED | ||
| M-HERLOA | ||
| ASIC-based multiplier | AAM01 with V-cut | |
| FPGA-based adder | HEAA | |
| HOERAA | ||
| HOAANED | ||
| M-HERLOA | ||
| Error analysis | Approximate adders | HEAA |
| HOERAA | ||
| HOAANED | ||
| M-HERLOA | ||
| Approximate multiplier | AAM01 with V-cut | |
| Accuracy analysis | Approximate adders | HEAA |
| HOERAA | ||
| HOAANED | ||
| M-HERLOA | ||
| Approximate multiplier | AAM01 with V-cut |
| Package | Version Used |
|---|---|
| Jinja2 | 2.11.2 |
| MarkupSafe | 1.1.1 |
| NumPy | 1.19.3 |
| Ply | 3.11 |
| PySimpleGUI | 4.33.0 |
| Pyverilog | 1.3.0 |
| Veriloggen | 1.9.0 |
| Yapf | 0.30.0 |
| Verilog Code Generated | Approximate Adder or Multiplier | Total Number of Bits | # Bits for Inaccurate Part of Approximate Adder or V-Cut for Approximate Multiplier |
|---|---|---|---|
| ASIC (based) adder | HEAA | 4 ≤ total bits ≤ 32 | 3 ≤ inaccurate bits ≤ total bits—1 |
| HOERAA | |||
| HOAANED | |||
| M-HERLOA | |||
| FPGA (based) adder | HEAA | 4 ≤ total bits ≤ 32 | 3 ≤ inaccurate bits ≤ total bits—1 |
| HOERAA | |||
| HOAANED | |||
| M-HERLOA | |||
| ASIC (based) multiplier | AAM01 with V-cut | 3 ≤ multiplicand/multiplier bits ≤ 32 | 0 ≤ V-cut ≤ (multiplicand bits + multiplier bits—3) |
| Error Analysis | Approximate Adder or Multiplier | Total Number of Bits | # Bits for Inaccurate Part of Approximate Adder or V-Cut for Approximate Multiplier |
|---|---|---|---|
| Approximate adder | HEAA | 4 ≤ total bits ≤ 32 | 3 ≤ inaccurate bits ≤ total bits—1 |
| HOERAA | |||
| HOAANED | |||
| M-HERLOA | |||
| Approximate multiplier | AAM01 with V-cut | 3 ≤ multiplicand/multiplier bits ≤ 32 | 0 ≤ V-cut ≤ (multiplicand bits + multiplier bits—3) |
| Accuracy Analysis | Approximate Adder or Multiplier | Total Number of Bits | Number of Inaccurate Bits for Approximate Adder or V-Cut for Approximate Multiplier | First and Second Unsigned Decimal Number |
|---|---|---|---|---|
| Approximate adder | HEAA | 4 ≤ total bits ≤ 32 | 3 ≤ inaccurate bits ≤ total bits−1 | # |
| HOERAA | ||||
| HOAANED | ||||
| M-HERLOA | ||||
| Approximate multiplier | AAM01 with V-cut | 3 ≤ multiplicand/multiplier bits ≤ 32 | 0 ≤ V-cut ≤ (multiplicand bits + multiplier bits—3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramanian, P.; Nayar, R.; Min, O.; Maskell, D.L. Approximator: A Software Tool for Automatic Generation of Approximate Arithmetic Circuits. Computers 2022, 11, 11. https://doi.org/10.3390/computers11010011
Balasubramanian P, Nayar R, Min O, Maskell DL. Approximator: A Software Tool for Automatic Generation of Approximate Arithmetic Circuits. Computers. 2022; 11(1):11. https://doi.org/10.3390/computers11010011
Chicago/Turabian StyleBalasubramanian, Padmanabhan, Raunaq Nayar, Okkar Min, and Douglas L. Maskell. 2022. "Approximator: A Software Tool for Automatic Generation of Approximate Arithmetic Circuits" Computers 11, no. 1: 11. https://doi.org/10.3390/computers11010011
APA StyleBalasubramanian, P., Nayar, R., Min, O., & Maskell, D. L. (2022). Approximator: A Software Tool for Automatic Generation of Approximate Arithmetic Circuits. Computers, 11(1), 11. https://doi.org/10.3390/computers11010011








