Abstract
The number of processing elements per solution is growing. From embedded devices now employing (often heterogeneous) multi-core processors, across many-core scientific computing platforms, to distributed systems comprising thousands of interconnected processors, parallel programming of one form or another is now the norm. Understanding how to efficiently parallelize code, however, is still an open problem, and the difficulties are exacerbated across heterogeneous processing, and especially at run time, when it is sometimes desirable to change the parallelization strategy to meet non-functional requirements (e.g., load balancing and power consumption). In this article, we investigate the use of a programming model based on series-parallel partial orders: computations are expressed as directed graphs that expose parallelization opportunities and necessary sequencing by construction. This programming model is suitable as an intermediate representation for higher-level languages. We then describe a model of computation for such a programming model that maps such graphs into a stack-based structure more amenable to hardware processing. We describe the formal small-step semantics for this model of computation and use this formal description to show that the model can be arbitrarily parallelized, at compile and runtime, with correct execution guaranteed by design. We empirically support this claim and evaluate parallelization benefits using a prototype open-source compiler, targeting a message-passing many-core simulation. We empirically verify the correctness of arbitrary parallelization, supporting the validity of our formal semantics, analyze the distribution of operations within cores to understand the implementation impact of the paradigm, and assess execution time improvements when five micro-benchmarks are automatically and randomly parallelized across 2 × 2 and 4 × 4 multi-core configurations, resulting in execution time decrease by up to 95% in the best case.
1. Introduction
Code parallelization has long been a challenging aspect of programming technologies [1]. In single-core, single-thread systems, temporal parallelization is an effective way of addressing latency issues [2]. In multi-thread, and later in multi-core systems, temporal and spatial parallelizations have become the keys to addressing performance limitations in general [3]. However, as the number of parallel processors increases, moving from multi- to many-core, and as these cores become more and more distributed, the difficulty of parallelizing code (efficiently) increases accordingly [4].
The zeitgeist shows not just an increase in both the number of cores and the degree of distribution, but also an increase in heterogeneity [5] and the level of runtime reconfiguration of computing systems [6]. From the embedded to the high-performance computing domains, runtime reconfiguration across heterogeneous parallel computing cores is an inexorable strategy to address not just computing performance, but also power consumption, communication latencies, and predictability [7]. In this scenario, where “ideal” parallelism depends not just on program structure but also on target architecture, and where reconfiguration might impose parallelization at runtime [8], traditional parallelization technologies can no longer cope [9]. This is particularly relevant in modern embedded systems, constrained by several metrics [10].
In this article, we explore a programming model and an associated model of computation (MoC) for arbitrary code parallelization, i.e., a paradigm that allows expressing programs such that they can be arbitrarily partitioned across N parallel processing elements, maintaining semantic correctness. Moreover, the paradigm allows parallelization to be (re)applied at any stage of runtime, lending itself to use across heterogeneous, runtime-reconfigurable parallel systems. Specifically, this article
- Introduces Asynchronous Graph Programming (AGP), a programming paradigm based on dynamic asynchronous graphs. A graph represents the potential execution of a program, expressing it as a set of data dependencies, merges between branches, and graph-expansion rules. In order-theoretic mathematics, AGP is a series-parallel partial order. We show this by expressing programs in such a manner that it is possible to partition graphs (parallelize the program) efficiently using knowledge of the target architecture and graph structure to minimize dependencies. These properties hold at runtime, allowing for seamless re-application.
- Formally describes its model of computation for programs expressed as they are in the paradigm. AGP provides a mechanism for evaluating programs across N processing elements in parallel, guaranteeing semantic correctness; e.g., the MoC guarantees that sequential events are processed in the correct order, regardless of the parallel allocation, while performing a best-effort first come, first served evaluation across events of arbitrary order.
- We describe an implementation to empirically support this claim and evaluate the benefits of parallelization using a prototype open-source compiler, targeting a message-passing many-core simulation. We empirically verify the correctness of arbitrary parallelization, supporting the validity of our formal semantics, analyze the distribution of operations within cores to understand the implementation impact of the paradigm, and measure performance improvement of random parallelization across five micro-benchmarks with increasing levels of parallelization opportunities, showing that, on average, it is possible to reduce execution time between 28% and 87%, when moving from single-core to a 2 × 2 multi-core configuration and between 33% and 95%, when moving from single-core to a 4 × 4 multi-core configuration.
The remainder of this article is organized as follows: Section 2 provides a review of code-parallelization approaches to put our work into context. In Section 3, we introduce our programming model, describing how parallelization strategies might be applied. Section 4 formally describes the small-step semantics of our MoC (which implements our programming model), including a formal analysis of its parallelization. Section 5 describes our prototype implementation, where we elaborate on our empirical evaluation framework (a message-passing many-core simulation) and our experimental methodology and results. Section 6 describes current related work in the field, and Section 7 concludes this article, describing our ongoing research efforts in this domain.
2. Background: Code Parallelization Strategies
Code parallelization approaches can be broadly grouped into three different categories: source code, compilation, and models of computation for parallelization (our approach lies in the latter category).
Source-code parallelization consists of approaches to expressing parallelization opportunities at the source-code level (either automatically or manually). This includes clearly static approaches such as partitioning computations across functions and threads [11]; i.e., a programmer conceptually identifies parts of their program that can be run in parallel and implements them across threads. Other approaches are partially dynamic (i.e., potentially overlap with compilation parallelism), e.g., insertion of compiler pragmas for loop unrolling to exploit data parallelism or map-reduce patterns [12]. Approaches using higher-level paradigms mapped onto extant languages (e.g., task-based programming models such as OpenMP [13]) also fall into this category (interested readers may consult [14] for a full taxonomy of task-based programming models).
Compilation parallelization consists of optimizing parallelizing compilers [15] that perform static analysis (potentially combined with runtime profiling stages [16]) to identify opportunities for parallelization at the compile-time level (potentially invisible to the programmer). Both source code and compiler parallelization approaches can be applied to any model of computation, of course; however, the majority of these initiatives target extant languages based on traditional models of computation such as imperative [17] or functional [18] models (for good reason: advances in parallelizing C or Haskell code, for example, have immediate impacts on practitioners). The impetus behind Deep Learning, for example, has led to high demand for automatic parallelization of machine learning models [19]. A full description of source code and compiler-level parallelization strategies is beyond the scope of this paper, but we point interested readers to [20,21] for more comprehensive descriptions.
Models of computation for parallelization, on the other hand, explore new computing paradigms that are more amenable to parallelization. In some cases, new models of computation can be leveraged by extant languages [22] if operational semantics permit. In other cases, new models of computation require new languages with brand new operational semantics (there are many examples of these, particularly within Embedded Domain-Specific Languages (EDSLs) [23]). Most novel models of computation are variations/extensions of either the -calculus [24] or the -calculus [25], within functional languages, or variations/extensions of the operational semantics of imperative languages [26]. Our work, similarly to approaches like [27], explores more radical models of computation outside these families, hoping to shed light on strategies for parallel programming in reconfigurable systems. While most of the examples we give throughout this article are for multi-/many-core systems, our model should scale to more distributed systems.
3. Programming Model
Our programming model, Asynchronous Graph Programming (AGP), implements computations as a directed graph of single-assignment semantics (a past iteration of AGP is fully described in our previous work here [28], but we describe it in this article nonetheless, as several changes have occurred at the programming-model level as we further developed the model of computation). Listing 1 depicts a grammar for a possible AGP implementation, although this syntax is not as relevant as the semantics described below: this grammar is not intended for human-readable code but rather for specifying a specific push-down automata. Although we do not prove it here, the language is both context-free and Turing-complete.
| Listing 1: BNF grammar describing an AGP implementation. <op> (operations), <identifier> and <const> (constants) not defined for brevity. |
|
Each node in the graph is assigned once, as the result of a computation, or is expanded into a subgraph. Operands for computations are either other nodes in the graph, or the special input virtual node (output is also a special virtual node, that can be assigned like any other node: we elaborate on these in Section 3.1 below). Nodes are considered unconstructed if they exist in a graph, but their corresponding value has not yet been computed. Nodes are constructed only when all their dependencies (i.e., nodes whose values are required) have been constructed. Nodes can also be destroyed without ever having been constructed: for example, the operation “if condition result” (expressed here in Polish notation) has two dependencies, “condition” and “result”. When both operands are constructed, the operation constructs a node with the value of node “result” if the value of node “condition” is considered true; if the value of node “condition” is considered false, the operation destroys the corresponding node (removing it from the program) and subsequently destroys all nodes that depend on the current node, pruning this branch of the program. A special operation “merge” is used to propagate the result of one of two possible parallel paths: “merge” constructs a node with the value of whichever of its operands is constructed first.
Recursion is achieved by expanding a node into a complete subgraph, connecting nodes in the higher subgraph to input and output nodes in the lower graph; i.e., upon expansion, for all inputs and outputs listed in the expansion function, the expanded subgraph’s input nodes are replaced by the mapped nodes in the higher graph, and references from a mapped node to output are removed; a referencing node is placed in higher graph’s corresponding dependencies.
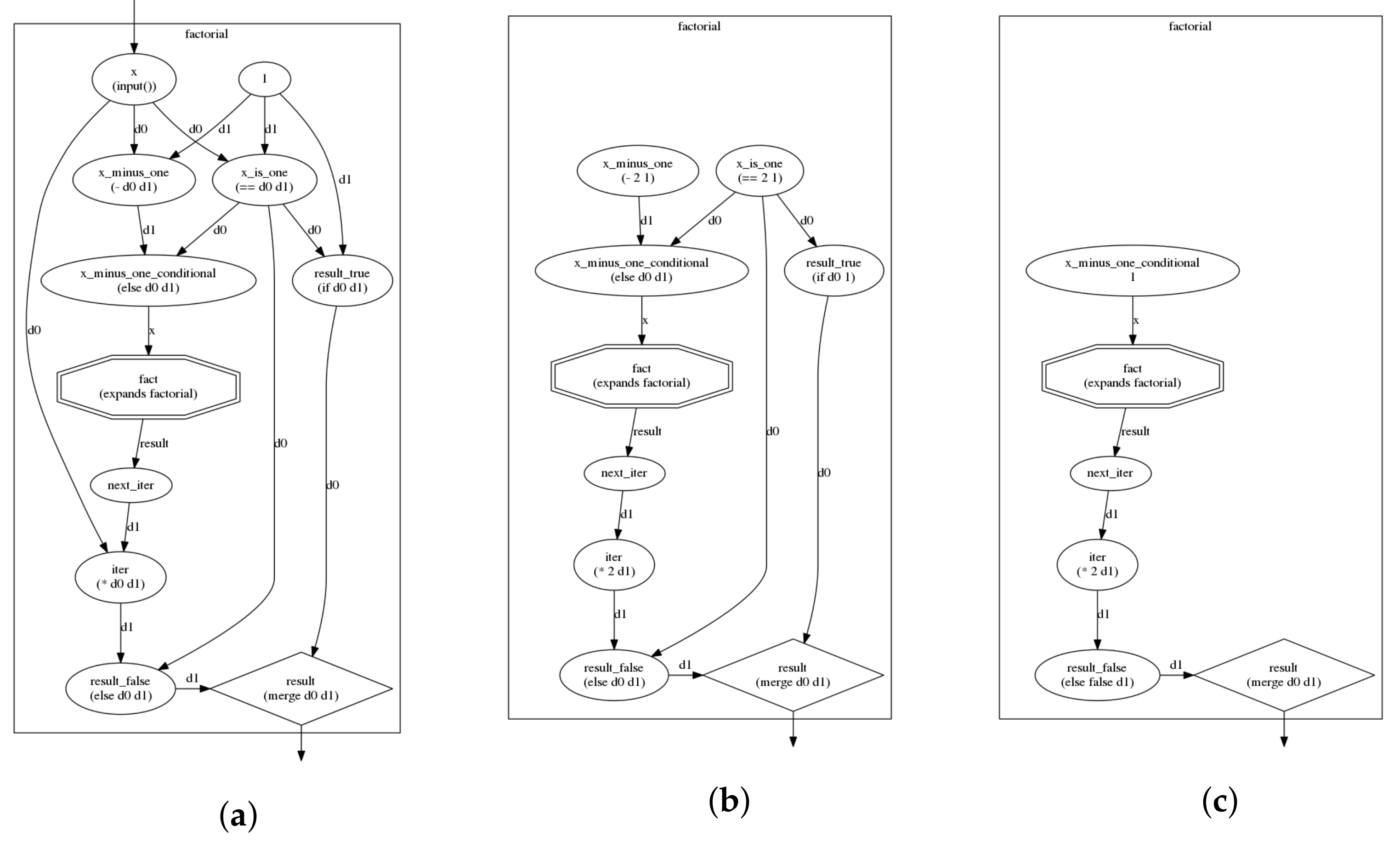
The example in Listing 2 below demonstrates the AGP paradigm for a subgraph that calculates the factorial of a number (assuming only positive integers are fed as input). Typical programming characters such as − and * represent arithmetic operations. The result of the computation, connected to the output node, is the result of a merge (line 14): it is either 1, if the input is 1 (base case of the recursion), or the result of the iteration, which is the current input multiplied by the next iteration (line 5). The next iteration is the result of a recursive expansion of the subgraph, where the lower graph’s input “x” is mapped to a higher graph node “x − 1” (line 11). The expansion in line 10 always occurs, as long as its inputs are constructed (i.e., node x_minus_one_conditional); however, because of the semantics of “if” and “else”, which destroy its unconstructed nodes and their dependencies if their respective logical tests fail (line 7), the expansion node is destroyed in the base case. Partial runtime evaluation is depicted in Figure 1.
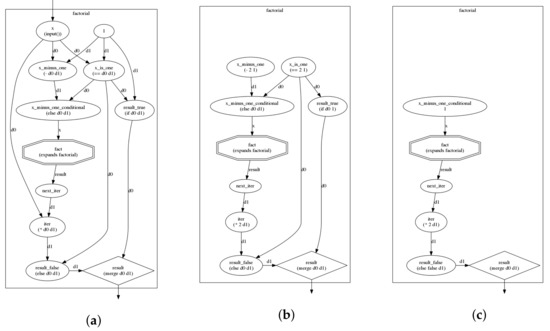
Figure 1.
Visual representation of the factorial graph and its evaluation. (a) initial (compile time) graph. (b) evaluation for input after one step; (c) evaluation after two steps (subgraph expansion will follow).
| Listing 2: “Factorial” function highlighting all aspects of AGP. Pseudo-syntax for legibility. |
|
3.1. Rationale
The AGP paradigm becomes reasonable when we examine how input and output are implemented at a lower level, within the context of the target use cases. Experience writing highly asynchronous code (e.g., interrupt-driven bare-metal code in C, with shared global state) shows the difficulty in preventing race conditions leading to erroneous local states [29]. Experience with parallelizing functional languages, while (more) easily correct by construction, shows less efficiency (read: performance) than imperative code [30], primarily due to memory hierarchy behavior [31], and especially when dealing with asynchronous events. These issues are likely to be exacerbated as the degree of parallelization and heterogeneity increases, thus the design decisions in AGP.
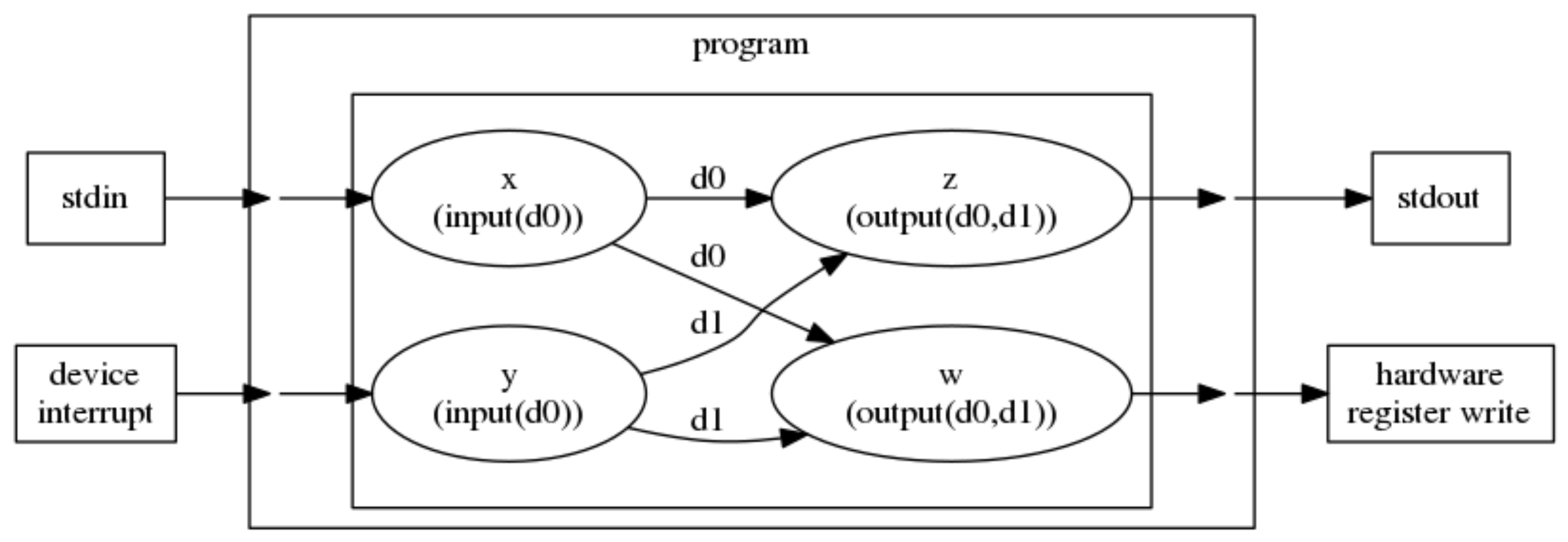
In AGP semantics, the behavior of input and output is undefined by construction. They are used for subgraph expansion: upon expansion, references to input and output are replaced by connections to existing nodes in the higher graph, if they have been mapped in expansion code (note that this does not necessarily have to happen: it is possible to expand a subgraph with more inputs and outputs than the ones mapped at expansion, resulting in a free IO node). Free IO nodes (i.e., nodes connected to input and output that must be evaluated) are evaluated according to custom rules, specified by the compiler and runtime system (Figure 2). For example, the compiler/runtime might map all inputs and outputs to stdio, i.e., as wrappers for low-level printf and scanf. Alternatively, the compiler/runtime might map an input to a peripheral device Interrupt Service Routine; i.e., if the node is constructed, that interrupt has occurred and whatever value it returned is bound to the node. In this fashion, an asynchronous shared state is handled by construction: a merge operator would connect results for computations interrupt occurred and interrupt did not occur (probably expanding a new node to deal with the next interrupt in the case of interrupt occurred; this expansion does not need to be synchronous as long as it is performed at the same point in time, during graph processing, when interrupt-related nodes are merged, to ensure no interrupts are lost). Similarly, the compiler/runtime might map an output to a write to a hardware device. These examples are for bare-metal code, but they scale to abstractions up the stack. For example, in a distributed system, input and output can be mapped to message passing ports for send and receive (it is, of course, possible to map inputs and output from different nodes to several different physical media at the same time). Thus, we envision AGP being used across highly parallel systems with heterogeneous interfaces, where low-level interface code merely populates or responds to a node value: state logic and synchronization are embedded in the AGP graph structure.
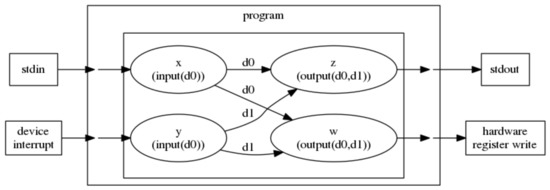
Figure 2.
Mapping of program input/output operations to external I/O.
Regarding parallelization, within AGP semantics, the problem of parallelizing code across processing elements becomes a problem of partitioning a graph. Thus, we can borrow from graph theory to decide on parallelization strategies in the function of requirements. For example, we suspect that for shared memory multi-core performance, the best parallelization strategy will be based on minimizing edges between partitioned graphs, as this corresponds to minimizing the shared memory requirements that are incurred with costly cache coherency mechanisms [32]. Examining these strategies is outside the scope of this paper and is reserved for future work, but we hope they illustrate hypothetical AGP applications. Note that because of the dependency semantics, ordering of operations is guaranteed, regardless of the parallelization.
AGP is certainly not intended for programmers, but rather as an intermediate and/or target representation for higher-level languages whose semantics can be expressed (and take advantage of the AGP paradigm). Expressing Intermediate Representations as dependency graphs is, of course, not new [33,34]: what is different in AGP, compared to typical compiler optimization passes, is that the graph representation is preserved in target-code generation and manipulated at runtime. While this is not necessarily useful in other representations, which are instead leveraged for optimization prior to code generation, AGP’s semantics allow the graph representation to be employed for parallelization in a unique way. Although all single assignment languages should be able to compile down to AGP (this is a hypothesis only; we have not tested it), we believe its true potential will be achieved by languages with explicit parallelism.
4. Model of Computation
Directed graphs, unfortunately, are not easily mapped onto a flat memory space as employed by virtually all von Neumann machines. Thus, to efficiently execute AGP programs, we need to map a graph onto a “flat” (or linear) data structure, where every element can be assigned a unique address, as per random access memory architecture. Furthermore, the properties of AGP that lend themselves to parallelization (i.e., construction rules) should be preserved. The following subsection shows how to transform an AGP graph into a stack-based model, easily mapped onto random access memory, that can be concurrently evaluated by N processing elements in a safe manner.
4.1. AGP Semantics
Our MoC maps a graph onto a stack. Connections between graph nodes correspond to references from one stack element to another. Each element on the stack contains references to all other elements that depend on it and a rule for its construction, as a function of the elements it depends on. Evaluation proceeds by finding a ready element on the stack (i.e., one whose dependencies have been fully evaluated) and evaluating it according to its construction rule. Evaluating an element marks it as dead and populates all its dependencies with its value for subsequent construction. Destroying an element (i.e., removing it without constructing it, due to the requirements for its construction having been deemed impossible) marks it as dead and recursively marks all the elements that depend on it. Whenever the top of the stack is a dead element, it is removed from the stack. Evaluating an expansion pushes a sub-stack corresponding to the expanded subgraph on top of the existing stack. Evaluation terminates when the stack is empty.
Let denote the stack as an ordered set of n elements, such that , and E denote an element on the stack. E is a tuple of the form or , where f is the function that rules the construction of E; d is either a set of primitive types (i.e., integers) that constitute the dependencies of E, or a set of tuples of the form that map an element on the stack and a primitive type; and is the set of elements in the stack (such that ) that depend on E (the destinations of the constructed value of E), and the optional special element . The construction function f is of one of the types (the primitive operations in our MoC), and its type dictates which evaluation rule is applied on the stack. denotes the type of the function f in E. These rules were implicitly alluded to in Listing 2 and Figure 1.
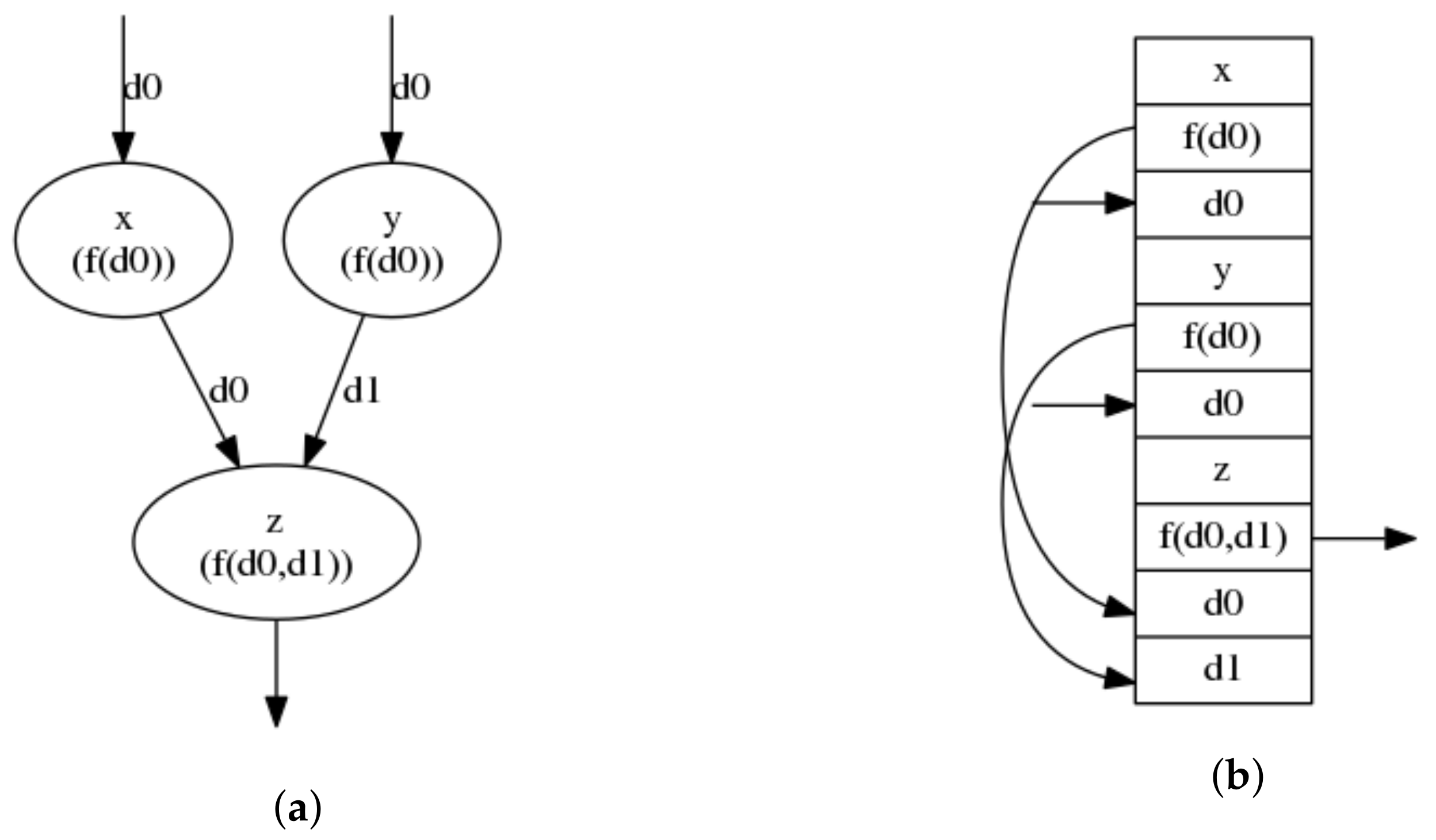
Each evaluation transforms the stack such that . We use the following notation for stack transformations: describes the removal of from the stack, such that ; describes appending (pushing) the stack to the top of stack , such that . The notation is the application of the primitive value x to the dependencies d of all elements in the stack present in the set e, i.e., to the set . The notation is the transformation of , such that all its ordered elements are constructed using the ordered values d, and all its output references in elements are replaced with references to the elements . We use parenthesis to sequentialize successive stack transformations. An example mapping between graph form and stack form is depicted in Figure 3.
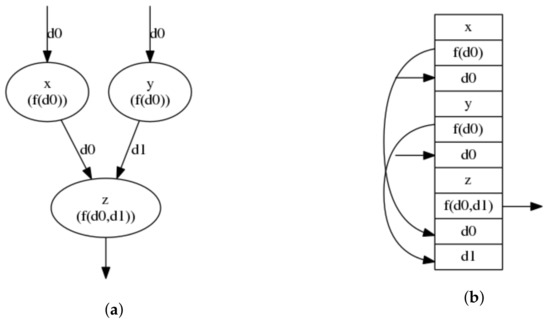
Figure 3.
Mapping of a directed graph onto a stack. (a) Graph depiction. (b) Equivalent stack depiction. Here, node names are used to identify stack elements (each element name is at the top of its respective field).
We can now start describing the small-step semantics of AGP. For any , where d is a set of primitive types:
That is, arithmetic functions always construct an element value from its sources d, remove it from the stack, and propagate its value to all the elements that depend on it. If , the value is also propagated to the output of the program (although the medium is not specified in the semantics, and we do not describe it in our rules). The construction function f might be an input function, in which case it constructs the element from a value obtained by a program input (for example, in the case of output, the medium is not specified in the semantics): its arguments d are only evaluated as necessary preconditions for computing input (i.e., to guarantee ordering).
For any , where f is either “if” or “else” and where d is a set of primitive types:
That is, boolean functions (that examine a boolean dependency) either propagate a second dependency to all the elements that depend on it or remove them (destroy them) from the stack, depending on the boolean value. Elements that are constructed by a merge function are never destroyed. If , the value is also propagated to the output of the program (although the medium is not specified in the semantics and we do not describe it in our rules).
For any , where d is a set of primitive types:
That is, merge functions propagate a single value to all the elements that depend on it. An element constructed by a merge function may depend on several elements: the first dependency that is constructed is the dependency used (this is used, for example, to merge the results of “if” and “else” branches: only one of these would propagate its value to a merge element, while the other will destroy all its dependents except ones constructed by the merge).
For any , the only case where d is a set of tuples of the form that map an element on the stack and a primitive type is the following:
where
That is, an expansion pushes a new sub-stack on top of the current stack, replacing a set of elements in the sub-stack with constructed values and replacing output destinations with references to elements already in the stack (although this small-step semantic rule seems complex, it represents nothing more than subgraph IO re-mapping).
4.2. Parallelizing AGP
We now have the tools to examine the parallelization of computations modeled through AGP. At any given element evaluation, one of three transformations is applied on the stack: removal of a single (evaluated) element with value application (denoted by ), removal of several elements (evaluated element, and the elements that depend on it, recursively, denoted by ), or removal of evaluated element and pushing a new set of elements on top of the stack (denoted by ). Let us examine the concurrent application of these rules by two parallel threads (if rules A and B can be safely applied in parallel by two threads, it is easy to observe rules A, A, and B can be safely applied in parallel by three threads).
Let be a stack evaluated concurrently by two computational threads. At any point during evaluation, either a single evaluation rule will be applied on the stack at any one time (if a second thread is, e.g., traversing the stack searching for a ready element) or two rules will be applied simultaneously. Thus, we can examine all possibilities of concurrent rule application, to determine the safety of parallel execution.
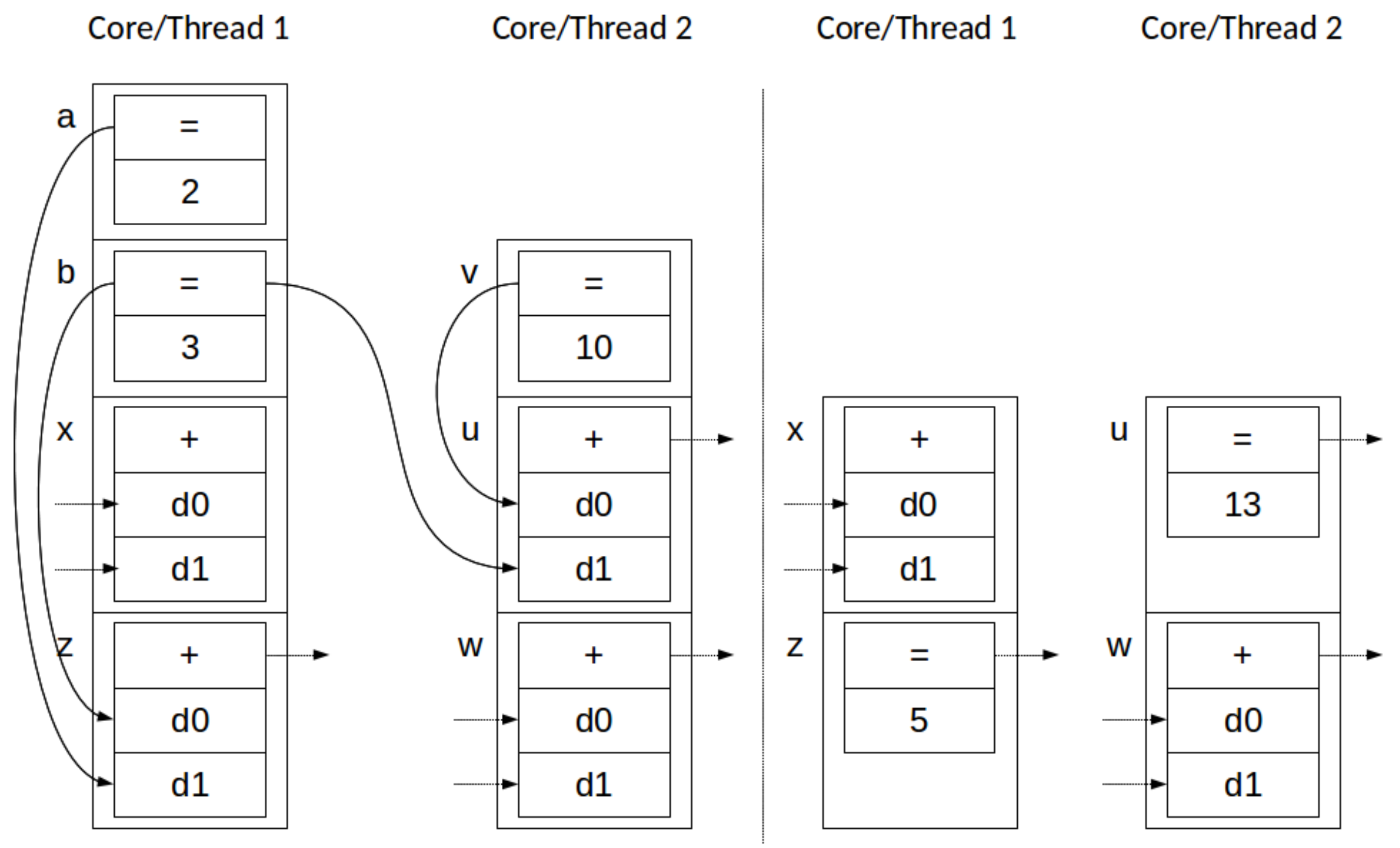
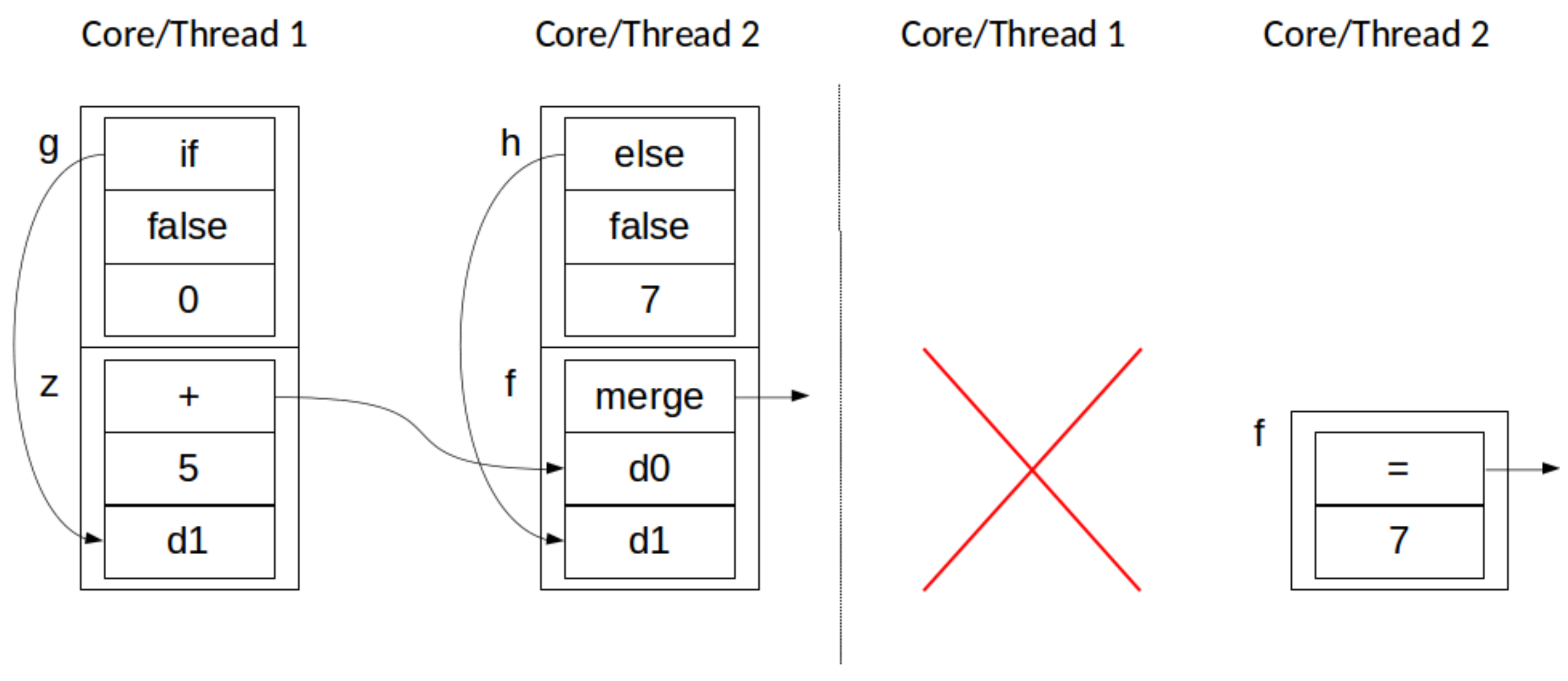
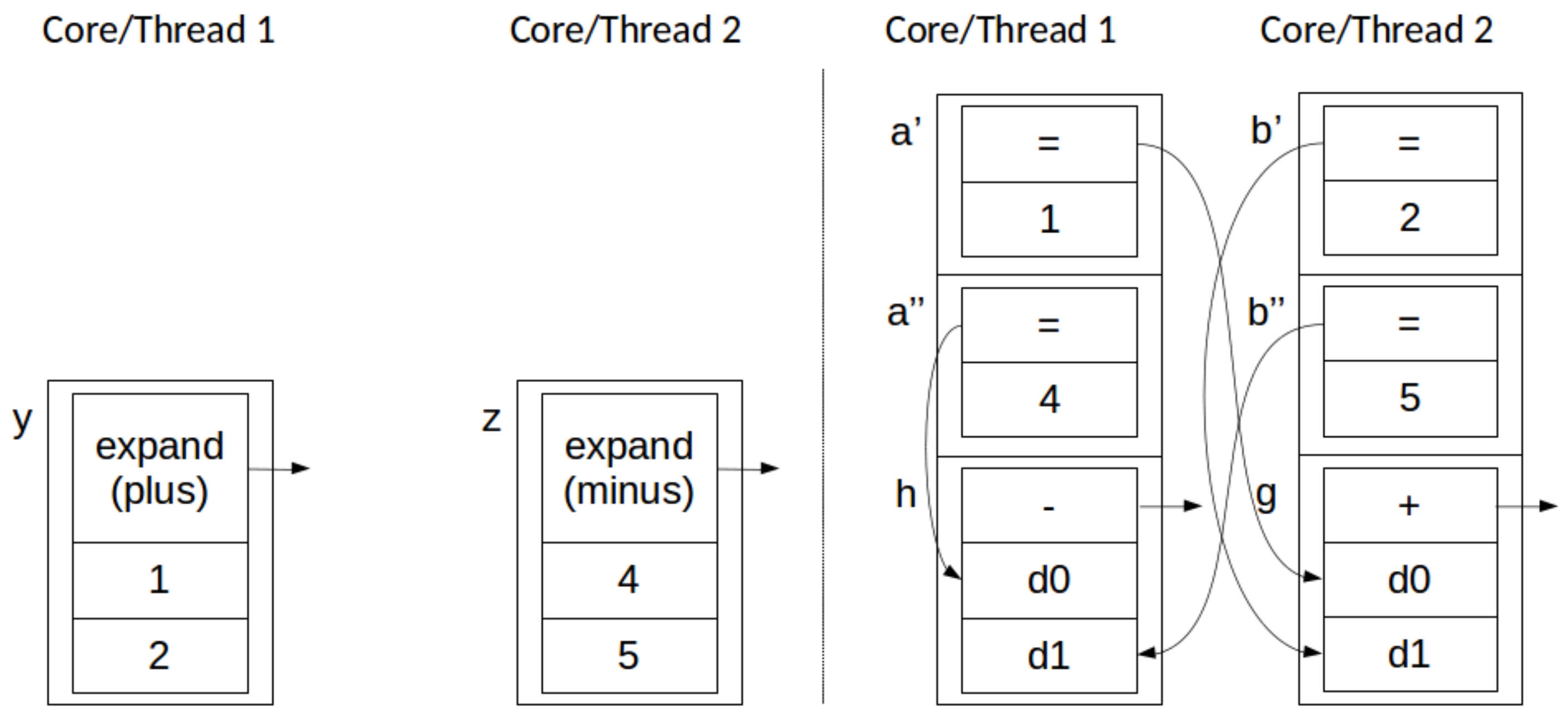
Application and Application: i.e., two concurrent stack transformations, both of the form . Removal from a set is commutative, so . The same property applies to the application of the primitive value x to the dependencies d of all elements in the stack present in the set e, such that , since syntactic rules in our programming model enforce that while and might have overlap, the position in the respective sets d is unique. Thus, two Application transformations can be applied in any order, or at the same time, with the same result. This behavior is depicted, in stack form, in Figure 4.
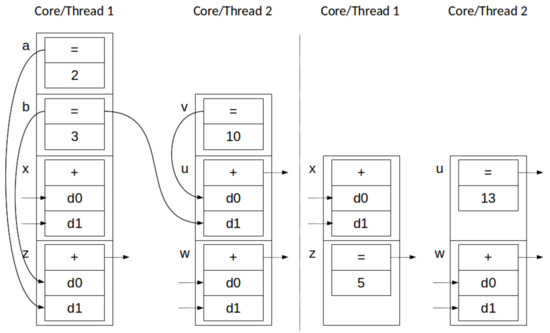
Figure 4.
Simultaneous applications across two parallel threads: before (left) and after (right).
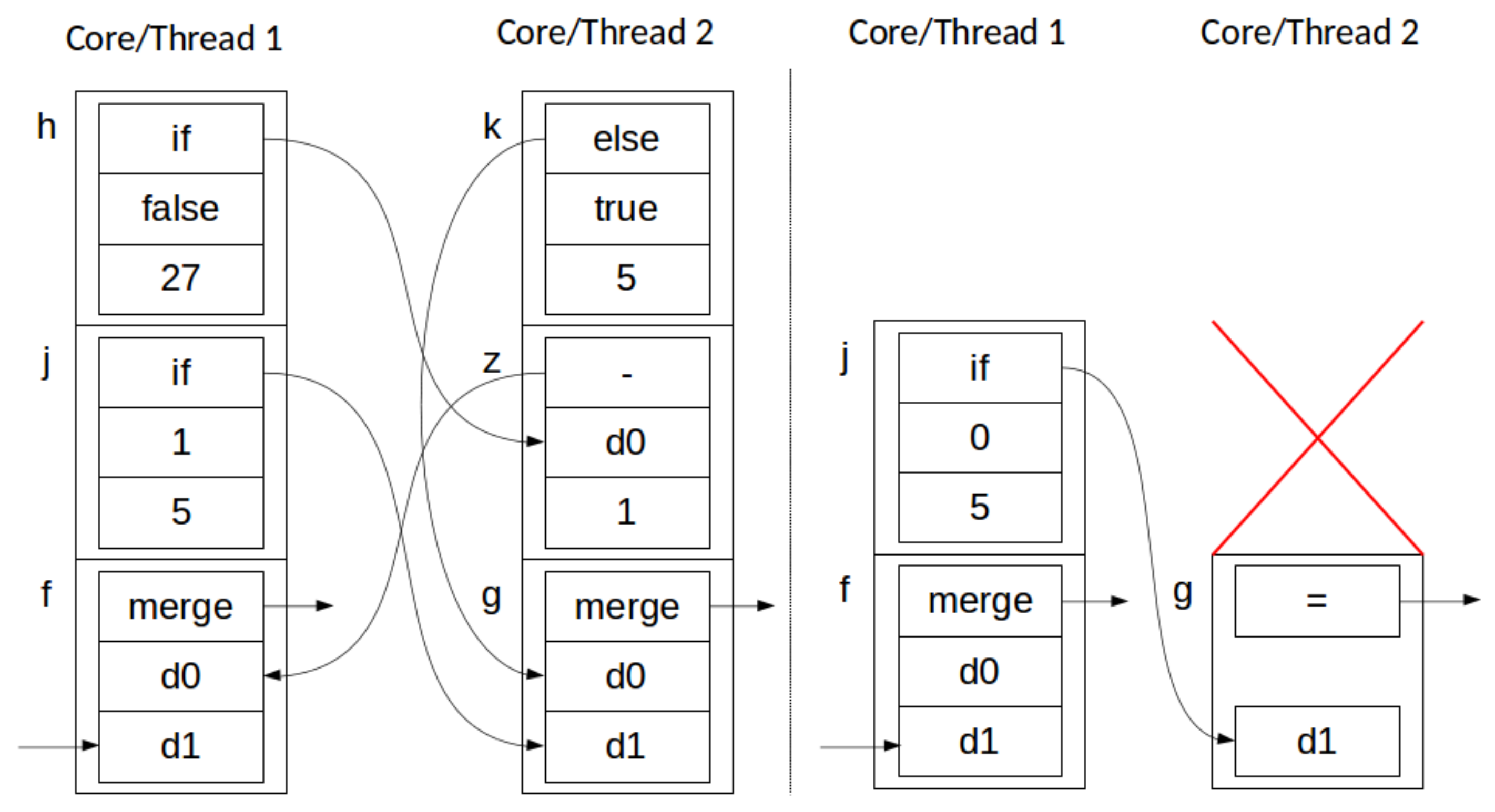
Application and Destruction, i.e., two concurrent stack transformations of the forms and . As before, removal is commutative. The relationship between and is less clear, but it becomes intuitive by realizing that ; i.e., the application of the value x to elements no longer on the stack has no effect. Because of this property, removal and value application are also commutative; thus, an Application transformation and a Destruction transformation can be applied in any order, or at the same time, with the same result (the exception to this is if a result of both applications is the same element with a merge construction function, but that would correspond to a poorly constructed program in our programming model). This behavior is depicted, in stack form, in Figure 5.
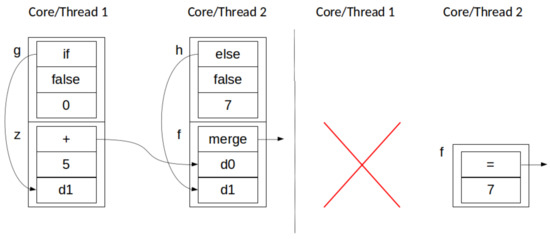
Figure 5.
Simultaneous application (thread 2) and destruction (thread 1) across two parallel threads: before (left) and after (right). Red arrow denotes a destroyed node.
Destruction and Destruction, i.e., two concurrent stack transformations, both of the form . Since set removal is commutative, two Destruction transformations can be applied in any order, or at the same time, with the same result (there is a potential exception to this, in the case that the element being evaluated, resulting in one of the transformations, is marked for removal in the other one, but this would correspond to a syntactic error in our programming model, so that case is not considered here). This behavior is depicted, in stack form, in Figure 6.
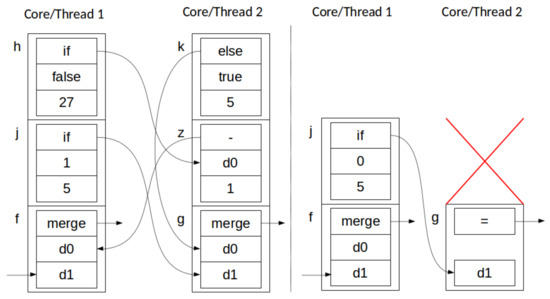
Figure 6.
Simultaneous destructions across two parallel threads: before (left) and after (right). Red arrow denotes destroyed node. One of the inputs of the merge node is destroyed, but the node remains in the stack. This example shows one core destroyed a node in another core’s stack.
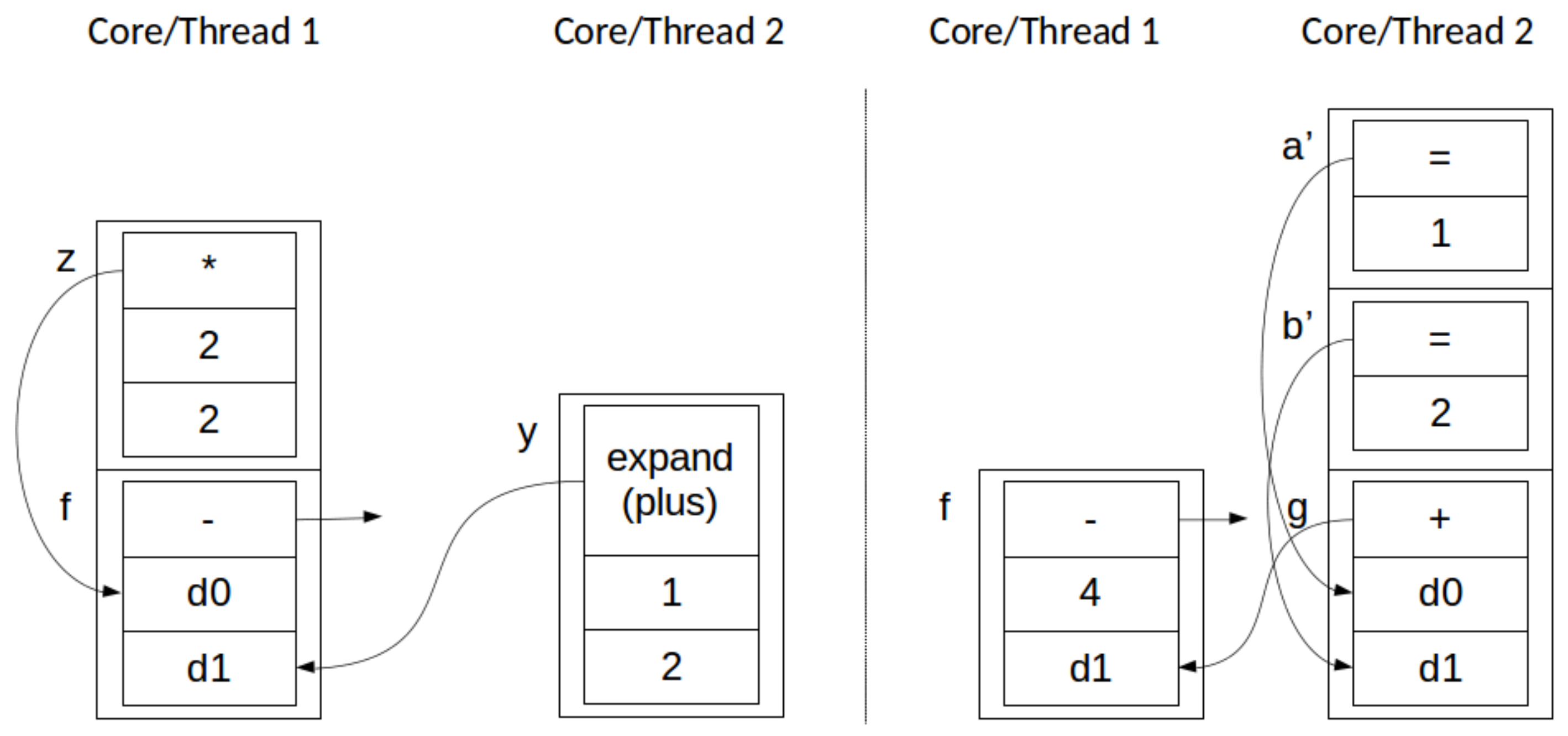
Application and Push, i.e., two concurrent stack transformations of the forms and . As before, removal is commutative. Since expansion is only evaluated if its dependencies are fully constructed, . Since arithmetic functions are only evaluated if its dependencies are fully constructed, . Because of these properties, and are commutative. Thus, an Application transformation and a Push transformation can be applied in any order, or at the same time, with the same result. This behavior is depicted, in stack form, in Figure 7.
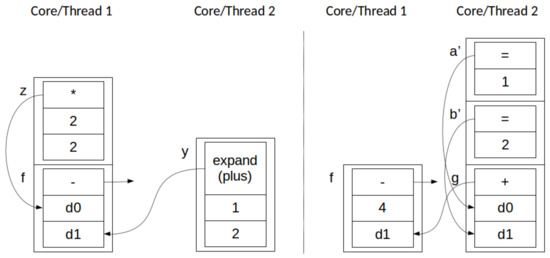
Figure 7.
Simultaneous application (thread 1) and push (thread 2) across two parallel threads: before (left) and after (right). Pushed (expanded) code is a simple addition of two newly-mapped nodes ( and in this example).
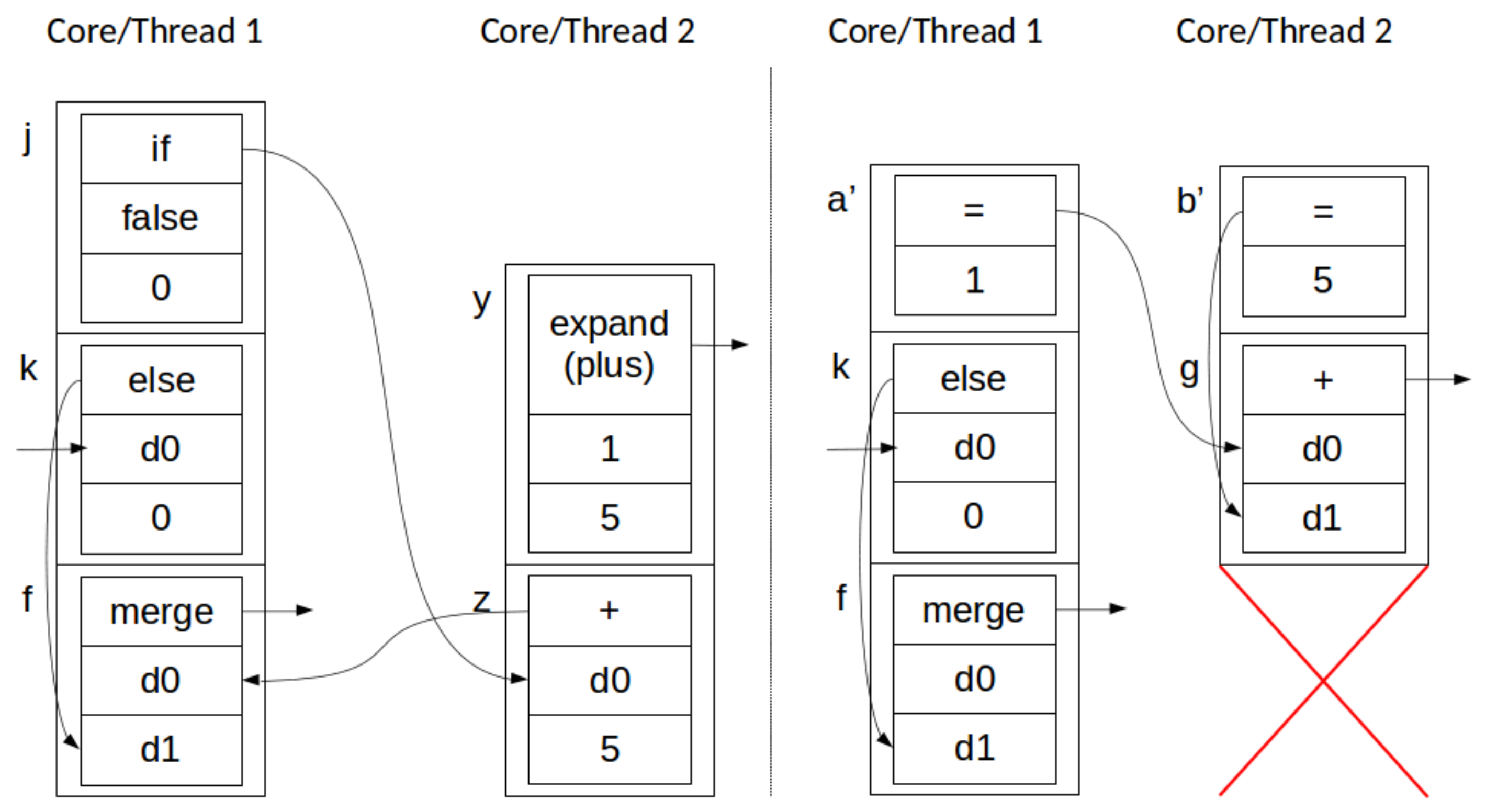
Destruction and Push, i.e., two concurrent stack transformations of the forms and . As before, removal is commutative. Since destruction is only applied to unconstructed elements (i.e., ones whose dependencies have not been fulfilled) and expansion is only evaluated if its dependencies are fully constructed, . It is possible that (resulting in an expansion that eventually results in an Application to non-existing elements), but as previously described, , i.e., the application of the value x to elements no longer on the stack has no effect. Thus, a Destruction transformation and a Push transformation can be applied in any order, or at the same time, with the same result. This behavior is depicted, in stack form, in Figure 8.
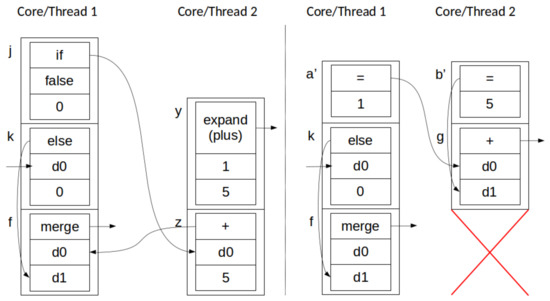
Figure 8.
Simultaneous destruction (thread 1) and push (thread 2) across two parallel threads: before (left) and after (right). Example depicts thread 1 destroying a node in thread 2’s memory, and thread 2 pushing nodes allocated to thread 1’s stack ().
Push and Push, i.e., two two concurrent stack transformations. In this case, both transformations are of the form . This is the only case where operations are not commutative, for strict ordering, as . However, if stack order is not important (and for the purposes of AGP, it is not), as long as graph structure is preserved, then the transformations are indeed commutative, resulting in the same elements pushed onto the top of respective stacks, preserving program structure and behavior. This behavior is depicted, in stack form, in Figure 9.
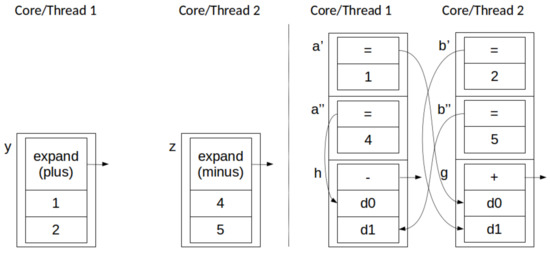
Figure 9.
Simultaneous pushes across two parallel threads: before (left) and after (right). Example depicts threads pushing nodes to their own and to one another’s stacks.
5. Experimental Evaluation
5.1. Evaluation Framework
We have implemented a prototype AGP compiler, chc, (publicly available here (https://github.com/paulofrgarcia-carleton/chc-public-release, last verified 14 November 2022)). The supported syntax is slightly different from the one presented in Listing 2, but the semantics are equivalent. chc generates a stack, populated by program nodes, following the transformation rules described in the previous sections. chc can also generate (posix-based) multithreaded C code that evaluates this stack in a portable manner, but that feature is meant for prototyping and quick evaluation rather than for deployment.
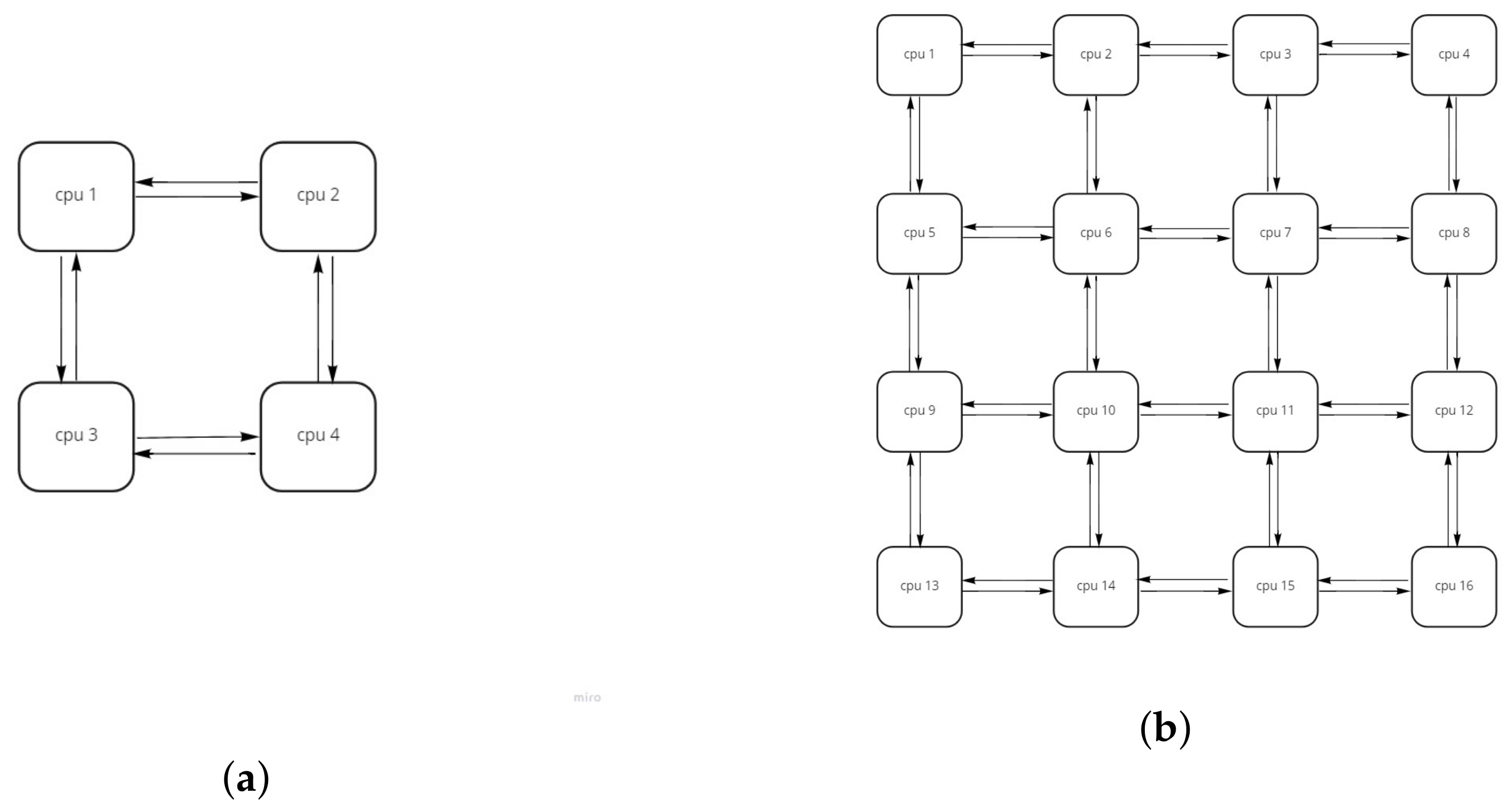
To properly empirically verify that AGP semantics guarantee correct parallelization by construction, we have set up a message-passing many-core simulation. Cores are organized in a grid-like fashion (e.g., Figure 10), with each core equipped with its own local memory; there is no shared memory across different cores. Each core can communicate with its neighbors through queues; i.e., core (i, j) can communicate with cores (i − 1, j), (i + 1, j), (i, j − 1), and (i, j + 1), if they exist. Rather than implementing functinal/cycle-accurate simulation of a given instruction set, each virtual core merely implements an evaluation algorithm to process AGP programs, as depicted in Algorithm 1. This model can be realized in silico using several possible implementation architectures, e.g., [35].
| Algorithm 1: Core evaluation loop. | |
| allocated nodes | |
| ifthen | ▹ Communication block |
| if N should be forwarded then | |
| else | |
| ▹ Update local stack with N | |
| end if | |
| end if | |
| whiledo | |
| while do | |
| ▹ Garbage Collect top of stack | |
| end while | |
| if = expansion() then | ▹ Should expand graph |
| ▹ Propagate nodes allocated elsewhere | |
| else | |
| results ← process(S) | |
| ▹ Update local stack and forward results to other cores | |
| end if | |
| end while |
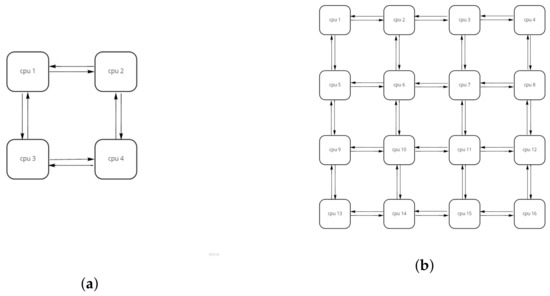
Figure 10.
Evaluation architecture: message-passing many-core simulation. (a) 2 × 2, (b) 4 × 4.
Nodes are allocated to cores at random at compile time. Node-allocation strategies are one of the fundamental properties to be explored within AGP, but they are outside the scope of this article and are reserved for future work. We make no claims about the quality of allocation strategies many are possible, within AGP, but our purpose in this article is to show that the paradigm allows for any feasible strategy to be employed, still resulting in correct program execution. Throughout our experiments, we allocate nodes randomly. All possible program nodes (i.e., even nodes from subgraphs not yet expanded) are mapped to cores, i.e., placed in their program memory. Each core traverses its internal stack, attempting to evaluate ready nodes. When a node is evaluated, its result is propagated to its dependents (either in local memory, if dependents are mapped to the same core, or across the message-passing channels). Each core also acts as a relay for messages.
When subgraphs are expanded, the core responsible for processing expansion populates its internal stack with all the subgraph nodes allocated to it and broadcasts a message so all other cores, if they have allocated subgraph nodes, do the same in their local stacks. Expanding core is then responsible for recalculating subgraph offsets and destinations, as well as propagating that information through the message-passing channels so other cores can update the newly pushed nodes as well accordingly.
5.2. Experiments and Results
We are interested in evaluating several things:
- Empirically verifying the correctness of arbitrary parallelization, supporting the validity of our formal semantics.
- Analyzing the distribution of operations within cores to understand the implementation impact of the paradigm (i.e., identify optimization opportunities for compilers).
- Measuring speedup compared to single-core execution, for various different node allocations.
To evaluate these properties, we constructed five micro-benchmarks. The first micro-benchmark (“Linear”) was constructed to offer very few parallelization opportunities: during most of its runtime, few data can be processed, as there is a direct sequential dependency between data. The second micro-benchmark (“Cascade”) presents four identical, and independent, computational streams. Third, fourth, and fifth benchmarks are matrix multiplications, for matrix sizes of 2 × 2, 4 × 4, and 8 × 8, respectively.
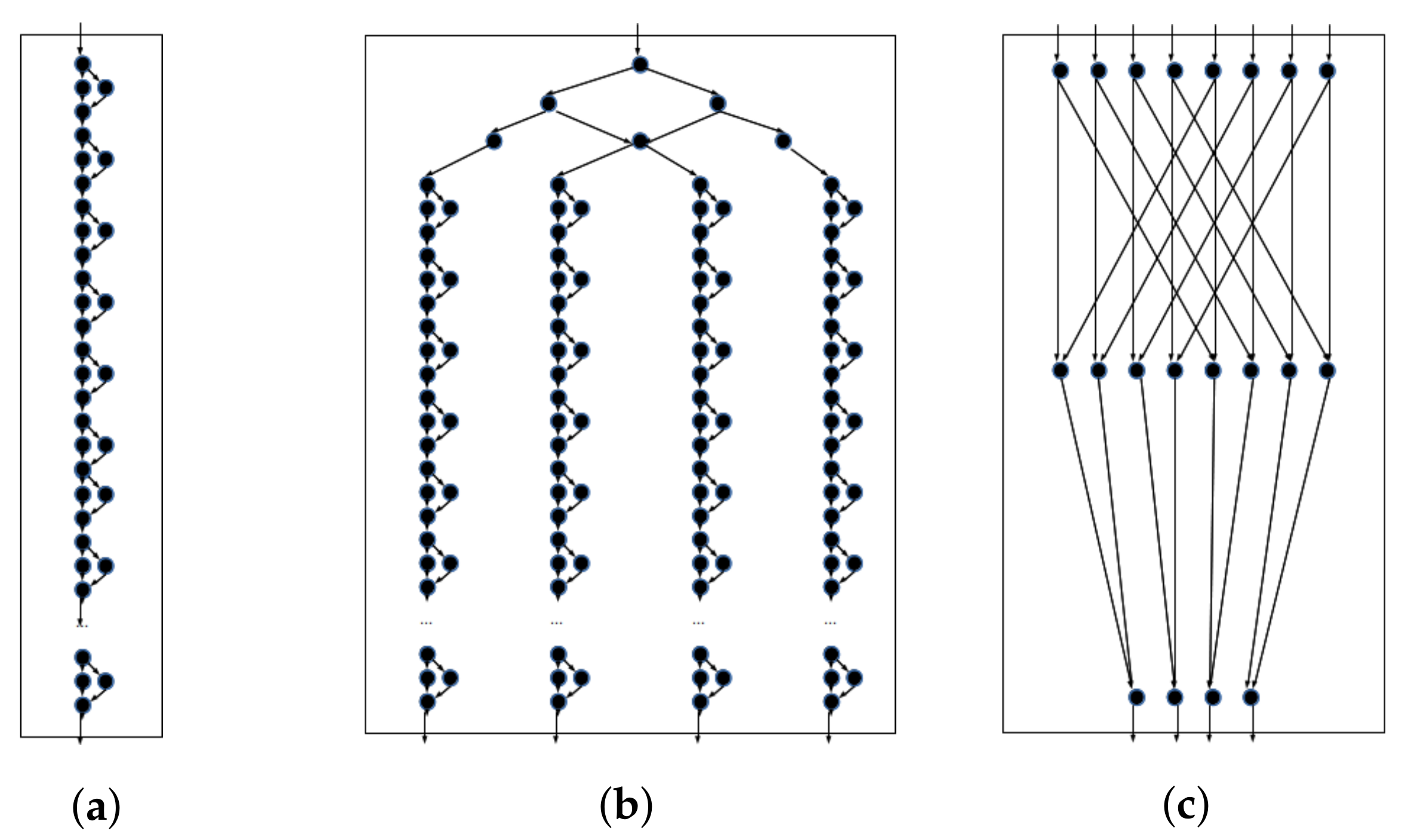
Benchmarks’ execution profiles are depicted in Figure 11 (matrix multiplication for sizes 4 × 4 and 8 × 8 are omitted, for brevity: these are similar to the 2 × 2 version, but with wider, and a higher number of, rows). These are not canonical program representations expressed in AGP, as was the case in Figure 1; rather, they are visual depictions of the lifetime of complete programs, to illustrate runtime data dependencies. AGP source code for these benchmarks are included in the simulation architecture, available here (https://github.com/layeghimahsa/AGP_compiler_chc, last verified 14 November 2022), for those interested in replicating/extending our results or repurposing chc and the simulation framework for other purposes.
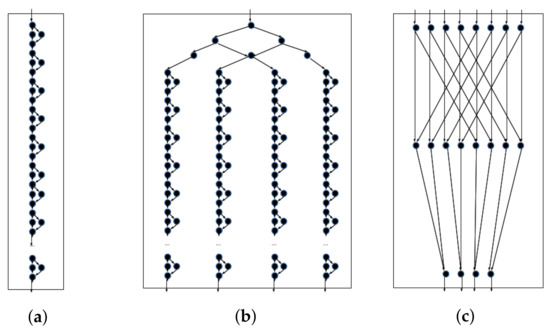
Figure 11.
Benchmarks’ execution profile. These plots do not represent canonical program implementations: rather, they depict full graph expansions throughout program runtime. Input nodes are depicted on the top and output nodes at the bottom. (a) Linear. (b) Cascade. (c) Matrix multiplication 2 × 2.
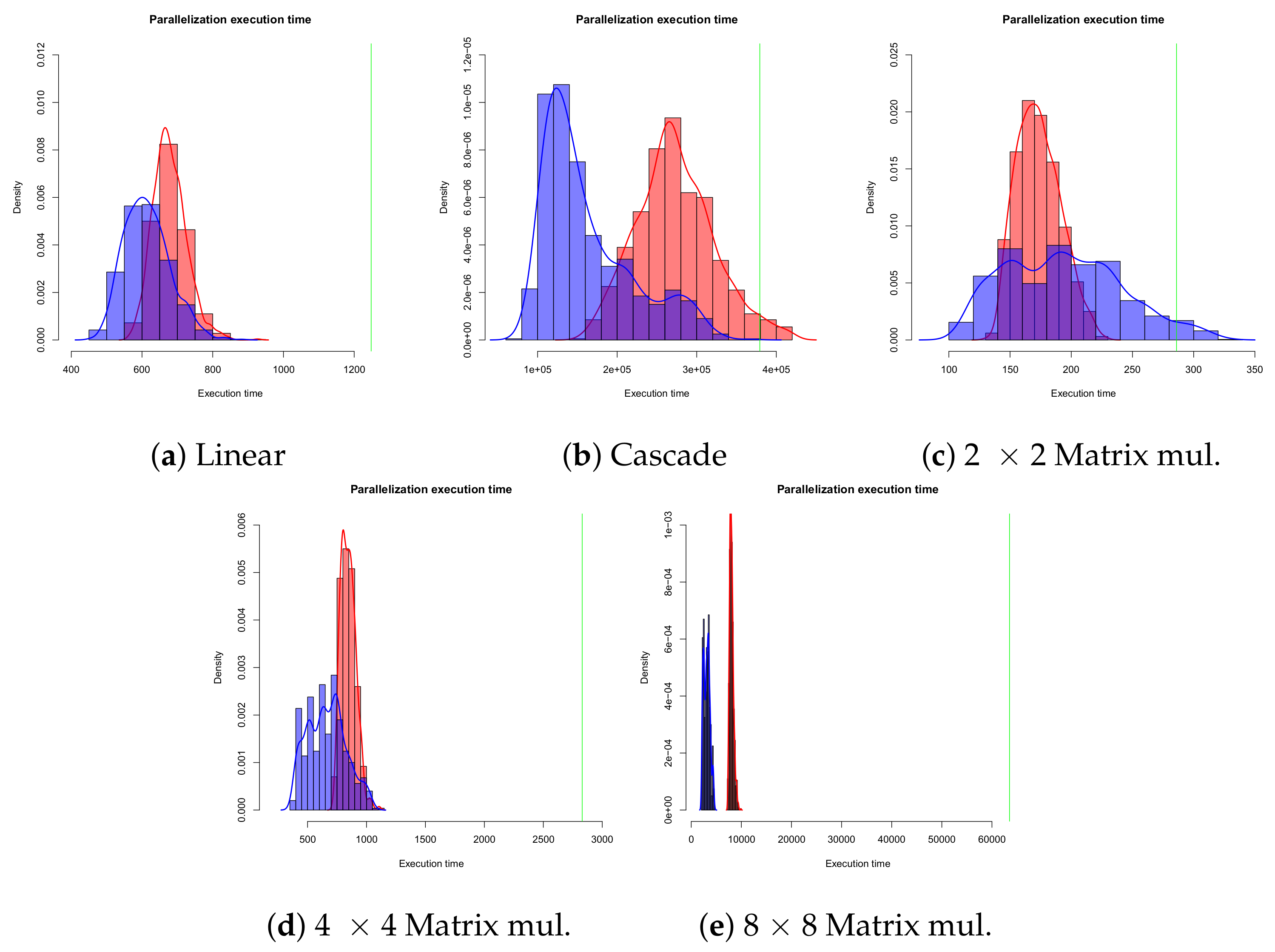
We ran 1000 instances of each benchmark, randomly allocating nodes across cores, for 1, 2 × 2, 4 × 4 and 8 × 8 multi-core configurations. While the solution space is far too large to be comprehensively covered, random allocation allows us to sample the space without designer biases. For every run, we confirmed that programs terminated and returned the correct results (they did), supporting the validity of our claim that AGP programs can be arbitrarily parallelized as described in our formal semantics. Figure 12 depicts execution time histograms for each benchmark (single-core execution time is marked by the vertical green line). Average results, with standard deviations, are depicted in Table 1.
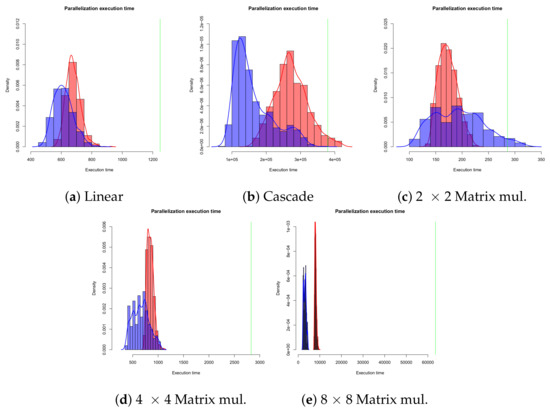
Figure 12.
Execution time histograms for each benchmark. Single-core execution time is marked by the vertical green line. Red bars represent runs in the 2 × 2 configuration; blue bars represent runs in the 4 × 4 configuration.

Table 1.
Average Execution Time (in simulation ticks) per benchmark across configurations.
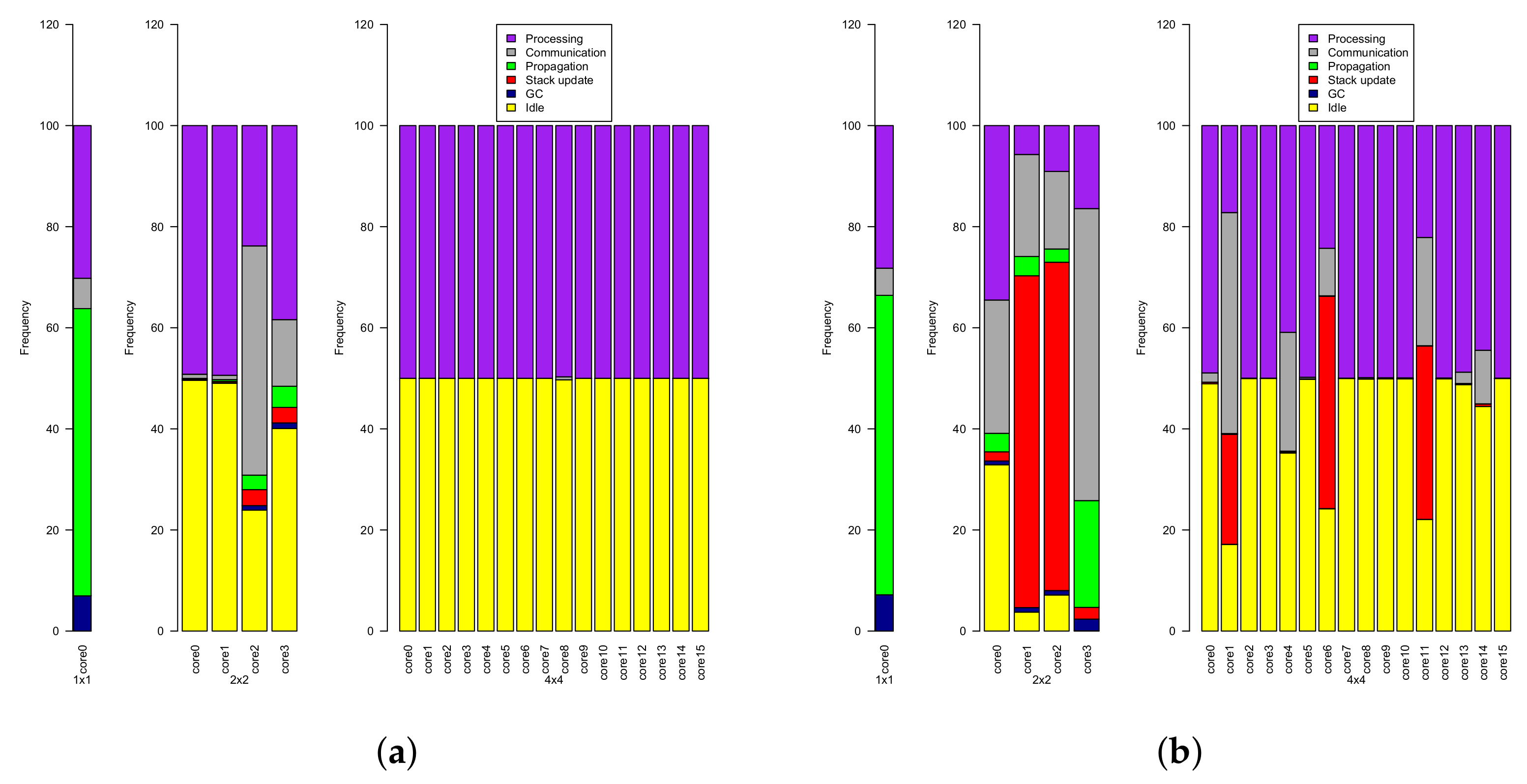
We then instrumented the simulation framework to profile cores’ states during program execution to analyze the distribution of operations within cores. Results for a randomly selected run of Linear and Cascade are depicted in Figure 13 for 1, 2 × 2 and 4 × 4 configurations.
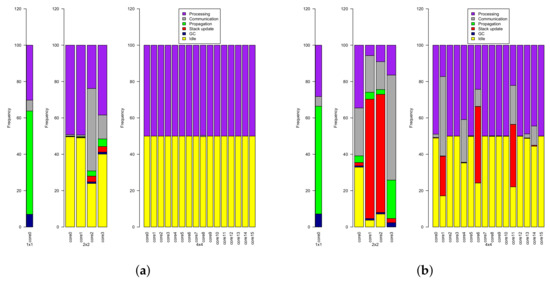
Figure 13.
Core utilization for different dimensionalities across two synthetic benchmarks (a) Linear and (b) Cascade.
In Figure 13, idle time (yellow) depicts the percentage of time spent when a core is certain it has no ready nodes to process. Processing time (purple) includes the percentage of time actually evaluating a node, as well as the percentage of time traversing a core’s allocated nodes to determine whether or not some node is valid (as they may change as a result of communication from other cores). Stack update (red) is the percentage of time spent pushing nodes to its local stack, as a result of an expansion triggered by another core that is communicating that information, and communication time (grey) is the percentage of time spent processing messages (either reading to self, transmitting from self, or relaying).
5.3. Discussion of Results
Our results support our formal semantics; i.e., AGP can be arbitrarily parallelized with guaranteed correct execution. We have not provided a full formal proof derivation that guarantees correctness of arbitrary parallelization but a clear formulation of the computational model that is used to explain the supporting empirical results.
Analysis of processor state reveals more interesting properties (Figure 13). Unsurprisingly, single-core execution spends most of the time processing nodes and propagating results across the graph. We observe a small amount of communication time, despite having a single core, because of how garbage collection is implemented (node pruning broadcasts a message to all cores to eliminate dead nodes, even if there is just one core). As the number of cores increases, several spend a significant amount of time communicating data to others (as a result of processing subgraph expansion), which in turn leads to other cores spending a significant amount of time updating their local stack (this is especially visible in Figure 13 for benchmark (b), which is highly recursive, expanding multiple subgraphs, in 2 × 2 and 4 × 4 configurations). Essentially, the allocation separates subgraphs across cores, resulting in significant communication overhead to process a subgraph expansion. This is consistent with the graph-partitioning strategies we alluded to previously: node allocation must take into account graph locality to better utilize parallelism.
On average, execution time significantly decreases as the degree of parallelism increases: experiments show it is possible to reduce execution time between 28% and 87%, when moving from single-core to a 2 × 2 multi-core configuration, and between 33% and 95%, when moving from single-core to a 4 × 4 multi-core configuration. As our simulation does not implement a specific instruction set, but rather a direct interpretation of AGP semantics, these results abstract important real runtime details; nonetheless, they showcase the potential of the model of computation. Future work must assess how concrete implementations fare.
5.4. Deployment Considerations
We have not yet performed an in-depth evaluation of how processor architectural features affect the execution of AGP programs, but it is worth discussing expectations and preliminary experiences.
Subsections of AGP programs that can be evaluated synchronously (because there are no asynchronous dependencies within the subgraph) are essentially equivalent to imperative programs: an optimizing compiler would produce fundamentally equivalent code. Thus, architectural considerations are not relevant to a comparison of AGP and other paradigms.
Asynchronous subsections, where parallelization can be beneficially employed, are relevant. If parallelization is ideally performed, then the instruction stream on any given core would be locally synchronous; i.e., equivalent to imperative execution. If parallelization is not ideally performed (either because of the parallelization strategy or because the degree of possible parallelization, in function of number of cores, exceeds program possibilities), then a core would be executing an asynchronous instruction stream: from the machine code perspective, a sequence of fairly independent instructions. Deeply pipelined cores are then not likely to be negatively affected by AGP execution: for example, branch mis-prediction penalties are likely to be negligible. In superscalar, speculative, out-of-order execution, the asynchronous nature of this instruction stream is likely to offer higher possibilities for keeping processors busy, as there are few dependencies between instructions. The caveat is that, because of this independence, cache locality (both spatial and temporal) is likely to be small: thus, we can likely expect low cache hit-rate. Whether processor utilization or cache utilization is the bigger contributor to performance in an AGP program is not yet known.
6. Related Work
In Section 2, we categorized the different approaches to the automatic parallelization of programs, which we group under source code, compilation, and models of computation for parallelization. Here, we focus our attention on recent endeavors in each category, comparing and contrasting them with the approach described in this article.
6.1. Source Code Parallelization
At the program source level, recent advances have proposed new memory models [36] (in contrast with the traditional sequential consistency model) that allow for aggressive compiler optimizations, supported by novel exception mechanisms that incur little cognitive overhead for programmers. Similar work, at the hardware level but with implications on programmability, is explored in [37]. Source analysis to guarantee parallel program correctness (i.e., pre-compilation checkers) is described in [38], in the context of a source data-race checker. AGP takes a very different approach: the programmer needs to be concerned not with parallelization but instead with data dependencies and control flow within single assignment semantics. Interpreting the written graph as a series-parallel partial order, parallelism is then automatically (and correctly) extracted from the program representation by graph analysis, and sequentiality (as explicitly implied by the programmer) is preserved by node dependencies.
6.2. Compile-Time Parallelization
The fundamental challenge in compile-time parallelization is to guarantee that program partitioning will result in correct execution, and this is primarily driven by the synchronization constructs between parallel portions. The use of impredicative Concurrent Abstract Predicates is explored in [39] to verify the correctness of both standard and custom synchronization constructs. Similarly, [40] describes a high-level language and a compiler optimization methodology for automatic parallelization in a conflict-free manner. At a lower level of granularity, affine transformations have shown great promise in loop restructuring, especially when driven by architecture-informed cost functions [41]; within this research track, fusion conflict graphs seem to implement a subset of AGP functionality [42]. The use of graphs as compiler tools is, of course, not new; a domain-specific language compiler for the transformation of graphs into message-passing implementations is described in [43], and similar technology targeting GPUs are presented in [44]. Technologies such as Tapir [45] allow fork-join parallelism (e.g., as supported by Cilk and OpenMP) to be embedded into LLVM’s intermediate representation. AGP again takes a different approach from verifying synchronization constructs: rather than focusing on the correct implementation of a given parallelization strategy, AGP enforces a parallelization strategy that is correct by construction (see Section 4).
Compiler-time parallelism is now focusing on speculative parallelization (particularly to take advantage of runtime information): a comprehensive review of existing techniques is presented in [46]. Whil not necessarily a method for parallelization, [47] is a compile-time technique (technically design time, as it includes pre-compilation simulations and cross-checking) for the verification of concurrent system design, particularly focused on guaranteeing that bottom layers obey the parallel architectures specified at higher levels. Similarly, the toolchain described in [16] takes advantage of hardware side-channels to extract multi-core profiles without disturbing software, and technologies for highly parallel, heterogeneous systems simulation such as [11] are driving compiler optimizations. These techniques and technologies are orthogonal to AGP and in fact will be leveraged in future work to drive compile-time and runtime parallelization strategies.
6.3. Parallel Models of Computation
Different parallel models of computation (referred to as concurrency models in [48]) such as the actor model, futures, and transactions, are combined in the Chocola language, a unified language that attempts to maintain the guarantees of each model, even when they are combined. This multi-model approach lends itself quite well to fine-tuning for particular applications, but still requires cognitive effort by the programmer to select and implement the appropriate model. The streaming model of computation, already well-established in image processing, is now being applied for big data across large, distributed systems through novel paradigms, supported, of course, by implementations such as SPL [49]. More generally, OpenMP [50] seems to continue to summarize the parallelization zeitgeist, as its model of computation can be leveraged across several toolchains. OpenMP targets coarse-grained parallelization, where the allocation across parallel threads occurs pre-compilation (either heuristically or supported by profiling). In contrast, AGP takes the approach of fine-grained parallelization, using a model that can, theoretically, allocate processing to threads regardless of which conceptual computation those nodes belong to. Much like OpenMP, however, AGP does not restrict itself to shared memory machines, as the IO model can be mapped across myriad input/output strategies. Formal parallel methods such as BSP [51] are orthogonal to AGP and are good sources of node-allocation strategies.
7. Conclusions
This article introduced Asynchronous Graph Programming, a programming model and an associated MoC for arbitrary code parallelization. AGP allows expressing programs such that they can be arbitrarily partitioned across N parallel processing elements, maintaining semantic correctness. Moreover, the paradigm allows parallelization to be (re)applied at any stage of runtime, lending itself to use across heterogeneous, runtime-reconfigurable parallel systems. We have shown how AGP, an instance of series-parallel partial order, can be used to express programs, and how its graph architecture can be mapped onto a stack-based flat address space. We formally described how stack operations, used to evaluate AGP programs, are parallel-safe, and empirically verified the correctness of and evaluated improvements for automatic parallelization of five micro-benchmarks. Our prototype AGP compiler, chc, is open-source, and we expect to extend it in the near future and maintain it for the foreseeable future.
Our experiments suggest that node allocation must take into account graph locality to better utilize parallelism; node allocation should reflect program dependencies, which can be inferred from graph connections when expressed in AGP.
Our ongoing research encompasses several directions. Our work on the chc prototype continues: we are extending the generated runtime system with low-level IO hooks and on compiler mechanisms to map (and remap) nodes’ input/output operations onto those IOs. Runtime reconfiguration (re-allocation of nodes across threads and dynamically spawning new threads) is being prototyped on heterogeneous multi-cores driven by performance-energy profiles. Finally, we are experimenting with high-level languages that compile down to AGP, and what sorts of semantics and properties can be leveraged at that level.
Author Contributions
Conceptualization, P.G.; methodology, P.G.; software, S.C. and P.G.; validation, S.C. and P.G.; formal analysis, P.G.; writing—original draft preparation, P.G.; writing—review and editing, P.G.; visualization, P.G.; supervision, P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Babak Esfandiari provided invaluable feedback on an early draft of this article. The ideas behind AGP came from long discussions about programming paradigms with Robert Stewart, frequently at the pub.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rau, B.R.; Fisher, J.A. Instruction-level parallel processing: History, overview, and perspective. In Instruction-Level Parallelism; Springer: Berlin/Heidelberg, Germany, 1993; pp. 9–50. [Google Scholar]
- Krishnaiyer, R.; Kultursay, E.; Chawla, P.; Preis, S.; Zvezdin, A.; Saito, H. Compiler-based data prefetching and streaming non-temporal store generation for the intel (r) xeon phi (tm) coprocessor. In Proceedings of the 2013 IEEE International Symposium on Parallel & Distributed Processing, Workshops and Phd Forum, Cambridge, MA, USA, 20–24 May 2013; pp. 1575–1586. [Google Scholar]
- Cho, S.; Melhem, R.G. On the interplay of parallelization, program performance, and energy consumption. IEEE Trans. Parallel Distrib. Syst. 2009, 21, 342–353. [Google Scholar] [CrossRef]
- Diaz, J.; Munoz-Caro, C.; Nino, A. A survey of parallel programming models and tools in the multi and many-core era. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1369–1386. [Google Scholar] [CrossRef]
- Lukefahr, A.; Padmanabha, S.; Das, R.; Dreslinski, R., Jr.; Wenisch, T.F.; Mahlke, S. Heterogeneous microarchitectures trump voltage scaling for low-power cores. In Proceedings of the Proceedings of the 23rd International Conference on Parallel Architectures and Compilation, Edmonton, AB, Canada, 24–27 August 2014; pp. 237–250. [Google Scholar]
- El-Araby, E.; Gonzalez, I.; El-Ghazawi, T. Exploiting partial runtime reconfiguration for high-performance reconfigurable computing. ACM Trans. Reconfigurable Technol. Syst. (TRETS) 2009, 1, 21. [Google Scholar] [CrossRef]
- Liu, S.; Pittman, R.N.; Forin, A.; Gaudiot, J.L. Achieving energy efficiency through runtime partial reconfiguration on reconfigurable systems. ACM Trans. Embed. Comput. Syst. (TECS) 2013, 12, 72. [Google Scholar] [CrossRef]
- Leung, S.T.; Zahorjan, J. Improving the performance of runtime parallelization. In Proceedings of the Fourth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, New York, NY, USA, 19–23 May 1993; pp. 83–91. [Google Scholar]
- Dogan, H.; Ahmad, M.; Kahne, B.; Khan, O. Accelerating Synchronization Using Moving Compute to Data Model at 1,000-Core Multicore Scale. ACM Trans. Archit. Code Optim. 2019, 16, 1–27. [Google Scholar] [CrossRef]
- Gamatié, A.; Devic, G.; Sassatelli, G.; Bernabovi, S.; Naudin, P.; Chapman, M. Towards energy-efficient heterogeneous multicore architectures for edge computing. IEEE Access 2019, 7, 49474–49491. [Google Scholar] [CrossRef]
- Tampouratzis, N.; Papaefstathiou, I.; Nikitakis, A.; Brokalakis, A.; Andrianakis, S.; Dollas, A.; Marcon, M.; Plebani, E. A Novel, Highly Integrated Simulator for Parallel and Distributed Systems. ACM Trans. Archit. Code Optim. 2020, 17, 1–28. [Google Scholar] [CrossRef]
- Scaife, N.; Horiguchi, S.; Michaelson, G.; Bristow, P. A parallel SML compiler based on algorithmic skeletons. J. Funct. Program. 2005, 15, 615. [Google Scholar] [CrossRef]
- Butko, A.; Bruguier, F.; Gamatié, A.; Sassatelli, G. Efficient programming for multicore processor heterogeneity: Openmp versus ompss. In Proceedings of the OpenSuCo, Frankfurt, Germany, 20 June 2017. [Google Scholar]
- Thoman, P.; Dichev, K.; Heller, T.; Iakymchuk, R.; Aguilar, X.; Hasanov, K.; Gschwandtner, P.; Lemarinier, P.; Markidis, S.; Jordan, H.; et al. A taxonomy of task-based parallel programming technologies for high-performance computing. J. Supercomput. 2018, 74, 1422–1434. [Google Scholar] [CrossRef]
- Ying, V.A.; Jeffrey, M.C.; Sanchez, D. T4: Compiling sequential code for effective speculative parallelization in hardware. In Proceedings of the 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 30 May–3 June 2020; pp. 159–172. [Google Scholar]
- France-Pillois, M.; Martin, J.; Rousseau, F. A Non-Intrusive Tool Chain to Optimize MPSoC End-to-End Systems. ACM Trans. Archit. Code Optim. (TACO) 2021, 18, 21. [Google Scholar] [CrossRef]
- Rasch, A.; Schulze, R.; Steuwer, M.; Gorlatch, S. Efficient Auto-Tuning of Parallel Programs with Interdependent Tuning Parameters via Auto-Tuning Framework (ATF). ACM Trans. Archit. Code Optim. 2021, 18, 1. [Google Scholar] [CrossRef]
- Muller, S.K.; Singer, K.; Goldstein, N.; Acar, U.A.; Agrawal, K.; Lee, I.T.A. Responsive parallelism with futures and state. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, London, UK, 15–20 June 2020; pp. 577–591. [Google Scholar]
- Wang, Y.E.; Wu, C.J.; Wang, X.; Hazelwood, K.; Brooks, D. Exploiting Parallelism Opportunities with Deep Learning Frameworks. ACM Trans. Archit. Code Optim. 2021, 18, 9. [Google Scholar] [CrossRef]
- Röger, H.; Mayer, R. A comprehensive survey on parallelization and elasticity in stream processing. ACM Comput. Surv. (CSUR) 2019, 52, 36. [Google Scholar] [CrossRef]
- Hou, N.; Yan, X.; He, F. A survey on partitioning models, solution algorithms and algorithm parallelization for hardware/software co-design. Des. Autom. Embed. Syst. 2019, 23, 57–77. [Google Scholar] [CrossRef]
- Hanxleden, R.V.; Mendler, M.; Aguado, J.; Duderstadt, B.; Fuhrmann, I.; Motika, C.; Mercer, S.; O’brien, O.; Roop, P. Sequentially Constructive Concurrency—A Conservative Extension of the Synchronous Model of Computation. ACM Trans. Embed. Comput. Syst. 2014, 13, 144. [Google Scholar] [CrossRef]
- Hokkanen, J.; Kraus, J.; Herten, A.; Pleiter, D.; Kollet, S. Accelerated hydrologic modeling: ParFlow GPU implementation. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 4–8 May 2020; p. 12904. [Google Scholar]
- Forster, Y.; Smolka, G. Weak call-by-value lambda calculus as a model of computation in Coq. In Proceedings of the International Conference on Interactive Theorem Proving, Brasília, Brazil, 26–29 September 2017; Springer: Cham, Switzerland, 2017; pp. 189–206. [Google Scholar]
- Cristescu, I.D.; Krivine, J.; Varacca, D. Rigid Families for CCS and the Pi-calculus. In Proceedings of the International Colloquium on Theoretical Aspects of Computing, Cali, Colombia, 29–31 October 2015; Springer: Cham, Switzerland, 2015; pp. 223–240. [Google Scholar]
- Burckhardt, S.; Leijen, D.; Sadowski, C.; Yi, J.; Ball, T. Two for the price of one: A model for parallel and incremental computation. ACM SIGPLAN Not. 2011, 46, 427–444. [Google Scholar] [CrossRef]
- Gao, G.R.; Sterling, T.; Stevens, R.; Hereld, M.; Zhu, W. ParalleX: A Study of A New Parallel Computation Model. In Proceedings of the 2007 IEEE International Parallel and Distributed Processing Symposium, Long Beach, CA, USA, 26–30 March 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Fryer, J.; Garcia, P. Towards a Programming Paradigm for Reconfigurable Computing: Asynchronous Graph Programming. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; Volume 1, pp. 1721–1728. [Google Scholar]
- Engler, D.; Ashcraft, K. RacerX: Effective, static detection of race conditions and deadlocks. ACM SIGOPS Oper. Syst. Rev. 2003, 37, 237–252. [Google Scholar] [CrossRef]
- Coelho, R.; Tanus, F.; Moreira, A.; Nazar, G. ACQuA: A Parallel Accelerator Architecture for Pure Functional Programs. In Proceedings of the 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 6–8 July 2020; pp. 346–351. [Google Scholar] [CrossRef]
- Lifflander, J.; Krishnamoorthy, S. Cache locality optimization for recursive programs. In Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, Barcelona, Spain, 18–23 June 2017; pp. 1–16. [Google Scholar]
- Molka, D.; Hackenberg, D.; Schone, R.; Muller, M.S. Memory performance and cache coherency effects on an intel nehalem multiprocessor system. In Proceedings of the 2009 18th International Conference on Parallel Architectures and Compilation Techniques, Raleigh, NC, USA, 12–16 September 2009; pp. 261–270. [Google Scholar]
- Cyphers, S.; Bansal, A.K.; Bhiwandiwalla, A.; Bobba, J.; Brookhart, M.; Chakraborty, A.; Constable, W.; Convey, C.; Cook, L.; Kanawi, O.; et al. Intel ngraph: An intermediate representation, compiler, and executor for deep learning. arXiv 2018, arXiv:1801.08058. [Google Scholar]
- Tiganourias, E.; Mavropoulos, M.; Keramidas, G.; Kelefouras, V.; Antonopoulos, C.P.; Voros, N. A Hierarchical Profiler of Intermediate Representation Code based on LLVM. In Proceedings of the 2021 10th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 7–10 June 2021; pp. 1–5. [Google Scholar]
- Wang, P.; McAllister, J. Streaming elements for FPGA signal and image processing accelerators. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 2262–2274. [Google Scholar] [CrossRef]
- Marino, D.; Singh, A.; Millstein, T.; Musuvathi, M.; Narayanasamy, S. DRFx: An Understandable, High Performance, and Flexible Memory Model for Concurrent Languages. ACM Trans. Program. Lang. Syst. 2016, 38, 16. [Google Scholar] [CrossRef]
- Puthoor, S.; Lipasti, M.H. Systems-on-Chip with Strong Ordering. ACM Trans. Archit. Code Optim. 2021, 18, 15. [Google Scholar] [CrossRef]
- Bora, U.; Das, S.; Kukreja, P.; Joshi, S.; Upadrasta, R.; Rajopadhye, S. LLOV: A Fast Static Data-Race Checker for OpenMP Programs. ACM Trans. Archit. Code Optim. 2020, 17, 35. [Google Scholar] [CrossRef]
- Dodds, M.; Jagannathan, S.; Parkinson, M.J.; Svendsen, K.; Birkedal, L. Verifying Custom Synchronization Constructs Using Higher-Order Separation Logic. ACM Trans. Program. Lang. Syst. 2016, 38, 4. [Google Scholar] [CrossRef]
- Liu, Y.A.; Stoller, S.D.; Lin, B. From Clarity to Efficiency for Distributed Algorithms. ACM Trans. Program. Lang. Syst. 2017, 39, 12. [Google Scholar] [CrossRef]
- Bondhugula, U.; Acharya, A.; Cohen, A. The Pluto+ Algorithm: A Practical Approach for Parallelization and Locality Optimization of Affine Loop Nests. ACM Trans. Program. Lang. Syst. 2016, 38, 12. [Google Scholar] [CrossRef]
- Acharya, A.; Bondhugula, U.; Cohen, A. Effective Loop Fusion in Polyhedral Compilation Using Fusion Conflict Graphs. ACM Trans. Archit. Code Optim. 2020, 17, 26. [Google Scholar] [CrossRef]
- Rajendran, A.; Nandivada, V.K. DisGCo: A Compiler for Distributed Graph Analytics. ACM Trans. Archit. Code Optim. 2020, 17, 28. [Google Scholar] [CrossRef]
- Zhang, Y.; Liao, X.; Gu, L.; Jin, H.; Hu, K.; Liu, H.; He, B. AsynGraph: Maximizing Data Parallelism for Efficient Iterative Graph Processing on GPUs. ACM Trans. Archit. Code Optim. 2020, 17, 29. [Google Scholar] [CrossRef]
- Schardl, T.B.; Moses, W.S.; Leiserson, C.E. Tapir: Embedding Fork-Join Parallelism into LLVM’s Intermediate Representation. SIGPLAN Not. 2017, 52, 249–265. [Google Scholar] [CrossRef]
- Yiapanis, P.; Brown, G.; Luján, M. Compiler-Driven Software Speculation for Thread-Level Parallelism. ACM Trans. Program. Lang. Syst. 2015, 38, 5. [Google Scholar] [CrossRef]
- Sanan, D.; Zhao, Y.; Lin, S.W.; Yang, L. CSim2: Compositional Top-down Verification of Concurrent Systems Using Rely-Guarantee. ACM Trans. Program. Lang. Syst. 2021, 43, 2. [Google Scholar] [CrossRef]
- Swalens, J.; Koster, J.D.; Meuter, W.D. Chocola: Composable Concurrency Language. ACM Trans. Program. Lang. Syst. 2021, 42, 17. [Google Scholar] [CrossRef]
- Hirzel, M.; Schneider, S.; Gedik, B. SPL: An Extensible Language for Distributed Stream Processing. ACM Trans. Program. Lang. Syst. 2017, 39, 5. [Google Scholar] [CrossRef]
- de Supinski, B.R.; Scogland, T.R.; Duran, A.; Klemm, M.; Bellido, S.M.; Olivier, S.L.; Terboven, C.; Mattson, T.G. The ongoing evolution of openmp. Proc. IEEE 2018, 106, 2004–2019. [Google Scholar] [CrossRef]
- Gerbessiotis, A.; Valiant, L. Direct Bulk-Synchronous Parallel Algorithms. J. Parallel Distrib. Comput. 1994, 22, 251–267. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).