Multi-Period Optimal Reactive Power Dispatch Using a Mean-Variance Mapping Optimization Algorithm
Abstract
:1. Introduction
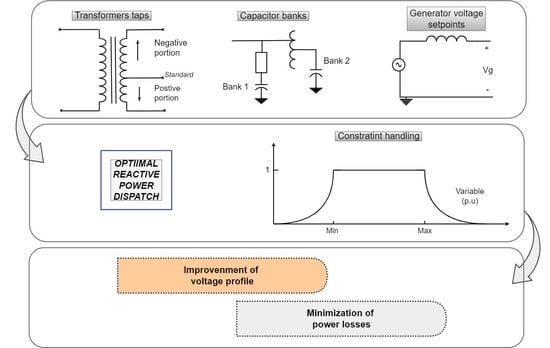
2. Mathematical Modeling
2.1. Objective Function
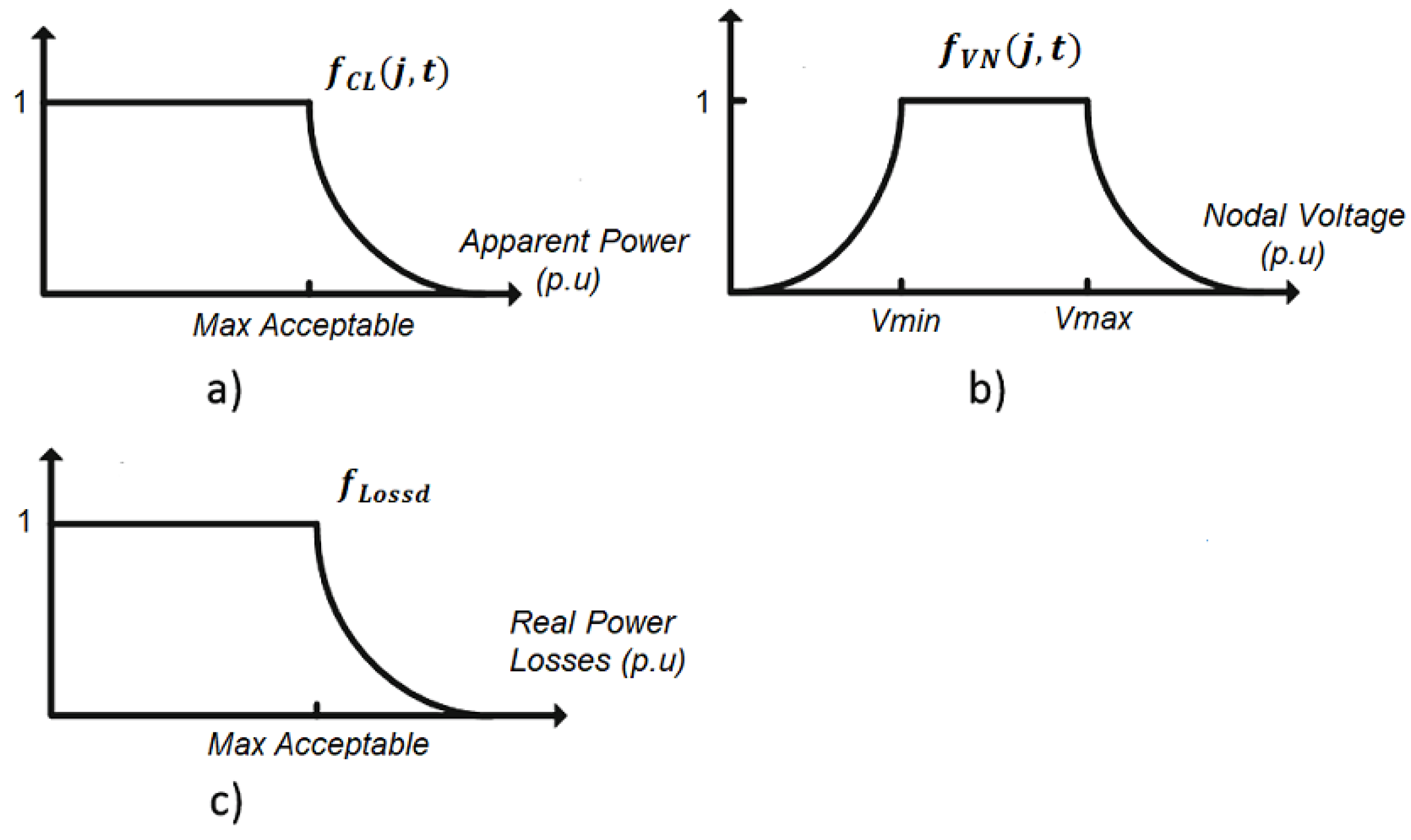
2.2. Enforcement of Voltage Limits
2.3. Enforcement of Power Flow Limits
2.4. Active Power Losses Target
2.5. Limits on Transformer Taps Maneuvers
2.6. Daily Limit of Transformer Tap Operations
2.7. Capacitor Banks Daily Switching Limit
3. Solution Approach
3.1. Fitness Evaluation and Constraint Handling
3.2. Enhanced Mapping
3.3. Solution Archive
3.4. Offspring Generation and Stopping Criterion
3.5. MVMO Swarm Variant
4. Tests and Results
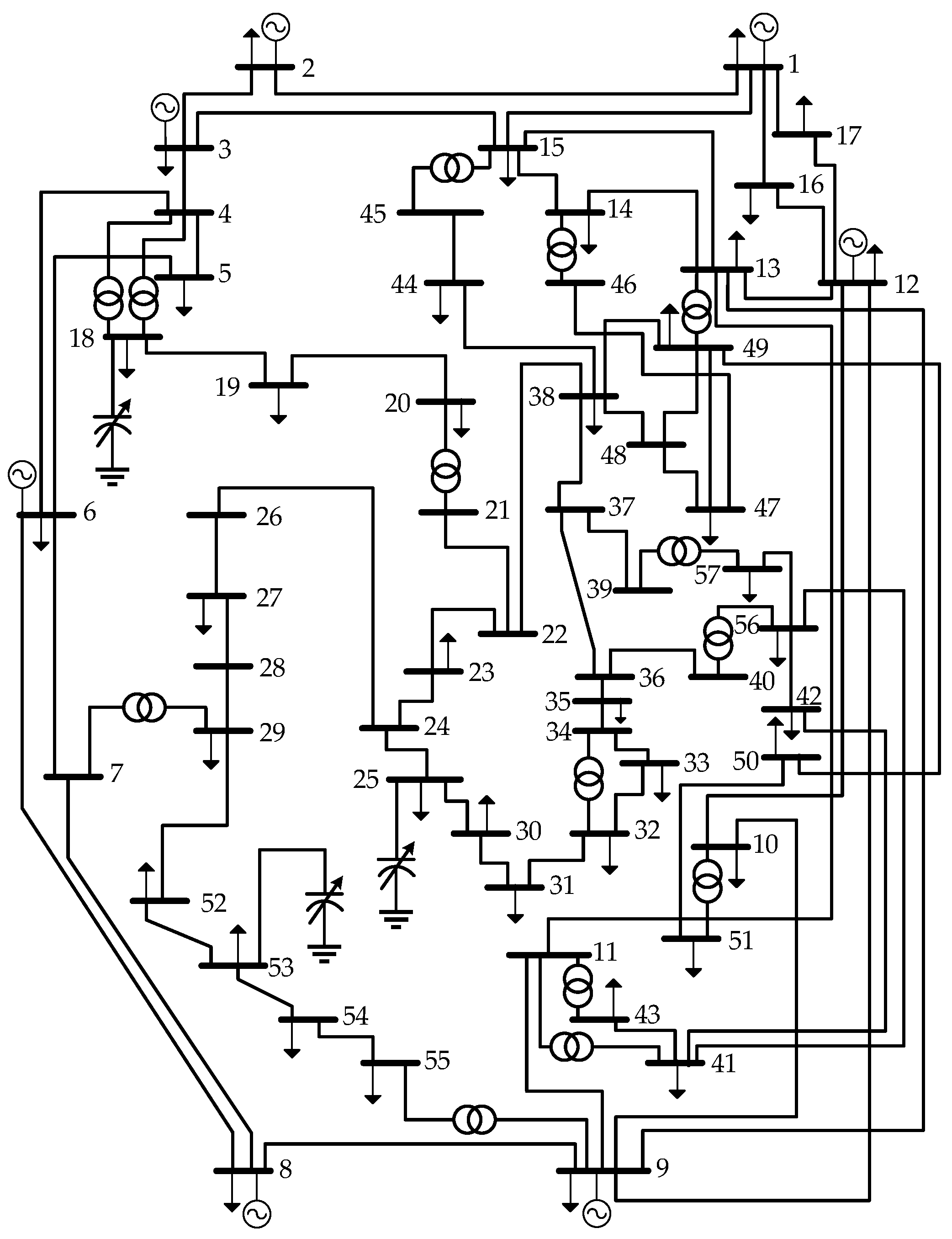
4.1. Description of the Test Systems
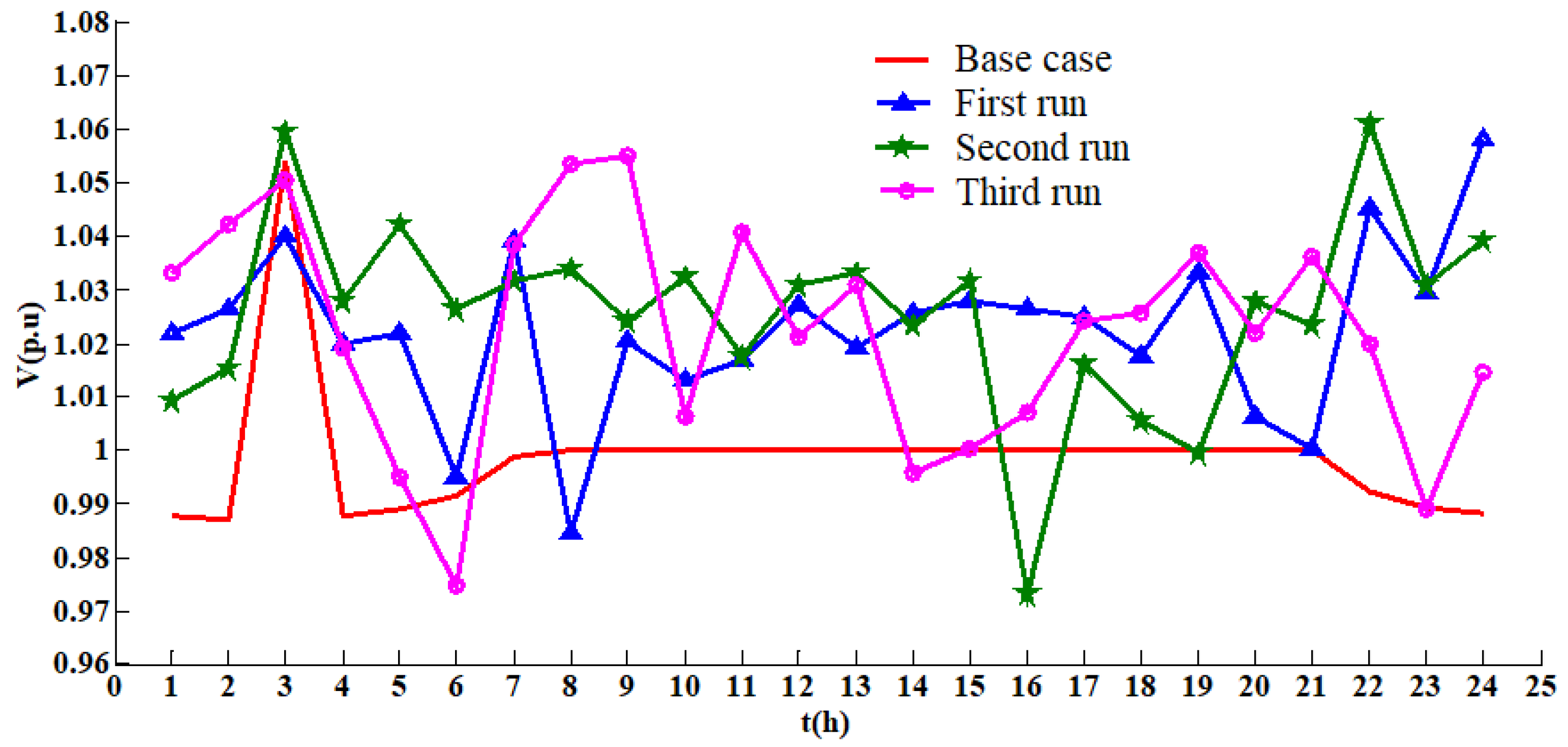
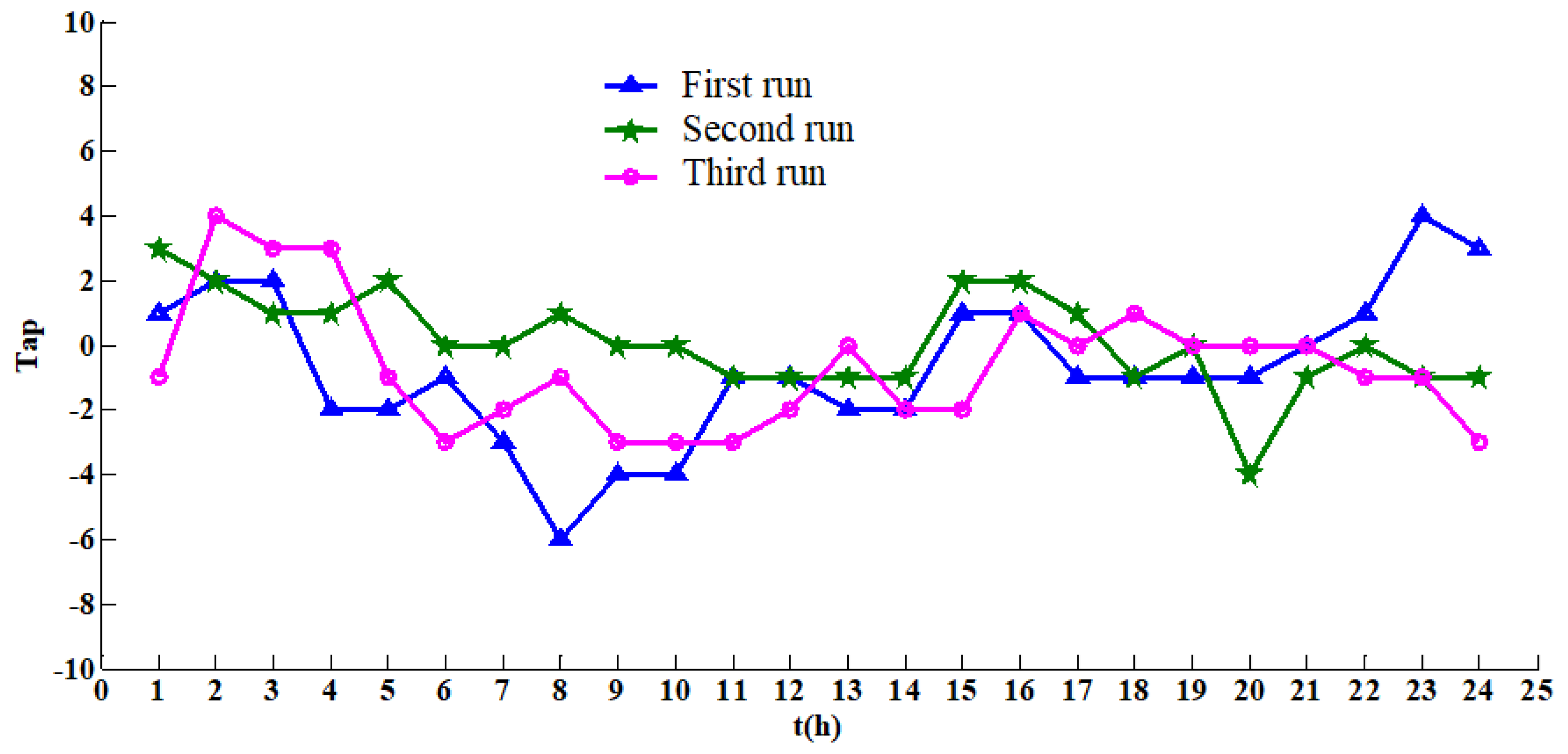
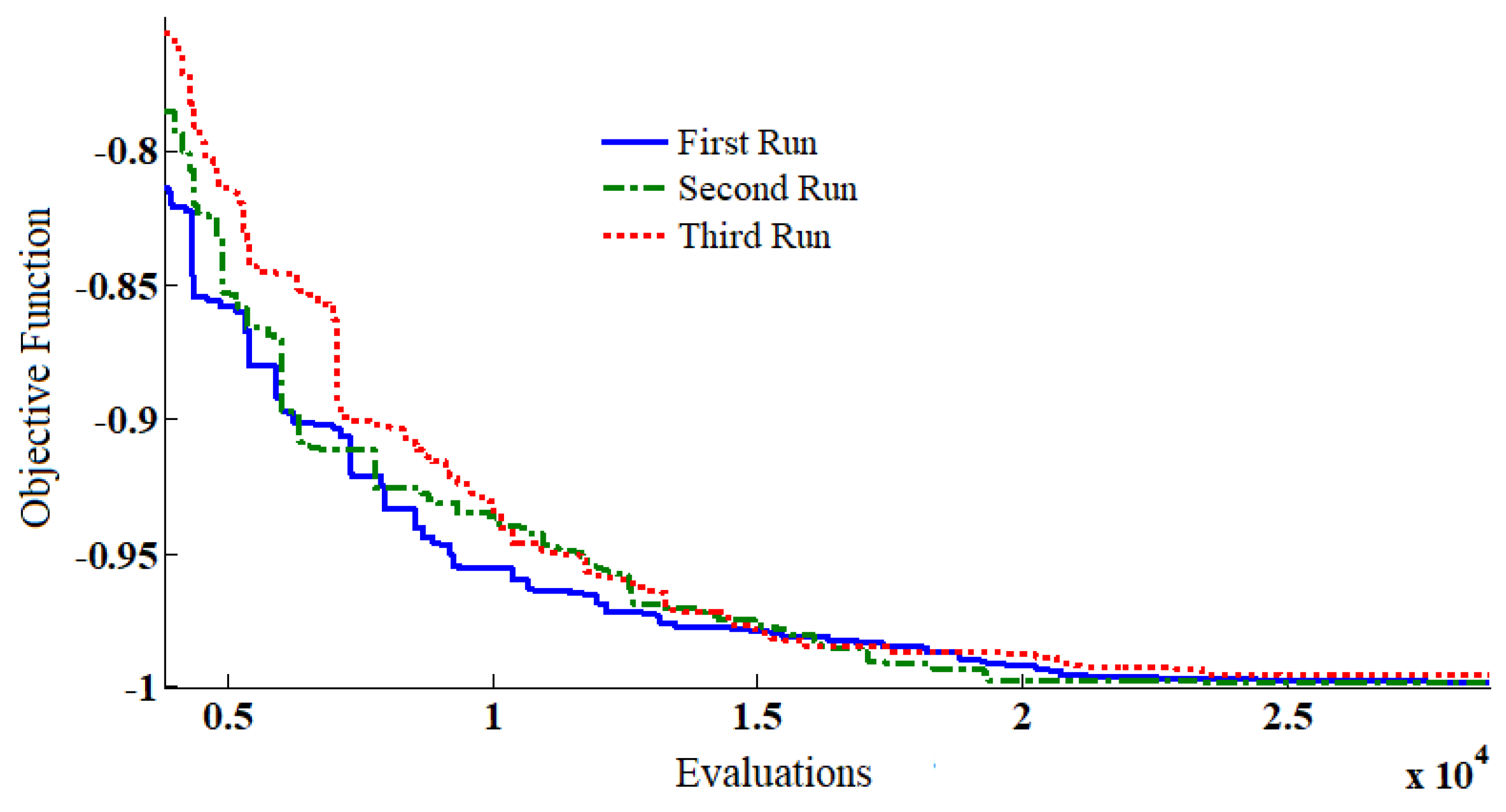
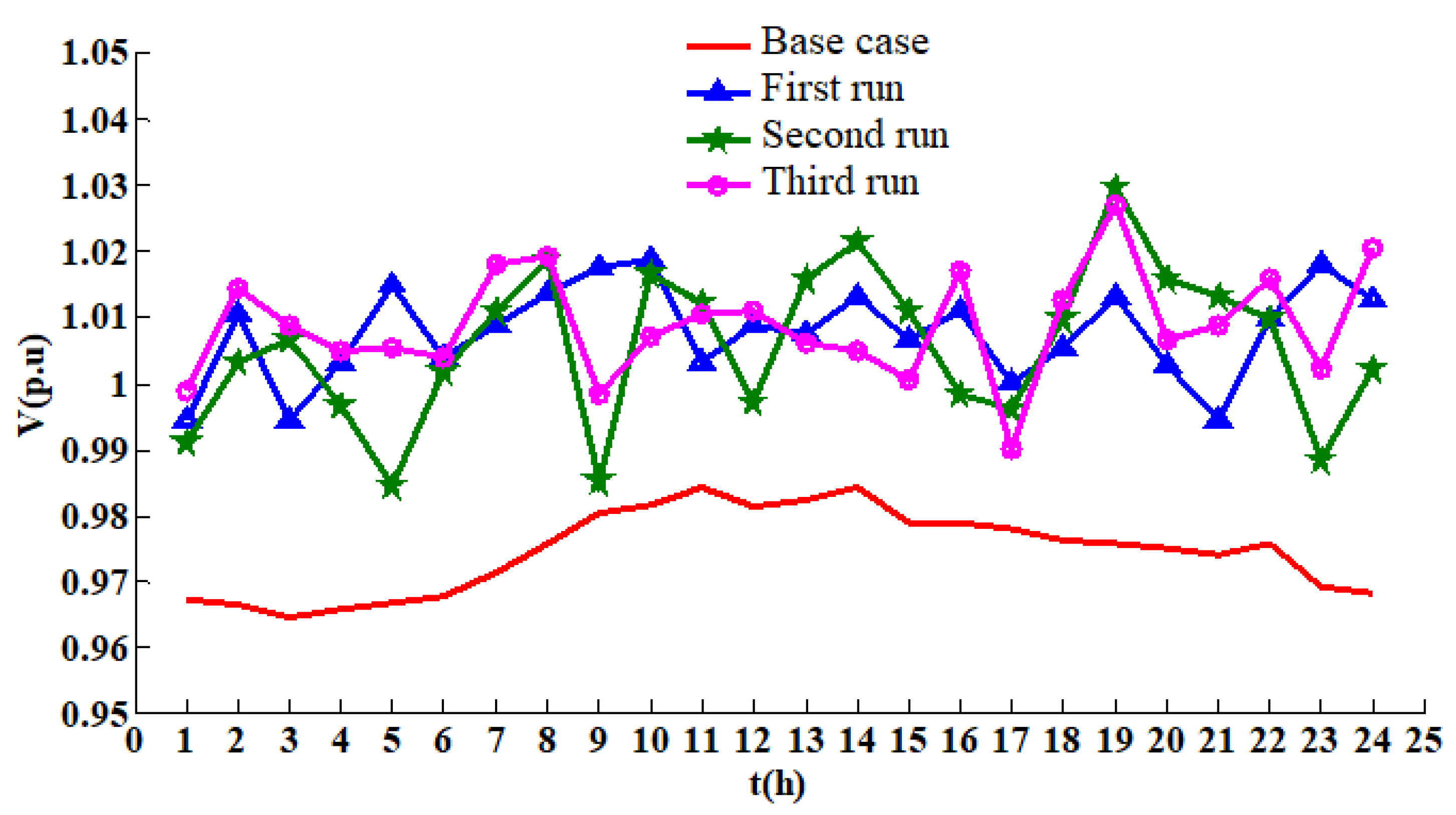
4.2. Results with the IEEE 30-Bus Test System
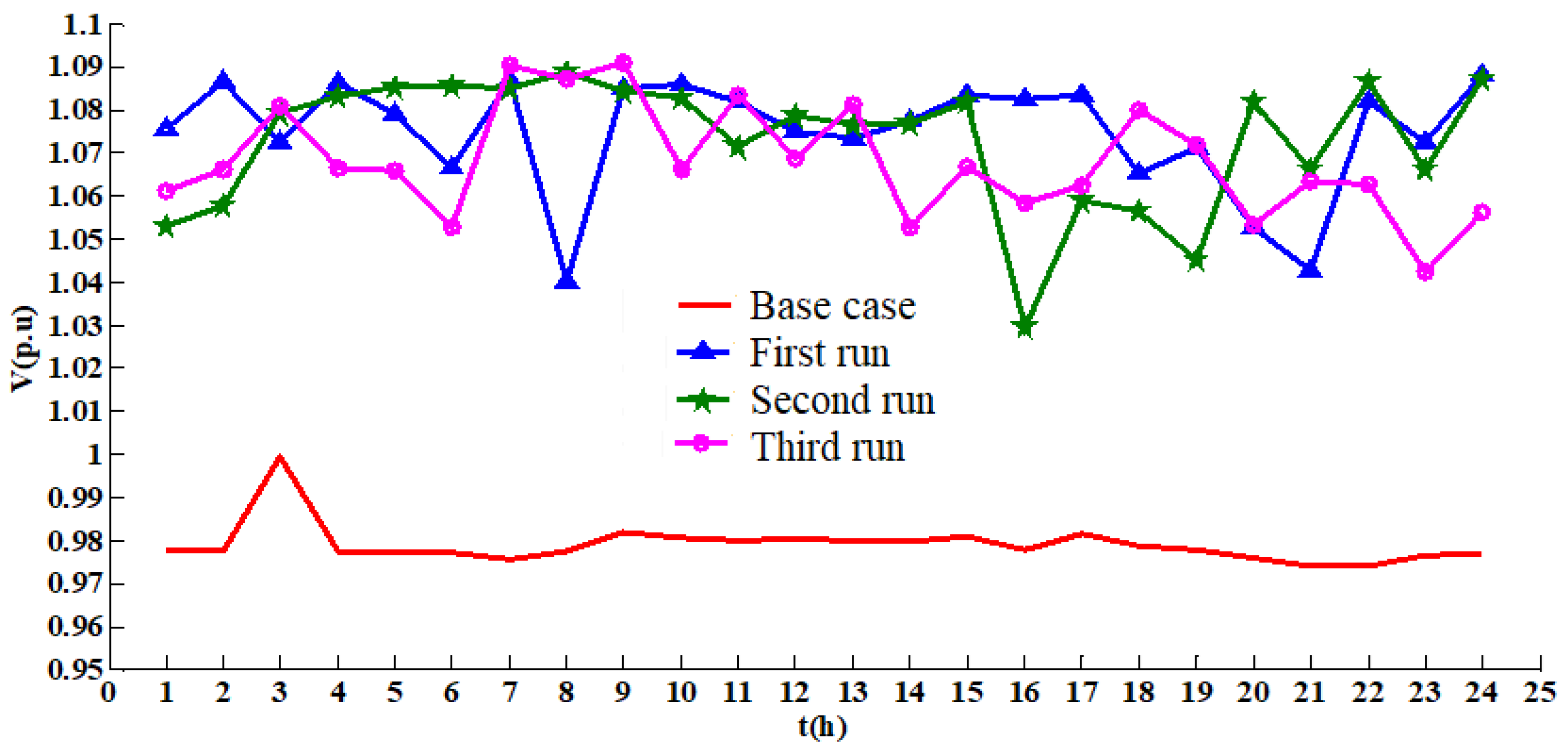
4.3. Results with the IEEE 57-Bus Test System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassan, M.H.; Kamel, S.; El-Dabah, M.A.; Khurshaid, T.; Domínguez-García, J.L. Optimal Reactive Power Dispatch with Time-Varying Demand and Renewable Energy Uncertainty Using Rao-3 Algorithm. IEEE Access 2021, 9, 23264–23283. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal Reactive Power Dispatch Using Chaotic Bat Algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Constante, F.S.G.; López, J.C.; Rider, M.J. Optimal Reactive Power Dispatch With Discrete Controllers Using a Branch-and-Bound Algorithm: A Semidefinite Relaxation Approach. IEEE Trans. Power Syst. 2021, 36, 4539–4550. [Google Scholar] [CrossRef]
- Deeb, N.I.; Shahidehpour, S.M. An Efficient Technique for Reactive Power Dispatch Using a Revised Linear Programming Approach. Electr. Power Syst. Res. 1988, 15, 121–134. [Google Scholar] [CrossRef]
- Sachdeva, S.S.; Billinton, R. Optimum Network Var Planning by Nonlinear Programming. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1217–1225. [Google Scholar] [CrossRef]
- Grudinin, N. Reactive power optimization using successive quadratic programming method. IEEE Trans. Power Syst. 1998, 13, 1219–1225. [Google Scholar] [CrossRef]
- Quintana, V.; Santos-Nieto, M. Reactive-power dispatch by successive quadratic programming. IEEE Trans. Energy Convers. 1989, 4, 425–435. [Google Scholar] [CrossRef]
- Granville, S. Optimal reactive dispatch through interior point methods. IEEE Trans. Power Syst. 1994, 9, 136–146. [Google Scholar] [CrossRef]
- Bjelogrlic, M.; Calovic, M.; Ristanovic, P.; Babic, B. Application of Newton’s optimal power flow in voltage/reactive power control. IEEE Trans. Power Syst. 1990, 5, 1447–1454. [Google Scholar] [CrossRef]
- Zhu, J.; Xiong, X. Optimal reactive power control using modified interior point method. Electr. Power Syst. Res. 2003, 66, 187–192. [Google Scholar] [CrossRef]
- Yu, D.C.; Fagan, J.E.; Foote, B.; Aly, A.A. An optimal load flow study by the generalized reduced gradient approach. Electr. Power Syst. Res. 1986, 10, 47–53. [Google Scholar] [CrossRef]
- Deeb, N.; Shahidehpour, S. Linear reactive power optimization in a large power network using the decomposition approach. IEEE Trans. Power Syst. 1990, 5, 428–438. [Google Scholar] [CrossRef]
- López-Lezama, J.M.; Cortina-Gómez, J.; Muñoz-Galeano, N. Assessment of the Electric Grid Interdiction Problem using a nonlinear modeling approach. Electr. Power Syst. Res. 2017, 144, 243–254. [Google Scholar] [CrossRef]
- Saldarriaga-Zuluaga, S.D.; López-Lezama, J.M.; Muñoz-Galeano, N. Adaptive protection coordination scheme in microgrids using directional over-current relays with non-standard characteristics. Heliyon 2021, 7, e06665. [Google Scholar] [CrossRef] [PubMed]
- Agudelo, L.; López-Lezama, J.M.; Muñoz-Galeano, N. Vulnerability assessment of power systems to intentional attacks using a specialized genetic algorithm. Dyna 2015, 82, 78–84. [Google Scholar] [CrossRef]
- Niu, M.; Xu, N.Z.; Dong, H.N.; Ge, Y.Y.; Liu, Y.T.; Ngin, H.T. Adaptive Range Composite Differential Evolution for Fast Optimal Reactive Power Dispatch. IEEE Access 2021, 9, 20117–20126. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y. Multi-Objective Optimal Reactive Power Dispatch of Power Systems by Combining Classification-Based Multi-Objective Evolutionary Algorithm and Integrated Decision Making. IEEE Access 2020, 8, 38198–38209. [Google Scholar] [CrossRef]
- Zhihuan, L.; Yinhong, L.; Xianzhong, D. Non-dominated sorting genetic algorithm-II for robust multi-objective optimal reactive power dispatch. IET Gener. Transm. Distrib. 2010, 4, 1000–1008. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Gupta, V. Fuzzy based evolutionary algorithm for reactive power optimization with FACTS devices. Int. J. Electr. Power Energy Syst. 2014, 61, 39–47. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H. A Novel Nature Inspired Meta-Heuristic Optimization Approach of GWO Optimizer for Optimal Reactive Power Dispatch Problems. IEEE Access 2020, 8, 202596–202610. [Google Scholar] [CrossRef]
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment. IEEE Trans. Power Syst. 2000, 15, 1232–1239. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Rojas, M.; Sumper, A.; Bellmunt, O.; Sudria-Andreu, A. Reactive power dispatch in wind farms using particle swarm optimization technique and feasible solutions search. Appl. Energy 2011, 88, 4678–4686. [Google Scholar] [CrossRef]
- Liang, R.H.; Wang, J.C.; Chen, Y.T.; Tseng, W.T. An enhanced firefly algorithm to multi-objective optimal active/reactive power dispatch with uncertainties consideration. Int. J. Electr. Power Energy Syst. 2015, 64, 1088–1097. [Google Scholar] [CrossRef]
- De, M.; Goswami, S.K. Optimal Reactive Power Procurement With Voltage Stability Consideration in Deregulated Power System. IEEE Trans. Power Syst. 2014, 29, 2078–2086. [Google Scholar] [CrossRef]
- Malakar, T.; Goswami, S. Active and reactive dispatch with minimum control movements. Int. J. Electr. Power Energy Syst. 2013, 44, 78–87. [Google Scholar] [CrossRef]
- Duman, S.; Sonmez, Y.; Guvenc, U.; Yorukeren, N. Optimal reactive power dispatch using a gravitational search algorithm. IET Gener. Transm. Distrib. 2012, 6, 563. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Azizipanah-Abarghooee, R.; Bahmani-Firouzi, B. Multiobjective Optimal Reactive Power Dispatch and Voltage Control: A New Opposition-Based Self-Adaptive Modified Gravitational Search Algorithm. IEEE Syst. J. 2013, 7, 742–753. [Google Scholar] [CrossRef]
- Khazali, A.; Kalantar, M. Optimal reactive power dispatch based on harmony search algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 684–692. [Google Scholar] [CrossRef]
- Kn, L.; Reddy, B.; Kalavathi, M. A New charged system Search for Solving Optimal Reactive Power Dispatch Problem. Int. J. Comput. 2014, 14, 22–40. [Google Scholar]
- Yan, W.; Liu, F.; Chung, C.; Wong, K. A hybrid genetic algorithm-interior point method for optimal reactive power flow. IEEE Trans. Power Syst. 2006, 21, 1163–1169. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.M.; Huang, Y.C. Combined Differential Evolution Algorithm and Ant System for Optimal Reactive Power Dispatch. Energy Procedia 2012, 14, 1238–1243. [Google Scholar] [CrossRef] [Green Version]
- Laouafi, F.; Boukadoum, A.; Leulmi, S. Reactive Power Dispatch with Hybrid Formulation: Particle Swarm Optimization and Improved Genetic Algorithms with Real Coding. Int. Rev. Electr. Eng. 2010, 5, 601–607. [Google Scholar]
- Jamal, R.; Men, B.; Khan, N.H.; Raja, M.A.Z.; Muhammad, Y. Application of Shannon Entropy Implementation Into a Novel Fractional Particle Swarm Optimization Gravitational Search Algorithm (FPSOGSA) for Optimal Reactive Power Dispatch Problem. IEEE Access 2021, 9, 2715–2733. [Google Scholar] [CrossRef]
- Kanna, B.; Singh, S.N. Towards reactive power dispatch within a wind farm using hybrid PSO. Int. J. Electr. Power Energy Syst. 2015, 69, 232–240. [Google Scholar] [CrossRef]
- Vlachogiannis, J.; Lee, K. A Comparative Study on Particle Swarm Optimization for Optimal Steady-State Performance of Power Systems. IEEE Trans. Power Syst. 2006, 21, 1718–1728. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, L.; Singh, H. Hybrid multi-swarm particle swarm optimisation based multi-objective reactive power dispatch. IET Gener. Transm. Distrib. 2015, 9, 727–739. [Google Scholar] [CrossRef]
- Gutierrez Rojas, D.; Lopez Lezama, J.; Villa, W. Metaheuristic Techniques Applied to the Optimal Reactive Power Dispatch: A Review. IEEE Latin Am. Trans. 2016, 14, 2253–2263. [Google Scholar] [CrossRef]
- Marín-Cano, C.C.; Sierra-Aguilar, J.E.; López-Lezama, J.M.; Jaramillo-Duque, A.; Villegas, J.G. A Novel Strategy to Reduce Computational Burden of the Stochastic Security Constrained Unit Commitment Problem. Energies 2020, 13, 3777. [Google Scholar] [CrossRef]
- Yang, B.; Cao, X.; Cai, Z.; Yang, T.; Chen, D.; Gao, X.; Zhang, J. Unit Commitment Comprehensive Optimal Model Considering the Cost of Wind Power Curtailment and Deep Peak Regulation of Thermal Unit. IEEE Access 2020, 8, 71318–71325. [Google Scholar] [CrossRef]
- Naghdalian, S.; Amraee, T.; Kamali, S.; Capitanescu, F. Stochastic Network-Constrained Unit Commitment to Determine Flexible Ramp Reserve for Handling Wind Power and Demand Uncertainties. IEEE Trans. Ind. Inform. 2020, 16, 4580–4591. [Google Scholar] [CrossRef]
- Sierra-Aguilar, J.E.; Marín-Cano, C.C.; López-Lezama, J.M.; Jaramillo-Duque, A.; Villegas, J.G. A New Affinely Adjustable Robust Model for Security Constrained Unit Commitment under Uncertainty. Appl. Sci. 2021, 11, 3987. [Google Scholar] [CrossRef]
- Zhao, J.; Ju, L.; Dai, Z.; Chen, G. Voltage stability constrained dynamic optimal reactive power flow based on branch-bound and primal–dual interior point method. Int. J. Electr. Power Energy Syst. 2015, 73, 601–607. [Google Scholar] [CrossRef]
- Liu, M.B.; Canizares, C.A.; Huang, W. Reactive Power and Voltage Control in Distribution Systems With Limited Switching Operations. IEEE Trans. Power Syst. 2009, 24, 889–899. [Google Scholar] [CrossRef]
- Agalgaonkar, Y.P.; Pal, B.C.; Jabr, R.A. Distribution Voltage Control Considering the Impact of PV Generation on Tap Changers and Autonomous Regulators. IEEE Trans. Power Syst. 2014, 29, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Wang, X.; Chen, H.; Taylor, G. Volt/VAR control in distribution systems using a time-interval based approach. IEE Proc. Gener. Transm. Distrib. 2003, 150, 548–554. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, S.K. Day-ahead optimal reactive power ancillary service procurement under dynamic multi-objective framework in wind integrated deregulated power system. Energy 2021, 223, 120028. [Google Scholar] [CrossRef]
- Kim, Y.J.; Ahn, S.J.; Hwang, P.I.; Pyo, G.C.; Moon, S.I. Coordinated Control of a DG and Voltage Control Devices Using a Dynamic Programming Algorithm. IEEE Trans. Power Syst. 2013, 28, 42–51. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Wu, Q. Fully decentralized multiarea reactive power optimization considering practical regulation constraints of devices. Int. J. Electr. Power Energy Syst. 2019, 105, 351–364. [Google Scholar] [CrossRef]
- Morán-Burgos, J.A.; Sierra-Aguilar, J.E.; Villa-Acevedo, W.M.; López-Lezama, J.M. A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals. Appl. Sci. 2021, 11, 8535. [Google Scholar] [CrossRef]
- Ahmadi, H.; Martí, J.R.; Dommel, H.W. A Framework for Volt-VAR Optimization in Distribution Systems. IEEE Trans. Smart Grid 2015, 6, 1473–1483. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Ren, Z. Optimal reactive power dispatch considering costs of adjusting the control devices. IEEE Trans. Power Syst. 2005, 20, 1349–1356. [Google Scholar] [CrossRef]
- Yang, W.; Chen, L.; Deng, Z.; Xu, X.; Zhou, C. A multi-period scheduling strategy for ADN considering the reactive power adjustment ability of DES. Int. J. Electr. Power Energy Syst. 2020, 121, 106095. [Google Scholar] [CrossRef]
- Ibrahim, T.M.S.; De Rubira, T.T.; Del Rosso, A.; Patel, M.; Guggilam, S.; Mohamed, A. Alternating Optimization Approach for Voltage-Secure Multi-Period Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2021, 1. [Google Scholar] [CrossRef]
- Villa-Acevedo, W.M.; López-Lezama, J.M.; Valencia-Velásquez, J.A. A Novel Constraint Handling Approach for the Optimal Reactive Power Dispatch Problem. Energies 2018, 11, 2352. [Google Scholar] [CrossRef] [Green Version]
- Londoño, D.C.; Villa-Acevedo, W.M.; López-Lezama, J.M. Assessment of Metaheuristic Techniques Applied to the Optimal Reactive Power Dispatch. In Proceedings of the Applied Computer Sciences in Engineering; Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2019; pp. 250–262. [Google Scholar] [CrossRef]
- Nakawiro, W.; Erlich, I.; Rueda, J.L. A novel optimization algorithm for optimal reactive power dispatch: A comparative study. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 1555–1561. [Google Scholar] [CrossRef]
- Rueda, J.L.; Erlich, I. Optimal dispatch of reactive power sources by using MVMO optimization. In Proceedings of the 2013 IEEE Computational Intelligence Applications in Smart Grid (CIASG), Singapore, 16–19 April 2013; pp. 29–36. [Google Scholar] [CrossRef]
- Erlich, I. Mean-Variance Mapping Optimization Algorithm Home Page. Available online: https://www.uni-due.de/mvmo/ (accessed on 10 November 2020).
- Erlich, I.; Venayagamoorthy, G.K.; Worawat, N. A Mean-Variance Optimization algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Cepeda, J.C.; Rueda, J.L.; Erlich, I. Identification of dynamic equivalents based on heuristic optimization for smart grid applications. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Rueda, J.L.; Erlich, I. Evaluation of the mean-variance mapping optimization for solving multimodal problems. In Proceedings of the 2013 IEEE Symposium on Swarm Intelligence (SIS), Singapore, 16–19 April 2013; pp. 7–14. [Google Scholar] [CrossRef]
- University of Illinois. ICSEG Power Case 1—IEEE 30 Bus Systems. Available online: https://uofi.app.box.com/s/frjqsg9vpe6dvv7ufodd (accessed on 10 November 2020).
- University of Washington. Power Systems Test Case Archive—UWEE. Available online: https://labs.ece.uw.edu/pstca/ (accessed on 10 November 2020).
- ABB. Cambiador de Tomas en Carga, Tipo UBB Guía de Mantenimiento; Technical Report; 1ZSE 5492-127 es, Rev. 5; ABB: Ludvika, Suecia, 2005. [Google Scholar]
- ABB. Interruptores de Tanque Vivo; Guia de Usuario Edición 4, 2008-10; ABB: Ludvika, Suecia, 2008. [Google Scholar]
- Ela, A.A.E.; Abido, M.; Spea, S. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]







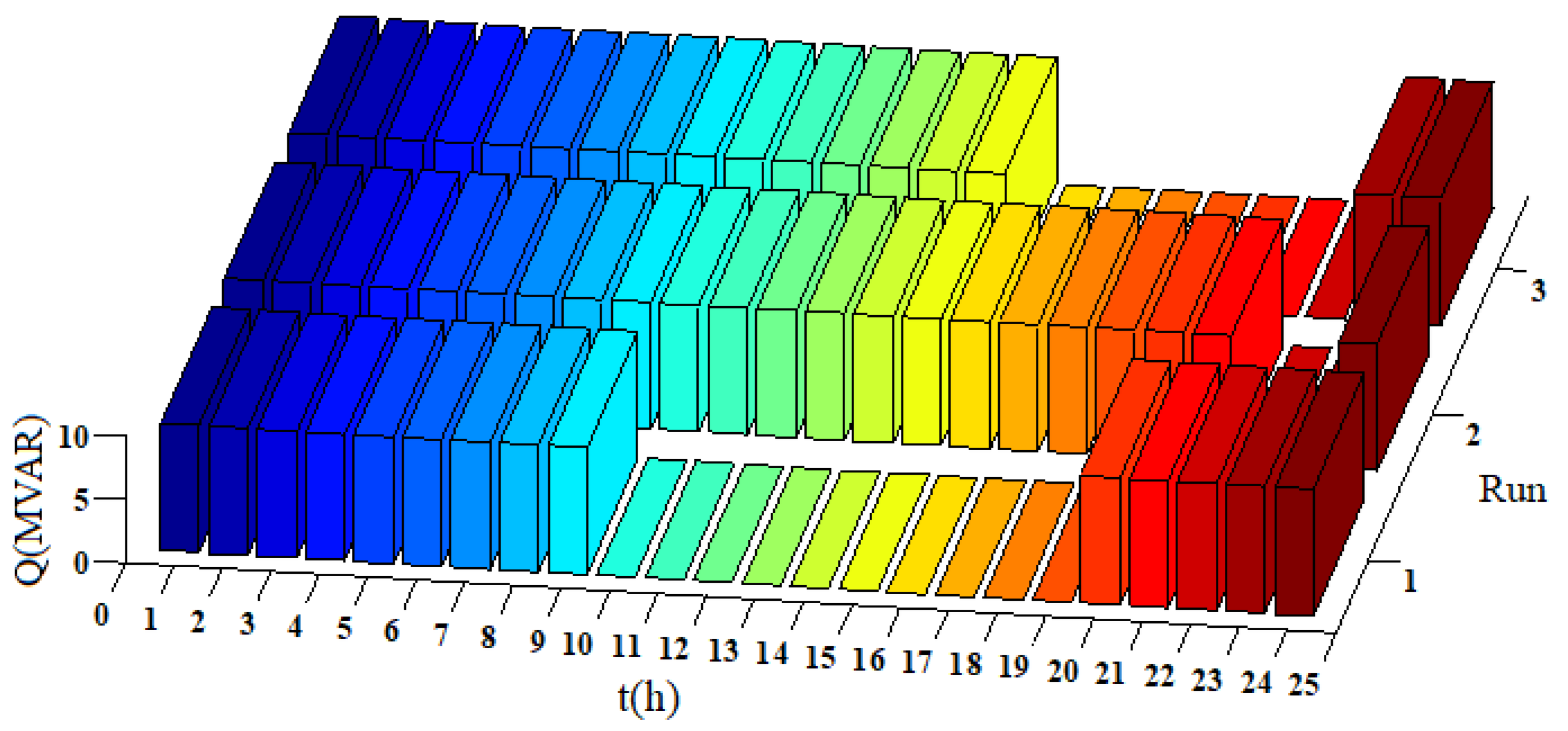
| Paper | Transformers | Reactive Compensation | Stopping Criterion | |||
|---|---|---|---|---|---|---|
| Daily | Inter-Hour | Daily | Inter-Hour | Number of Evaluations | Goal Accomplished | |
| [43] | X | X | X | X | ||
| [44,46,48,50] | X | X | X | |||
| [45,49,51,52,53,54] | X | X | X | |||
| [47] | X | X | ||||
| Proposed | X | X | X | X | X | X |
| Test System | Power Losses (Base Case [MW]) | Power Losses (Goal [MW]) |
|---|---|---|
| IEEE-30 Bus | 65.36 | 59.9 |
| IEEE-57 Bus | 241.7 | 219.5 |
| IEEE 30-Bus Test System | Power Losses (MW) | Time (s) |
|---|---|---|
| Best Solution | 59.9128 | 3611 |
| Worst Solution | 59.9999 | 10,340 |
| Mean | 59.9838 | 7000 |
| Standard Deviation | 0.0186 | 1699 |
| IEEE 57-Bus Test System | Power Losses (MW) | Time (s) |
|---|---|---|
| Best Solution | 219.8989 | 9922 |
| Worst Solution | 219.9972 | 20,619 |
| Mean | 219.9838 | 14,285 |
| Standard Deviation | 0.0256 | 2893 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Londoño Tamayo, D.C.; Villa-Acevedo, W.M.; López-Lezama, J.M. Multi-Period Optimal Reactive Power Dispatch Using a Mean-Variance Mapping Optimization Algorithm. Computers 2022, 11, 48. https://doi.org/10.3390/computers11040048
Londoño Tamayo DC, Villa-Acevedo WM, López-Lezama JM. Multi-Period Optimal Reactive Power Dispatch Using a Mean-Variance Mapping Optimization Algorithm. Computers. 2022; 11(4):48. https://doi.org/10.3390/computers11040048
Chicago/Turabian StyleLondoño Tamayo, Daniel C., Walter M. Villa-Acevedo, and Jesús M. López-Lezama. 2022. "Multi-Period Optimal Reactive Power Dispatch Using a Mean-Variance Mapping Optimization Algorithm" Computers 11, no. 4: 48. https://doi.org/10.3390/computers11040048
APA StyleLondoño Tamayo, D. C., Villa-Acevedo, W. M., & López-Lezama, J. M. (2022). Multi-Period Optimal Reactive Power Dispatch Using a Mean-Variance Mapping Optimization Algorithm. Computers, 11(4), 48. https://doi.org/10.3390/computers11040048