Energy-Efficient Cluster Head Selection in Wireless Sensor Networks Using an Improved Grey Wolf Optimization Algorithm

Abstract

The internet of things (IoT) and industrial IoT (IIoT) play a major role in today’s world of intelligent networks, and they essentially use a wireless sensor network (WSN) as a perception layer to collect the intended data. This data is processed as information and send to cloud servers through a base station, the challenge here is the consumption of minimum energy for processing and communication. The dynamic formation of cluster heads and energy aware clustering schemes help in improving the lifetime of WSNs. In recent years, grey wolf optimization (GWO) became the most popular feature selection optimizing, swarm intelligent, and robust metaheuristics algorithm that gives competitive results with impressive characteristics. In spite of several studies in the literature to enhance the performance of the GWO algorithm, there is a need for further improvements in terms of feature selection, accuracy, and execution time. In this paper, we have proposed an energy-efficient cluster head selection using an improved version of the GWO (EECHIGWO) algorithm to alleviate the imbalance between exploitation and exploration, lack of population diversity, and premature convergence of the basic GWO algorithm. The primary goal of this paper is to enhance the energy efficiency, average throughput, network stability, and the network lifetime in WSNs with an optimal selection of cluster heads using the EECHIGWO algorithm. It considers sink distance, residual energy, cluster head balancing factor, and average intra-cluster distance as the parameters in selecting the cluster head. The proposed EECHIGWO-based clustering protocol has been tested in terms of the number of dead nodes, energy consumption, number of operating rounds, and the average throughput. The simulation results have confirmed the optimal selection of cluster heads with minimum energy consumption, resolved premature convergence, and enhanced the network lifetime by using minimum energy levels in WSNs. Using the proposed algorithm, there is an improvement in network stability of 169.29%, 19.03%, 253.73%, 307.89%, and 333.51% compared to the SSMOECHS, FGWSTERP, LEACH-PRO, HMGWO, and FIGWO protocols, respectively.

1. Introduction

WSNs became the backbone of all the smart IoT applications, and their reliable deployment is very important for diverse real-time applications like the military, industry, wide-area surveillance, environmental monitoring factors, and health monitoring. WSNs play an important role in the Industry 4.0 revolution and they are essential in the perception/sensing layer of IoT systems for sensing the physical environment and collecting the data using SNs. Due to the short span of battery life in the SNs of WSNs, optimal energy consumption has been always a challenge. The energy efficiency of sensor nodes plays a major role due to their constrained resources in terms of processing and communication. Therefore, it is essential to propose efficient energy consumption algorithms to extend the lifetime and stability of WSNs. Clustering is a prominent mechanism to achieve energy efficiency in WSNs. Clustering-based architecture in WSNs reduces the number of data transmissions using intra-cluster and inter-cluster communications [1]. However, the performance of clustering depends on the process of CH selection and the formation of optimal number of clusters. In a cluster-based architecture, a random selection of CHs causes poor connectivity, unexpected node failures, and reduces network lifetime. On the other hand, optimal selection of CHs enhances the performance and lifetime in WSNs. An optimized routing algorithm through an efficient CH selection process is essential for larger-scale WSNs. Clustering-based routing supports load balancing, reliable communication, and fault tolerance to prolong the life time of a WSN. CH selection based on node position, centrality of nodes, residual energy, number of neighbors, and node rank (rank is assigned depends on number of links, link cost) overcomes the drawbacks of the LEACH protocol [2]. Dynamic and on-demand CH selection based on the occurrence of events minimizes the message and computational overhead, and also ensures energy balancing among CHs [3]. Optimal clustering replaces one-hop communication between the CHs and sink node by an optimal multi-hop distance in order to mitigate energy consumption and enhance the network lifetime by 35% in WSNs [4]. Adaptive CH selection in heterogeneous WSNs, based on residual energy and node location, ensures that the node which has higher residual energy and is close to the BS becomes the CH with the highest probability [5].

In recent years, GWO became the most popular feature selection optimization, swarm intelligent, and robust metaheuristics algorithm that gives competitive results in solving engineering problems. In spite of several studies in the literature to enhance the performance of the GWO algorithm, there is a need for further improvements in terms of the balance between exploitation and exploration, lack of population diversity, and premature convergence of the basic GWO algorithm. In this paper, we have proposed an energy-efficient CH selection using an improved version of the GWO (EECHIGWO) algorithm to enhance the energy efficiency, average throughput, network stability, and the network lifetime in WSNs with an optimal selection of CHs. It considers sink distance, residual energy, CH balancing factor, and average intra-cluster distance as the parameters in selecting the CH. The simulation results have confirmed the optimal selection of the CH with minimum energy consumption, resolved premature convergence, and enhanced the network lifetime by using minimum energy levels in WSNs.

The definition of fitness functions plays a key role in selecting optimal CHs in WSNs. In the existing literature, the fitness functions are defined with equal or random weight values irrespective of the SN’s position and its available energy. The novelty towards the proposed work include the computation of optimal fitness value for a given SN based on the residual energy and its distance to BS. For optimal clustering and routing, objective functions are considered where routing fitness is computed based on the minimum number of hops, mean load, and distance between gateways and BS. In this paper, the minimum value of all fitness functions of gateways is considered as clustering fitness function.

The remainder paper is organized as follows: the main contributions and literature survey of this work are described in Section 2 and Section 3, respectively. The clustering based on the proposed EECHIGWO algorithm is explained in Section 4. Section 5 explains the results and discussions of the proposed method and comparison with the recently proposed GWO-based CH selection methods. Finally, the conclusions and future scope are made in Section 6.

2. Contributions

Motivation

Due to the limited resources of SNs in WSNs and applications where recharging or replacing the battery is not a feasible solution, it is essential to design and implement energy-efficient schemes to improve the key performance parameters. Even though clustering is considered to be the most prominent technique to prolong the lifetime expectancy in WSNs, the process of CH selection in order to enhance the network lifetime is still a challenge. The conventional clustering-based routing algorithms support fault tolerance, load balancing, and reliable communications at the cost of decreased lifetime of the CH. To overcome this, there has been a continuous research on designing efficient CH selection techniques, data acquisition, and routing optimization algorithms.

In this article, an improved version of the GWO algorithm is applied for an optimal CH selection in WSNs to minimize the energy levels used for computation and communication. The performance of the proposed protocol is evaluated in terms of the number of dead nodes, energy consumption levels, the number of operating rounds, and the average throughput. A rigorous statistical analysis and simulations are carried out by taking the average of fifteen readings for each result to prove the proposed algorithm’s efficiency. In addition, a comparative analysis is performed with the recently proposed GWO-based algorithms. The simulation results prove that the proposed algorithm outperforms in terms of energy preservation and an enhanced network lifetime.

The main contributions of this article are as follows:

(a)

Rigorous literature study of algorithms and protocols are conducted that enhances the WSN lifetime with an optimal CH selection and energy-efficient techniques.

(b)

Study of the futuristic algorithms proposed based on the GWO algorithm for CH selection and optimal energy utilization in WSNs.

(c)

Proposed a novel method based on an improved GWO algorithm, distance between BS and SN for CH selection, and efficient energy utilization.

(d)

Defined the fitness function based on the IGWO algorithm that considers residual energy at SN to avoid randomness in CH selection for energy-efficient data deliveries.

(e)

Compared the performance of the proposed algorithm with existing GWO-based algorithms in terms of the number of dead nodes, number of operating rounds, energy consumption, and the average throughput.

(f)

Proved that the proposed EECHIGWO algorithm outperforms the existing GWO-based algorithms in WSNs.

3. Literature Survey

Efficient energy utilization is one of the primary goals to maximize the network lifetime in WSNs. Clustering is known to be one of the efficient techniques in WSNs to enhance energy efficiency by designing an energy-efficient protocol in CHs selection. There are various techniques present in the literature for electing CHs in WSNs to enhance the network lifetime, but this still remains a major challenge in WSNs.

3.1. Energy Efficient Techniques for WSNs

The energy efficiency is a critical parameter to be addressed in WSNs, as the individual SNs operate with limited energy sources and optimizing the energy consumption of SNs has been a challenging design issue in WSNs. Energy-efficient WSNs compromise with network stability as a crucial factor in ensuring long lasting and reliable network coverage. Clustering and routing are essential aspects to be considered for the efficient energy consumption of SNs in WSNs [6]. An adaptive hierarchical routing and hybrid clustering based on the fuzzy C-means method, residual energy, BS location, and Euclidean distance improves coverage and lifetime of the network [7]. Fuzzy-based clustering provides energy-efficient routing capabilities that enhances the network lifetime [8].

Equalized CH election routing ensures the energy conservation in a balanced fashion and enhances the network lifetime [9]. A neuro-fuzzy-based energy-aware clustering is proposed in WSNs that consist of neural networks and a fuzzy subsystem to achieve energy-efficient clusters and CHs. The performance of these systems are measured based on residual energy, transmission range, and trust factor (for security) [10]. Multi-level route-aware clustering minimizes routing control packets and moderates the energy consumption at relay nodes present near the BS [11]. Formation of clusters in WSNs based on the Voronoi diagram minimizes the energy consumption for communication. This method can enhance the FND by 14.5% compared to SEP [12].

3.2. Energy Aware Clustering and Performance Optimization Using Metahueristic Approach

In this section, the importance of metaheuristic algorithms to solve the engineering problems and the role of GWO in enhancing the performance of WSNs are highlighted. The energy constraints in measuring network lifetime pose a challenge in a widely spread applications of WSNs. Network stability and energy efficiency are two typical trade-off parameters in WSNs. There have been continuous efforts by researchers in achieving the energy efficiency in WSNs that includes state-of-the-art metaheuristic algorithms [13].

In recent years, swarm intelligence metaheuristic optimization techniques have proved the outstanding performers in solving a wide range of engineering and science problems. GWO is one such technique, and it became popular due to the involvement of only few parameters and no derivation information. It provides right balance between exploitation and exploration that leads to favorable convergence. It has applications in the fields of networking, image processing, machine learning, bioinformatics, global optimization, environmental applications, etc. [14]. For enhancing the efficient usage of computational resources, an adaptive GWO tunes the exploitation and exploration parameters automatically based on fitness function, and this reduces the number of iterations needed [15].

There have been many energy-efficient clustering protocols based on the GWO algorithm proposed in the recent times towards optimal CH selection [16,17]. GWO-based methods are proposed for energy optimizations in WSNs by finding the optimal positions of SNs to achieve maximum connectivity and coverage. It has been shown that the GWO-based CH selection algorithm performs better than PSO, GA, and Greedy approaches [18,19]. Precision improvement of the SN positions improves the data transmission among SNs in the network, saves the node’s energy, and also enhances the network lifetime [20].

The GWO algorithm is used to define a connected dominating set based on distance and it is used to achieve energy efficiency and stability in cluster-based WSNs [21]. A GWO algorithm-based approach enhances the energy efficiency compared to ABC and AFS algorithms [22]. The GWO-based game theoretical approach gives better solutions in selecting optimal aggregation points to improve the SN’s battery lifetime [23]. The SMO algorithm is proposed based on the sampling population for energy efficient CH selection [24]. Multi-object-based SMO is an energy efficient clustering and routing algorithm that balances the load at gateways for an improved network lifetime compared to PSO and GWO algorithms [25]. A combination of using GWO and whale optimization algorithms for clustering and dynamic CH selection increases the capabilities in terms of exploitation and exploration [26]. A whale optimization-based algorithm improves the rate of utilization of SNs and coverage in heterogeneous WSNs [27]. To reduce the energy consumption in CH selection, an objective function in GWO is defined based on residual energy, intra-cluster distance, CH balancing factor, and sink distance [28]. Topology control based on binary GWO introduces a fitness function that reduces the number of active nodes and enhances the network lifetime [29].

In the literature, the state-of-the-art metaheuristic algorithms like ACO, BA, GA, PSO, WOA, MFO, etc., are proposed to solve the optimization problems in engineering applications. COA integrated with a dimension learning-based hunting strategy maintains diversity and enhances the balance between exploration and exploitation. It effectively provides the optimization of energy constraints in WSNs [30]. CSA is used to select the optimal CHs in heterogeneous WSNs in order to improve the energy efficiency and network lifetime compared to PSO, GA, and LEACH algorithms [31]. A BSO swarm-based algorithm helps in selecting best possible CHs for enhancing the coverage, data rate, and energy efficiency in WSNs [32]. An ARSH-FATI-based CH selection dynamically (at run-time) switches between exploitation and exploration of the search process. It enhances the network lifetime by 25% compared to a PSO algorithm [33]. Network coverage optimization in heterogeneous WSNs using a sine-cosine-based WOA balances the local and global search capabilities, speeds up the search process, and enhances the optimization accuracy. It also maximizes the utilization rate of nodes, thereby mitigating the network cost.

Out of all the existing well-known metaheuristic algorithms (such as PSO, GSA, DE, EP, and ES), GWO has proved to be a powerful swarm-intelligent algorithm introduced to handle continuous and discrete optimization problems in the field of engineering. It is a unique metaheuristic algorithm that mimics the leadership hierarchy and attacking strategy of grey wolves. It is used for solving classic, real engineering design problems in unknown search spaces [34]. It improves the deterministic approach of a stochastic optimization for multi-robot exploration in the given space [35].

The GWO algorithm can be applied effectively in various fields of engineering and has many applications. It is applied in the image processing domain that includes image segmentation, image compression, image classification, and medical imaging to enhance efficiency and robustness [36]. GWO is used to enhance the accuracy of the IDS by 81% in detecting anomalous traffic in the network [37,38,39]. It improves the task allocation process and minimizes runtimes of the serverless frameworks for cloud applications at varied load conditions [40]. It is used for the secure transfer of data in IoT applications in which the GWO-based security algorithms offer lower memory and time for encryption/decryption [41]. GWO is useful for text clustering in text mining application to improve convergence rate and avoid trapping into local minima. The combination of GWO and GO algorithms give 87.6% efficiency in terms of precision, accuracy, recall, and sensitivity compared to individual algorithms [42].

3.3. Role of GWO Algorithm in Optimal CH Selection

The optimal CH selection using GWO greatly enhances network performance in terms of coverage, throughput, energy consumption, and network lifetime in WSNs [43]. It formulates the objective function and its weights based on intra-cluster distance, CH balancing factor, residual energy, and sink distance [44,45,46]. GWO addresses clustering and routing issues by formulating an optimal fitness function so that the number of hops and overall distance traversed are minimized, and also load balancing is achieved. The fitness functions for routing and clustering give higher values compared to GA and PSO algorithms [47]. A hybrid approach of GWO and WOA provides effective cluster formation, dynamic CH selection, and an optimal number of CHs in WSNs. It has better exploration and exploitation capabilities than the individual optimization approaches. CH selection based on the combination of GWO and CSO algorithms avoids premature convergence in exploring the search space. It gives a trade-off between the exploration and exploitation in CH selection to enhance the network lifetime expectancy more than FFO, ABCO, FGGWO algorithms [48].

Distance-based stable CDS along with GWO provides an enhanced performance of 70.5% over the GA-based algorithms in terms of energy efficiency and network stability. A three-level hybrid clustering is proposed for WSNs using the GWO algorithm. At level 1, BS selects the CHs; in level 2, there is GWO-based optimal data routing; and in level 3, distributed clustering takes place. This hybrid clustering enhances the network performance in terms of residual energy, stability, and lifetime [49]. The network coverage optimization using a minimal distribution of redundant nodes can enhance the stability and lifetime in WSNs. The GWO algorithm embedded with SA can achieve better coverage optimization than PSO in terms of optimization speed, energy consumption, and network lifetime [50]. The coverage optimization in WSNs using a Virtual Force Levy-embedded GWO algorithm performs better than CSA and Chaotic PSO techniques in terms of scalability, adaptability, uniformity, and coverage rate [51].

GWO is used to compute the threshold levels of sensor decision rules at the fusion center without depending on initial values and provides lower complexity in WSNs [52]. It is used to localize the SNs with minimal position errors, and with a quicker convergence than PSO and MBA algorithms [53]. The quantum computing with a clone operation in the GWO algorithm avoids falling it into a local optimal solution. The optimal design of the sensor duty cycle in industrial WSNs using the quantum clone GWO improves convergence speed and network lifetime compared to GA and SA algorithms [54].

3.4. Enhanced Versions of GWO Algorithms for WSNs

The conventional GWO algorithm may give sub-optimal/local optimal solutions because of its minimal exploration at early stages. An improved GWO aims to enhance the optimization accuracy, accelerating the convergence of the GWO algorithm, and balancing between exploration and exploitation. There are various attempts that have been made to address the limitations of the GWO algorithm in terms of convergence speed, convergence accuracy, and instability [55]. The improved versions of the GWO algorithm are applied to WSNs for enhancing the convergence speed and precision. The features of these algorithms are presented in Table 1, and they attempted to overcome the issues of slow convergence, falling into local minima, and low search precision of the GWO algorithm [56].

Dimension-based learning in GWO addresses the drawbacks of the conventional GWO algorithm, i.e., a lack of population diversity, premature convergence, and the imbalance between exploration and exploitation. It demonstrates applicability and efficiency in solving engineering design problems in a superior way compared to the conventional GWO algorithm [57]. Weighted GWO enhances the convergence rate with higher exploration and exploitation in the searching space. A weighted GWO algorithm with an MLP neural network further enhances the classification accuracy with optimal weights [58]. Binary GWO with SVM is used to improve the intrusion detection rate and accuracy in WSNs. It improves the intrusion detection rate and detection accuracy, and at the same time it minimizes the processing time, number of features, and false alarm rates [59]. “Differential evolution” is introduced to update the wolf pack at each iteration based on the fitness value. ‘R’ wolves with the least fitness values are eliminated and new set of (randomly generated) wolves are introduced. It gives better optimization accuracy and convergence speed than CSA, PSO, and ABCO algorithms [60]. An improved version of the GWO algorithm supports an energy-efficient, balanced CH structure in WSNs based on fitness values, and it extends the network stability period and throughput by 31.5% compared to the SEP algorithm. Behavior-based GWO performs better in terms of population diversity and convergence. The objective function for this algorithm is defined by considering the connectivity rate, coverage rate, and total energy consumption in WSNs [61]. A fuzzy-extended, GWO algorithm-based, threshold-sensitive, energy-efficient clustering protocol enhances the network stability. A modified GWO algorithm for heterogeneous WSNs selects the initial clusters depending on the values of the fitness functions for energy nodes. The fitness values are considered as initial weights in GWO and these weights are updated dynamically based on the distance between the wolves and their prey. It ensures the selection of optimal CHs and enhances the network lifetime by 55.7% and 31.9%, compared to SEP and the distributed energy-efficient clustering algorithm, respectively [62].

Table 1. Comparison of the relevant algorithms and their features.

Protocol	Nodes Type	Inter-Cluster Topology	Need of Energy Awareness	CH Selection	Heuristic Approach
SSMOECHS [24]	Homogeneous	Single-hop	No	Probabilistic	No
GWO-C [43]	Homogeneous	Single-hop	No	Probabilistic	Yes
GWO-based clustering [44]	Homogeneous	Dual-hop	No	Probabilistic	Yes
GWO [47]	Heterogeneous	Multi-hop	Yes	Probabilistic	Yes
HGWCSOA [48]	Homogeneous	Single-hop	Yes	Probabilistic	Yes
QCGWO [54]	Homogeneous	Not applicable	No	Not applicable	Yes
BGWO [61]	Homogeneous	Single-hop	No	Probabilistic	Yes
FGWSTERP [62]	Homogeneous	Single-hop	Yes	Fuzzy based	Yes
LEACH-PRO [63]	Homogeneous	Single-hop	Yes	Probabilistic	No
HMGWO [64]	Heterogeneous	Single-hop	Yes	Probabilistic	Yes
FIGWO [65]	Homogeneous	Single-hop	Yes	Deterministic	Yes

Table 1. Comparison of the relevant algorithms and their features.

Protocol	Nodes Type	Inter-Cluster Topology	Need of Energy Awareness	CH Selection	Heuristic Approach
SSMOECHS [24]	Homogeneous	Single-hop	No	Probabilistic	No
GWO-C [43]	Homogeneous	Single-hop	No	Probabilistic	Yes
GWO-based clustering [44]	Homogeneous	Dual-hop	No	Probabilistic	Yes
GWO [47]	Heterogeneous	Multi-hop	Yes	Probabilistic	Yes
HGWCSOA [48]	Homogeneous	Single-hop	Yes	Probabilistic	Yes
QCGWO [54]	Homogeneous	Not applicable	No	Not applicable	Yes
BGWO [61]	Homogeneous	Single-hop	No	Probabilistic	Yes
FGWSTERP [62]	Homogeneous	Single-hop	Yes	Fuzzy based	Yes
LEACH-PRO [63]	Homogeneous	Single-hop	Yes	Probabilistic	No
HMGWO [64]	Heterogeneous	Single-hop	Yes	Probabilistic	Yes
FIGWO [65]	Homogeneous	Single-hop	Yes	Deterministic	Yes

4. Methodology

In this section, the proposed EECHIGWO algorithm is presented with details to enhance the network lifetime using an optimal CH selection process. This network model is meant mainly for industrial applications where the different manufacturing segments of a plant are located at different geographical places and the assumptions are as follows:

1.

The SNs are randomly deployed in a two-dimensional geographical space.

2.

The BS is located at the center of the network terrain and there is multi-hop communication from CHs to the BS.

3.

The SNs are divided into approximately equal groups, and they are randomly distributed within the group.

4.

The SNs are homogeneous within the group and their mobility is limited to 0.2 m/s.

5.

BS and the nodes who participate in multi-path communication only will have uninterrupted power supply.

6.

BS executes the algorithm for CH selection and also it collects the aggregated data from all CHs.

Figure 1 shows the radio energy model of an SN using two different channel models: free space path loss (d²) model for a single-hop communication and multipath propagation fading (d⁴) model for the multi-hop path communication. Therefore, the energy consumption for transmitting an n-bit packet over distance ‘d’ is computed as

$$E_{TX}\left(n, d\right)=\{\begin{array}{c}n{E}_{elec}+n e_{fs} d^2 d<d_0\\ n{E}_{elec}+n e_{mp} d^4 d\ge d_0\end{array}$$

(1)

where

• e_fs → energy dissipation coefficient of free-space attenuation model
• n → packet length
• e_mp → energy dissipation coefficient of multipath attenuation model
• d → distance between sender and receiving node
• d₀ = $\sqrt{e_{fs} /e_{mp}}$ → threshold distance
• E_elec → energy needed to transmit/receive 1-bit data.

At Rx, the amount of energy consumption for receiving n-bit data packet is computed as

$$E_{RX}\left(n\right)=n\times E_{elec}$$

(2)

There are three parameters that contribute to the energy consumption at CH: number of data packets received from SNs which are members of a particular cluster, data aggregation performed by CH, and number of aggregated packets transmitted from CH to BS. Therefore, the energy consumption at CH is given as

$$E_{CH}=E_{RX}\left(n, d\right)\times S{N}_{num}+E_{DF}\times n \times \left(S{N}_{num}+1\right)+E_{TX}\left(n, d\right)$$

(3)

SN_num→ SN’s number in a particular cluster E_DF → data fusion energy/bit.

For all SNs other than CHs, the energy consumption is E_TX (n, d).

The total remaining energy during the k^th round is computed as:

$$E_R(k)=E_R(k-1)-({\displaystyle \sum _{l=1}^{C{H}_{num}(l)}{E}_{CH}(l)}+{\displaystyle \sum _{m=1}^{S{N}_{alive}(k)-C{H}_{num}(k)}{E}_{SN}(m))}$$

(4)

• E_R(k − 1) → total remaining energy at (k − 1)^th round
• CH_num(k) → number of CHs in the k^th round
• SN_alive (k) → total number of alive nodes in the k^th round
• E_CH(l) → energy consumed by l^th CH
• E_CH(m) → energy consumed by m^th SN

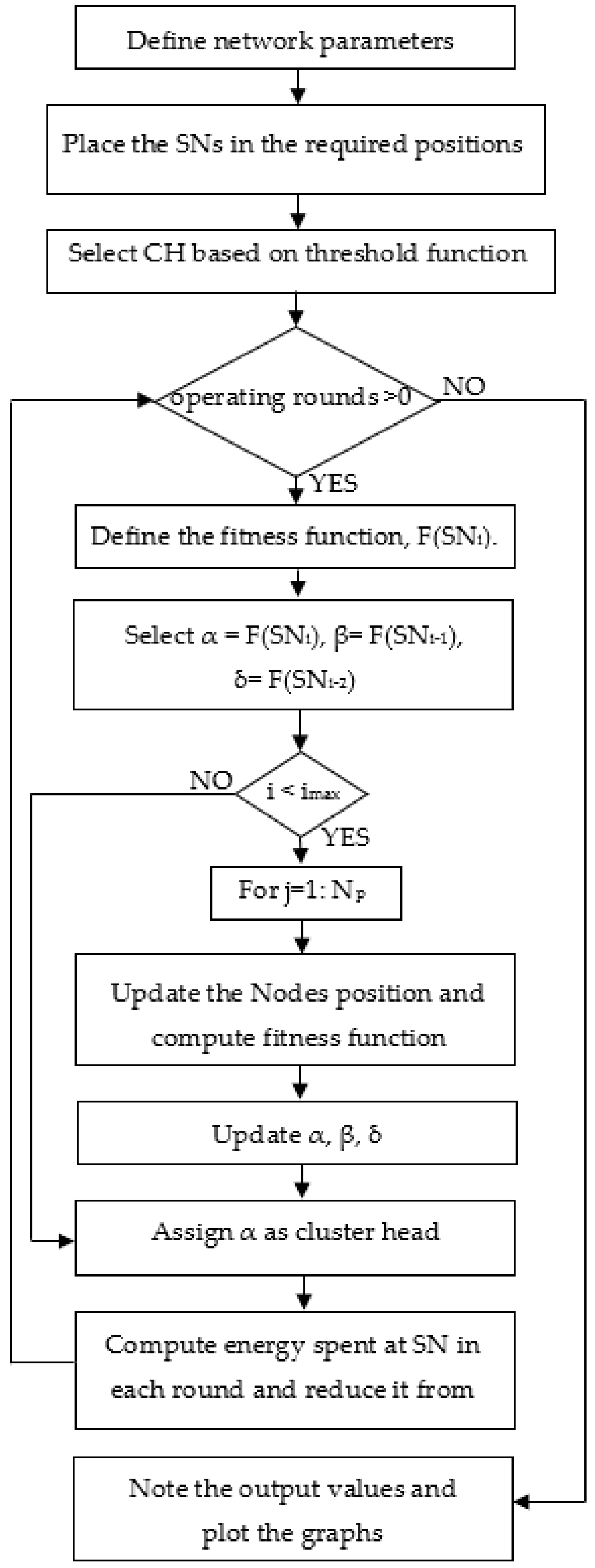
Proposed EECHIGWO Algorithm

To overcome the randomness in CH selection, BS performs CH selection based on the proposed EECHIGWO algorithm. The information about the selected CHs are broadcasted to all SNs through the multi-hop communication nodes. The total number of SNs are divided into four subsets (approximately) based on fitness value and out of which the location of sixteen SNs are declared as fixed to support multi-hop paths. The SNs are considered as grey wolves and CH is the prey. The EECHIGWO algorithm is defined in terms of rounds, and each round consists of CH formation stage and data transmission stage. The fitness value of an SN is computed based on the residual energy and its distance to BS.

$$F= \{\begin{array}{c}0.8 \times \left(\frac{E_{residual}}{E_{initial}}\right)+0.2 \times \left(\frac{d_{max} - d}{d_{max}-d_{min}}\right), E_{residual} <0\\ 0.2 \times \left(\frac{E_{residual}}{E_{initial}}\right)+0.8 \times \left(\frac{d_{max} - d}{d_{max}-d_{min}}\right), E_{residual} \ge d_0\end{array}$$

(5)

where

• E_inital → initial energy of SN,
• E_residual → residual energy at SN after each round,
• d → distance between SN and BS,
• d_max → maximum distance between SN and BS,
• d_min → minimum distance between SN and BS.

The Equation (5) represents the fitness function in which 80% weightage is given to residual energy at SN and 20% weightage is given to the distance between the SN and BS.

The initial position of BS is computed as

$$\overrightarrow{X_{CH}}=\left|{\omega }_{\alpha }\overrightarrow{X_{\alpha }}+{\omega }_{\beta }\overrightarrow{X_{\beta }}+{\omega }_{\delta }\overrightarrow{X_{\alpha }}\right|$$

(6)

where ω_α, ω_β, ω_δ are the initial weights and they are calculated as follows:

$${\omega }_{\alpha }=\frac{F_{\alpha }}{F_{\alpha }+F_{\beta }+F_{\delta }},{\omega }_{\beta }=\frac{F_{\beta }}{F_{\alpha }+F_{\beta }+F_{\delta }},{\omega }_{\delta }=\frac{F_{\delta }}{F_{\alpha }+F_{\beta }+F_{\delta }}$$

(7)

F_α, F_β, F_δ are the first three optimal fitness values of the SNs.

To enhance the capabilities of global search using the GWO algorithm, the weights ω_α, ω_β, ω_δ are dynamically updated using the vectors $\overrightarrow{D}$, $\overrightarrow{A}$ and at the i^th iteration, the weights are calculated as:

$${\omega }_{\alpha }^{i+1}=\frac{\overrightarrow{D_{\alpha }^{i+1}}\times \overrightarrow{A_{\alpha }^{i+1}}}{\overrightarrow{D_{\alpha }^{i+1}}\times \overrightarrow{A_{\alpha }^{i+1}}+\overrightarrow{D_{\beta }^{i+1}}\times \overrightarrow{A_{\beta }^{i+1}}+\overrightarrow{D_{\delta }^{i+1}}\times \overrightarrow{A_{\delta }^{i+1}}}$$

(8a)

$${\omega }_{\beta }^{i+1}=\frac{\overrightarrow{D_{\beta }^{i+1}}\times \overrightarrow{A_{\beta }^{i+1}}}{\overrightarrow{D_{\alpha }^{i+1}}\times \overrightarrow{A_{\alpha }^{i+1}}+\overrightarrow{D_{\beta }^{i+1}}\times \overrightarrow{A_{\beta }^{i+1}}+\overrightarrow{D_{\delta }^{i+1}}\times \overrightarrow{A_{\delta }^{i+1}}}$$

(8b)

$${\omega }_{\delta }^{i+1}=\frac{\overrightarrow{D_{\delta }^{i+1}}\times \overrightarrow{A_{\delta }^{i+1}}}{\overrightarrow{D_{\alpha }^{i+1}}\times \overrightarrow{A_{\alpha }^{i+1}}+\overrightarrow{D_{\beta }^{i+1}}\times \overrightarrow{A_{\beta }^{i+1}}+\overrightarrow{D_{\delta }^{i+1}}\times \overrightarrow{A_{\delta }^{i+1}}}$$

(8c)

During the CH selection process, the location of the CH is computed using α, β, ω wolves, and the other SNs compute their distances with respect to BS as shown in Figure 2.

The updated position of SN in the (i + 1)^th iteration is computed as:

$$\overrightarrow{X^{i+1}}=\overrightarrow{X_{CH}^i}-\overrightarrow{A}\times \overrightarrow{D}$$

(9)

where $\overrightarrow{A}$ is the convergence vector and it is given as $\overrightarrow{A}=2\overrightarrow{\alpha }\times \overrightarrow{r_1}-\overrightarrow{\alpha }$, $\overrightarrow{X_{CH}^i}$ is the CH position in the previous iteration, i.e., i^th iteration.

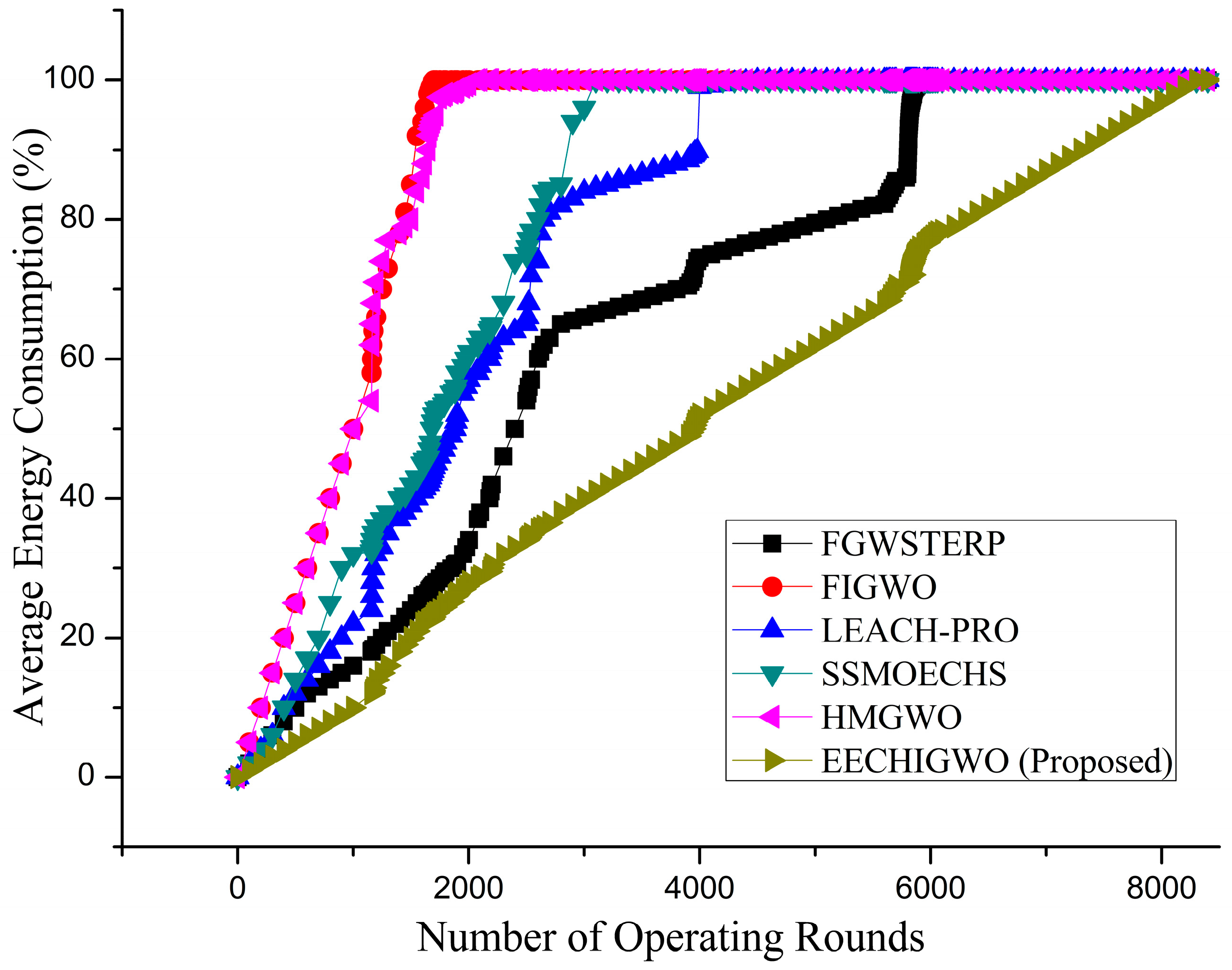
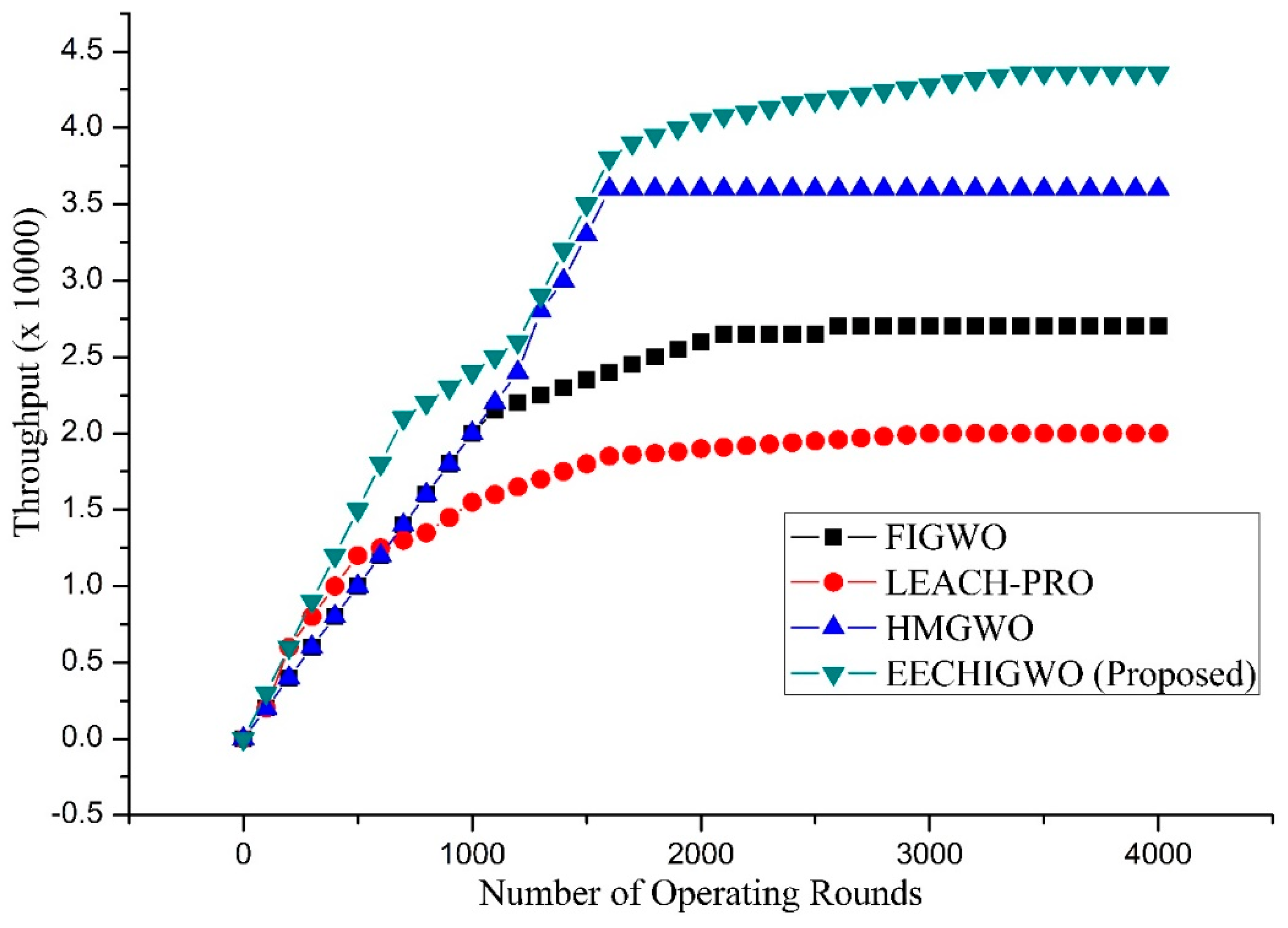
5. Results and Discussions

The performance of the proposed EECHIGWO algorithm is evaluated by conducting extensive simulations in MATLAB 2022B. Each simulation reading is considered by taking an average of fifteen simulation runs and the results are compared with the existing state-of-the-art literature in enhancing the energy efficiency of WSNs using GWO-based techniques. With the same experimental parameters as shown in

Table 2. Initial parameters of EECHIGWO protocol for simulations.

Parameter	Value
Network Terrain	100 m2
Network size	100
Initial Energy (E0)	1 J
Probability to become CH (P)	0.1
Number of CHs	P × 100
Efs, Eelec, Eamp	10 pJ/bit/m2, 50 nJ/bit, 0.0013 pJ/bit/m4
Dcritical, Dmax	20 m, 100 m
Data Packet size	500-Bytes
BS Position	(50, 50)

, the EECHIGWO algorithm’s performance is compared with the SSMOECHS [24], FGWSTERP [62], LEACH-PRO [63], HMGWO [64], and FIGWO [65] algorithms. For ease of comparison, the number of SNs are considered as 100 in the network terrain of 100 m². The metrics considered for analyzing the performance of the proposed algorithm include average energy consumption, number of dead nodes to define the network stability, and average throughput which defines the number of data packets delivered to BS. During the operation of WSNs, the SNs send the sensed information to their respective CHs and each CH forwards the aggregated information from various SNs to BS through fixed intermediate nodes.

Network lifetime can be defined based on stable and unstable periods. The stable period is the time at which network starts operating till the FND. The unstable period is the time duration between the FND and LND. In Figure 3, the FND, HND, and LND are observed at 5940th, 6604th, 7908th operating rounds, respectively. The reason for this enhanced lifetime of the proposed EECHIGWO protocol is that it eliminates the random selection of CH. The BS selects the CHs based on the optimal fitness values of the SNs, and the CHs’ selection information is broadcasted to all SNs through only the multi-hop communication nodes, which are placed in the fixed locations with an uninterrupted power supply. Therefore, the SNs with lower residual energy levels have a lower probability of being elected as CH. It enhances the network lifetime by avoiding the sudden death of SNs who have lower residual energies.

The global optimization capabilities of the proposed protocol give balanced energy consumption among SNs and leads to minimal average energy consumption at each round, as shown in Figure 4. The energy consumption is minimized due to optimal intra-cluster communication, uniform distribution of clusters, and multi-hop routing based on the distance between CH and BS. The multi-hop communication feature of the proposed algorithm enhances the load balancing capabilities and mitigates the energy consumption at CHs located far away from BS. From Figure 4, it can be seen that the first SN’s death was much later than the other protocols. Similarly, in the given network size of 100 SNs, the 50% SNs death, 100% SNs death was significantly increased compared to other protocols. The overall observation is that the proposed EECHIGWO protocol gives superior performance in terms of network lifetime compared to other protocols shown in Figure 4.

The throughput is measured in terms of the number of data packets delivered to BS from the SNs. The proposed EECHIGWO protocol provides higher throughput than other protocols as shown in Figure 5. This is due to the fact that it adopts an optimal CH selection and the SNs have the highest survival time. The even distribution of energy consumption at SNs improves the network throughput as well as prolongs the network life. At the given number of rounds, the number of alive SNs in the network are higher than that of the other algorithms; therefore, more data groups are generated, and the number of data packets delivered at the BS also increases. At a higher number of operating rounds, particularly after the round number 1600, the throughput using EECHIGWO is much higher than other protocols where more data packets are generated towards the BS.

Table 3. Network stability comparison in terms of number of rounds.

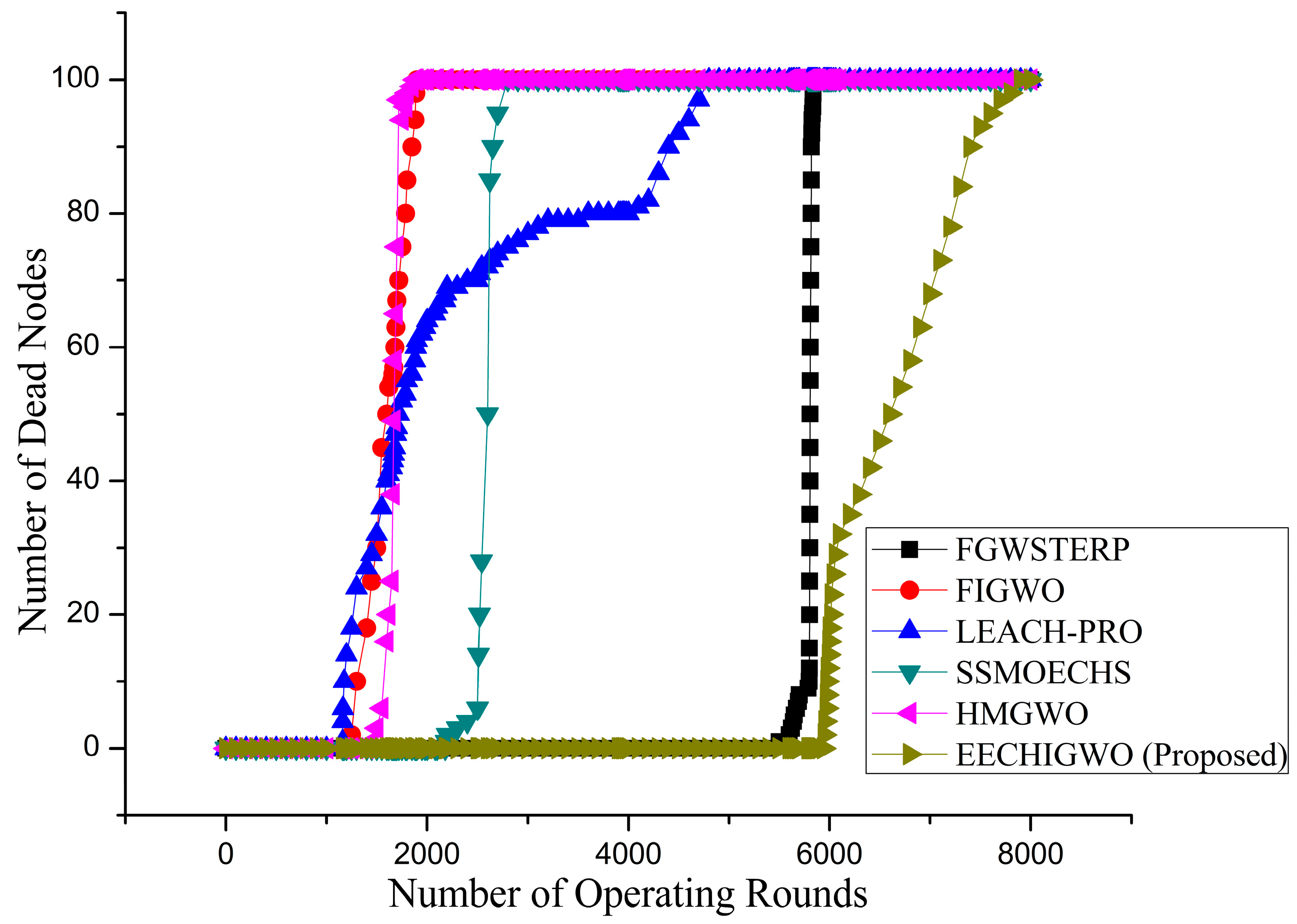
Algorithm	FND	FND Improvement (%)	HND	HND Improvement (%)	LND	LND Improvement (%)	Overall Improvement (%)
SSMOECHS [24]	2190	171.23	2600	154	2798	182.63	169.29
FGWSTERP [62]	5500	8	5807	13.72	5841	35.38	19.03
LEACH-PRO [63]	1159	412.5	1720	283.95	4800	64.75	253.73
HMGWO [64]	1450	309.65	1675	294.27	1884	319.75	307.89
FIGWO [65]	1248	375.96	1612	309.68	1906	314.9	333.51
EECHIGWO [Proposed]	5940	----	6604	----	7908	----	----

shows the network stability in terms of FND, HND, and LND of the proposed protocol and compares with various existing protocols. From the readings shown in Table 3, the rapid death of SNs is reduced from the round where FND occurs using the proposed algorithm. This is because of the criteria that the SN with lower residual energies become CH with very minimal probability. There is an improvement in network stability of 169.29%, 19.03%, 253.73%, 307.89%, and 333.51% compared to the SSMOECHS, FGWSTERP, LEACH-PRO, HMGWO, and FIGWO protocols, respectively.

6. Conclusions

In this paper, an energy-efficient CH selection using an improved version of the GWO algorithm is proposed which considers sink distance, residual energy, balancing factor, and average intra-cluster distance as the parameters in selecting the CH. The proposed EECHIGWO protocol has multi-hop features and provides optimal fitness function values to improve the WSN’s lifetime. The design of fitness function for CH selection is based on both the amount of residual energy at SNs and their Euclidean distance to BS. It supports deterministic and even selection of CHs in each round that leads to balanced energy consumption and avoids premature deaths of SNs. The performance of the protocol is tested in terms of number of dead nodes to define the network stability, average energy consumption, number of operating rounds, average throughput, and network lifetime. The simulation results have confirmed the optimal selection of CH with minimum energy consumption. It is proved that the network throughput, stability, and the network lifetime are enhanced compared to the existing state-of-the-art energy-efficient routing protocols for WSNs such as FGWSTERP [62], FIGWO [65], LEACH-PRO [63], SSMOECHS [24], and HMGWO [64], which are single-hop protocols with higher energy consumption and provide lower network lifetime. Using the proposed algorithm, there is an improvement in network stability of 169.29%, 19.03%, 253.73%, 307.89%, and 333.51% compared to the SSMOECHS, FGWSTERP, LEACH-PRO, HMGWO, and FIGWO protocols, respectively. As a future scope of the current research, the performance of the proposed algorithm can be tested for heterogeneous WSNs with larger number of SNs and higher node densities.