Temporal-Logic-Based Testing Tool Architecture for Dual-Programming Model Systems

Abstract

Today, various applications in different domains increasingly rely on high-performance computing (HPC) to accomplish computations swiftly. Integrating one or more programming models alongside the used programming language enhances system parallelism, thereby improving its performance. However, this integration can introduce runtime errors such as race conditions, deadlocks, or livelocks. Some of these errors may go undetected using conventional testing techniques, necessitating the exploration of additional methods for enhanced reliability. Formal methods, such as temporal logic, can be useful for detecting runtime errors since they have been widely used in real-time systems. Additionally, many software systems must adhere to temporal properties to ensure correct functionality. Temporal logics indeed serve as a formal frame that takes into account the temporal aspect when describing changes in elements or states over time. This paper proposes a temporal-logic-based testing tool utilizing instrumentation techniques designed for a dual-level programming model, namely, Message Passing Interface (MPI) and Open Multi-Processing (OpenMP), integrated with the C++ programming language. After a comprehensive study of temporal logic types, we found and proved that linear temporal logic is well suited as the foundation for our tool. Notably, while the tool is currently in development, our approach is poised to effectively address the highlighted examples of runtime errors by the proposed solution. This paper thoroughly explores various types and operators of temporal logic to inform the design of the testing tool based on temporal properties, aiming for a robust and reliable system.

1. Introduction

High-performance computing (HPC) enables powerful computing resources to solve complex and computationally demanding problems by improving performance and achieving high levels of speed and parallelism. Parallel processing enables HPC to achieve higher computing power and greater augmented performance compared to traditional computing systems. Utilizing parallel processing for performing tasks requires programmers to reconsider how they write programs to deploy them effectively on the different available processing units. Programmers must transform serial code to parallel code to achieve high-performance computing and a low execution time. Exascale systems, the latest HPC technologies, operate at speeds of 10 quintillion (10¹⁸) floating-point operations per second (FLOPS) [1]. The high speed of the Exascale systems can be achieved by adding more parallelism to the system using multi-level programming models integrated with the programming language to exploit the available hardware resources effectively [2].

Multi-level programming includes single-level, dual-level, and tri-level models. A single-level model uses one programming model, such as Message Passing Interface (MPI) or Open Multi-Processing (OpenMP). A dual-level approach uses two programming models, while in a tri-level programming model three models are combined with the programming language. Typically, various programming models can be applied to serve various purposes, including passing messages between multiple processes, such as MPIs, and shared-memory multi-processing, such as OpenMP.

Although using multi-level programming models when writing programs increases the system parallelism and improves its performance, it can lead to more synchronization errors in the system. Thus, testing these programs becomes extremely important [3]. Employing a combination of MPI and OpenMP can be viewed as encompassing both task parallelism and data parallelism. Task parallelism involves breaking down the workload into independent tasks that can be executed simultaneously with OpenMP threads, while data parallelism involves partitioning a substantial data set into smaller parts and processing them concurrently using OpenMP threads. OpenMP threads are used for computationally intensive tasks executed locally on a node. In contrast, MPI is used for inter-node communication to exchange data and synchronize computations across the distributed system. However, initiating many MPI calls using various OpenMP threads simultaneously increases these systems’ complexity and chance of errors.

While current HPC systems commonly use the dual model (MPI + OpenMP) to achieve more efficient computations, most of the available testing tools target either MPI or OpenMP and do not fully consider the dual model [4]. In a dual (MPI + OpenMP) model, there are new possible errors that may emerge, and identifying these errors requires an understanding of MPI and OpenMP and consideration of the interaction between these programming models. However, using testing techniques, such as integration testing or unit testing, cannot guarantee that the system is free of all types of errors, especially in parallel applications that have nondetermined behavior. Thus, applying effective logical formulas to ensure that the system is running without any violation may increase the reliability over the entire system.

Currently, temporal logic is used for various applications and in different research areas. It is powerful due to the fact that it includes a time element, which is an important factor to be considered in parallel systems. There are several types of temporal logic, such as propositional, linear, interval, and branching temporal logic, each with their own specific properties.

This research sets out to explore the selection of an appropriate temporal logic approach to serve as an assertion language, considering its properties and operators. The primary objective is to identify runtime errors, specifically those elusive to compiler detection due to the integration of C++, MPI, and OpenMP code. Our proposed solution is grounded in a robust theoretical foundation and a deep understanding of temporal logic properties. Indeed, it is crucial to note that the implementation of the proposed testing tool is currently in progress and the practical validation of the tool is the next step in our research agenda. The ultimate aim is to design an effective testing tool architecture capable of dynamically detecting runtime errors, such as race conditions and deadlocks, in the programs under examination. The subsequent sections will delve into the theoretical foundations, design considerations, and the envisioned potential of the proposed tool.

The rest of this paper is organized as follows. Section 2 offers a concise summary of the related research. Then, Section 3 identifies some of the runtime errors that occur in MPI and OpenMP programming models. In Section 4, the types of temporal logic are discussed, and the type chosen to be followed in our approach is specified and its selection justified. The proposed architecture is introduced in Section 5, followed by a discussion in Section 6. Lastly, Section 7 presents the conclusion.

2. Related Work

Temporal logic defines statements that trace state changes over time in formal methods using mathematical or logical terms. It has been shown to be useful in different areas including computer science, artificial intelligence, robotics, and many other fields. In addition, it has been used for program specification and verification since the early 1980s [5]. S. Ramakrishnan and J. McGregor [6] claimed that expressing chain events is extremely significant in both the modeling and testing of parallel and distributed systems. The authors presented a useful approach that aims to improve the quality of the testing and modeling of object-oriented distributed systems using temporal logic. In recent times, extensive attention has been drawn to the use of temporal logic and model checking, which depends on temporal logic, in different application areas for the purpose of identifying time properties.

B. Koteska et al. [7] proposed enhancing the testing process for complex and challenging scientific applications by employing formal specification and verification. The researchers specifically chose to utilize interval temporal logic for this purpose. Generally, researchers are interested in verifying different object-oriented languages, such as C, C++, and Java using different model checkers that depend on temporal logic. N. Mahmud et al. [8] emphasized the significance of formal methods in enhancing the rigorous analysis of requirements in embedded systems. They proposed an approach involving deep semantic analysis for requirements, which was manifested in the specification representation defined by description logic formulae. Additionally, the utilization of Timed Computation Tree Logic was suggested for model-checking embedded systems.

In [9], a tool that works with two model checkers to analyze the implementations in C/C++ web service systems is proposed to detect any violations determined using LTL. This tool is able to debug very complex distributed C/C++ web service systems and check high-level properties, such as safety and liveness, that are specified by LTL. Additionally, the tool can directly analyze implementations written in C and C++ languages. However, for finite-trace LTL, there are difficulties at the end of the trace.

Baumeister et al. [10] introduced A-HLTL, a temporal logic specifically designed for handling asynchronous hyperproperties—a collection of trace properties applied in computational systems. A-HLTL employs two temporal logics, namely, HyperLTL and HyperCTL*, along with two model checkers to assess hyperproperties in computational systems. This logic is particularly adept at describing asynchronous hyperproperties and enables the analysis of systems with traces that can proceed at different speeds and take stuttering steps independently. A-HLTL can address a wide range of security requirements. However, there is a model-checking problem in that it is undecidable, which presents a challenge in verifying properties expressed in this logic.

M. S. Khan et al. [11] highlighted the recent exploitation of temporal logic in various areas, including software engineering. The authors presented different viewpoints to researchers in the UML domain, giving significant consideration to temporal logic.

The JPAX tool, presented in [12], verified that the implemented program in Java complies with the properties formulated in temporal logic and provided by the user via specialized algorithms described in the paper. This tool can detect any errors related to concurrency, such as deadlocks and data races, but it does not provide a solution to correct the behavior of a program when the specified properties are not satisfied.

Aljehani et al. [13] proposed the IMATT tool that uses both static and dynamic testing to detect errors in web applications implemented in Java. The static tester analyzed the source code of a web application to detect violations and report them to the programmer, and then the dynamic tester used temporal logic to examine the application under test.

In [14], specification-based testing with LTL is applied in real-world systems, where system requirements are encoded in the LTL and a suitable model checker for LTL is applied. While this approach provides model checking for testing linear temporal properties in implementations, the scalability of LTL model checking is limited. This restricts its suitability for large-scale real-world systems, making it challenging to effectively handle faults.

In [15], Panizo and Gallardo presented STAN, a tool that can be applied in hybrid systems exhibiting both continuous and discrete behavior. STAN performs the runtime verification of non-functional properties in event-driven systems, where the system changes its state as a result of events. It used a model checker to verify properties described by Event-Driven Interval Temporal Logic. The tool has the ability to analyze data traces of hybrid systems, model some of their sub-classes, and analyze them against LTL properties. Furthermore, it is flexible, as it can be easily extended to support new types of data traces and temporal logic operators. However, the model checker that is used to verify properties is usually undecidable, even if there are some tools that deal with that problem but do not completely solve it. Moreover, it is difficult to represent some continuous variables. In addition, there are difficulties in predicting the exposed environment that relates to these hybrid systems.

More recently, researchers investigated the use of temporal logic in various control applications like robotics. Human actions can be produced repeatedly using specifications from LTL [16]. In [17], a runtime monitoring algorithm is presented that is generally used in robotics and automation tasks and motion planning. The algorithm uses time window temporal logic (TWTL) for the specification and decides whether the TWTL specification is satisfied or not. The tool is effective with an increased number of traces, efficient in consuming memory, and efficient in reducing the execution time. The proposed algorithm includes an offline version designed for logged traces, but it may need adjustments if applied to online monitoring. This aspect should be considered as a potential limitation. Some tools that are based on temporal logic are summarized in

Table 1. Tools based on temporal logic.

Solution/Tool	Applied to	Techniques	Advantages	Disadvantages
[9] Hybrid model checking	C/C++ web services	dynamically search violations specified by LTL	checks the high-level properties	difficulties at the end of the trace
[10] A-HLTL	computational systems	uses two temporal logics and two model checkers	covers a rich set of security requirements	undecidable model-checking
[12] JPAX	Java	verified properties in temporal logic	detects concurrency errors	does not clarify next step if properties not satisfied
[13] IMATT	Java	apply static and dynamic testing	tests agent security	temporal assert statements inserted manually
[14] Specification testing with LTL	real-world systems	system requirements are encoded in LTL	offers a practical method for testing	not suitable for big real-world systems
[15] STAN	hybrid systems	performs runtime verification data traces	efficiency and flexibility	difficult to represent continuous variables
[17] Runtime monitoring algorithm	motion planning	uses TWTL	increasing number of traces	It is offline version

.

In the realm of testing tools and techniques for detecting runtime errors in parallel systems using programming models, a variety of tools employ static or dynamic analyses, or a combination of both. For our focus, we will specifically explore tools targeting the MPI or OpenMP programming models, or both.

H. Ma et al. [18] argued that the most common runtime errors that can arise in MPI and OpenMP programs are deadlocks and race conditions. They introduced the HOME tool, which employs both static and dynamic analyses on a dual-level programming model involving MPI and OpenMP. HOME is designed to identify concurrency issues and improve the detection of data race conditions in the programming models. Marmot and PARCOACH [19,20] are testing techniques that target the hybrid MPI and OpenMP models. Marmot employs a dynamic testing approach, while PARCOACH utilizes hybrid testing techniques.

Additionally, Atzeni et al. [21] presented ARCHER, a hybrid testing tool applicable to OpenMP programs specifically designed to uncover critical data races common in multi-threaded programming. Additionally, various tools consider the runtime error violations in multi-threaded applications in general, which can also be employed to detect race conditions and deadlocks in OpenMP or MPI programs, even if not explicitly designed for them. Notable examples include Intel Inspector [22], ThreadSanitizer (TSan) [23], and Helgrind [24], all considered to be dynamic analyzing tools. Extensive work has been carried out on the OpenMP programming model to detect data races using static tools such as ompVerify [25], DRACO [26], PolyOMP [27,28], OMPRacer [29], and LLOV [30], as well as dynamic race detection techniques such as SWORD [31], ROMP [32], and OMPSanitizer [33].

There are different tools that target the deadlock in programming models, such as Magiclock [34] and Sherlock [35] for deadlock detection. S. Royuela et al. [36] argued that the best deadlock detector is the static deadlock analysis approach developed in [37], which is designed for applications whose behaviors are specified based on the C standard and P-threads specification.

For MPI applications, tools like Nasty-MPI [38], MUST [39], and MEMCHECKER [40] serve as dynamic testing tools to detect runtime errors. Effort is still continuing to design tools that can effectively detect runtime errors in MPI and other programming models. In this vein, MPI-RCDD was suggested by [41] to identify the main causes of the deadlock problem in MPI programs by implementing two techniques: process dependency and message timeout. MUST-RMA is a dynamic analyzer proposed by [42] that combines two tools, i.e., MUST and ThreadSanitizer. It concentrates on data race errors that occur across multiple processes in the Remote Memory Access of MPI.

In the context of the existing literature, to the best of our knowledge, it has been identified that no testing tool leveraging temporal logic has been put forth for the explicit purpose of detecting runtime errors within the dual-programming model, particularly in scenarios involving MPI and OpenMP. In response to this gap, our study introduces a novel testing approach based on temporal logic to identify and address runtime errors within the dual-programming model implemented in C++ with MPI and OpenMP. Detailed insights into the proposed technique will be presented in Section 5. In

Table 2. Some testing tools used for MPI, OpenMP, or hybrid programming models.

Tool	Targeted Errors	Programming Models	Technique	Temporal Logic Based
HOME [18]	data races and incorrect synchronization	MPI/OpenMP	hybrid	no
Marmot [19]	deadlock, race condition and mismatching	MPI/OpenMP	dynamic	no
PARCOACH [20]	deadlock, data race and mismatching	MPI/OpenMP	hybrid	no
ARCHER [21]	data race	OpenMP	hybrid	no
ompVerify [25]	data race	OpenMP	static	no
MUST [39]	deadlock and data race	MPI	dynamic	no
MPI-RCDD [41]	deadlock	MPI	dynamic	no
MUST-RMA [42]	data race	MPI	dynamic	no
Our tool	deadlock and data race	MPI/OpenMP	dynamic	yes

below, the summary of some testing tools used for MPI, OpenMP, or hybrid programming models is displayed.

Despite the advancements in software testing tools for parallel applications, a notable void persists in addressing runtime errors in a dual-programming model. The models chosen for our study, namely, MPI and OpenMP, align with the prevailing practices in current HPC systems striving for Exascale speeds. However, it is noteworthy that existing testing tools predominantly concentrate on either MPI or OpenMP, overlooking the unique challenges posed by the dual model. Specifically, our proposed tool, which is still in the developmental phase, builds upon temporal logic properties, which are crucial for addressing the temporal requirements of parallel systems to ensure accurate functionality. The envisioned development of this tool is designed to enhance system reliability by unveiling a diverse range of runtime errors within C++ programs that integrate the MPI and OpenMP programming models.

3. Runtime Errors

The compiler is able to detect syntax and semantics errors; however, it cannot detect runtime errors, which can cause serious problems when running the program. It is the programmer’s task to check any probability of runtime errors in a parallel program and design the program to prevent such errors from occurring. In addition, the probability of runtime errors is even higher, and their causes vary when using programming models integrated with a programming language. Various papers discuss the common runtime errors that arise when using single- [43], dual- [2], or tri-level programming models [44,45]. This section focuses on the cases in which runtime errors may occur in MPI and OpenMP programming models integrated with C++ programs. These cases are to be targeted by our proposed detection tool.

Typically, threads are susceptible to race conditions and deadlocks. A deadlock arises when multiple threads are in a state of waiting for each other to receive data, resulting in a halt in their execution without any progress. Deadlocks can be categorized as either actual or potential deadlocks. An actual deadlock, also called real or deterministic, is a deadlock that is certain to occur. A potential deadlock, also called non-deterministic, is a deadlock that may or may not occur. The race condition occurs when two or more threads or processes compete to access a shared resource concurrently without enforcing appropriate synchronization rules that prohibit the race condition [36].

3.1. MPI Errors

The Message Passing Interface (MPI) programming model provides a high level of parallelization for the code. However, when threads perform send and receive operations, the MPI is susceptible to certain errors that are not detected by the compiler, such as deadlock and race condition errors. The main arguments of send and receive operations in the MPI programming model are illustrated in Listing 1. In the first argument, both the send and receive operations represent the data buffer. Then, the second and third arguments specify the number and kind of data in the buffer. The fourth argument represents the rank of the destination/source process, while the fifth represents an integer tag that is used to identify the message being received/sent. Then, the communicator that defines the group of processes involved in the communication is defined in the sixth argument. Finally, a status object that contains information about the received message is only defined in the receive operation.

Listing 1. MPI send and receive.

1: MPI_Send(void* data, int count, MPI_Datatype datatype, int destination, int tag,

2:     MPI_Comm communicator);

3: MPI_Recv( void* data, int count,MPI_Datatype datatype, int source, int tag, 4:     MPI_Comm communicator, MPI_Status* status);

3.1.1. MPI Deadlock

The causes of deadlocks can vary. One scenario occurs when data are sent and received with inconsistent types or tags in the send and receive operations. Deadlocks may also arise based on the size of the transmitted data; if the data size exceeds the buffer size, a deadlock will occur. To prevent deadlocks, each send operation must have a corresponding receive operation. Another potential deadlock occurs if the programmer specifies an incorrect source number in the receive operation or a wrong destination number in the send operation. In MPI, a deadlock may arise with (Send–Send) operations when the data size exceeds the buffer size.

Listing 2 shows an actual deadlock caused by simultaneously implementing two processes, starting with receive operations (Recv–Recv). Each process will wait to receive data, causing the system to hang forever.

Listing 2. Recv–Recv error in MPI.

1: if(rank==0) 2:   { 3: MPI_Recv (&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD, &status); 4: msg=42; 5: MPI_Send (&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD); 6:   } 7:    else if (rank == 1) 8:   { 9: MPI_Recv (&msg, 1, MPI_INT, 0, 0, MPI_COMM_WORLD, &status); 10: msg=23; 11: MPI_Send (&msg, 1, MPI_INT, 0, 0, MPI_COMM_WORLD); 12:   }

Listing 3 illustrates the application of Synchronous Send (Ssend), where the send operation becomes blocked until a handshake between the sender and the receiver takes place. Failure to establish this handshake can potentially lead to a deadlock.

Listing 3. Synchronous send in MPI.

1: if (rank==0) 2: { 3:   msg=42; 4:   MPI_SSend (&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD); 5:   MPI_ Recv (&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD, &status); 6: } 7:   else if (rank == 1) 8: { 9:   msg=23; 10:   MPI_SSend (&msg, 1, MPI_INT,0, 0, MPI_COMM_WORLD); 11:  MPI_ Recv (&msg, 1, MPI_INT, 0, 0, MPI_COMM_WORLD, &status); 12:  }

3.1.2. MPI Race Condition

The Immediate Send (Isend) is used in asynchronous (non-blocking) communication to achieve a high level of parallelization, since neither the sender nor the receiver will be blocked. However, this type of communication may cause a race condition, such as in the example illustrated in Listing 4. In this example, the value of “msg” is changed before it is received; therefore, incorrect data are received and an incorrect result is obtained.

Listing 4. Isend in MPI.

1: msg=42; 2: // send message asynchronously 3: MPI_ISend (&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD); 4: 5: // Do some other work while message is being sent 6: 7: msg=23; 8: 9: MPI_Wait(&request, MPI_STATUS_IGNORE); // it return when operation or request is complete

Furthermore, using the wildcard (MPI_ANY_SOURCE) as the source argument in a receive call can result in a race condition. In the wildcard, no specific source is determined, as shown in Listing 5, where the order of the receive operations made by the process with rank 1 could cause a potential race condition, which may lead to potential deadlock.

Listing 5. Wildcard in MPI.

1: if (rank == 0) 2:  { 3:  msg = 42; 4: MPI_Send(&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD); 5: MPI_Recv(&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD, &status); 6:  } 7: else if (rank == 1) 8:  { 9: msg = 23; 10: MPI_Send(&msg, 1, MPI_INT, 0, 0, MPI_COMM_WORLD); 11: MPI_Recv(&msg, 1, MPI_INT, MPI_ANY_SOURCE, 0, MPI_COMM_WORLD, &status); 12: MPI_Recv(&msg, 1, MPI_INT, 2, 0, MPI_COMM_WORLD, &status); 13:  } 14: else if (rank == 2) 15:  { 16: msg = 99; 17: MPI_Send(&msg, 1, MPI_INT, 1, 0, MPI_COMM_WORLD); 18:  }

3.2. OpenMP Errors

The Open Multi-Processing (OpenMP) programming model provides a high level of parallelization by exploiting the multi-core CPUs and shared memory. It distributes the workload over multiple threads and, therefore, will achieve a faster execution. However, it is susceptible to errors such as the deadlock and race condition, which are not detected by the compiler.

3.2.1. OpenMP Deadlock

Basically, generating locks in any program is subject to errors; in particular, using nested locks can cause deadlock. The programmer must be aware of how to use locks in OpenMP and understand that locks must be properly initialized to avoid defects. If a thread acquires a lock, then all other threads will be prohibited from calling that lock until it is released by the owner thread through the execution of “omp_unset_lock”. It is the programmer’s responsibility to check for these types of errors, as they may not be detected by the compiler. Furthermore, using locks incorrectly may lead to deadlock, which is caused by the race condition, as in Listing 6. A deadlock is caused when there are two threads running concurrently and each thread attempts to obtain a lock owned by the other thread that cannot be released. Thus, these threads will infinitely wait for each other, causing a deadlock situation. The same deadlock error may occur with nested locks within if–else blocks.

Listing 6. Deadlock caused by nested locks within sections.

1: #pragma omp sections 2:   { 3: #pragma omp section 4:      { 5:    omp_set_lock(&lockk1); 6:    omp_set_lock(&lockk2); 7:    omp_unset_lock(&lockk1); 8:    omp_unset_lock(&lockk2); 9:      } 10:  #pragma omp section 11:    { 12:    omp_set_lock(&lockk2); 13:    omp_set_lock(&lockk1); 14:    omp_unset_lock(&lockk2); 15:    omp_unset_lock(&lockk1); 16:    } 17:   }

Moreover, a barrier construct is set to synchronize all threads such that each thread will be forced to wait until all threads have arrived to ensure the integrity of the data. However, using a barrier inside a for-loop in OpenMP will lead to a potential deadlock (see Listing 7).

Listing 7. Barrier within for-loop error in OpenMP.

1: void calculate(int *A, int size) 2:  { 3:  #pragma omp parallel for 4:    for (int i = 0; i < size; i++) 5:    { 6:      // Perform some calculations on array A 7:      A[i] = i * 2; 8:      #pragma omp barrier // Potential deadlock here 9:    } 10:  }

Using the same name for nested critical directives may lead to a deadlock. In addition, not specifying the names of nested critical regions will lead to them being dealt with as if they have the same name (see Listing 8).

Listing 8. Nested critical directives.

1: int x = 0; 2: #pragma omp parallel num_threads(2) 3:   { 4:    #pragma omp critical 5:    { 6:    // Critical section 1 7:    x++; 8: 9:    #pragma omp critical 10:      { 11:       // Critical section 2 (nested) 12:       x--; 13:      } 14:    } 15:   }

In OpenMP applications, there will be a deadlock if a lock is set twice in different places without being released. Furthermore, a deadlock situation will occur in a system if the programmer has locked a variable in a section and released it in another section, or if a variable is locked inside a for-loop but it is unlocked outside the block of the for-loop. Moreover, Listing 9 shows a potential deadlock situation because of the unlocking statement that is placed inside the if (or else) statement. Depending on the input variable value, the deadlock may or may not occur.

Listing 9. A potential deadlock situation in OpenMP.

1: #pragma omp parallel 2:  { 3:  #pragma omp critical 4:  { 5:    omp_set_lock(&lock1); 6:    if (input_variable == value) 7:    { 8:     omp_unset_lock(&lock1); 9:     } 10:    else 11:    { 12:       // perform some code 13:    } 14:  } 15:  }

The incorrect use of the master directive, which is a block executed only by the master thread within the parallel region, could lead to a deadlock and may also cause a potential race condition. The deadlock occurs if the master thread meets a barrier construct within the nonparallel region. The master thread will not be continued until all threads arrive at the synchronization construct. However, these threads will not arrive at the barrier construct because they are executed outside the nonparallel region. Additionally, a race condition can occur when shared data are modified by both the master thread in the non-parallel region and the threads outside of it, as illustrated in Listing 10. Furthermore, the barrier construct should not be utilized within critical, ordered, and explicit task regions, for similar reasons.

Listing 10. Barrier inside a master directive-caused deadlock.

1: #pragma omp parallel 2:  { 3:   // Do some parallel work 4:   #pragma omp master 5:   { 6:     // Do some sequential work 7:     #pragma omp barrier // Potential deadlock 8:      // Modify shared data 9:   } 10:   // Do more parallel work 11:   // Modify shared data lead to potential race condition 12:  }

In addition, there is potential for a deadlock if the master construct is defined within a single region, which is a block that is only executed by the thread that arrives first, while the other threads cannot proceed until the single-region execution is complete. The deadlock in this case occurs because the thread accessing the single region is not the master thread. Therefore, the master construct becomes stuck and will never be executed. This results in a conflict, as the master must be implemented by the master thread, and the single construct executed by the first arriving thread (see Listing 11).

Listing 11. Potential deadlock caused by a master construct.

1: /* Master thread attempts to enter the single region which is executed 2:  by the first arrived thread */ 3:  #pragma omp single 4:   { 5:    #pragma omp master 6:    { 7:  // Code must be executed by the master thread within the single region 8:    } 9:   }

Additionally, a deadlock might occur if the programmer is not aware of the order in which the locks are accessed. Not releasing locks before encountering a task scheduling point, such as a “taskwait” directive or a barrier, leads to a potential deadlock resulting from a race on a lock. The “taskwait” directive is a construct that prevents the parent thread from continuing with the remaining portion of the program until all child operations have been completed (see Listing 12).

Listing 12. Potential deadlock caused by a race on a lock.

1: #pragma omp parallel 2: { 3:    #pragma omp master 4:   { 5:    #pragma omp task 6:    { 7:      #pragma omp task 8:      { 9:          omp_set_lock(&lock); 10:         // Perform some action 11:         // Release the lock 12:        omp_unset_lock(&lock); 13:      } 14:      omp_set_lock(&lock); 15:       // Perform some action 16:      #pragma omp taskwait 17:      // Release the lock 18:      omp_unset_lock(&lock); 19:    } 20:   } 21: } 22: omp_destroy_lock(&lock);

The single directive must be reached by all threads, and this is stated in the specification of the OpenMP [46]. However, as seen from Listing 13, it is not guaranteed that all threads will reach the single directive, as this depends on whether the condition of the “if” statement is satisfied. Therefore, some of the threads will stop at the end of the single directive block while other threads will stop at the explicit barrier construct, resulting in a potential deadlock. Similarly, if a barrier is placed within a function, and the code by which this function is called is within an “if” statement block, according to the “if” statement condition, some threads will reach the barrier inside the function, while others will reach the implicit barrier at the end of the parallel region, potentially leading to a deadlock.

Listing 13. Potential deadlock caused by if statement.

1: void performAction() 2:  { 3:    if( /*...*/ ) 4:    { 5:      #pragma omp parallel 6:      { 7:        If() 8:        { 9:         /*...*/ 10:          #pragma omp single 11:          { 12:             /*...*/ 13:          } // implicit barrier 14:         #pragma omp barrier // explicit barrier 15:        } 16:      } 17:    } 18:  }

3.2.2. OpenMP Race Condition

Typically, all programming models suffer from the race condition problem. In particular, the race condition in OpenMP occurs when read and write operations are performed on shared data. The example in Listing 14 shows a race condition occurring because of the attempt of multiple threads to alter the shared variable “sum” at same time. As a result, the value of “sum” may be different from run to run. In another scenario, data dependency could lead to a data race in OpenMP, especially when dependencies exist between two or more arrays placed within a nested for-loop. The iterations of the for-loop are executed by a group of threads simultaneously. Consequently, a data race may occur when multiple threads concurrently access an array, and its execution depends on another array. In other words, if one thread reads the variable and other thread writes to the same variable, then the result will be incorrect because of the race condition. In addition, a race condition can occur due to the use of nested loops that belong to one parallel directive, whether the for-loop is preceded by a for-directive or not.

Listing 14. Race condition caused by dependent computation.

1: int main() 2:  { 3:  int sum = 0; 4:  #pragma omp parallel for 5:  for (int i = 0; i < 10; i++) 6:  { 7:    sum += i; 8:  } 9:  }

The “nowait” clause allows threads to continue their execution without waiting for other threads at the implicit barrier in constructs such as parallel, for, sections, and single, leading to an increase in system parallelism. However, the incorrect use of the “nowait” directive can cause a race condition in OpenMP. In Listing 15, two tasks attempt to access a shared datum and alter it simultaneously. However, due to the “nowait” directive, the implicit barrier at the end of the single directive will be revoked, which means the second task will proceed with its execution and not wait for the first one to complete, resulting in an unexpected output.

Listing 15. Race condition caused by “nowait” directive.

1:  // shared variable x 2: #pragma omp parallel 3:  { 4:  #pragma omp single 5:  { 6:    #pragma omp task shared(x) 7:    { 8:      // Task 1: access and modify shared variable x 9:    } 10:     #pragma omp nowait 11:  } 12:  //.... 13:  #pragma omp task shared(x) 14:  { 15:    // Task 2: access and modify shared variable x 16:  } // ...... 17:  }

In Figure 1 and Figure 2 below, some of the errors in MPI and OpenMP that were discussed in this paper are summarized.

3.3. Errors in Dual MPI and OpenMP Model

In this section, we will discuss how a system written in MPI and OpenMP in addition to C++ code will be affected by the errors existing in either MPI or OpenMP. For example, if a deadlock occurs in MPI code, how will this affect the whole system? Let us consider Listing 16, in which the array C values depend on the values of array A, and array A needs to complete its calculation before being used in C to avoid a data race. However, there is a possibility that some threads may start the calculation of array C before finishing the calculation of array A. Furthermore, a race condition may also occur if the “nowait” clause is used after the for-loop construct. In addition, in the MPI code, if the send operation did not specify the receiver, a deadlock will occur. As a result, the entire system will enter a deadlock situation because of these errors.

Listing 16. (MPI + OpenMP) program with deadlock situation.

1: void calculateA(int *A, int size) 2:  { 3:  #pragma omp parallel for 4:  for (int i = 0; i < size; i++) 5:  { 6:     // Perform some calculations on array A 7:    A[i] = i * 2; 8:  } 9:  } 10: 11: void calculateC(int *C, int *A, int size) 12:  { 13:  #pragma omp parallel for 14:  for (int i = 0; i < size; i++) 15:  { 16:    // Perform some calculations on array C based on array A 17:     C[i] = A[i] + 1; 18:  } // Potential race condition occur if the ‘nowait’ clause is used 19:  } 20: 21: int main(int argc, char **argv) 22:  { 23:  int rank, size; 24:  MPI_Init(&argc, &argv); 25:  MPI_Comm_rank(MPI_COMM_WORLD, &rank); 26:  MPI_Comm_size(MPI_COMM_WORLD, &size); 27:  int *A = new int[size]; 28:  int *C = new int[size]; 29:  calculateA(A, size); 30:  // Potential data race here if threads writing to C before A is fully updated 31:  calculateC(C, A, size); 32:  // Potential deadlock here if not specifying the receiver in MPI_Send 33:  if (rank == 0) 34:  { 35:    MPI_Send(C, size, MPI_INT, 1, 0, MPI_COMM_WORLD); 36:  } 37:  else if (rank == 1) 38:  { 39:    MPI_Recv(C, size, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE); 40:  } 41:  }

MPI specification allows the creation of multiple threads within an MPI process. Ensuring the correctness of this process is a challenging task because it is hard to properly synchronize threads and processes. In addition, the resulting synchronization errors may not cause any conflict with the MPI specification, and, thus, these errors are usually not detected before running the system. Considering the example in Listing 17, there are two processes, each of which run a thread: one for send and other for receive. Nevertheless, one of these threads will be executed because of the use of “MPI_Init()”, which is used to initialize the MPI library. It restricts the execution to only a master thread within each process. Therefore, undefined behavior can occur because of a deadlock that will be raised. This is dissimilar to the extended “MPI_Init_Thread()” function, which is compatible with the OpenMP as it supports the execution of multiple threads within a single process. Therefore, the programmer must implement the “MPI_Init_Thread()” function instead of “MPI_Init()” in order to solve this issue.

Listing 17. Deadlock by MPI_Init().

1: int MPI_Init() 2: omp_set_num_threads(2); 3: #pragma omp parallel 4:  { 5:  #pragma omp sections 6:  { 7:    #pragma omp section 8:    if (rank == 0 ) 9:      MPI_Send(rank1); 10:    #pragma omp section 11:    if (rank ==0) 12:      MPI_Recv(rank1); 13:  } 14:  }

To distinguish between different threads running in different processes, their tags must not be the same, in order to avoid a potential deadlock. In the example shown in Listing 18, it is possible that certain MPI_Recv calls are prevented; therefore, a deadlock may arise because the corresponding thread does not receive any incoming messages. This can happen when all incoming messages have the same tag and cannot be distinguished from each other. To solve this issue, it is possible to initialize the tag variable with the thread_ID.

Listing 18. Potential deadlock in (MPI + OpenMP) program.

1: MPI_Init_thread(0,0,MPI_THREAD_MULTIPLE, & provided); 2: MPI_Comm_rank(MPI_COMM_WORLD, &rank); 3: 4: int tag=0; omp_set_num_threads(2); 5: #pragma omp parallel for private(i) 6: for(j = 0; j < 2; j++) 7:  { 8:  if(rank==0) 9:   { 10:    MPI_Send(&a, 1, MPI_INT, 1, tag, MPI_COMM_WORLD); 11:    MPI_Recv(&a, 1, MPI_INT, 1, tag, MPI_COMM_WORLD, MPI_STATUS_IGNORE); 12:   } 13:   if(rank==1) 14:   { 15:    MPI_Recv(&a, 1, MPI_INT, 0, tag, MPI_COMM_WORLD,MPI_STATUS_IGNORE ); 16:    MPI_Send(&a, 1, MPI_INT, 0, tag, MPI_COMM_WORLD); 17:   } 18:  }

The dependency errors for the dual-level programming model (MPI + OpenMP) and their effect on the system are illustrated in

Table 3. Dependency errors for dual-level programming model (MPI + OpenMP).

MPI	OpenMP	Effect on Entire System
no error	no error	no error
deadlock	no error	deadlock in system
potential deadlock	no error	potential deadlock in system
race condition	no error	race condition in system
potential race condition	no error	potential race condition in system
no error	deadlock	deadlock in system
no error	potential deadlock	potential deadlock in system
no error	race condition	race condition.
no error	potential race condition	potential race condition in system
deadlock	deadlock	deadlock in system
deadlock	OpenMP race condition	deadlock in system
race condition	deadlock	deadlock in system
race condition	race condition	potential deadlock or potential race condition in system

. According to the runtime errors discussed in Section 3, the chance of errors in a program that is written using a dual-programming model, in our case MPI and OpenMP, will be increased and its causes are varied. Errors may be caused by the MPI programming model, OpenMP programming model, or a combination of both.

4. Temporal Logic

After studying and analyzing runtime errors and investigating their causes and impact on a hybrid system that uses MPI and OpenMP, it is essential to understand the types and properties of temporal logic. This understanding will help specify the most suitable type that can be applied in our research.

Temporal logic is a mathematical or logical framework that describes how statements change over time. It has been proven to be a valuable tool in various fields due to its ability to formally express and analyze state changes. Konur categorized temporal logic with respect to time flow and different standards, considering aspects such as “discrete time versus continuous time”, “points versus intervals”, “linear time versus branching time”, and “past versus future” [47].

In the next subsections, we further discuss the most important types of temporal logic related to our proposed research tool, which are linear, interval, and branching temporal logic. Each type of temporal logic is designed to serve a specific scope of a system. For instance, interval time logic was developed to cater to the needs of real-time systems, and linear temporal logic can address concurrent systems’ specification and validation. Every type of temporal logic has a level of expressive power, which is the capability to precisely depict temporal properties or relationships in a system. Additionally, selecting the suitable type of temporal logic involves sacrificing one property out of two: expressiveness or complexity. Therefore, finding a balance between these two properties is essential [47].

4.1. Linear Temporal Logic

Linear temporal logic (LTL) is a set of possible instants that can be discrete or continuous. These instants are ordered sequentially such that only one possible time instant follows each predecessor. LTL is particularly expressive for natural language analysis models and finds utility in the specification and validation of concurrent systems. Indeed, it is useful for expressing the behavioral relationship specification based on time rather than functional dependencies.

LTL has proven its worth in verifying infinite state systems (proof systems). Its capabilities extend to describing properties related to sequences of states that follow a linear order. For example, LTL can articulate statements like: “p holds at some state in the sequence” [47]. The LTL language is composed of a set of propositional variables, Boolean operators such as not (¬), and (∧), or (∨), and implies (→), and temporal operators such as next, until, eventually, and always, which are denoted as ○, U, ◇, and □, respectively.

Table 4. LTL operators.

System Properties	LTL Properties
q holds at all states after p holds	p → q
p and q cannot hold at the same time	□ ((¬q) ∨ (¬p))
q holds at some time after p holds	p → ◇q
If p repeatedly holds, q holds after some time	□◇ p → q
If p always holds, q holds after some time	□ p → ◇q

shows some examples of how LTL operators can be used to express different system properties.

Temporal logic was initially created to represent tense in natural language. However, under the field of computer science, LTL has gained substantial importance in concurrent reactive systems, particularly in designing formal specifications and testing validity. In addition, LTL is widely used for the formal verification of concurrent systems. The popularity of temporal logic, in this context, stems from its ability to succinctly and formally express a variety of useful concepts such as safety, liveness, and fairness properties.

The safety property indicates a specific condition that must never be satisfied, such as “no deadlock”. The liveness property, on the other hand, indicates a specific condition that must be satisfied at a specific time or any time in the future, such as “a system eventually terminates”. The fairness property describes assumptions that are necessary to guarantee that a subsystem moves forward, usually helpful for scheduling processes or responding to messages, for instance, “at the end of any request, it will be satisfied” [48].

4.2. Branching Temporal Logic

Another classification of temporal logic is branching time logic (BTL). In BTL, the time structure will be implemented as a tree of states, where each path in the tree is a possible execution sequence. Thus, a number of instants can follow a predecessor in a binary order.

BTL finds efficiency in many applications, such as in artificial intelligence, especially in planning systems in which a number of strategies are produced based on different states. The BTL is efficient in verifying finite state systems. Unlike LTL, which is restricted to only one path, the BTL syntax allows path quantification. Thus, formulas can be evaluated through different branches. It can express a program property efficiently, and it can be used with model checking with less complexity and less model size, where BTL is linear with the number of states, and LTL is exponential. BTL is very efficient for use in model-checking procedures [49].

In addition, computational temporal logic (CTL) is a type of branching and point logic which has more syntax. This additional syntax allows CTL to express the more useful and complex specification properties of a system. BTL can also be used to specify the properties of concurrent programs. It is particularly used when the states to be represented are uncertain, implying several potential alternative futures for a state.

In BTL, the main operators, or path quantifiers, are “there exist” (∃), which implies some paths, and “for all” (∀), which implies all paths in the execution branches.

Table 5. Branching operators.

System Properties	BTL Properties
There exists a state where p holds but q does not hold	∃(p ∧ ¬q)
At all paths p holds after some time	∀ □(∃◇p)

indicate examples of the properties expressed in BTL:

Although BTL can express the different properties of concurrent systems, it cannot express the fairness property, which can be expressed using LTL [47,48].

4.3. Interval Temporal Logic

Interval temporal logic (ITL) presents the concept of intervals, providing a means to represent continuous periods of time. Temporal logics that can describe events in time intervals are considered more expressive than those that only deal with single time instances because of their ability to describe events that occur over a period of time, and even a single moment can be described in ITL such that the interval size will be equal to one.

In contrast to points-based temporal logics that describe a system’s evolution state-by-state, ITL efficiently defines temporal models and properties for concurrent systems, particularly those with time-dependent behaviors. This makes ITL especially valuable for real-time critical systems. Moreover, describing the relations between events is possible using interval-based methods, which are considered to be more expressive, abstractive, and simpler than points-based approaches such as LTL, as well as being more comprehensive and easier to understand. Researchers noted that ITL is more appropriate for describing natural language in terms of time than the point-based temporal logic.

ITL is richer in terms of representation formalism than point-based logic, allowing it to represent real-time system behavior. Contrary to many temporal logic models, ITL has the ability to address sequential and parallel composition. It provides robust specifications that can be expanded and properties that can be investigated in terms of their safety, liveness, and timeliness.

However, the drawback of ITL is that properties can only be verified during the specified interval and cannot be verified outside of it. Several operators can be used to describe the ordering and combination of intervals, including meets, before, and during. These operators signify the sequencing of intervals. Additionally, chop operators can indicate the merging of two intervals, and the interval length can be represented by the duration operator [47,50].

4.4. LTL for Dual MPI and OpenMP

After a comprehensive review of temporal logic types, operators, and their properties, and a detailed study of runtime errors in MPI and OpenMP discussed in Section 3, we have concluded that linear temporal logic (LTL) is the most suitable temporal logic to form the basis of our tool. In this section, we will delve into the rationale behind selecting LTL.

Z. Manna et al. [51] initially proposed using LTL for reasoning about concurrent programs. Since then, researchers have extensively utilized LTL to prove the correctness of concurrent programs, protocols, and hardware. This approach has led to the development of powerful tools leveraging LTL, such as Temporal Rover. Temporal Rover serves as a specification-based verification tool for applications written in C, C++, and Java and hardware description languages like Verilog and VHDL. The tool combines formal specification using LTL and metric temporal logic (MTL) [52], playing a crucial role in verifying and validating temporal properties in software and hardware systems.

Another significant tool, Java Path Explorer (JPaX), has emerged from NASA research. JPaX is a runtime verification tool capable of verifying past and future time linear temporal properties, as well as detecting deadlocks and data races [12].

Recent research [16] introduces innovative applications of LTL, such as automatically generating human motions based on LTL specifications. Moreover, the LTL is known for its expressive simplicity and rich syntax. This logic allows for the derivation of sub-logics, such as Generalized Possibilistic Linear–Temporal Logic (GPoLTL), which is discussed in [53] along with its path semantics and introduces the concept of GPoLTL with schedulers.

LTL for Runtime Errors in MPI and OpenMP

Our analysis of runtime errors in MPI and OpenMP systems revealed the effectiveness of applying rules based on LTL. These rules not only prevent certain errors, but also detect violations that may lead to runtime errors. For example, the actual deadlock after the (Recv–Recv) code in MPI can be represented based on an LTL rule, as illustrated in Figure 3. This rule specifies to “always not to follow receive by receive from a different process”.

Another example is using MTL, an extension of LTL with timing restrictions, to prevent a potential deadlock. This situation may arise when a process executes a blocking point-to-point routine, specifically Ssend (Synchronous send), where the execution halts until data exchange is assured. Employing the next operator (represented by a circle), which ensures that two threads (p, q) occur next to each other with a specified time constraint, helps detect and prevent the deadlock (refer to Figure 4). The temporal logic formula asserts that “if p occurs then q will be the next within 10-time units”.

The potential race condition resulting from the wildcard (MPI_ANY_SOURCE) code in MPI, as shown in Listing 5, can be represented by LTL, as depicted in Figure 5. In a process with rank 1, the order of the receive operations may cause a potential race condition, leading to a deadlock. To prevent this race condition, the process with rank 1 must ensure receiving from the process with rank 0 first and then from the process with rank 2. The temporal logic formula, utilizing the always operator, asserts that “within the same process, it is always not to follow a receive operation with another receive operation from the same rank”.

Furthermore, the race condition caused by Immediate Send (Isend) in asynchronous communication, as illustrated in Listing 4, can be represented by the LTL formula shown in Figure 6 below.

Using locks incorrectly within if–else blocks or section directives can potentially cause a deadlock, as illustrated in Listing 6. To represent this scenario in LTL, let us denote omp_set_lock(&lock1), omp_unset_lock(&lock1), omp_set_lock(&lock2), and omp_unset_lock(&lock2) as p, q, r, and s, respectively. The temporal logic formula asserts that “it is always the case that, if p hold, then r, then q, then s, then after some time, r, then p, then s, then q, cannot hold” (see Figure 7).

Additionally, LTL proves valuable in representing conditions that must not be satisfied within specific blocks of code. In the context of Listings 7 and 10, where applying a barrier inside a for-loop, critical, ordered, or task region can lead to a deadlock. This constraint can be precisely expressed using LTL.

Consider the following temporal logic formula that “If p, q, r, or s holds, then always x must not hold”, where: p represents the for-loop, q represents the critical region, r represents the ordered region, s represents the task region, and x represents the barrier construct. This LTL formula succinctly captures the requirement that the barrier should not be applied within the specified code regions to prevent deadlocks (see Figure 8). Similarly, in Listings 8 and 11, where a deadlock may arise in case of nested critical directives or master construct within single directive, the same principle applies.

Furthermore, when employing the “taskwait” directive or the barrier construct, it is crucial to ensure that these are not followed by the release of locks, as doing so could potentially lead to a deadlock resulting from a race on a lock, as exemplified in Listing 12. To express this constraint in LTL, the formula asserts: “if p or q holds, then in the next moment in time, always x must not occur”. In this context, p and q represent the “taskwait” directive and the barrier, respectively, and x denotes the released lock (see Figure 9).

To detect OpenMP deadlocks due to setting the same lock twice in different places without releasing it, using the formula based on LTL states that “it is always the case that if p holds, then q is eventually hold”. This is illustrated in Figure 10.

In general, most of the runtime errors discussed in Section 3 can be represented using LTL. Notably, to the best of our knowledge, currently no testing tool exists based on temporal logic designed to detect runtime errors in a dual-programming model involving MPI and OpenMP. Therefore, we are proposing a tool based on LTL that enhances system correctness by detecting some of the runtime errors, such as deadlocks and race conditions, that are not detected by the compiler.

5. Proposed System Architecture

In this section, we propose a testing tool based on temporal logic assertion language for a dual-programming model integrating MPI and OpenMP with the C++ programming language. The proposed tool detects violations that cause runtime errors, which cannot be detected by the compiler. The architecture for the proposed testing tool is shown in Figure 11.

The temporal logic assertion language will be added to the source code, which includes MPI + OpenMP and C++, and it will be passed as input to the instrumental subsystem divided into four phases, as illustrated in Figure 12.

In the instrumental subsystem, the initial phase involves the lexical analyzer, also known as the scanner. This module reads the user source code, including assertion statements, line by line, to group the character stream into units or tokens. The scanner module is revealed in Algorithm 1.

Algorithm 1: The scanner module

1: SELECT Folder() 2: FOREACH SourceFile in Folder 3: CREATE DestinationFile 4: WHILE line = SourceFile.ReadLine() != null 5:  IF line HasAssert 6:   IF line HasTemporalOperator 7:    SendFileToParser(sourceFile) 8:    SendLineToParser(line) 9:   END IF 10:    PerformOperations() 11:   END IF 12:  ELSE 13:    WriteLineToDestinationFile(destinationFile, line) 14:  END WHILE 15: generatedCodeFile = receiveGeneratedCodeFile() 16: 17: IF generatedCodeFile is != null 18:    copyGeneratedCodeToFile(sourceFile, generatedCodeFile) 19: END IF 20: End FOREACH

Next is the parser, in which the syntax of the tokens that are generated from the last phase will be checked and grouped into syntactical units. The parser examines the tokens, determining whether they constitute user code statements or assert statements. If the tokens correspond to user code statements, they are written to the destination file, which exclusively contains MPI, OpenMP, and C++ code without any temporal assertions. On the other hand, if the statements begin with a double slash followed by the assert keywords and one of the temporal logic operators (temporal logic syntax), the source code is generated according to the type of temporal operators involved. The temporal logic syntax will be further explained in next subsection. Algorithm 2 reveals the parser module.

Algorithm 2: The parser module

1: RECEIVE (SourceFile, DestinationFile, line) 2: StrLine = Line 3: DECLARE (Label, Temporal, Condition, Semantic) 4: Array = StrLine.ToCharArray() 5: 6: FOR char in Array 7: IF char == ’(’ 8:  WHILE char != ’)’ 9:    Condition += char 10:   END WHILE 11:   END IF 12: END FOR 13: Array = StrLine.split([" "]+) 14: Label = Array[0] 15: Temporal = Array[1] 16: 17: SWITCH Temporal 18:  case "[]": 19:   Semantic = "Always CodeGenerator" 20:  case "U": 21:   Semantic = "Until CodeGenerator" 22:  case "N": 23:   Semantic = "Next CodeGenerator" 24:  case "~": 25:   Semantic = "Eventually CodeGenerator" 26:  default: 27:   Semantic = "Precede CodeGenerator" 28: END SWITCH 29: 30: SendToSemanticModule(SourceFile, DestinationFile, Label, Condition, Semantic)

Then, the semantic module will check the meaning (semantics) of the units that are generated from the last phase. This module produces code corresponding to each temporal assert statement, contingent on the specific temporal logic operators involved.

Finally, the translator or convertor module will translate the temporal logic statement into the used programming language and programming models.

After passing all of the levels of the instrumental subsystem, the output, at this point, will be the user source code in addition to the translated temporal logic statements that are in C++ (MPI + OpenMP). The translated temporal logic statements will be used to test a specific scope of the user code, determined by the developer, in which errors are expected. The code, after instrumentation, undergoes compilation and linking, generating executable (EXE) code that encompasses both an EXE user function and EXE runtime subsystem. The semantic and translator modules are shown in Algorithm 3.

Algorithm 3: The semantic and translator modules

1:  RECEIVE (SourceFile, DestinationFile, Label, Condition, Semantic) 2: 3: WHILE (Line = SourceFile.readLine() != null) 4: IF Line == "Assert" 5:  Continue 6: END IF 7: 8: IF Line == Label 9:  Break 10: END IF 11: 12: ConditionArray = ExtractVariables(Condition) 13: TokenizeArray = Tokenize(Line) 14: 15: FOR i = 0 to ConditionArray.length 16:  FOR j = 0 to TokenizeArray.length 17:   IF ConditionArray [i] == TokenizeArray [j] 18:    WRITE Line to DestinationFile 19:    WRITE Corresponding_C++_MPI_OpenMP_Code to DestinationFile 20:   ELSE 21:    WRITE Line to DestinationFile 22:   END IF 23:  END FOR 24: END FOR 25: 26: END WHILE 27: 28: SEND GeneratedCode to Compiler

Subsequently, this EXE code is executed, revealing a list of runtime errors. In our tool, we use an instrumentation technique in which the instrument statements will be added to the user code for testing purposes. However, this technique will cause the file size to be bigger and therefore degrade the performance in terms of system response time.

On the other hand, another technique for the instrumentation is to add the assertion statements as API function calls to check the specific portion of the code that requires testing. Applying the latest technique results in the small size of the code file, as a function will be called each time it is needed, and better response time. However, it has some disadvantages, such as the fact that it is single point of failure, as it is based on a centralized controller for detecting errors. In addition, it has a scalability issue whereby there is a tradeoff between the number of tests and the performance of the whole system in terms of efficiency.

Our distributed testing tool strives to achieve accurate code where the reliability of the system is prioritized over the increase in the size of the code file due to the addition of the instrument statements to each part of the code that needs to be tested.

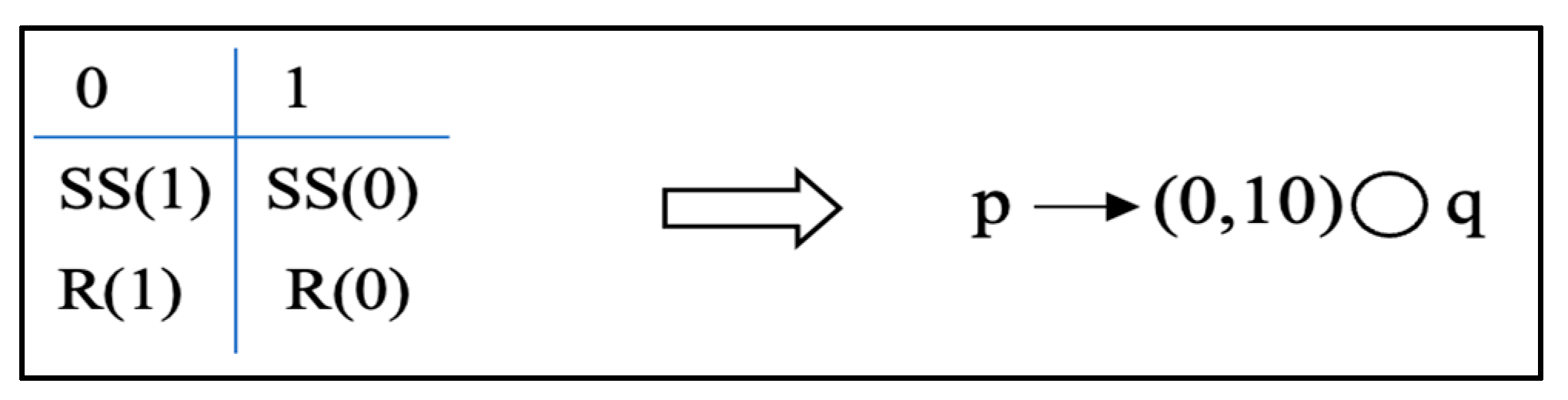
The Proposed Temporal Assertion Language

The proposed assertion language, constructed from scratch, is based on linear temporal logic. It incorporates five fundamental operators: always, eventually, next, until, and precede. The syntax of the assertion language is defined using Backus Naur Form (BNF). The “[]” symbolizes the always operator (safety property), indicating that a condition must consistently hold within a specified scope in the system being tested. On the other hand, the “~” symbol, representing the eventually operator (fairness property), implies that a specific condition should be met at least once within the testing scope. The “N” notation corresponds to the next operator, signifying that the assertion remains true in the subsequent step. Introducing the “U” symbol for the until operator, which operates across two threads, mandates that once the first thread no longer holds, the second must take over. Lastly, the “P” symbolizes the precede operator, functioning across two threads and specifying that the first thread begins execution before the second, with a potential overlap between them. To ensure the proper scoping of the assert statement, each temporal assert statement must be accompanied by an end-assert statement. Figure 13 depicts the grammar of the language, presented in BNF.

Each assert statement begins and ends with the “assert_token”, which is the comment character in C++, intended to be ignored by the C++ compiler. The semantics of each operator will be determined to carry out its intended functionality. Referring to Figure 3, which represents the (Recv–Recv) in LTL, its assertion language syntax is illustrated in Listing 19 below.

Listing 19. Assertion language syntax for recv–recv.

1:  // A1.1 Assert [] ! (thread 1 and 2 start with receive operation) 2: { block of user code under testing } 3: // A1.1 End Assert

In Listing 19, the beginning and the end of the system scope being tested is identified by “//”, and then the block ID “A1.1”. This serves as a marker for the beginning and end of the temporal assert statements in the code. Additionally, “Assert” and “End” are keywords, providing further distinguished and clear boundaries for the temporal assert statement. The used operator is “always” followed by the condition that must be satisfied within this identified scope.

Furthermore, the potential race condition resulting in a deadlock, depicted in Figure 5, can be detected by ensuring that process 1 does not receive from process 2 first. Therefore, this condition is specified within the assert statement after the used operator. It must always be checked in each line within the assert block. Figure 14 below shows an example of the instrumentation of the always operator, displaying the assert statements before and after passing through the convertor module (included in the instrumental sub-system), which translates the temporal logic statements into the programming language used.

6. Discussion

In HPC, the dual MPI and OpenMP programming model, which involves running several OpenMP threads within each MPI process, is gaining popularity. However, this will cause the system to be subject to errors that may not be detected during the compilation process. Therefore, it is essential to test this dual-programming model using different tools to ensure that these models are safe to use and free from critical errors that may lead to disastrous results. According to a survey study, there are many tools used to test single-level programming models (MPI and OpenMP) because of their widespread use; however, only a few (about four) testing tools target the dual MPI and OpenMP programming models, and none of these tools are based on temporal logic [54].

After a comprehensive study of temporal logic and its various types, we determined that it is suitable to base our tool on. LTL, in particular, is well suited as the foundation for our tool. This paper delved into the study of the dual MPI and OpenMP programming model. Through experiments and application analysis, we aimed to unravel how runtime errors manifest within the MPI and OpenMP framework and how they interact. Once our proposed testing tool is implemented, these identified errors will be specifically targeted for detection.

Drawing from our findings after analyzing these errors, we specified the appropriate LTL operators for testing. Building upon this groundwork, we propose a testing tool architecture designed to dynamically test the intended applications in a distributed manner. In addition, our tool is designed to perform a dynamic testing approach that tests the user’s source code by inserting assertion statements based on LTL. After integrating the user source code with the assertion language, it will be instrumented by several phases, starting with the lexical analyzer, and then the parser, followed by the semantic analyzer and, finally, the convertor, which translates the assertion statements to the user programming language.

Subsequently, these assertion statements were executed to test the program and detect any violations. It is important to note that our proposed tool is currently in the conceptual stage and not yet implemented. Developing our tool will require extensive effort to cover a broad spectrum of errors and anticipate various scenarios in which runtime errors may manifest. This is due to the fact that parallel application handling is a challenging and demanding task due to the inherent characteristics and behavior. Thus, proper techniques for runtime error detection must be selected based on the type and behavior of the encountered errors. To our knowledge, there is currently no testing tool based on temporal logic designed to detect runtime errors in hybrid programming models. Furthermore, the proposed tools represented by [44,45,55] utilize simple assert statements to detect runtime errors in hybrid programming models.

Table 6. Comparative study summary.

Testing Tool	Assertion Technique	Programming Models	Targeted Errors
[44] (dynamic approach)	simple assert statements	MPI, OpenMP, and OpenACC	potential runtime errors
[45] (dynamic approach)	simple assert statements	MPI, OpenMP, and CUDA	potential runtime errors
[55] ACC_TEST (dynamic approach)	simple assert statements	MPI and OpenACC	potential runtime errors
our tool	assertion language based on temporal logic	MPI and OpenMP	potential and real runtime errors

presents a detailed comparison between our proposed tool architecture and that of other tools.

In our proposed testing tool, a distinctive feature lies in the construction of the assertion language from scratch, specifically based on LTL. This marks a departure from existing tools that rely on simple assert statements. By opting for a tailored assertion language built on LTL, we aim to enhance the tool’s precision and effectiveness in uncovering runtime errors. The upcoming practical validation will further substantiate the tool’s capabilities, marking a crucial step in our research agenda.

7. Conclusions and Future Work

Recently, the demand for high-performance computing has surged, especially with the advent of Exascale supercomputers. The importance of constructing parallel systems has grown significantly. However, there exists a gap in the adequate testing of these systems, necessitating the exploration of new techniques to design high-speed and reliable software. While the dual MPI and OpenMP model is widely used in various parallel systems to achieve high performance, this combination may increase the probability of runtime errors that are challenging to detect before the execution process.

In this paper, we conduct an analysis and categorization of runtime errors and their underlying causes resulting from the integration of MPI + OpenMP and C++. Additionally, we perform a comprehensive study of temporal logic, including its operators and properties, to determine the most suitable one as the foundation for our tool, namely, LTL. We introduce an assertion language based on LTL to be used in detecting runtime errors. Moreover, we propose the architecture of our tool specifically designed for detecting runtime errors in the dual MPI and OpenMP programming model. This architecture utilizes the proposed assertion language. The tool, based on dynamic testing methods, aims to enhance the system reliability by uncovering a diverse spectrum of runtime errors. This approach is motivated by the necessity to address runtime errors that are often not detected by the compiler.

In our future work, we plan to implement the proposed architecture of our tool and assess its effectiveness in detecting runtime errors resulting from the integration of MPI and OpenMP, along with the C++ programming language. The implemented tool will be evaluated and compared with existing testing tools using specific criteria such as error detection accuracy, performance, and execution time. We anticipate that our tool will offer improvements over existing tools, providing enhanced reliability and the capability to detect more runtime errors.