Dealing with Class Overlap Through Cluster-Based Sample Weighting
Abstract
1. Introduction
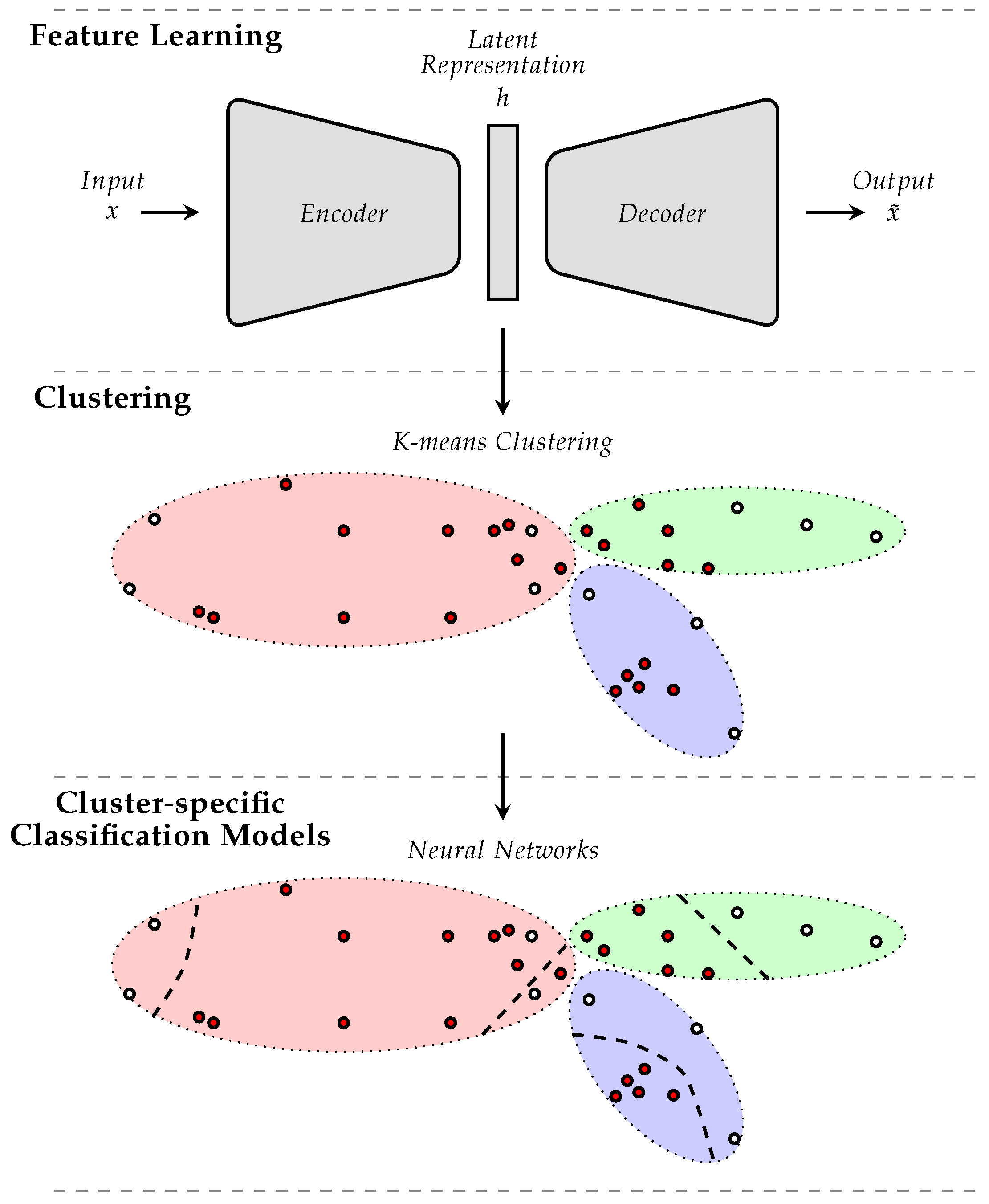
2. Proposed Approach
- A latent space is generated using feature learning; this process is undertaken in order to reduce the dimensionality of the input data, which is crucial for the extraction of meaningful clusters; moreover, feature learning is performed in such a way that the knowledge relevant for the classification task at hand is preserved within the latent space.
- Data clustering is performed within the generated latent space; each cluster is characterized by a cluster center and a spread that is subsequently used to define the weights of each sample; more specifically, each sample is weighted according to its distance to each of the cluster centers; this is done in order to avoid the negative effects of any form of class imbalance within each clusters, which could impact the performance of the subsequently trained classification models.
- Cluster-specific classification models are optimized using a weighted loss function; the weights used for the optimization of each model correspond to the cluster related sample-specific weights, defined using a specific weighting function.
2.1. Feature Learning
2.2. Cluster-Based Sample Weighting (CbSW)
2.3. Cluster-Specific Model Optimization
3. Experiments
3.1. BioVid Heat Pain Database
3.2. SenseEmotion Dataset
3.3. Data Preprocessing
- BioVid Part A: ;
- BioVid Part B: ;
- SenseEmotion: .
3.4. Experimental Settings
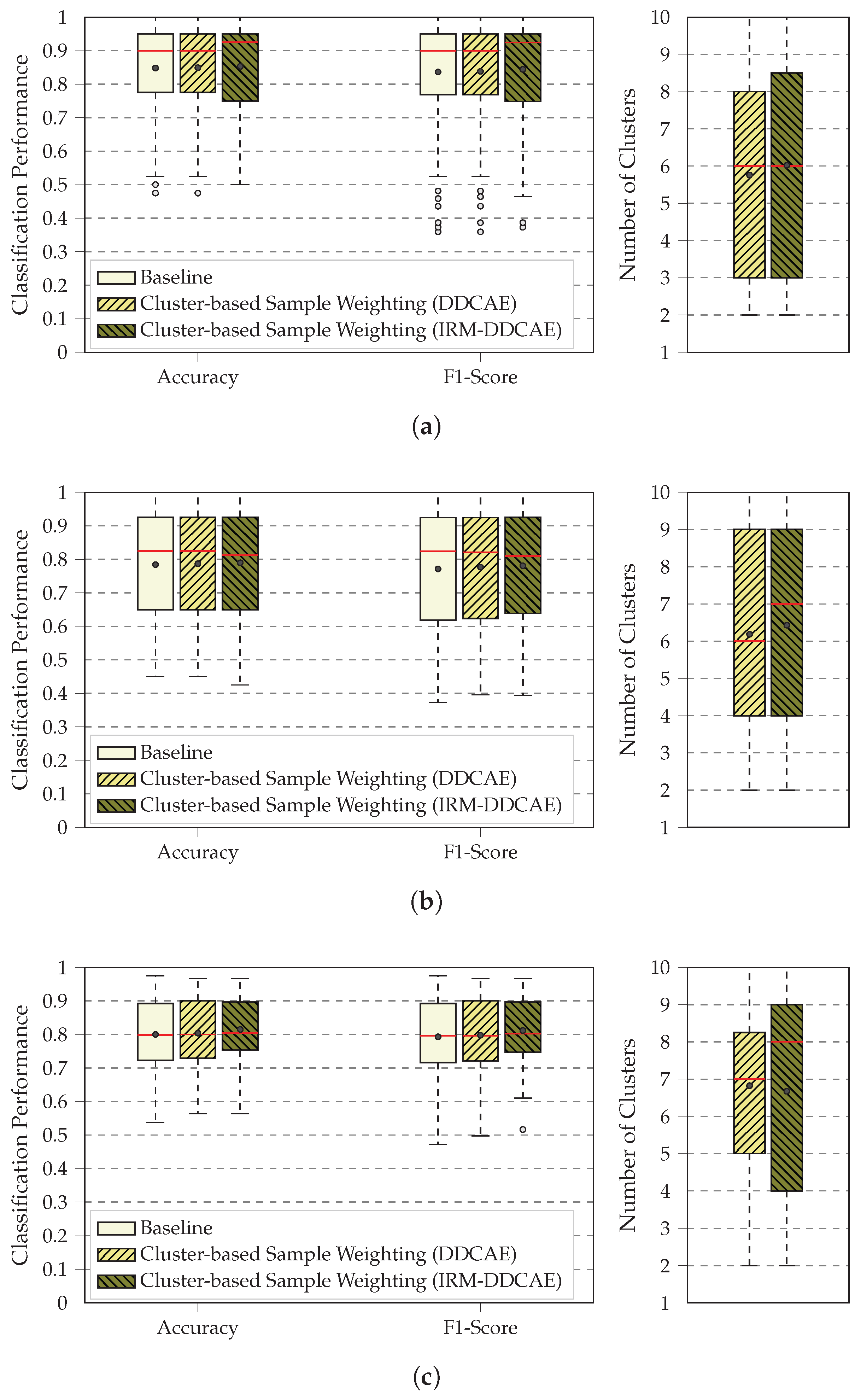
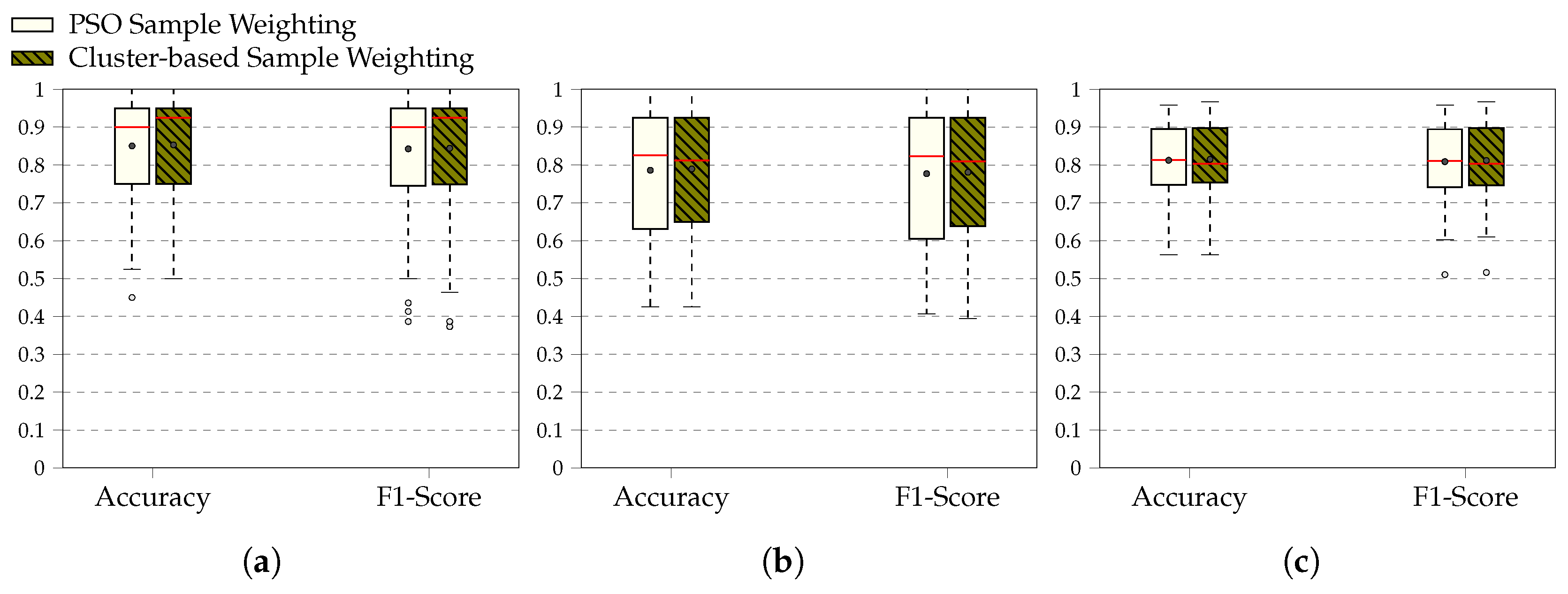
4. Results
5. Discussion
| Approach | Accuracy (%) |
|---|---|
| Werner et al. [39]: Random Forests Classifier with 100 Trees | |
| Kächele et al. [40]: Random Forests Classifier with 500 Trees | |
| Thiam et al. [27]: 1-Dimensional Convolutional Neural Network (1-D CNN) | |
| Phan et al. [41]: 1-D CNN & Bidirectional Long Short-Term Memory (BiLSTM) | |
| Lu et al. [42]: Multiscale Convolutional Networks & Squeeze-Excitation Residual Networks & Transformer Encoder (PainAttnNet) | |
| Li et al. [43]: Multi-Dimensional Temporal Convolutional Network & Activate Channels Feature Network & Cross-Attention Temporal Convolutional Network (EDAPainNet) | |
| Current Approach: Cluster-based Sample Weighting (IRM-DDCAE) |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MLP | multi-layer perceptron |
| MW-Net | meta-weight-net |
| CIEL | cluster-based intelligence ensemble learning |
| PSO | particle swarm optimization |
| LOW | learning optimal sample weights |
| CMW-Net | class-aware meta-weight-net |
| DDCAE | deep denoizing convolutional auto-encoder |
| AE | auto-encoder |
| DCNN | deep convolutional neural network |
| IRM | implicit rank-minimizing |
| IRM-DDCAE | implicit rank-minimizing deep denoizing convolutional auto-encoder |
| BN | batch normalization |
| ELU | exponential linear unit |
| MSE | mean squared error |
| EDA | electrodermal activity |
| ECG | electrocardiography |
| EMG | electromyography |
| Hz | Hertz |
| LOSO | leave one subject out |
| CbSW | cluster-based sample weighting |
| PSOSW | particle swarm optimization sample weighting |
| GNNs | graph neural networks |
References
- Vuttipittayamongkol, P.; Elyan, E.; Petrovski, A. On the Class Overlap Problem in Imbalanced Data Classification. Knowl.-Based Syst. 2021, 212, 106631. [Google Scholar] [CrossRef]
- Soltanzadeh, P.; Feizi-Derakhshi, M.R.; Hashemzadeh, M. Addressing the Class-Imbalance and Class-Overlap Problems by a Metaheuristic-based Under-Sampling Approach. Pattern Recognit. 2023, 143, 109721. [Google Scholar] [CrossRef]
- Santos, M.S.; Abreu, P.H.; Japkowicz, N.; Fernández, A.; Santos, J. A Unifying View of Class Overlap and Imbalance: Key Concepts, Multi-View Paranoma, and Open Avenues for Research. Inf. Fusion 2023, 89, 228–253. [Google Scholar] [CrossRef]
- Thrun, S.; Pratt, L. Learning to Learn: Introduction and Overview. In Learning to Learn; Springer: Boston, MA, USA, 1998; pp. 3–17. [Google Scholar] [CrossRef]
- De Jong, K.A. Evolutionary Computation: A Unified Approach; The MIT Press: Cambridge, MA, USA, 2006; Available online: https://ieeexplore.ieee.org/servlet/opac?bknumber=6267245 (accessed on 22 October 2025).
- Ren, M.; Zeng, W.; Yang, B.; Urtasun, R. Learning to Reweight Examples for Robust Deep Learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Sweden, 10–15 July 2018; Volume 80, pp. 4334–4343. Available online: https://proceedings.mlr.press/v80/ren18a/ren18a.pdf (accessed on 22 October 2025).
- Shu, J.; Xie, Q.; Yi, L.; Zhao, Q.; Zhou, S.; Xu, Z.; Meng, D. Meta-Weight-Net: Learning an Explicit Mapping For Sample Weighting. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–19 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2019; Volume 32. Available online: https://proceedings.neurips.cc/paper_files/paper/2019/file/e58cc5ca94270acaceed13bc82dfedf7-Paper.pdf (accessed on 22 October 2025).
- Cui, S.; Wang, Y.; Yin, Y.; Cheng, T.; Wang, D.; Zhai, M. A Cluster-based Intelligence Ensemble Learning Method for Classification Problems. Inf. Sci. 2021, 560, 386–409. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhardt, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 25 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Santiago, C.; Barata, C.; Sasdelli, M.; Carneiro, G.; Nascimento, J.C. LOW: Training Deep Neural Networks by Learning Sample Weights. Pattern Recognit. 2021, 110, 107585. [Google Scholar] [CrossRef]
- Shu, J.; Yuan, X.; Meng, D.; Xu, Z. CMW-Net: Learning a Class-Aware Sample Weighting Mapping for Robust Deep Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11521–11539. [Google Scholar] [CrossRef]
- Thiam, P.; Kestler, H.A.; Schwenker, F. Multimodal Deep Denoising Convolutional Autoencoders for Pain Intensity Classification based on Physiological Signals. In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM), Valetta, Malta, 22–24 February 2020; INSTICC: Lisboa, Portugal; SciTePress: Setubal, Portugal, 2020; Volume 1, pp. 289–296. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R.S. Autoencoders, Minimum Description Length and Helmholtz Free Energy. In Proceedings of the 7th International Conference on Neural Information Processing Systems NIPS’93, Denver, CO, USA, 29 November–2 December 1993; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; pp. 3–10. Available online: https://proceedings.neurips.cc/paper/1993/file/9e3cfc48eccf81a0d57663e129aef3cb-Paper.pdf (accessed on 22 October 2025).
- Hinton, G.E.; Salakhutdinov, R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Jing, L.; Zbontar, J.; LeCun, Y. Implicit Rank-Minimizing Autoencoder. In Proceedings of the 34th International Conference of Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Curran Associates Inc.: Red Hook, NY, USA, 2020; pp. 14736–14746. Available online: https://proceedings.neurips.cc/paper/2020/file/a9078e8653368c9c291ae2f8b74012e7-Paper.pdf (accessed on 22 October 2025).
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In 5th Berkeley Symposium on Mathematical Statistics and Probability; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Oakland, CA, USA, 1967; Volume 1, pp. 281–297. Available online: https://projecteuclid.org/ebooks/berkeley-symposium-on-mathematical-statistics-and-probability/Proceedings-of-the-Fifth-Berkeley-Symposium-on-Mathematical-Statistics-and/chapter/Some-methods-for-classification-and-analysis-of-multivariate-observations/bsmsp/1200512992 (accessed on 22 October 2025).
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Śmieja, M.; Wiercioch, M. Constrained Clustering with a Complex Cluster Structure. Adv. Data Anal. Classif. 2017, 11, 493–518. [Google Scholar] [CrossRef]
- Coghill, R.C.; McHaffie, J.G.; Yen, Y.F. Neural Correlates of Interindividual Differences in the Subjective Experience of Pain. Proc. Natl. Acad. Sci. USA 2003, 100, 8538–8542. [Google Scholar] [CrossRef]
- Nielsen, C.S.; Stubhaug, A.; Price, D.D.; Vassend, O.; Czajkowski, N.; Harris, J.R. Individual Differences in Pain Sensitivity: Genetic and Environment Contributions. Pain 2008, 136, 21–29. [Google Scholar] [CrossRef]
- Walter, S.; Gruss, S.; Ehleiter, H.; Tan, J.; Traue, H.C.; Crawcour, S.; Werner, P.; Al-Hamadi, A.; Andrade, A. The BioVid Heat Pain Database: Data for the Advancement and Systematic Validation of an Automated Pain Recognition System. In Proceedings of the 2013 IEEE International Conference on Cybernetics (CYBCO), Lausanne, Switzerland, 13–15 June 2013; pp. 128–131. [Google Scholar] [CrossRef]
- Velana, M.; Gruss, S.; Layher, G.; Thiam, P.; Zhang, Y.; Schork, D.; Kessler, V.; Gruss, S.; Neumann, H.; Kim, J.; et al. The SenseEmotion Database: A Multimodal Database for the Development and Systematic Validation of an Automatic Pain- and Emotion-Recognition System. In Proceedings of the Multimodal Pattern Recognition of Social Signals in Human-Computer-Interaction, Cancun, Mexico, 4 December 2016; Schwenker, F., Scherer, S., Eds.; Springer: Cham, Switzerland, 2017; pp. 127–139. [Google Scholar] [CrossRef]
- Pouromran, F.; Radhakrishnan, S.; Kamarthi, S. Exploration of Physiological Sensors, Features, and Machine Learning Models for Pain Intensity Estimation. PLoS ONE 2021, 16, e0254108. [Google Scholar] [CrossRef] [PubMed]
- Werner, P.; Lopez-Martinez, D.; Walter, S.; Al-Hamadi, A.; Gruss, S.; Picard, R.W. Automatic Recognition Methods Supporting Pain Assessment: A Survey. IEEE Trans. Affect. Comput. 2022, 13, 530–552. [Google Scholar] [CrossRef]
- Rojas, R.F.; Hirachan, N.; Brown, N.; Waddington, G.; Murtagh, L.; Seymour, B.; Goecke, R. Multimodal Physiological Sensing for the Assessment of Acute Pain. Front. Pain Res. 2023, 4, 1150264. [Google Scholar] [CrossRef] [PubMed]
- Thiam, P.; Hihn, H.; Braun, D.A.; Kestler, H.A.; Schwenker, F. Multi-Modal Pain Intensity Assessment Based on Physiological Signals: A Deep Learning Perspective. Front. Physiol. 2021, 12, 720464. [Google Scholar] [CrossRef]
- Thiam, P.; Bellmann, P.; Kestler, H.A.; Schwenker, F. Exploring Deep Physiological Models for Nociceptive Pain Recognition. Sensors 2019, 20, 4503. [Google Scholar] [CrossRef] [PubMed]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Neural Network Learning by Exponential Linear Units (ELUs). In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016; Conference Track Proceedings. Available online: http://arxiv.org/abs/1511.07289 (accessed on 22 October 2025).
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018. Proceedings, Part VII. pp. 3–19. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings. Available online: https://arxiv.org/abs/1412.6980 (accessed on 22 October 2025).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 1–4 November 2016; pp. 265–283. Available online: https://www.usenix.org/system/files/conference/osdi16/osdi16-abadi.pdf (accessed on 22 October 2025).
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 3 September 2025).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter Selection in Particle Swarm Optimization. In Proceedings of the 7th International Conference on Evolutionary Programming, San Diego, CA, USA, 25–27 March 1998; Lecture Notes in Computer Science. Porto, V.W., Saravanan, N., Waagen, D., Eiben, A.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1447, pp. 591–600. [Google Scholar] [CrossRef]
- Arasomwan, M.A.; Adewumi, A.O. On the Performance of Linear Decreasing Inertia Weight Particle Swarm Optimization for Global Optimization. Sci. World J. 2013, 1, 860289. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems NIPS’ 17, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Von Luxburg, U., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 6000–6010. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 22 October 2025).
- Chen, Z.; Xiao, T.; Kuang, K.; Lv, Z.; Zhang, M.; Yang, J.; Lu, C.; Yang, H.; Wu, F. Learning To Reweight for Generalizable Graph Neural Networks. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, Vancouver, BA, Canada, 20–27 February 2024; Volume 38, pp. 8320–8328. [Google Scholar] [CrossRef]
- Li, W.; Wei, W.; Wang, P.; Pan, L.; Yang, B.; Xu, Y. Research on GNNs with Stable Learning. Sci. Rep. 2025, 15, 29002. [Google Scholar] [CrossRef]
- Werner, P.; Al-Hamadi, A.; Niese, R.; Walter, S.; Gruss, S.; Traue, H.C. Automatic Pain Recognition from Video and Biomedical Signals. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 4582–4587. [Google Scholar] [CrossRef]
- Kächele, M.; Amirian, M.; Thiam, P.; Werner, P.; Walter, S.; Palm, G.; Schwenker, F. Adaptive Confidence Learning for the Personalization of Pain Intensity Estimation Systems. Evol. Syst. 2017, 8, 71–83. [Google Scholar] [CrossRef]
- Phan, K.N.; Iyortsuun, N.K.; Pant, S.; Yang, H.J.; Kim, S.H. Pain Recognition with Physiological Signals Using Multi-Level Context Information. IEEE Access 2023, 11, 20114–20127. [Google Scholar] [CrossRef]
- Lu, Z.; Ozek, B.; Kamarthi, S. Transformer Encoder with Multiscale Deep Learning for Pain Classification using Physiological Signals. Front. Physiol. 2023, 14, 1294577. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Luo, J.; Wang, Y.; Jiang, Y.; Chen, X.; Quan, Y. Automatic Pain Assessment based on Physiological Signals: Application of Multi-Scale Networks and Cross-Attention Cross-Attention. In Proceedings of the 13th International Conference on Bioinformatics and biomedical Science ICBBS ’24, Hong Kong, China, 18–20 October 2024; pp. 113–122. [Google Scholar] [CrossRef]

| Encoder | |
|---|---|
| Block | No. Kernels/Units |
| 16 | |
| 32 | |
| 64 | |
| 128 | |
| Flatten | |
| Decoder | |
| Block | No. Kernels/Units |
| Reshape | |
| 128 | |
| 64 | |
| 32 | |
| 16 | |
| 1 | |
| Dataset | BioVid Part A ( vs. ) | ||
| Approach | Baseline | CbSW (DDCAE) | CbSW (IRM-DDCAE) |
| Accuracy | |||
| F1-Score | |||
| Dataset | BioVid Part B ( vs. ) | ||
| Approach | Baseline | CbSW (DDCAE) | CbSW (IRM-DDCAE) |
| Accuracy | |||
| F1-Score | |||
| Dataset | SenseEmotion ( vs. ) | ||
| Approach | Baseline | CbSW (DDCAE) | CbSW (IRM-DDCAE) |
| Accuracy | |||
| F1-Score | |||
| Dataset | BioVid Part A ( vs. ) | BioVid Part B ( vs. ) | SenseEmotion ( vs. ) | |||
|---|---|---|---|---|---|---|
| Approach | PSOSW | CbSW | PSOSW | CbSW | PSOSW | CbSW |
| Accuracy | ||||||
| F1-Score | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiam, P.; Schwenker, F.; Kestler, H.A. Dealing with Class Overlap Through Cluster-Based Sample Weighting. Computers 2025, 14, 457. https://doi.org/10.3390/computers14110457
Thiam P, Schwenker F, Kestler HA. Dealing with Class Overlap Through Cluster-Based Sample Weighting. Computers. 2025; 14(11):457. https://doi.org/10.3390/computers14110457
Chicago/Turabian StyleThiam, Patrick, Friedhelm Schwenker, and Hans Armin Kestler. 2025. "Dealing with Class Overlap Through Cluster-Based Sample Weighting" Computers 14, no. 11: 457. https://doi.org/10.3390/computers14110457
APA StyleThiam, P., Schwenker, F., & Kestler, H. A. (2025). Dealing with Class Overlap Through Cluster-Based Sample Weighting. Computers, 14(11), 457. https://doi.org/10.3390/computers14110457








