Direct Reciprocity and Model-Predictive Strategy Update Explain the Network Reciprocity Observed in Socioeconomic Networks
Abstract
:1. Introduction
2. The Model
2.1. Tit-for-tat vs. D
- her own strategy, T or D, to be used at round t (in Table 1, second column, Tn and Dn denote the fact that the agent changed strategy after round ); and
- for each neighbor j, the strategy, T or D, that i expects j to use at round t and the last actions, C or D, played by i and j at round .
2.2. Tit-for-two-tats vs. D
2.3. New-tit-for-two-tats vs. D
3. Results
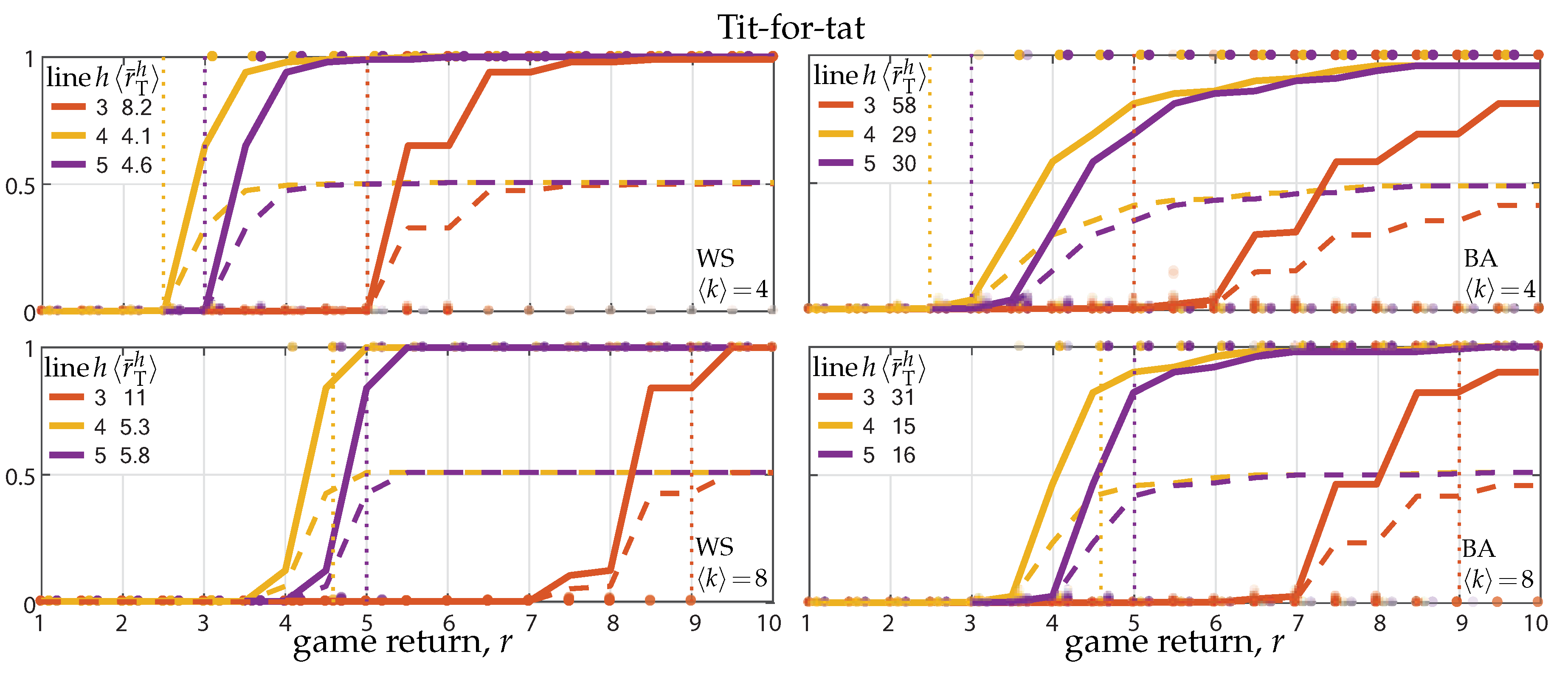
3.1. Tit-for-tat vs. D
3.2. Tit-for-two-tats vs. D
3.3. New-tit-for-two-tats vs. D
4. Discussion and Conclusions
4.1. Three Versions of the T-strategy
4.2. Comparison with the T-strategy in Dercole et al. (2019)
4.3. Impact on Applied Behavioral Science
4.4. Future Directions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Theorems and Proofs of Results in Section 3
Appendix A.1. Tit-for-tat vs. D
Appendix A.2. Tit-for-two-tats vs. D
Appendix A.3. New-tit-for-two-tats vs. D
References
- Trivers, R.L. The Evolution of Reciprocal Altruism. Q. Rev. Biol. 1971, 46, 35–37. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The Evolution of Cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R. The Evolution of Cooperation; American Association for the Advancement of Science: Washington, DC, USA, 2006. [Google Scholar]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Nowak, M.; Highfield, R. SuperCooperators: Altruism, Evolution, and Why We Need Each Other to Succeed; Simon and Schuster: New York, NY, USA, 2011. [Google Scholar]
- Ocampo-Martinez, C.; Quijano, N. Game-Theoretical Methods in Control of Engineering Systems: An Introduction to the Special Issue. IEEE Control Syst. 2017, 37, 30–32. [Google Scholar]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 687, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Perc, M.; Gómez-Gardeñes, J.; Szolnoki, A.; Floría, L.M.; Moreno, Y. Evolutionary dynamics of group interactions on structured populations: A review. J. R. Soc. Interface 2013, 10, 20120997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Szabó, G.; Fath, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef] [Green Version]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [Green Version]
- Nowak, M.A.; May, R. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef]
- Konno, T. A condition for cooperation in a game on complex networks. J. Theor. Biol. 2011, 269, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Allen, B.; Lippner, G.; Chen, Y.T.; Fotouhi, B.; Momeni, N.; Yau, S.T.; Nowak, M.A. Evolutionary dynamics on any population structure. Nature 2017, 544, 227–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roca, C.P.; Cuesta, J.A.; Sánchez, A. Promotion of cooperation on networks? The myopic best response case. Eur. Phys. J. B 2009, 71, 587. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, E.; Hauert, C.; Nowak, M.A. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 2005, 95, 098104. [Google Scholar] [CrossRef] [Green Version]
- Santos, F.C.; Pacheco, J.M. A new route to the evolution of cooperation. J. Evol. Biol. 2006, 19, 726–733. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M.; Tom, L. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [Green Version]
- Santos, F.C.; Rodrigues, J.F.; Pacheco, J.M. Graph topology plays a determinant role in the evolution of cooperation. Proc. R. Soc. B 2006, 273, 51–55. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Gardeñes, J.; Campillo, M.; Floría, L.M.; Moreno, Y. Dynamical Organization of Cooperation in Complex Topologies. Phys. Rev. Lett. 2007, 98, 108103. [Google Scholar] [CrossRef] [Green Version]
- Ohtsuki, H.; Nowak, M.A. Direct reciprocity on graphs. J. Theor. Biol. 2007, 247, 462–470. [Google Scholar] [CrossRef] [Green Version]
- Poncela, J.; Gómez-Gardeñes, J.; Floria, L.M.; Moreno, Y. Robustness of cooperation in the evolutionary prisoner’s dilemma on complex networks. New J. Phys. 2007, 9, 184. [Google Scholar] [CrossRef] [Green Version]
- Assenza, S.; Gómez-Gardeñes, J.; Latora, V. Enhancement of cooperation in highly clustered scale-free networks. Phys. Rev. E 2008, 78, 017101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gómez-Gardeñes, J.; Poncela, J.; Floría, L.M.; Moreno, Y. Natural selection of cooperation and degree hierarchy in heterogeneous populations. J. Theor. Biol. 2008, 253, 296–301. [Google Scholar] [CrossRef] [PubMed]
- Pusch, A.; Weber, S.; Porto, M. Impact of topology on the dynamical organization of cooperation in the prisoner’s dilemma game. Phys. Rev. E 2008, 77, 036120. [Google Scholar] [CrossRef]
- Santos, F.C.; Santos, M.D.; Pacheco, J.M. Social diversity promotes the emergence of cooperation in public goods games. Nature 2008, 454, 213–216. [Google Scholar] [CrossRef]
- Devlin, S.; Treloar, T. Evolution of cooperation through the heterogeneity of random networks. Phys. Rev. E 2009, 79, 016107. [Google Scholar] [CrossRef] [Green Version]
- Devlin, S.; Treloar, T. Cooperation in an evolutionary prisoner’s dilemma on networks with degree-degree correlations. Phys. Rev. E 2009, 80, 026105. [Google Scholar] [CrossRef] [Green Version]
- Floría, L.; Gracia-Lázaro, C.; Gómez-Gardenes, J.; Moreno, Y. Social network reciprocity as a phase transition in evolutionary cooperation. Phys. Rev. E 2009, 79, 026106. [Google Scholar] [CrossRef] [Green Version]
- Perc, M. Evolution of cooperation on scale-free networks subject to error and attack. New J. Phys. 2009, 11, 033027. [Google Scholar] [CrossRef]
- Cardillo, A.; Gómez-Gardeñes, J.; Vilone, D.; Sánchez, A. Co-evolution of strategies and update rules in the prisoner’s dilemma game on complex networks. New J. Phys. 2010, 12, 103034. [Google Scholar] [CrossRef]
- Débarre, F.; Hauert, C.; Doebeli, M. Social evolution in structured populations. Nat. Commun. 2014, 5, 3409. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.D. The genetical evolution of social behaviour. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Wilson, D.S. A general theory of group selection. Proc. Natl. Acad. Sci. USA 1975, 72, 143–146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jansen, V.A.; van Baalen, M. Altruism through beard chromodynamics. Nature 2006, 440, 663–666. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.A.; Doebeli, M. A simple and general explanation for the evolution of altruism. Proc. R. Soc. Lond. B 2009, 276, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Bolton, G.E.; Ockenfels, A. A theory of equity, reciprocity and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef] [Green Version]
- Capraro, V. A model of human cooperation in social dilemmas. PLoS ONE 2013, 8, e72427. [Google Scholar] [CrossRef] [Green Version]
- Capraro, V.; Rand, D.G. Do the Right Thing: Experimental evidence that preferences for moral behavior, rather than equity or efficiency per se, drive human prosociality. Judgm. Decis. Mak. 2018, 13, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Vanberg, V.J.; Congleton, R.D. Rationality, Morality, and Exit. Am. Polit. Sci. Rev. 1992, 86, 418–431. [Google Scholar] [CrossRef]
- Batali, J.; Kitcher, P. Evolution of altriusm in optional and compulsory games. J. Theor. Biol. 1995, 175, 161–171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyd, R.; Gintis, H.; Bowles, S.; Richerson, P.J. The Evolution of Altruistic Punishment. Proc. Natl. Acad. Sci. USA 2003, 100, 3531–3535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dercole, F.; De Carli, M.; Della Rossa, F.; Papadopoulos, A.V. Overpunishing is not necessary to fix cooperation in voluntary public goods games. J. Theor. Biol. 2013, 326, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Semmann, D. Conditional cooperation can hinder network reciprocity. Proc. Natl. Acad. Sci. USA 2012, 109, 12846–12847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grujić, J.; Fosco, C.; Araujo, L.; Cuesta, J.A.; Sánchez, A. Social experiments in the mesoscale: Humans playing a spatial prisoner’s dilemma. PLoS ONE 2010, 5, e13749. [Google Scholar] [CrossRef] [Green Version]
- Grujić, J.; Röhl, T.; Semmann, D.; Milinski, M.; Arne, T. Consistent Strategy Updating in Spatial and Non-Spatial Behavioral Experiments Does Not Promote Cooperation in Social Networks. PLoS ONE 2012, 7, e47718. [Google Scholar] [CrossRef] [Green Version]
- Gracia-Lázaro, C.; Ferrer, A.; Ruiz, G.; Tarancón, A.; Cuesta, J.A.; Sánchez, A.; Moreno, Y. Heterogeneous networks do not promote cooperation when humans play a Prisoner’s Dilemma. Proc. Natl. Acad. Sci. USA 2012, 109, 12922–12926. [Google Scholar] [CrossRef] [Green Version]
- Gracia-Lazaro, C.; Cuesta, J.A.; Sanchez, A.; Moreno, Y. Human behavior in Prisoner’s Dilemma experiments suppresses network reciprocity. Sci. Rep. 2012, 2, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Grujić, J.; Gracia-Lazaro, C.; Milinski, M.; Semmann, D.; Traulsen, A.; Cuesta, J.A.; Moreno, Y.; Sanchez, A. A comparative analysis of spatial Prisoner’s Dilemma experiments: Conditional cooperation and payoff irrelevance. Sci. Rep. 2014, 4, 4615. [Google Scholar] [CrossRef]
- Rand, D.G.; Nowak, M.A.; Fowler, J.H.; Christakis, N.A. Static network structure can stabilize human cooperation. Proc. Natl. Acad. Sci. USA 2014, 111, 17093–17098. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Jusup, M.; Wang, Z.; Li, H.; Shi, L.; Podobnik, B.; Stanley, H.E.; Havlin, S.; Boccaletti, S. Punishment diminishes the benefits of network reciprocity in social dilemma experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 30–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dercole, F.; Della Rossa, F.; Piccardi, C. Direct Reciprocity and Model-Predictive Rationality Explain Network Reciprocity over Social Ties; Scientific Report; Nature Publishing Group: London, UK, 2019. [Google Scholar]
- DiMeglio, A.; Dercole, F.; Della Rossa, F. Direct reciprocity and model-predictive rationality: A setup for network reciprocity over social ties. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1531–1536. [Google Scholar]
- Grilo, C.; Luís, C. Effects of asynchronism on evolutionary games. J. Theor. Biol. 2011, 269, 109–122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.H. Complex networks: Structure and dynamics. Phys. Rev. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Traulsen, A.; Semmann, D.; Sommerfeld, R.D.; Krambeck, H.J.; Milinski, M. Human strategy updating in evolutionary games. Proc. Natl. Acad. Sci. USA 2010, 107, 2962–2966. [Google Scholar] [CrossRef] [Green Version]
- Melamed, D.; Harrell, A.; Simpson, B. Cooperation, clustering, and assortative mixing in dynamic networks. Proc. Natl. Acad. Sci. USA 2018, 115, 951–956. [Google Scholar] [CrossRef] [Green Version]
- Perc, M.; Szolnoki, A. Coevolutionary games—A mini review. BioSystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [Green Version]
- Fehl, K.; van der Post, D.J.; Semmann, D. Co-evolution of behaviour and social network structure promotes human cooperation. Ecol. Lett. 2009, 14, 546–551. [Google Scholar] [CrossRef]


| At Round t | Class of after Round t | ||||
|---|---|---|---|---|---|
| Class of | Strat. of | Act. of | Act. of | Act. of | |
| (Expected) | |||||
| TCC | T | C | C | C | TCC |
| D | DCD | ||||
| Dn | D | C | TDC | ||
| D | DDD | ||||
| DCD | T,Dn | D | D | C | TDC |
| D | DDD | ||||
| TDC | T,Tn | C | D | D | TCD |
| D,Dn | D | D | TDD | ||
| DDD | T | D | D | C | TDC |
| D | DDD | ||||
| Tn | C | C | TCC | ||
| D | DCD | ||||
| D,Dn | D | C | TDC | ||
| D | DDD | ||||
| TCD | T,Dn | D | C | C | TDC |
| D | DDD | ||||
| TDD | Tn | C | D | C | TCC |
| D | TCD | ||||
| D | D | C | TDC | ||
| D | TDD | ||||
| When Computing | Class of j Updated after Round t | Contribution per Neighbor per Round | Number of Neighbors | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | ||||||
| TCC | … | ||||||
| TCD | r | … | r | ||||
| TDC | r | … | r | ||||
| DCD, DDD | 0 | 0 | … | 0 | 0 | – | |
| TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TCC, TCD | r | 0 | … | 0 | 0 | ||
| TDC, DCD, DDD | 0 | 0 | … | 0 | 0 | – | |
| TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TDC, TDD, DDD | 0 | 0 | … | 0 | 0 | – | |
| TCC, TCD, DCD | Revising Ds have no such neighbors | 0 | |||||
| TDC, TDD | r | … | r | ||||
| DDD | 0 | … | 0 | 0 | |||
| TCC, TCD, DCD | Revising Ds have no such neighbors | 0 | |||||
| At Round t | Class of after Round t | ||||
|---|---|---|---|---|---|
| Class of | Strat. of | Act. of | Act. of | Act. of | |
| (Expected) | |||||
| TCC | T | C | C | C | TCC |
| D | DCD1 | ||||
| Dn | D | C | TDC1 | ||
| D | DDD | ||||
| DCD1 | T | C | D | C | TCC |
| D | DCD | ||||
| Dn | D | C | TDC1 | ||
| D | DDD | ||||
| TDC1 | T,Tn | C | C | C | TCC |
| D | DCD1 | ||||
| D,Dn | D | C | TDC | ||
| D | DDD | ||||
| DDD | T,D,Dn | D | D | C | TDC1 |
| D | DDD | ||||
| Tn | C | C | TCC | ||
| D | DCD1 | ||||
| DCD | T,Dn | D | D | C | TDC1 |
| D | DDD | ||||
| TDC | Tn | C | D | D | TCD1 |
| D,Dn | D | D | TDD | ||
| TCD1 | T | C | C | C | TCC |
| D | DCD | ||||
| Dn | D | C | TDC1 | ||
| D | DDD | ||||
| TDD | Tn | C | D | C | TCC |
| D | TCD1 | ||||
| D | D | C | TDC1 | ||
| D | TDD | ||||
| When Computing | Class of j updated after Round t | Contribution per Neighbor per Round | Number of Neighbors | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | h | ||||
| TCC, TCD1, TDC1 | … | ||||||
| DCD1 | 0 | 0 | … | 0 | |||
| DCD, DDD | 0 | 0 | 0 | … | 0 | – | |
| TDC, TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TCC, TCD1 | r | r | 0 | … | 0 | ||
| TDC1 | r | 0 | 0 | … | 0 | ||
| DCD, DCD1, DDD | 0 | 0 | 0 | … | 0 | – | |
| TDC, TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TDC1 | r | 0 | … | 0 | 0 | ||
| TDC, TDD, DDD | 0 | 0 | … | 0 | 0 | – | |
| TCC, TCD1, DCD, DCD1 | Revising Ds have no such neighbors | 0 | |||||
| TDC1 | … | ||||||
| TDC, TDD | … | ||||||
| DDD | 0 | … | 0 | ||||
| TCC, DCD1, DCD, TCD1 | Revising Ds have no such neighbors | 0 | |||||
| At Round t | Class of after Round t | ||||
|---|---|---|---|---|---|
| Class of | Strat. of | Act. of | Act. of | Act. of | |
| (Expected) | |||||
| TCC | T | C | C | C | TCC |
| D | DCD | ||||
| Dn | D | C | TDC | ||
| D | DDD | ||||
| DCD | T,Dn | D | D | C | TDC1 |
| D | DDD | ||||
| TDC | Tn | C | D | D | TCD1 |
| D,Dn | D | D | TDD | ||
| DDD | T,D,Dn | D | D | C | TDC1 |
| D | DDD | ||||
| Tn | C | C | TCC | ||
| D | DCD1 | ||||
| TDC1 | T,Tn | C | C | C | TCC |
| D | DCD1 | ||||
| Tn | D | D | TCD1 | ||
| D,Dn | D | C | C | TDC | |
| D | DDD | ||||
| D | D | D | TDD | ||
| TCD1 | T | C | C | C | TCC |
| D | DCD | ||||
| Dn | D | C | TDC | ||
| D | DDD | ||||
| TDD | Tn | C | D | C | TCC |
| D | TCD1 | ||||
| D | D | C | TDC1 | ||
| D | TDD | ||||
| DCD1 | T,Dn | D | D | C | TDC1 |
| D | DDD | ||||
| When Computing | Class of j Updated after Round t | Contribution per Neighbor per Round | Number of Neighbors | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | h | ||||
| TCC, TCD1, TDC1 | … | ||||||
| DCD, DCD1, DDD | 0 | 0 | 0 | … | 0 | – | |
| TDC, TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TCC,TCD1,TDC1 | r | 0 | 0 | … | 0 | ||
| DCD, DCD1, DDD | 0 | 0 | 0 | … | 0 | – | |
| TDC, TDD | Revising Ts have no TDD-neigbors | 0 | |||||
| TDC1 | r | 0 | … | 0 | 0 | ||
| TDC, TDD, DDD | 0 | 0 | … | 0 | 0 | – | |
| TCC, TCD1, DCD, DCD1 | Revising Ds have no such neighbors | 0 | |||||
| TDC1 | … | ||||||
| TDC, TDD | … | ||||||
| DDD | 0 | 0 | … | 0 | |||
| TCC, TCD1, DCD, DCD1 | Revising Ds have no such neighbors | 0 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Della Rossa, F.; Dercole, F.; Di Meglio, A. Direct Reciprocity and Model-Predictive Strategy Update Explain the Network Reciprocity Observed in Socioeconomic Networks. Games 2020, 11, 16. https://doi.org/10.3390/g11010016
Della Rossa F, Dercole F, Di Meglio A. Direct Reciprocity and Model-Predictive Strategy Update Explain the Network Reciprocity Observed in Socioeconomic Networks. Games. 2020; 11(1):16. https://doi.org/10.3390/g11010016
Chicago/Turabian StyleDella Rossa, Fabio, Fabio Dercole, and Anna Di Meglio. 2020. "Direct Reciprocity and Model-Predictive Strategy Update Explain the Network Reciprocity Observed in Socioeconomic Networks" Games 11, no. 1: 16. https://doi.org/10.3390/g11010016
APA StyleDella Rossa, F., Dercole, F., & Di Meglio, A. (2020). Direct Reciprocity and Model-Predictive Strategy Update Explain the Network Reciprocity Observed in Socioeconomic Networks. Games, 11(1), 16. https://doi.org/10.3390/g11010016





