Reactive Strategies: An Inch of Memory, a Mile of Equilibria
Abstract
:1. Introduction
- (Q1)
- What are all possible NE profiles in stochastic RSs?
- (Q2)
- What are all possible symmetric games admitting NE in stochastic RSs?
- (Q3)
- Do equilibrium profiles in conditional stochastic RSs Pareto improve over equilibrium profiles in unconditional RSs?
1.1. Related Literature
1.2. Results and Structure of the Article
- If there exists an NE formed by a profile of conditional SRSs, then there are infinitely many NE profiles generated by conditional SRSs that, in general, have distinct payoffs, but we do not have a folk theorem.
- If there exists an NE formed by a profile of unconditional SRSs, then NE profiles in conditional SRSs either Pareto improve over it or provide the same payoff profile.
1.3. Definitions of Repeated Games

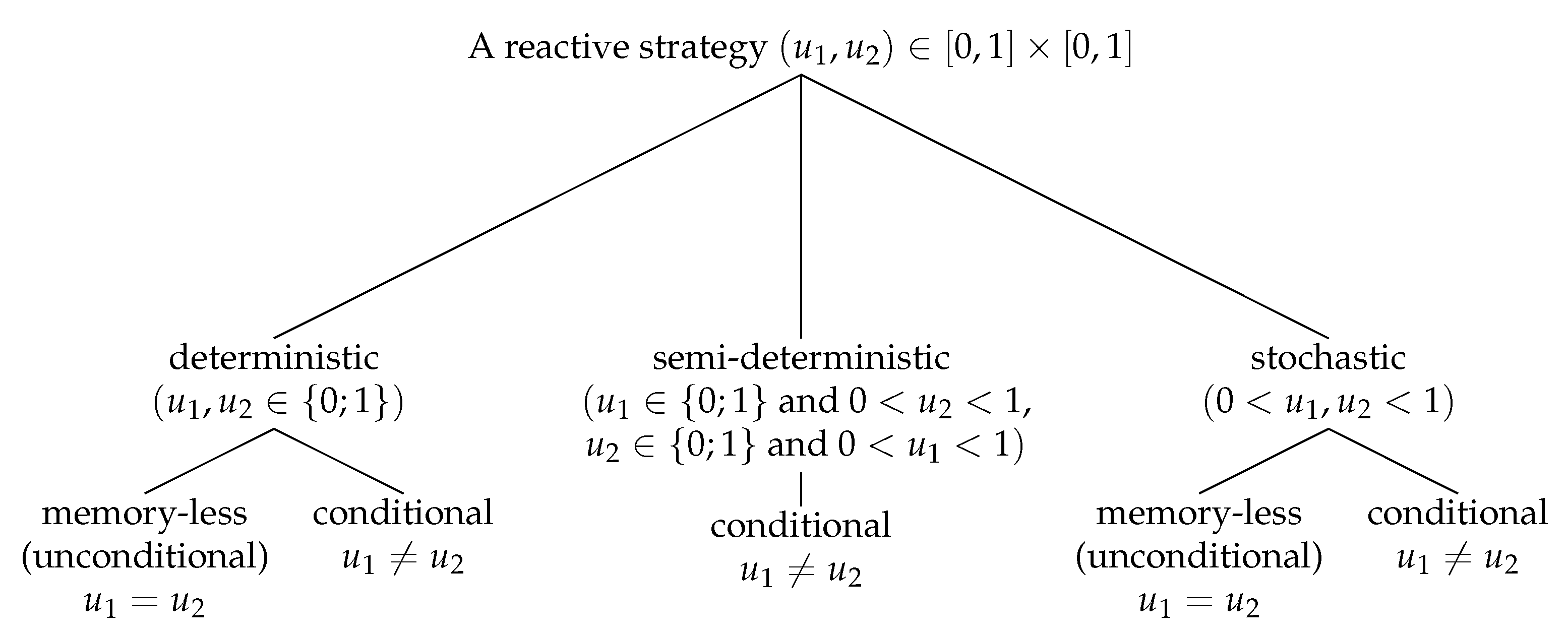
1.3.1. Strategies
1.3.2. Payoffs
- 1.
- In contrast to semi-deterministic and deterministic RSs, the payoffs for profiles of SRSs do not depend on the opening move;
- 2.
- SRSs capture non-deterministic behavior that is the most natural for the domain of evolutionary game theory, where RSs originated to model real-life processes.
1.3.3. Equilibria
2. Characterization of Nash Equilibria
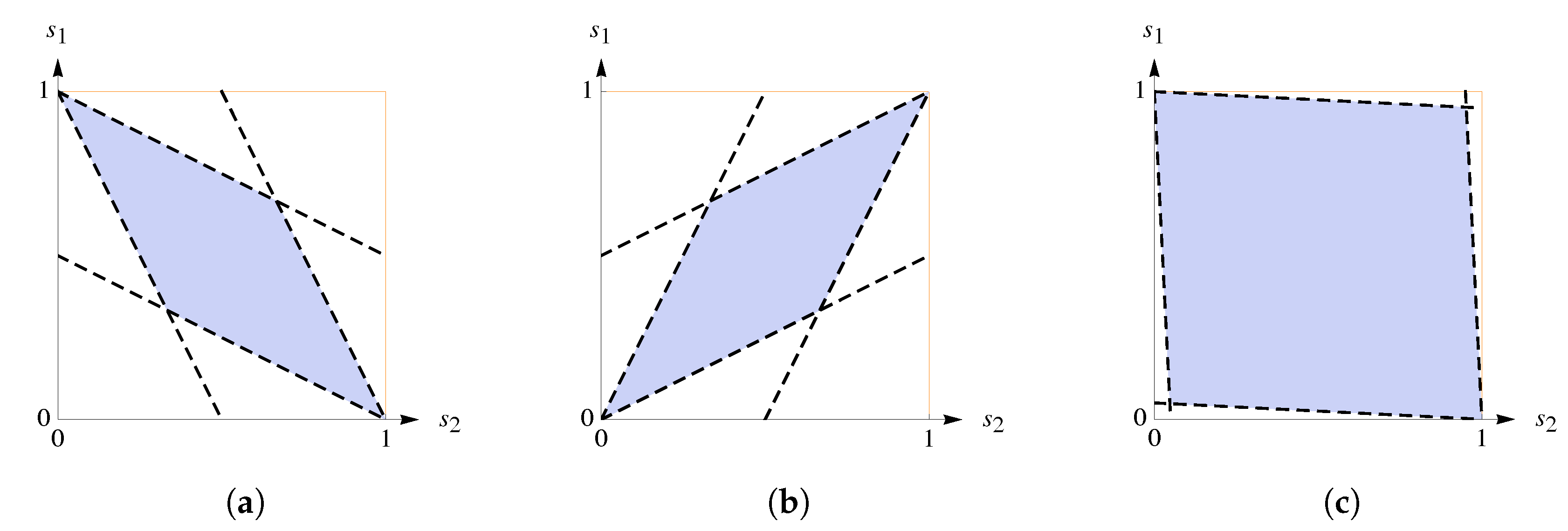
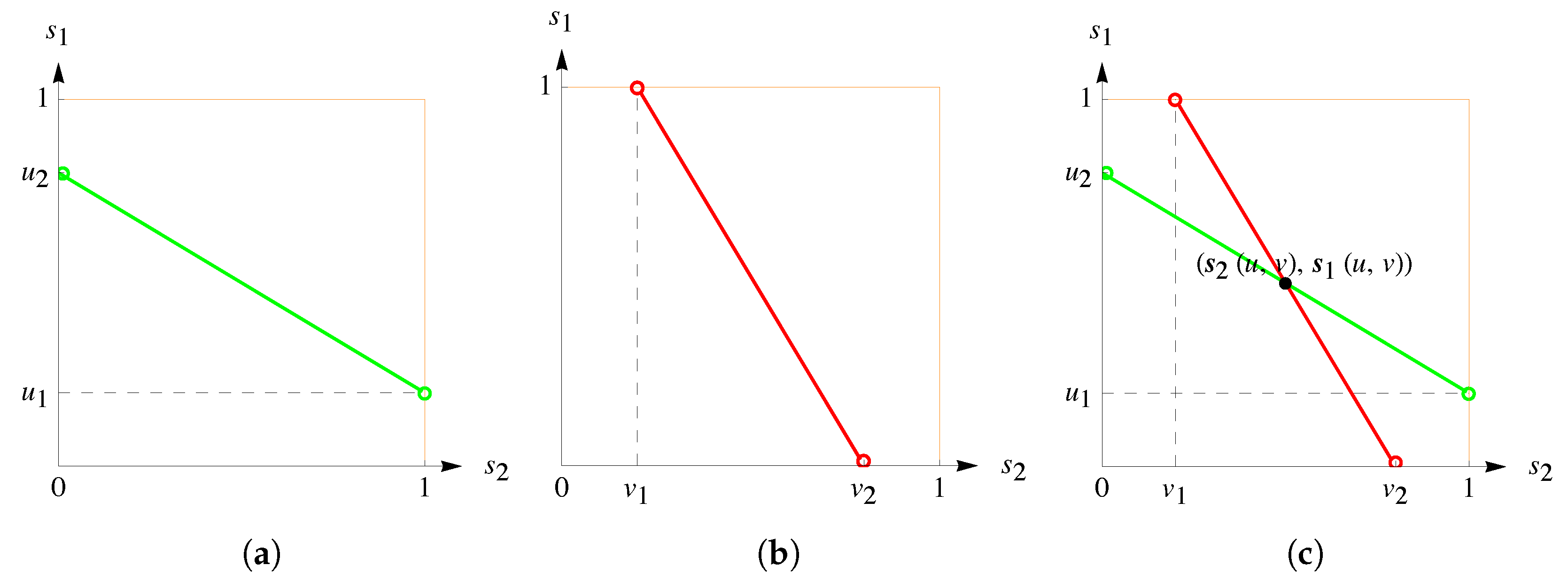
2.1. Geometric Intuition and Attainable Sets
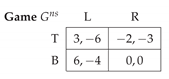
2.2. Prisoner’s Dilemma with Equal Gains from Switching

2.3. Characterization of Nash Equilibria in
- 1.
- and
- 2.
- and (or, symmetrically, and ),
- 3.
- and
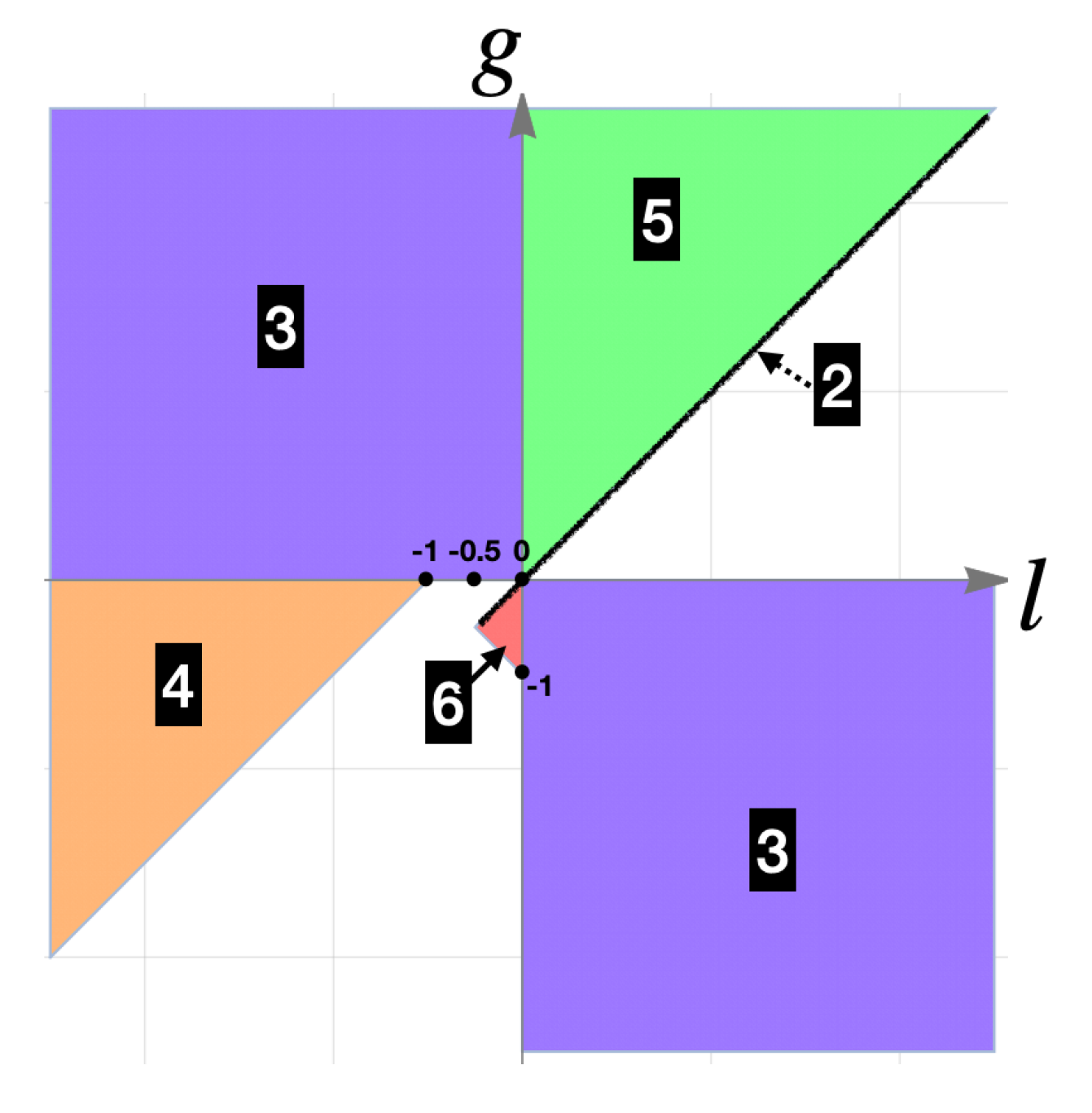
2.4. Existence of Nash Equilibria in Symmetric Games

- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
2.5. If All RSs Are Available
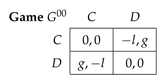
3. Equilibrium Payoffs in Conditional SRSs
3.1. Payoffs for NE Profiles of Unconditional and Conditional SRSs
3.2. Symmetric Games

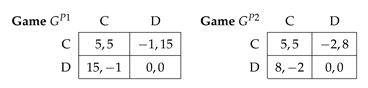
3.3. A Game with Pareto-Efficient Equilibrium and Dominant Strategies

4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ESD | Equilibrium stationary distribution |
| NE | Nash equilibrium |
| RS (SRS) | Reactive strategy (stochastic reactive strategy) |
| SME | Strong mixed equilibrium |
| SPE | Subgame perfect equilibrium |
| ZD | Zero-determinant (strategies) |
Appendix A. Existence of Equilibria in Symmetric Games
Appendix A.1. Case a = 0

Appendix A.2. Case a < 0
Appendix A.3. Case a > 0
Appendix B. Theorem 2 for Symmetric Games with Equal Payoffs on the Leading Diagonal

| Condition of the Theorem | One-Shot Game Description | The Benchmark in Memory-Less RSs | NE Payoffs in Conditional SRSs |
|---|---|---|---|
| 1 | A trivial stage game with identical payoffs | Any profile of memory-less RSs forms a NE with payoffs | Any profile of conditional RSs forms an NE with payoffs |
| 2, 6, and 7 | Can not hold for | ||
| 3 | Coordination and anti-coordination stage games with two pure equilibria | There is an NE profile in memory-less SRSs with payoffs | If then there exists an NE profile of conditional SRSs Pareto dominating the memory-less benchmark. If then there is an unique ESD ; all payoff profiles of equilibria in SRSs coincide. |
| 4 and 5 | Stage games having one dominant pure strategy; any symmetric profile of mixed strategies Pareto improves the NE payoffs | Payoff profile of dominant strategies | Any NE profile of conditional SRSs Pareto dominates the memory-less benchmark. |
Appendix C. Additional Examples
Appendix C.1. Non-Symmetric Equilibria in Prisoner’s Dilemma and Folk Theorem


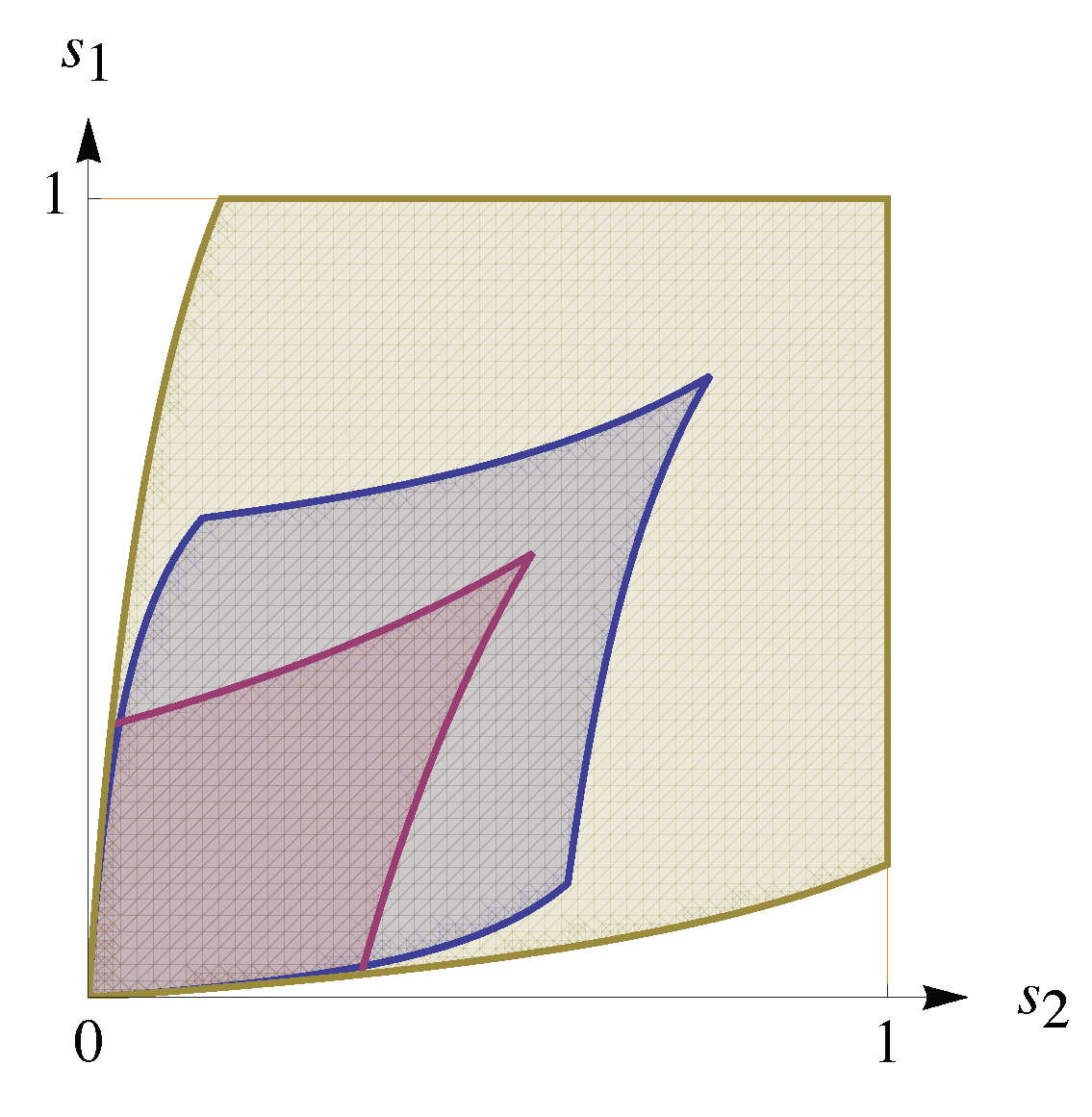
Appendix C.2. Symmetric ESD in Non-Symmetric Games
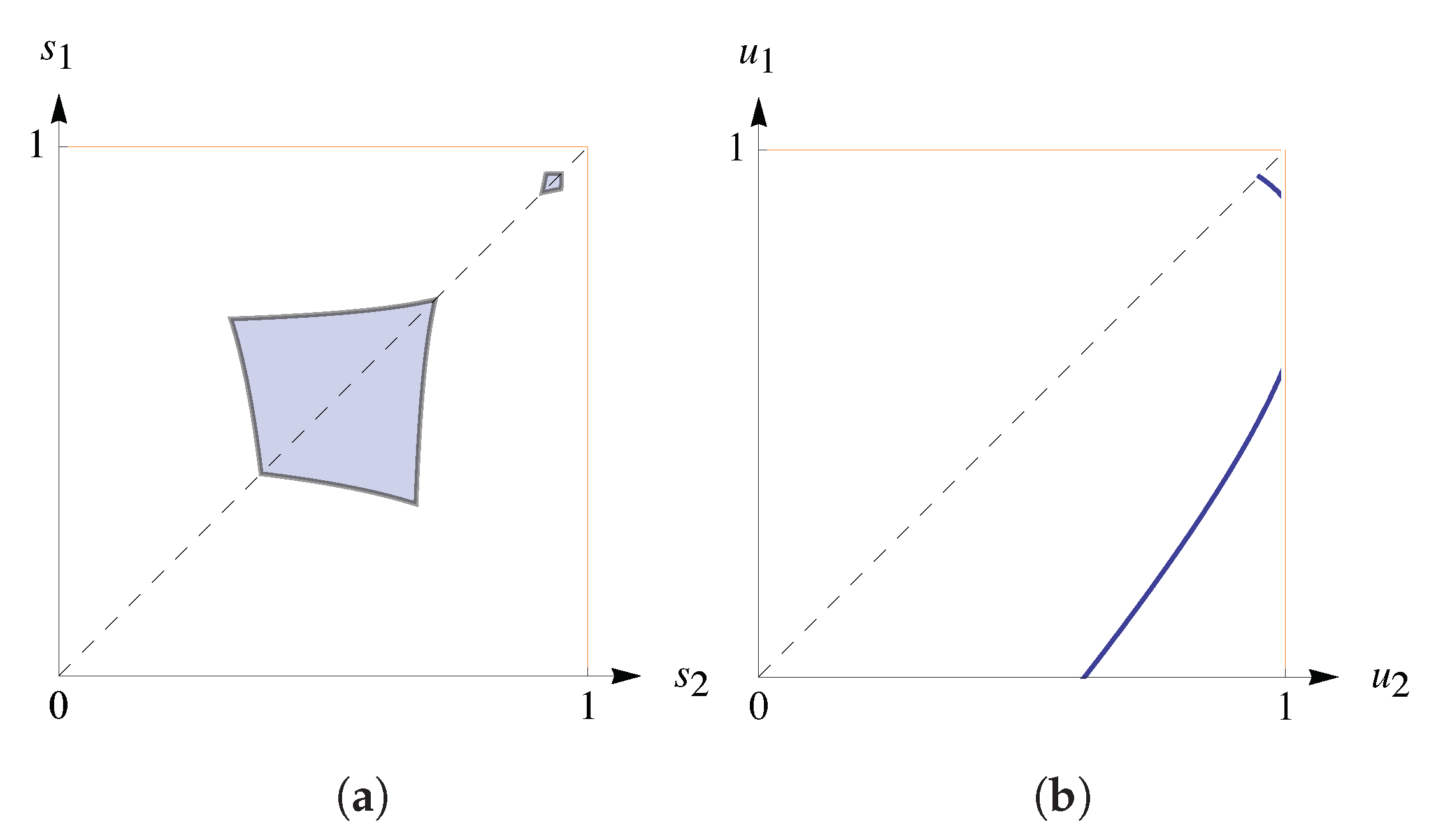
 admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.
admitting a continuum of ESDs of the form We say that ESDs of this form are symmetric ESDs (though this may be not a good choice of words). Symmetric ESDs have an intriguing property. Imagine that in a repeated game, players are in an equilibrium, and we observe only action frequencies (but not conditional frequencies). If the frequencies are symmetric, then it would be natural to conclude that we are observing a symmetric game. This following example, however, shows that the last assumption may not be true.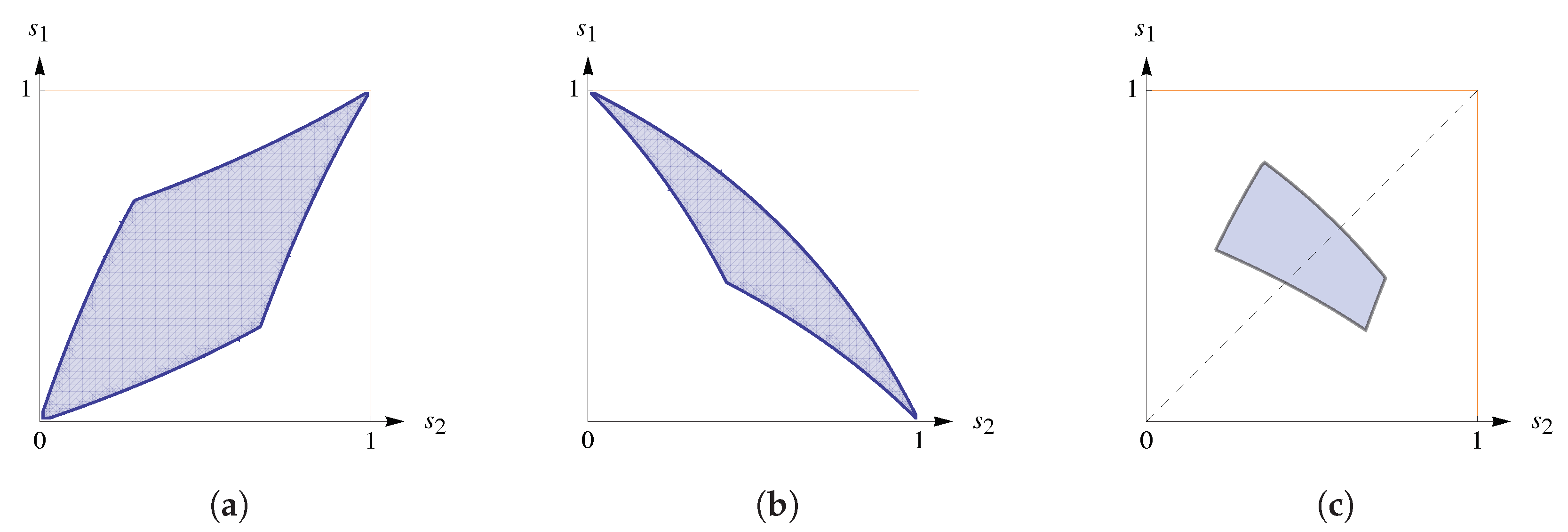
Appendix C.3. Games with Disconnected Regions of ESDs

References
- Mailath, G.J.; Samuelson, L. Repeated Games and Reputations: Long-Run Relationships; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kalai, E. Bounded Rationality and Strategic Complexity in Repeated Games. In Game Theory and Applications; Academic Press, Inc.: San Diego, CA, USA, 1990; Chapter V; pp. 131–157. [Google Scholar]
- Dal Bó, P.; Fréchette, G.R. Strategy Choice in the Infinitely Repeated Prisoner’s Dilemma. Am. Econ. Rev. 2019, 109, 3929–3952. [Google Scholar] [CrossRef] [Green Version]
- Nowak, M.; Sigmund, K. The evolution of stochastic strategies in the Prisoner’s Dilemma. Acta Appl. Math. 1990, 20, 247–265. [Google Scholar] [CrossRef]
- Nowak, M. Stochastic strategies in the Prisoner’s Dilemma. Theor. Popul. Biol. 1990, 38, 93–112. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. Evolutionary Dynamics of Biological Games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofbauer, J.; Sigmund, K. Adaptive dynamics and evolutionary stability. Appl. Math. Lett. 1990, 3, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Kalai, E.; Samet, D.; Stanford, W. A note on reactive equilibria in the discounted prisoner’s dilemma and associated games. Int. J. Game Theory 1988, 17, 177–186. [Google Scholar] [CrossRef]
- Aumann, R.J. Repeated Games. In Issues in Contemporary Microeconomics and Welfare; Feiwel, G.R., Ed.; Palgrave Macmillan: London, UK, 1985; Chapter 5; pp. 209–242. [Google Scholar] [CrossRef]
- Friedman, J.W. Reaction Functions and the Theory of Duopoly. Rev. Econ. Stud. 1968, 35, 257–272. [Google Scholar] [CrossRef]
- Stanford, W.G. Subgame perfect reaction function equilibria in discounted duopoly supergames are trivial. J. Econ. Theory 1986, 39, 226–232. [Google Scholar] [CrossRef]
- Kamihigashi, T.; Furusawa, T. Global dynamics in repeated games with additively separable payoffs. Rev. Econ. Dyn. 2010, 13, 899–918. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.W.; Samuelson, L. Continuous Reaction Functions in Duopolies. Games Econ. Behav. 1994, 6, 55–82. [Google Scholar] [CrossRef]
- Kryazhimskiy, A. Equilibrium stochastic behaviors in repeated games. In Abstracts of International Conference Stochastic Optimization and Optimal Stopping; Steklov Mathematical Institute: Moscow, Russia, 2012; pp. 38–41. [Google Scholar]
- Press, W.H.; Dyson, F.J. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hilbe, C.; Traulsen, A.; Sigmund, K. Partners or rivals? Strategies for the iterated prisoner’s dilemma. Games Econ. Behav. 2015, 92, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Dutta, P.K.; Siconolfi, P. Mixed strategy equilibria in repeated games with one-period memory. Int. J. Econ. Theory 2010, 6, 167–187. [Google Scholar] [CrossRef]
- Ely, J.C.; Välimäki, J. A Robust Folk Theorem for the Prisoner’s Dilemma. J. Econ. Theory 2002, 102, 84–105. [Google Scholar] [CrossRef] [Green Version]
- D’Arcangelo, C. Too Much of Anything Is Bad for You, Even Information: How Information Can Be Detrimental to Cooperation and Coordination. Ph.D. Thesis, University of Trento, Trent, Italy, 2018. [Google Scholar]
- Abreu, D.; Rubinstein, A. The Structure of Nash equilibrium in Repeated Games with Finite Automata. Econom. J. Econom. Soc. 1988, 56, 1259–1281. [Google Scholar] [CrossRef]
- Marks, R. Repeated games and finite automata. In Recent Developments in Game Theory; Edward Elgar Publishing: Cheltenham, UK, 1992; pp. 43–64. [Google Scholar]
- Baek, S.K.; Jeong, H.C.; Hilbe, C.; Nowak, M.A. Comparing reactive and memory-one strategies of direct reciprocity. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, M. An evolutionarily stable strategy may be inaccessible. J. Theor. Biol. 1990, 142, 237–241. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Moulin, H.; Vial, J.P. Strategically zero-sum games: The class of games whose completely mixed equilibria cannot be improved upon. Int. J. Game Theory 1978, 7, 201–221. [Google Scholar] [CrossRef]
- Kleimenov, A.; Kryazhimskiy, A. Normal Behavior, Altruism and Aggression in Cooperative Game Dynamics; IIASA: Laxenburg, Austria, 1998. [Google Scholar]
- McAvoy, A.; Nowak, M.A. Reactive learning strategies for iterated games. Proc. R. Soc. A 2019, 475, 20180819. [Google Scholar] [CrossRef] [Green Version]
- Barlo, M.; Carmona, G.; Sabourian, H. Repeated games with one-memory. J. Econ. Theory 2009, 144, 312–336. [Google Scholar] [CrossRef] [Green Version]


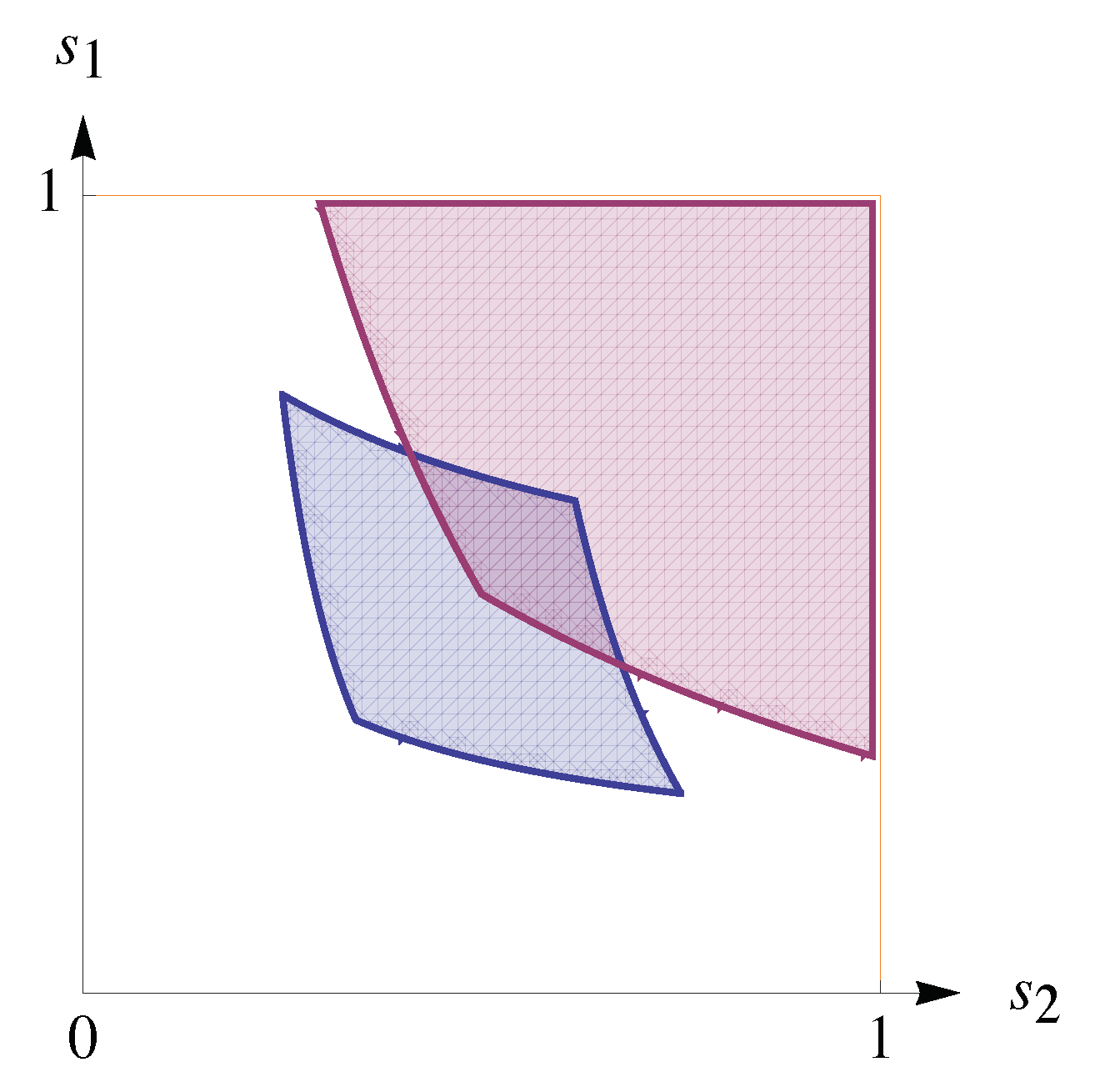
| Game | Setting | Strategies | Payoffs | Description |
|---|---|---|---|---|
| One-shot | Mixed strategies | A one-shot game | ||
| Repeated | Unconditional RSs | the memory-less play of that is infinitely repeated; is ‘equivalent’ to but formalised as repeated interaction. | ||
| Repeated | Stochastic and unconditional RSs | The repeated modification of where probabilities of actions can be conditioned by the preceding opponent’s action. In addition to memory-less strategies from , players get conditional ones. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baklanov, A. Reactive Strategies: An Inch of Memory, a Mile of Equilibria. Games 2021, 12, 42. https://doi.org/10.3390/g12020042
Baklanov A. Reactive Strategies: An Inch of Memory, a Mile of Equilibria. Games. 2021; 12(2):42. https://doi.org/10.3390/g12020042
Chicago/Turabian StyleBaklanov, Artem. 2021. "Reactive Strategies: An Inch of Memory, a Mile of Equilibria" Games 12, no. 2: 42. https://doi.org/10.3390/g12020042
APA StyleBaklanov, A. (2021). Reactive Strategies: An Inch of Memory, a Mile of Equilibria. Games, 12(2), 42. https://doi.org/10.3390/g12020042






