The Evolution of Ambiguity in Sender—Receiver Signaling Games
Abstract
:1. Introduction
1.1. Related Work
1.2. Structure of the Article
2. The Game Models
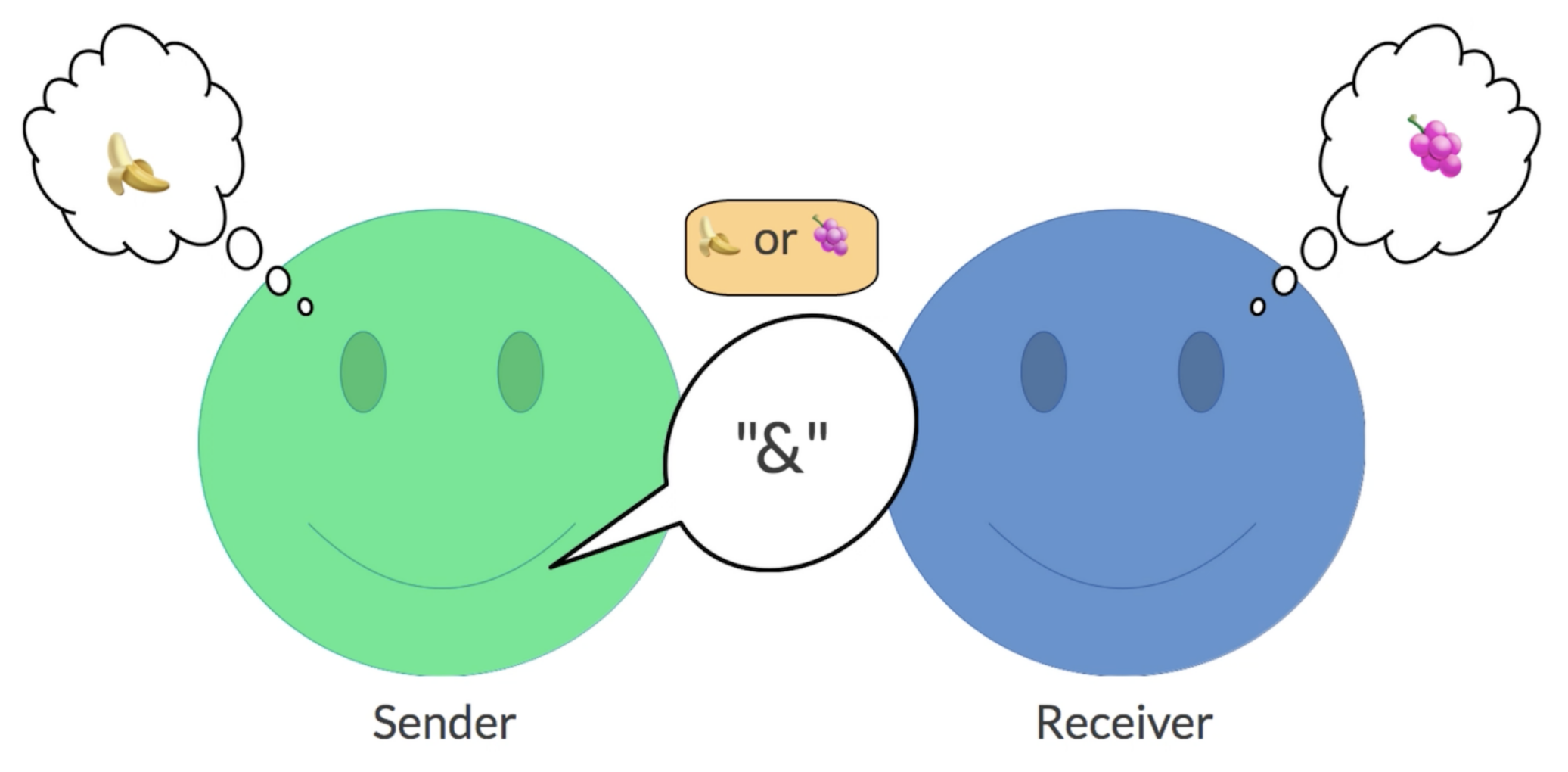
2.1. Lewis Signaling Game
2.2. Context-Signaling Game
- ,
- ,
- ,
2.3. Context Bottleneck Game
3. Formal and Computational Analysis
- for all
- If for some , then
3.1. Strategy Spaces and Equilibria
3.2. Emergence Rates under Evolutionary Dynamics
4. Online Experiments
4.1. Experimental Setup
- player 1 is sender, information state is ;
- player 2 is sender, information state is ;
- player 1 is sender, information state is ;
- player 2 is sender, information state is ;
- player 1 is sender, information state is ;
- player 2 is sender, information state is .
4.2. Experimental Results
4.3. Discussion
5. Conclusions
6. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CS game | context-signaling game |
| LS game | Lewis signaling game |
| CB game | context bottleneck game |
| expected utility | |
| communicative utility | |
| EGT | evolutionary game theory |
| ESS | evolutionarily stable strategy |
| PDI | pairwise difference imitation |
| CoS | communicative success |
| PS | perfect signaling |
| PA | perfect ambiguity |
| nPA | non-perfect ambiguity |
Appendix A. Pairwise Differential Imitation (PDI) Dynamics

Appendix B. Experimental Procedure
- In this experiment you will play a communication game with an other participant for a number of 30 rounds.
- In each round you both can score 10 points if you play successfully, otherwise you both receive 0 points.
- Your final total score will be converted into real money (100 points = 1£) and added to your participation fee.
- Please take your time and play carefully. Press ’Next’ to go to the video tutorial (<2 min) that explains how to play the game.

References
- Lewis, D. Convention. A Philosophical Study; Blackwell: Cambridge, MA, USA, 1969. [Google Scholar]
- Barrett, J.A. Numerical Simulations of the Lewis Signaling Game: Learning Strategies, Pooling Equilibria, and the Evolution of Grammar; Technical Report; Institute for Mathematical Behavioral Sciences, University of California: Irvine, UK, 2006. [Google Scholar]
- Skyrms, B. Signals: Evolution, Learning and Information; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Huttegger, S.M.; Zollman, K.J.S. Signaling Games: Dynamics of Evolution and Learning. In Language, Games, and Evolution; Benz, A., Ebert, C., Jäger, G., van Rooij, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 160–176. [Google Scholar]
- Wärneryd, K. Cheap Talk, Coordination, and Evolutionary Stability. Games Econ. Behav. 1993, 5, 532–546. [Google Scholar] [CrossRef]
- Huttegger, S.M. Evolution and the Explanation of Meaning. Philos. Sci. 2007, 74, 1–27. [Google Scholar] [CrossRef]
- Santana, C. Ambiguity in Cooperative Signaling. Philos. Sci. 2014, 81, 398–422. [Google Scholar] [CrossRef]
- Mühlenbernd, R. Evolutionary stability of ambiguity in context-signaling games. Synthese 2021, 198, 11725–11753. [Google Scholar] [CrossRef]
- Skyrms, B. Evolution of the Social Contract; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Skyrms, B.; Pemantle, R. A dynamic model of social network formation. Proc. Natl. Acad. Sci. USA 2000, 97, 9340–9349. [Google Scholar] [CrossRef] [Green Version]
- Zollman, K.J.S. Talking to Neighbors: The Evolution of Regional Meaning. Philos. Sci. 2005, 72, 69–85. [Google Scholar] [CrossRef] [Green Version]
- Hofbauer, J.; Huttegger, S.M. Feasibility of communication in binary signaling games. J. Theor. Biol. 2008, 245, 843–849. [Google Scholar] [CrossRef]
- Pawlowitsch, C. Why Evolution does not always lead to an optimal signaling system. Games Econ. Behav. 2008, 63, 203–226. [Google Scholar] [CrossRef]
- Barrett, J.A.; Zollman, K.J.S. The Role of Forgetting in the Evolution and Learning of Language. J. Exp. Theor. Artif. Intell. 2009, 21, 293–309. [Google Scholar] [CrossRef]
- Mühlenbernd, R. Learning with Neighbours. Synthese 2011, 183, 87–109. [Google Scholar] [CrossRef]
- Mühlenbernd, R.; Franke, M. Meaning, evolution and the structure of society. In Proceedings of the European Conference on Social Intelligence, Barcelona, Spain, 3–5 November 2014; Herzig, A., Lorini, E., Eds.; Volume 1283, pp. 28–39. [Google Scholar]
- Mühlenbernd, R.; Nick, J. Language change and the force of innovation. In Pristine Perspectives on Logic, Language, and Computation; Katrenko, S., Rendsvig, K., Eds.; Springer: Heidelberg, Germany; New York, NY, USA, 2014; Volume 8607, pp. 194–213. [Google Scholar]
- Mühlenbernd, R.; Enke, D. The grammaticalization cycle of the progressive—A game-theoretic analysis. Morphology 2017, 27, 497–526. [Google Scholar] [CrossRef]
- Mühlenbernd, R. The change of signaling conventions in social networks. AI Soc. 2019, 34, 721–734. [Google Scholar] [CrossRef]
- Macy, M.W.; Flache, A. Learning dynamics in social dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99, 7229–7236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skyrms, B. The Stag Hunt and the Evolution of Social Structure; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorini, E.; Mühlenbernd, R. The long-term benefits of following fairness norms under dynamics of learning and evolution. Fundam. Inform. 2018, 158, 121–148. [Google Scholar] [CrossRef]
- LiCalzi, M.; Mühlenbernd, R. Categorization and cooperation across games. Games 2019, 10, 5. [Google Scholar] [CrossRef] [Green Version]
- Harré, M. Utility, Revealed Preferences Theory, and Strategic Ambiguity in Iterated Games. Entropy 2017, 19, 201. [Google Scholar] [CrossRef] [Green Version]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Evolution of Communication with Partial Common Interest. Games Econ. Behav. 2001, 37, 79–120. [Google Scholar] [CrossRef] [Green Version]
- Bruner, J.; O’Connor, C.; Rubin, H.; Huttegger, S.M. David Lewis in the lab: Experimental results on the emergence of meaning. Synthese 2018, 195, 603–621. [Google Scholar] [CrossRef]
- Rubin, H.; Bruner, J.; O’Connor, C.; Huttegger, S.M. Communication without common interest: A signaling experiment. Stud. Hist. Philos. Sci. Part C Stud. Hist. Philos. Biol. Biomed. Sci. 2020, 83, 101295. [Google Scholar] [CrossRef]
- Blume, A.; Lai, E.; Lim, W. Strategic information transmission: A survey of experiments and theoretical foundations. In Handbook of Experimental Game Theory; Capra, C.M., Croson, R., Rigdon, M., Rosenblat, T., Eds.; Edward Elgar Publishing: Cheltenham, UK; Northampton, MA, USA, 2020; pp. 311–347. [Google Scholar]
- Rohde, H.; Seyfarth, S.; Clark, B.; Jaeger, G.; Kaufmann, S. Communicating with cost-based implicature: A game-theoretic approach to ambiguity. In Proceedings of the 16th Workshop on the Semantics and Pragmatics of Dialogue, Paris, France, 19–21 September 2012. [Google Scholar]
- Schumann, A. Payoff Cellular Automata and Reflexive Games. J. Cell. Autom. 2014, 9, 287–313. [Google Scholar]
- Schumann, A. Towards Context-Based Concurrent Formal Theories. Parallel Process. Lett. 2015, 25, 1540008. [Google Scholar] [CrossRef]
- Mertens, J.F.; Neyman, A. Stochastic games. Internatioanl J. Game Theory 1981, 10, 53–66. [Google Scholar] [CrossRef]
- Hilbe, C.; Štěpán, Š.; Chatterjee, K.; Nowak, M.A. Evolution of cooperation in stochastic games. Nature 2018, 559, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Jäger, G. Evolutionary Game Theory and Typology. A Case Study. Language 2007, 83, 74–109. [Google Scholar] [CrossRef]
- Deo, A. The semantic and pragmatic underpinnings of grammaticalization paths: The progressive to imperfective shift. Semant. Pragmat. 2015, 8, 1–52. [Google Scholar] [CrossRef] [Green Version]
- Bruner, J.; O’Connor, C.; Rubin, H. Experimental economics for philosophers. In Methodological Advances in Experimental Philosophy; Fischer, M.C.E., Ed.; Bloomsbury Academic: New York, NY, USA, 2019. [Google Scholar]
- Spence, M. Job market signaling. Q. J. Econ. 1973, 87, 355–374. [Google Scholar] [CrossRef]
- Farrell, J.; Rabin, M. Cheap Talk. J. Econ. Perspect. 1996, 10, 103–118. [Google Scholar] [CrossRef]
- Jäger, G. Applications of Game Theory in Linguistics. Lang. Linguist. Compass 2008, 2/3, 408–421. [Google Scholar]
- Mühlenbernd, R.; Quinley, J. Language change and network games. Lang. Linguist. Compass 2017, 11, e12235. [Google Scholar] [CrossRef]
- Grafen, A. Biological signals as handicaps. J. Theor. Biol. 1990, 144, 517–546. [Google Scholar] [CrossRef]
- Maynard Smith, J. The concept of information in biology. Philos. Sci. 2000, 67, 177–194. [Google Scholar] [CrossRef]
- Maynard Smith, J.; Price, G. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Nowak, M.A.; Krakauer, D.C. The evolution of language. Proc. Natl. Acad. Sci. USA 1999, 96, 8028–8033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, P.D.; Jonker, L.B. Evolutionarily Stable Strategies and Game Dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Balkenborg, D.; Schlag, K.H. Evolutionarily stable sets. Int. J. Game Theory 2001, 29, 571–595. [Google Scholar] [CrossRef]
- Izquierdoy, L.R.; Izquierdoz, S.S.; Sandholm, W.H. An Introduction to ABED: Agent-Based Simulation of Evolutionary Game Dynamics. Games Econ. Behav. 2019, 118, 434–462. [Google Scholar] [CrossRef]
- Skyrms, B. Signals, evolution and the explanatory power of transient information. Philos. Sci. 2002, 69, 407–428. [Google Scholar] [CrossRef] [Green Version]
- Aumann, R. Nash equilibria are not self-enforcing. In Economic Decision Making, Games, Econometrics and Optimization; Gabzewicz, J.J., Richard, J.F., Wolsey, L.A., Eds.; North Holland: Amsterdam, The Netherlands, 1990; pp. 201–206. [Google Scholar]
- Roth, A.E.; Erev, I. Learning in Extensive-Form Games: Experimental Data and Simple Dynamic Models in the Intermediate Term. Games Econ. Behav. 1995, 8, 164–212. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. The Theory of Learning in Games; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]





| Symbol | Description |
|---|---|
| information states of set T | |
| signals of set S | |
| response actions of set R | |
| contextual cues of set C | |
| probability function over T given | |
| utility function | |
| sender strategy | |
| receiver strategy (standard signaling game) | |
| receiver strategy (context-signaling game) | |
| communicative strategy (pair of sender + receiver strategy) |
| LS Game | CS Game | CB Game | |
|---|---|---|---|
| number of states | 3 | 3 | 3 |
| number of signals | 3 | 3 | 2 |
| contextual cues | no | yes | yes |
| LS Game | CB Game | CS Game | |
|---|---|---|---|
| number of sender strategies | 27 | 8 | 27 |
| number of receiver strategies | 27 | 81 | 729 |
| total number of strategies | 729 | 648 | 19,683 |
| perfect signaling systems | 6 () | - | 54 () |
| perfect ambiguous systems | - | 2 () | 54 () |
| (non-perfect) evolutionarily stable sets | no | yes | yes |
| LS Game | CB Game | CS Game | |
|---|---|---|---|
| perfect signaling system | - | ||
| perfect ambiguous systems | - | ||
| non-perfect ambiguous systems |
| Game | Recruitment | Participants | |
|---|---|---|---|
| Session I | LS game | Prolific | 10 () |
| Session II | CS game | Invitation | 10 () |
| Session III | CS game | Prolific | 10 () |
| Session IV | CB game | Prolific | 10 () |
| Session V | CB game | Prolific | 10 () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mühlenbernd, R.; Wacewicz, S.; Żywiczyński, P. The Evolution of Ambiguity in Sender—Receiver Signaling Games. Games 2022, 13, 20. https://doi.org/10.3390/g13020020
Mühlenbernd R, Wacewicz S, Żywiczyński P. The Evolution of Ambiguity in Sender—Receiver Signaling Games. Games. 2022; 13(2):20. https://doi.org/10.3390/g13020020
Chicago/Turabian StyleMühlenbernd, Roland, Sławomir Wacewicz, and Przemysław Żywiczyński. 2022. "The Evolution of Ambiguity in Sender—Receiver Signaling Games" Games 13, no. 2: 20. https://doi.org/10.3390/g13020020
APA StyleMühlenbernd, R., Wacewicz, S., & Żywiczyński, P. (2022). The Evolution of Ambiguity in Sender—Receiver Signaling Games. Games, 13(2), 20. https://doi.org/10.3390/g13020020






