Firms 1 and 2 play a two-stage game. In our notation, subscript i identifies one of the firms and subscript j identifies that firm’s competitor. In stage I, each owner maximizes profit () by deciding whether to search for and hire a CEO who may make a biased estimate of the degree of substitutability between competing products. A CEO’s type is identified by parameter , which indexes the extent of estimation bias. In our specification, CEOi is unbiased when . Overestimation of product substitutability occurs when and underestimation occurs when . It is assumed that there is a pool of potential CEOs with varying degrees of bias. In stage II, owners delegate corporate decisions to CEOs. At this stage, CEOs compete in the product market where they make output () or price () decisions, depending on the mode of competition: Cournot, Bertrand, and Cournot–Bertrand. Each CEO maximizes expected profit, based on their type and the mode of competition. At each stage, decisions are made simultaneously, and economic agents have perfect and complete information.
The first set of terms on the right-hand side of the equality is the own effect on firm i’s profit that results from a marginal increase in . It equals zero, given profit maximization . The second set of terms identifies the strategic effect that occurs because of the resulting change in the action of firm j. If Equation (1) is zero, then it pays to hire an unbiased CEO. If it is positive (negative), however, it is optimal to hire a CEO who overestimates (underestimates) product substitutability.
Equation (1) demonstrates that market structure can influence an owner’s decision. In the absence of strategic effects, as in perfect competition and monopoly markets, the strategic effect is zero and owners hire unbiased CEOs. In an imperfectly competitive setting, however, the strategic effect need not be zero and its sign depends on the mode of competition and the extent to which the CEO’s bias affects rival behavior.
When discussing the various models below, we consider general and specific functional forms. The specific cases build from the duopoly framework found in Dixit [
24] and Singh and Vives [
25] that is commonly used in the overconfidence literature. In this model, product demand derives from a representative consumer who has a quadratic and concave utility function. The resulting inverse demand functions are:
where
and
. Given symmetry, firm
i’s demand can be written as
. For simplicity, let
, where parameter
d is an index of product differentiation or substitutability. Products are homogeneous or perfect substitutes when
and are unrelated when
(i.e., each firm is a monopolist). Thus, the degree of substitutability increases as
and decreases as
. Given that the Nash equilibrium in the product market is identical to the competitive outcome in the Bertrand case for homogeneous goods, we assume that products are imperfect substitutes,
. A firm’s cost of production,
, is normalized to zero to simplify the discussion.
2.1. Estimation Bias in a Cournot Game
We first consider Cournot competition in the output market, where firms optimize by simultaneously choosing quantities. For firm i, the owner’s goal is to maximize true profit: . Once hired, the CEO of firm i maximizes expected profit, , which depends on the degree of CEO bias. Expected profit equals true profit only when .
To analyze the case where owners consider hiring biased CEOs, we use backwards induction to obtain the SPNE. In stage II, where CEOs optimize over output, Nash equilibrium values are and . In stage I, firm i’s profit depends upon first-stage choices, and , and the anticipated actions in the second period, and . That is, . This model implies the following results:
Proposition 1. Consider this two-stage game with Cournot competition in stage II and where both firms have the option of hiring a biased CEO [, ] in stage I.
- A.
If a change in has no direct effect on in the neighborhood of the simple Cournot outcome where , then both firms hire CEOs who underestimate the degree of product substitutability ().
- B.
If a change in directly effects by shifting firm j’s best-reply function, then the sign of CEO estimation bias is indeterminate.
Proof. When
corresponds to output, Equation (1) becomes:
With profit maximization,
; therefore, the first set of terms on the right-hand side of the equality equals 0. Given that products are substitutes,
. Because firm
j’s best-reply function has a negative slope with Cournot competition,
.
Given that underestimation of the degree of product substitutability induces CEO
i to increase production,
in the neighborhood of the simple Cournot outcome where
. As a result,
and both firms hire CEOs who underestimate the degree of product substitutability (
).
In this case, the sign of
is indeterminant without knowing the sign and the relative magnitude of the direct effect
. □
To further illustrate, we consider the linear model of Dixit [
24] and Singh and Vives [
25], as discussed above. This specification provides an example of Part A of Proposition 1, because a change in
has no direct effect on firm
j’s best-reply function. In stage II, CEOs simultaneously maximize expected profit with respect to output. Recall that when biased, CEO
i believes that
and, therefore, expects profit to be
. In this symmetric game, firm
i’s first-order condition of profit maximization is
. Firm
i’s best-reply function (
BRi) is:
Notice that there are no direct effects in this model, as
does not depend on
. In terms of
, firm
i’s best-reply function can be written as
8:
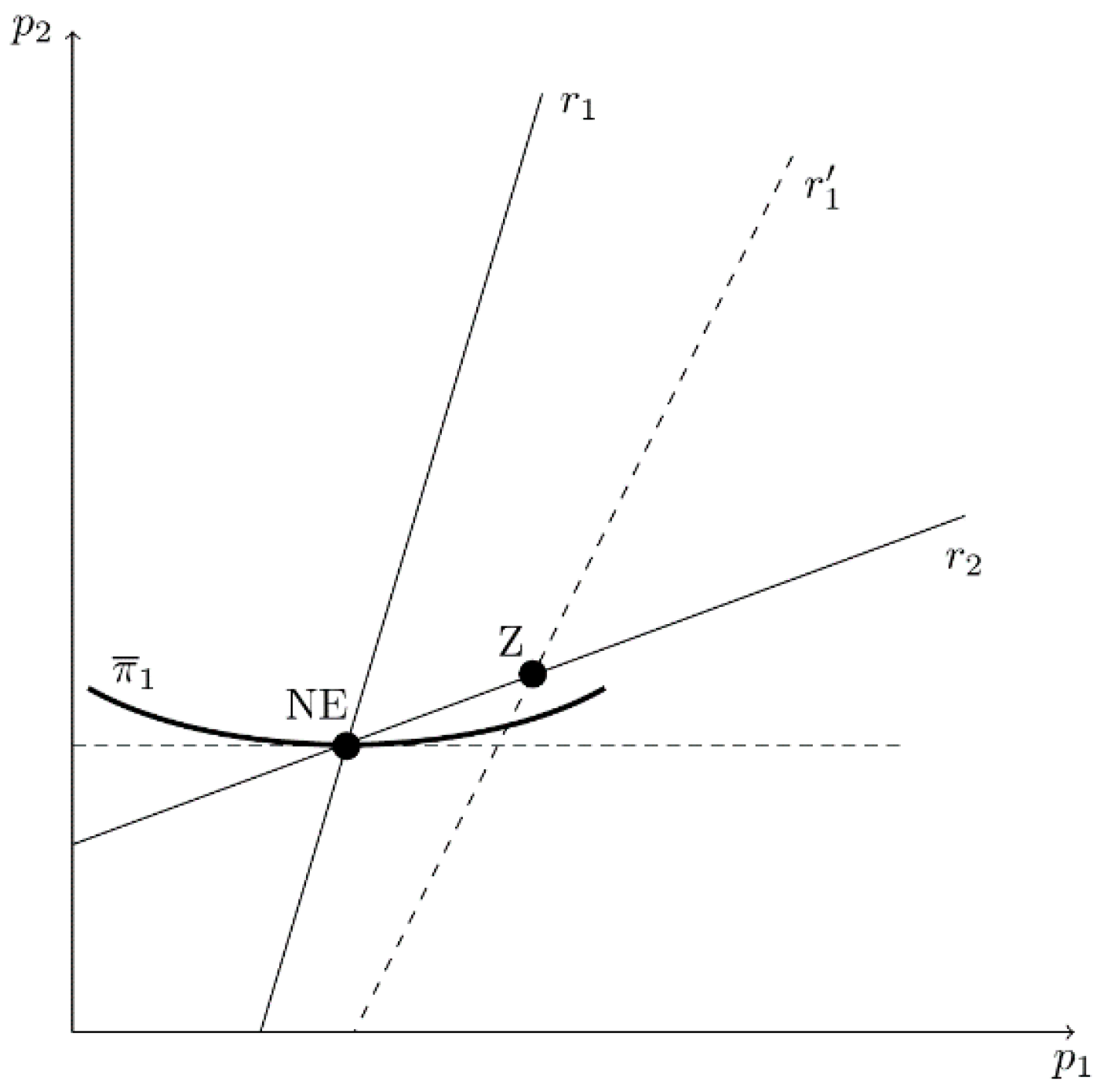
Figure 1 provides a graph of firm 1’s best-reply curve (
r1), with
on the horizontal axis and
on the vertical axis. Note that the
-intercept equals the simple monopoly output level,
, which is optimal when
. Furthermore, if the CEO of firm 1, CEO
1, underestimates the degree of product substitutability to a greater extent (i.e.,
decreases),
r1 becomes steeper and rotates around the
-intercept (from
r1 to
in
Figure 1). That is, firm 1 is willing to produce more output for a given
. In stage II, the Nash equilibrium (
NE) level of output is:
In stage I, owners simultaneously choose
to maximize true profit, given the anticipated output choices of CEOs in stage II, which are identified as
and
. Thus, owner
i anticipates profit to be:
Firm
i’s first-order condition of profit maximization is:
In this model, when evaluated at the simple Nash equilibrium where . Thus, the optimal value of is less than 1 (i.e., each owner has an incentive to hire a CEO who underestimates ).
The intuition behind this result can be seen from the following Figures.
Figure 2 identifies each firm’s best-reply curve, labeled
and
, and the simple Cournot (
NE) outcome when there is no bias (
). Firm
i’s iso-profit curve (
) is concave to its own (
) axis, and an iso-profit curve that is closer to the firm’s own axis signifies higher profit. By definition of a best-reply function, at
NE the slope of the tangent line to firm 1’s iso-profit curve is horizontal and the slope of the tangent to firm 2’s iso-profit curve is vertical. A marginal decrease in
(underestimation of product substitutability) causes firm 1’s best reply to become steeper. As illustrated in
Figure 3,
rotates away from the origin and moves the equilibrium down firm 2’s best-reply curve toward point
Z, the Stackelberg-type equilibrium. By underestimating the degree of substitutability between products, firm 2’s optimal output level increases
9. This enables Firm 1 to reach a lower iso-profit curve,
, representing higher profit. In other words, in this strategic setting, a marginal decrease in
induces firm 2 to produce less output, which benefits firm 1. The same incentive applies to firm 2. Therefore, each owner has an incentive to hire a CEO who underestimates strategic effects. This is consistent with Part A of Proposition 1, because a change in
has no effect on firm
j’s best-reply curve.
When both owners simultaneously optimize over
,
SPNE values are listed in
Table 1. It shows that it is optimal for owners to hire CEOs who underestimate strategic effects (
. The table also includes the simple Cournot, cartel, and competitive outcomes in the absence of bias
10. Note that the
SPNE price is lower than the cartel and simple Cournot prices but exceeds the competitive price.
Figure 4 provides a graphical depiction of the
SPNE, where
NE identifies the simple Cournot outcome. When owners have the option of hiring biased CEOs in stage I, each owner chooses
to maximize profit given the best reply of its competitor. Each firm hires a CEO who underestimates strategic effects, which rotates each firm’s best-reply function away from the origin. The
SPNE is reached when these conditions simultaneously hold for both owners, which occurs when firm
i’s iso-profit curve is tangent to firm
j’s best-reply curve at
SPNE in
Figure 4. The reduction in
below 1 leads to greater production and lower profits for both firms. Thus, the
SPNE is superior to the simple Cournot and cartel outcomes from society’s perspective.
The intuition of Part B of Proposition 1 is apparent for a non-linear example where a change in
causes both
r1 and
r2 to shift. Suppose that an increase in
causes both
r1 and
r2 to rotate toward the origin, as illustrated in
Figure 5. This means that the overestimation of product substitutability by CEO
1 causes firm 2 to behave less aggressively (i.e., firm 2 produces less output for a given
). If this causes the new equilibrium point
Z to lie below
as illustrated in
Figure 5, then
and it would benefit the owner of firm 1 to hire a CEO who overestimates product substitutability (
. Alternatively, if point
Z is on
, then it would pay the owner to hire an unbiased CEO (
. Finally, if point
Z is above
, then it would pay the owner to hire a CEO who underestimates product substitutability (
. A similar argument applies to firm 2, making it clear that the sign of the estimation bias is indeterminate.
2.2. Strategic Bias in a Bertrand Game
We use the same approach to investigate the Bertrand-type game. In this model, demand and profit equations depend on choice variables, and . Firm i’s true profit function is . CEOi’s price decision is based on expected profit, , which depends on the degree of CEO bias.
To analyze an owner’s decision to hire a biased CEO, we use backwards induction to identify the characteristics of the SPNE. In stage II, the Nash equilibrium prices are and . In stage I, firm i’s profit depends upon first-stage choices, and , and the anticipated actions in the second period, such that . In this model, the results are:
Proposition 2. Consider this two-stage game with Bertrand competition in stage II and where both firms have the option of hiring a biased CEO [, ] in stage I.
- A.
If a change in has no direct effect on
in the neighborhood of the simple Bertrand outcome where , then both firms hire CEOs who underestimate the degree of product substitutability ().
- B.
If a change in directly affects by shifting firm j’s best-reply function, then the sign of CEO estimation bias is indeterminate.
Proof. When
corresponds to price, Equation (1) becomes:
With profit maximization,
; therefore, the first set of terms on the right-hand side of the equality equals 0. Given that products are substitutes,
. Because firm
j’s best-reply function has a positive slope with Bertrand competition,
.
Given that the underestimation of the degree of product substitutability induces CEO
i to raise the price,
in the neighborhood of the simple Bertrand outcome where
. As a result,
and both firms hire CEOs who underestimate the degree of product substitutability (
).
In this case, the sign of
is indeterminant without knowing the sign and relative magnitude of the direct effect
. □
To illustrate, we continue to use the linear model described above. As in the Cournot case, it provides an example that is consistent with Part A of Proposition 2, because a change in
has no effect on firm
j’s best-reply function. Firms face the same inverse demand system as before. In the Bertrand game, demand functions are obtained by inverting the inverse demand functions, Equations (2) and (3), for
and
. The true demand functions are:
With the potential for bias, which occurs when CEO
i believes that
, CEOs expect demand functions to be:
Solving the stage II problem first, CEOs simultaneously maximize expected profit with respect to price, where CEO
i expects profit to be
. Given symmetry and the first-order condition of profit maximization, the best-reply function for firm
i in terms of
is:
Figure 6 provides a graph of firm 1’s best-reply function, with
on the horizontal axis and
on the vertical axis. In the Bertrand case, the best-reply function has a positive slope and
r1 does not depend on the value of
. As
decreases (i.e., CEO
1 underestimates product substitutability),
r1 becomes flatter and the
-intercept increases. In the stage II subgame, firm
i’s
NE price is:
Figure 7 depicts best-reply curves and the simple Nash (Bertrand) equilibrium assuming no estimation bias (
). In this case, each firm’s iso-profit curve is convex to its own axis and exhibits greater profit for iso-profit curves that are further from its own axis.
In stage I, owners simultaneously choose
to maximize true profit, given the anticipated equilibrium prices in stage II,
and
. Thus, owner
i anticipates profit to be:
The first-order condition of profit maximization is:
As in the Cournot case, when evaluated at the simple Bertrand equilibrium where . Thus, the optimal value of is less than 1.
When the owners of both firms consider hiring biased CEOs,
SPNE values are listed in
Table 2. It demonstrates that it is optimal for owners to hire CEOs who underestimate product substitutability (
. The table also includes the simple Bertrand (
NE) outcome. (The simple cartel and competitive outcomes are the same as in
Table 1.) In this model, the
SPNE price exceeds the simple Bertrand price but falls short of the cartel price.
Figure 8 provides intuition for this result. It shows the best-reply curves (
and
), firm 1’s iso-profit curve, and the simple Bertrand equilibrium (
NE). A marginal decrease in
causes firm 1’s best reply to shift right from
to
. In this case, CEO
1 believes that products 1 and 2 are less substitutable than is actually true, causing the firm’s optimal price to be greater for a given
. By underestimating product substitutability, price competition is reduced and firm 1 earns greater profit as the equilibrium moves to a point such as
Z11. In other words, a marginal decrease in
induces firm 2 to charge a higher price, which benefits firm 1. The same argument applies to firm 2. Thus, each owner has an incentive to hire a CEO who underestimates product substitutability, a result that is consistent with Part A of Proposition 2.
Figure 9 identifies the
NE without bias and the
SPNE. With the potential for bias, each owner chooses
to maximize profit given the best reply of its competitor. As described in
Figure 9, the
SPNE is reached when each owner hires a CEO who underestimates product substitutability to the point where firm
i’s iso-profit curve is tangent to firm
j’s best-reply curve. In this two-stage game, each firm’s optimal
is less than 1, a bias that leads to higher prices and profits for both firms (i.e., each firm’s iso-profit curve is further away from its own axis).
Figure 10 provides intuition for Part B of Proposition 2. In this example, a change in
causes both
r1 and
r2 to shift. If an increase in
causes both
and
to shift up so that the new equilibrium point
Z lies below
, then
and it would benefit the owner of firm 1 to hire a CEO who overestimates product substitutability (
. If point
Z is on
, then it would pay the owner to hire an unbiased CEO. Finally, if point
Z is above
, then it would pay the owner to hire a CEO who underestimates product substitutability. A similar argument applies to firm 2, making it clear that the sign of the estimation bias is indeterminate.
2.3. Strategic Bias in a Cournot–Bertrand Game
In this section, we assume Cournot–Bertrand competition in the product market. For concreteness, let firm 1 compete in output and firm 2 compete in price. With this mode of competition, demand and profit equations depend upon choice variables, and . Firm i’s true profit is , while CEOi bases decisions on expected profit: . Given the strategic asymmetry between firms, firm 1’s best-reply function has a positive slope and firm 2’s best-reply function has a negative slope, even when firms face the same cost and inverse demand functions.
As in the previous models, backwards induction is used to obtain the
SPNE. In stage II, the Nash equilibrium values are
and
. In stage I, firm
i’s profit depends on first-stage choices,
and
, and the anticipated actions in the second period, such that
.
Figure 11 describes each firm’s best-reply curve and the simple Nash (Cournot–Bertrand) equilibrium, assuming no estimation bias (
).
Figure 11 also depicts firm 1’s iso-profit curve, which is convex to the
-axis, and firm 2’s iso-profit curve, which is concave to the
-axis. In this model, firm 1’s profit is greater for a higher iso-profit curve (i.e., the firm’s profit increases with
); firm 2’s profit is greater for an iso-profit curve that is further left (i.e., the firm’s profit increases as
decreases).
Given that firms optimize over different choice variables, the effect of estimation bias on profit may differ by firm. Thus, we first consider the effect of bias for each individual firm before investigating the case where both owners have the option of hiring biased CEOs. Regarding the Cournot-type firm (firm 1):
Proposition 3. Consider this two-stage game with Cournot–Bertrand competition in stage II and where only the Cournot-type firm has the option of hiring a biased CEO [, ] in stage I.
- A.
If a change in has no direct effect on
in the neighborhood of the simple Cournot–Bertrand outcome where , then firm 1 hires a CEO who overestimates the degree of product substitutability ().
- B.
If a change in directly affects by shifting firm 2’s best-reply function, then the sign of CEO1’s estimation bias is indeterminate.
Proof. When
corresponds to output for firm 1 and price for firm 2, Equation (1) becomes the following for firm 1:
With profit maximization,
; therefore, the first set of terms on the right-hand side of the equality equals 0. Given that products are substitutes,
. Because firm 2’s best-reply function has a negative slope in the Cournot–Bertrand model,
.
Given that the underestimation of the degree of product substitutability induces CEO
1 to increase output,
in the neighborhood of the simple Cournot–Bertrand outcome where
. As a result,
and firm 1 hires a CEO who overestimates the degree of product substitutability (
).
In this case, the sign of
is indeterminant without knowing the sign and relative magnitude of the direct effect
. □
The intuition behind Part A of Proposition 3 is evident from
Figure 11, where
NE assumes no bias. If a marginal increase in
, signifying an overestimation of product substitutability, causes
to shift left and has no effect of
, then firm 1’s profit rises as the equilibrium moves up
to a point that is above the iso-profit curve
12. Thus,
. Part B is relevant when the change
also causes
to shift. If the increase in
causes
to shift left (i.e., firm 2 behaves less aggressively by setting a lower price for a given level of
), then firm 1’s profit may increase, decrease, or remain the same depending on whether the new equilibrium is above, below, or on iso-profit curve
. In this case, the sign of
is indeterminate.
The following proposition considers the case where only the Bertrand-type firm (firm 2) can hire a biased CEO.
Proposition 4. Consider this two-stage game with Cournot–Bertrand competition in stage II and where only the Bertrand-type firm has the option of hiring a biased CEO [] in stage I.
- A.
If a change in has no direct effect on
in the neighborhood of the simple Cournot–Bertrand outcome where , then firm 2 hires a CEO who overestimates the degree of product substitutability ().
- B.
If a change in directly affects by shifting firm 1’s best-reply function, then the sign of CEO2’s estimation bias is indeterminate.
Proof. When
corresponds to output for firm 1 and to price for firm 2, Equation (1) becomes the following for firm 2:
With profit maximization,
and the first set of terms on the right-hand side of the equality equals 0. Given that products are substitutes,
. Because firm 1’s best-reply function has a positive slope in the Cournot–Bertrand model,
.
Given that the underestimation of the degree of product substitutability causes CEO
2 to increase the price,
in the neighborhood of the simple Cournot–Bertrand outcome where
. As a result,
and firm 2 hires a CEO who overestimates the degree of product substitutability (
).
In this case, the sign of
is indeterminant without knowing the sign and magnitude of the direct effect
. □
Part A of Proposition 4 is evident from
Figure 11 when
NE assumes no bias. If a marginal increase in
, signifying an overestimation of product substitutability, causes
to shift left and has no effect on
, then firm 2’s profit rises as the equilibrium moves down
to a point that is left of the iso-profit curve
13. Thus,
. Part B is relevant when the change
also causes
to shift. If the increase in
causes
to shift right (i.e., firm 1 behaves more aggressively by producing more output for a given
), then firm 2’s profit may increase, decrease, or remain the same depending on whether the new equilibrium is to the left of, to the right of, or on iso-profit curve
. In this case, the sign of
is indeterminate.
Finally, when the owners of both firms have the option of hiring a strategically biased CEOs in stage I, the resulting SPNE has the following characteristics.
Proposition 5. Consider this two-stage game with Cournot–Bertrand competition in stage II and where both firms have the option of hiring a biased CEO in stage I.
- A.
In the absence of direct effects in the neighborhood of the simple Cournot–Bertrand outcome where , both firms hire CEOs who overestimate the degree of product substitutability ().
- B.
When direct effects are present, the sign of CEO estimation bias is indeterminate.
The proof of Part A follows from Propositions 3 and 4
14. It is difficult to verify Part B directly, but we use the linear model of Dixit [
24] and Singh and Vives [
25] to prove it indirectly.
In this specification, the firm demand equations depend on choice variables and are derived by solving Equations (2) and (3) for
and
. The true demand equations are:
The resulting profit equations are:
In the presence of bias, which occurs when CEO
i believes that
, CEOs expect the demand equations to be
15:
The expected profit equations are:
We use backwards induction to obtain the SPNE. In stage II, CEOs simultaneously maximize expected profits with respect to their particular choice variable, for CEO1 and for CEO2.
Because the best-reply functions in stage II differ by firm, we examine them separately. Solving firm 1’s first-order condition for
yields its best-reply function:
Figure 12 graphs this function when
is on the horizontal axis and
is on the vertical axis. In this model,
has a positive slope. A decrease in
(i.e., CEO
1 underestimates product substitutability by a greater degree) causes
to become steeper and its
-intercept
16 to shift right (e.g., shifting
to
in
Figure 12). More importantly, unlike the linear specifications of the Cournot and Bertrand models, firm 1’s best reply depends on
as well as
. A decrease in
causes firm 1’s best reply to become steeper and the
-intercept to shift left, as is illustrated in
Figure 13. That is, an underestimation of the degree of product substitutability by CEO
2 causes firm 1 to behave less aggressively (i.e., firm 1 produces less output for a given
). We see that it is this influence of
on firm 1’s best-reply function that drives the result in Part B of Proposition 5.
Firm 2’s best-reply function in the stage II problem derives from its first-order condition and is described below.
Figure 14 illustrates firm 2’s best reply. It has a negative slope, and a decrease in
(i.e., the underestimation of strategic effects) causes
to shift to
. Firm 2’s best reply becomes flatter, while the
-intercept remains constant at the simple monopoly price (
). In the linear model, a change in
has no effect on
.
Solving the best-reply functions simultaneously for
and
yields Nash equilibrium values in stage II:
In stage I, owners simultaneously choose
to maximize true profit, given anticipated CEO choices in stage II,
and
. Thus, owners anticipate profits to be:
In this game, there are two
SPNE, identified as
SPNE-A and
SPNE-B17.
Table 3 lists equilibrium values for
SPNE-A and the simple Cournot–Bertrand outcome (
NE). (The simple cartel and competitive outcomes are the same as in
Table 1). Note that in this case, the parameter restrictions of the model [
and
] require that
. This means that there can only be a mild degree of product differentiation (i.e.,
is sufficiently close to
). At
SPNE-A,
: it is optimal for owners to hire CEOs who underestimate the degree of product substitutability. In the limit, however,
as
: it pays the owner of the Bertrand-type firm to hire an unbiased CEO
18. In addition, the presence of CEO bias reduces competition. For both firms,
SPNE-A prices exceed
NE prices but fall short of the cartel price.
Table 4 lists the optimal values for the equilibrium
SPNE-B. (The simple cartel and competitive outcomes can be found in
Table 1, and the simple Cournot–Bertrand outcome is the same as in
Table 3). In this equilibrium, whether it pays an owner to hire a biased CEO depends on the degree of product differentiation and whether the firm competes in output or price. At this equilibrium:
When , it is optimal for both owners to hire CEOs who underestimate the degree of product substitutability ().
When , it is optimal for the owner of the Cournot-type firm to hire an unbiased CEO and the owner of the Bertrand-type firm to hire a CEO who underestimates product substitutability ().
When (i.e., there is considerable product differentiation), it is optimal for the owner of firm 1 to hire a CEO who overestimates product substitutability and the owner of firm 2 to hire a CEO who underestimates product substitutability ().
When , ; when , ; when , .
Unlike in the Cournot and the Bertrand models, it is impossible to know the direction of bias in SPNE-B without additional information. This is consistent with Part B of Proposition 5, because a change in causes the best-reply curves of both firms to shift. The fundamental prediction of the Cournot–Bertrand case is that an owner is likely to hire a CEO who overestimates strategic effects when the firm competes in output and there is a substantial degree of product differentiation.
Figure 15 provides an illustration when
and
.
NE identifies the simple Cournot–Bertrand equilibrium in the absence of bias (
). When owners have the option of hiring biased CEOs in stage I, each owner chooses
to maximize profit given the best reply of its competitor. The
SPNE is reached when this simultaneously holds for each owner and occurs where firm
i’s iso-profit curve is tangent to firm
j’s best-reply curve at
SPNE. Identifying the
SPNE relative to
NE is difficult because
shifts with changes in both
and
. That is, the increase in
causes
to become flatter and the
-intercept to decrease. The decrease in
causes
to become steeper and the
-intercept to decrease
19. Thus, the resulting shift in
is indeterminate.
Figure 15 provides an example where overestimation of product substitutability by CEO
1 and underestimation of product substitutability by CEO
2 lead to a decrease in
and an increase in
. Thus, competition is diminished, and each firm earns greater profit
20.