Evolution of “Pay-It-Forward” in the Presence of the Temptation to Free-Ride
Abstract
1. Introduction
2. Brief Literature Review
3. Model
3.1. Game
3.2. Game, Strategies and Payoff Matrix
3.3. Payoff Matrix
3.4. Strategy Switching
3.5. Probability Distribution on and Expected Payoff
3.5.1. Linear Expected Utility Theory
3.5.2. Prospect Theory
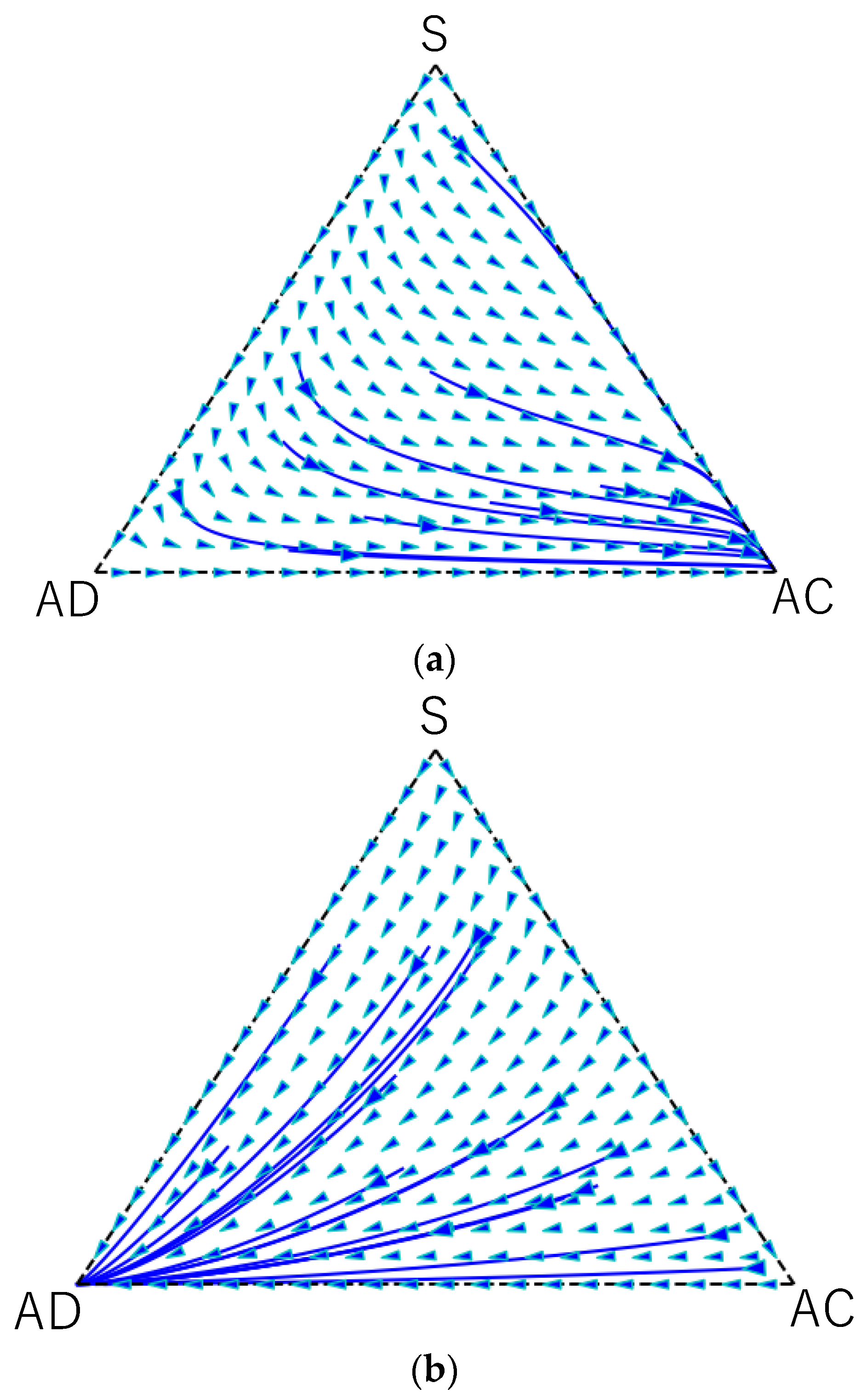
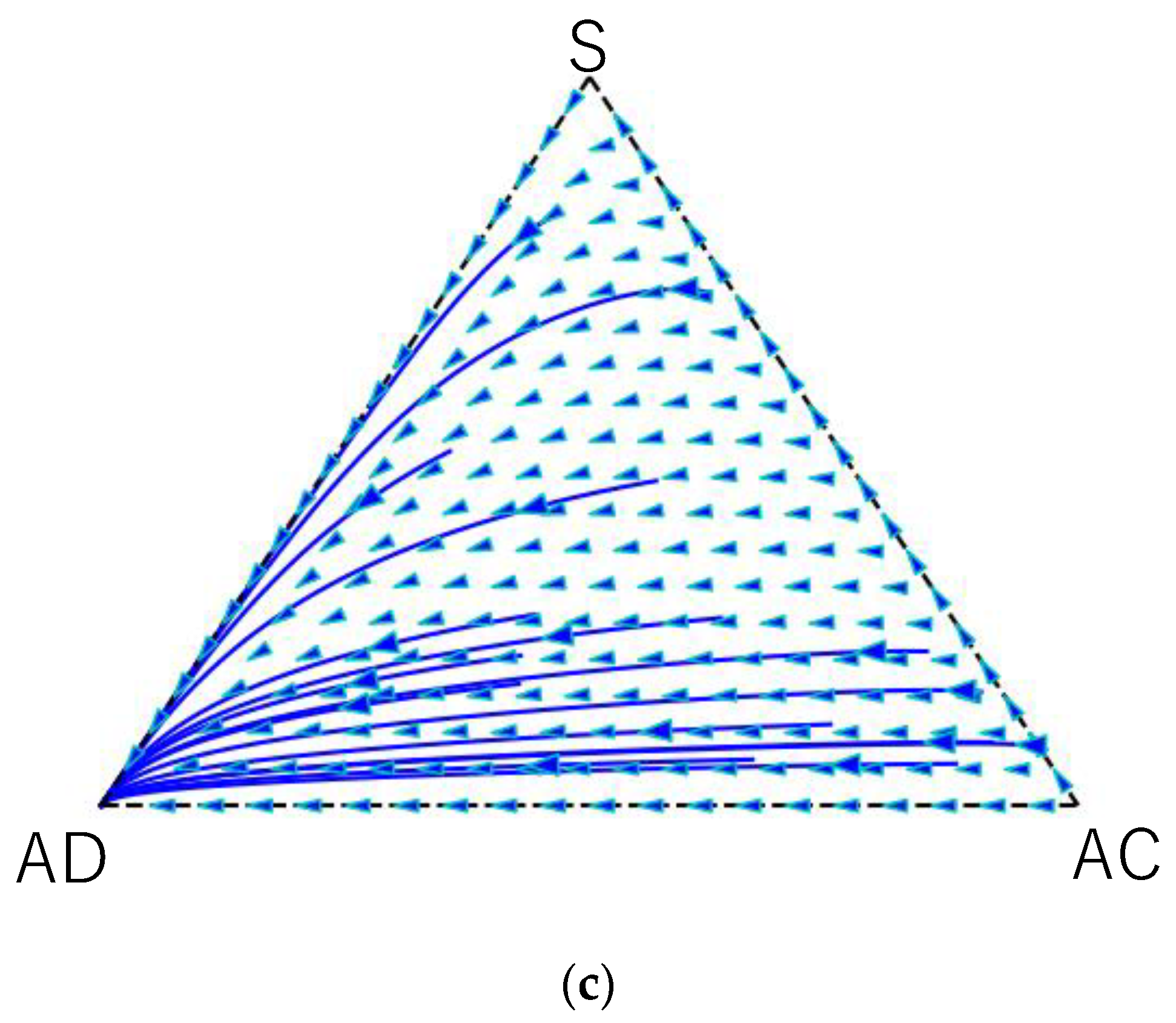
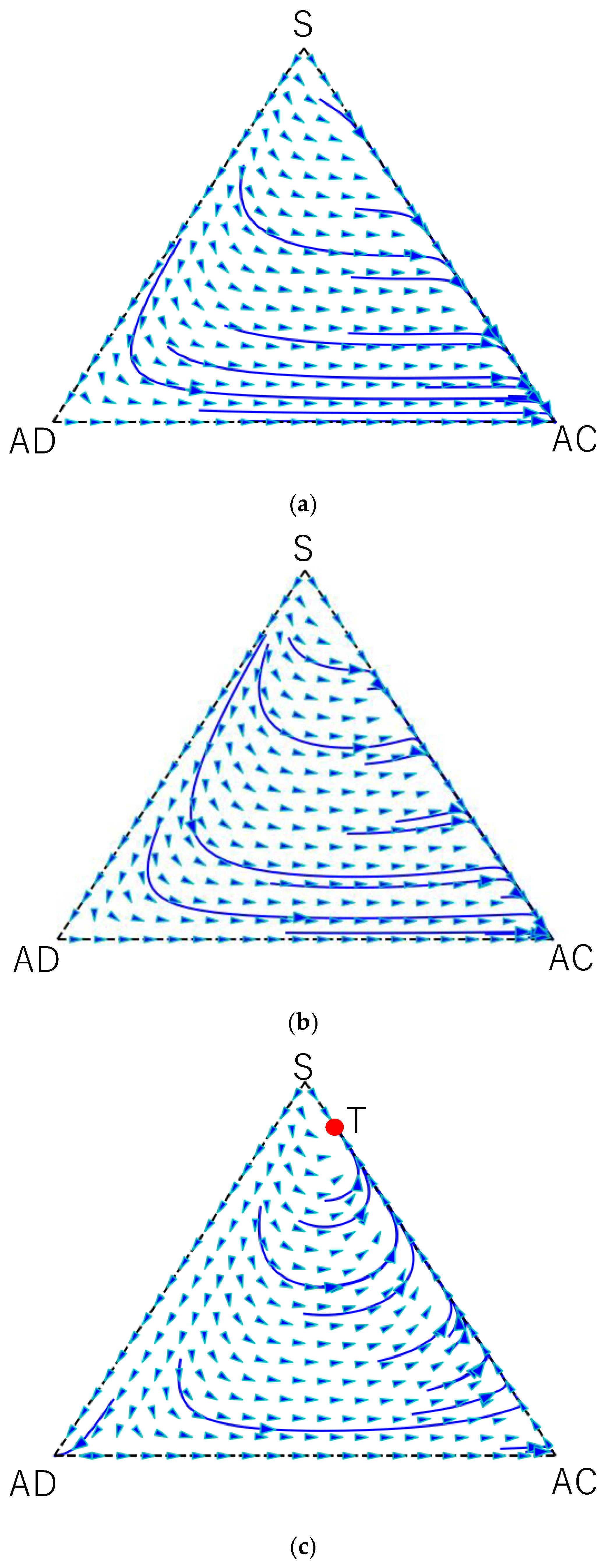
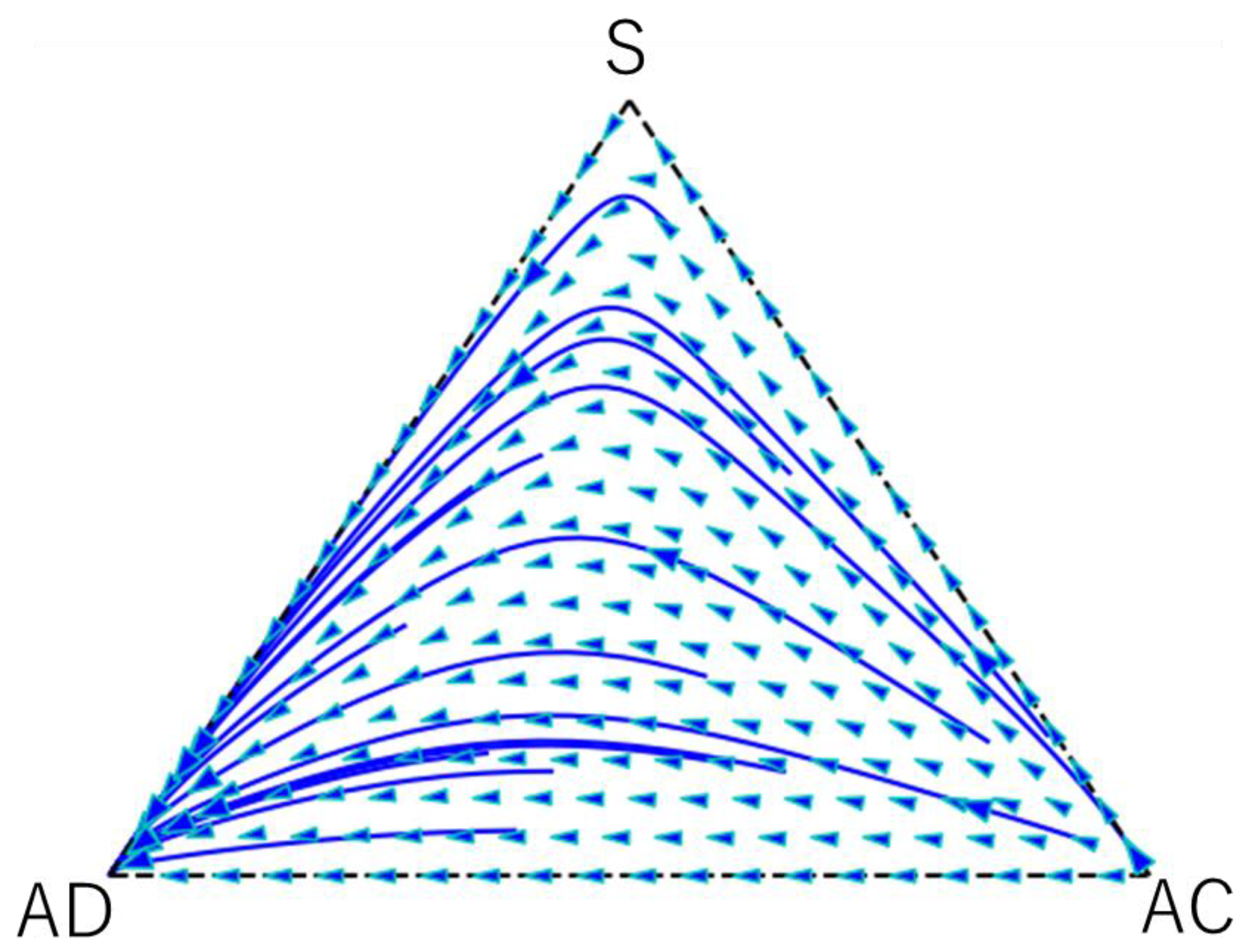
4. Results
4.1. Analysis in Case of EUT
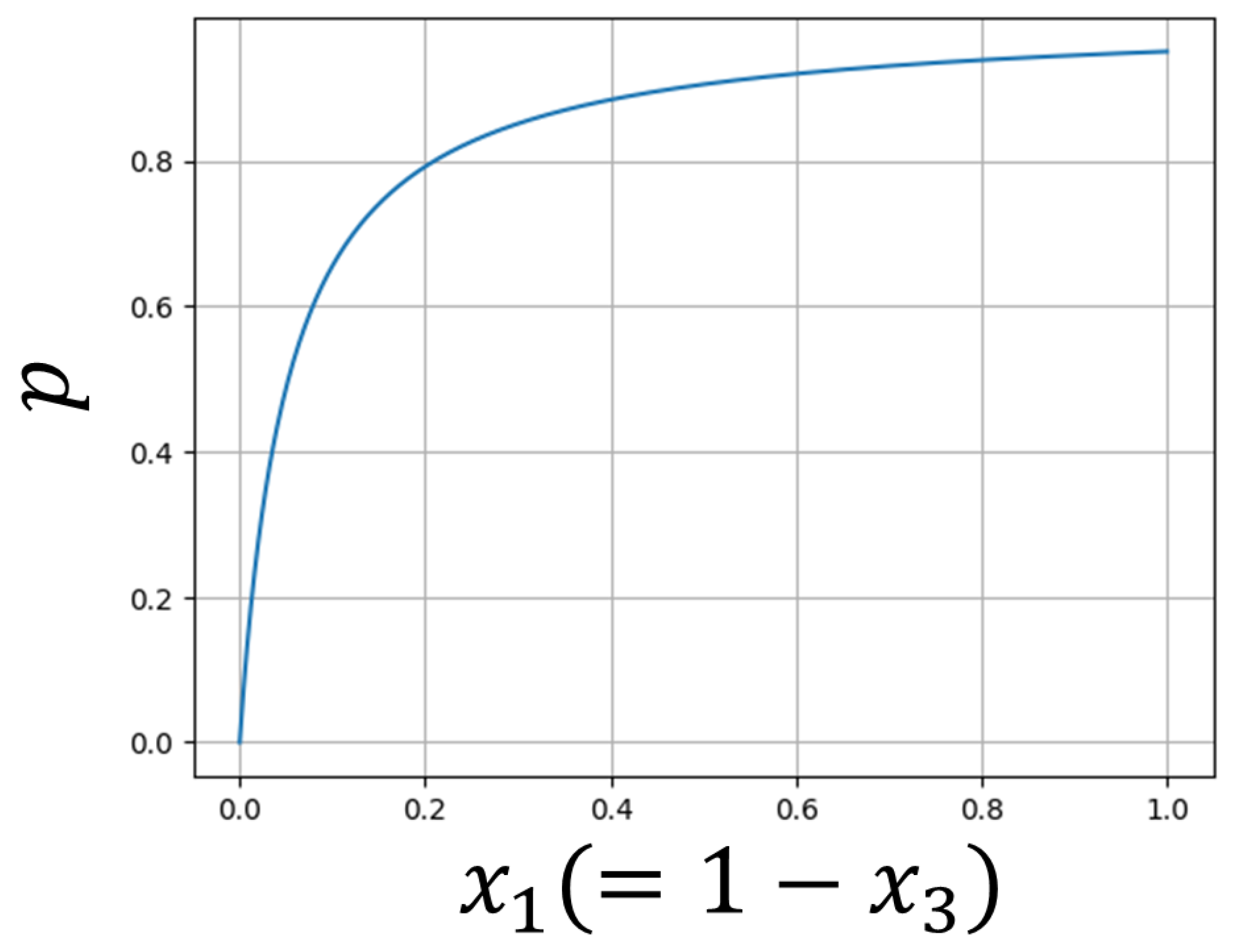
4.2. Numerical Results in Case of PT
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Fowler, J.H.; Christakis, N.A. Cooperative behavior cascades in human social networks. Proc. Natl. Acad. Sci. USA 2010, 107, 5334–5338. [Google Scholar] [CrossRef]
- Pressman, S.D.; Kraft, T.L.; Cross, M.P. It’s good to do good and receive good: The impact of a “pay it forward” style kindness intervention on giver and receiver well-being. J. Posit. Psychol. 2015, 10, 293–302. [Google Scholar] [CrossRef]
- Nowak, M.A.; Roch, S. Upstream reciprocity and the evolution of gratitude. Proc. R. Soc. B 2007, 274, 605–610. [Google Scholar] [CrossRef]
- Ostrom, E. Governing the Commons: The Evolution of Institutions for Collective Action; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, UK; Oxford, UK, 2010. [Google Scholar]
- Nowak, M.A.; Highfield, R. Super Cooperators; Free Press: New York, NY, USA, 2011. [Google Scholar]
- Bowls, S.; Gintis, H. A Cooperative Species; Princeton University Press: Princeton, UK; Oxford, UK, 2011. [Google Scholar]
- Yamagishi, T. Trust: The Evolutionary Game of Mind and Society; Springer: New York, NY, USA, 2011. [Google Scholar]
- Perc, M.; Jordan, J.J.; Rand, D.G.; Wang, Z.; Boccaletti, S.; Szolnoki, A. Statistical physics of human cooperation. Phys. Rep. 2017, 68, 1–51. [Google Scholar] [CrossRef]
- Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. Evolution of Cooperation with Peer Punishment under Prospect Theory. Games 2019, 10, 11. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: Analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Loss aversion in riskless choice: A reference-dependent model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]
- Wakker, P.P. Prospect Theory: For Risk and Ambiguity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gilboa, I. Theory of Decision under Uncertainty; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gilboa, I. Making Better Decisions: Decision Theory in Practice; John Wiley and Sons: Tokyo, Japan, 2010. [Google Scholar]
- Tversky, A.; Kahneman, D. Judgement under uncertainty: Heuristics and biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef]
- Machina, M.J. Expected utility analysis without the independence axiom. Econometrica 1982, 50, 277–323. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Extensional vs. intuitive reasoning: The conjunction fallacy in probability judging. Psychol. Rev. 1983, 90, 293–315. [Google Scholar] [CrossRef]
- Schmeidler, D. Subjective probability and expected utility without additivity. Econometrica 1989, 57, 571–587. [Google Scholar] [CrossRef]
- Gilboa, I.; Schmeidler, D. Maxmin expected utility with a non-unique prior. J. Math. Econ. 1989, 18, 141–153. [Google Scholar] [CrossRef]
- Starmer, C. Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. J. Econ. Lit. 2000, 38, 332–382. [Google Scholar] [CrossRef]
- Yang, G.; Chen, J. Research on Enterprise Radical Technology Innovation Behavior—Evolutionary Game Analysis Based on Prospect Theory. J. Ind. Technol. Econ. 2020, 39, 57–64. [Google Scholar]
- Sun, H.; Gao, G.; Li, Z. Evolutionary Game Analysis of Enterprise Carbon Emission Regulation Based on Prospect Theory. Soft Comput. 2022, 26, 13357–13368. [Google Scholar] [CrossRef]
- Shen, J.; Gao, X.; He, W.; Sun, F.; Zhang, Z.; Kong, Y.; Wan, Z.; Zhang, X.; Li, Z.; Wang, J.; et al. Prospect Theory in an Evolutionary Game: Construction of Watershed Ecological Compensation System in Taihu Lake Basin. J. Clean. Prod. 2021, 291, 125929. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J. Evolutionary Game Analysis of Low-Carbon Incentive Behaviour of Power Battery Recycling Based on Prospect Theory. Sustainability 2024, 16, 2793. [Google Scholar] [CrossRef]
- Sigmund, K. Games of Life; Dover Publications: Mineora, NY, USA, 2017. [Google Scholar]
- Ferreira, P.L.; Santos, F.C.; Pequito, S. Risk sensitivity and theory of mind in human coordination. PLoS Comput. Biol. 2021, 17, e1009167. [Google Scholar] [CrossRef]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1292–1298. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. The dynamics of indirect reciprocity. J. Theor. Biol. 1998, 194, 561–574. [Google Scholar] [CrossRef]
- Leimar, O.; Hammerstein, P. Evolution of cooperation through indirect reciprocity. Proc. R. Soc. B 2001, 268, 745–753. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. How should we define goodness?—Reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004, 231, 107–120. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006, 239, 435–444. [Google Scholar] [CrossRef]
- Sasaki, T.; Okada, I.; Nakai, Y. The evolution of conditional moral assessment in indirect reciprocity. Sci. Rep. 2017, 7, 41870. [Google Scholar] [CrossRef]
- Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. A theoretical approach to norm ecosystems: Two adaptive architectures of indirect reciprocity show different paths to the evolution of cooperation. Front. Phys. 2018, 6, 14. [Google Scholar] [CrossRef]
- Yamamoto, H.; Okada, I.; Uchida, S.; Sasaki, T. Exploring norms indispensable for both emergence and maintenance of cooperation in indirect reciprocity. Front. Phys. 2022, 10, 1019422. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Ohtsuki, H. Evolutionary stability of cooperation in indirect reciprocity under noisy and private assessment. Proc. Natl. Acad. Sci. USA 2023, 120, e2300544120. [Google Scholar] [CrossRef]
- Iwagami, A.; Masuda, N. Upstream reciprocity in heterogeneous networks. J. Theor. Biol. 2010, 265, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, T.; Rutte, C.; Killingback, T.; Taborsky, M.; Bonhoeffer, S. Evolution of cooperation by generalized reciprocity. Proc. R. Soc. B 2005, 272, 1115–1120. [Google Scholar] [CrossRef] [PubMed]
- Okada, I. A review of theoretical studies on indirect reciprocity. Games 2020, 11, 27. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J. Theor. Biol. 2007, 244, 518–531. [Google Scholar] [CrossRef]
- Uchida, S.; Sigmund, K. The competition of assessment rules for indirect reciprocity. J. Theor. Biol. 2010, 263, 13–19. [Google Scholar] [CrossRef]
- Murase, Y.; Kim, M.; Baek, S.K. Social norms in indirect reciprocity with ternary reputations. Sci. Rep. 2022, 12, 455. [Google Scholar] [CrossRef]
- Yamagishi, T. The provision of a sanctioning system as a public good. J. Personal. Soc. Psychol. 1986, 51, 110–116. [Google Scholar] [CrossRef]
- Boyd, R.; Richerson, P.J. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethol. Sociobiol. 1992, 13, 171–195. [Google Scholar] [CrossRef]
- Milinski, M.; Rockenbach, B. Human behaviour: Punisher pays. Nature 2008, 452, 297–298. [Google Scholar] [CrossRef]
- Casari, M.; Luini, L. Cooperation under alternative punishment institutions: An experiment. J. Econ. Behav. Organ. 2009, 71, 273–282. [Google Scholar] [CrossRef]
- Kosfeld, M.; Okada, A.; Riedl, A. Institution formation in public goods games. Am. Econ. Rev. 2009, 99, 1335–1355. [Google Scholar] [CrossRef]
- Sigmund, K.; de Silva, H.; Traulsen, A.; Hauert, C. Social learning promotes institutions for governing the commons. Nature 2010, 466, 861–863. [Google Scholar] [CrossRef]
- Traulsen, A.; Röhl, T.; Milinski, M. An economic experiment reveals that humans prefer pool punishment to maintain the commons. Proc. Biol. Sci. 2012, 279, 3716–3721. [Google Scholar] [CrossRef]
| Player B’s Option Player A’s Option | Cooperate (C) | Defect (D) |
|---|---|---|
| Cooperate (C) | b − c | −c |
| Defect (D) | b | 0 |
| Outcome Player A’s Option | Cooperate Not-Punish (CN) | Cooperate Punish (CP) | Defect Not-Punish (DN) | Defect Punish (DP) |
|---|---|---|---|---|
| Cooperate (C) | 0 | 0 | ||
| Defect (D) | 0 |
| (a) | ||||
| Outcome Player A’s option | Cooperate Not-Punish (CN) | Cooperate Punish (CP) | Defect Not-Punish (DN) | Defect Punish (DP) |
| Cooperate (C) | ||||
| Defect (D) | ||||
| (b) | ||||
| Outcome Player A’s option | Cooperate Not-Punish (CN) | Cooperate Punish (CP) | Defect Not-Punish (DN) | Defect Punish (DP) |
| Cooperate (C) | 0 | 0 | 0 | 0 |
| Defect (D) | ||||
| (c) | ||||
| Outcome Player A’s option | Cooperate Not-Punish (CN) | Cooperate Punish (CP) | Defect Not-Punish (DN) | Defect Punish (DP) |
| Cooperate (C) | ||||
| Defect (D) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uchida, S.; Sasaki, T.; Yamamoto, H.; Okada, I. Evolution of “Pay-It-Forward” in the Presence of the Temptation to Free-Ride. Games 2024, 15, 16. https://doi.org/10.3390/g15030016
Uchida S, Sasaki T, Yamamoto H, Okada I. Evolution of “Pay-It-Forward” in the Presence of the Temptation to Free-Ride. Games. 2024; 15(3):16. https://doi.org/10.3390/g15030016
Chicago/Turabian StyleUchida, Satoshi, Tatsuya Sasaki, Hitoshi Yamamoto, and Isamu Okada. 2024. "Evolution of “Pay-It-Forward” in the Presence of the Temptation to Free-Ride" Games 15, no. 3: 16. https://doi.org/10.3390/g15030016
APA StyleUchida, S., Sasaki, T., Yamamoto, H., & Okada, I. (2024). Evolution of “Pay-It-Forward” in the Presence of the Temptation to Free-Ride. Games, 15(3), 16. https://doi.org/10.3390/g15030016









