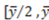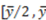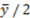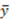Modeling Inequity Aversion in a Dictator Game with Production
Abstract
:1. Introduction
2. Results and Discussion
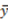 ≥ 0 between herself and her counterpart. The size of this surplus depends on both the subjects' monetary contributions, which are denoted by yi≥ 0 for iϵ{d,r}, in particular,
≥ 0 between herself and her counterpart. The size of this surplus depends on both the subjects' monetary contributions, which are denoted by yi≥ 0 for iϵ{d,r}, in particular,

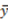 , where xi≥ 0 denotes the monetary payoff that subject i will receive, for i ϵ{d,r}. The model of inequality aversion of Fehr and Schmidt [1] builds on the assumption that the dictator dislikes unequal outcomes (see Nielsen [26]). More specifically, the authors posit the following utility function for the dictator:
, where xi≥ 0 denotes the monetary payoff that subject i will receive, for i ϵ{d,r}. The model of inequality aversion of Fehr and Schmidt [1] builds on the assumption that the dictator dislikes unequal outcomes (see Nielsen [26]). More specifically, the authors posit the following utility function for the dictator:
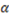 and β, which are assumed to satisfy
and β, which are assumed to satisfy 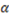 > β ≥ 0 and β ≤1. This implies that the dictator cares more for inequality when she has less than half of the surplus than the dictator does when she has more.
> β ≥ 0 and β ≤1. This implies that the dictator cares more for inequality when she has less than half of the surplus than the dictator does when she has more. 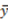 - xd , equation (2) can be rewritten as follows:
- xd , equation (2) can be rewritten as follows:

 if
if  > 0.5. Otherwise, the dictator behaves selfishly,
> 0.5. Otherwise, the dictator behaves selfishly,  ).5
).5 
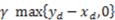 if she does not take her own production, whereas
if she does not take her own production, whereas  represents the cost of taking more than what she produces.6 The new parameters are assumed to satisfy γ ≥
represents the cost of taking more than what she produces.6 The new parameters are assumed to satisfy γ ≥  >0. The authors note that if
>0. The authors note that if 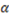 and β are both zero, then just deserts affect the dictator's choice when γ >1 or ψ>1. If
and β are both zero, then just deserts affect the dictator's choice when γ >1 or ψ>1. If 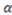 $ and β are not zero, two different contexts are at stake: when the dictator accumulates less money than the recipient (
$ and β are not zero, two different contexts are at stake: when the dictator accumulates less money than the recipient ( 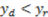 ), and when the dictator accumulates more (
), and when the dictator accumulates more ( 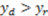 ). In either case, when 2β + ψ <1, the dictator behaves selfishly and keeps the entire surplus,
). In either case, when 2β + ψ <1, the dictator behaves selfishly and keeps the entire surplus,  ). If the dictator accumulates less money than the recipient and 2β + ψ > 1, the model predicts that the dictator will either keep half of the surplus or her own production, depending on whether ψ – 1 > 2
). If the dictator accumulates less money than the recipient and 2β + ψ > 1, the model predicts that the dictator will either keep half of the surplus or her own production, depending on whether ψ – 1 > 2 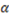 or ψ – 1 < 2
or ψ – 1 < 2 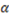 . Both the egalitarian allocation,
. Both the egalitarian allocation,  and the libertarian allocation
and the libertarian allocation 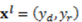 can also be predicted if the dictator accumulates more money than the recipient.
can also be predicted if the dictator accumulates more money than the recipient.  . Arguably, the prediction of this model contrasts with liberal egalitarian ethics, which states that subjects should only be rewarded for factors under their control. In that vein, the accountability principle as first proposed by Konow [13] states that the dictator will choose a division that gives to each subject the amount of money that is generated by her input. We denote this amount predicted by the accountability principle as
. Arguably, the prediction of this model contrasts with liberal egalitarian ethics, which states that subjects should only be rewarded for factors under their control. In that vein, the accountability principle as first proposed by Konow [13] states that the dictator will choose a division that gives to each subject the amount of money that is generated by her input. We denote this amount predicted by the accountability principle as 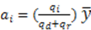 for iϵ{d,r}, so that if the dictator ignores those factors beyond the subjects’ control, she will choose the allocation
for iϵ{d,r}, so that if the dictator ignores those factors beyond the subjects’ control, she will choose the allocation 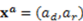 . We propose to model the dictator's utility function as follows:
. We propose to model the dictator's utility function as follows:

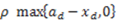 if she free-rides on the recipient's effort, but she also suffers a cost
if she free-rides on the recipient's effort, but she also suffers a cost  if she takes less money than what corresponds to her input, where ρ ≥
if she takes less money than what corresponds to her input, where ρ ≥  > 0 is assumed to be satisfied (i.e., the dictator cares less about the recipient’s disadvantage than about her own).
> 0 is assumed to be satisfied (i.e., the dictator cares less about the recipient’s disadvantage than about her own). 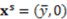 (ii) choose the egalitarian allocation and divide the surplus in two identical parts
(ii) choose the egalitarian allocation and divide the surplus in two identical parts  , (iii) choose the libertarian allocation that is based on subjects' production
, (iii) choose the libertarian allocation that is based on subjects' production 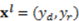 or (iv) behave according to the accountability principle that is based solely on factors under the subjects’ control
or (iv) behave according to the accountability principle that is based solely on factors under the subjects’ control 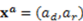 .7 We summarize our results in Table 1. As we argue, the dictator's choice depends on the relationship between factors within and beyond the subjects’ control, which determines the relationship between
.7 We summarize our results in Table 1. As we argue, the dictator's choice depends on the relationship between factors within and beyond the subjects’ control, which determines the relationship between  ,
, 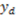 and
and 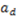 , as well as the values of the parameters.
, as well as the values of the parameters.  ) so that the dictator's production in terms of money
) so that the dictator's production in terms of money 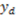 would be greater than her production in terms of inputs
would be greater than her production in terms of inputs 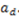 The values of qi ≥ 0 and pi > 0 determine in this framework whether these contributions (
The values of qi ≥ 0 and pi > 0 determine in this framework whether these contributions ( 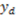 and
and 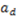 ) are above half of the surplus (
) are above half of the surplus (  ) or not. Assume that
) or not. Assume that 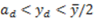 is satisfied. It is clear that the dictator gets the highest monetary payoff by choosing the egalitarian allocation
is satisfied. It is clear that the dictator gets the highest monetary payoff by choosing the egalitarian allocation 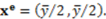 The dictator will choose this division of the surplus as long as the cost of deviating from the accountability principle (that yields the smallest payoff) is small enough. More precisely,
The dictator will choose this division of the surplus as long as the cost of deviating from the accountability principle (that yields the smallest payoff) is small enough. More precisely, 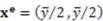 will be chosen if ω < 1 + 2
will be chosen if ω < 1 + 2 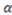 – ψ. If the cost is very high and the condition ω > 1 + 2
– ψ. If the cost is very high and the condition ω > 1 + 2 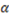 + γ holds, the dictator will choose to divide the surplus according to the accountability principle
+ γ holds, the dictator will choose to divide the surplus according to the accountability principle 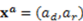 that yields the dictator the smallest monetary payoff. If
that yields the dictator the smallest monetary payoff. If 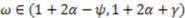 , then the libertarian allocation will be chosen because it would be very costly to divide the surplus according to the egalitarian allocation, but the cost is not sufficiently high to enforce the use of the accountability principle. We can follow this reasoning so as to explain the prediction of our model in Table 1. We observe that there always exists a tradeoff between a higher monetary payoff and the cost of deviating from the fairness ideal that yields the smallest payoff.
, then the libertarian allocation will be chosen because it would be very costly to divide the surplus according to the egalitarian allocation, but the cost is not sufficiently high to enforce the use of the accountability principle. We can follow this reasoning so as to explain the prediction of our model in Table 1. We observe that there always exists a tradeoff between a higher monetary payoff and the cost of deviating from the fairness ideal that yields the smallest payoff.  |
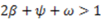 . Otherwise, the dictator behaves selfish,
. Otherwise, the dictator behaves selfish,  . We do not consider the possibility of
. We do not consider the possibility of 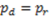 , because (by definition)
, because (by definition) 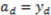 in that case our predictions would be identical to the ones in Frohlich et al. (2004).
in that case our predictions would be identical to the ones in Frohlich et al. (2004).3. Applications of our model
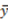 = 30 and the subjects’ contributions to the surplus is given by yd = yr =15. Since both subjects contribute the same (i.e., yd = yr =
= 30 and the subjects’ contributions to the surplus is given by yd = yr =15. Since both subjects contribute the same (i.e., yd = yr =  ), the models of Fehr and Schmidt [1] and Frohlich et al. [2] predict that the recipient will receive at most half of the surplus. It is worth noting, however, that the dictator might consider this allocation as unfair because the recipient has more questions correct at a lower reward level. Liberal egalitarian ethics states that the recipient ought to receive the part of the surplus that is due to her performance, which would compensate recipients for the lower reward. In our example,
), the models of Fehr and Schmidt [1] and Frohlich et al. [2] predict that the recipient will receive at most half of the surplus. It is worth noting, however, that the dictator might consider this allocation as unfair because the recipient has more questions correct at a lower reward level. Liberal egalitarian ethics states that the recipient ought to receive the part of the surplus that is due to her performance, which would compensate recipients for the lower reward. In our example, 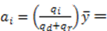 18. This amount represents 60-percent of the surplus. Importantly, our model is able to predict this allocation, although this behavior cannot be predicted by equations (3) or (4). In fact, the nonlinear versions of our model in the supplementary material can predict any dictator's giving xr in the interval [15,18], which are above the equal split allocation.
18. This amount represents 60-percent of the surplus. Importantly, our model is able to predict this allocation, although this behavior cannot be predicted by equations (3) or (4). In fact, the nonlinear versions of our model in the supplementary material can predict any dictator's giving xr in the interval [15,18], which are above the equal split allocation. 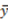 ). We use the vertical axis to represent the proportion of the surplus that the dictator gives away to the recipient (xr/
). We use the vertical axis to represent the proportion of the surplus that the dictator gives away to the recipient (xr/ 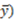 . As a consequence, the 45-degree line represents the appropriate theoretical prediction in Frohlich et al. [2], because observations on this line indicate that recipients are being transferred exactly the proportion of the surplus that they have contributed, i.e., the 45-degree line represents the libertarian allocation xr = yr. In Figure 1, we also plot the horizontal line (xr/
. As a consequence, the 45-degree line represents the appropriate theoretical prediction in Frohlich et al. [2], because observations on this line indicate that recipients are being transferred exactly the proportion of the surplus that they have contributed, i.e., the 45-degree line represents the libertarian allocation xr = yr. In Figure 1, we also plot the horizontal line (xr/ 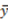 = 0.5), which represents the egalitarian allocation xr =
= 0.5), which represents the egalitarian allocation xr = 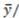 2 (Fehr and Schmid [1]). The dotted curve depicts the accountability principle xr=ar. Therefore, allocations on this curve indicate that recipients are being transferred exactly the proportion of the surplus that is due to their effort.9 The difference between pd and pr establishes the concavity of the dotted curve xr = ar and determines those allocations that cannot be predicted by Fehr and Schmidt [1] or Frohlich et al. [2]. In particular, the nonlinear version of these models predicts no allocations above both “just dessert” and the horizontal line xr =
2 (Fehr and Schmid [1]). The dotted curve depicts the accountability principle xr=ar. Therefore, allocations on this curve indicate that recipients are being transferred exactly the proportion of the surplus that is due to their effort.9 The difference between pd and pr establishes the concavity of the dotted curve xr = ar and determines those allocations that cannot be predicted by Fehr and Schmidt [1] or Frohlich et al. [2]. In particular, the nonlinear version of these models predicts no allocations above both “just dessert” and the horizontal line xr =  . Graphically, this implies that the models predict any giving in the shadowed area, except the striped area (i.e., the models predict xr ≤ max{
. Graphically, this implies that the models predict any giving in the shadowed area, except the striped area (i.e., the models predict xr ≤ max{  ,yr}). However, our model takes into account the accountability principle so that our prediction includes the striped area (i.e., our model predict xr ≤ max{
,yr}). However, our model takes into account the accountability principle so that our prediction includes the striped area (i.e., our model predict xr ≤ max{  ,yr,ar}).
,yr,ar}). 
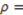
 = 0 is assumed).
= 0 is assumed).  ,yr}.10
,yr}.10 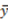 / 2, xr = ar and xr = yr. This feature of our model generalizes the idea that each dictator is motivated by a single fairness view (i.e., by a single “line”), with dictators being heterogeneous in what they consider as fair, and the marginal utility loss of deviating from this fairness ideal increasing in the size of the deviation. Our way of modeling social preference is also valid under the assumptions that fairness ideals are tradeoffs against each other, and heterogeneity lies inside each subject rather, than taking place across subjects. It remains to be discussed whether we should expect subjects to hold different fairness ideals at each time. Using a questionnaire, the seminal paper of Yaari [25] provides evidence that subjects choose different solutions for the same distribution problems, depending on the prevalence of tastes or needs in the story underlying each question (see also Messick and Sentis [23]). Recent experimental findings are also in line with the idea of within-subject heterogeneity (e.g., Croson and Konow [22], Konow [16], Ubeda [24], Blanco et al. [33] and Miller and Ubeda [10]). In their paper, Blanco et al. (2011) test the consistency of the Fehr and Schmidt's model and find that it fails to predict behavior at the individual level, as subjects exhibit different fairness attitudes across games (i.e., the estimation of and
/ 2, xr = ar and xr = yr. This feature of our model generalizes the idea that each dictator is motivated by a single fairness view (i.e., by a single “line”), with dictators being heterogeneous in what they consider as fair, and the marginal utility loss of deviating from this fairness ideal increasing in the size of the deviation. Our way of modeling social preference is also valid under the assumptions that fairness ideals are tradeoffs against each other, and heterogeneity lies inside each subject rather, than taking place across subjects. It remains to be discussed whether we should expect subjects to hold different fairness ideals at each time. Using a questionnaire, the seminal paper of Yaari [25] provides evidence that subjects choose different solutions for the same distribution problems, depending on the prevalence of tastes or needs in the story underlying each question (see also Messick and Sentis [23]). Recent experimental findings are also in line with the idea of within-subject heterogeneity (e.g., Croson and Konow [22], Konow [16], Ubeda [24], Blanco et al. [33] and Miller and Ubeda [10]). In their paper, Blanco et al. (2011) test the consistency of the Fehr and Schmidt's model and find that it fails to predict behavior at the individual level, as subjects exhibit different fairness attitudes across games (i.e., the estimation of and  and β for a given subject changes depending on the game). The work of Miller and Ubeda [10] focuses on a repeated dictator game with production and highlight that women are likely to switch between the three different fairness ideals presented in the current paper.
and β for a given subject changes depending on the game). The work of Miller and Ubeda [10] focuses on a repeated dictator game with production and highlight that women are likely to switch between the three different fairness ideals presented in the current paper. 4. Conclusion
Acknowledgments
- 1 Hereafter we focus our exposition on the dictator game with production, which has been an important device for studying social preferences and distributional justice. We note that the existence of the production stage is important to disentangle the effect of fairness concerns and property rights in the final outcome. As noted by Cherry et al. [6], if there is not a production stage, then dictators might give money away, because they are fair-minded, or simply because the surplus to be divided is "manna from heaven", and dictators do not feel any right to keep the entire surplus for themselves.
- 2 Frohlich et al. [2] use the concept of “just desert” to identify the division of the surplus that corresponds to the subjects’ production. We borrow the terminology in Cappelen et al. [5,14] and refer to this division as the libertarian allocation. Hereafter, we follow Cappelen et al. [5,14] in labeling the rest of the fairness ideals presented in the paper.
- 3 The approach in Cappelen et al. [5,14] relies on the assumption of between-subject heterogeneity; i.e., subjects differ with respect to their consideration of fairness ideals (see also Engel [4] or Visser [21] for evidence of between-subject heterogeneity). However, there exists experimental evidence suggesting the existence of within-subject heterogeneity; i.e., the same subject might choose different allocations (or fairness ideals) depending on the context (see, among others, in Croson and Konow [22], Konow [16], Messick and Sentis [23], Miller and Ubeda [10], Ubeda [24] or Yaari [25]).
- 4 We acknowledge that it might be hard to disentangle which variables are under the subjects’ control and which variables are outside their control in some situations. We find, however, that the classification of factors within and beyond individuals’ control is beyond the scope of this paper. For further discussion on this topic, the interested reader can see Fleurbaey and Maniquet [18]. Konow [27] is also an excellent overview of various theories of justice that deals with this feature.
- 5 For the special case in which β = 0.5, the dictator is indifferent between any share xdϵ
]. As Fehr and Schmidt [1] argue, the nonlinear versions of their model lead also to predictions x= (xd, xr) that satisfy xdϵ
] and xr =
- xd≥ 0. The models of Bolton and Ockenfelds [28] and Charness and Rabin [29] do also integrate equality as an argument. In particular, Bolton and Ockenfelds [28] show that the results of Fehr and Schmidt [1] are robust to non-linearity as well as incomplete information.
- 6 We note that we have rewritten the original equation in Frohlich et al. [2] so as to follow our reasoning in equation (3). In particular, because yd + yr = xd + xr, the latter term in equation (4) can also be thought of as the cost of not giving to the recipient her production.
- 7 Nonlinear versions of our model would predict interior results that lead to compromises between these fairness ideals. The interested reader can find a brief discussion about the linearity assumption in the supplementary material. We note that Bolton and Ockenfelds [28] is an extension of Fehr and Schmidt [1] to the non-linear case. The model of Bolton et al. [32] incorporates an idea that is related to the accountability principle in the context of procedural fairness; i.e., the authors use different games and investigate the extent to which subjects care about fair procedures.
- 8 The experimental design in Rodriguez-Lara and Moreno-Garrido [11] relies on this production stage. In Konow [7], subjects are differently rewarded for a real-effort task that involves stuffing letters into envelops. In Ubeda [24], the task consists of solving puzzles, whereas in Cappelen et al. [5], subjects have to choose how much money to invest in an investment game in which the rate of return is exogenously determined.
- 9 Recall that we focus on the case in which the dictator is rewarded at a higher rate; therefore the recipient's monetary contribution to the surplus will be below her contribution in terms of inputs (ar > yr). Graphically, this implies that the dotted curve (the accountability principle) is above the 45-degree line (the libertarian principle). Both principles coincide when (yr /
) = 0 and (yr /
) = 1. In the first case, all the available surplus is due to the dictators' inputs (qr = 0). The contrary is true if (yr /
) = 1.We also note that we represent (yr /
) on the horizontal line and assume that pd = 1.5 and pr = 1. Thus, the egalitarian principle and the libertarian one coincide when (yr /
) = 0.5 (i.e., when yr =
), whereas the egalitarian principle and the accountability one coincide if ar /
= 0.5 (i.e., when ar =
). In order to satisfy this latter condition, both subjects should have exactly the same number of correct answers (qd = qr), which implies that yr /
= 0.4.
References
- Fehr, E.; Schmidt, K. A theory of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Frohlich, N.; Oppenheimer, J.; Kurki, A. Modeling other-regarding preferences and an experimental test. Public Choice 2004, 119, 91–117. [Google Scholar] [CrossRef]
- Camerer, C. Behavioral Game Theory; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Engel, C. Dictator games: A meta study. Exp. Econ. 2011, 14, 583–610. [Google Scholar] [CrossRef]
- Cappelen, A.W.; Hole, A.D.; Sorensen, E.; Tungodden, B. The pluralism of fairness ideals: An experimental approach. Am. Econ. Rev. 2007, 97, 818–827. [Google Scholar] [CrossRef]
- Cherry, T.L.; Frykblom, P.; Shogren, J.F. Hardnose the dictator. Am. Econ. Rev. 2002, 92, 1218–1221. [Google Scholar] [CrossRef]
- Konow, J. Fair shares: Accountability and cognitive dissonance in allocation decisions. Am. Econ. Rev. 2000, 90, 1072–1091. [Google Scholar] [CrossRef]
- Oxoby, R.J.; Spraggon, J. Mine and yours: Property rights in dictator games. J. Econ. Behav. Organ. 2008, 65, 703–713. [Google Scholar] [CrossRef]
- Ruffle, B.J. More is better, but fair is fair: Tipping in dictator and ultimatum game. Games Econ. Behav. 1998, 23, 247–265. [Google Scholar] [CrossRef]
- Miller, L.; Ubeda, P. Are women more sensitive to the decision-making context? J. Econ. Behav. Organ. 2011, 83, 98–104. [Google Scholar] [CrossRef]
- Rodriguez-Lara, I.; Moreno-Garrido, L. Self-Interest and fairness: Self-serving choices of justice principles. Exp. Econ. 2012, 15, 158–175. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K. Theories of fairness and reciprocity: Evidence and economic applications. In Advances in Economics and Econometrics; Dewatripont, M.e.A., Ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 208–257. [Google Scholar]
- Konow, J. A positive theory of economic fairness. J. Econ. Behav. Organ. 1996, 31, 13–35. [Google Scholar] [CrossRef]
- Cappelen, A.W.; Moene, K.O.; Sorensen, E.; Tungodden, B. Rich meets poor: An international fairness experiment. CMI working paper, Mimeo. CMI: Bergen, Norway, 2008. [Google Scholar]
- Cappelen, A.W.; Sorensen, E.; Tungodden, B. Responsability for what? Fairness and individual responsibility. European Econ. Rev. 2010, 54, 429–441. [Google Scholar] [CrossRef] [Green Version]
- Konow, J. Fair and square: The four sides of distributive justice. J. Econ. Behav. Organ. 2001, 46, 137–164. [Google Scholar] [CrossRef]
- Cappelen, A.W.; Tungodden, B. Rewarding effort. Econ. Theory 2009, 39, 425–441. [Google Scholar] [CrossRef]
- Fleurbaey, M.; Maniquet, F. Compensation and responsability. In Handbook of Social Choice and Welfare; Arrow, K., Sen, A., Suzumura, K., Eds.; Northe-Holland: Amsterdam, The Netherlands, 2010; Volume 2. [Google Scholar]
- Rawls, J. A Theory of Justice; Harvard University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Roemer, J.E. Equality of Opportunity; Harvard University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Visser, M.S.; Roelofs, M.R. Heterogeneous preferences for altruism: Gender and personality, social status, giving and taking. Exp Econ. 2011, 14, 490–506. [Google Scholar] [CrossRef]
- Croson, R.; Konow, J. Social preferences and moral biases. J. Econ. Behav. Organization 2009, 69, 201–212. [Google Scholar] [CrossRef]
- Messick, D.; Sentis, K. Fairness, preference and fairness biases. In Equity Theory, Psychological and Sociological Perspectives; Messick, D., Cook, K.S., Eds.; Praeger: New York, NY, USA, 1983; pp. 61–94. [Google Scholar]
- Ubeda, P. The consistency of fairness rules: An experimental study. Working Paper DPEB No. 10/10. Nuffield College, University of Oxford: Oxford, UK, 2010. [Google Scholar]
- Yaari, M.; Bar-Hillel, M. On dividing justly. Soc. Choice Welfare 1984, 1, 1–24. [Google Scholar]
- Nielsen, K. Equality and Liberty: A Defense of Radical Egalitarianism; Rowman and Littlefield Publishers, Inc.: Lanham, MD, USA, 1984. [Google Scholar]
- Konow, J. Which is the fairest one of all? A positive analysis of justice theories. J. Econ. Literature 2003, 41, 1188–1239. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 30, 166–193. [Google Scholar]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ 2002, 117, 817–869. [Google Scholar] [CrossRef]
- Selten, R. The equity principle in economic behavior. In Decision Theory and Social Ethics, Issues in Social Choice; Gottinger, H.W., Leinfellner, W., Eds.; Springer: Berlin, Germany, 1984; pp. 289–301. [Google Scholar]
- Nozick, R. Anarchy, State and Utopia; Wiley-Blackwell: New York, NY, USA, 1974. [Google Scholar]
- Bolton, G.E.; Brandts, J.; Ockenfels, A. Fair procedures: Evidence from games involving lotteries. Econ. J. 2005, 115, 1054–1076. [Google Scholar] [CrossRef]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. Games Econ. Behav. 2011, 7, 321–338. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rodriguez-Lara, I.; Moreno-Garrido, L. Modeling Inequity Aversion in a Dictator Game with Production. Games 2012, 3, 138-149. https://doi.org/10.3390/g3040138
Rodriguez-Lara I, Moreno-Garrido L. Modeling Inequity Aversion in a Dictator Game with Production. Games. 2012; 3(4):138-149. https://doi.org/10.3390/g3040138
Chicago/Turabian StyleRodriguez-Lara, Ismael, and Luis Moreno-Garrido. 2012. "Modeling Inequity Aversion in a Dictator Game with Production" Games 3, no. 4: 138-149. https://doi.org/10.3390/g3040138
APA StyleRodriguez-Lara, I., & Moreno-Garrido, L. (2012). Modeling Inequity Aversion in a Dictator Game with Production. Games, 3(4), 138-149. https://doi.org/10.3390/g3040138