Belief Heterogeneity and the Restart Effect in a Public Goods Game
Abstract
1. Introduction
2. Experimental Design and Procedure
3. Results
- Hypothesis 1:
- (a) Higher contributions and stronger restarts in Partner-Control compared to Stranger-Control; (b) Higher contributions and stronger restarts in Partner-Belief compared to Stranger-Belief.
- Hypothesis 2:
- (a) Higher contributions and stronger restarts in Partner-Control compared to Partner-Belief; (b) Higher contributions and stronger restarts in Stranger-Control compared to Stranger-Belief.
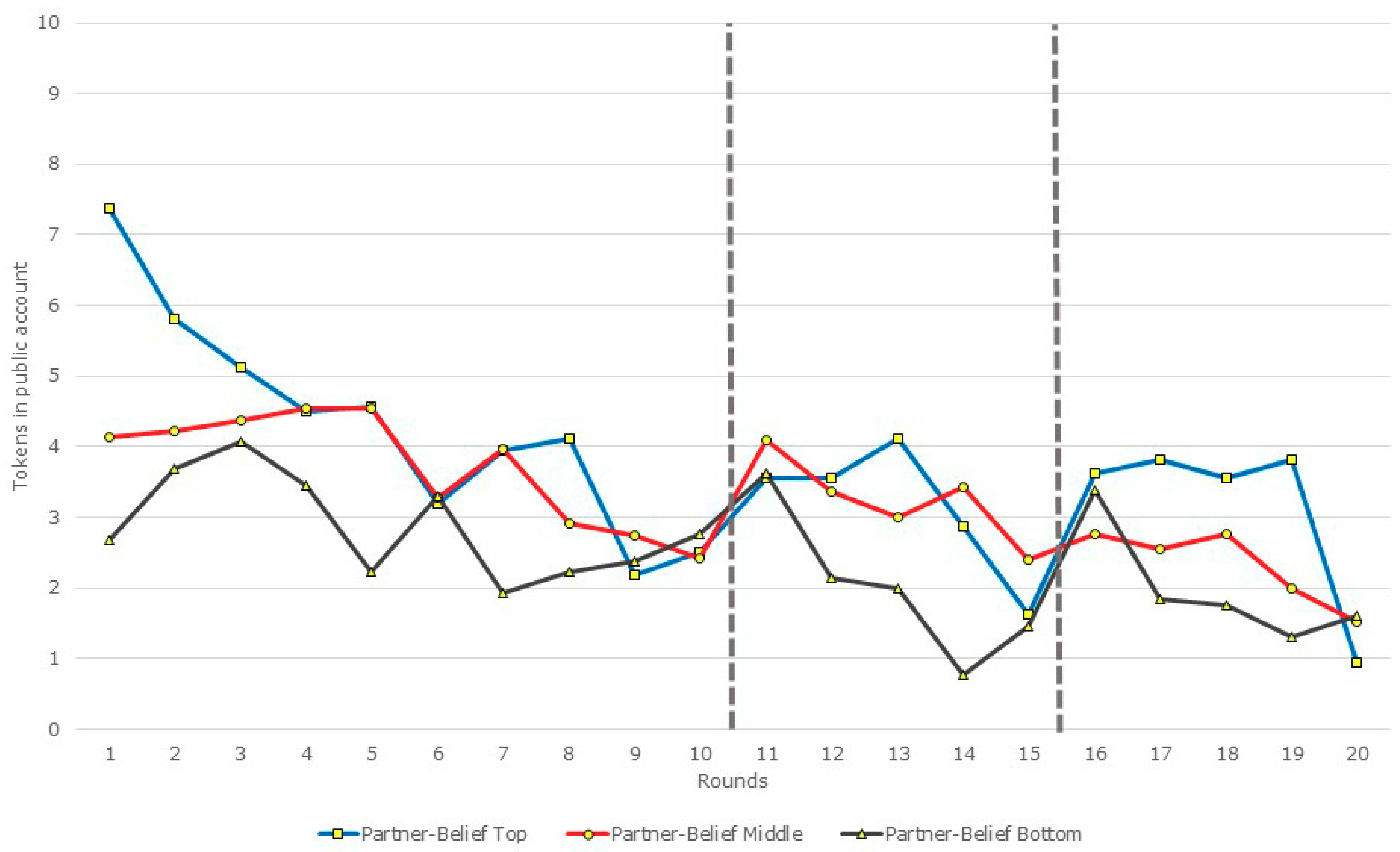
3.1. Restart, Beliefs, and Contributions
3.2. Restarts, Beliefs, and Contributions: A Disaggregated View
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Additional Regression Results
| Dependent variable: Tokens contributed to the public account | ||||
| Regressors | (1) | (2) | (3) | (4) |
| Round | −0.09 *** | −0.09 *** | −0.09 *** | −0.09 *** |
| (0.03) | (0.01) | (0.01) | (0.02) | |
| Stranger Matching | −1.02 | |||
| (0.72) | ||||
| Belief | −1.36 ** | |||
| (0.37) | ||||
| Stranger-Belief | −2.49 *** | −2.37 *** | ||
| (0.36) | (0.44) | |||
| Partner-Belief | −2.21 *** | −2.03 *** | ||
| (0.52) | (0.40) | |||
| Stranger-Control | −2.13 *** | −1.76 *** | ||
| (0.55) | (0.5) | |||
| Lag Avg. Contribution by Others | 0.68 *** | |||
| (0.04) | ||||
| Constant | 5.03 *** | 5.34 *** | 6.34 *** | 2.93 *** |
| (0.29) | (0.32) | (0.38) | (0.43) | |
| Number of observations | 3760 | 3760 | 3760 | 3572 |
| Wald χ2 | 20.13 | 35.51 | 81.78 | 483.36 |
| Probability > χ2 | 0.00 | 0.00 | 0.00 | 0.00 |
| R2 | 0.03 | 0.03 | 0.03 | 0.10 |
| Wald test for equality of coefficients | ||||
| Stranger-Belief = Partner-Belief | χ2 = 0.2 | χ2 = 0.76 | ||
| (p = 0.66) | (p = 0.38) | |||
| Stranger-Belief = Stranger-Control | χ2 = 0.29 | χ2 = 1.84 | ||
| (p = 0.59) | (p = 0.17) | |||
| Partner-Belief = Stranger-Control | χ2 = 0.01 | χ2 = 0.42 | ||
| (p = 0.92) | (p = 0.52) | |||
| Treatments | Groups | Avg. Diff Rounds 10–11 | Avg. Diff Rounds 15–16 | Rank Sum Tests | ||
|---|---|---|---|---|---|---|
| Partner Matching | Top (n = 16) | 1.06 | 2 | Middle (n = 35) | Bottom (n = 13) | |
| Middle (n = 35) | 1.66 | 0.37 | Top (n = 16) | (a) |z| = 0.72; p = 0.47 (b) |z| = 1.4; p = 0.16 | (a) |z| = 0.15; p = 0.88 (b) |z| = 0.15; p = 0.88 | |
| Bottom (n = 13) | 0.85 | 1.92 | Middle (n = 35) | --- | |z| = 0.36; p = 0.72 (b) |z| = 1.01; p = 0.31 | |
| Stranger Matching | Top (n = 8) | 0.25 | 0.88 | Middle (n = 26) | Bottom (n = 10) | |
| Middle (n = 26) | 1.08 | 0.31 | Top (n = 8) | (a) |z| = 0.35; p = 0.73 (b) |z| = 0.59; p = 0.56 | (a) |z| = 0.4; p = 0.89 (b) |z| = 0.67; p = 0.5 | |
| Bottom (n = 10) | −0.9 | 1.6 | Middle (n = 26) | --- | (a) |z| = 0.89; p = 0.37 (b) |z| = 1.08; p = 0.28 | |
| Treatments | Groups | Avg. Diff Rounds 10–11 | Rank Sum Tests | ||
|---|---|---|---|---|---|
| Partner Matching | Top (n = 16) | 1.13 | Middle (n = 35) | Bottom (n = 13) | |
| Middle (n = 35) | 0.74 | Top (n = 16) | |z| = 0.71; p = 0.48 | |z| = 0.24; p = 0.81 | |
| Bottom (n = 13) | 0.92 | Middle (n = 35) | --- | |z| = 0.34; p = 0.74 | |
| Stranger Matching | Top (n = 8) | 0.75 | Middle (n = 26) | Bottom (n = 10) | |
| Middle (n = 26) | 0.00 | Top (n = 8) | |z| = 0.56; p = 0.58 | |z| = 0.18; p = 0.86 | |
| Bottom (n = 10) | −0.40 | Middle (n = 26) | --- | |z| = 0.66; p = 0.51 | |
| ____ 0 | ____ 3 | ____ 6 | _____ 9 |
| ____ 1 | ____ 4 | ____ 7 | ____ 10 |
| ____ 2 | ____ 5 | ____ 8 |
| ____ 0 | ____ 3 | ____ 6 | _____ 9 |
| ____ 1 | ____ 4 | ____ 7 | ____ 10 |
| ____ 2 | ____ 5 | ____ 8 |
| Round | Predicted Average | Actual Average | Difference | Square of Difference | Earnings ($1 – Square of Difference) |
- A “restart” works in the following way: Participants are initially told that they will play for a certain number of rounds. (They are also alerted at the outset that there may be other parts to the study following the conclusion of the game in question. They are told that they will get further instructions if they are asked to participate in further tasks.) Once the preannounced number of rounds are completed, participants are told how much they have earned up to that point. Then, they are asked if they are willing to take part and play a few more rounds of the same game, with no changes to the underlying parameters of the game or the payment scheme. This is the “restart”; in the sense that participants thought the game was over, but now they are asked to play for more rounds.
- We need to add a word about our use of experimental cents in the instructions, rather than saying that each token is worth NZ $0.05. If we did this, then for each token contributed to the public account, the token gets doubled in value to NZ $0.10; redistributed equally among the four group members, this nets NZ $0.025 per player. However, the software does not allow three decimal points and rounds this up to NZ $0.03. As a result, we denote payoffs in experimental currency, but then make the actual payoff equal to 50% of the experimental payoffs.
- These two types of matching protocols—fixed groups versus random rematching within a session—are commonly used in such experimental studies. However, under such protocols, each participant interacts with every other participant within the group. There is now a large related literature that looks at social networks where participants may be constrained to interact with one or more immediate neighbors (incomplete networks) [50,51,52], as opposed to interacting with every other group member (complete network, as in the present study). This literature suggests that the nature of the network architecture and the ability to monitor and/or punish one or more members of the group has important implications for the ability of punishments to sustain cooperation over time as well as the efficacy of such punishments. We eschew a detailed discussion of this line of work as being beyond the scope of the current study.
References
- Andreoni, J. Why free ride? Strategies and learning in public goods experiments. J. Public Econ. 1988, 37, 291–304. [Google Scholar] [CrossRef]
- Croson, R. Partners and strangers revisited. Econ. Lett. 1996, 53, 25–32. [Google Scholar] [CrossRef]
- Ledyard, J. Public goods: A survey of experimental results. In Handbook of Experimental Economics; Kagel, J., Roth, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1995; Chapter 2; pp. 111–194. [Google Scholar]
- Cookson, R. Framing effects in public goods experiments. Exp. Econ. 2000, 3, 55–79. [Google Scholar] [CrossRef]
- Brandts, J.; Schram, A. Cooperation and noise in public goods experiments: Applying the contribution function approach. J. Public Econ. 2001, 79, 399–427. [Google Scholar] [CrossRef]
- Brandts, J.; Saijo, T.; Schram, A. How universal is behavior? A four country comparison of spite, cooperation and errors in voluntary contribution mechanisms. Public Choice 2004, 119, 381–424. [Google Scholar] [CrossRef]
- Burlando, R.; Hey, J. Do Anglo–Saxons free-ride more? J. Public Econ. 1997, 64, 41–60. [Google Scholar] [CrossRef]
- Keser, C.; van Winden, F. Conditional co-operators and voluntary contributions to public goods. Scand. J. Econ. 2000, 102, 23–39. [Google Scholar] [CrossRef]
- Palfrey, T.; Prisbrey, J. Altruism, reputation, and noise in linear public goods experiments. J. Public Econ. 1996, 61, 409–427. [Google Scholar] [CrossRef]
- Palfrey, T.; Prisbrey, J. Anomalous behavior in public goods experiments: How much and why? Am. Econ. Rev. 1997, 87, 829–846. [Google Scholar]
- Sonnemans, J.; Schram, A.; Offerman, T. Strategic behavior in public good games: When partners drift apart. Econ. Lett. 1999, 62, 35–41. [Google Scholar] [CrossRef]
- Weimann, J. Individual behavior in a free riding experiment. J. Public Econ. 1994, 54, 185–200. [Google Scholar] [CrossRef]
- Andreoni, J.; Croson, R. Partners versus strangers: Random rematching in public goods experiments. In Handbook of Experimental Economics Results; Plott, C., Smith, V., Eds.; Elsevier (North-Holland): Amsterdam, The Netherlands, 2008; Volume 1, Chapter 82; pp. 776–783. [Google Scholar]
- Yamagishi, T. The provision of a sanctioning system in the United States and Japan. Soc. Psychol. Q. 1988, 51, 265–271. [Google Scholar] [CrossRef]
- Yamagishi, T. The provision of a sanctioning system as a public good. J. Pers. Soc. Psychol. 1986, 51, 110–116. [Google Scholar] [CrossRef]
- Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Gächter, S. Cooperation and punishment in public goods experiments. Am. Econ. Rev. 2002, 90, 980–994. [Google Scholar] [CrossRef]
- Gächter, S.; Renner, E.; Sefton, M. The long run benefits of punishment. Science 2008, 322, 1510. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R.; Gintis, H.; Bowles, S.; Richerson, P. The evolution of altruistic punishment. Proc. Natl. Acad. Sci. USA 2003, 100, 3531–3535. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. Punish or Perish? Retaliation and collaboration among humans. Trends Ecol. Evol. 2007, 22, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Egas, M.; Riedl, A. The economics of altruistic punishment and the maintenance of cooperation. Proc. R. Soc. B: Biol. Sci. 2008, 275, 871–878. [Google Scholar] [CrossRef] [PubMed]
- Nikiforakis, N.; Normann, H.-T. A comparative statics analysis of punishment in public good experiments. Exp. Econ. 2008, 11, 358–369. [Google Scholar] [CrossRef]
- Nikiforakis, N. Feedback, punishment and cooperation in public goods experiments. Games Econ. Behav. 2010, 68, 689–702. [Google Scholar] [CrossRef]
- Hermann, B.; Thöni, C.; Gächter, S. Antisocial punishments across societies. Science 2008, 319, 1362–1367. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, A. Sustaining cooperation in laboratory public goods experiments: A selective survey of the literature. Exp. Econ. 2011, 14, 47–83. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Paichayontvijit, T. On the long-run efficacy of punishments and recommendations in a laboratory public goods game. Nat. Sci. Rep. 2017, 7, 12286. [Google Scholar] [CrossRef] [PubMed]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Gächter, S. Conditional Cooperation: Behavioral Regularities from the Lab and the Field and their Policy Implications. In Economics and Psychology. A Promising New Cross-Disciplinary Field; Frey, B., Stutzer, A., Eds.; CESifo Seminar Series; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Fischbacher, U.; Gächter, S. Social preferences, beliefs, and the dynamics of free riding in public good experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Gunnthorsdottir, A.; Houser, D.; McCabe, K. Disposition, history and contributions in public goods experiments. J. Econ. Behav. Organ. 2007, 62, 304–315. [Google Scholar] [CrossRef]
- Ambrus, A.; Pathak, P. Cooperation over finite horizons: A theory and experiments. J. Public Econ. 2011, 95, 500–512. [Google Scholar] [CrossRef]
- Gächter, S.; Thöni, C. Social learning and voluntary cooperation among like-minded people. J. Eur. Econ. Assoc. 2005, 3, 303–314. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Paichayontvijit, T.; Smith, A. Belief heterogeneity and contributions decay among conditional co-operators in public goods games. J. Econ. Psychol. 2017, 58, 15–30. [Google Scholar] [CrossRef]
- Neugebauer, T.; Perote, J.; Schmidt, U.; Loos, M. Selfish-biased conditional cooperation: On the decline of contributions in repeated public goods experiments. J. Econ. Psychol. 2009, 30, 52–60. [Google Scholar] [CrossRef]
- Ones, U.; Putterman, L. The ecology of collective action: A public goods and sanctions experiment with controlled group formation. J. Econ. Behav. Organ. 2007, 62, 495–521. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Quercia, S. The behavioral validity of the strategy method in public good experiments. J. Econ. Psychol. 2012, 33, 897–913. [Google Scholar] [CrossRef]
- Brañas-Garza, P.; Paz Espinosa, M. Unraveling Public Good Games. Games 2011, 2, 434–451. [Google Scholar] [CrossRef]
- Smith, A. Estimating the causal effect of beliefs on contributions in repeated public good games. Exp. Econ. 2013, 16, 414–425. [Google Scholar] [CrossRef]
- Frankl, V. Man’s Search for Meaning. An Introduction to Logotherapy; Beacon Press: Boston, MA, USA, 2006. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Strouss and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Kahneman, D.; Slovic, P.; Tversky, A. Judgement under Uncertainty: Heuristics and Biases; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Rand, D.; Greene, J.D.; Nowak, M.A. Spontaneous giving and calculated greed. Nature 2012, 489, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Croson, R. Thinking like a game theorist: Factors affecting the frequency of equilibrium play. J. Econ. Behav. Organ. 2000, 41, 299–314. [Google Scholar] [CrossRef]
- Gächter, S.; Renner, E. The effects of (incentivized) belief elicitation in public goods experiments. Exp. Econ. 2010, 13, 364–377. [Google Scholar] [CrossRef]
- Chaudhuri, A. Experiments in Economics: Playing Fair with Money; Routledge: London, UK; New York, NY, USA, 2009. [Google Scholar]
- Clark, K.; Sefton, M. Repetition and signalling: Experimental evidence from games with efficient equilibria. Econ. Lett. 2001, 70, 357–362. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Chaudhuri, A.; Schotter, A.; Sopher, B. Talking ourselves to efficiency: Coordination in inter-generational minimum effort games with private, almost common and common Knowledge of Advice. Econ. J. 2009, 119, 91–122. [Google Scholar] [CrossRef]
- Van Huyck, J.B.; Battalio, R.C.; Beil, R.O. Tacit coordination games, strategic uncertainty, and coordination failure. Am. Econ. Rev. 1990, 80, 234–248. [Google Scholar]
- Carpenter, J. Punishing free-riders: How group size affects mutual monitoring and the provision of public goods. Games Econ. Behav. 2007, 60, 31–51. [Google Scholar] [CrossRef]
- Carpenter, J.; Kariv, S.; Schotter, A. Network architecture, cooperation and punishment in public goods games. Rev. Econ. Des. 2012, 95, 1–26. [Google Scholar]
- Leibbrandt, A.; Ramalingam, A.; Sääksvuori, L.; Walker, J. Incomplete punishment networks in public goods games: Experimental evidence. Exp. Econ. 2015, 8, 15–37. [Google Scholar] [CrossRef]


| Stranger Matching | Partner Matching | Total | |
|---|---|---|---|
| Belief Treatment | (Stranger-Belief) Session 1: 20 Session 2: 24 Total: 44 | (Partner-Belief) Session 1: 20 Session 2: 16 Session 3: 28 Total: 64 | 108 |
| Control Treatment (no belief elicitation) | (Stranger-Control) Session 1: 16 Session 2: 20 Total: 36 | (Partner-Control) Session 1: 20 Session 2: 24 Total: 44 | 80 |
| Total | 80 | 108 | 188 |
| First Restart | Second Restart | ||||||
|---|---|---|---|---|---|---|---|
| Round 1 | Round 10 | Round 11 | Round 15 | Round 16 | Round 20 | AVERAGE | |
| Stranger-Belief (n = 44) | 3.77 | 2.59 | 3.07 | 2.32 | 3.02 | 1.98 | 2.91 |
| Significance of restart effect | |z| = 0.77 p = 0.44 | |z| = 1.28 p = 0.20 | |||||
| Partner-Belief (n = 64) | 4.66 | 2.52 | 3.86 | 2.02 | 3.11 | 1.39 | 3.2 |
| Significance of restart effect | |z| = 2.37 p = 0.02 | |z| = 2.41 p = 0.02 | |||||
| Stranger-Control (n = 36) | 4.31 | 2.78 | 3.03 | 2.22 | 2.78 | 1.75 | 3.27 |
| Significance of restart effect | |z| = 0.83 p = 0.41 | |z| = 1.42 p = 0.15 | |||||
| Partner-Control (n = 44) | 5.46 | 2.23 | 6.77 | 5.32 | 7.27 | 2.69 | 5.4 |
| Significance of restart effect | |z| = 5.24 p < 0.01 | |z| = 2.03 p = 0.04 | |||||
| Dependent variable: Tokens contributed to the public account | ||||
| Regressors | (1) | (2) | (3) | (4) |
| Round | −0.14 *** | −0.14 *** | −0.14 *** | −0.09 *** |
| (0.01) | (0.01) | (0.01) | (0.02) | |
| Stranger Matching | −1.64 *** | |||
| (0.4) | ||||
| Belief | −2.28 *** | |||
| (0.37) | ||||
| Stranger-Belief | −4.09 *** | −2.37 *** | ||
| (0.49) | (0.44) | |||
| Partner-Belief | −3.45 *** | −2.03 *** | ||
| (0.45) | (0.40) | |||
| Stranger-Control | −3.18 *** | −1.76 *** | ||
| (0.51) | (0.5) | |||
| Lag Avg. Contribution by Others | 0.68 *** | |||
| (0.04) | ||||
| Constant | 5.2 *** | 5.81 *** | 7.25 *** | 2.93 *** |
| (0.29) | (0.32) | (0.38) | (0.43) | |
| Number of observations | 3760 | 3760 | 3760 | 3572 |
| Wald χ2 | 121.95 | 141.26 | 188.17 | 483.36 |
| Probability > χ2 | 0.00 | 0.00 | 0.00 | 0.00 |
| Number left-censored | 1084 | 1084 | 1084 | 1064 |
| Number uncensored | 2254 | 2254 | 2254 | 2108 |
| Number right-censored | 422 | 422 | 422 | 400 |
| Wald test for equality of coefficients | ||||
| Stranger-Belief = Partner-Belief | χ2 = 2.03 | χ2 = 0.76 | ||
| (p = 0.15) | (p = 0.38) | |||
| Stranger-Belief = Stranger-Control | χ2 = 3.14 * | χ2 = 1.84 | ||
| (p = 0.08) | (p = 0.17) | |||
| Partner-Belief = Stranger-Control | χ2 = 0.32 | χ2 = 0.42 | ||
| (p = 0.57) | (p = 0.52) | |||
| Treatments | Rounds | Average Belief about Others’ Contributions | Sign Rank Tests | ||
|---|---|---|---|---|---|
| Round 10 | Round 11 | Round 16 | |||
| Partner Matching (n = 64) | Round 1 | 5.12 | |z| = 3.99; p < 0.01 | --- | --- |
| Round 10 | 3.39 | --- | |z| = 2.08; p = 0.04 | --- | |
| Round 11 | 4.27 | --- | --- | |z| = 1.23; p = 0.22 | |
| Round 16 | 3.75 | --- | --- | --- | |
| Stranger Matching (n = 44) | Round 1 | 4.68 | |z| = 2.22; p = 0.03 | --- | --- |
| Round 10 | 3.77 | --- | |z| = 0.25; p = 0.80 | --- | |
| Round 11 | 3.82 | --- | --- | |z| = 0.51; p = 0.95 | |
| Round 16 | 3.82 | --- | --- | --- | |
| Partner Matching | Stranger Matching | Combined | |
|---|---|---|---|
| Top | 16 (25%) | 8 (18%) | 24 (22%) |
| Middle | 35 (55%) | 26 (59%) | 61 (57%) |
| Bottom | 13 (20%) | 10 (23%) | 23 (21%) |
| Total | 64 | 44 | 108 |
| Round 10 Beliefs | Round 11 Beliefs | Sign Rank Test | |
|---|---|---|---|
| Partner Matching | |||
| Top (n = 16) | 3.44 | 4.56 | |z| = 1.58; p = 0.12 |
| Middle (n = 35) | 3.54 | 4.29 | |z| = 1.18; p = 0.23 |
| Bottom (n = 13) | 2.92 | 3.85 | |z| = 0.96; p = 0.34 |
| Overall (n = 64) | 3.39 | 4.27 | |z| = 2.08; p = 0.04 |
| Stranger Matching | |||
| Top (n = 8) | 4 | 4.75 | |z| = 0.53; p = 0.59 |
| Middle (n = 26) | 3.58 | 3.58 | |z| = 0.02; p = 0.98 |
| Bottom (n = 10) | 4.1 | 3.7 | |z| = 0.04; p = 0.97 |
| Overall (n = 44) | 3.77 | 3.82 | |z| = 0.25; p = 0.80 |
| Round 10 | Round 11 | Sign Rank Test | Round 15 | Round 16 | Sign Rank Test | |
|---|---|---|---|---|---|---|
| Partner Matching | ||||||
| Top (n = 16) | 2.5 | 3.56 | |z| = 0.65; p = 0.52 | 1.63 | 3.63 | |z| = 2.27; p = 0.02 |
| Middle (n = 35) | 2.43 | 4.09 | |z| = 2.34; p = 0.02 | 2.4 | 2.77 | |z| = 0.85; p = 0.39 |
| Bottom (n = 13) | 2.77 | 3.62 | |z| = 0.60; p = 0.55 | 1.46 | 3.39 | |z| = 1.4; p = 0.16 |
| Overall (n = 64) | 2.52 | 3.86 | |z| = 2.37; p = 0.02 | 2.02 | 3.11 | |z| = 2.4; p = 0.02 |
| Stranger Matching | ||||||
| Top (n = 8) | 1.63 | 1.88 | |z| = 0.29; p = 0.77 | 0.88 | 1.75 | |z| = 0.97; p = 0.33 |
| Middle (n = 26) | 2.19 | 3.27 | |z| = 1.43; p = 0.15 | 2.46 | 2.76 | |z| = 0.74; p = 0.46 |
| Bottom (n = 10) | 4.4 | 3.5 | |z| = 0.69; p = 0.49 | 3.1 | 4.7 | |z| = 0.9; p = 0.37 |
| Overall (n = 44) | 2.59 | 3.07 | |z| = 0.77; p = 0.44 | 2.32 | 3.02 | |z| = 1.28; p = 0.20 |
| Round 11 Beliefs | Round 11 Contributions | Sign Rank Test | Round 16 Beliefs | Round 16 Contributions | Sign Rank Test | |
|---|---|---|---|---|---|---|
| Partner Matching | ||||||
| Top (n = 16) | 4.56 | 3.57 | |z| = 1.09; p = 0.27 | 4.06 | 3.63 | |z| = 0.70; p = 0.48 |
| Middle (n = 35) | 4.29 | 4.09 | |z| = 0.07; p = 0.95 | 3.83 | 2.77 | |z| = 1.87; p = 0.06 |
| Bottom (n = 13) | 3.85 | 3.62 | |z| = 0.11; p = 0.92 | 3.15 | 3.38 | |z| = 0.35; p = 0.72 |
| Overall (n = 64) | 4.27 | 3.86 | |z| = 0.76; p = 0.45 | 3.75 | 3.11 | |z| = 1.55; p = 0.12 |
| Stranger Matching | ||||||
| Top (n = 8) | 4.75 | 1.88 | |z| = 2.34; p = 0.02 | 3.38 | 1.75 | |z| = 1.7; p = 0.09 |
| Middle (n = 26) | 3.58 | 3.27 | |z| = 0.27; p = 0.79 | 4.23 | 2.77 | |z| = 2.49; p = 0.01 |
| Bottom (n = 10) | 3.7 | 3.5 | |z| = 0.46; p = 0.64 | 3.1 | 4.7 | |z| = 1.02; p = 0.31 |
| Overall (n = 44) | 3.82 | 3.07 | |z| = 1.37; p = 0.17 | 3.82 | 3.02 | |z| = 1.82; p = 0.07 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhuri, A. Belief Heterogeneity and the Restart Effect in a Public Goods Game. Games 2018, 9, 96. https://doi.org/10.3390/g9040096
Chaudhuri A. Belief Heterogeneity and the Restart Effect in a Public Goods Game. Games. 2018; 9(4):96. https://doi.org/10.3390/g9040096
Chicago/Turabian StyleChaudhuri, Ananish. 2018. "Belief Heterogeneity and the Restart Effect in a Public Goods Game" Games 9, no. 4: 96. https://doi.org/10.3390/g9040096
APA StyleChaudhuri, A. (2018). Belief Heterogeneity and the Restart Effect in a Public Goods Game. Games, 9(4), 96. https://doi.org/10.3390/g9040096





