Abstract
Novel two-dimensional (2D) materials have received extensive attention in the field of photocatalysis due to their unique properties. Traditional ZnO material with wurtzite structure transforms into a stable graphite-like structure that has the characteristics of 2D material when its thickness is less than a few atomic layers. In this work, using first-principles calculations, we investigated the potential of multilayer graphite-like ZnO as a photocatalyst for water splitting. The results showed that multilayer ZnO is a series of direct bandgap semiconductors, and their band edge positions all straddle the redox potential of water. Increasing with the number of layers, the bandgap of multilayer ZnO decreased from 3.20 eV for one layer to 2.21 eV for six layers, and visible light absorption capacity was significantly enhanced. Hence, multilayer ZnO was indeed promising for photocatalytic water splitting. Furthermore, suitable biaxial tensile strain could decrease the bandgap and maintain the stable graphite-like structure at a broader thickness range. In contrast, excessive biaxial tensile strain could change the redox capacity of multilayer ZnO and prevent it from catalyzing water splitting. Our theoretical results show that six-layer ZnO under 1% biaxial strain had direct bandgap of 2.07 eV and represents the most excellent photocatalytic performance among these multilayer ZnO materials.
1. Introduction
As a possible way to alleviate the energy crisis, photocatalytic water splitting to produce hydrogen has attracted more and more attention [1,2]. Since utilizing solar energy to generate photogenerated electron-hole pairs could participate in the redox reaction on the surface of the material to catalyze water splitting, synthesizing and developing efficient photocatalysts has great significance for hydrogen production. High-efficiency photocatalysts in solar energy conversion applications need a suitable bandgap that can absorb visible light energy, and their band edge position must straddle the redox potential of water to ensure sufficient redox capacity [3].
ZnO is a potential photocatalytic material with a proper bandgap and has been widely investigated, owing to its high carrier mobility and excellent optical characteristics [4]. In its normal state, bulk ZnO is a stable wurtzite structure with a direct bandgap of 3.37 eV [5]. Due to its excellent properties, ZnO has wide applications in the fields of electronics, optoelectronics, and photocatalysis [6,7]. In recent years, with the advent of 2D ZnO, the application potential of ZnO in photocatalysts has gradually improved [8]. Compared with the bulk structure, 2D ZnO has a larger specific surface area and sufficient reaction surface. Photogenerated electron-hole pairs migrate to the surface to participate in the reaction more quickly. Thus, a good deal of 2D ZnO has been applied as the photocatalyst for hydrogen production. Freeman et al. predicted that wurtzite materials such as ZnO would undergo structural phase transition from a wurtzite structure to a graphite-like layered structure as the number of layers decreases [9]. Subsequently, ZnO thin films with a graphite-like layered structure were successfully grown on Ag (111) substrates by Tushce’s group, and they observed that ZnO transitioned to wurtzite structure as the number of layers increased [10]. The structural transformation found by this experiment proved the existence of 2D graphite-like layered ZnO.
Due to the significant influence of interlayer interaction and the quantum confinement effect on the energy band structure of the material, 2D multilayer structure material often has unique electronic characteristics, and it has gradually become a new research hotspot in the field of photocatalysis [11,12,13,14,15,16,17,18,19,20]. Meanwhile, research studies on their 2D structures are also proceeding rapidly and productively, ever since the successful experimental synthesis of their graphene-like 2D counterparts. Despite some reports on 2D graphite-like structures, the reported details remain controversial, and a thorough understanding is still lacking. In the case of ZnO, for instance, due to surface depolarization, ZnO films that are only a few atomic layers thick favor a stable graphite-like multilayer structure. Furthermore, when the number of layers increases, ZnO films begin transforming into the bulk structure at a certain critical thickness [21,22,23,24,25]. Theoretically, some previous first-principles calculation studies predicted the existence of graphite-like multilayer ZnO [9,26]. Moreover, an experiment by Lee et al. showed that the bandgap of ZnO thin films could be tuned by the number of layers before the phase transformation from the graphite-like structure to the bulk wurtzite structure occurred [27]. This provided a new method for tuning the photocatalytic performance of materials. In recent years, a few studies on the effect of layer number on photocatalytic performance of multilayer materials have been reported. Guan et al. found that the bandgap of multilayer Janus MoSSe decreased monotonically with the increase of the number of layers and explored its potential as an efficient photocatalyst through theoretical calculations [28]. Zhao et al. investigated selective adsorption and photocatalytic reduction of CO2 using 2D ZnO films with different layers [29]. Although 2D ZnO has many unique advantages as a photocatalyst, a method that can flexibly tune the bandgap of 2D material and avoid widening of the bandgap caused by two-dimensionalization is still desirable in order to improve its photocatalytic performance in sunlight.
At present, epitaxial strain is considered a powerful and practical method for tuning the band structure of 2D materials [30,31,32]. Regarding monolayer ZnO, there are some reports on tuning the physical and chemical properties of the material via strain. Kaewmaraya et al. found that the bandgap of a ZnO monolayer nanosheet varied almost linearly with uniaxial strain, and it showed a parabola-like behavior under homogeneous biaxial strain [33]. Chen et al. tuned the bandgap of monolayer ZnO via biaxial strain and found that monolayer ZnO at 10% biaxial tensile strain had better photocatalytic water splitting performance [34]. Interestingly, Wu et al. found that the bandgap of strained graphitic multilayer films could be tuned over a wide range, either above or below that of the bulk wurtzite phase, and, importantly, the thickness range of both freestanding and substrate-supported stable graphitic films depended sensitively on the strain and could be substantially extended [26]. This research showed that, for multilayer ZnO, the strain might be able to tune its photocatalytic performance more effectively.
In this article, using first-principles calculations, we investigated the photocatalytic performance of multilayer ZnO combined with biaxial strain. Based on the proper band edge position, we focused on the changes in bandgap and the light absorption spectrum. Above all, we studied the electronic properties of multilayer ZnO. The bandgap of multilayer ZnO decreased when the number of layers increased. When the thickness of ZnO was six layers, the direct bandgap calculated by the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional and van der Waals interaction was 2.21 eV. Six-layer ZnO also had a suitable band edge position and excellent visible light absorption to be a promising photocatalyst for water splitting. After that, by applying biaxial strain to multilayer ZnO, we found that 1% biaxial tensile strain reduced the bandgap of six-layer ZnO from 2.21 to 2.07 eV, and the band edge position still straddled the redox potential of water. Hence, suitable biaxial strain could enhance the photocatalytic performance of multilayer ZnO for water splitting.
2. Results and Discussions
2.1. Geometric Structures and Electronic Properties of Multilayer ZnO
The structures we studied are shown in Figure 1. In this article, the graphite-like multilayer ZnO films are labeled nL ZnO (n is the number of layers, n = 1–6). The optimized lattice constant of 1L was 3.288 Å, as the number of layers increased, the lattice constant decreased, and the stable value 3.273 Å was reached when the number of layers reached about 5 or 6 layers. For n = 3–6, the optimized vertical distance between adjacent layers was relatively stable, and the average distance was 3.347 Å. For all nL ZnO, the bond length of Zn-O was 1.891 Å.
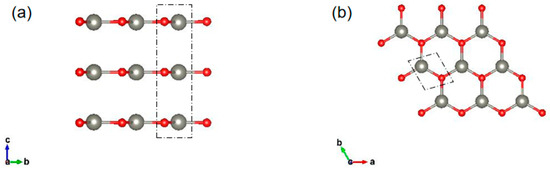
Figure 1.
(a) Side view of the optimized geometrical structure of three-layer (3L) ZnO; (b) Top view of 2D graphite-like layered ZnO. The red and gray balls represent O and Zn, respectively.
From the total energy point of view, the stability enhancement of nL ZnO as the number of layers increased was expected. However, it was still necessary to pay attention to the phase transition process of ZnO [9,26]. Past studies have shown that, theoretically, phase transition from the 2D graphite phase of ZnO to the bulk wurtzite phase of ZnO occurs roughly at eight layers, which means that up to eight layers the graphite-like structure is more stable than the wurtzite structure [26]. Furthermore, the calculated formation energies of nL ZnO are listed in Table 1 as inversely related to the number of layers. Many studies have successfully synthesized monolayer or few-layer ZnO [21,27]. therefore, these formation energies might indicate that several layers of ZnO were more stable and more comfortable to synthesize than monolayer ZnO.

Table 1.
Bandgaps, total energies, formation energies, and binding energies of nL ZnO.
For electronic properties, we calculated the band structures of nL ZnO using the HSE06 functional, as shown in Figure 2. From the band structures we find that all nL ZnO (n = 1–6) were direct bandgap semiconductors. Moreover, the valence band maximum (VBM) and the conduction band minimum (CBM) were located at the point in the Brillouin zone, suggesting that excited-state electrons easily transitioned from VBM to CBM, generating electron-hole pairs. The bandgap of 1L ZnO was 3.20 eV, which meant that 1L ZnO had a weak energy absorption capacity for visible light, and this was consistent with previous research results [35]. As the number of layers increased, the nL ZnO bandgap decreased due to the quantum confinement effect and interaction between interlayers. Figure 3b shows the trend of the bandgap, from 3.20 eV of 1L ZnO to 2.21 eV of 6L ZnO. When the number of layers reached four, the bandgap variation amplitude began decreasing significantly. It could be predicted that as the number of layers continued to increase, the bandgap of multilayer ZnO would gradually approach the theoretical bandgap value of bulk ZnO. As the size (number of layers) of multilayer ZnO gradually increased, the ZnO originally existing in the graphite-like structure would transform into a bulk wurtzite structure [26]. At this time, even if the size (number of layers) continued to increase, the bandgap of ZnO would not continue to decrease.
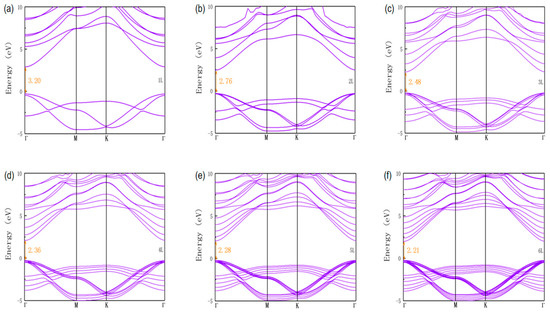
Figure 2.
Band structures of (a) 1L, (b) 2L, (c) 3L, (d) 4L, (e) 5L, and (f) 6L ZnO were calculated using the HSE06 functional. Fermi level was set to 0 eV.
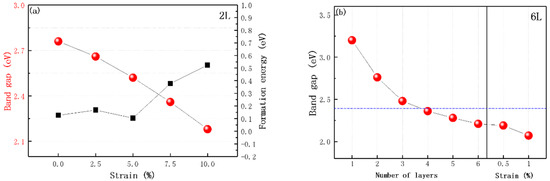
Figure 3.
(a) Bandgap and formation energy of 2L ZnO under different strains are represented by red balls and black squares, respectively. (b) The bandgap of nL ZnO and 6L ZnO under 0.5% and 1% strains; the blue dashed line indicates the bandgap of bulk ZnO calculated using the HSE06 functional.
2.2. Effect of the Biaxial Strain
As mentioned above, there was a limit to the nL ZnO bandgap decrease caused by the increase in layer number, so the bandgap had only a narrow tune range. We intended to solve this problem by applying biaxial strain to multilayer ZnO. Through some studies on strained monolayer ZnO, we learned that the edge states of the conduction band and valence band of ZnO would undergo charge localization by applying biaxial strain. The bandgap of monolayer ZnO varies with biaxial strain similarly to a parabola—the bandgap of unstrained ZnO is the largest, and increases in tensile and compressive strain would reduce the bandgap value. Bandgap values under the same magnitude of tensile and compressive strain are not equal: the effect of tensile strain on the bandgap is more obvious [30,33]. Our research object was graphite-like multilayer ZnO. The atomic structure of each layer was similar to that of monolayer ZnO. Therefore, we guessed that nL ZnO bandgap change under biaxial tensile strain was similar to strained monolayer ZnO. To ensure that our guess was reasonable, we studied the effect of biaxial strain on 2L ZnO. It should be noted that our purpose was only to narrow the bandgap and improve the light absorption capacity of the material, so our calculation only considered tensile strain, which had a more obvious effect on bandgap. Biaxial tensile strain ranged from 0% to 10% in 2.5% increments, and we calculated the electronic structures of 2L ZnO under different biaxial strains. The calculation results in Figure 3a showed that our guess was reasonable. Biaxial tensile strain did not change the positions of VBM and CBM in the Brillouin zone, and 2L ZnO under different strains was still a direct bandgap semiconductor. With the strain increasing, the bandgap of 2L ZnO gradually decreased from 2.76 to 2.18 eV, as shown in Figure 3a. However, biaxial tensile strain not only narrowed the bandgap, but also shifted the band edge position, which meant that while looking for narrow-bandgap ZnO, we must pay attention to its band edge position [34].
The formation energies of 2L ZnO under 2.5%, 5%, 7.5% and 10% strains are presented in Figure 3a. Only at 5% strain was the formation energy of 2L ZnO lower than that of the initial structure, and the overall trend of formation energy was upward, which was consistent with previous research [26]. Interestingly, nL ZnO under biaxial strain, compared with pristine nL ZnO, could maintain the stable graphite-like structure at a larger maximum number of layers, which illustrated the feasibility of our research.
According to the general law of multilayer ZnO under biaxial strain, we applied biaxial tensile strain to 6L ZnO and looked for the ideal bandgap that satisfied visible light absorption in a more extensive tune range. Because the bandgap was very sensitive to the change in biaxial strain, we used a smaller step size of 0.5%. Through testing, we discovered that 6L ZnO under 1% biaxial tensile strain had direct bandgap of 2.07 eV, which should be an appropriate visible-light-absorbing material, and its formation energy was 0.099 eV smaller than that of 6L ZnO, demonstrating that it was still stable. Fortunately, 6L ZnO under 1% biaxial tensile strain could also catalyze water splitting; the details will be discussed in the next section.
2.3. Photocatalytic Water Splitting
Based on the above discussion, the photocatalytic performance of nL ZnO for water splitting was systematically investigated. First of all, we calculated the band edge positions of nL ZnO (n = 1–6) and 6L ZnO under biaxial strain relative to the vacuum level using the HSE06 functional, as shown in Figure 4. For water splitting, the redox potential of water needed to be marked. Relative to the vacuum level, the standard reduction potential of is −4.44 eV, and the standard oxidation potential of is −5.67 eV [36,37]. We found that nL ZnO CBM and VBM values straddled the redox potential of water, indicating that they were suitable for catalyzing the water splitting reaction. Specifically, the energy difference between CBM and the reduction potential of decreased significantly as the number of layers increased. It can be seen from Figure 4 that CBM values of 5L ZnO and 6L ZnO were above the reduction potential by 0.41 and 0.29 eV, respectively. This meant that the excited electrons had sufficient reduction capacity to participate in the reduction reaction on the surface of the material to produce hydrogen. After applying tensile strain, the position adjustment of CBM was approximately linearly dependent on the strain, and the energy difference was further reduced. CBM of 6L ZnO under 1% biaxial strain was only 0.08 eV above the reduction potential. On the other hand, there was a slight change in VBM positions with the number of layers and even strain. The energy differences between these VBM values and the oxidation potential were mostly between 0.64 and 0.76 eV, so they had sufficiently strong oxidation power in the photocatalytic water splitting process.
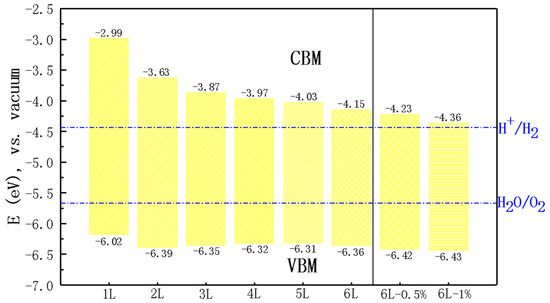
Figure 4.
Band edge positions of nL ZnO (n = 1–6) and 6L ZnO under 0.5% and 1% biaxial strain relative to the vacuum level calculated using the HSE06 functional. The redox potential of water relative to the vacuum level is indicated by blue dotted lines.
Furthermore, we studied the optical absorption spectra of nL ZnO (n = 1–6) and 6L ZnO under 0.5% and 1% biaxial strain, another critical factor affecting photocatalytic capability. Figure 5 shows that the first absorption peak of 1L ZnO was around 3.32 eV, which was in the ultraviolet energy region. In contrast, the absorption coefficient was small in the energy range of visible light. As the number of layers increased, bandgap decreased, and light absorption range gradually moved towards the visible energy region. For instance, the first absorption peaks of 2, 4, and 6L ZnO were around 2.82, 2.61, and 2.46 eV, respectively, and all were in the visible energy region. The first absorption peaks of 6L ZnO under 0.5% biaxial strain and 6L ZnO under 1% biaxial strain were located at 2.47 and 2.43 eV, respectively. Compared with unstrained 6L ZnO, the corresponding absorption coefficients increased from 0.588 to 0.591 and from 0.588 to 0.600, respectively. In our work, 6L under 1% strain had the best light absorption capacity.
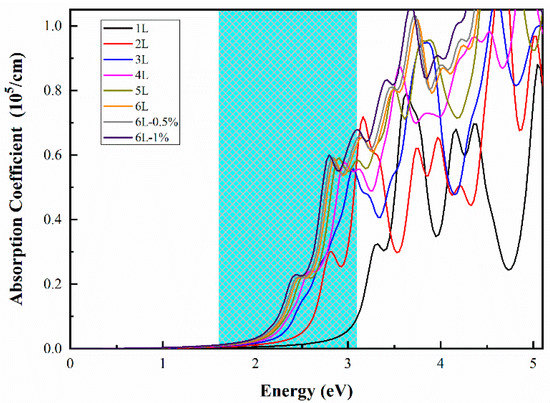
Figure 5.
Optical absorption spectra of nL ZnO (n = 1–6) and 6L ZnO under 0.5% and 1% biaxial strain obtained using HSE06 calculations. The energy range of visible light is shown on the blue background.
3. Computational Methods
First-principles calculations were performed by using the Vienna Ab initio Simulation Package (VASP) [38]. The projector augmented wave (PAW) potentials were used for core–electron interactions, and the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional was used to treat the exchange and correlation interactions [39,40]. The DFT-D2 scheme with Grimme correction was adopted to describe the van der Waals (vdW) interactions between adjacent layers [41,42,43]. In all calculations, the cut-off energy was set to 520 eV, and the energy convergence of geometry optimization was set to 10−5 eV. The thickness of the vacuum layer along the z-direction was set to 20 Å to ensure the interactions among layers were negligible. The k-point sampling of the Brillouin zone was implemented using a gamma-centered Monkhorst–Pack grid with 5 × 5 × 1 for geometry optimization and 15 × 15 × 1 for the calculations of optical properties. Because PBE functional would underestimate the bandgap of materials, electronic structures and optical properties were calculated by using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional [44].
Biaxial tensile strain was achieved by simultaneously changing the lattice constants in the orthogonal basis vector direction in the plane of ZnO thin layers. The percentage of biaxial tensile strain was expressed as
where and are the lattice constants before and after biaxial strain is applied, respectively. The stability of the multilayer structures was evaluated according to binding energy Eb and formation energy Ef [45], which were defined as
where , , and are the total energies of multilayer ZnO, bulk ZnO, and monolayer ZnO, respectively. and are the number of atoms in the multilayers and bulk unit cells, and is the layers of multilayer ZnO.
4. Conclusions
To sum up, through first-principles calculations we explored the possibility of 2D graphite-like multilayer ZnO films (nL ZnO, n = 1–6) as a photocatalyst for water splitting. The results of the geometry structures, electronic properties, and optical absorption characteristics indicated that nL ZnO was a series of direct bandgap semiconductors with appropriate band edge positions. Within a smaller thickness range, as the number of layers increased, the bandgap gradually decreased, and the visible light absorption capacity was greatly enhanced. For 6L ZnO, the bandgap of 2.21 eV and more suitable band edge position, compared to that of other nL ZnO, made it a potentially excellent photocatalyst for water splitting. Furthermore, electronic structures, band edge positions, and light absorption characteristics of nL ZnO could be further tuned by biaxial strain. nL ZnO under epitaxial tensile strain could maintain the stable graphite-like structure at a broader thickness range. Appropriate biaxial tensile strain could decrease the bandgap and enhance utilization of visible light. However, excessive biaxial tensile strain would destroy the position of the band edge and prevent nL ZnO from catalyzing water splitting. After testing, 6L ZnO under 1% biaxial tensile strain had direct bandgap of 2.07 eV, the best light absorption spectrum in this study, and it also had a suitable band edge position. Thus, with a suitable bandgap and band edge position, the stability and light absorption capacity can be tuned by biaxial strain, and nL ZnO is a promising material for photocatalytic water splitting.
Author Contributions
Conceptualization, X.C.; methodology, J.H.; formal analysis, S.Z. and Y.H.; investigation, X.T. and C.T.; data curation, K.Z.; writing—original draft preparation, G.J.; writing—review and editing, X.C. and Y.Z.; supervision, Z.F.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript. Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.
Funding
This research was funded by the National Key Research and Development Program of China, grant number: 2019YFA0705204, and the Heilongjiang Students’ Platform for innovation and entrepreneurship training program (No.201910214020), China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Christoforidis, K.C.; Fornasiero, P. Photocatalytic Hydrogen Production: A Rift into the Future Energy Supply. ChemCatChem 2017, 9, 1523–1544. [Google Scholar] [CrossRef]
- Hoffmann, M.R.; Martin, S.T.; Choi, W.; Bahnemann, D.W. Environmental Applications of Semiconductor Photocatalysis. Chem. Rev. 1995, 95, 69–96. [Google Scholar] [CrossRef]
- Chen, S.; Wang, L.-W. Thermodynamic Oxidation and Reduction Potentials of Photocatalytic Semiconductors in Aqueous Solution. Chem. Mater. 2012, 24, 3659–3666. [Google Scholar] [CrossRef]
- Hamid, S.B.A.; Teh, S.J.; Lai, C.W. Photocatalytic Water Oxidation on ZnO: A Review. Catalysts 2017, 7, 93. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef]
- Hoffman, R.L.; Norris, B.J.; Wager, J.F. ZnO-based transparent thin-film transistors. Appl. Phys. Lett. 2003, 82, 733–735. [Google Scholar] [CrossRef]
- Qiu, Y.; Yan, K.; Deng, H.; Yang, S. Secondary Branching and Nitrogen Doping of ZnO Nanotetrapods: Building a Highly Active Network for Photoelectrochemical Water Splitting. Nano Lett. 2011, 12, 407–413. [Google Scholar] [CrossRef]
- Kalantar-Zadeh, K.; Ou, J.Z.; Daeneke, T.; Mitchell, A.; Sasaki, T.; Fuhrer, M.S. Two dimensional and layered transition metal oxides. Appl. Mater. Today 2016, 5, 73–89. [Google Scholar] [CrossRef]
- Freeman, C.L.; Claeyssens, F.; Allan, N.L.; Harding, J.H. Graphitic Nanofilms as Precursors to Wurtzite Films: Theory. Phys. Rev. Lett. 2006, 96, 066102. [Google Scholar] [CrossRef]
- Tusche, C.; Meyerheim, H.L.; Kirschner, J. Observation of depolarized ZnO(0001) mono-layers: Formation of unreconstructed planar sheets. Phys. Rev. Lett. 2007, 99, 026102. [Google Scholar] [CrossRef]
- Wang, G.; Li, D.; Sun, Q.; Dang, S.; Zhong, M.-M.; Xiao, S.; Liu, G. Hybrid Density Functional Study on the Photocatalytic Properties of Two-dimensional g-ZnO Based Heterostructures. Nanomaterials 2018, 8, 374. [Google Scholar] [CrossRef]
- Peng, R.; Ma, Y.; Huang, B.; Dai, Y. Two-dimensional Janus PtSSe for photocatalytic water splitting under the visible or infrared light. J. Mater. Chem. A 2019, 7, 603–610. [Google Scholar] [CrossRef]
- Drmosh, Q.; Hezam, A.; Hossain, M.; Qamar, M.; Yamani, Z.; Byrappa, K. A novel Cs2O–Bi2O3–TiO2–ZnO heterostructure with direct Z-Scheme for efficient photocatalytic water splitting. Ceram. Int. 2019, 45, 23756–23764. [Google Scholar] [CrossRef]
- Ren, K.; Yu, J.; Tang, W. Two-dimensional ZnO/BSe van der waals heterostructure used as a promising photocatalyst for water splitting: A DFT study. J. Alloys Compd. 2020, 812, 152049. [Google Scholar] [CrossRef]
- Wang, S.; Ren, C.; Tian, H.; Yu, J.; Sun, M. MoS2/ZnO van der Waals heterostructure as a high-efficiency water splitting photocatalyst: A first-principles study. Phys. Chem. Chem. Phys. 2018, 20, 13394–13399. [Google Scholar] [CrossRef]
- Ren, K.; Luo, Y.; Yu, J.; Ren, K. Theoretical prediction of two-dimensional ZnO/GaN van der Waals heterostructure as a photocatalyst for water splitting. Chem. Phys. 2020, 528, 110539. [Google Scholar] [CrossRef]
- Deng, D.; Novoselov, K.S.; Fu, Q.; Zheng, N.; Tian, Z.; Bao, X. Catalysis with two-dimensional materials and their heterostructures. Nat. Nanotechnol. 2016, 11, 218–230. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Huang, W.; Hu, W.; Yang, K.; Zhou, B.-X.; Pan, A.; Huang, G. Two-Dimensional MoS2-Graphene-Based Multilayer van der Waals Heterostructures: Enhanced Charge Transfer and Optical Absorption, and Electric-Field Tunable Dirac Point and Band Gap. Chem. Mater. 2017, 29, 5504–5512. [Google Scholar] [CrossRef]
- Yu, W.; Wang, X.; Li, C. Tuning the Electronic Structure of ZnO Bilayer: A First-Principles Study. J. Nanosci. Nanotechnol. 2019, 19, 2839–2843. [Google Scholar] [CrossRef]
- Gao, X.; Shen, Y.; Ma, Y.; Wu, S.; Zhou, Z. ZnO/g-GeC van der Waals heterostructure: Novel photocatalyst for small molecule splitting. J. Mater. Chem. C 2019, 7, 4791–4799. [Google Scholar] [CrossRef]
- Wang, C.; Wang, W.-H.; Lu, F.; Cheng, Y.; Ren, L.; Wang, W.; Liu, H. Pure and Oxidized Ag Substrate Influence on the Phase Transformation and Semiconducting Behaviors of Layered ZnO: A First-Principles Study. J. Phys. Chem. C 2015, 119, 4891–4897. [Google Scholar] [CrossRef]
- Tom, K.B.; Lin, S.; Wan, L.F.; Wang, J.; Ahlm, N.; N’Diaye, A.T.; Bustillo, K.C.; Huang, J.; Liu, Y.; Lou, S.; et al. Solution-Based, Template-Assisted Realization of Large-Scale Graphitic ZnO. ACS Nano 2018, 12, 7554–7561. [Google Scholar] [CrossRef]
- Niemelä, J.-P.; Aghaee, M.; Kessels, W.E.; Creatore, M.; Verheijen, M.A. Transition in layer structure of atomic/molecular layer deposited ZnO-zincone multilayers. J. Vac. Sci. Technol. A 2019, 37, 040602. [Google Scholar] [CrossRef]
- Quang, H.T.; Bachmatiuk, A.; Dianat, A.; Ortmann, F.; Zhao, J.; Warner, J.H.; Eckert, J.; Cuniberti, G.; Rümmeli, M.H. In Situ Observations of Free-Standing Graphene-like Mono- and Bilayer ZnO Membranes. ACS Nano 2015, 9, 11408–11413. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Bhatti, K.; Qindeel, R.; Alonizan, N.; Althobaiti, H.S. Characterizations of multilayer ZnO thin films deposited by sol-gel spin coating technique. Results Phys. 2017, 7, 651–655. [Google Scholar] [CrossRef]
- Wu, D.; Lagally, M.G.; Liu, F. Stabilizing Graphitic Thin Films of Wurtzite Materials by Epitaxial Strain. Phys. Rev. Lett. 2011, 107, 236101. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Sorescu, D.C.; Deng, X. Tunable Lattice Constant and Band Gap of Single- and Few-Layer ZnO. J. Phys. Chem. Lett. 2016, 7, 1335–1340. [Google Scholar] [CrossRef]
- Guan, Z.; Ni, S.; Hu, S. Tunable Electronic and Optical Properties of Monolayer and Multilayer Janus MoSSe as a Photocatalyst for Solar Water Splitting: A First-Principles Study. J. Phys. Chem. C 2018, 122, 6209–6216. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, N.; Zhou, S.; Zhao, J. Two-dimensional ZnO for the selective photoreduction of CO2. J. Mater. Chem. A 2019, 7, 16294–16303. [Google Scholar] [CrossRef]
- Behera, H.; Mukhopadhyay, G. Strain-tunable band parameters of ZnO mono-layer in graphene-like honeycomb structure. Phys. Lett. A 2012, 376, 3287–3289. [Google Scholar] [CrossRef]
- Zhuang, H.L.; Hennig, R.G. Single-Layer Group-III Monochalcogenide Photocatalysts for Water Splitting. Chem. Mater. 2013, 25, 3232–3238. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B.; Wang, J.; Yuan, Y.; Zhang, Q.; Gao, Z.; Liu, L.-M.; Chen, L. The stabilities and electronic structures of single-layer bismuth oxyhalides for photocatalytic water splitting. Phys. Chem. Chem. Phys. 2014, 16, 25854–25861. [Google Scholar] [CrossRef] [PubMed]
- Kaewmaraya, T.; De Sarkar, A.; Sa, B.; Sun, Z.; Ahuja, R. Strain-induced tunability of optical and photocatalytic properties of ZnO mono-layer nanosheet. Comput. Mater. Sci. 2014, 91, 38–42. [Google Scholar] [CrossRef]
- Chen, H.F.; Tan, C.L.; Zhang, K.; Zhao, W.B.; Tian, X.H.; Huang, Y.W. Enhanced photocatalytic performance of ZnO mono-layer for water splitting via biaxial strain and external electric field. Appl. Surf. Sci. 2019, 481, 1064–1071. [Google Scholar] [CrossRef]
- Tu, Z. First-Principles Study on Physical Properties of a Single ZnO Monolayer with Graphene-Like Structure. J. Comput. Theor. Nanosci. 2010, 7, 1182–1186. [Google Scholar] [CrossRef]
- Trasatti, S. The absolute electrode potential: An explanatory note (Recommendations 1986). Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar] [CrossRef]
- Kanan, D.K.; Carter, E.A. Band Gap Engineering of MnO via ZnO Alloying: A Potential New Visible-Light Photocatalyst. J. Phys. Chem. C 2012, 116, 9876–9887. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Abinitio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 13115–13118. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- White, J.A.; Bird, D. Implementation of gradient-corrected exchange-correlation potentials in Car-Parrinello total-energy calculations. Phys. Rev. B 1994, 50, 4954–4957. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Jurecka, P.; Cerny, J.; Hobza, P.; Salahub, D.R. Density functional theory augmented with an empirical dispersion term. Interaction energies and geometries of 80 noncovalent complexes compared with ab initio quantum mechanics calculations. J. Comp. Chem. 2007, 28, 555–569. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Yang, J. First-principles study of two-dimensional van der Waals heterojunctions. Comput. Mater. Sci. 2016, 112, 518–526. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Chowdhury, C.; Karmakar, S.; Datta, A. Monolayer Group IV–VI Monochalcogenides: Low-Dimensional Materials for Photocatalytic Water Splitting. J. Phys. Chem. C 2017, 121, 7615–7624. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).