New Method of Determining Kinetic Parameters for Decomposition of Hydrogen Peroxide by Catalase

Abstract

The presented study investigates the kinetic properties of catalase during hydrogen peroxide decomposition reaction. A novel and simple method is hereby proposed for the determination of the enzyme deactivation rate constant (k_d) and the decomposition of H₂O₂ reaction rate constant (k_r). Available methods allow the k_d constant to be determined only based on previously experimentally determined k_r. The presented method differs from the conventional procedure. Known initial and final concentrations of hydrogen peroxide enable determination of both constants at the same time based on data from only one experiment. The correctness of the new method proposed here in determining the reaction rate constant was checked by comparing the obtained constant values with the calculated values according to the commonly used Aebi method. The method was used to analyze in detail the effect of pH (3–10) and temperature (10–45 °C) of the reaction medium on kinetic constants. The value of the constant k_d increases together with the value of pH and temperature. In addition, the activation energy for decomposition reaction and deactivation reaction was found to be E_r = 14 kJ mol⁻¹ and E_d = 56.8 kJ mol⁻¹ respectively.

1. Introduction

Enzymes are highly efficient and selective biological catalysts under specific conditions, which makes their use extremely popular in various bioprocesses [1,2]. One of the common enzymes ubiquitously found in all living organisms is catalase [3,4]. Enzymes from various sources exhibit some differences in structure and properties [5,6,7]; nevertheless, all of them decompose hydrogen peroxide into molecular oxygen and water in the two-step process shown in Equation (1). In the first step, the heme-containing catalase bonds with and breaks up a molecule of hydrogen peroxide into harmless water and oxygen atom. This oxygen atom is joined to the iron atom present in the heme (Compound I). In the next step, a second hydrogen peroxide molecule binds and is also divided into two parts. After the second oxygen atom is attached to the iron atom the molecules of water and oxygen gas are released [8].

$$\mathrm{Catalase}\stackrel{+{\mathrm{H}}_2{\mathrm{O}}_2;-{\mathrm{H}}_2\mathrm{O}}{\to }\mathrm{Compound}\mathrm{I}\stackrel{+{\mathrm{H}}_2{\mathrm{O}}_2;-{\mathrm{H}}_2\mathrm{O},-{\mathrm{O}}_2}{\to }\mathrm{Catalase}$$

(1)

When H₂O₂ concentration is low, catalase can return to the native enzyme oxidizing secondary two-electron donors, e.g., low molecular alcohols (peroxidatic activity). A secondary two-electron donor participates in the second step of Equation (1) [9]. However, under certain conditions, Compound II can be created, but it cannot be effectively reduced to the native enzyme and therefore its accumulation leads to the catalase deactivation. Catalases may also form another intermediate product known as Compound III and are generally inactive towards most electron donors. Compound III structurally resembles oxy forms of mioglobin and hemoglobin. It can be generated in the reactions of Compound II with hydrogen peroxide, or ferric catalases with superoxide [9].

Catalase has a number of uses including food processing, the pharmaceutical and cosmetics industry, textiles, paper production, medical fields and also the bioremediation field [10,11]. Application of catalase in industrial processes is limited by the inability to withstand harsh operating conditions, e.g., high temperatures, extreme pH values, high detergent concentrations and high organic solvent concentrations [12]. The activity of the enzyme is lost due to changes in its spatial structure or polypeptide chain ruptures. Many operations have been applied in order to improve the use of enzymes in industry processes. The most popular of these is immobilization [13,14,15,16], which not only improves the catalytic stability of the enzyme but also allows its repeated use. There are also many reports on the improvement of enzyme activity using molecular biology methods [17,18]. Each technique is based on knowledge of the catalytic reaction mechanisms and the accompanying deactivation processes. Therefore, it is so important to look for new methods for determining the kinetic parameters of reactions that give us better understanding of the phenomena occurring during the reaction.

Decomposition of hydrogen peroxide using enzymes and deactivation of catalase follow first order kinetics with respect to the enzyme and substrate [19]. It has been shown that bovine liver catalase is both reversibly inhibited and irreversibly deactivated at high hydrogen peroxide concentration. Kinetic modeling has highlighted the role of Compound III in both types of activity loss [20]. Due to the phenomenon of substrate catalase deactivation, the use of this first order kinetics equation is only valid for low concentrations of hydrogen peroxide [21]. Information regarding the deactivation of catalase during the decomposition of hydrogen peroxide available in the literature refers mainly to deactivation using the substrate. There is no research concerning the effect of pH and temperature of the reaction mixture on bovine liver catalase deactivation rate.

Deactivation of catalase using substrate can be caused by the creation of inactive Compound II. Compound I from Equation (1) is an enzyme from an oxyferryl group with a π-cationic porphyrin radical. Forming of Compound II can result from the reduction of Compound I using a single electron (Equation (2) [22]).

$$\mathrm{Compound}\mathrm{I}({\mathrm{por}}^{+●}-{\mathrm{Fe}}^{\mathrm{IV}}=\mathrm{O})+{\mathrm{e}}^{-}\to \mathrm{Compound}\mathrm{II}(\mathrm{por}-{\mathrm{Fe}}^{\mathrm{IV}}=\mathrm{O})$$

(2)

The possibility of creating a hydroxyferryl form of Compound II was also demonstrated [23]:

$$\mathrm{Compound}\mathrm{I}({\mathrm{por}}^{+●}-{\mathrm{Fe}}^{\mathrm{IV}}=\mathrm{O})+\mathrm{H}({\mathrm{H}}^{+}+{\mathrm{e}}^{-})\to \mathrm{Compound}\mathrm{II}(\mathrm{por}-{\mathrm{Fe}}^{\mathrm{IV}}-\mathrm{OH})$$

(3)

Based on the above equations, the catalase deactivation is described using first order kinetics, and the dependence of the reaction rate, v_d, on H₂O₂ concentration assumes the following form:

$${\mathrm{v}}_{\mathrm{d}}={\mathrm{k}}_{\mathrm{d}}{\mathrm{C}}_{\mathrm{S}}{\mathrm{C}}_{\mathrm{E}}$$

(4)

where C_S and C_E represent the hydrogen peroxide concentration and active enzyme concentration respectively and k_d is the enzyme deactivation rate constant.

This article provides a general mathematical procedure for the simulation of biochemical reactors operated batchwise when both the enzyme catalyzed reaction and the enzyme deactivation reaction take place. A novel method is proposed in order to calculate the kinetic parameters of enzyme reaction and deactivation. The effect of pH and temperature on the reaction rate constant of H₂O₂ decomposition and the rate constant of deactivation during the enzymatic process were analyzed in detail. Unlike the ordinary kinetic assays performed in a short time, the presented method requires determination of the final substrate concentration when the enzyme is completely deactivated. The method is based on experimental data from the decomposition of hydrogen peroxidase using bovine liver catalase.

Catalase is one of the first enzymes obtained in crystalline form and a series of studies have been carried out on its activity, applications and methods of immobilization. However, the mechanism of action on H₂O₂ and the effects of environmental factors is still unclear. Catalase activity is significantly affected by the pH values of the aqueous medium and temperature [24]. So far, no one has studied the impact of these two factors on the kinetic parameters for hydrogen peroxide decomposition reaction using bovine liver catalase in wide range. Literature data is fragmentary and inconsistent [21,25,26,27,28]. Therefore, this study analyzed in detail the effect of pH and temperature on the reaction rate constant of H₂O₂ decomposition and the rate constant of deactivation during the enzymatic process.

2. Results and Discussion

A new element in the presented study is the method of determining k_d. In other works [21,25,26], the algorithm of operation assumes determining first the value k based on the known initial concentration of the enzyme and on the initial linear slope of a first-order plot. Then, the value of k_d was calculated. In this work there is no need to know the reaction rate constant of H₂O₂ decomposition, but one has to be sure that all the used enzyme is engaged and the final concentration of H₂O₂ is achieved.

2.1. Effect of pH

To determine the kinetic parameters of the decomposition of H₂O₂, the reaction has to run with the excess substrate (Figure 1). The presented method also requires that the reaction has to last long enough to find a final concentration (C_SF) of H₂O₂ after total deactivation of the enzyme (

Table 1. Initial (C_S0) and final (C_SF) concentration of hydrogen peroxide at different pH.

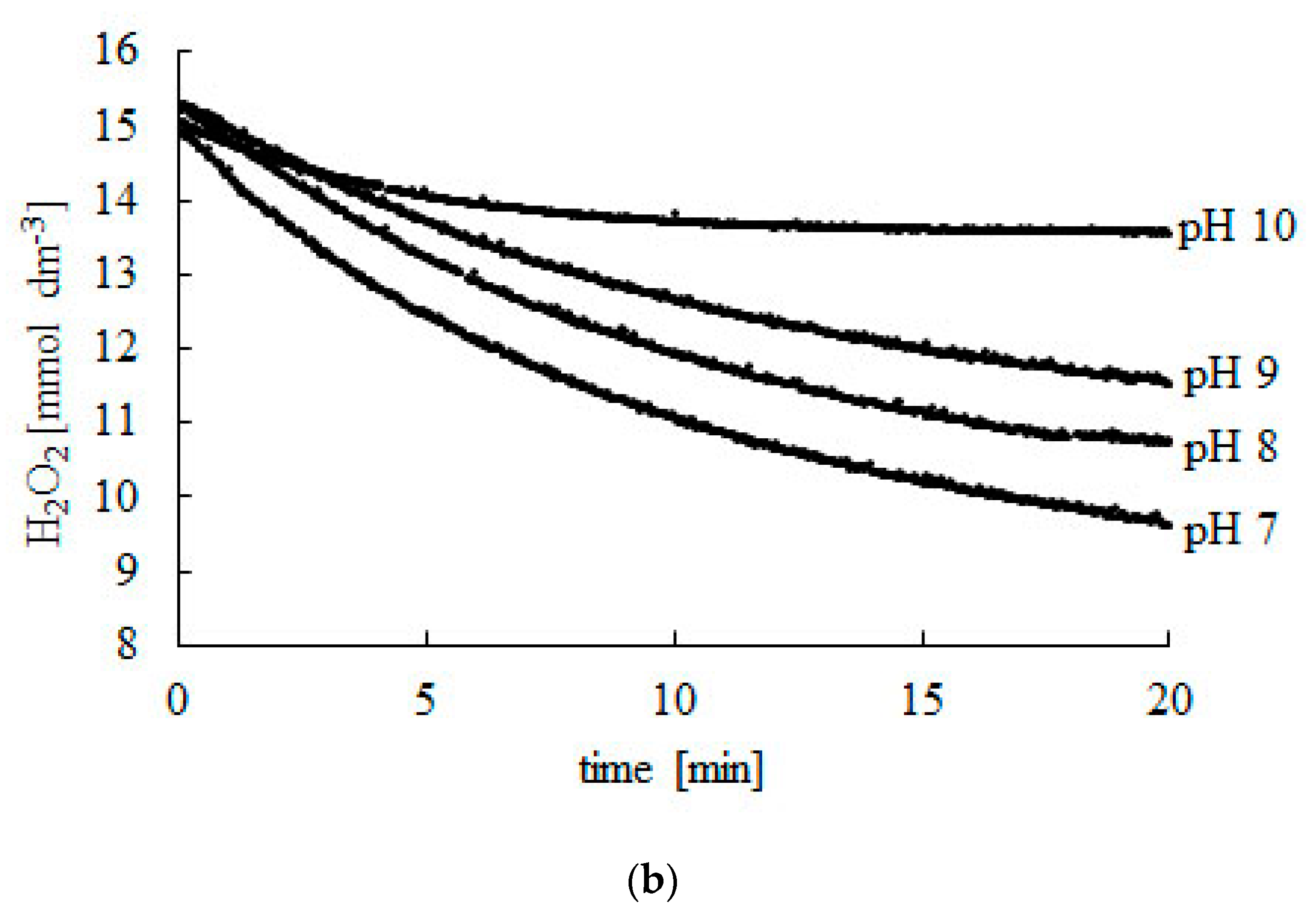
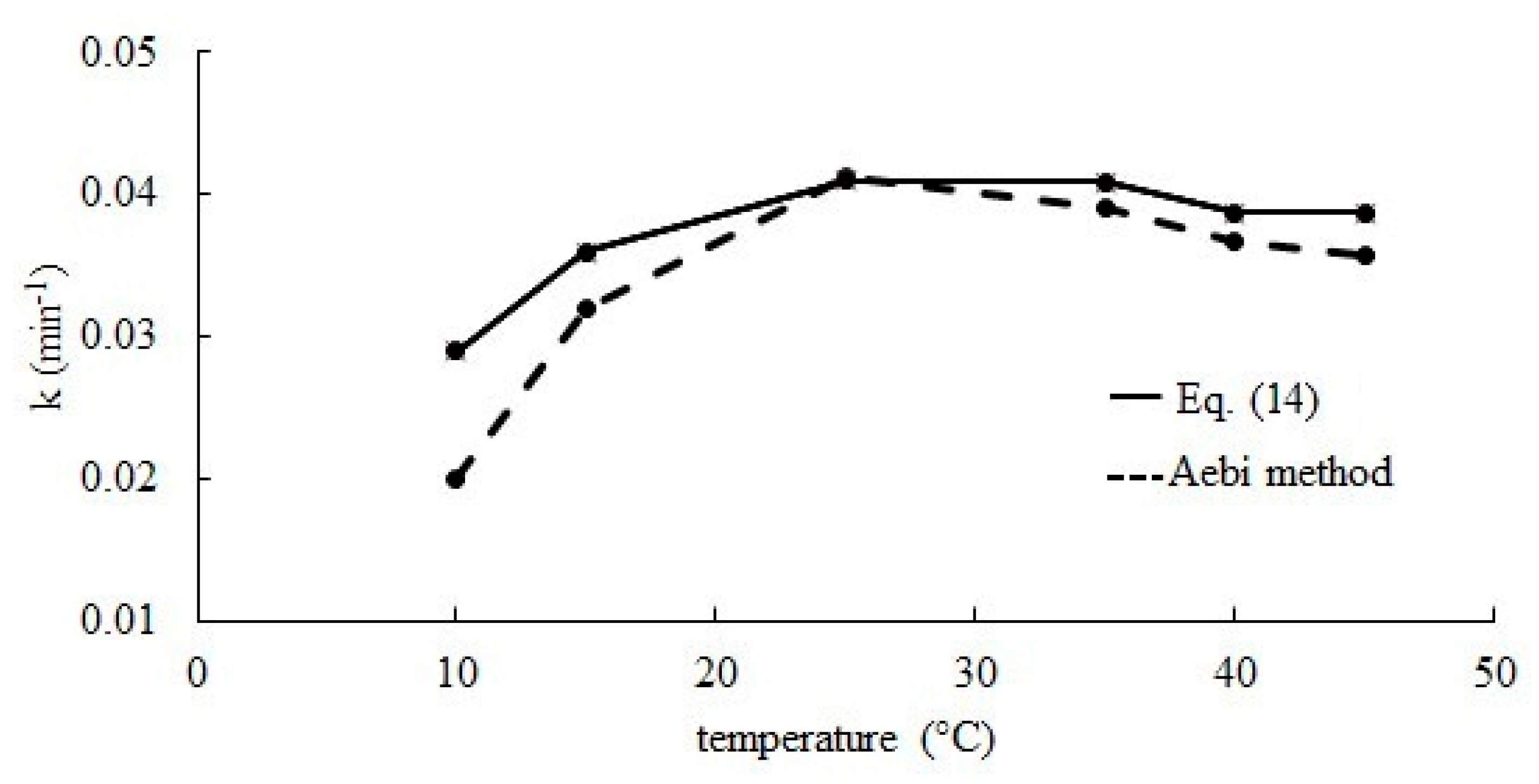
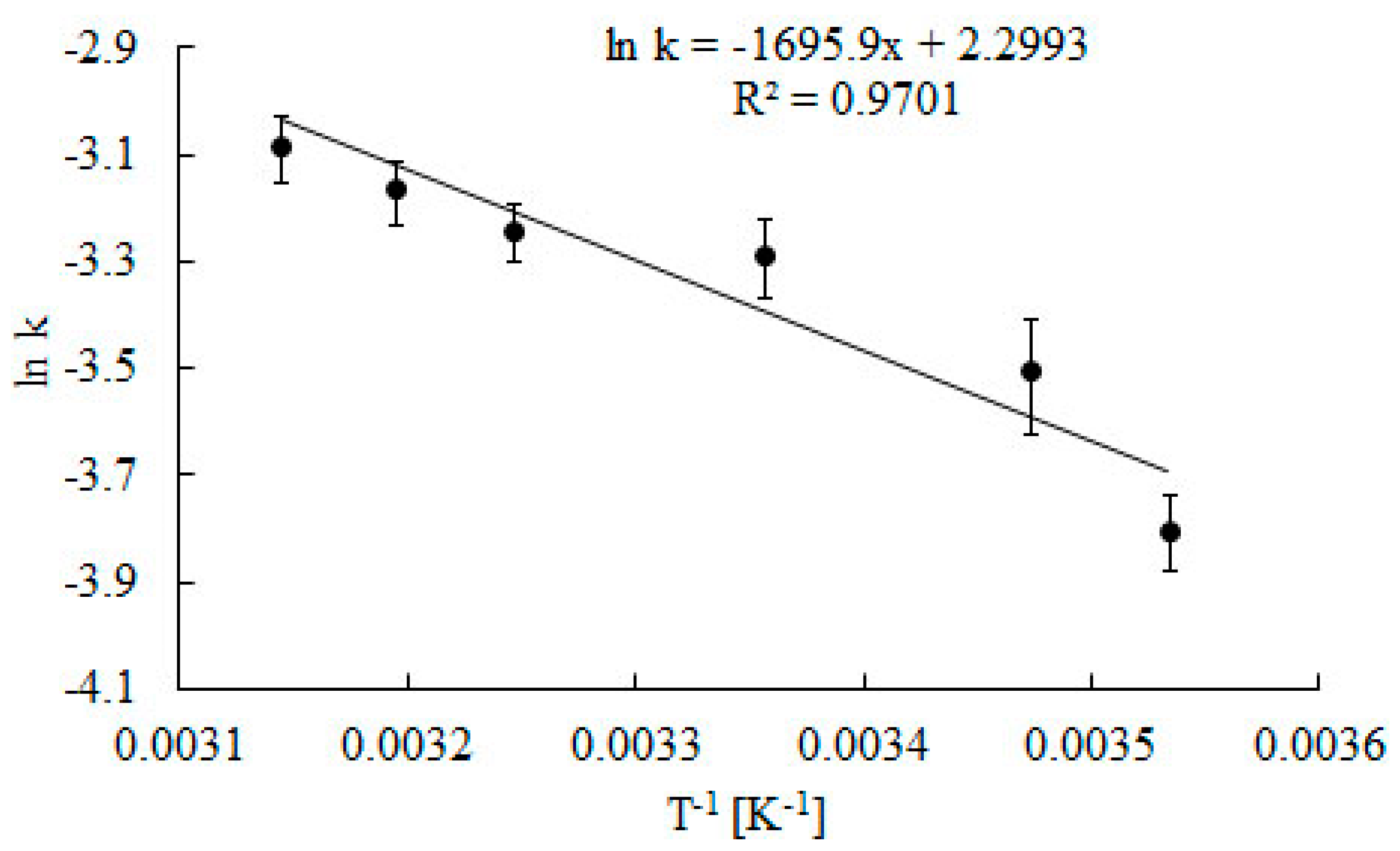
pH	CS0 (mmol dm−3)	CSF (mmol dm−3)	Time (min)
3	15.06	11.79	40
4	15.02	11.61	50
5	15.17	10.25	60
6	15.08	9.39	70
7	14.98	8.70	80
8	15.10	9.04	40
9	14.96	10.66	40
10	15.05	13.48	12

).

For known values of C_S0 and ΔC_S, based on Equation (14) the plots of f(C_S) vs. time for each pH were created (Figure 2). Afterwards, linear regressions were performed and the values of k_d were determined from the slope of the solid line. The R² coefficients were determined, and their values were higher than 0.98 for each case. These results demonstrate that the regressions are highly significant. The closer the R² is to 1, the stronger the model is and the better it predicts the response.

Figure 3 shows the effect of the pH of the reaction medium on the rate constant of the deactivation process. Changing the buffer used to ensure an adequate pH value may affect catalase activity [29]. To ensure the reliability of the results, experiments were performed using two different buffers on the border of their operation. Values of k_d were very similar. In accordance to the line of the graph, the value of the constant k_d increases together with pH.

So far, no one has presented research on the effect of pH on deactivating bovine liver catalase for the H₂O₂ decomposition reaction. In the literature, the deactivation constant can only be found for pH 7. The value of the constant k_d determined by the presented method for this pH is 7.85 dm³ mol⁻¹ min⁻¹ and is ca. 13% and 6% lower than those determined by Deluca et al. [26] and Feuers et al. [25].

For known values of the enzyme deactivation rate constant (k_d) and ΔC_S, based on Equation (12) the reaction rate constants k were determined. The reaction rate constant was also calculated using the Aebi method [30], based on the results of the decrease in the substrate concentration during the first minute of the experiment. The calculation results for both methods are presented in Figure 4.

Figure 4 shows changes in the hydrogen peroxide decomposition rate constant value, which depends on the pH ranging from 3 to 10. The results obtained for the constant k using the presented method, based on Equation (12), are in all cases slightly higher and do not differ much from those calculated according to the Aebi method [30]; this result proves the correctness of the presented method. The Aebi method assumes that deactivation can be omitted because the measurement time is very short. In fact, with about a one-minute measurement time, slight deactivation should occur, and a lower reaction rate constant (97% to 99%) can be explained in this way. From the plot we can observe a high k value within the range of 6–8, while below and above this range, a significant decrease of rate constant is noticed. The curve shape from Figure 4 will be identical for the relation k_r to pH, therefore it can be compared with the results presenting activity. Similar results were obtained by Kaushal et al. [11]. Activity of catalase decreased by 50% at pH 9, but in the acid region it decreased by ca. 80%. The acid segment of the curve also differs from what was obtained by Chance [27]; this result can be caused by usage of different buffer in this range of pH. Most studies on catalase activity at various pH were conducted in a narrow pH range. The curve (Figure 4) is also consistent with the Góth’s [28] results, however a comparison is only possible in the range of 6–8.

2.2. Effect of Temperature

Among the parameters affecting enzyme activity, temperature is the most important because it can be easily manipulated, and it affects not only the catalytic reaction rate but also the rate of deactivation of the enzyme [24]. The effect of temperature on the kinetic parameters of decomposition of H₂O₂ was studied in this work by carrying out the reaction at different temperatures of reaction medium, in the range of 10–45 °C. The rate constant of deactivation during the enzymatic process and reaction rate constant of H₂O₂ decomposition were determined in the same way as for pH effect analysis. The rate constants k_d were calculated as the slope of the line from Figure 2. The results, with their standard deviations SD and determination coefficients R², are presented in

Table 2. Effect of the temperature of the reaction medium on the rate constant of deactivation during the enzymatic process, pH = 7. Data for which R² values are not reported are from the literature cited.

Temperature (°C)	kd ± SD (dm3 mol−1 min−1)	R2
10	1.83 ± 0.15	0.989
15	2.32 ± 0.21	0.994
25	7.85 ± 0.22	0.998
35	13.04 ± 0.54	0.991
40	16.42 ± 1.90	0.990
45	24.81 ± 3.30	0.989
25	8.9	Deluca et al. [26]
25	8.34	Feuers et al. [25]
27	6.86	Ghadermarzi and Moosavi-Movahedi [21]

.

From the data shown in Table 2, it was observed that the constant k_d increases together with temperature. It was detected that k_d increased ca. 14 times whilst temperature increased from 10 °C to 45 °C. It is clear that in the conditions adopted in these tests, 45 °C is not a convenient temperature for the process and a lower value should be adopted.

The rate constant of deactivation k_d values for catalase from bovine liver are much higher than those obtained by Miłek [31] for fungal catalase. Comparing the results (Figure 5) confirms that catalase from animal tissues more easily tends to convert into a catalytically inactive form than those obtained from microorganisms.

Rate constants of catalase deactivation were presented as an Arrhenius plot (Figure 6), and the activation energy for catalase deactivation was estimated (E_d = 56.8 kJ mol⁻¹).

Values of the determination coefficient (R² = 0.9813) points out goodness of regression, which can be used to explain 98.13% of total variation in the response. The activation energy of catalase deactivation is three times lower than the activation energy for catalase deactivation in water in the presence of substrate estimated by Cantemir et al. [29].

Based on known values of k_d, ΔC_S and Equation (12) reaction rate constants k were determined. The obtained results were compared with those calculated according to the Aebi method [30]. The results obtained with both methods do not differ significantly from each other. Effect of the temperature of the reaction medium on the hydrogen peroxide decomposition rate constant is presented in Figure 7 for temperatures of 10–45 °C. Together with temperature increase, a large increase of the reaction rate constant value is observed, but after exceeding 25 °C, constant k does not change significantly.

Figure 8, the Arrhenius activation energy for decomposition of H₂O₂ was determined. Value of E_r was calculated to be 14 kJ mol⁻¹ and is slightly higher than estimated by Góth [28]. For an enzyme from the same supplier (Sigma), the activation energy is reduced by 5.8 kJ mol⁻¹. However, catalase activity was measured using a different method. Moreover, activation energy was calculated according to the Arrhenius plot, based on determination of enzyme activities at four temperatures in a narrow range between 20 and 33 °C. The value of calculated activation energy for decomposition of H₂O₂ is four times lower than the catalase deactivation energy. The energy necessary to start the deactivation reaction is much higher than the energy needed to initiate the catalytic reaction. This result confirms other authors’ findings [31,32,33].

3. Materials and Methods

3.1. Materials

For all experiments, bovine liver catalase (EC 1.11.1.6) was purchased from Sigma Aldrich (Poznań, Poland). Hydrogen peroxide (H₂O₂, 30%), monosodium phosphate (NaH₂PO₄), sodium phosphate dibasic heptahydrate (Na₂HPO₄∙7H₂O), acetic acid (CH₃COOH, 99%), sodium acetate (CH₃COONa), phosphoric acid (H₃PO₄, 85%), boric acid (H₃BO₃, 99%) were purchased from Avantor Performance Materials Poland S.A. (Gliwice, Poland).

3.2. Decomposition of Hydrogen Peroxide

Decomposition of hydrogen peroxide was measured using the method of Beers and Sizer [34]. Spectrophotometer Helios was used to measure the decrease in the absorbance (at 240 nm) during the decomposition of H₂O₂. The system allows for continuous reading of absorbance. Reaction was carried out within the isothermal batch reactor with mixing. Decomposition of hydrogen peroxide was started by adding a buffered catalase solution (pH 7, 17.5 U mL⁻¹). Initial concentration of H₂O₂ in the reaction mixture was chosen to be 15 mmol dm⁻³. The substrate concentrations were calculated using the Lambert-Beer law, with extinction coefficient 39.4 M⁻¹ cm⁻¹. A number of preliminary tests were performed to ensure that observed effects were caused by enzyme deactivation and not due to exhaustion of substrate, inhibition by reaction byproducts or slow heating of samples.

3.3. Determination of Kinetic Parameters

Consideration of an isothermal reactor with perfect mixing gives a system of two ordinary differential equations

$$-\frac{\mathrm{d}{C}_S}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{r}}{\mathrm{C}}_{\mathrm{E}}{\mathrm{C}}_{\mathrm{S}}$$

(5)

$$-\frac{{\mathrm{dC}}_{\mathrm{E}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}{\mathrm{C}}_{\mathrm{E}}{\mathrm{C}}_{\mathrm{S}}$$

(6)

where C_S and C_E represent the hydrogen peroxide concentration and active enzyme concentration respectively. The initial conditions are C_S (t = 0) = C_S0 and C_E (t = 0) = C_E0. First one kinetic model (Equation (5)) describes decomposition of hydrogen peroxide reaction with k_r as a rate constant. The second model (Equation (6)) defines deactivation of catalase with k_d as a rate constant. Measurement of active enzyme concentration during the experiment is not possible. It is convenient to introduce the fraction of catalase activity

$$\mathrm{A}=\frac{{\mathrm{C}}_{\mathrm{E}}}{{\mathrm{C}}_{\mathrm{E}0}}$$

(7)

where k = k_rC_E0, and the initial conditions are C_S (t = 0) = C_S0 and A (t = 0) = 1 for Equations (5) and (6) are as follows:

$$-\frac{{\mathrm{dC}}_{\mathrm{S}}}{\mathrm{dt}}={\mathrm{kAC}}_{\mathrm{S}}$$

(8)

$$-\frac{\mathrm{dA}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}{\mathrm{AC}}_{\mathrm{S}}$$

(9)

Integration of differential Equations (5) and (6) for k ≠ k_dC_S0 gives

$$\mathrm{A}=1-\frac{{\mathrm{k}}_{\mathrm{d}}}{\mathrm{k}}({\mathrm{C}}_{S_0}-C_S)$$

(10)

In a certain case where k = k_dC_S0 hydrogen peroxide concentration is given by

$${\mathrm{C}}_{\mathrm{S}}=\frac{{\mathrm{C}}_{\mathrm{S}0}}{\mathrm{kt}+1}$$

(11)

The determination of the k and k_d constants can easily be carried out when the amount of used catalase is not sufficient to decompose the total amount of H₂O₂ because the enzyme will be completely deactivated. In such a case, the difference in substrate concentrations for the final activity of catalase A = 0 is described based on Equation (10) in the following way:

$${\mathrm{C}}_{\mathrm{S}0}-{\mathrm{C}}_{\mathrm{SF}}={\Delta \mathrm{C}}_{\mathrm{S}}=\frac{\mathrm{k}}{{\mathrm{k}}_{\mathrm{d}}}$$

(12)

Based on Equations (10) and (12) and after rearranging (supplement material) we obtain

$$\frac{\ln \left(\frac{{\mathrm{C}}_{\mathrm{S}}{\Delta \mathrm{C}}_{\mathrm{S}}}{{\mathrm{C}}_{\mathrm{S}0}({\mathrm{C}}_{\mathrm{S}}+{\Delta \mathrm{C}}_{\mathrm{S}}-{\mathrm{C}}_{\mathrm{S}0})}\right)}{{\mathrm{C}}_{\mathrm{S}0}-{\Delta \mathrm{C}}_{\mathrm{S}}}={\mathrm{k}}_{\mathrm{d}}\mathrm{t}$$

(13)

From Equation (13), the enzyme deactivation rate constant k_d can be taken from linear regression on Equation (14).

$$\mathrm{f}(C_S)=\frac{\ln \left(\frac{{\mathrm{C}}_{\mathrm{S}}{\Delta \mathrm{C}}_{\mathrm{S}}}{{\mathrm{C}}_{\mathrm{S}0}({\mathrm{C}}_{\mathrm{S}}+{\Delta \mathrm{C}}_{\mathrm{S}}-{\mathrm{C}}_{\mathrm{S}0})}\right)}{{\mathrm{C}}_{\mathrm{S}0}-{\Delta \mathrm{C}}_{\mathrm{S}}}={\mathrm{k}}_{\mathrm{d}}\mathrm{t}$$

(14)

where the slope is equal to the enzyme deactivation rate constant. Using the known values of k_d and ΔC_S, reaction rate constant k can be calculated.

3.4. Effect of pH and Temperature

The effect of pH on the kinetic parameters was analyzed by carrying out the decomposition reaction of buffered hydrogen peroxide solution 15 mmol dm⁻³ at 25 °C over the pH range 3–10 using the following buffers: 0.05 M Britton and Robinson (pH 3–4, pH 8–10), 0.05 M acetate (pH 4–6) and 0.05 M phosphate (pH 6–8).

Further insight into details of the decomposition of hydrogen peroxide and deactivation of catalase was gained from the temperature dependence of rate constants. The effect of temperature was tested performing decomposition reactions in various temperatures ranging from 10 to 45 °C. The experimental data analysis was based on the Arrhenius relationship

$${\mathrm{k}}_{\mathrm{d}}={\mathrm{k}}_{\mathrm{d}0}\exp \left(\frac{-{\mathrm{E}}_{\mathrm{D}}}{\mathrm{RT}}\right)$$

(15)

where k_d0 is specific constant for the deactivation, E_D is an activation energy for enzyme deactivation, R is the universal gas constant and T is the absolute temperature. The E_D was evaluated from the linear regression ln(k_d) vs. T⁻¹. Catalase activation energy E_r for H₂O₂ decomposition was also determined using the Arrhenius equation

$$\mathrm{k}={\mathrm{k}}_0\exp \left(\frac{-{\mathrm{E}}_{\mathrm{r}}}{\mathrm{RT}}\right)$$

(16)

where k₀ is specific constant for the reaction of H₂O₂ decomposition. After plotting ln(k) vs. T⁻¹, the activation energy was estimated from the slope of the linear portion of the plot.

3.5. Statistical Analysis

Calculations for rate constants and activation energy were performed using Microsoft Excel 2016 and StatSoft Statistica (Krakow, Poland). The value of rate constants for deactivation of catalase were determined using linear regression using the least squares method (Levenberg-Marquardt). Basic descriptive statistics have been used, such as mean standard deviations and determination coefficient R². Fisher’s least significant difference (LSD) was carried out at a 95% confidence interval to check the significance difference among the means—the mean square due to regression and the mean square due to error.

4. Conclusions

This study presents a new method to establish the kinetic parameters for hydrogen peroxide decomposition reaction using catalase from bovine liver. It has been shown that it is possible to determine the k_d constant only using data of H₂O₂ concentration changes. In addition, this method allows the determination of both k_d and k_r constants at the same time based on one experiment. The results of the constant reaction rate of H₂O₂ decomposition obtained using the presented method are very close to the results calculated using the popular Aebi method [30]. Research confirms the range of pH to achieve the high values of the rate constant, i.e., 6–8. Studies have also shown the degree of deactivation of the enzyme which occurs in parallel with the reaction of hydrogen peroxide decomposition. The method might be applicable to enzymes in general and can be used to determine if the enzyme exposed to external factors undergoes mechanisms of deactivation.