Solid Oxide Fuel Cell Performance Analysis through Local Modelling
Abstract
:1. Introduction
2. Electrochemical Process Modelling
2.1. The SIMFC Code and its Kinetic Core
2.2. The Reference Equivalent Circuit
3. Result and Discussion
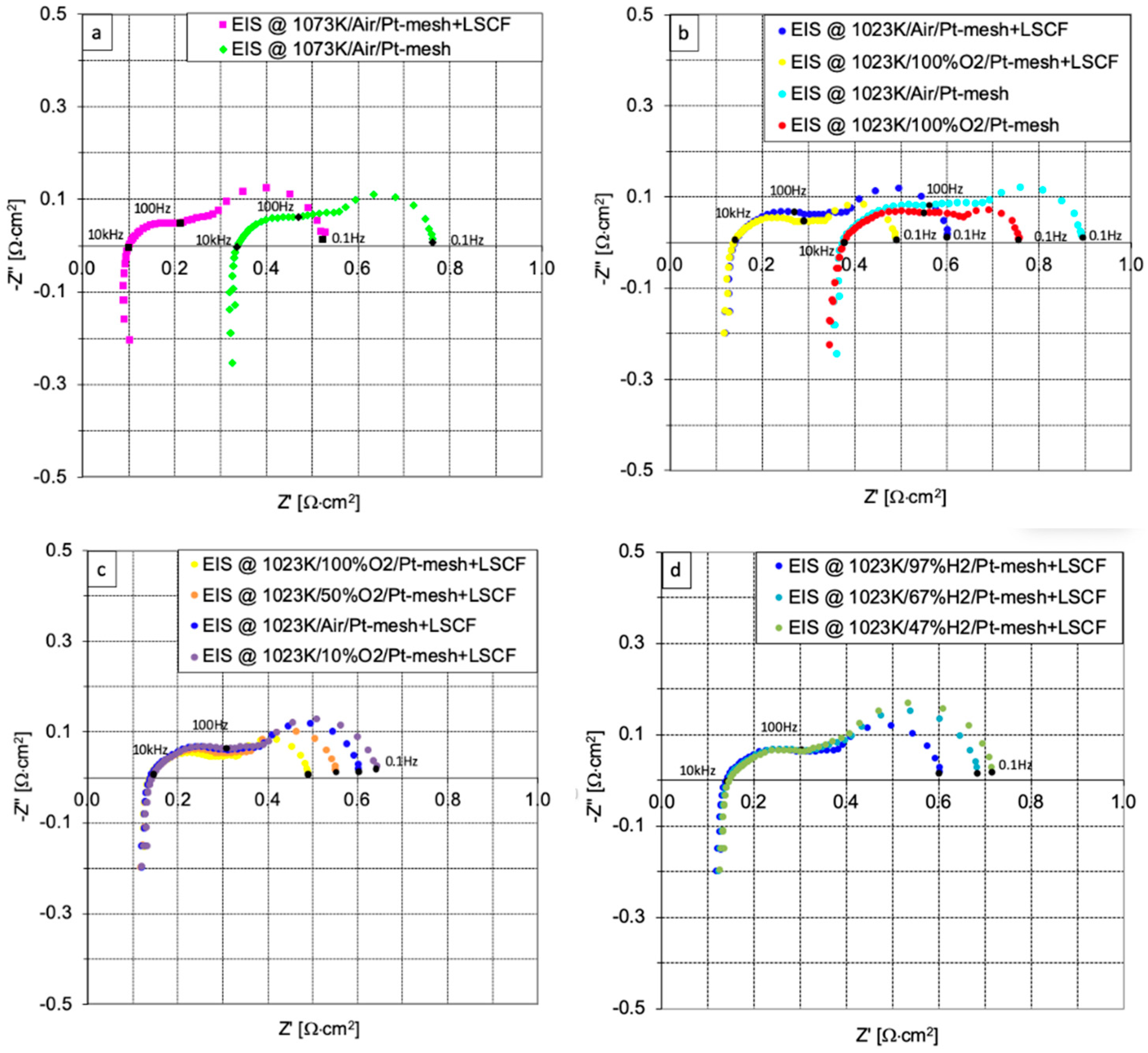
3.1. EIS Analysis and Kinetics Parameter Identification
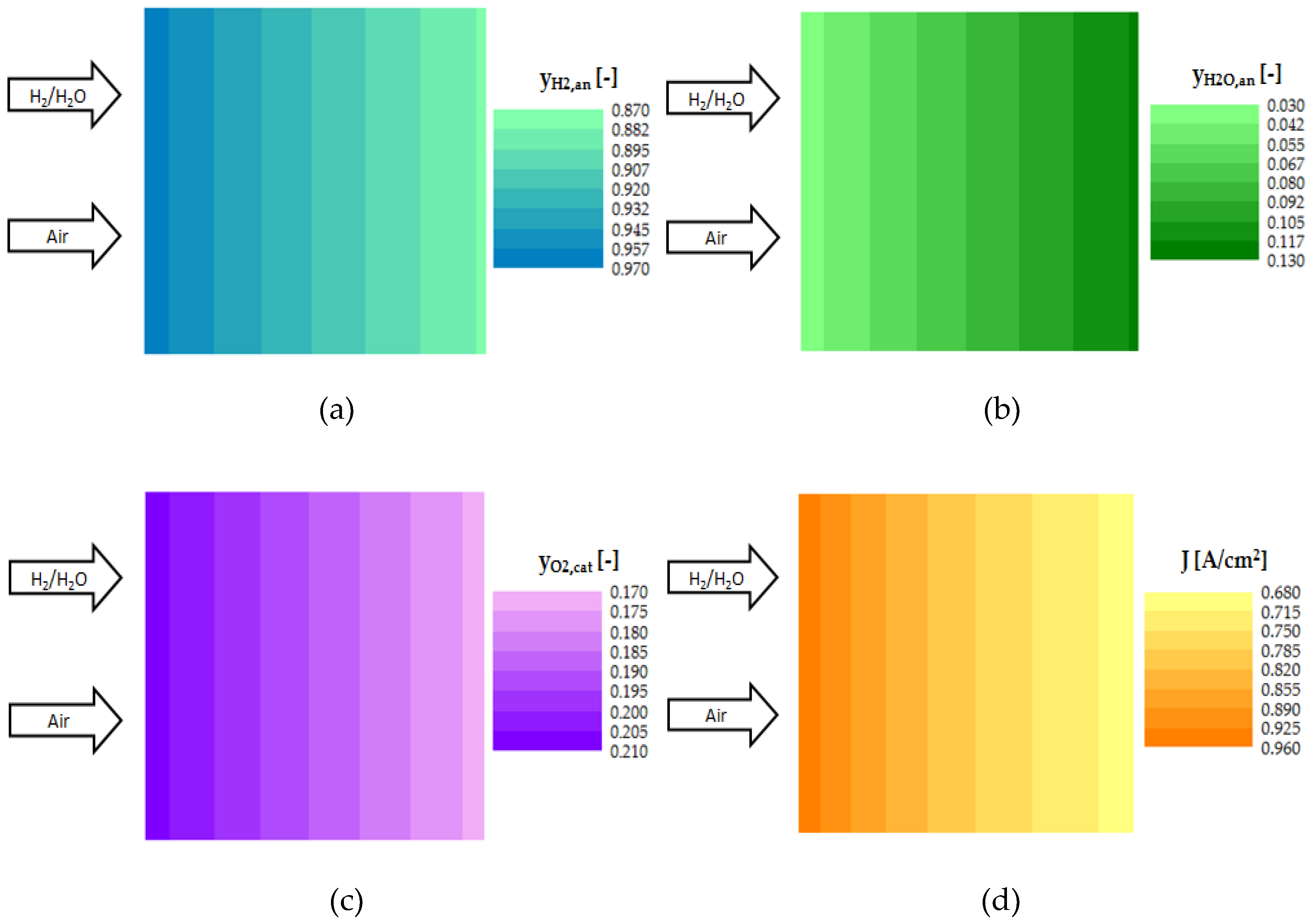
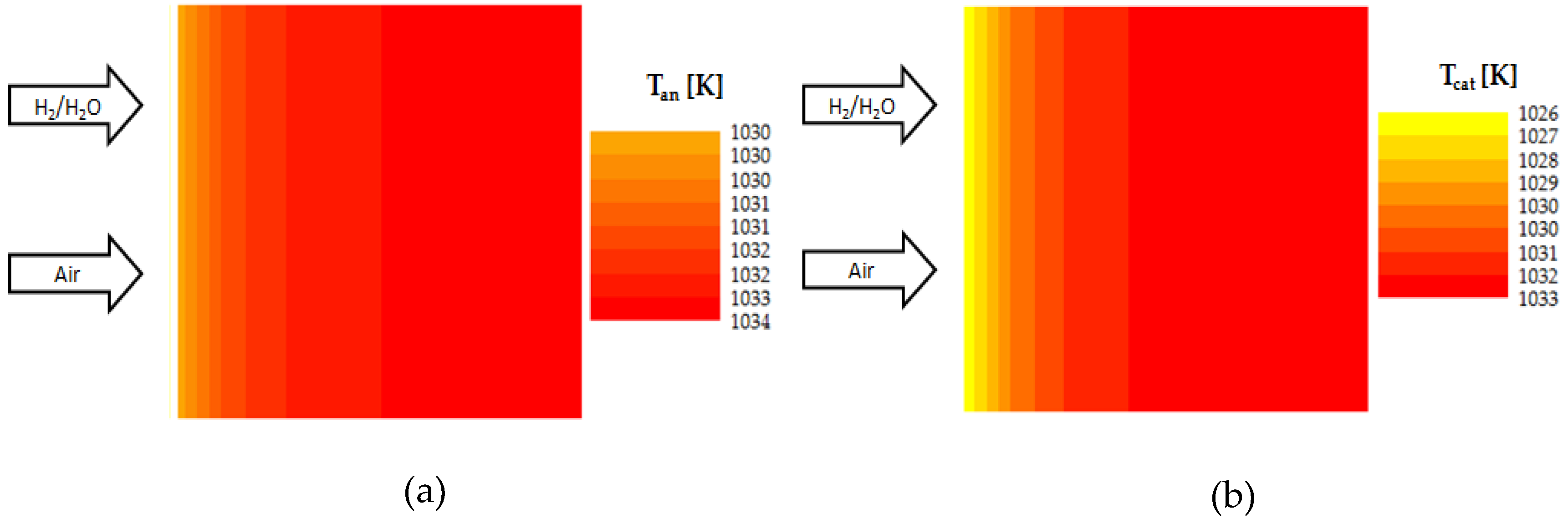
3.2. SOFC Local Performance Evaluation
4. Materials and Methods
4.1. Anode-Supported Cells and Current Collectors
4.2. LSCF Contacting Paste
4.3. Cell Testing
4.4. Post-Experimental Characterization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A, B, C | Kinetics orders for exchange current density [-] |
| a | Pore radius [m] |
| D | Diffusion coefficient [m2/s] |
| d | Thickness [m] |
| E | Potential [V] |
| E0 | Reversible voltage [V] |
| Eact | Activation energy [J/mol] |
| F | Faraday constant [C/mol] |
| J | Current density [A/m2] |
| J0 | Exchange current density [A/m2] |
| M | Molecular weight [mol/g] |
| P | Electrochemical parameters |
| p | Pressure [atm] |
| R | Gas constant [J/(molK)] |
| T | Temperature [K] |
| V | Cell voltage [V] |
| v | Diffusion volume [-] |
| y | Molar fraction [-] |
| z | Number of transferred electrons [-] |
| Greek letters | |
| γ | Pre-exponential coefficient in exchange current density [A/m2] |
| ε | Porosity [-] |
| η | Overpotential [V] |
| ξ | Tortuosity [-] |
| Subscript | |
| Act | Activation |
| An | Anode |
| Cat | Cathode |
| Conc | Concentration |
| Eff | Effective |
| El | Electrode |
| K | Knudsen |
| Mix | Mixture |
| Ohm | Ohmic |
References
- Debe, M.K. Electrocatalyst approaches and challenges automotive fuel cells. Nature 2012, 486, 43–51. [Google Scholar] [CrossRef]
- Steele, B.C.H.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Laosiripojana, N.; Wiyaratn, W.; Kiatkittipong, W.; Arpornwichanop, A.; Soottitantawat, A.; Assabumrungrat, S. Review on solid oxide fuel cell technology. Eng. J. 2009, 13, 65–82. [Google Scholar] [CrossRef]
- Handoko, A.D.; Steinmann, S.N.; Seh, Z.W. Theory-guided materials design: Two-dimensional MXenes in electro- and photocatalysis. Nanoscale Horiz. 2019, 4, 809–827. [Google Scholar] [CrossRef]
- Da Silva, F.S.; de Souza, T.M. Novel materials for solid oxide fuel cell technologies: A literature review. Int. J. Hydrog. Energy 2017, 42, 26020–26036. [Google Scholar] [CrossRef] [Green Version]
- Irshad, M.; Siraj, K.; Raza, R.; Ali, A.; Tiwari, P.; Zhu, B.; Rafique, A.; Ali, A.; Ullah, M.K.; Usman, A. A brief description of high temperature solid oxide fuel cells operation, materials, design, fabrication, technologies and performance. Appl. Sci. 2016, 6, 75. [Google Scholar] [CrossRef] [Green Version]
- She, Z.W.; Kibsgaard, J.; Dickens, C.F.; Chorkendorff, I.; Nørskov, J.K.; Jaramillo, T.F. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 2017, 355. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, T.; Sahu, M.; Sanjay, P. CFD modeling of SOFC cogeneration system for building applications. Energy Procedia 2017, 109, 361–368. [Google Scholar] [CrossRef]
- Fong, K.F.; Lee, C.K. System analysis and appraisal of SOFC-primed micro cogeneration for residential application in subtropical region. Energy Build. 2016, 128, 819–826. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ottaviano, A. Integration of SOFC/GT hybrid systems in Micro-Grids. Energy 2017, 118, 716–728. [Google Scholar] [CrossRef]
- Hauck, M.; Herrmann, S.; Spliethoff, H. Simulation of a reversible SOFC with Aspen Plus. Int. J. Hydrog. Energy 2017, 42, 10329–10340. [Google Scholar] [CrossRef]
- Aguiar, P.; Adjiman, C.S.; Brandon, N.P. Anode-supported intermediate temperature direct internal reforming solid oxide fuel cell. I: Model-based steady-state performance. J. Power Sources 2004, 138, 120–136. [Google Scholar] [CrossRef]
- Luo, X.J.; Fong, K.F. Development of 2D dynamic model for hydrogen-fed and methane-fed solid oxide fuel cells. J. Power Sources 2016, 328, 91–104. [Google Scholar] [CrossRef]
- Tang, S.; Amiri, A.; Vijay, P.; Tadé, M.O. Development and validation of a computationally efficient pseudo 3D model for planar SOFC integrated with a heating furnace. Chem. Eng. J. 2016, 290, 252–262. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, J.; Yue, D.; Yang, G.; Ye, S.; He, C.; Wang, W.; Yuan, J.; Huang, N. Three-dimensional CFD modeling of transport phenomena in a cross-flow anode-supported planar SOFC. Energies 2014, 7, 80–98. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Chen, T.; Wang, Y.; Peng, Z.; Wang, W.G. Electrochemical analysis of an anode-supported SOFC. Int. J. Electrochem. Sci. 2013, 8, 2330–2344. [Google Scholar]
- Kazempoor, P.; Braun, R.J. Model validation and performance analysis of regenerative solid oxide cells for energy storage applications: Reversible operation. Int. J. Hydrog. Energy 2014, 39, 5955–5971. [Google Scholar] [CrossRef]
- Yoon, K.J.; Gopalan, S.; Pal, U.B. Analysis of electrochemical performance of SOFCs using polarization modeling and impedance measurements. J. Electrochem. Soc. 2009, 156, B311–B317. [Google Scholar] [CrossRef]
- Stoynov, Z.B.; Vladikova, D.E.; Burdin, B.G.; Laurencin, J.; Montinaro, D.; Nakajo, A.; Piccardo, P.; Thorel, A.; Hubert, M.; Spotorno, R. Differential resistance analysis—A new tool for evaluation of solid oxide fuel cells degradation. MRS Adv. 2017, 2, 3991–4003. [Google Scholar] [CrossRef]
- Huang, Q.A.; Hui, S.R.; Wang, B.; Zhang, J. A review of AC impedance modeling and validation in SOFC diagnosis. Electrochim. Acta 2007, 52, 8144–8164. [Google Scholar] [CrossRef]
- Leonide, A.; Sonn, V.; Weber, A.; Ivers-Tiffée, E. Evaluation and modeling of the cell resistance in anode-supported solid oxide fuel cells. J. Electrochem. Soc. 2008, 155, B36–B41. [Google Scholar] [CrossRef]
- Choi, J.H.; Lee, T.; Choi, M.; Yoo, Y.S.; Baek, S.W.; Bae, J. Long-term performance of anode-supported SOFC integrated with metal interconnect by joining process. Int. J. Hydrog. Energy 2010, 35, 4285–4291. [Google Scholar] [CrossRef]
- Spotorno, R.; Piccardo, P.; Costa, R.; Han, F.; Schiller, G. LaNi0.6Fe0.4O3 as cathode contacting material: Effect on anode supported cell performances. ECS Trans. 2017, 78, 1689–1699. [Google Scholar] [CrossRef]
- Audasso, E.; Bosio, B.; Nam, S. Extension of an effective MCFC kinetic model to a wider range of operating conditions. Int. J. Hydrog. Energy 2016, 41, 5571–5581. [Google Scholar] [CrossRef]
- Conti, B.; Bosio, B.; McPhail, S.J.; Santoni, F.; Pumiglia, D.; Arato, E. A 2-D model for intermediate temperature solid oxide fuel cells preliminary validated on local values. Catalysts 2019, 9, 36. [Google Scholar] [CrossRef] [Green Version]
- Bove, R.; Lunghi, P.; Sammes, N.M. SOFC mathematical model for systems simulations. Part one: From a micro-detailed to macro-black-box model. Int. J. Hydrog. Energy 2005, 30, 181–187. [Google Scholar] [CrossRef]
- Fuel Cell Handbook, 7th ed.; EG&G Technical Services Inc.: Pittsburgh, PA, USA; Morgantown, WV, USA, 2004; ISBN 0442319266.
- Noren, D.A.; Hoffman, M.A. Clarifying the Butler-Volmer equation and related approximations for calculating activation losses in solid oxide fuel cell models. J. Power Sources 2005, 152, 175–181. [Google Scholar] [CrossRef]
- Yonekura, T.; Tachikawa, Y.; Yoshizumi, T.; Shiratori, Y.; Ito, K.; Sasaki, K. Exchange current density of solid oxide fuel cell electrodes. ECS Trans. 2011, 35, 1007–1014. [Google Scholar] [CrossRef]
- Leonide, A.; Apel, Y.; Ivers-Tiffée, E. SOFC modelling and parameter identification by means of impedance spectroscopy. ECS Trans. 2009, 19, 81–109. [Google Scholar]
- Bianchi, F.R.; Bosio, B.; Baldinelli, A.; Barelli, L. Optimization of a reference kinetic model for solid oxide fuel cells. Catalyst 2020, 10, 104. [Google Scholar] [CrossRef] [Green Version]
- Gu, W.; Cheng, P.; Tang, M. Compilation and evaluation of gas phase diffusion coefficients of halogenated organic compounds. R. Soc. Open. Sci. 2018, 5, 171936. [Google Scholar] [CrossRef] [PubMed]
- DiGiuseppe, G. An electrochemical model of a solid oxide fuel cell using experimental data for validation of material properties. In Proceedings of the ASME 2010, 8th International Fuel Cell Science, Engineering and Technology Conference, Brooklyn, NY, USA, 14–16 June 2010. [Google Scholar] [CrossRef]
- Spotorno, R.; Piccardo, P.; Schiller, G. Effect of cathode contacting on anode supported cell performance. J. Electrochem. Soc. 2016, 163, F872–F876. [Google Scholar] [CrossRef] [Green Version]
- Boigues Muñoz, C.; Pumiglia, D.; McPhail, S.J.; Santori, G.; Montinaro, D.; Comodi, G.; Carlini, M.; Polonara, F. More accurate macro-models of solid oxide fuel cells through electrochemical and microstructural parameter estimation—Part II: Parameter estimation. J. Power Sources 2015, 286, 321–329. [Google Scholar] [CrossRef] [Green Version]
- Zabihian, F.; Fung, A.S. Macro-level modeling of solid oxide fuel cells, approaches and assumptions revisited. J. Renew. Sustain. Energy 2017, 9, 054301. [Google Scholar] [CrossRef]
- Okamoto, H.; Kawamura, G.; Kudo, T. Study of oxygen adsorption on platinum through observation of exchange current in a solid electrolyte concentration cell. Electrochim. Acta 1983, 28, 379–382. [Google Scholar] [CrossRef]
- Barelli, L.; Barluzzi, E.; Bidini, G. Diagnosis methodology and technique for solid oxide fuel cells: A review. Int. J. Hydrog. Energy. 2013, 38, 5060–5074. [Google Scholar] [CrossRef]
- Spotorno, R.; Piccardo, P.; Perrozzi, F. Interaction between Crofer 22 APU current collector and LSCF cathode contacting layer under cell operation. ECS Trans. 2015, 68, 1633–1640. [Google Scholar] [CrossRef]
- Spotorno, R.; Piccardo, P.; Schiller, G. Effect of cathode contacting on anode supported cell performances and degradation. ECS Trans. 2015, 68, 2429–2439. [Google Scholar] [CrossRef]
- Boukamp, B.A. A nonlinear least squares fit procedure for analysis of immittance data of electrochemical systems. Solid State Ion. 1986, 20, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, J.R.; Potter, L.D., Jr. A flexible procedure for analyzing impedance spectroscopy results: Description and illustration. Solid State Ion. 1987, 24, 61–79. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Comminges, C.; Fu, Q.X.; Zahid, M.; Steiner, N.Y.; Bucheli, O. Monitoring the degradation of a solid oxide fuel cell stack during 10,000 h via electrochemical impedance spectroscopy. Electrochim. Acta 2012, 59, 367–375. [Google Scholar] [CrossRef]




| Parameter | Pt-Mesh+LSCF Cell | Pt-Mesh Cell |
|---|---|---|
| P1 [Ωm2/K] | 3.1 × 10−12 | 1.6 × 10−9 |
| P2 [K] | 8597.9 | 3216.0 |
| Eact,an [kJ/mol] | 119 | 119 |
| Eact,cat [kJ/mol] | 120 | 120 |
| A [-] | 0.3 | 0.3 |
| B [-] | 0 | 0 |
| C [-] | 0.2 | 0.2 |
| γan [A/m2] | 5 × 109 | 5 × 109 |
| γcat [A/m2] | 8.8 × 109 | 1.5 × 109 |
| ηleakage [V] | 0.03 | 0.03 |
| Layer | ε [%] | d [μm] |
|---|---|---|
| Ni/8YSZ-cermet anode | 32.602 | 295.401 |
| 8YSZ electrolyte | 1.378 | 10.056 |
| GDC interlayer | 23.798 | 3.546 |
| LSCF cathode | 30.717 | 24.201 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi, F.R.; Spotorno, R.; Piccardo, P.; Bosio, B. Solid Oxide Fuel Cell Performance Analysis through Local Modelling. Catalysts 2020, 10, 519. https://doi.org/10.3390/catal10050519
Bianchi FR, Spotorno R, Piccardo P, Bosio B. Solid Oxide Fuel Cell Performance Analysis through Local Modelling. Catalysts. 2020; 10(5):519. https://doi.org/10.3390/catal10050519
Chicago/Turabian StyleBianchi, Fiammetta Rita, Roberto Spotorno, Paolo Piccardo, and Barbara Bosio. 2020. "Solid Oxide Fuel Cell Performance Analysis through Local Modelling" Catalysts 10, no. 5: 519. https://doi.org/10.3390/catal10050519
APA StyleBianchi, F. R., Spotorno, R., Piccardo, P., & Bosio, B. (2020). Solid Oxide Fuel Cell Performance Analysis through Local Modelling. Catalysts, 10(5), 519. https://doi.org/10.3390/catal10050519








