2.1. Characterization and Performances of N@AC Catalysts
This study of DCE dehydrochlorination is based on our previous work, and details of characterization of the N@AC catalysts are available in our previously published paper [
19]. The textural properties of the catalysts were investigated by performing N
2 adsorption–desorption isothermal analysis. The N@AC catalysts contained mainly micropores (<2 nm) and small mesopores (2–4 nm). The total specific surface areas (650–1000 m
2 g
−1), specific volumes (0.34–0.49 cm
3 g
−1), and micropore volumes (0.26–0.40 cm
3 g
−1) decreased significantly with increasing nitrogen content. X-ray diffraction (XRD) patterns showed a high degree of surface graphitization of the N@AC catalysts, and N-doping did not affect the diffraction peaks. Raman spectroscopy showed that the number of defects formed during graphitization increased with increasing number of nitrogen atoms on the N@AC catalyst surface. These defects can contribute to the catalytic activity. Transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HRTEM) showed graphitization of the N@AC surface, in agreement with the XRD results. The catalyst chemical states were investigated by X-ray photoelectron spectroscopy (XPS). The high-resolution C1s XP spectra of the N@AC catalysts were divided into four individual peaks after fitting, i.e., C–C (~284.5 eV), C–N (~285.2 eV), C–O (~286.3 eV), and C=O (~288.3 eV). The high-resolution N1s spectrum showed that the nitrogen in the N@AC catalysts was present in three states, i.e., pyridinic-N (~398.5 eV), pyrrolic-N (~400.2 eV), and graphitic-N (~401.1 eV).
It has previously been reported that N-doped carbon can catalyze the dehydrochlorination of DCE to VCM. However, there have been no reports of the effects of the nitrogen precursor species on the catalytic performances of N-doped carbon catalysts. We selected seven nitrogen compounds as precursors, namely pyrrole, pyridine, acrylamide, melamine, urea, ammonium hydroxide (NH
3°H
2O), and imidazole. These compounds have different molecular sizes, molecular structures, solubilities, and boiling points.
Table 1 showed that the actual nitrogen content doped on activated carbon was 0.6–0.7 wt.% when nitrogen atom content was controlled by 2.0 wt.% in the impregnation. As shown in
Figure 1a, the seven N-doped catalysts gave similar catalytic performances, with DCE conversions of 50–55% at 260 °C; the DCE conversion over AC was only ~22%. The results showed that different N-resources had no obvious effect on the catalytic activity of the N@AC catalysts for DCE dehydrochlorination if there were same N contents doped on carbon. The results further implied that there should be a common catalytic active site generated in the seven N@AC catalysts in the calcination. As shown in
Figure 2, there were the same nitrogen chemical states formed in the N@AC catalysts in the calcination, i.e., pyridinic-N, pyrrolic-N, and graphitic-N. It is certain that the catalytic activity of the N@AC catalysts is closely related to the existence of these nitrogen chemical states.
Figure 1b shows that the performances of the N@AC catalysts were much better than that of AC (dosage of pyrrole = 0). The DCE conversion over AC without an added nitrogen precursor was only ~22%. The DCE conversion increased from 22.0% to 61.8% with increasing pyrrole content from 0 to 40.0 g/100 g AC. The 30Pyrrole/AC (30 g pyrrole/100 g AC) catalyst gave the best catalytic performance in DCE dehydrochlorination, and the result was better than that achieved by pyrolysis of DCE [
2]. When the pyrrole content was further increased, no increases in the N@AC catalytic activity were observed. This may be related to a decrease in the specific surface area [
19].
Figure 1c shows that the catalytic activity of N@AC was sensitive to the calcination temperature. The DCE conversion increased as the calcination temperature increased from 250 to 850 °C, with only ~20% conversion at 250 °C. Initially, as the calcination temperature increased to 450 °C, the conversion increased gradually to ~35%. When the temperature was increased to 650 °C, the DCE conversion increased abruptly to ~65%. There was no obvious change in the conversion at temperatures between 650 and 850 °C. The results (
Figure 1c) indicate that catalytic sites were formed on the N@AC surface at 250 to 650 °C, but catalytic site formation almost stopped at temperatures above 650 °C.
Figure 1d shows that the DCE conversion decreased with increasing liquid hourly space velocity (LHSV). The DCE conversion increased from 39.9% to 83.6% with decreasing LHSV from 1.0 to 0.25 h
−1.
Figure 1e shows that the catalytic performance of N@AC improved, and the DCE conversion increased from 25.1% to 61.5%, with increasing reaction temperature from 240 to 260 °C. The DCE conversion reached 87.0% at 280 °C, which is better than that achieved by DCE pyrolysis at 500–550 °C. As shown in
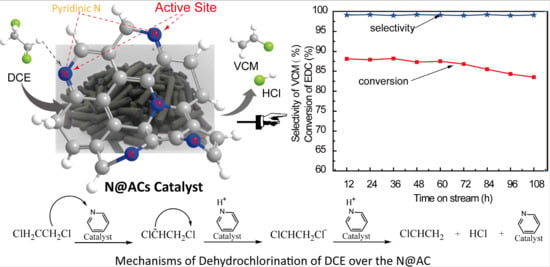
Figure 1f, the N@AC catalysts delivered stable performances, with DCE conversions greater than 80% and VCM selectivity greater than 99%, at 280 °C in 110 h.
2.2. Active Sites of N@AC Catalysts for DCE Conversion to VCM
The N@AC catalysts clearly gave excellent catalytic performances in DCE dehydrochlorination. It is important to identify the active sites involved in N@AC-catalyzed dehydrochlorination. The active sites were investigated by using an incipient wetness impregnation method to prepare N@AC catalysts with AC as the carrier and pyrrole as the nitrogen precursor. The AC was impregnated in 30% (
w/
w) pyrrole for 12 h and then the crude products were carbonized at 250, 450, 650, and 850 °C, respectively. The obtained N@AC catalysts are denoted by catalyst-1, catalyst-2, catalyst-3, and catalyst-4, respectively. The high-resolution N1s XP spectra of the N@AC catalysts are shown in
Figure 3a,c. The spectrum of catalyst-1 (
Figure 3a) contained only a pyrrolic-N peak (~400.2 eV); this indicates that pyrrole hardly decomposed at 250 °C.
Figure 3c shows that the pyrrolic-N atom content was ~3.25%. However, the DCE conversion was only ~20% (
Figure 3b), which indicates that pyrrolic-N did not provide the active sites for DCE dehydrochlorination.
Pyridinic-N formation on the N@AC catalyst surface gradually increased with increasing calcination temperature (
Figure 3a). At 450 °C, i.e., catalyst-2, ~0.25% pyridinic-N was generated and the amount of pyrrolic-N decreased (
Figure 3c). The DCE conversion increased to 35.3% from ~20%, which shows that pyridinic-N might provide active sites for DCE dehydrochlorination. When the calcination temperature was increased to 650 °C, ~0.60% pyridinic-N and 0.50% graphitic-N (~401.1 eV) were generated, but the amount of pyrrolic-N (~400.2 eV) decreased to 1.60% from 3.25% (
Figure 3c). The DCE conversion over catalyst-3 suddenly increased to 61.2%, which implies that pyridinic-N and graphitic-N might be the active sites of N@AC for dehydrochlorination. When the calcination temperature was increased to 850 °C, a large amount of graphitic-N (~1.26%) was generated, and the amount of pyridinic-N only increased to about ~0.70% (
Figure 3c). Although a large amount of graphitic-N was generated, catalyst-4 did not give an excellent performance. The DCE conversion was only 63.9% (
Figure 3b), which is similar to that achieved with catalyst-3. This indicates that graphitic-N almost did not provide active sites for catalytic dehydrochlorination. Compared with pyrrolic-N and graphitic-N, pyridinic-N was obviously the main active for catalytic dehydrochlorination.
We further investigated whether pyridinic-N was critical in providing active sites for dehydrochlorination by preparing pyrrole-AC, pyridine-AC, and 10Pyrrole/AC and assessed their abilities to catalyze DCE dehydrochlorination. The pyrrole-AC and pyridine-AC were prepared by an incipient wetness impregnation and dry, not by calcination. In contrast, 10Pyrrole/AC was prepared under calcination. Because calcination did not occur, pyrrole-AC gave a poor catalytic performance, with ~20% DCE conversion. However, pyridine-AC gave an excellent catalytic performance, which strongly suggests that pyridinic-N is the critical active site for dehydrochlorination. The catalytic performance of 10Pyrrole/AC was similar to that of pyridine-AC, and pyridinic-N was generated under calcination. The XP spectra and catalytic performances of N@AC further show that pyridinic-N generated under calcination provides the N@AC active sites for dehydrochlorination.
2.3. Reaction Mechanism of N@AC-Catalyzed DCE Conversion to VCM
Further experiments were performed to determine why pyridinic-N provides the active sites for dehydrochlorination. There is one p-electron in pyridinic-N, provided to the aromatic π-system. Because of the role of pyridinic-N, the carbon matrix has a lone electron pair, which contributes to an increase of the electron-donating ability of the catalyst [
20]. The introduction of pyridinic-type nitrogen species into the carbon network increases the basicity [
21], and the derived carbon can be used as a solid basic catalyst [
22]. The mechanism of the catalytic dehydrochlorination of DCE can be controlled by the basicity of the catalyst.
The surface basic properties of the N@AC catalysts were researched by CO
2-TPD (
Figure 4a). For comparison, the basic properties of AC were also investigated. According to literature reports, the desorption peaks at about 120–150 °C can be attributed to interactions between CO
2 and weakly basic sites on the catalyst. The desorption peak temperature clearly shifted with increasing N-doping, which indicates that the N@AC surface basicity increased with increasing N-doped content. In addition, weak desorption peaks were observed at ~300 °C for the N@AC catalysts but not for AC. This indicates generation of much stronger basic sites on N@AC. The high-resolution N1s XP spectrum showed that pyridinic-N contributes to the basicity of the N@AC catalyst, and this improves the catalytic performance in DCE dehydrochlorination. The mechanism of dehydrochlorination was investigated by performing DCE-TPD (
Figure 4b). TPD as an effective technology is often to directly compare the adsorption and activation of reactants on the surface of the different catalysts, and is used to explain the reaction mechanism. The temperature of desorption in the TPD diagram reflects the binding force of the adsorbed molecules and the catalyst surface. The peak area is related to the adsorption quantity. The desorption temperatures of DCE on AC was about 160 °C, but the corresponding temperature on the 30Pyrrole/AC catalyst was about 190 °C. The result of comparison shows that DCE is more likely to adsorb on N@AC than on AC (
Figure 4b). The desorption peak areas of both samples confirmed the improved ability of N@AC to activate DCE molecules compared with that of AC; this is consistent with the activity data. As shown in
Figure 4b, the pyridinic-N basic sited in N@AC can effectively adsorb and activate DCE to produce VCM.
On the basis of the above discussion, we propose the following reaction scheme for DCE dehydrochlorination to VCM on the pyridinic-N active sites of the N@AC catalyst (
Figure 4c). First, a DCE molecule approaches the N@AC surface through internal diffusion. The C–H bond of the neighboring pyridinic-N is polarized and hydrogen interacts with the pyridinic-N basic site. Next, the C–H bond is cleaved to generate ClC
−HCH
2Cl. Because of the high electronegativity of the Cl atom, the electron cloud of C
− is transferred to Cl to generate the intermediate state ClCHCH
2Cl
−. The active intermediate states ClCHCH
2Cl
− and pyridinic-NH
+ react to form ClCHCH
2 (VCM) and HCl, and N@AC is reduced. This completes DCE dehydrochlorination on the N@AC catalyst.
2.4. Kinetics of DCE Dehydrochlorination over N@AC Catalyst
To enable a deeper understanding of the dehydrochlorination mechanism, optimization of the reaction process parameters, and improvement of the reactor design, we investigated the kinetics of DCE dehydrochlorination over N@AC catalysts. The reaction formula was shown in
Scheme 1.
DCE, VCM, and HCl are denoted by A, B, and C, respectively. In addition, the N@AC active site is denoted by σ.
In the intrinsic kinetic study, we investigated the following three reaction processes.
Absorption of DCE on N@AC:
Desorption of VCM from N@AC:
The following kinetic equations were derived by using the Langmuir adsorption model.
Adsorption rate equation:
where,
is the net adsorption rate of A.
and
are the adsorption and desorption rate constants of A, respectively.
is the partial pressure of A.
denotes the content of exposed active sites and
is the content of adsorption A.
Surface reaction rate equation:
where,
is net reaction rate.
and
are the forward and reverse reaction rate constants, respectively.
is the partial pressure of C.
Desorption rate equation:
where,
is the net desorption rate.
and
are the desorption and adsorption rate constants of B, respectively.
is the partial pressure of B.
In the following equation:
If adsorption control is the rate-limiting step, the kinetic equation is derived as follows.
The remaining steps are balanced, i.e.,
Equations (7)–(10) were used to derive (11).
If the surface reaction is the rate-limiting step, the kinetic equation, which was derived by the same method as (11), is
If desorption is the rate-limiting step, the kinetic equation, which was derived by the same method as (11), is
If the initial amount of DCE is 1 mol and the DCE conversion is
XA,
XA mol of VCM and HCl, respectively, are generated, the DCE surplus is (1 −
XA) mol, the total amount of materials after the reaction is (1 +
XA) mol, and
PA and
PB can be converted to
XA.
Finally, by substituting (14) and (15) in (11)–(13), respectively, three reaction rate equations, i.e., (16)–(18) are obtained.
To solve the kinetic equations, it is necessary to determine a series of
XA values (DCE conversions) at different
values (the ratio of the catalyst quantity to the DCE flow) by performing DCE dehydrochlorination experiments. We used the data to solve the kinetic equations, with the help of computer software. To obtain an intrinsic kinetic equation that was as accurate as possible, we had to minimize negative effects from sources such as the reactor, catalyst loading, and external and internal diffusion of DCE.
Figure 5a shows that the value of
XA tended to be constant, which indicates that external diffusion had been eliminated, when the value of
FA was greater than 0.04 mol h
−1.
Figure 5b shows that DCE conversion gradually increased with decreasing amount of catalyst. When the mesh was greater than 120, the DCE conversion tended to be constant, which indicates that internal diffusion was eliminated. To eliminate diffusion, kinetic experiments were performed at 250–290 °C. The experimental dynamic data are shown in
Table 2. The results show that the catalytic performance in DCE dehydrochlorination clearly increased with increasing
W/
FA.
In these experiments, the DCE conversions were all greater i.e., >15%. On the basis of theoretical and experimental results, this reactor was defined as an integral reactor, and can be represented by
Substitution of Equations (16), (17), and (18) into (19) gives the following kinetic equations:
The computer software 1stOpt was used to fit Equations (20)–(22) to obtain the parameters
KA,
KB, and
k by using the data in
Table 2. The fitting was carried out with the Universal Global Optimization Algorithm (UGO). The fitting results show that some of the parameters
KA,
KB, and
k in Equations (20) and (22) had negative values. This indicates that the hypothetical kinetic models (20) and (22) are not reasonable. The surface reaction rate is therefore the limiting step in DCE dehydrochlorination over N@AC. The fitting results for Equation (21) are shown in
Table 3. The
R2 value is close to 1.0, which indicates that the intrinsic kinetic process followed this dynamic model. The data in
Table 3 show that
k was clearly lower than
KA and
KB, which shows that the surface reaction rate was far slower than the rates of adsorption on N@AC and desorption from N@AC. The intrinsic kinetic rate greatly increased with increasing surface reaction rate.
Figure 5c shows that the calculated value of
is close to the experimental value, which shows that the kinetic model is appropriate, and supports the hypothesis that the surface reaction is the controlling step in DCE dehydrochlorination over N@AC.
The linear equation
was used to determine the activation energy of DCE dehydrochlorination over N@AC catalysts and the parameter
A, with the help of 1stOpt software. The Arrhenius equation was then obtained.
Figure 5d and the data in
Table 4 show good linear correlations between 1/
T and ln
k, ln
KA, and ln
KB, with correlation coefficients of 0.9979, 0.9897, and 0.9986, respectively. The kinetic data in the temperature range 250–290 °C therefore fit the reaction mechanism model fairly well. The Arrhenius equation,
, was used to determine the activation energy of DCE dehydrochlorination over N@AC, and gave a value of 254.09 kJ mol
−1 in the temperature range 250–290 °C;
k,
KA and
KB can be expressed as:
This kinetic study enables a deeper understanding of the mechanism of DCE dehydrochlorination over N@AC. The surface reaction is the rate-limiting step in DCE dehydrochlorination. DCE adsorption on and desorption from the N@AC surface are faster than the surface reaction.