A Model for Correcting the Pressure Drop between Two Monoliths
Abstract
:1. Introduction
2. Computational Model
2.1. Grid Quality
2.2. Corroboration of the Flow Regime
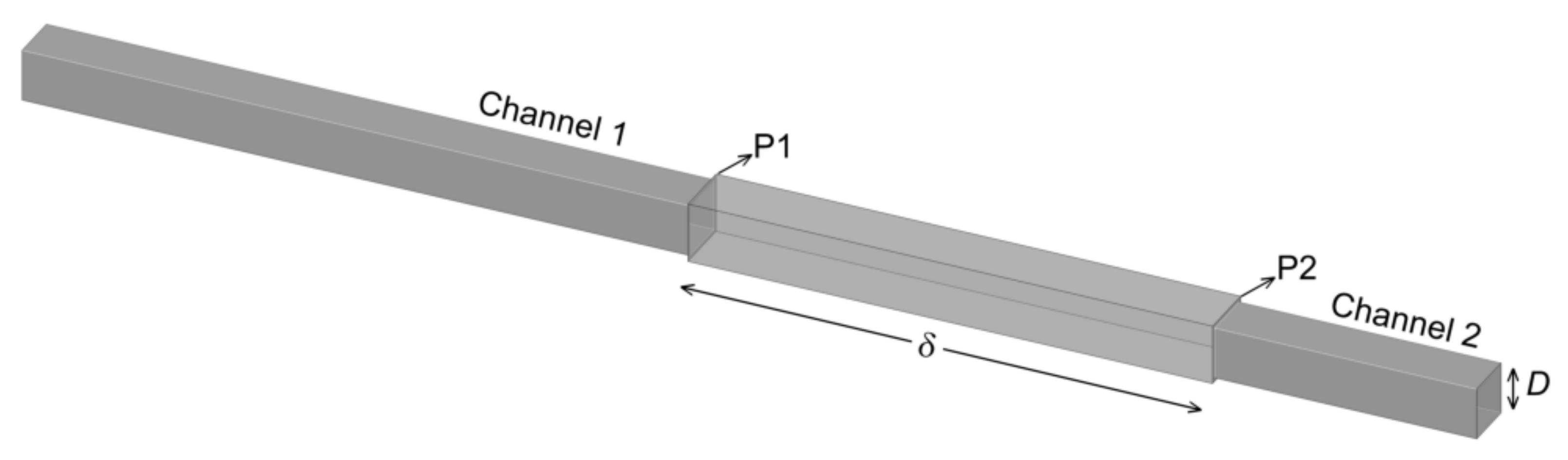
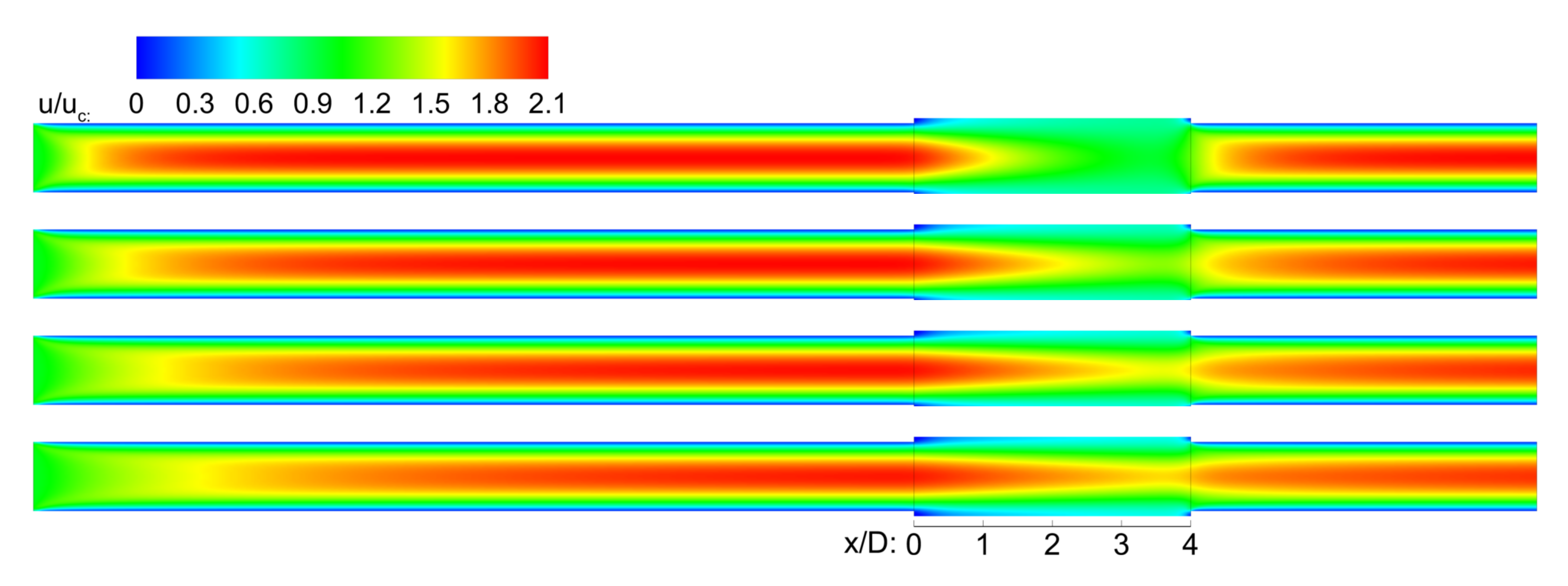
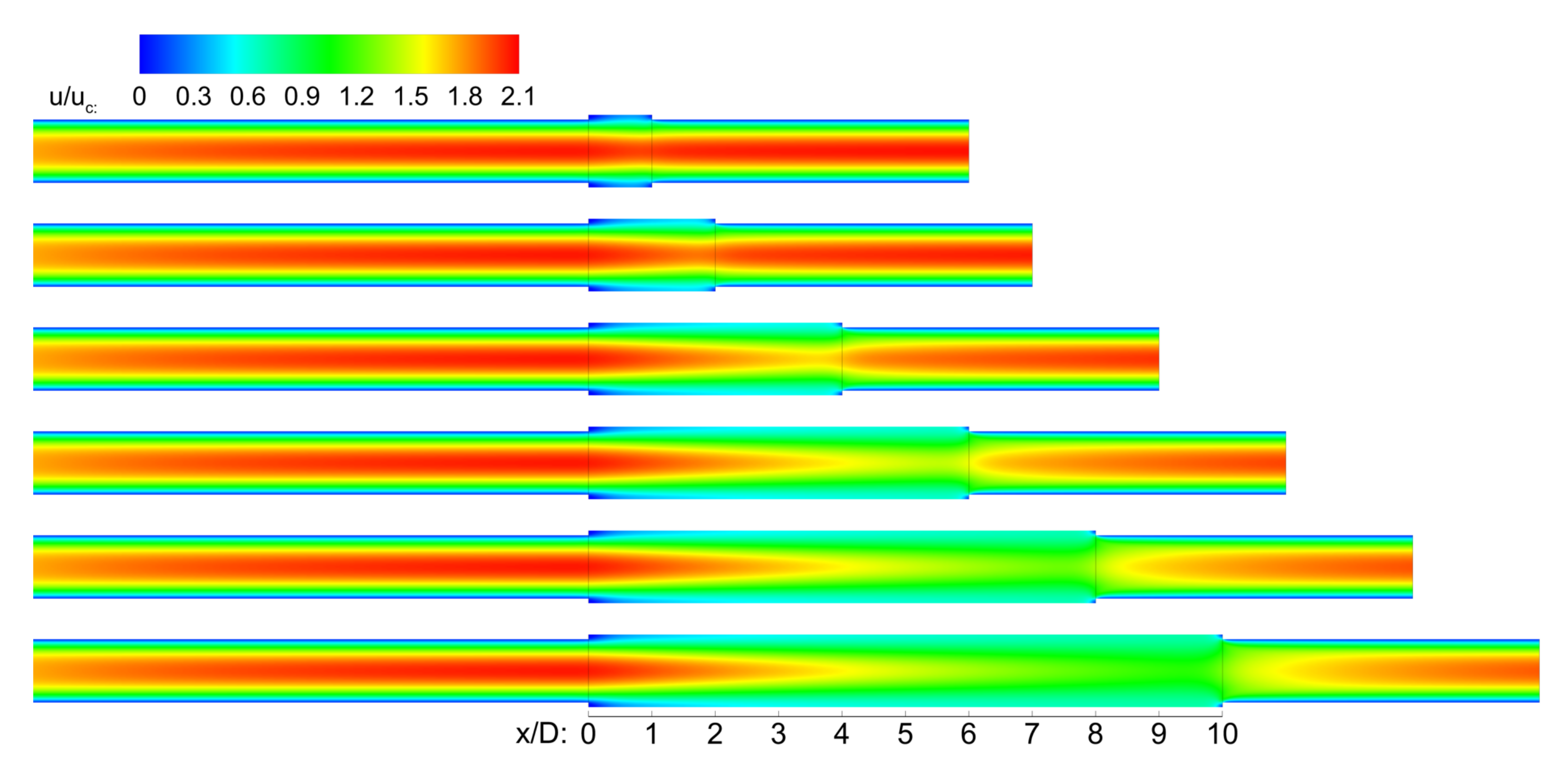
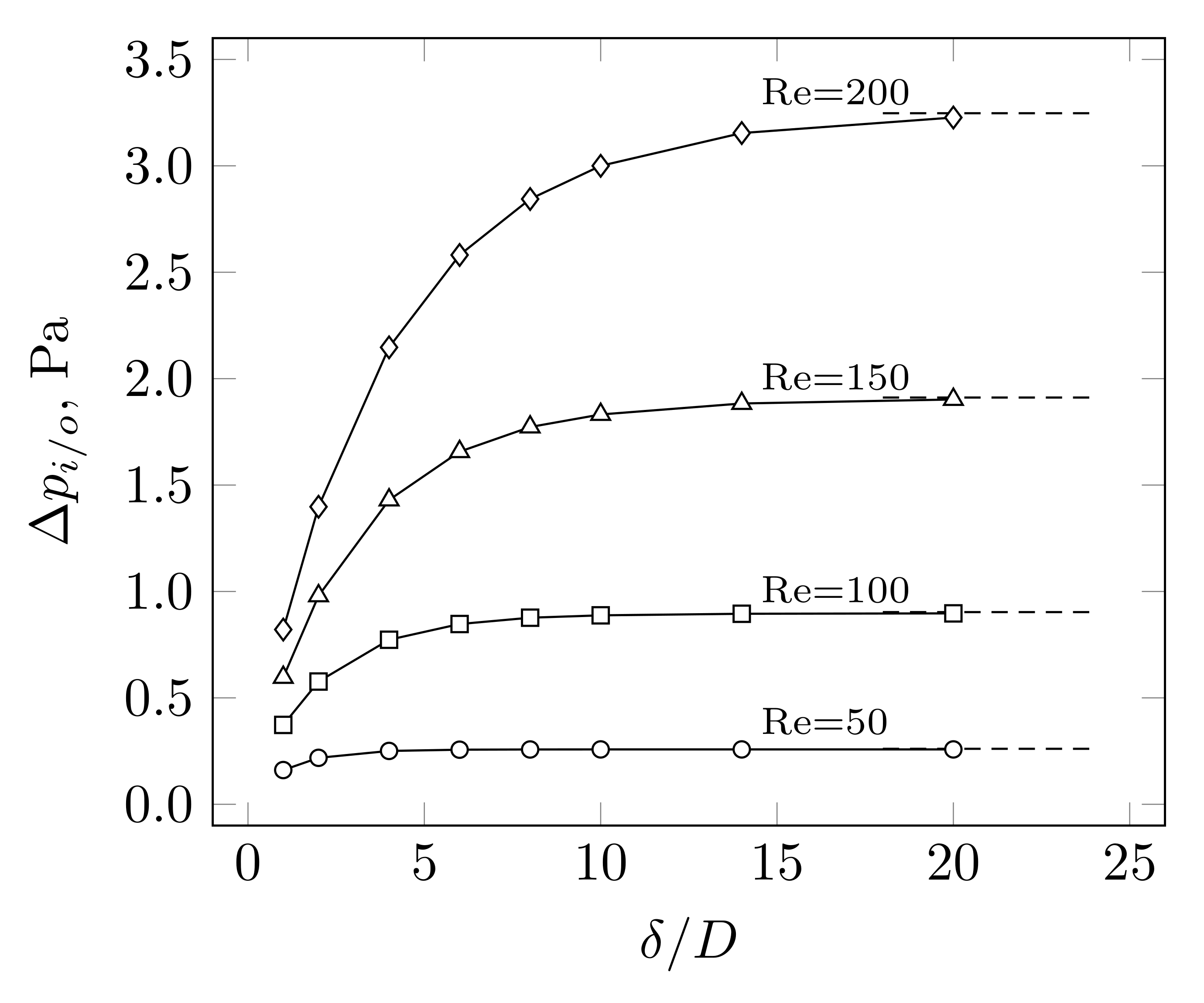
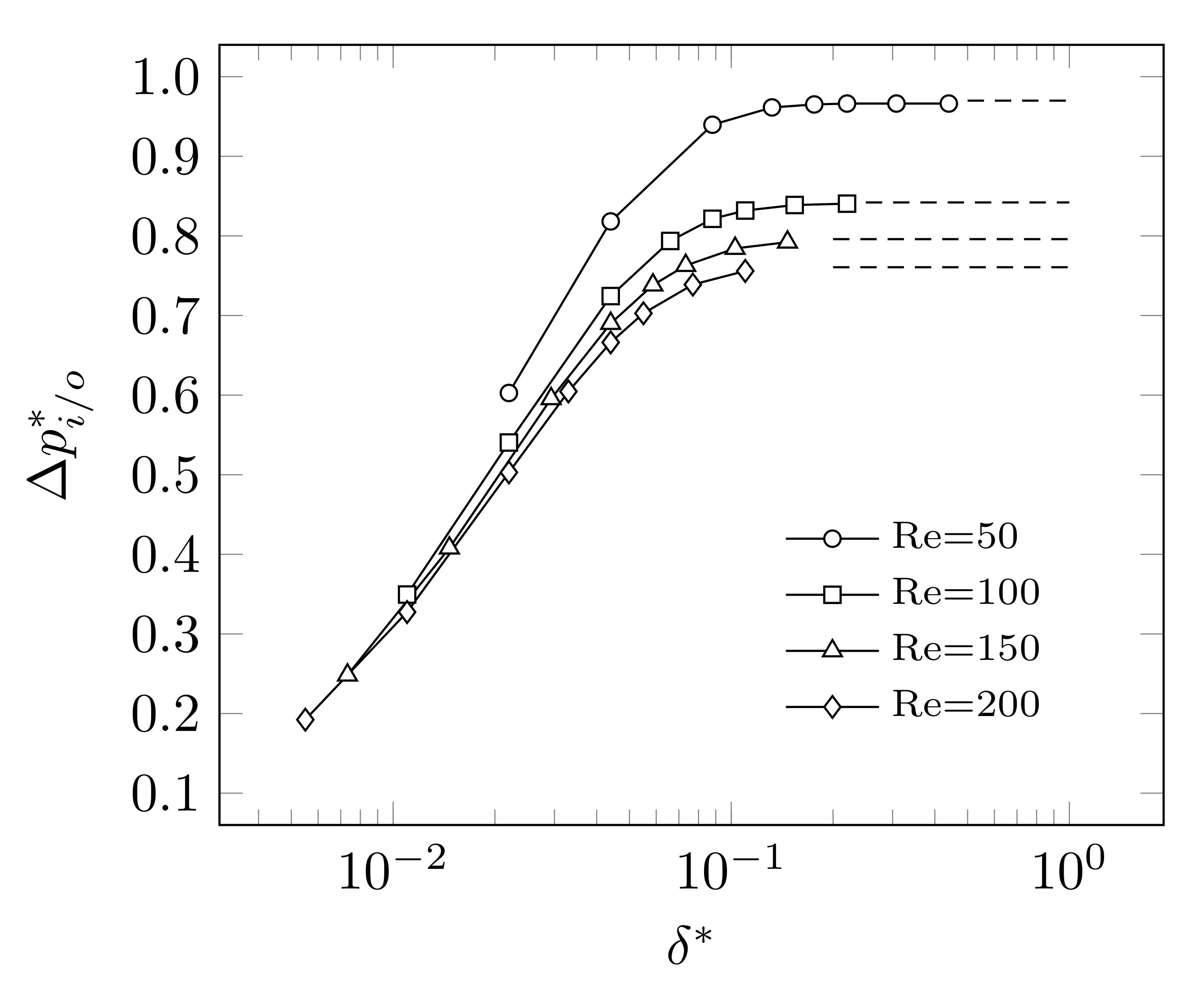
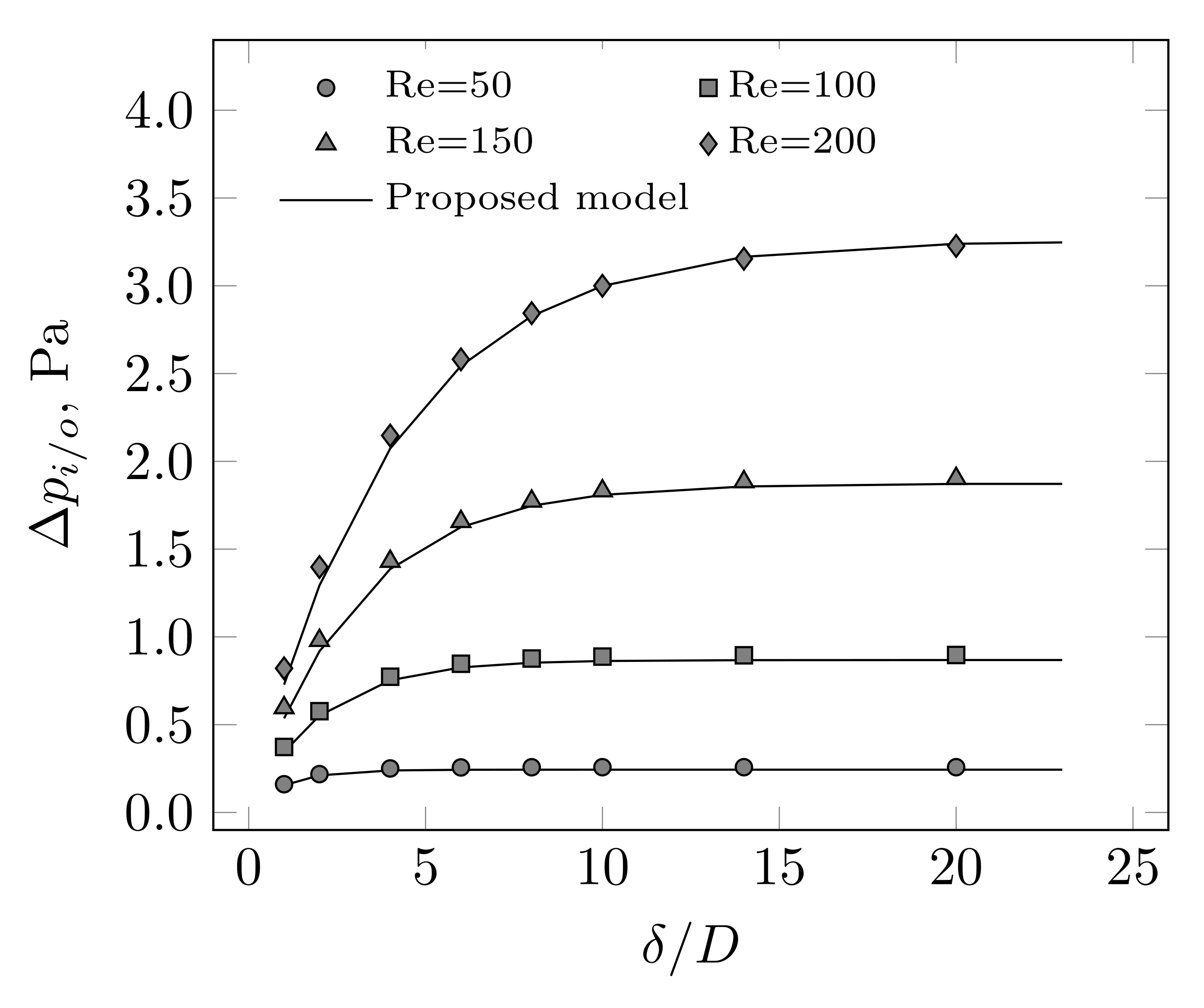
3. Results
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Channel hydraulic diameter, m |
| f | Darcy friction factor, - |
| f1,f2 | Model parameters, - |
| fδ | Correction factor, - |
| kc | Model parameter, - |
| k | Turbulence kinetic energy, m2/s2 |
| ksgs | Sub-grid turbulence kinetic energy, m2/s2 |
| Lw | Substrate wall thickness, m |
| LH | Hydraulic entrance length, m |
| p | Pressure, Pa |
| pT | Total pressure, Pa |
| pS | Static pressure, Pa |
| Δpc | Pressure drop inside of the substrate, Pa |
| Δpi | Pressure drop when entering the substrate, Pa |
| Δpo | Pressure drop when leaving the substrate, Pa |
| Δpi/o | Combined effect of Δpi and Δpo, Pa |
| Re | Reynolds number, - |
| t | Time, s |
| u | Velocity magnitude, m/s |
| uc | Channel velocity, m/s |
| δ | Length of the gap between substrates, m |
| δij | Kronecker delta, - |
| ϕ | Substrate void fraction, - |
| ρ | Fluid density, kg/m3 |
| τc | Model parameter, - |
| μ | Fluid viscosity, Pa·s |
| μsgs | Sub-grid turbulence viscosity, Pa·s |
References
- Williams, J.L. Monolith structures, materials, properties and uses. Catal. Today 2001, 69, 3–9. [Google Scholar] [CrossRef]
- Hayes, R.E.; Cornejo, I. Multi-scale modelling of monolith reactors: A 30-year perspective from 1990 to 2020. Can. J. Chem. Eng. 2021. [Google Scholar] [CrossRef]
- Lock, J.; Clasén, K.; Sjoblom, J.; McKelvey, T. A Control-Oriented Spatially Resolved Thermal Model of the Three-Way-Catalyst; SAE International: Warrendale, PA, USA, 2021; Available online: https://www.sae.org/publications/technical-papers/content/2021-01-0597 (accessed on 1 August 2021).
- Clarkson, R.J. A Theoretical and Experimental Study of Automotive Catalytic Converters. Ph.D. Thesis, Coventry University, Coventry, UK, 1997. [Google Scholar]
- Della Torre, A.; Montenegro, G.; Onorati, A.; Cerri, T.; Tronconi, E.; Nova, I. Numerical Optimization of a SCR System Based on the Injection of Pure Gaseous Ammonia for the NOx Reduction in Light-Duty Diesel Engines. In Proceedings of the SAE 2020 World Congress Experience, Detroit, MI, USA, 21–23 April 2020; pp. 1–11. [Google Scholar]
- Benjamin, S.F.; Clarkson, R.; Haimad, N.A.; Girgis, N. An experimental and predictive study of the flow field in axisymmetric automotive exhaust catalyst systems. SAE Trans. 1996, 105, 1008–1019. [Google Scholar]
- Tahay, P.; Khani, Y.; Jabari, M.; Bahadoran, F.; Safari, N. Highly porous monolith/TiO2 supported Cu, Cu-Ni, Ru, and Pt catalysts in methanol steam reforming process for H2 generation. Appl. Catal. A Gen. 2018, 554, 44–53. [Google Scholar] [CrossRef]
- Chatterjee, D.; Burkhardt, T.; Rappe, T.; Güthenke, A.; Weibel, M. Numerical simulation of DOC+ DPF+ SCR systems: DOC influence on SCR performance. SAE Int. J. Fuels Lubr. 2009, 1, 440–451. [Google Scholar] [CrossRef]
- Arab, S.; Commenge, J.M.; Portha, J.F.; Falk, L. Methanol synthesis from CO2 and H2 in multi-tubular fixed-bed reactor and multi-tubular reactor filled with monoliths. Chem. Eng. Res. Des. 2014, 92, 2598–2608. [Google Scholar] [CrossRef]
- Jang, J.; Lee, J.; Choi, Y.; Park, S. Reduction of particle emissions from gasoline vehicles with direct fuel injection systems using a gasoline particulate filter. Sci. Total Environ. 2018, 644, 1418–1428. [Google Scholar] [CrossRef]
- Martínez, F.L.D.; Julcour, C.; Billet, A.M.; Larachi, F. Modelling and simulations of a monolith reactor for three-phase hydrogenation reactions—Rules and recommendations for mass transfer analysis. Catal. Today 2016, 273, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Quintanilla, A.; Casas, J.; Miranzo, P.; Osendi, M.I.; Belmonte, M. 3D-Printed Fe-doped silicon carbide monolithic catalysts for wet peroxide oxidation processes. Appl. Catal. B Environ. 2018, 235, 246–255. [Google Scholar] [CrossRef]
- Ibáñez, M.; Sanz, O.; Egaña, A.; Reyero, I.; Bimbela, F.; Gandía, L.M.; Montes, M. Performance comparison between washcoated and packed-bed monolithic reactors for the low-temperature Fischer-Tropsch synthesis. Chem. Eng. J. 2021, 425, 130424. [Google Scholar] [CrossRef]
- Busse, C.; Freund, H.; Schwieger, W. Intensification of heat transfer in catalytic reactors by additively manufactured periodic open cellular structures (POCS). Chem. Eng. Process.-Process. Intensif. 2018, 124, 199–214. [Google Scholar] [CrossRef]
- Negri, M.; Wilhelm, M.; Hendrich, C.; Wingborg, N.; Gediminas, L.; Adelöw, L.; Maleix, C.; Chabernaud, P.; Brahmi, R.; Beauchet, R.; et al. New technologies for ammonium dinitramide based monopropellant thrusters–The project RHEFORM. Acta Astronaut. 2018, 143, 105–117. [Google Scholar] [CrossRef]
- Souliotis, T.; Koltsakis, G.; Samaras, Z. Catalyst Modeling Challenges for Electrified Powertrains. Catalysts 2021, 11, 539. [Google Scholar] [CrossRef]
- Cornejo, I.; Hayes, R.E. A Review of the Critical Aspects in the Multi-Scale Modelling of Structured Catalytic Reactors. Catalysts 2021, 11, 89. [Google Scholar] [CrossRef]
- Walander, M.; Nygren, A.; Sjöblom, J.; Johansson, E.; Creaser, D.; Edvardsson, J.; Tamm, S.; Lundberg, B. Use of 3D-printed mixers in laboratory reactor design for modelling of heterogeneous catalytic converters. Chem. Eng. Process.-Process. Intensif. 2021, 164, 108325. [Google Scholar] [CrossRef]
- Cornejo, I.; Nikrityuk, P.; Hayes, R.E. The influence of channel geometry on the pressure drop in automotive catalytic converters: Model development and validation. Chem. Eng. Sci. 2020, 212, 115317. [Google Scholar] [CrossRef]
- Carter, R.N.; Menacherry, P.; Pfefferle, W.C.; Muench, G.; Roychoudhury, S. Laboratory Evaluation of Ultra-Short Metal Monolith Catalyst; Technical Report; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1998. [Google Scholar]
- Quadri, S. The Effect of Oblique Entry Flow in Automotive Catalytic Converters. Ph.D. Thesis, Coventry University, Coventry, UK, 2008. [Google Scholar]
- Cornejo, I.; Nikrityuk, P.; Hayes, R.E. Pressure correction for automotive catalytic converters: A multi-zone permeability approach. Chem. Eng. Res. Des. 2019, 147, 232–243. [Google Scholar] [CrossRef]
- Hettel, M.; Daymo, E.; Schmidt, T.; Deutschmann, O. CFD-Modeling of fluid domains with embedded monoliths with emphasis on automotive converters. Chem. Eng. Process.-Process. Intensif. 2020, 147, 107728. [Google Scholar] [CrossRef]
- Hayes, R.E.; Fadic, A.; Mmbaga, J.; Najafi, A. CFD modelling of the automotive catalytic converter. Catal. Today 2012, 188, 94–105. [Google Scholar] [CrossRef]
- Cornejo, I.; Nikrityuk, P.; Lange, C.; Hayes, R.E. Influence of upstream turbulence on the pressure drop inside a monolith. Chem. Eng. Process.-Process. Intensif. 2020, 147, 107735. [Google Scholar] [CrossRef]
- Cornejo, I.; Hayes, R.E.; Nikrityuk, P. A new approach for the modeling of turbulent flows in automotive catalytic converters. Chem. Eng. Res. Des. 2018, 140, 308–319. [Google Scholar] [CrossRef]
- Cornejo, I.; Nikrityuk, P.; Hayes, R.E. Effect of substrate geometry and flow condition on the turbulence generation after a monolith. Can. J. Chem. Eng. 2020, 98, 947–956. [Google Scholar] [CrossRef]
- ANSYS Fluent Theory Guide Release 2021R1; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Tyldesley, J.R. An Introduction to Tensor Analysis for Engineers and Applied Scientists; Longman Publishing Group: Upper Saddle River, NJ, USA, 1975. [Google Scholar]
- Kauzmann, W. Kinetic Theory of Gases; Courier Corporation: New York, NY, USA, 2012. [Google Scholar]
- ANSYS Fluent Software Package v2021R1; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Malalasekera, W.; Versteeg, H. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; PEARSON Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Shah, R. A correlation for laminar hydrodynamic entry length solutions for circular and noncircular ducts. J. Fluids Eng. 1978, 100, 177–179. [Google Scholar] [CrossRef]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Durst, F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Cornejo, I.; Nikrityuk, P.; Hayes, R.E. Turbulence generation after a monolith in automotive catalytic converters. Chem. Eng. Sci. 2018, 187, 107–116. [Google Scholar] [CrossRef]
- Menon, S.; Yeung, P.K.; Kim, W.W. Effect of subgrid models on the computed interscale energy transfer in isotropic turbulence. Comput. Fluids 1996, 25, 165–180. [Google Scholar] [CrossRef]
- Menon, S.; Kim, W.W. High Reynolds number flow simulations using the localized dynamic subgrid-scale model. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; p. 425. [Google Scholar]
- Kim, W.W.; Menon, S.; Kim, W.W.; Menon, S. Application of the localized dynamic subgrid-scale model to turbulent wall-bounded flows. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–10 January 1997; p. 210. [Google Scholar]
- Afzal, N.; Seena, A.; Bushra, A. Power law velocity profile in fully developed turbulent pipe and channel flows. J. Hydraul. Eng. 2007, 133, 1080–1086. [Google Scholar] [CrossRef]
- Peszynski, K.; Tesař, V. Algebraic model of turbulent flow in ducts of rectangular cross-section with rounded corners. Flow Meas. Instrum. 2020, 75, 101790. [Google Scholar] [CrossRef]
- Blanchard, P.; Devaney, R.; Hall, G. Differential Equations; Richard Stratton: Boston, MA, USA, 2011. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Iwaniszyn, M.; Jodłowski, P.J.; Sindera, K.; Gancarczyk, A.; Korpyś, M.; Jędrzejczyk, R.J.; Kołodziej, A. Entrance effects on forced convective heat transfer in laminar flow through short hexagonal channels: Experimental and CFD study. Chem. Eng. J. 2021, 405, 126635. [Google Scholar] [CrossRef]
- Groppi, G.; Tronconi, E. Theoretical analysis of mass and heat transfer in monolith catalysts with triangular channels. Chem. Eng. Sci. 1997, 52, 3521–3526. [Google Scholar] [CrossRef]
- Watling, T.C. Flow and Forced Convection Heat and Mass Transfer Characteristics of Developed Laminar Flow in Square Channels with Rounded Corners: A Model for Flow in Washcoated Monolith Channels. Ind. Eng. Chem. Res. 2020, 59, 19770–19780. [Google Scholar] [CrossRef]
- Watling, T.C.; Van Lishout, Y.; Rees, I.D. Backpressure Prediction for Flow-Through Monoliths and Wall-Flow Filters Using 1-Dimensional Models: Entrance Effect Pressure Change, Developing Flow and Validation Using Length-Varying Techniques. Emiss. Control. Sci. Technol. 2021, 1–18. [Google Scholar] [CrossRef]


| N | Re | /D | N | Re | /D | N | Re | /D | N | Re | /D |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 1 | 9 | 50 | 4 | 17 | 50 | 8 | 25 | 50 | 14 |
| 2 | 100 | 1 | 10 | 100 | 4 | 18 | 100 | 8 | 26 | 100 | 14 |
| 3 | 150 | 1 | 11 | 150 | 4 | 19 | 150 | 8 | 27 | 150 | 14 |
| 4 | 200 | 1 | 12 | 200 | 4 | 20 | 200 | 8 | 28 | 200 | 14 |
| 5 | 50 | 1 | 13 | 50 | 6 | 21 | 50 | 10 | 29 | 50 | 20 |
| 6 | 100 | 2 | 14 | 100 | 6 | 22 | 100 | 10 | 30 | 100 | 20 |
| 7 | 150 | 2 | 15 | 150 | 6 | 23 | 150 | 10 | 31 | 150 | 20 |
| 8 | 200 | 2 | 16 | 200 | 6 | 24 | 200 | 10 | 32 | 200 | 20 |
| Gap Length () | Correction () | |
|---|---|---|
| Re | 1 | + |
| ( + ) | ||
| Re | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornejo, I. A Model for Correcting the Pressure Drop between Two Monoliths. Catalysts 2021, 11, 1314. https://doi.org/10.3390/catal11111314
Cornejo I. A Model for Correcting the Pressure Drop between Two Monoliths. Catalysts. 2021; 11(11):1314. https://doi.org/10.3390/catal11111314
Chicago/Turabian StyleCornejo, Ivan. 2021. "A Model for Correcting the Pressure Drop between Two Monoliths" Catalysts 11, no. 11: 1314. https://doi.org/10.3390/catal11111314
APA StyleCornejo, I. (2021). A Model for Correcting the Pressure Drop between Two Monoliths. Catalysts, 11(11), 1314. https://doi.org/10.3390/catal11111314






