Crystal Imperfections of Industrial Vanadium Phosphorous Oxide Catalysts
Abstract
:1. Introduction
2. Results
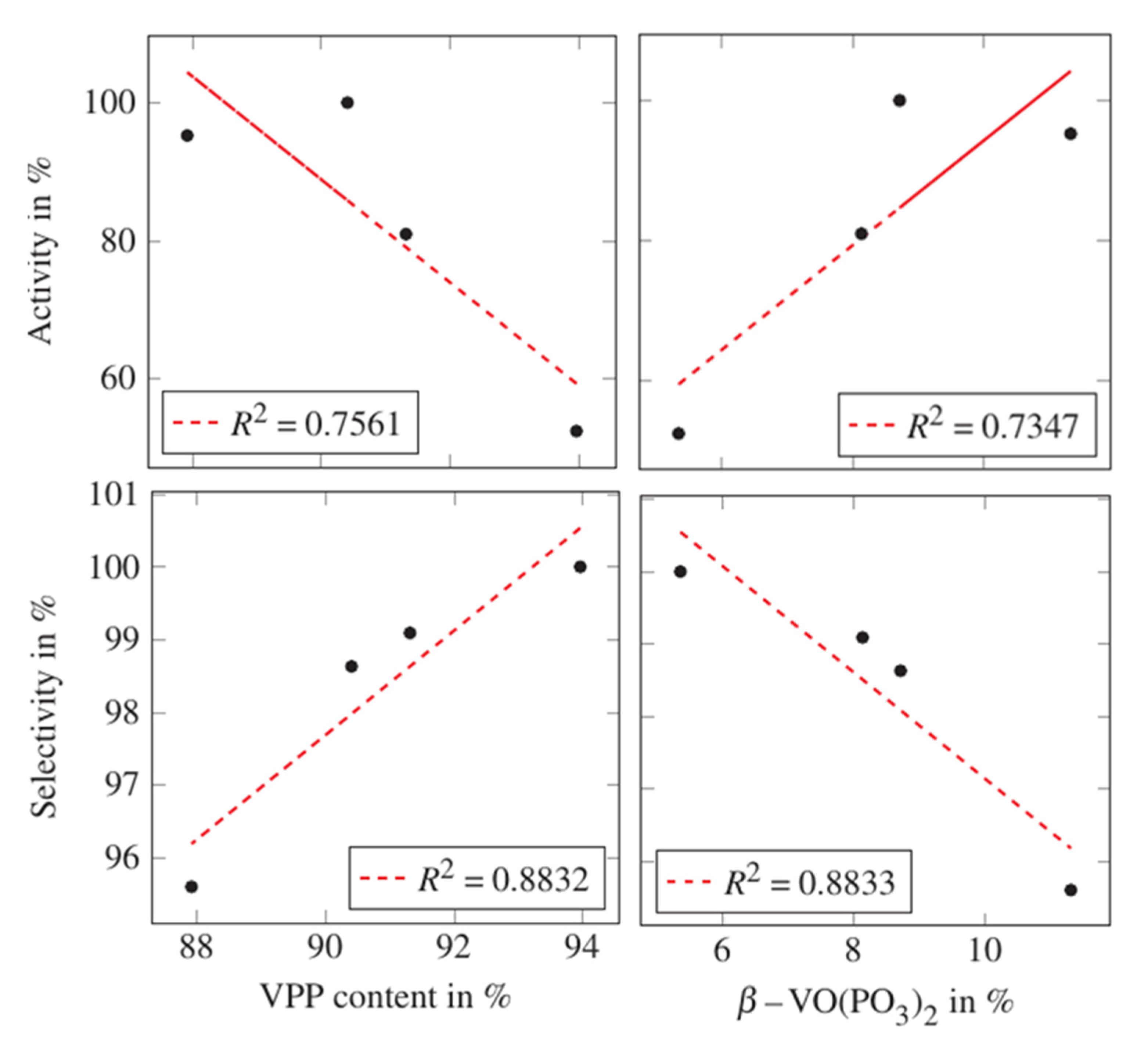
2.1. Changing the Catalyst Preparation Conditions
2.2. Results of the Powder Diffraction Full Profile Analysis
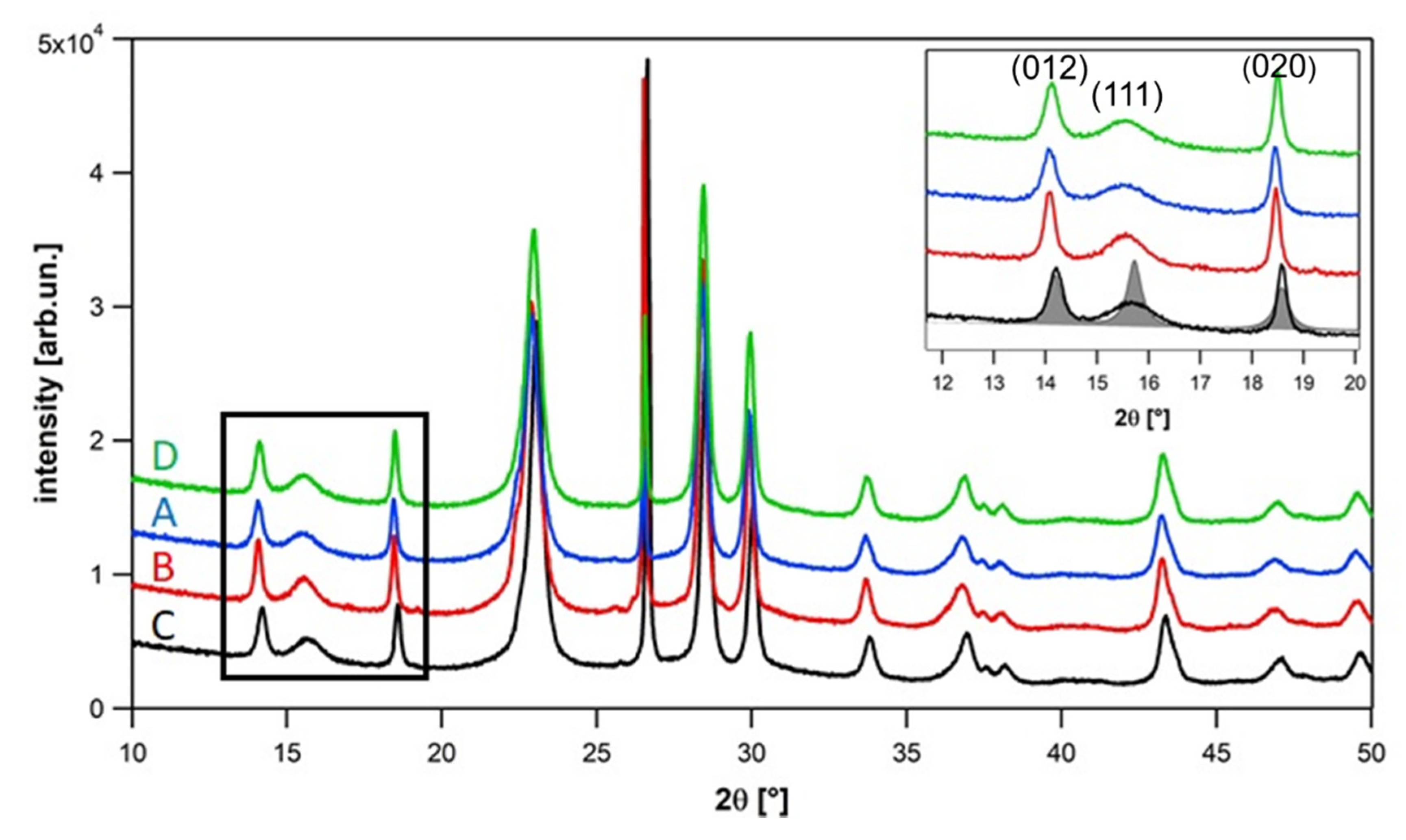
2.2.1. Phase Identification
2.2.2. Refinement with Isotropic Particle Size Effect
2.2.3. Refinement with Anisotropic Particle Size Effect
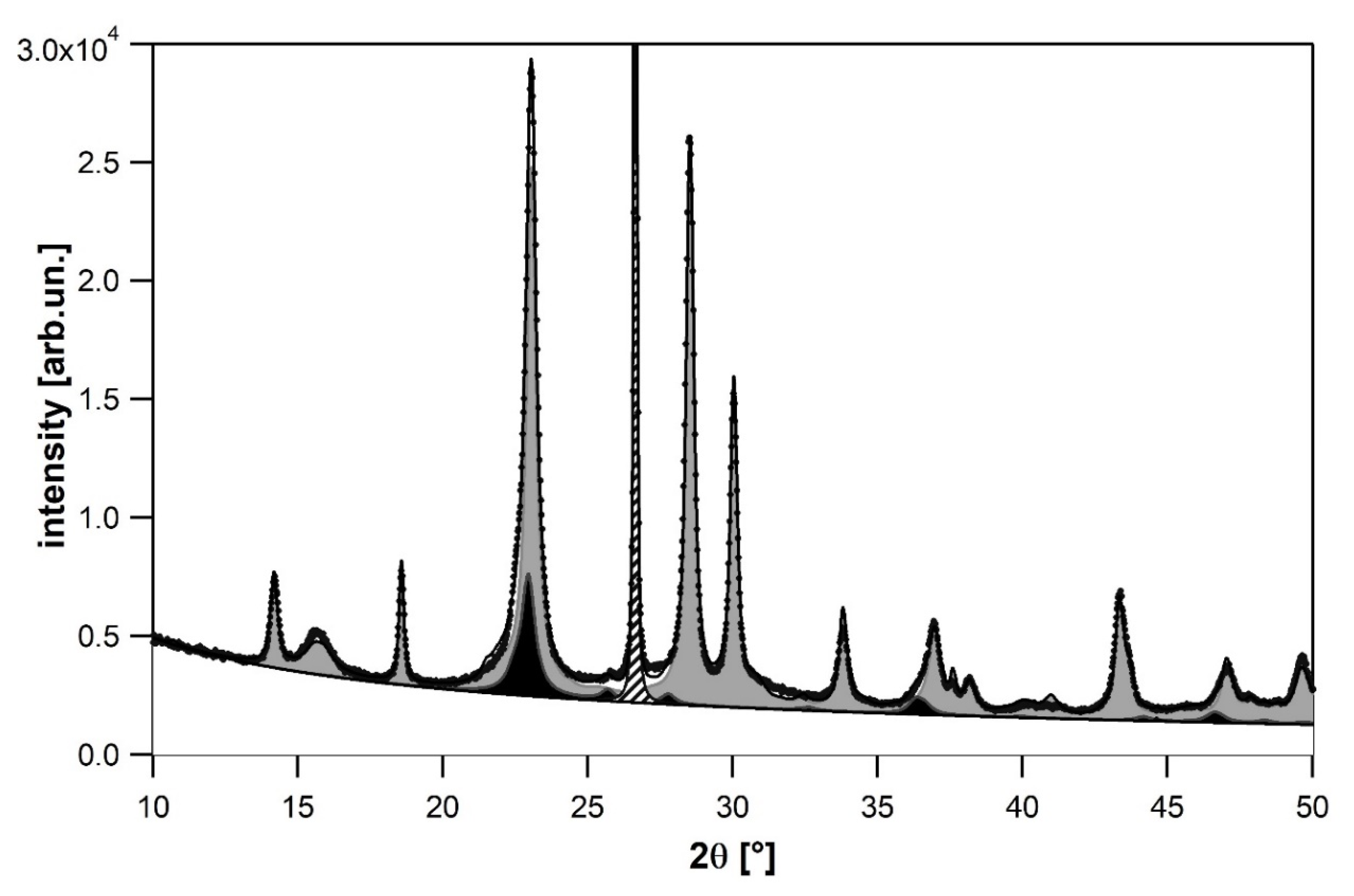
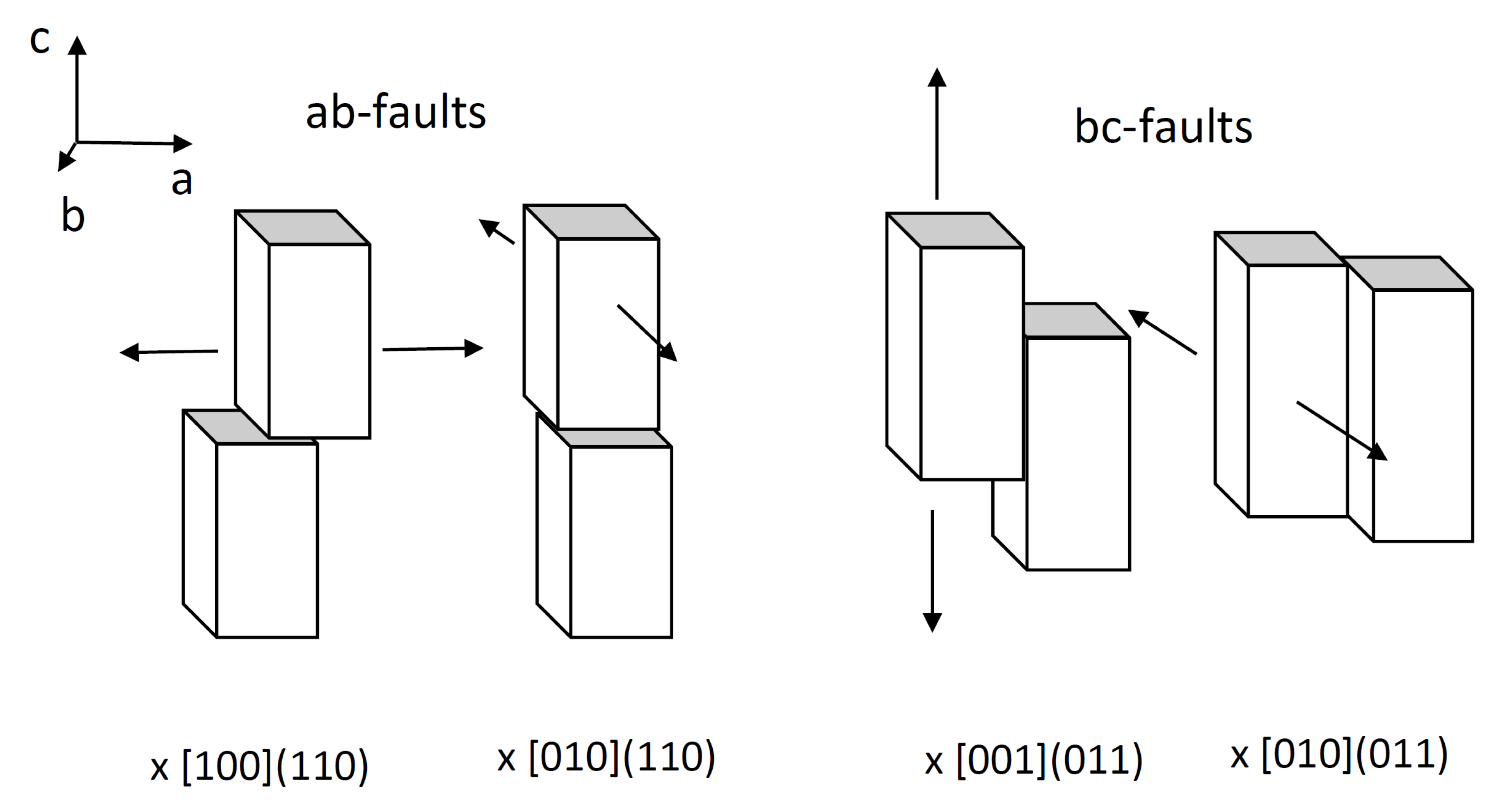
2.2.4. Refinement with Stacking Faults
3. Discussion
4. Materials and Methods
4.1. Bench-Scale Performance Test
4.2. Single Crystal Diffraction
4.3. Powder Crystal Diffraction
4.4. Stacking Fault Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Centi, G.; Trifiro, F.; Ebner, J.R.; Franchetti, V.M. Mechanistic aspects of maleic anhydride synthesis from C4 hydrocarbons over phosphorus vanadium oxide. Chem. Rev. 1988, 88, 55–80. [Google Scholar] [CrossRef]
- Lesser, D.; Mestl, G.; Turek, T. Transient behavior of vanadyl pyrophosphate catalysts during the partial oxidation of n-butane in industrial-sized, fixed bed reactors. Appl. Catal. A Gen. 2016, 510, 1–10. [Google Scholar] [CrossRef]
- Nguyen, P.; Sleight, A.; Roberts, N.; Warren, W. Modeling of extended defects in the vanadium phosphate catalyst for butane oxidation, (VO)2P2O7. J. Solid State Chem. 1996, 122, 259–265. [Google Scholar] [CrossRef]
- van Smaalen, S.; Dinnebier, R.; Hanson, J.; Gollwitzer, J.; Büllesfeld, F.; Prokofiev, A.; Assmus, W. High-temperature behavior of vanadyl pyrophosphate (VO)2P2O7. J. Solid State Chem. 2005, 178, 2225–2230. [Google Scholar] [CrossRef]
- Bordes, E.; Courtine, P.; Johnson, J. On the topotactic dehydration of VOHPO4·0.5H2O into vanadyl pyrophosphate. J. Solid State Chem. 1984, 55, 270–279. [Google Scholar] [CrossRef]
- Guliants, V.; Holmes, S.; Benziger, J.; Heaney, P.; Yates, D.; Wachs, I. In situ studies of atomic, nano-and macroscale order during VOHPO4·0.5 H2O transformation to (VO)2P2O7. J. Mol. Catal. A Chem. 2001, 172, 265–276. [Google Scholar] [CrossRef]
- Torardi, C.; Li, Z.; Horowitz, H.; Liang, W.; Whangbo, M.-H. Transformation of VOHPO4·1/2H2O to (VO)2P2O7: Crystallographic, microstructural, and mechanistic aspects. J. Solid State Chem. 1995, 119, 349–358. [Google Scholar] [CrossRef]
- Guliants, V.V.; Carreon, M.A. Vanadium-Phosphorus-Oxides: From Fundamentals of n-Butane Oxidation to Synthesis of New Phases; The Royal Society of Chemistry: Cambridge, UK, 2005. [Google Scholar]
- Weng, W.; Al Otaibi, R.; Alhumaimess, M.; Conte, M.; Bartley, J.K.; Dummer, N.F.; Hutchings, G.J.; Kiely, C.J. Controlling vanadium phosphate catalyst precursor morphology by adding alkane solvents in the reduction step of VOPO4·2H2O to VOHPO4·0.5H2O. J. Mater. Chem. 2011, 21, 16136–16146. [Google Scholar] [CrossRef] [Green Version]
- Sithamparappillai, U.; Nuno, J.L.; Dummer, N.F.; Weng, W.; Kiely, C.J.; Bartley, J.K.; Hutchings, G.J. Effect on the structure and morphology of vanadium phosphates of the addition of alkanes during the alcohol reduction of VOPO4·2H2O. J. Mater. Chem. 2010, 20, 5310–5318. [Google Scholar] [CrossRef] [Green Version]
- Hannour, F.; Martin, A.; Kubias, B.; Lücke, B.; Bordes, E.; Courtine, P. Vanadium phosphorus oxides with P/V = 2 used as oxidation and ammoxidation catalysts. Catal. Today 1998, 40, 263–272. [Google Scholar] [CrossRef]
- Cavani, F.; Luciani, S.; Esposti, E.D.; Cortelli, C.; Leanza, R. Surface Dynamics of A Vanadyl Pyrophosphate Catalyst for n-Butane Oxidation to Maleic Anhydride: An In Situ Raman and Reactivity Study of the Effect of the P/V Atomic Ratio. Chem. Eur. J. 2010, 16, 1646–1655. [Google Scholar] [CrossRef] [PubMed]
- Cavani, F.; De Santi, D.; Luciani, S.; Löfberg, A.; Bordes-Richard, E.; Cortelli, C.; Leanza, R. Transient reactivity of vanadyl pyrophosphate, the catalyst for n-butane oxidation to maleic anhydride, in response to in-situ treatments. Appl. Catal. A Gen. 2010, 376, 66–75. [Google Scholar] [CrossRef]
- Böcklein, S.; Mestl, G.; Auras, S.V.; Wintterlin, J. On the correlation of structure and catalytic performance of VPO catalysts. Top. Catal. 2017, 60, 1682–1697. [Google Scholar] [CrossRef]
- Thompson, D.J.; Fanning, M.; Hodnett, B. Modelling the active sites in vanadyl pyrophosphate. J. Mol. Catal. A Chem. 2003, 198, 125–137. [Google Scholar] [CrossRef]
- Cheng, M.-J.; Goddard, W.A.; Fu, R. The reduction-coupled oxo activation (ROA) mechanism responsible for the catalytic selective activation and functionalization of n-butane to maleic anhydride by vanadium phosphate oxide. Top. Catal. 2014, 57, 1171–1187. [Google Scholar] [CrossRef]
- Gai, P.L.; Kourtakis, K. Solid-state defect mechanism in vanadyl pyrophosphate catalysts: Implications for selective oxidation. Science 1995, 267, 661–663. [Google Scholar] [CrossRef]
- Cotter, T.; Reitzmann, A.; Mestl, G.; Donabauer, G.; Röhrer, S. Alkali Metal-Modified Vanadium-Phosphorus Oxide (VPO) Catalyst. U.S. Patent No. 9,931,618, 3 April 2018. [Google Scholar]
- Hiroi, Z.; Azuma, M.; Fujishiro, Y.; Saito, T.; Takano, M.; Izumi, F.; Kamiyama, T.; Ikeda, T. Structural study of the quantum-spin chain compound (VO)2P2O7. J. Solid State Chem. 1999, 146, 369–379. [Google Scholar] [CrossRef]
- Geupel, S.; Pilz, K.; Smaalen, S.v.; Büllesfeld, F.; Prokofiev, A.; Assmus, W. Synchrotron-radiation study of the two-leg spin-ladder (VO)2P2O7 at 120 K. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2002, 58, i9–i13. [Google Scholar] [CrossRef] [Green Version]
- Koo, H.-J.; Whangbo, M.-H.; VerNooy, P.D.; Torardi, C.C.; Marshall, W.J. Flux Growth of Vanadyl Pyrophosphate, (VO)P2O7, and Spin Dimer Analysis of the Spin Exchange Interactions of (VO)2P2O7 and Vanadyl Hydrogen Phosphate, VO(HPO4)·0.5H2O. Inorg. Chem. 2002, 41, 4664–4672. [Google Scholar] [CrossRef]
- Saito, T.; Terashima, T.; Azuma, M.; Takano, M.; Goto, T.; Ohta, H.; Utsumi, W.; Bordet, P.; Johnston, D. Single crystal growth of the high pressure phase of (VO)2P2O7 at 3 GPa. J. Solid State Chem. 2000, 153, 124–131. [Google Scholar] [CrossRef]
- Nguyen, P.; Hoffman, R.; Sleight, A. Structure of (VO)2P2O7. Mater. Res. Bull. 1995, 30, 1055–1063. [Google Scholar] [CrossRef]
- Gorbunova, Y.E.; Linde, S. Structure of crystals of vanadyl pyrophosphate (VO)2P2O7. Dokl. Akad. Nauk SSSR 1979, 245, 584–588. [Google Scholar]
- Ectors, D.; Goetz-Neunhoeffer, F.; Neubauer, J. A generalized geometric approach to anisotropic peak broadening due to domain morphology. J. Appl. Crystallogr. 2015, 48, 189–194. [Google Scholar] [CrossRef]
- Gao, Z.; Odstrcil, M.; Böcklein, S.; Palagin, D.; Holler, M.; Sanchez, D.F.; Krumreich, F.; Menzel, A.; Stampanoni, M.; Mestl, G.; et al. Sparse ab initio x-ray transmission spectrotomography for nanoscopic compositional analysis of functional materials. Sci. Adv. 2021, 7, eabf6971. [Google Scholar] [CrossRef] [PubMed]
- Ihli, J.; Bloch, L.; Böcklein, S.; Rzepka, P.; Burghammer, M.; da Silva, J.C.; Mestl, G.; van Bokhoven, J.A. Evolution of Heterogeneity in Industrial Selective Oxidation Catalyst Pellets. ACS Catal. 2021, 11, 8274–8283. [Google Scholar] [CrossRef]
- Coelho, A.A. TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Momma, K. VESTA, ver. 3.4.6. 27 January 2019. Available online: https://jp-minerals.org/vesta/en/ (accessed on 18 February 2019).
- Rigaku, Matsubara-cho, 3-9-12 Akishima-shi, Tokyo, Japan. CrysAlis Pro. Available online: https://www.rigaku.com/products/crystallography/crysalis (accessed on 18 February 2019).
- Herbst-Irmer, R.; Spek, A.; Schneider, T.; Sawaya, M. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; Oxford University Press: Oxford, UK, 2006; Volume 8. [Google Scholar]
- Coelho, A.A.; Evans, J.S.; Lewis, J.W. Averaging the intensity of many-layered structures for accurate stacking-fault analysis using Rietveld refinement. J. Appl. Crystallogr. 2016, 49, 1740–1749. [Google Scholar] [CrossRef] [Green Version]

| Sample | Temperature | Steam Content | Oxygen Content | Normalized Activity [%] | Normalized Selectivity [%] |
|---|---|---|---|---|---|
| A | hot | medium | medium | 95.2 | 95.6 |
| B | medium | low | high | 81.0 | 99.1 |
| C | medium | medium | high | 100.0 | 98.6 |
| D | medium | medium | low | 52.4 | 100.0 |
| Publication Pearson’s Crystallographic Database | Space Group | Lattice Parameter a [Å] | Lattice Parameter b [Å] | Lattice Parameter c [Å] |
|---|---|---|---|---|
| [4] | Pca21 | 7.7288 | 9.5787 | 16.5873 |
| [20] | Pca21 | 7.7004 | 9.5777 | 16.5825 |
| [21] | Pca21 | 7.729 | 9.583 | 16.581 |
| [19] | Pca21 | 7.7381 | 9.587 | 16.5895 |
| [22] | Pbcn | 8.362 | 9.536 | 7.571 |
| [23] * | P1211 | 7.7276 | 16.5885 | 9.5796 |
| [24] | Pca21 | 7.725 | 9.572 | 16.576 |
| Publication ICSD Database | ||||
| [20] | Pca21 | 7.7004 | 9.5777 | 16.5825 |
| [21] | Pca21 | 7.729 | 9.583 | 16.581 |
| [19] | Pca21 | 7.73808 | 9.58698 | 16.58949 |
| [23] * | P1211 | 7.7276 | 16.58849 | 9.5796 |
| [24] | Pb21a | 7.725 | 16.5760 | 9.573 |
| Own single crystal structure | Pca21 | 7.7362(2) | 9.5842(2) | 16.5897(4) |
| rx [nm] | ry [nm] | rz [nm] | Rwp | |
|---|---|---|---|---|
| model 1 | 6.655(8) | 10.652(7) | 5.409(1) | 10.338(1) |
| model 2 | 4.7789(9) | 13.3614(6) | 5.6058(6) | 9.820(8) |
| model 3 | 3.888(4) | 8.9027(7) | 6.354(3) | 9.301(3) |
| A | B | C | D | |
|---|---|---|---|---|
| VPP [%] | 87.92 | 91.32 | 90.41 | 94.10 |
| β-VO(PO3)2 [%] | 11.32 | 8.14 | 8.72 | 5.23 |
| Graphite [%] | 0.77 | 0.54 | 0.78 | 0.68 |
| Model | 3 | 3 | 3 | 3 |
| rx [nm] | 2.928(7) | 2.802(5) | 3.870(3) | 3.095(3) |
| ry [nm] | 11.252(4) | 9.576(1) | 9.272(8) | 10.437(7) |
| rz [nm] | 7.527(3) | 5.881(4) | 6.546(4) | 6.085(5) |
| pa [%] | 0.94 | 0.94 | 0.90 | 0.94 |
| Rwp | 6.128 | 5.538 | 5.710 | 5.652 |
| Refinement Strategy | Rwp Value |
|---|---|
| Isotropic crystallite size (10 nm) | 23.827 |
| Anisotropic crystallite size (mod3) | 9.301 |
| ab-stacking fault | 7.101 |
| bc-stacking fault | 5.710 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kappel, I.; Böcklein, S.; Park, S.; Wharmby, M.; Mestl, G.; Schmahl, W.W. Crystal Imperfections of Industrial Vanadium Phosphorous Oxide Catalysts. Catalysts 2021, 11, 1325. https://doi.org/10.3390/catal11111325
Kappel I, Böcklein S, Park S, Wharmby M, Mestl G, Schmahl WW. Crystal Imperfections of Industrial Vanadium Phosphorous Oxide Catalysts. Catalysts. 2021; 11(11):1325. https://doi.org/10.3390/catal11111325
Chicago/Turabian StyleKappel, Isabella, Sebastian Böcklein, SoHyun Park, Michael Wharmby, Gerhard Mestl, and Wolfgang W. Schmahl. 2021. "Crystal Imperfections of Industrial Vanadium Phosphorous Oxide Catalysts" Catalysts 11, no. 11: 1325. https://doi.org/10.3390/catal11111325
APA StyleKappel, I., Böcklein, S., Park, S., Wharmby, M., Mestl, G., & Schmahl, W. W. (2021). Crystal Imperfections of Industrial Vanadium Phosphorous Oxide Catalysts. Catalysts, 11(11), 1325. https://doi.org/10.3390/catal11111325






