Steps toward Rationalization of the Enantiomeric Excess of the Sakurai–Hosomi–Denmark Allylation Catalyzed by Biisoquinoline N,N’-Dioxides Using Computations
Abstract
:1. Introduction
2. Computational Methods
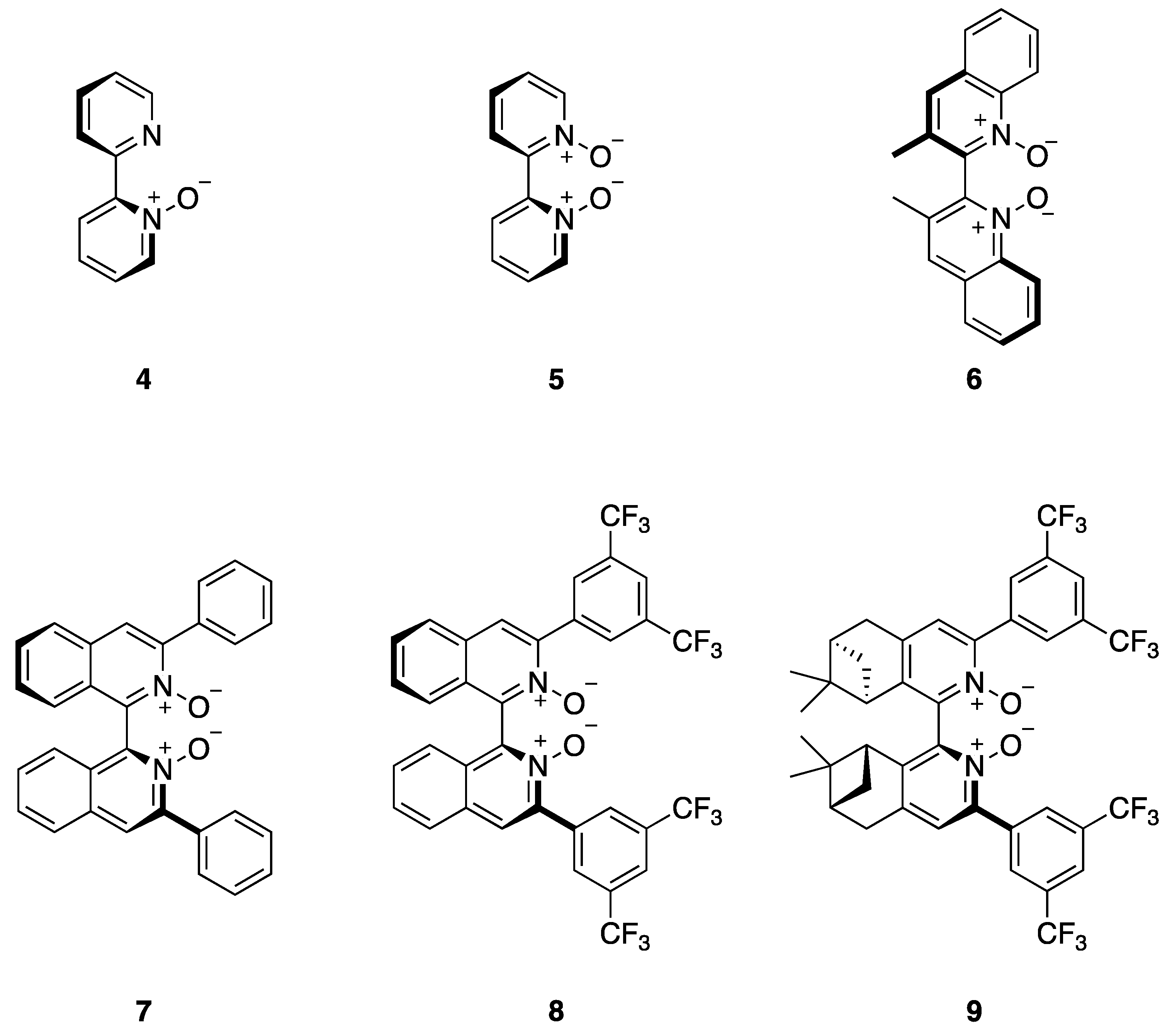
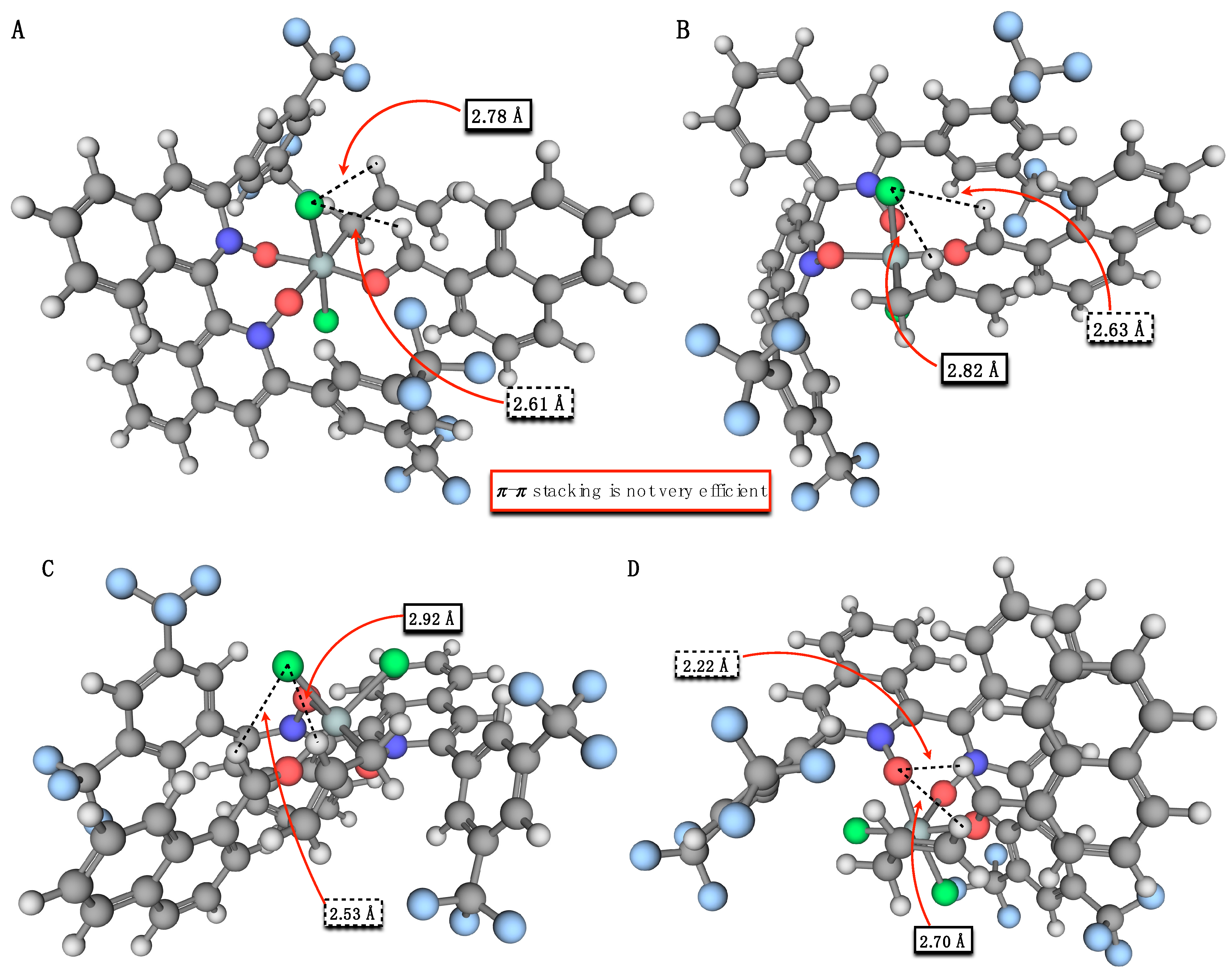
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rossi, S.; Benaglia, M.; Genoni, A. Organic Reactions Mediated by Tetrachlorosilane. Tetrahedron 2014, 70, 2065–2080. [Google Scholar] [CrossRef]
- Denmark, S.E.; Beutner, G.L. Lewis Base Catalysis in Organic Synthesis. Angew. Chem. Int. Ed. 2008, 47, 1560–1638. [Google Scholar] [CrossRef] [PubMed]
- Orito, Y.; Nakajima, M. Lewis Base Catalyzed Asymmetric Reactions Involving Hypervalent Silicate Intermediates. Synthesis 2006, 2006, 1391–1401. [Google Scholar] [CrossRef]
- Nakajima, M.; Saito, M.; Shiro, M.; Hashimoto, S. (S)-3,3’-Dimethyl-2,2’-Biquinoline N,N’-Dioxide as an Efficient Catalyst for Enantioselective Addition of Allyltrichlorosilanes to Aldehydes. J. Am. Chem. Soc. 1998, 120, 6419–6420. [Google Scholar] [CrossRef]
- Malkov, A.V.; Orsini, M.; Pernazza, D.; Muir, K.W.; Langer, V.; Meghani, P.; Kočovský, P. Chiral 2,2‘-Bipyridine-Type N-Monoxides as Organocatalysts in the Enantioselective Allylation of Aldehydes with Allyltrichlorosilane. Org. Lett. 2002, 4, 1047–1049. [Google Scholar] [CrossRef] [PubMed]
- Malkov, A.V.; Kočovský, P. Lewis Base-Catalyzed Reactions of SiX 3 -Based Reagents with C=O, C=N (n → σ*). In Lewis Base Catalysis in Organic Synthesis; Vedejs, E., Denmark, S.E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 1011–1038. ISBN 978-3-527-67514-2. [Google Scholar]
- Kočovský, P.; Malkov, A.V. Lewis Bases as Catalysts in the Reduction of Imines and Ketones with Silanes (n → σ *). In Lewis Base Catalysis in Organic Synthesis; Vedejs, E., Denmark, S.E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 1077–1112. ISBN 978-3-527-67514-2. [Google Scholar]
- Denmark, S.E.; Beutner, G.L. Principles, Definitions, Terminology, and Orbital Analysis of Lewis Base-Lewis Acid Interactions Leading to Catalysis. In Lewis Base Catalysis in Organic Synthesis; Vedejs, E., Denmark, S.E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 31–54. ISBN 978-3-527-67514-2. [Google Scholar]
- Fu, J.; Fujimori, S.; Denmark, S.E. Bifunctional Lewis Base Catalysis with Dual Activation of X 3 Si-Nu and C=O (n → σ *). In Lewis Base Catalysis in Organic Synthesis; Vedejs, E., Denmark, S.E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 281–338. ISBN 978-3-527-67514-2. [Google Scholar]
- Rossi, S.; Denmark, S.E. Lewis Base-Catalyzed, Lewis Acid-Mediated Reactions (n → σ*). In Lewis Base Catalysis in Organic Synthesis; Vedejs, E., Denmark, S.E., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 1039–1076. ISBN 978-3-527-67514-2. [Google Scholar]
- Reep, C.; Morgante, P.; Peverati, R.; Takenaka, N. Axial-Chiral Biisoquinoline N,N´-Dioxides Bearing Polar Aromatic C-H Bonds as Catalysts in Sakurai-Hosomi-Denmark Allylation. Org. Lett. 2018, 20, 5757–5761. [Google Scholar] [CrossRef]
- Malkov, A.V.; Ramírez-López, P.; Biedermannová (née Bendová), L.; Rulíšek, L.; Dufková, L.; Kotora, M.; Zhu, F.; Kočovský, P. On the Mechanism of Asymmetric Allylation of Aldehydes with Allyltrichlorosilanes Catalyzed by QUINOX, a Chiral Isoquinoline N -Oxide. J. Am. Chem. Soc. 2008, 130, 5341–5348. [Google Scholar] [CrossRef]
- Lu, T.; Porterfield, M.A.; Wheeler, S.E. Explaining the Disparate Stereoselectivities of N-Oxide Catalyzed Allylations and Propargylations of Aldehydes. Org. Lett. 2012, 14, 5310–5313. [Google Scholar] [CrossRef]
- Sepúlveda, D.; Lu, T.; Wheeler, S.E. Performance of DFT Methods and Origin of Stereoselectivity in Bipyridine N,N′-Dioxide Catalyzed Allylation and Propargylation Reactions. Org. Biomol. Chem. 2014, 12, 8346–8353. [Google Scholar] [CrossRef] [PubMed]
- Doney, A.C.; Rooks, B.J.; Lu, T.; Wheeler, S.E. Design of Organocatalysts for Asymmetric Propargylations through Computational Screening. ACS Catal. 2016, 6, 7948–7955. [Google Scholar] [CrossRef]
- Vaganov, V.Y.; Fukazawa, Y.; Kondratyev, N.S.; Shipilovskikh, S.A.; Wheeler, S.E.; Rubtsov, A.E.; Malkov, A.V. Optimization of Catalyst Structure for Asymmetric Propargylation of Aldehydes with Allenyltrichlorosilane. Adv. Synth. Catal. 2020, 362, 5467–5474. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Mapping the Genome of Meta-Generalized Gradient Approximation Density Functionals: The Search for B97M-V. J. Chem. Phys. 2015, 142, 074111-32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mardirossian, N.; Head-Gordon, M. ωB97M-V: A Combinatorially Optimized, Range-Separated Hybrid, Meta-GGA Density Functional with VV10 Nonlocal Correlation. J. Chem. Phys. 2016, 144, 214110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham Global-Hybrid Exchange–Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.S.; He, X.; Truhlar, D.G. MN15-L: A New Local Exchange-Correlation Functional for Kohn–Sham Density Functional Theory with Broad Accuracy for Atoms, Molecules, and Solids. J. Chem. Theory Comput. 2016, 12, 1280–1293. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A Generally Applicable Atomic-Charge Dependent London Dispersion Correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Goerigk, L.; Mehta, N. A Trip to the Density Functional Theory Zoo: Warnings and Recommendations for the User. Aust. J. Chem. 2019, 72, 563. [Google Scholar] [CrossRef] [Green Version]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; International Series of Monographs on Chemistry; Oxford Science Publications: Oxford, UK, 1994. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Morgante, P.; Peverati, R. The devil in the details: A tutorial review on some undervalued aspects of density functional theory calculations. J. Comput. Chem. 2020, 120, e26332. [Google Scholar] [CrossRef]



| Structure | ∆G≠, kcal mol−1 | ∆∆G≠,a kcal mol−1 | Structure | ∆G≠, kcal mol−1 | ∆∆G≠,a kcal mol−1 |
|---|---|---|---|---|---|
| Trans-1-Boat-Si | 13.0 | 1.78 | Trans-1-Boat-Re | 13.6 | 2.41 |
| Trans-1-Chair-Si | 11.2 | 0.00 | Trans-1-Chair-Re | 13.0 | 1.74 |
| Cis-2-Boat-Si | 16.3 | 5.03 | Cis-2-Boat-Re | 14.5 | 3.25 |
| Cis-2-Chair-Si | 15.2 | 3.96 | Cis-2-Chair-Re | 13.0 | 1.81 |
| Cis-3-Boat-Si | 20.4 | 9.18 | Cis-3-Boat-Re | 18.9 | 7.69 |
| Cis-3-Chair-Si | 17.1 | 5.88 | Cis-3-Chair-Re | 20.9 | 9.70 |
| Cis-4-Boat-Si | 28.6 b | 17.3 | Cis-4-Boat-Re | 25.6 | 14.4 |
| Cis-4-Chair-Si | 23.8 | 12.6 | Cis-4-Chair-Re | 21.3 | 10.0 |
| Cis-5-Boat-Si | 23.0 | 11.8 | Cis-5-Boat-Re | c | N/A |
| Cis-5-Chair-Si | 25.4 | 14.2 | Cis-5-Chair-Re | 19.5 | 8.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgante, P.; Deluca, C.; Jones, T.E.; Aldrich, G.J.; Takenaka, N.; Peverati, R. Steps toward Rationalization of the Enantiomeric Excess of the Sakurai–Hosomi–Denmark Allylation Catalyzed by Biisoquinoline N,N’-Dioxides Using Computations. Catalysts 2021, 11, 1487. https://doi.org/10.3390/catal11121487
Morgante P, Deluca C, Jones TE, Aldrich GJ, Takenaka N, Peverati R. Steps toward Rationalization of the Enantiomeric Excess of the Sakurai–Hosomi–Denmark Allylation Catalyzed by Biisoquinoline N,N’-Dioxides Using Computations. Catalysts. 2021; 11(12):1487. https://doi.org/10.3390/catal11121487
Chicago/Turabian StyleMorgante, Pierpaolo, Coty Deluca, Tegla E. Jones, Gregory J. Aldrich, Norito Takenaka, and Roberto Peverati. 2021. "Steps toward Rationalization of the Enantiomeric Excess of the Sakurai–Hosomi–Denmark Allylation Catalyzed by Biisoquinoline N,N’-Dioxides Using Computations" Catalysts 11, no. 12: 1487. https://doi.org/10.3390/catal11121487
APA StyleMorgante, P., Deluca, C., Jones, T. E., Aldrich, G. J., Takenaka, N., & Peverati, R. (2021). Steps toward Rationalization of the Enantiomeric Excess of the Sakurai–Hosomi–Denmark Allylation Catalyzed by Biisoquinoline N,N’-Dioxides Using Computations. Catalysts, 11(12), 1487. https://doi.org/10.3390/catal11121487






