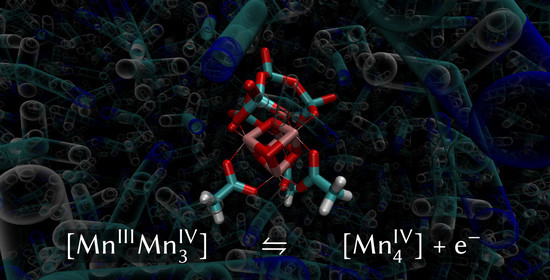
A Force Field for a Manganese-Vanadium Water Oxidation Catalyst: Redox Potentials in Solution as Showcase
Abstract
:1. Introduction
2. Theory
2.1. Force Field Parameters
2.2. Redox Potentials
3. Computational Details
3.1. Reference Ab Initio Calculations
3.2. QM/MM MD Reference Simulations
3.3. MM MD Simulations
3.4. Parameter Setup
3.5. Redox Potential Calculations
4. Results
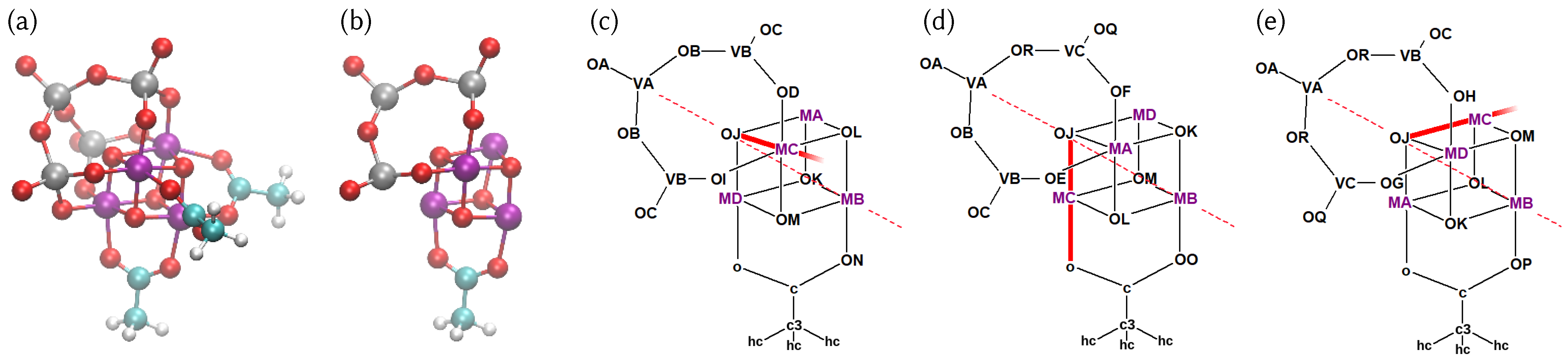
4.1. Structure of the Catalyst and Atom Type Labeling
4.2. Force Field Parameters and Geometries
4.3. Energy Distributions and Redox Potentials
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hagedorn, G.; Kalmus, P.; Mann, M.; Vicca, S.; den Berge, J.V.; van Ypersele, J.P.; Bourg, D.; Rotmans, J.; Kaaronen, R.; Rahmstorf, S.; et al. Concerns of young protesters are justified. Science 2019, 364, 139–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cook, T.R.; Dogutan, D.K.; Reece, S.Y.; Surendranath, Y.; Teets, T.S.; Nocera, D.G. Solar energy supply and storage for the legacy and nonlegacy worlds. Chem. Rev. 2010, 110, 6474–6502. [Google Scholar] [CrossRef] [PubMed]
- Tachibana, Y.; Vayssieres, L.; Durrant, J.R. Artificial photosynthesis for solar water-splitting. Nat. Photonics 2012, 6, 511–518. [Google Scholar] [CrossRef]
- Berardi, S.; Drouet, S.; Francàs, L.; Gimbert-Suriñach, C.; Guttentag, M.; Richmond, C.; Stoll, T.; Llobet, A. Molecular artificial photosynthesis. Chem. Soc. Rev. 2014, 43, 7501–7519. [Google Scholar] [CrossRef]
- Kärkäs, M.D.; Verho, O.; Johnston, E.V.; Åkermark, B. Artificial photosynthesis: Molecular systems for catalytic water oxidation. Chem. Rev. 2014, 114, 11863–12001. [Google Scholar] [CrossRef]
- Blakemore, J.D.; Crabtree, R.H.; Brudvig, G.W. Molecular catalysts for water oxidation. Chem. Rev. 2015, 115, 12974–13005. [Google Scholar] [CrossRef] [PubMed]
- Roger, I.; Shipman, M.A.; Symes, M.D. Earth-abundant catalysts for electrochemical and photoelectrochemical water splitting. Nat. Rev. Chem. 2017, 1, 0003. [Google Scholar] [CrossRef]
- Matheu, R.; Garrido-Barros, P.; Gil-Sepulcre, M.; Ertem, M.Z.; Sala, X.; Gimbert-Suriñach, C.; Llobet, A. The development of molecular water oxidation catalysts. Nat. Rev. Chem. 2019, 3, 331–341. [Google Scholar] [CrossRef]
- Gao, D.; Trentin, I.; Schwiedrzik, L.; González, L.; Streb, C. The reactivity and stability of polyoxometalate water oxidation electrocatalysts. Molecules 2019, 25, 157. [Google Scholar] [CrossRef] [Green Version]
- Limburg, B.; Bouwman, E.; Bonnet, S. Molecular water oxidation catalysts based on transition metals and their decomposition pathways. Coord. Chem. Rev. 2012, 256, 1451–1467. [Google Scholar] [CrossRef]
- Vinyard, D.J.; Brudvig, G.W. Progress toward a molecular mechanism of water oxidation in photosystem II. Annu. Rev. Phys. Chem. 2017, 68, 101–116. [Google Scholar] [CrossRef]
- Kok, B.; Forbush, B.; Mcgloin, M. Cooperation of charges in photosynthetic O2 evolution–I. A linear four step mechanism. Photochem. Photobiol. 1970, 11, 457–475. [Google Scholar] [CrossRef] [PubMed]
- Åhrling, K.A.; Peterson, S.; Styring, S. An oscillating manganese electron paramagnetic resonance signal from the S0 state of the oxygen evolving complex in photosystem II. Biochemistry 1997, 36, 13148–13152. [Google Scholar] [CrossRef] [PubMed]
- Krewald, V.; Retegan, M.; Cox, N.; Messinger, J.; Lubitz, W.; DeBeer, S.; Neese, F.; Pantazis, D.A. Metal oxidation states in biological water splitting. Chem. Sci. 2015, 6, 1676–1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lubitz, W.; Chrysina, M.; Cox, N. Water oxidation in photosystem II. Photosynth. Res. 2019, 142, 105–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cox, N.; Pantazis, D.A.; Lubitz, W. Current understanding of the mechanism of water oxidation in photosystem II and its relation to XFEL data. Annu. Rev. Biochem. 2020, 89, 795–820. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, B.; Forster, J.; Goetz, M.K.; Yücel, D.; Berger, C.; Jacob, T.; Streb, C. Visible-light-driven water oxidation by a molecular manganese vanadium oxide cluster. Angew. Chem. Int. Ed. 2016, 55, 6329–6333. [Google Scholar] [CrossRef]
- Romanenko, I.; Rajagopal, A.; Neumann, C.; Turchanin, A.; Streb, C.; Schacher, F.H. Embedding molecular photosensitizers and catalysts in nanoporous block copolymer membranes for visible-light driven hydrogen evolution. J. Mater. Chem. A 2020, 8, 6238–6244. [Google Scholar] [CrossRef]
- Nabiyan, A.; Schulz, M.; Neumann, C.; Dietzek, B.; Turchanin, A.; Schacher, F.H. Photocatalytically active block copolymer hybrid micelles from double hydrophilic block copolymers. Eur. Polym. J. 2020, 140, 110037. [Google Scholar] [CrossRef]
- Quiñonero, D.; Kaledin, A.L.; Kuznetsov, A.E.; Geletii, Y.V.; Besson, C.; Hill, C.L.; Musaev, D.G. Computational studies of the geometry and electronic structure of an all-inorganic and homogeneous tetra-Ru-polyoxotungstate catalyst for water oxidation and its four subsequent one-electron oxidized forms. J. Phys. Chem. A 2010, 114, 535–542. [Google Scholar] [CrossRef]
- Soriano-López, J.; Musaev, D.G.; Hill, C.L.; Galán-Mascarós, J.R.; Carbó, J.J.; Poblet, J.M. Tetracobalt-polyoxometalate catalysts for water oxidation: Key mechanistic details. J. Catal. 2017, 350, 56–63. [Google Scholar] [CrossRef] [Green Version]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to the dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 799. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The AMBER biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [Green Version]
- Boresch, S.; Karplus, M. The Jacobian factor in free energy simulations. J. Chem. Phys. 1996, 105, 5145–5154. [Google Scholar] [CrossRef]
- Warshel, A. Dynamics of reactions in polar solvents. Semiclassical trajectory studies of electron-transfer and proton-transfer reactions. J. Phys. Chem. 1982, 86, 2218–2224. [Google Scholar] [CrossRef]
- King, G.; Warshel, A. Investigation of the free energy functions for electron transfer reactions. J. Chem. Phys. 1990, 93, 8682–8692. [Google Scholar] [CrossRef]
- Blumberger, J.; Tavernelli, I.; Klein, M.L.; Sprik, M. Diabatic free energy curves and coordination fluctuations for the aqueous Ag+/Ag2+ redox couple: A biased Born-Oppenheimer molecular dynamics investigation. J. Chem. Phys. 2006, 124, 064507. [Google Scholar] [CrossRef] [PubMed]
- Diamantis, P.; Gonthier, J.F.; Tavernelli, I.; Röthlisberger, U. Study of the redox properties of singlet and triplet tris(2,2′-bipyridine) ruthenium(II) ([Ru(bpy)3]2+) in aqueous solution by full quantum and mixed quantum/classical molecular dynamics simulations. J. Phys. Chem. B 2014, 118, 3950–3959. [Google Scholar] [CrossRef]
- Diamantis, P.; Tavernelli, I.; Rothlisberger, U. Redox properties of native and damaged DNA from mixed quantum mechanical/molecular mechanics molecular dynamics simulations. J. Chem. Theory Comput. 2020, 16, 6690–6701. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef] [Green Version]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. III. Applications to data on the rates of organic redox reactions. J. Chem. Phys. 1957, 26, 872–877. [Google Scholar] [CrossRef] [Green Version]
- Marcus, R.A. On the theory of electron-transfer reactions. VI. Unified treatment for homogeneous and electrode reactions. J. Chem. Phys. 1965, 43, 679–701. [Google Scholar] [CrossRef] [Green Version]
- Matyushov, D.V.; Voth, G.A. Modeling the free energy surfaces of electron transfer in condensed phases. J. Chem. Phys. 2000, 113, 5413. [Google Scholar] [CrossRef]
- Small, D.W.; Matyushov, D.V.; Voth, G.A. The theory of electron transfer reactions: What may be missing? J. Am. Chem. Soc. 2003, 125, 7470–7478. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-electron scalar relativistic basis sets for third-row transition metal atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two–component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2017, 8, e1327. [Google Scholar] [CrossRef]
- Ames, W.; Pantazis, D.A.; Krewald, V.; Cox, N.; Messinger, J.; Lubitz, W.; Neese, F. Theoretical evaluation of structural models of the S2 state in the oxygen evolving complex of photosystem II: Protonation states and magnetic interactions. J. Am. Chem. Soc. 2011, 133, 19743–19757. [Google Scholar] [CrossRef]
- Neese, F. Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Greene, D.; Homeyer, N.; et al. AMBER 2017. Available online: http://ambermd.org/ (accessed on 21 April 2017).
- Ufimtsev, I.S.; Martinez, T.J. Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics. J. Chem. Theory Comput. 2009, 5, 2619–2628. [Google Scholar] [CrossRef]
- Titov, A.V.; Ufimtsev, I.S.; Luehr, N.; Martinez, T.J. Generating efficient quantum chemistry codes for novel architectures. J. Chem. Theory Comput. 2012, 9, 213–221. [Google Scholar] [CrossRef]
- Dunning, T.H.; Hay, P.J. Gaussian basis sets for molecular calculations. In Methods of Electronic Structure Theory; Springer: New York, NY, USA, 1977; pp. 1–27. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Song, C.; Wang, L.P.; Martínez, T.J. Automated code engine for graphical processing units: Application to the effective core potential integrals and gradients. J. Chem. Theory Comput. 2015, 12, 92–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caleman, C.; van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force field benchmark of organic liquids: Density, enthalpy of vaporization, heat capacities, surface tension, isothermal compressibility, volumetric expansion coefficient, and dielectric constant. J. Chem. Theory Comput. 2011, 8, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kovalenko, A. Application of the approximate 3D-reference interaction site model (RISM) molecular solvation theory to acetonitrile as solvent. J. Phys. Chem. B 2020, 124, 4590–4597. [Google Scholar] [CrossRef] [PubMed]
- Joung, I.S.; Cheatham, T.E. Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Roberts, B.P.; Chakravorty, D.K.; Merz, K.M. Rational design of particle mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent. J. Chem. Theory Comput. 2013, 9, 2733–2748. [Google Scholar] [CrossRef] [Green Version]
- Menke, C.; Diemann, E.; Müller, A. Polyoxovanadate clusters and cages: Force-field parameterization. J. Mol. Struct. 1997, 436-437, 35–47. [Google Scholar] [CrossRef]
- Manchanda, R.; Zimmer, M.; Brudvig, G.W.; Crabtree, R.H. A modified MM2 force field for high-valent di-μ-oxo manganese dimers. J. Mol. Struct. 1994, 323, 257–266. [Google Scholar] [CrossRef]
- Seminario, J.M. Calculation of intramolecular force fields from second-derivative tensors. Int. J. Quantum Chem. 1996, 60, 1271–1277. [Google Scholar] [CrossRef]
- Grimme, S. A general quantum mechanically derived force field (QMDFF) for molecules and condensed phase simulations. J. Chem. Theory Comput. 2014, 10, 4497–4514. [Google Scholar] [CrossRef]
- Brunken, C.; Reiher, M. Self-parametrizing system-focused atomistic models. J. Chem. Theory Comput. 2020, 16, 1646–1665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schütt, K.T.; Tkatchenko, A.; Müller, K.R. Machine learning force fields. Chem. Rev. 2021. [Google Scholar] [CrossRef]
- Westermayr, J.; Marquetand, P. Machine learning for electronically excited states of molecules. Chem. Rev. 2020. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Götz, A.W.; Clark, M.A.; Walker, R.C. An extensible interface for QM/MM molecular dynamics simulations with AMBER. J. Comput. Chem. 2013, 35, 95–108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Namazian, M.; Lin, C.Y.; Coote, M.L. Benchmark calculations of absolute reduction potential of ferricinium/ferrocene couple in nonaqueous solutions. J. Chem. Theory Comput. 2010, 6, 2721–2725. [Google Scholar] [CrossRef]
- Cox, N.; Retegan, M.; Neese, F.; Pantazis, D.A.; Boussac, A.; Lubitz, W. Electronic structure of the oxygen-evolving complex in photosystem II prior to O–O bond formation. Science 2014, 345, 804–808. [Google Scholar] [CrossRef] [PubMed]
- Brese, N.E.; O’Keeffe, M. Bond-valence parameters for solids. Acta Crystallogr. Sect. B 1991, 47, 192–197. [Google Scholar] [CrossRef]
- Brown, I.D. Recent developments in the methods and applications of the bond valence model. Chem. Rev. 2009, 109, 6858–6919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. Europhys. Lett. 1994, 26, 583–588. [Google Scholar] [CrossRef] [Green Version]
- Maurer, P.; Laio, A.; Hugosson, H.W.; Colombo, M.C.; Rothlisberger, U. Automated parametrization of biomolecular force fields from quantum mechanics/molecular mechanics (QM/MM) Simulations through force matching. J. Chem. Theory Comput. 2007, 3, 628–639. [Google Scholar] [CrossRef]
- Barbatti, M.; Sen, K. Effects of different initial condition samplings on photodynamics and spectrum of pyrrole. Int. J. Quantum Chem. 2016, 116, 762–771. [Google Scholar] [CrossRef] [Green Version]
- Blumberger, J. Free energies for biological electron transfer from QM/MM calculation: Method, application and critical assessment. Phys. Chem. Chem. Phys. 2008, 10, 5651. [Google Scholar] [CrossRef] [PubMed]
- König, G.; Hudson, P.S.; Boresch, S.; Woodcock, H.L. Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using non-Boltzmann Bennett reweighting schemes. J. Chem. Theory Comput. 2014, 10, 1406–1419. [Google Scholar] [CrossRef]
- Hudson, P.S.; Woodcock, H.L.; Boresch, S. Use of interaction energies in QM/MM free energy simulations. J. Chem. Theory Comput. 2019, 15, 4632–4645. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Farrokhnia, M.; Heimdal, J.; Shleev, S.; Rulíšek, L.; Ryde, U. Reorganization energy for internal electron transfer in multicopper oxidases. J. Phys. Chem. B 2011, 115, 13111–13126. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Property | BP86 | B3LYP |
|---|---|---|
| — from Figure 4 — | ||
| — Derived — | ||
| from Equation (11) | ||
| from Equation (12) | ||
| from Equation (13) | ||
| from Equation (13) | ||
| from Equation (14) | ||
| from Equations (7) and (8) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cárdenas, G.; Marquetand, P.; Mai, S.; González, L. A Force Field for a Manganese-Vanadium Water Oxidation Catalyst: Redox Potentials in Solution as Showcase. Catalysts 2021, 11, 493. https://doi.org/10.3390/catal11040493
Cárdenas G, Marquetand P, Mai S, González L. A Force Field for a Manganese-Vanadium Water Oxidation Catalyst: Redox Potentials in Solution as Showcase. Catalysts. 2021; 11(4):493. https://doi.org/10.3390/catal11040493
Chicago/Turabian StyleCárdenas, Gustavo, Philipp Marquetand, Sebastian Mai, and Leticia González. 2021. "A Force Field for a Manganese-Vanadium Water Oxidation Catalyst: Redox Potentials in Solution as Showcase" Catalysts 11, no. 4: 493. https://doi.org/10.3390/catal11040493
APA StyleCárdenas, G., Marquetand, P., Mai, S., & González, L. (2021). A Force Field for a Manganese-Vanadium Water Oxidation Catalyst: Redox Potentials in Solution as Showcase. Catalysts, 11(4), 493. https://doi.org/10.3390/catal11040493