A Simple and Straightforward Method for Activity Measurement of Carbonic Anhydrases

Abstract

Carbonic anhydrase (CA) is an enzyme of high interest due to its high implications relative to the medical and environmental sectors. In the current paper, an enzyme assay for the determination of CA activity is proposed and it is characterized by its simplicity and high practicability. It permits the straightforward comparison of CAs performance in physiological conditions. The methodology and the theoretical background of the evaluation method are explained in detail. Moreover, the presumed advantages over alternative assays are discussed. The assay has proven to be particularly useful for the screening of CA activity with respect to their application in CO₂, capturing processes for further utilization or storage.

1. Introduction

Carbonic anhydrases (CAs; EC 4.2.1.1) are a group of metalloenzymes that catalyze the inter-conversion of carbon dioxide and water into the bicarbonate ion and a proton. First isolated in 1933, CAs have been found to be abundant in algae, bacteria, archaea, plants and animal tissues [1,2]. Six different and evolutionarily unrelated classes have been identified, namely α, β, γ, δ, ζ and η [3]. Despite their structural differences, all CAs utilize the same catalytic mechanism involving a central metal (mostly zinc) atom [4].

Due to their importance in the medical sector, CAs are thoroughly studied enzymes. CAs play a crucial role in numerous physiological processes, such as respiration, pH and CO₂ homeostasis, secretion, gluconeogenesis, or ureagenesis. In addition to the established role of CA inhibitors such as diuretics and antiglaucoma drugs, it has been made apparent that such inhibitors could have potential as novel anticancer and anti-infective drugs [5]. More recently, CAs have become the focus of environmental research. Climate change mitigation scenarios desire technologies that can be immediately implemented. These include carbon capture, utilization and storage [6]. In this context, CAs have raised high interest as enzymatic accelerators while proposing significant enhancement of the CO₂ capturing process in the aqueous phase [7,8].

A wide range of methods have been developed for the measurement of CA activity [9]. However, two of them are most widely applied. These are the Wilbur-Anderson assay and a colorimetric method, which is the so-called p-nitrophenol assay [10]. The Wilbur-Anderson assay makes use of the pH decrease caused by the reaction. One unit is defined as a pH drop from 8.3 to 6.3 per minute at 0 °C within a 20 mmol·L₋₁ Tris-HCl buffer solution saturated with CO₂ [11]. However, the assay suffers certain drawbacks. It is conducted at non-physiological temperature conditions (0–3 °C) in order to increase CO₂ solubility to provide sufficient substrate concentration. It is obvious that a comparison at or near zero temperature does not necessarily reproduce the activity at ‘natural’ conditions. Moreover, the unit is empirical and provides little information on enzyme kinetics. The p-nitrophenol assay utilizes another feature of CAs: In addition to its natural reaction, i.e., CO₂ hydration, CAs also exhibit certain carboxylic esterase activity. The release of nitrophenol, which is a chromophore with two characteristic adsorption peaks, through the hydrolysis of p-nitrophenol acetate is followed by spectrophotometric measurement [12]. This easily performable test is a valuable tool allowing the rapid comparison of CA activities. Nonetheless, the employment of an alternative substrate renders correct predictions of the actual CO₂ conversion capacity tricky.

More precise methods are available that provide highly accurate results. Frequently stopped-flow devices in combination with absorbance or fluorescence spectroscopy have been used to study the kinetics of CAs. Moreover, radioactive labelling with ¹³C or ¹⁸O and sophisticated analytical tools such as mass spectrometry or NMR have been employed [13]. There is no doubt that the application of such high end methods is well justified to address specific scientific questions, e.g., the measurement of undisturbed enzyme activity and its physiological effects in animal or plant tissues. However, the analytical effort and/or the required instrumentation increases significantly. On the other hand, the simple tests also have their merits, in particular, with the focus relative to technical applications such as the mentioned carbon sequestration processes.

Here, we report on a simple procedure and evaluation method that allows rapid estimation of enzyme activity. Background and method development are explained in detail and data interpretation in terms of kinetic constants are discussed.

2. Results

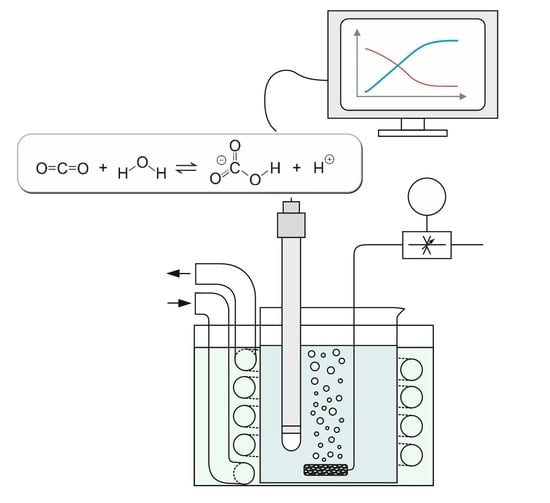
The presented assay is a modification of the Wilbur-Anderson protocol and the only analytical instrument employed is a pH meter with data recording. In order to allow adequate monitoring at higher temperatures by considering the associated enhanced enzyme activities, the time span necessary for a certain pH drop needs to be extended. For this purpose, the buffer concentration of the solution was raised from 20 to 100 mM. The buffer partially adsorbs the protons produced by the enzymatic conversion. In return, more CO₂ is also required for the overall reaction. Regarding the limited solubility of CO₂, it has to be continuously delivered by means of gas sparging instead of providing a specific amount at the beginning of the test.

The development and evaluation of the method are based on the considerations and assumptions presented in the following. In some equations, amounts (in mol) are addressed whereas concentrations (in mol·L⁻¹) are required for other equations describing equilibrium constants or kinetic reactions. However, taking a hypothetical reaction volume of 1 L allows the one-to-one interconversion of the two units.

2.1. Dependency of Bicarbonate Concentration on pH

The first step was to calculate the relation between measured pH and bicarbonate derived from conversion of CO₂. The apparent pK_a of carbonic acid, 6.35 at 25 °C, indicates a relatively weak acid being only slightly dissociated. However, it is well known that during the aqueous phase carbonic acid is in equilibrium with dissolved or aquatic CO₂ (CO₂(a)). Both species can hardly be distinguished and the above-named value is actually comprised of two equilibria: interconversion of CO₂(a)/H₂CO₃ and the true pK_a. In fact, carbonic acid is a relatively strong acid. The exact pK_a value cannot be determined but it lies between 3.4 and 3.9 at room temperature 20 °C < T < 25 °C and at zero ionic strength [14]. The pH range observed in the investigated test system, i.e., ≥6.4 is at least 2.5 units higher. Based on the given definition of the pK_a, Equation (1) can be developed.

[H₂CO₃] / [HCO₃⁻] = 10^{(pH – pKa)} ≤ 0.00316

(1)

Equation (1) shows that even at pH 6.4 less than 3.2‰, carbonic acid is present in the protonated form. It can therefore be simplified that the amount of CO₂ dissolved during the aquatic phase that undergoes further conversion corresponds to the HCO₃⁻ ions present in the solution and an equivalent number of released protons. These protons either interact with the TRIS buffer system and/or causes a change of pH.

x = a + b

(2)

X is the total protons released that is equivalent to bicarbonate ions [HCO₃⁻].

a denotes the H⁺ consumed by the buffer components.

b denotes the H⁺ resulting in a change of pH.

Equation (3) describes the dissociation equilibrium of the TRIS buffer at the initial conditions.

K_a = [TRIS]_i × [H⁺] / [TRISH⁺]_i

(3)

K_a denotes the acid constant of TRIS.

Index ‘i’ indicates initial the concentration values at the beginning of the test.

At a given time, the new equilibrium concentrations are described as follows.

[TRIS] = [TRIS]_I − a

(4)

[TRISH⁺] = [TRISH⁺]_i + a

(5)

Considering that the proton concentration at the beginning is very low, 10^−8.2, and is almost immediately outweighed by the protons released from H₂CO₃ dissociation, it can be simplified that the absolute proton concentration is equal to b. This simplification is a standard approach also used in pH calculations of weak acids or puffer systems described in the following.

B >> [H⁺]_i → [H⁺] ≈ b

(6)

Substituting Equations (4) and (5) into Equation (6) yields the following.

K_a = ([TRIS]_i − a) × b / ([TRISH⁺]_i + a)

(7)

Solving the set of Equations (2) and (7) for [HCO₃⁻] as a function of [H⁺] provides the following.

[HCO₃⁻] = (-[TRISH⁺]_i × K_a + (K_a + [TRIS]_i) × [H⁺] + [H⁺]²) / (K_a + [H⁺])

(8)

With pK_a = 8.1 (at 25 °C [15,16]) and a total buffer molarity of 0.1, the initial concentrations of the two buffer species at the start of pH (8.2) are the following: [TRIS]_i = 0.056 and [TRISH⁺]_i = 0.044. Inserting these values yields Equation (9), which allows the calculation of the bicarbonate concentration dependent on the measured pH as described as follows.

[HCO₃⁻] = (−3.495 × 10⁻¹⁰ + 0.056 × [H⁺] + [H⁺]²) / (7.943 × 10⁻⁹ + [H⁺])

(9)

Using pH data, the gained bicarbonate concentration can be plotted versus time.

In order to prove that the resulting simplifications does not produce any significant errors, a more comprehensive calculation was performed. This included two more equations covering the ion dissociation of water and the initial proton concentration, described as follows.

x = a + b – r

(10)

[H⁺] = b + [H⁺]_i – r

(11)

The value, r, denotes the re-association of H⁺ and OH^- to maintain the ion-product of water (=10⁻¹⁴).

Recalculated data almost completely matched the data obtained before. It was therefore concluded that the simpler Equation (9) is sufficiently accurate for the proposed method.

2.2. Correlation between Bicarbonate and Enzyme Reactivity

The second step is the correlation of the bicarbonate concentration to the activity of the CA considering the CO₂ transfer to the aquatic phase. In contrast to the buffer reaction above, the steps discussed in what follows are rate limiting. Consequently, the timely change of concentrations and not the concentrations at equilibrium needs to be addressed. Firstly, the time course of CO₂ in the liquid phase was regarded. The course of gas transfer to liquid is described by the well-known differential Equation (12). Therein, the transfer rate correlates to the difference between the saturation concentration of CO₂ in the liquid phase (C_sat, which depends on the Henry constant) and the actual concentration at a given time multiplied by the mass transfer rate from gas to liquid k₁ [17]. The latter is specific for a given set-up, which implying parameters such as gas flow rate, bubble size or mixing conditions, etc., while the saturation concentration can be calculated from the Henry coefficient or may otherwise be obtained from respective tables.

∂CO₂(a)’ / ∂t = k₁ × (C_sat − [CO₂(a)])

(12)

Solving this differential equation with a dissolved CO₂ concentration of zero at time zero results in Equation (13).

[CO₂(a)]’ = C_sat × (1 − e^{−k1 × t})

(13)

C_sat denotes the saturation concentration of CO₂(a).

This function describes the increasing form of an exponential decay and is generally valid for gas transfer reactions, e.g., for oxygenation. However, in the current case it is necessary to include the further reaction of dissolved CO₂ into bicarbonate and a proton. Following the law of mass action, both the forward and the backward reactions have to be taken into account. Therefore, Equation (12) needs to be extended by the following term.

∂CO₂(a)’’ / ∂t = −k₂ × [CO₂(a)] + k₋₂ [H⁺] × [HCO₃⁻]

(14)

k₂ is the rate constant of CO₂ conversion and k₋₂ is the rate constant of the back-reaction in the reverse direction. Combination of Equations (13) and (14) provides the timely change of CO₂ in the liquid phase. However, using Equation (9) to solve the complete differential equation is mathematically complex. Again, a simplification was employed: In the beginning, the back-reaction is very small due to the low concentrations of bicarbonate multiplied by the low concentration of protons. Therefore, the second part of the term can be neglected, which resulting in the following equation.

∂[CO₂(a)] / ∂t = k₁ × (C_sat − [CO₂(a)]) − k₂ × [CO₂(a)]

(15)

Rearrangement results in the following equation.

∂[CO₂(a)] / ∂t = (k₁ + k₂) × (C_sat × k₁ / (k₁ + k₂) − CO₂(a))

(16)

Integration of Equation (16) results in the same type of exponential function as Equation (12), however, with modified parameters.

[CO₂(a)] = k₁ / (k₁ + k₂) × C_sat × (1 − e ^{−(k1 + k2) × t})

(17)

Equation (17) describes the course of CO₂ concentration as long as the back reaction of bicarbonate is small. With this equation in mind, the use of a CO₂ sensitive electrode is another interesting option for following enzyme activity as it has been investigated by Botrè and Botrè [18]. However, this alternative was not tested here. In the current case, further development of the relationship between CO₂(a) and HCO₃⁻ concentration was worked out. In Equation (12), this context has already been addressed. Evidently, any CO₂ converted occurs in the form of bicarbonate. Again, disregarding the backreaction due to the distance to the equilibrium concentrations, Equation (18) and, subsequently, Equation (19) can be developed.

∂[HCO₃⁻] / ∂t = [CO₂(a)] × k₂

(18)

∂[HCO₃⁻] / ∂t = k₁ × k₂ / (k₁ + k₂) × C_sat × (1 − e ^{−(k1 + k2) × t})

(19)

In solving the differential equation with the initial condition, the concentration of zero at time zero yields Equation (20).

[HCO₃⁻] = k₁ × k₂ / (k₁ + k₂)² × C_sat × e ^{−(k1 + k2) × t} + k₁ × k₂/(k₁ + k₂) × C_sat × t − k₁ × k₂/(k₁ + k₂)²

(20)

2.3. Elaboration of the Rate Constant of Enzymatic Turnover

It might be possible to utilize a curve-fitting program and to investigate the individual constants. Nevertheless, an easier solution was sought here. The exponential term in the beginning of Equation (19) is another e-function. With a negative exponent, it gradually progresses towards zero and the HCO₃⁻ concentration becomes a straight line. The slope (m) of the graph is described as follows.

m = k₁ × k₂ / (k₁ + k₂) × C_sat

(21)

The value of m can be directly taken from the plot of the bicarbonate concentration. Using the blank experiment, k₁ can be elaborated from the rearranged Equation (21) employing literature data for C_sat. and k₂. C_sat is 0.0343 mol.L⁻¹ at 25 ° C and 1 atm pressure (calculated from the Henry coefficient provided by [19]). Regarding the second parameter, it must be noted that the actual situation is more complex and that k₂ is not a constant value. The reason is that there are two chemical reactions involved in the CO₂/HCO₃⁻ equilibrium: CO₂ + H₂O ⇔ HCO₃⁻ + H⁺ and CO₂ + OH⁻ ⇔ HCO₃⁻. According to Schulz et al. [20] the rate constant at 25 °C can be calculated by combining the two individual reaction constants: k₂ = k_2,1 + k_2,2 × [OH] with k_2,1 = 3.71 × 10⁻²·s⁻¹ and k_2,2 = 2.24 × 10³ L·mol⁻¹ s⁻¹. Despite these explanations, we presume that the assumption of a fixed k₂ is acceptable for the for the current purpose and keeping in mind all the other simplifications already made. In the given pH measurement range (~8–6.5), a k₂ value for the uncatalyzed reaction of 3.8 × 10⁻² is considered a reasonable approximation. According to these provisions, the estimated value for k₁ is 0.051 s⁻¹ for the specific set-up.

Modeling was employed to crosscheck the general validity of the described methodical approach. Firstly, model parameters were adjusted to fit the data for the blank experiment. Literature values or approximated values as listed in Table 1 (see Section 3. Materials and Methods) were applied. In a subsequent step, the CO₂ transfer rate, k₁, was adjusted to best possibly fit the observed data. Figure 1 shows an overlay of the predicated course and actually measured pH values (a) as well as the predicted and calculated HCO₃⁻ concentration (b) for two experiments with or without the addition of CA, respectively. Despite certain deviations, in particular, for the blank experiment, the model reproduces the data observed for the CA catalyzed reaction and the hydration of CO₂ dominates quite well. It should be noted that the final applied C_sat value was higher than initially considered. The locally higher dynamic pressure at the surface of the sparging device is a probable explanation for that.

An example of model predictions depicting an entire view of all involved chemical species is provided in Figure 2. Again, the practically linear increase in HCO₃⁻ concentration is demonstrated.

Knowing the slope of the graph and the elaboration of k₁ and C_sat from the blank experiment allows the theoretical calculation of the catalyzed rate constant k₂ in each test. However, it has to be considered that the provision of the exact values for the individual constants is complex. The difficulties related to k₂ were already mentioned. Moreover, C_sat is not only related to temperature and pressure but has also significant dependency on salinity or, more accurately, on the concentration and nature of the individual ions present in aquatic phase [21]. Even the pK_a of the Tris buffer is only valid in highly diluted solutions and has to be slightly corrected for ionic strength [22]. Finally, the last simplification made above which disregards the back reaction has some limitations. The back reaction sets in before the bicarbonate concentration reaches its highest inclination and, consequently, the maximum slope is slightly underestimated.

To summarize, there are certain imprecisions regarding the accuracy of the underlying parameters, as discussed previously. Nevertheless, the developed theory allows the reasonable estimation of the k₂ of the catalyzed reaction, which permits good judgement of the practical potential of a certain enzyme.

2.4. Calibration with a Standard Enzyme and Overall Assessment

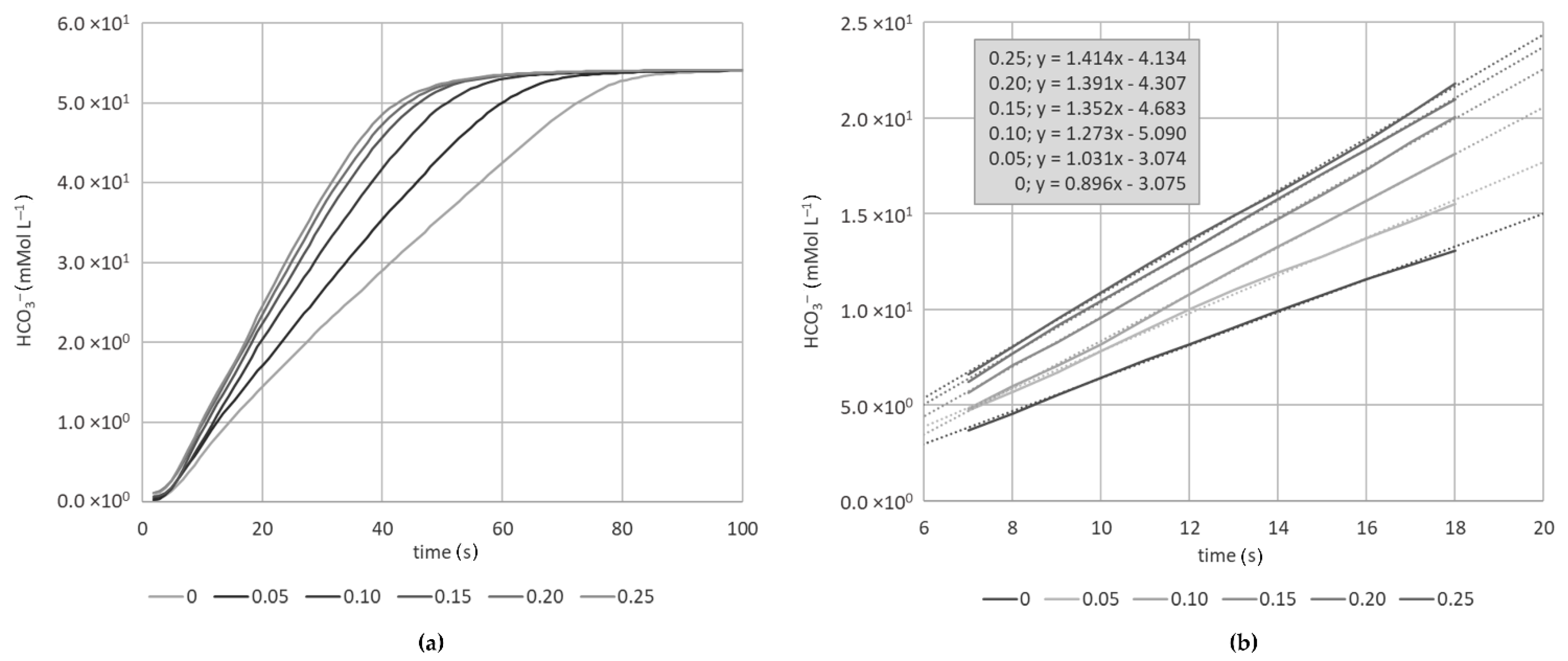
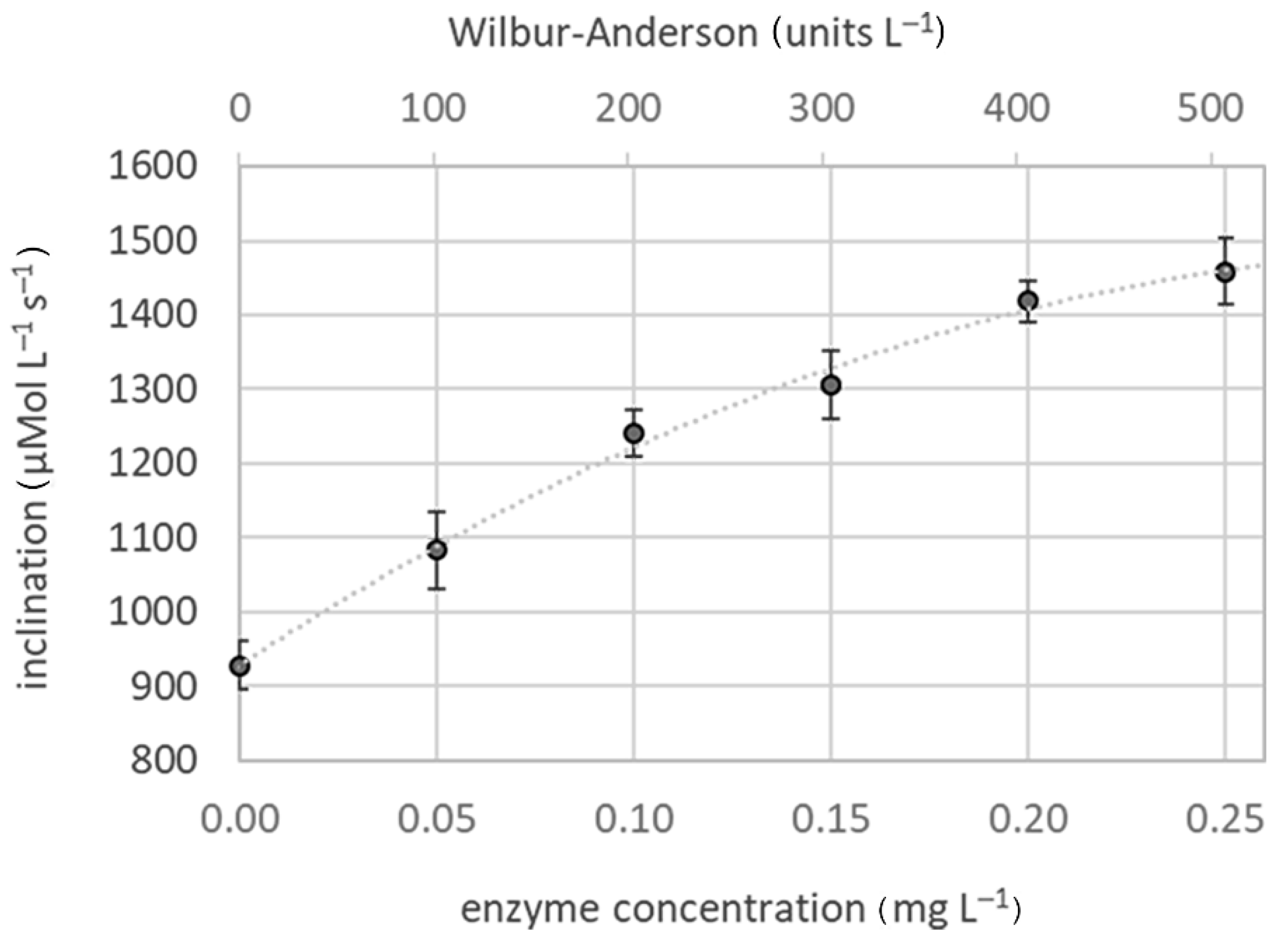
For practical purposes, it was more straightforward and convenient to calibrate the test system with a standard enzyme of known activity. For this purpose, different concentrations of CA from bovine erythrocytes were subjected to the test. The corresponding calculations using pH data and Equation (9) HCO₃⁻ concentrations are provided in Figure 3a. Figure 3b demonstrates data evaluation through the determination of the slope of the graph. Even if it might be hard to precisely define the linear range, the inclination within any reasonable time frame of reasonable linearity can be taken as calibration values. The final elaborated calibration curve presenting the applied enzyme amounts (primary x-axis) or the corresponding Wilbur-Andersen units (secondary x-axis) versus the slope of HCO₃⁻ is presented in Figure 4.

A comparison of the standard enzyme and three further CAs is presented in Figure 5. Despite an obvious correlation between the two assays, the figure also illustrates that the general assessment of the potential of different enzymes does not provide the same picture. This underlines our hesitations regarding the validity of data obtained by the WA assay conducted at 0–4 °C due to the difference in temperature sensitivity of CAs.

A certain disadvantage of the proposed method is that the pH is not constant throughout the test. Although the buffer provides a certain stabilization effect, pH still drops in the course of the enzyme reaction. Accordingly, enzyme activity is not a distinct value at fixed conditions but an average value over a certain pH range. However, it has to be emphasized that this disadvantage is shared with the other commonly applied test, which is the Wilbur-Anderson assay. It is, of course, possible to combine the presented method with a titration approach to maintain the pH at a fixed set-point. A corresponding attempt has been already suggested by Magid and Turbeck [23]. However, this would imply an exchange of simplicity for higher accuracy and this would give up the biggest asset of the proposed test system. Despite certain shortcomings and keeping in mind the downsides of other CA assays, we particularly acknowledge the high practicability of the test. In our lab, we found the proposed assay extremely helpful for the purpose of a quick routine method to straightforwardly crosscheck or compare the CO₂ conversion efficiency of different CAs.

Table 1. Types of reaction, rate laws and constants used for modeling the timely behavior of chemical species.

Name	Rate Law	Reaction	Rate Constants 1
CO2 transfer gas to liquid	Gas–liquid transfer according to Equation (11)	CO2(g) → CO2(a)	k1 = 5.1 × 10−2 (s−1) 2	Csat = 3.43 × 10−2 (mol L−1)
H2O dissociation	Mass action reversible	H2O H+ + OH-	kH2O_d = 2.53 × 10−5 (s−1) *	kH20_a = 1.4 × 1011 (L·mol−1 s−1) 3
CO2 hydration	Mass action reversible	CO2 + H2O H+ + HCO3−	k2_d = 3.8 × 10−2 (s−1) 4	k2_a = 8.51 × 104 (L·mol−1 s−1) *
TRIS buffer dissociation	Mass action reversible	TRISH+ TRIS + H+	kTris_d = 7.94 × 101 (s−1) *	kTris_a = 1.0 × 1010 (L·mol−1 s−1) 5

¹ For reversible mass action, the dissociation (index _d) and association rates (index _a) are provided. ² Estimated value for the given setup from Equation (21) and the blank experiment. ³ [24]. ⁴ Approximated value for the uncatalyzed reaction (see text). ⁵ Estimated from data upon dissociation of amines provided in [25]. * Calculated from the constant of the counter reaction and the dissociation constant at 25 °C.

Table 1. Types of reaction, rate laws and constants used for modeling the timely behavior of chemical species.

Name	Rate Law	Reaction	Rate Constants 1
CO2 transfer gas to liquid	Gas–liquid transfer according to Equation (11)	CO2(g) → CO2(a)	k1 = 5.1 × 10−2 (s−1) 2	Csat = 3.43 × 10−2 (mol L−1)
H2O dissociation	Mass action reversible	H2O H+ + OH-	kH2O_d = 2.53 × 10−5 (s−1) *	kH20_a = 1.4 × 1011 (L·mol−1 s−1) 3
CO2 hydration	Mass action reversible	CO2 + H2O H+ + HCO3−	k2_d = 3.8 × 10−2 (s−1) 4	k2_a = 8.51 × 104 (L·mol−1 s−1) *
TRIS buffer dissociation	Mass action reversible	TRISH+ TRIS + H+	kTris_d = 7.94 × 101 (s−1) *	kTris_a = 1.0 × 1010 (L·mol−1 s−1) 5

¹ For reversible mass action, the dissociation (index _d) and association rates (index _a) are provided. ² Estimated value for the given setup from Equation (21) and the blank experiment. ³ [24]. ⁴ Approximated value for the uncatalyzed reaction (see text). ⁵ Estimated from data upon dissociation of amines provided in [25]. * Calculated from the constant of the counter reaction and the dissociation constant at 25 °C.

3. Materials and Methods

3.1. Setup

Titration was performed in a 100 mL glass beaker enclosed by a temperature-controlled vessel to maintain 25 °C. Recording of the pH course was conducted with an automatic titration device (Titrino 702, pH electrode: LL-Viscotrode and Software TiNet 2.5 (2003), Metrohm, Herisau, Switzerland). All solutions were maintained at 25 °C prior to use. Gas sparging was conducted with bottled CO₂ (purity 99.5%, Messer, Gumpoldskirchen, Austria). In order to assure that enzymatic conversion is the rate-limiting step, CO₂ has to be delivered much faster than its consumption due to CA activity. Therefore, a stainless-steel aerator made of sintered metal (cylindric porous frit product no. 84026, outer diameter 5.8 mm, length 22 mm, Reichelt Chemie Technik, Heidelberg, Germany,) was employed in order to achieve fine bubble distribution. In addition, a high flow rate (200 mL min⁻¹) fixed by a mass flow controller (EL-Flow Select, Bronckhorst, Ruurlo, The Netherlands) was applied. Figure 6 illustrates the setup.

Tris buffer (0.1 mol·L⁻¹) was made from Tris-base (Tris(hydroxymethyl)aminomethane, ultrapure grade ≥ 99.9%, Sigma-Aldrich, Vienna, Austria) adjusted to pH 8.2 at 25 °C with 6 mol·L⁻¹ H₂SO₄ [14]. The measurement procedure was as follows. A 40 mL buffer was poured into the vessel. After a quick check of the appropriate temperature and pH, 0.1 mL enzyme solution was added and, at same time, gasification as well as pH recording begun. Due to the intensive mixing through the rising bubbles, no additional stirring was necessary. The experiment ended when a final stable pH below 6.5 was achieved.

3.2. Tested Enzymes

The utilized standard enzyme was CA from bovine erythrocytes (product no. C2624, Sigma-Aldrich, Vienna, Austria). The specific activity given by the provider was ≥3500 Wilbur-Anderson units.mg protein⁻¹; however, our own measurements only showed an activity of 2090 (+/−115) Wilbur-Anderson units per mg. The following concentrations were applied: Enzyme stock of 0.1, 0.08, 0.06, 0.04 and 0.02 mg/mL (in 0.1 M Tris buffer) resulting in a final concentration in the test of 0.25, 0.2, 0.15, 0.1 and 0.05 mg L⁻¹, respectively.

Three more microbial CAs derived from Persephonella marina EX-H1, Methanobacterium thermoautotrophicum and Acetobacterium woodii DSM 1030 were used for the evaluation of the method. CAs were obtained through the heterologous expression of the respective genes in E. coli. Detailed information on their preparation as well as the potential for CO₂ capturing will be provided in an upcoming publication.

3.3. Mathematical and Modeling Tools

Calculations were made or confirmed using the free online computing engine WolframAlpha available under https://www.wolframalpha.com/ (accessed on 11 January 2021). In order to verify the validity of the approach and to crosscheck the impact of simplifications, modeling of the timely behavior of the individual chemical species was made utilizing the program COPASI (version 4.29, Build 228), which is a free software application for the simulation and analysis of biochemical networks available under http://copasi.org/ (accessed on 10 February 2021). The simple model contained 4 reactions describing the rate of change of the involved chemical species. The types of reaction, rate laws and used constants are listed in Table 1. The software computes the timely development of the concentrations through iterative calculations for a given time interval.

4. Conclusions

In an era of growing concern relative to the record CO₂ levels in the atmosphere, the development of CO₂ capturing technologies is of high interest. On the path to full scale application, enzymatic enhancement is one of the options to improve efficiency of this approach. The CA activity assay proposed in the current paper resembles a simple method for judging enzyme activity requiring minimal analytical equipment. The continuous recording allows an accurate determination of conversion rates based on a larger set of data points compared to the Wilbur-Anderson assay. In contrast to this alternative routine method, activity is measured at an appropriate temperature and the gained values can be interpreted as thermodynamic constants. This allows easy and rapid comparison of CA activity. There are certainly assays of higher accuracy which, however, go hand in hand with elevated analytical effort. The introduced method is considered particularly useful for the screening of different CAs in environmental applications.