Accelerating the Design of Photocatalytic Surfaces for Antimicrobial Application: Machine Learning Based on a Sparse Dataset

Abstract

Nowadays, most experiments to synthesize and test photocatalytic antimicrobial materials are based on trial and error. More often than not, the mechanism of action of the antimicrobial activity is unknown for a large spectrum of microorganisms. Here, we propose a scheme to speed up the design and optimization of photocatalytic antimicrobial surfaces tailored to give a balanced production of reactive oxygen species (ROS) upon illumination. Using an experiment-to-machine-learning scheme applied to a limited experimental dataset, we built a model that can predict the photocatalytic activity of materials for antimicrobial applications over a wide range of material compositions. This machine-learning-assisted strategy offers the opportunity to reduce the cost, labor, time, and precursors consumed during experiments that are based on trial and error. Our strategy may significantly accelerate the large-scale deployment of photocatalysts as a promising route to mitigate fomite transmission of pathogens (bacteria, viruses, fungi) in hospital settings and public places.

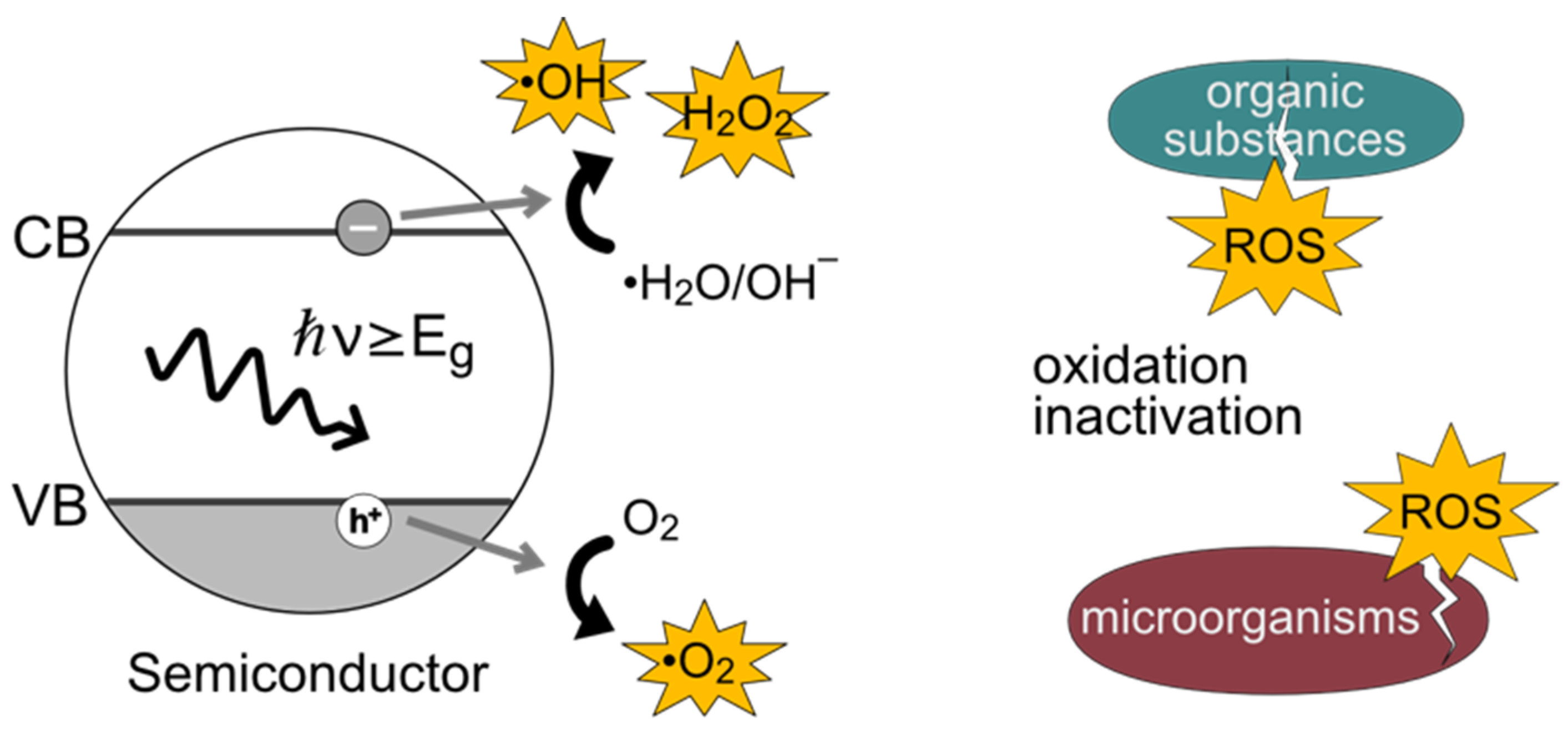
1. Introduction

Coronavirus disease 2019 (COVID-19), caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection, is the most impactful global pandemic of the 21st century to date and continues to infect and kill many individuals worldwide. Since its identification as a human pathogen in December 2019, SARS-CoV-2 has thus far infected more than 50 million people and caused more than 1.2 million deaths (https://coronavirus.jhu.edu/map.html, accessed on 6 November 2020). Due to limited access to COVID-19 testing, many countries screen only, if at all, symptomatic patients for COVID-19. Subsequently, the reported deaths associated with COVID-19 may be underestimated compared to the real numbers. The accurate scale of COVID-19 might be much higher because of missed diagnoses, data tracking anomalies, and indirectly related deaths [1]. The knowledge about COVID-19 disease remains limited thus far, especially because several virus mutants have emerged since the first diagnosed case, which has resulted in the subsequent waves of COVID-19 pandemic that are currently hitting several countries, calling for urgent interventions to suppress the spread of pathogens.

Pathogens can spread through direct (human-to-human transmission) and indirect contact via contaminated inanimate objects and airborne contagion. However, some pathogens remain intact and contagious even in smaller droplets ($<$5 $\mathsf{\mu }$m) and can be suspended in the air for up to three hours. Therefore, airborne isolation, room ventilation, and appropriate disinfectant application might restrict the aerosol spread of the pathogens [2]. However, the pathogens-laden droplets that are too heavy to remain in the air would fall on nearby floors or surfaces, creating fomites (or contaminated surfaces) [3]. A susceptible host touching these fomites could get infected [4]. It was found that the SARS-COV-2 virus, for example, could survive from 24 h on cardboard to 2 days on stainless steel and wood to even 7 days outside of surgical masks [5,6]. These findings indicate that the fomites can represent a considerable transmission path, mainly in closed areas [7].

Surfaces in hospital rooms of infected individuals or in toilets used by COVID-19 patients were shown to be contaminated by SARS-CoV-2 virus [8]. In crowded shopping malls, public restrooms, escalator handrails, food court trays, food court table surfaces, and food tray handles were previously shown to be contaminated by different bacteria [9]. They can therefore be a source of infection by SARS-CoV-2 as well [10]. International and national travel through airports is another potential source of fomite transmission. Indeed, surface contamination with respiratory viruses (e.g., influenza A and B viruses, respiratory syncytial virus, adenovirus, rhinovirus, and coronaviruses (229E, HKU1, NL63, and OC43)) at multiple sites associated with high touch, high traffic, and high density areas in Helsinki-Vantaa airport was shown recently [11], suggesting a potential risk of infection in the identified airport sites.

Consequently, fomite disinfection in closed settings and best practice cleaning measures are recommended to prevent the spread of microbial infections. Hydrogen peroxide (H₂O₂), at low concentrations (e.g., 0.5%), is known as a fast biocidal agent, including for severe acute respiratory syndrome (SARS) coronavirus, Middle East respiratory syndrome (MERS) coronavirus or endemic human coronaviruses (HCoV) [12], and H1N1 influenza virus [13].

Hence, there is an increasing interest in using photocatalytic systems as nanocoatings to disinfect surfaces, air, and water [14]. Photoactive agents such as titanium dioxide (TiO₂) loaded with metallic co-catalysts have been tested in many applications, including the removal of organic contaminants [15]. This technology relies on the production of reactive oxidative species (ROS) such as hydroxyl radicals, superoxide radical ions, and hydrogen peroxide (H₂O₂) in response to light excitation with energy greater than the band gap of the photoactive catalyst (see Figure 1).

Studies revealed that ROS oxidizes the proteins, lipids, and enzymatic systems of viruses and bacteria, leading to the loss of their function to reproduce either due to a damaged membrane or by damaging other key proteins such as the spike protein of SARS-CoV-2 [16]. When a pathogen comes into contact with the photocatalytic surface, the produced ROSs such as H₂O₂ would attack and oxidize key proteins leading to their inactivation [17]. To ensure the large-scale deployment of such photoactive antimicrobial nanocoatings, additional efforts are needed to explore the possibility of replacing rare and expensive co-catalysts such as platinum (Pt), palladium (Pd), and gold (Au) with less expensive metals such as silver (Ag), copper (Cu) and iron (Fe).

Furthermore, the adsorbed reactants on the surface induce the rearrangement of charges at the interface between the molecule and photocatalyst surface. Accordingly, the nanoparticles’ composition, such as Au-Ag/TiO₂ nanoparticles, determines not only ROS generation but also ROS degradation [18,19,20,21,22]. Therefore, because the overall reaction rate determines the efficacy of the photocatalyst, we explore the efficiency of ROS generation and degradation rates on the surface of the photocatalysts while targeting antimicrobial applications.

In hospitals and medical facilities, antimicrobial surfaces, specifically those coated with copper, were shown to reduce infection rates and contamination risk [23]. Some solid antimicrobial nanocoatings are manufactured using copper and silver and show quasi-instantaneous bacterial inactivation [24,25], while soft antimicrobial surfaces use silver-based compounds, triclosan, and zinc pyrithione. However, the potential risk of toxicity with high concentration silver and copper compounds constitutes the downside of some antimicrobial coatings [26,27]. This disadvantage calls for an accelerated material design for new, efficient, less toxic, and less expensive technologies.

During the lab-scale search for photocatalytic materials, finding the optimal composition is often limited to a few tens of experiments due to the limited time and cost of chemicals and precursors. Even when an optimal chemical composition is found, exhaustive rounds of lab-scale experiments are required. Delivering the conclusions with the predictions, this work demonstrates how machine learning (ML) schemes could help speed up the optimization and design of antimicrobial surfaces by learning then predicting photoactive pathogen inhibitors’ activity. We propose an experiment-to-machine-learning scheme applied to a limited experimental dataset and discuss its potential and applications.

2. From-Experiment-to-Machine-Learning Scheme

2.1. Handling Small Dataset with Machine Learning

Applying high-throughput experiments is gaining popularity to accelerate the optimization and discovery of the materials [28]. However, it is still limited in scope and to disciplines such as the pharma industry and catalysis. It often comes at the cost of installing fully automated synthesis setups, which are not within reach of the broad experimental community. The datasets generated during human-driven experiments vary between 5 and 20 data points resulting from a limited set of experimental conditions decided by the researcher or based on trials and errors. As a general rule, small datasets must be treated using low complexity models to avoid overfitting and are often well handled using polynomial fitting techniques [29]. Still, experimentally-generated small datasets might carry a high correlation and complexity level, requiring analysis using ML methods. The developed model, if successful, might serve as a predictive guide to explore other experimental conditions. In this respect, generalized additive models (GAM) are among the recommended techniques to deal with sparse and small sample/data sizes. Its use provides the flexibility to allow non-parametric fits with relaxed assumptions on the actual relationship between target and input variables and provides the potential for better fits to data than purely parametric models [30].

In this work, we train GAM models by using a small dataset reported in Ref. [31] of H₂O₂ production rates via TiO₂ photocatalyst loaded with different amounts of metallic Au_xAg_(1-x) nanoparticle co-catalysts, where $0\le x\le 1$. Because the dataset consists of a small number (∼15) of entries, we build our model using three input variables, which are the most physically and chemically relevant in this application. GAM is a generalization of the generalized linear model (GLM) in which the relationship between some input(s) $x_1$, $x_2$,$\cdots$ and $x_p$ and target $Y$ is not linear and for which an ordinary least squares (OLS) estimator does not capture the relationship very well. In this situation, one needs to relate nonlinear inputs to the expected value $\mathsf{\mu }=\mathrm{E}\left(Y|x\right)=\mathrm{g}\left(x\right)$, with a non-predefined link function $\mathrm{g}$ that might be appropriate. In other words, we can write the GAM structure as:

$$\mathrm{g}\left(\mathrm{E}\left(Y|x\right)\right)={\mathsf{\beta }}_0+s_1\left(x_1\right)+s_2\left(x_2\right)+\cdots +s_p\left(x_p\right)$$

(1)

where $x_1$, $x_2$, $\cdots$, and $x_p$ are the input variables, $Y$ is the dependent variable, $\mathrm{E}\left(Y\right)$ denotes the expected value, and $\mathrm{g}\left(Y\right)$ is the link function summing the smooth functions ($s_1$, $s_2$, $\cdots$, and $s_p$), of which shapes are fully determined by the data rather than predefined parametric functions, such as Gaussian, Poisson, or logistic. In addition, this method preserves the interpretability showing how the different input variables contribute to the expected value. We carried out also the GLM training, a conventional linear regression model, to showcase the enhanced performance that could be obtained from using generalized additive models GAM.

2.2. Dataset Preparation and ML Training

We considered the energy difference between the work function of Au-Ag nanoparticles and the redox potential of O₂/H₂O₂ [20,31,32,33,34,35,36,37]. (see “Mechanism of photocatalytic hydrogen peroxide production” in the Supplementary Information (SI)) While the reaction is expressed as ${\mathrm{O}}_2+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to {\mathrm{H}}_2{\mathrm{O}}_2$, it is understood that the reduction occurs through either a sequential two-step single-electron indirect reduction (${\mathrm{O}}_2\to {\mathrm{O}}^{•-}\to {\mathrm{H}}_2{\mathrm{O}}_2$) or a one-step two-electron direct reduction (${\mathrm{O}}_2\to {\mathrm{H}}_2{\mathrm{O}}_2$) route [38,39]. Moreover, the reaction is related to a decrease of H⁺ as well, and the redox potential level of O₂/H₂O₂ is more negative than the level of H⁺/H₂ by 0.69 V [34]. The trapped charges in the nanoparticles should transfer favorably to a reactant forming H₂O₂, while we keep the H⁺ oxidation reaction, preventing it from the backward reaction of $2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to {\mathrm{H}}_2$. Thus, it is challenging to determine with confidence the key factors governing the overall reaction mechanism. Moreover, one might need to take into consideration the adsorption of reactants on the surface of Au-Ag nanoparticles [18,19,20] since adsorbed reactants on the surface induce the rearrangement of charges at the interface between the molecule and Au-Ag nanoparticles, hence affecting the overall reaction rate.

In this work, we use the physical properties of the photocatalytic system such as Schottky barrier and work function to build a training set from a representative experimentally reported dataset. The work function difference between ${\mathsf{\Phi }}_{{\mathrm{Au}}_x{\mathrm{Ag}}_{\left(1-x\right)}}$ and ${\mathsf{\Phi }}_{{\mathrm{TiO}}_2}$ are the input variables expressed as

$${\mathsf{\phi }}_{\mathrm{B}}^{\mathrm{AuAg}}=\Delta E_{{\mathrm{TiO}}_2-\mathrm{M}}={\mathsf{\Phi }}_{{\mathrm{TiO}}_2}-{\mathsf{\Phi }}_{{\mathrm{Au}}_x{\mathrm{Ag}}_{\left(1-x\right)}}$$

(2)

and

$$\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}={\mathsf{\Phi }}_{{\mathrm{H}}_2{\mathrm{O}}_2}-{\mathsf{\Phi }}_{{\mathrm{Au}}_x{\mathrm{Ag}}_{\left(1-x\right)}}$$

(3)

where ${\mathsf{\Phi }}_{{\mathrm{H}}_2{\mathrm{O}}_2}$ is the redox potentials of H₂O₂, respectively, with respect to the vacuum level, and ${\mathsf{\Phi }}_{{\mathrm{Au}}_x{\mathrm{Ag}}_{\left(1-x\right)}}$ is the work function of the Au-Ag co-catalyst. The work function of Au-Ag alloy was obtained from the geometric mean between pure metals; in the case of Au_xAg_(1−x), the work function is given by:

$${\mathsf{\Phi }}_{{\mathrm{Au}}_x{\mathrm{Ag}}_{\left(1-x\right)}}={\left({\mathsf{\Phi }}_{\mathrm{Au}}\right)}^x\cdot {\left({\mathsf{\Phi }}_{\mathrm{Ag}}\right)}^{\left(1-x\right)}$$

(4)

Turning to input variables such $\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}$, the values of this metric are the lowest for pure Au nanoparticles ($\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}=0.09$), since the work function level is the closest to the O₂/H₂O₂ redox level. In contrast, for the pure Ag nanoparticles, $\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}=0.99$. At the same time, this metric reflects the high coverage of Ag on the nanoparticle active site as the values are significant. Thus, it represents the relative positions of work functions as well as the proportionate coverage of adsorbed nanoparticles. We employed an additional input variable $NP$ for the metallic nanoparticle loading. In addition to nanoparticles loading, we considered $\exp \left({\mathsf{\phi }}_{\mathrm{B}}\right)$ and $\exp \left(\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}\right)$ as the input variable during the GLM and GAM model training.

In summary, the dataset uses three input variables, the amount of nanoparticle loading $NP$, $\exp \left({\mathsf{\phi }}_{\mathrm{B}}^{\mathrm{AuAg}}\right)$, and $\exp \left(\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}\right)$, and as target variables, the H₂O₂ formation rate ($k_{\mathrm{f}}$) and decomposition rate ($k_{\mathrm{d}}$).

3. Results and Discussion

Our training dataset consists of experimentally reported data of Tsukamoto et al. [31] for Au_xAg_(1−x)/TiO₂ photocatalysts having as target values the formation of H₂O₂ and decomposition rates ($k_{\mathrm{f}}$ and $k_{\mathrm{d}}$) as well as the overall produced concentration ([H₂O₂]) at a few discreet co-catalyst compositions and loadings. We used the root mean square error (RMSE) and $R^2$ as metrics to evaluate the accuracy of each trained model. Rather than building one regression model for [H₂O₂], two separate models were built for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ separately. Subsequently, [H₂O₂] is computed according to the formula $\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]=\left(k_{\mathrm{f}}/k_{\mathrm{d}}\right)\left\{1-\exp \left(1-k_{\mathrm{d}}t\right)\right\}$ as in Ref. [31]. Our decision is well grounded by examining the Pearson correlation coefficients, as shown in Figure S3 in the Supplementary Materials. We found a significantly strong correlation between the input variables ($NP$, $\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}$ and $\Delta E_{{\mathrm{TiO}}_2-\mathrm{M}}$) and target variables ($k_{\mathrm{f}}$ and $k_{\mathrm{d}}$). While attempting to build a model to predict [H₂O₂] directly from the experimental data, we found a negligible correlation with $\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}$ and $\Delta E_{{\mathrm{TiO}}_2-\mathrm{M}}$, confirming that our adopted approach for performing two separate regressions for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ is well justified.

When comparing the accuracy of the predictive value with the GAM results, the GLM model demonstrated a limited predictive power for the rates of H₂O₂, in particular for $k_{\mathrm{f}}$ prediction (see Figure S4 in the Supplementary Materials for the GLM model). The computed $R^2$ values of $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ are 0.62 and 0.75, while the errors for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ values are $\pm$0.1 mM ${\mathrm{h}}^{-1}$ and $\pm$0.05 ${\mathrm{h}}^{-1}$, respectively. Because these GLM models behave poorly when the nonlinear correlation is dominant, the accuracy is worse when we assess the [H₂O₂] production via two-step $\left(k_{\mathrm{f}}/k_{\mathrm{d}}\right)$ computation or by simply building a GLM predictive model for [H₂O₂]. GLM model gives large residual errors because it fails to capture the non-linear relationship between the input and target. Subsequently, we moved to the GAM method, which, as shown in the next section, demonstrates significantly improved predictive power.

The GAM models give a higher predictive accuracy for both $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$, enabling us to reproduce the experimental data within an acceptable residual error, as shown in Figure 2a,b. The estimated RMSEs are 0.02 mM ${\mathrm{h}}^{-1}$ and 0.02 ${\mathrm{h}}^{-1}$ for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$, respectively. In other words, we reduce the RMSEs by 80% and 60% using the GAM models compared to GLM. Interestingly, these RMSEs are of the same order of magnitude as the error estimated during the experimental data acquisition for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$, which account for $\pm$0.03 mM ${\mathrm{h}}^{-1}$ and $\pm$0.02 ${\mathrm{h}}^{-1}$, respectively [31]. The steady state H₂O₂ production rate can be expressed as $\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]=\left(k_{\mathrm{f}}/k_{\mathrm{d}}\right)$, (when $\mathrm{t}=\infty$ in $\left[{\mathrm{H}}_2{\mathrm{O}}_2\right]=\left(k_{\mathrm{f}}/k_{\mathrm{d}}\right)\left\{1-\exp \left(1-k_{\mathrm{d}}\mathrm{t}\right)\right\}$. We thus combine the output of the GAM models we trained for $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ to generate a predictive model for [H₂O₂].

The power of the GAM model resides in its smooth functions that represent the attribution as a function of the corresponding input variables regardless of linear and nonlinear relations between input and dependent variables. As such, this method is flexible. In addition, the GAM framework controls the smooth functions to prevent overfitting by the regularization (also called degree of freedom). Moreover, it offers the possibility to interpret each contribution of a few input variables to the target values by plotting and analzing the smooth functions.

Turning to the second performance metric of the GAM model, $R^2$ values of $k_{\mathrm{f}}$ and $k_{\mathrm{d}}$ are 0.98 and 0.95 respectively, approaching unity and indicating an excellent prediction performance. The improved GAM performance originates from the fact that its smooth functions could express well the targets when using non-parametric means, empowering us to capture the nonlinear impact of the nanoparticle loading and band alignments input values on the overall H₂O₂ production.

The smooth functions (see Figure 3) depict the relationship between the $k_{\mathrm{f}}$ (and $k_{\mathrm{d}}$) and the input variables. The degrees of freedom for the smooth functions with respect to nanoparticle loading are higher compared to those for $\exp \left({\phi }_{\mathrm{B}}^{\mathrm{AuAg}}\right)$ and $\exp \left(\Delta E_{\mathrm{M}-{\mathrm{H}}_2{\mathrm{O}}_2}\right)$. This fact confirms our initially assumed non-linear impact of nanoparticle loading on the H₂O₂ production rates and explains why GLM performed poorly as shown earlier. Thus, GAM models reproduce well both rates and capture their non-linear dependence on the input variables.

Interestingly, the smooth function of $k_{\mathrm{f}}$ with respect to nanoparticle loading shows that the H₂O₂ production reaches its maximum when the amount of nanoparticle loading is at $NP=0.55$ (0.41 mol %). On the other hand, the H₂O₂ degradation rate $k_{\mathrm{d}}$ reaches its minimum when $NP=0.20$ (0.09 mol %) and its maximum when no co-catalysts are loaded, namely, when $NP=0.0$. Interestingly, this implies that one could target the desired H₂O₂ production for a given application guided by the results of our models by exploring the predicted H₂O₂ production over the entire range of nanoparticle loading and Au-Ag compositions. Such heatmaps of $k_{\mathrm{f}}$ and $k_d$ are presented in Figure 2c,d.

Figure 4a displays the scattered and small dataset reported experimentally for produced [H₂O₂] at discrete Au-Ag nanoparticle loading, while Figure 4b illustrates the calculated [H₂O₂] production map produced in this work. Despite a handful of data points of experimentally reported data our calculated [H₂O₂] production is consistent with the reported results: the maximum predicted [H₂O₂] production of 3.4 mM is recorded for Au₀.₁₆Ag₀.₈₄ alloy. Interestingly, we found that very high [H₂O₂] values could be achieved using nanoparticle loading as small as $NP=0.1$ mol %. The model predicts a high production rate at this concentration and loading while the decomposition rate is at its minimum, leading to an overall maximum efficiency in the [H₂O₂] production. Using this model, we constructed a full landscape of the photocatalytic production of [H₂O₂] by varying the nanoparticle loading and Au-Ag composition.

Figure 4c reports the RMSE and $R^2$ of the predicted vs. real data of the H₂O₂ production that achieves high accuracies in individual predictions between the observed and produced H₂O₂ concentrations as indicated by $R^2=0.95$, while the RMSE is as low as 0.22 mM. Therefore, the GAM models we built can capture the main trends governing [H₂O₂] as a function of the properties of the metallic co-catalyst concentration in the Au_xAg_y/TiO₂ system.

While we probe the optimal nanoparticle incorporation, the calculated map suggests that nanoparticles with lower loading of Au-Ag can produce H₂O₂ as efficiently as the TiO₂ catalyst with Au_0.2Ag_0.8 $NP=0.5$ mol %. The H₂O₂ production may be sustained by incorporating a smaller amount of Au and Ag since $k_{\mathrm{d}}$ is suppressed by reducing the loading while $k_{\mathrm{f}}$ is less affected by the loading reduction. Interestingly, Yang et al. recently reported the synthesis of the colloidal Au-Ag/TiO₂, which shows an excellent photocatalytic efficiency for the degradation of methylene blue [40]. The Au-Ag loading ranged from 0.4 to 1.0 mol % and the maximal photoactivity was achieved by using Au_0.21Ag_0.79 with $NP=0.82$ mol % TiO₂ catalyst. Such a high nanoparticle loading also supports the prediction made by our model, which was kept blind to this information, pointing out the strongest photocatalytic activity properly.

At this point, it is worth discussing whether these Au_xAg_y/TiO₂ photocatalysts can be used effectively as an antimicrobial surface. Disinfection of influenza virus on a steel surface achieved a 3 log₁₀ pathogen reduction within 15 min using 10 ppm (0.6 mM) of H₂O₂ in vapor. Increasing the concentration of H₂O₂ to 90 ppm (5.2 mM) boosted the pathogen reduction to 4.5 log₁₀ [13]. On the other hand, Fenton photocatalysts used for water treatment systems led to the degradation of dyes and pollutants in periods of time in the range of 30–200 min when used in solution containing a H₂O₂ concentration ranging from 4 mM to 90 mM depending on the used Fenton catalyst and illumination conditions [32].

Recently, a gas-liquid-solid (G-L-S) TiO₂ triphase system has been tested against the inactivation of Klebsiella pneumoniae Gram-negative bacteria (KPN) [41,42]. The system offered an H₂O₂ generation rate of 1003 ± 52 μM ${\mathrm{h}}^{-1}$ (∼1 mM ${\mathrm{h}}^{-1}$), which is 18 times higher than its corresponding diphase system. The G-L-S TiO₂ disactivated the KPN colony concentration with the following efficiency: at 10 min, the survival ratio was quickly reduced to 35% and within 30 min irradiation with ultraviolet light (UV), it achieved over 99% light-triggered removal efficiency. Hence, it is possible to increase the level of H₂O₂ production by at least one order of magnitude by using an G-L-S triphase photocatalytic system where the Au_xAg_y/TiO₂ photocatalysts are immobilized on porous superhydrophobic substrate to ensure a maximal flow of O₂ system and overcome the slow kinetics of O₂ in solution. The triphase system allows reactant O₂ to reach the reaction interface directly from the ambient atmosphere, greatly increasing the interface O₂ concentration, which in turn simultaneously enhanced the kinetics of H₂O₂ formation and suppresses the unwanted electron-hole recombination and the kinetics of H₂O₂ decomposition reaction.

The prospects of silver-rich Au_xAg_y bi-metallic nanoparticles photocatalysists to combat the spread of infection via the deployment of antibacterial coatings requires a careful analysis of the involved reaction kinetics [43]. For instance, accordingly, we estimate that for the efficient inactivation of enveloped viruses such as SARS-CoV-2, within 30 min, we need a material capable of producing at least 1 mM ${\mathrm{h}}^{-1}$ ${\mathrm{mg}}^{-1}$ using O₂ and H₂O from the air and releasing not more than 30 $\mathsf{\mu }$M of H₂O₂. Still, it is also important to account for various competing phenomena: (i) the affinity of the microorganism to water and to a particular surface [44]; (ii) the competition between the microorganism, water layer on the surfaces, and organic pollutant present in the air; and (iii) the spontaneous decomposition rate of ${\mathrm{H}}_2{\mathrm{O}}_2 \to {\mathrm{H}}_2\mathrm{O}+\frac{1}{2}{\mathrm{O}}_2$ on the surface as a function of temperature and humidity.

Despite their relatively modest H₂O₂ production rate, Au_xAg_y/TiO₂ photocatalysts could be used as a sustainable and continuous source of hydrogen peroxide in heterogeneous Fenton catalytic systems, ensuring a controlled production of H₂O₂ upon illumination [32]. It might find application for water and air decontamination as well as self-cleaning coating with the controlled release and degradation of H₂O₂ upon illumination, ensuring that the level of H₂O₂ never exceeds the internationally agreed health safety levels (1 ppm) [45]. The plasmonic effects due to the response of Au and Ag nanoparticles to visible light excitation are expected to increase the photocatalytic activity for Au_xAg_y/TiO₂ photocatalysts [46]. If combining with Fenton catalysts, one might expect to broaden the visible light absorption of the hybrid material under visible light illumination and hence its disinfection efficiency for indoor settings.

These identified open areas of investigation are needed to deploy antimicrobial surfaces for the disinfection of air and fomites. While it is urgent to explore the continuous range of chemical composition, the proposed ML-assisted approach would accelerate the deployment of antimicrobial coatings for high-touch surfaces as a promising route to mitigate the viral and bacterial transmission via fomites and possibly via aerosol by coating air conditioning and air cleaning filters.

4. Conclusions

Combining concepts from materials science, electrochemistry, and device physics with machine learning, we built a scheme to accelerate the estimation of reactive oxidative species (ROS) production and decomposition rates induced by photocatalytic materials upon illumination. The model built in this work can predict ROS production rates while scanning the entire range of all possible compositions and properties of the photocatalytic system, a task impossible to achieve experimentally. It also offers the possibility to estimate the self-degradation of H₂O₂ to enable its level to be kept within safe ranges. If tailored adequately, we estimate that the photocatalytic system proposed in this work could be efficient for the continuous inactivation of bacteria and possibly viruses. In addition, the proposed composition would give a balanced production of reactive oxygen species (ROS) upon controlled illumination, offering an opportunity for continuous disinfection of water, surfaces, and air, facilitating its integration in indoor environments such as offices, buildings, offices, malls, and airports.

The strategy we present in this work is adaptable to different concentrations and compositions of photoactive materials, which are relevant under experimental conditions but unreachable using conventional calculations. Our experiment-to-machine-learning scheme can be challenged in lab conditions with more data on the baseline materials as well as the novel materials, taking into consideration the cost and abundance of materials associated with a large-scale deployment of this solution.