Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study
Abstract
1. Introduction
- Hematite, i.e., Fe2O3, where iron is at the highest state of oxidation, 3 (Fe3+);
- Magnetite, i.e., Fe3O4, with a state of oxidation of 2.6 (mixture of Fe2+ and Fe3+);
- Wüstite, i.e., FeO, where iron is at the lowest state of oxidation, 2 (Fe2+).
2. Material and Methods
- The incoming energy flow on the focal area has a circular shape located at the midpoint of the tube. This energy flow comes from the second derivative of the heat flow on the surface. The value set in each simulation depends on the detected direct radiation value.
- An outward convective scattering flow was imposed on the outer surface section of the receiver, considering the average wind speed.
- The gas insertion and outflow were imposed in the outer section of the pipe. Due to the low pressures at which the system is operating, the gas can be considered almost uncompressed.
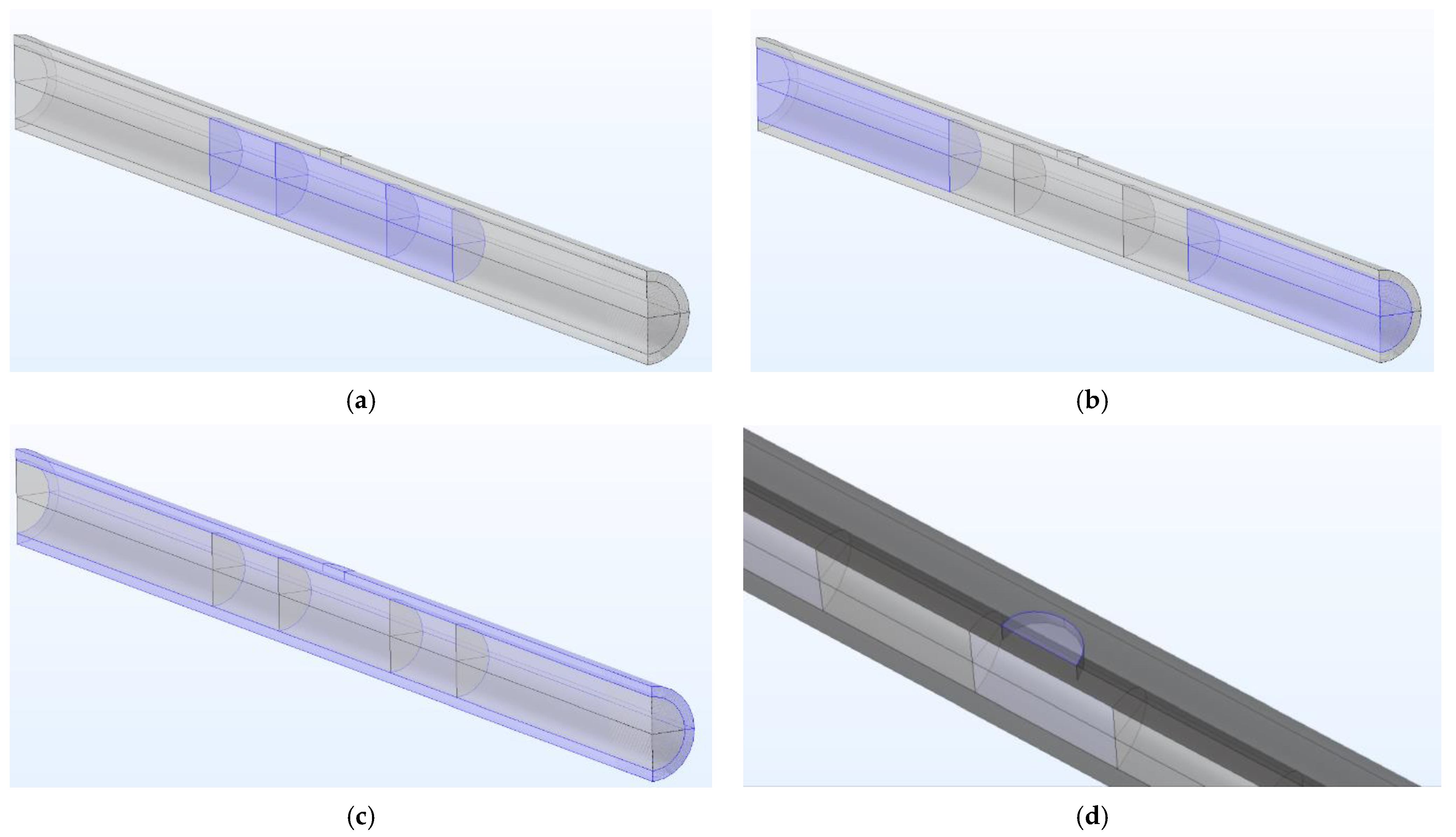
- The central part, hosting the powder, has the shape of a short cylinder with an L/D ratio of 1.5. The quantity of charged powders follows, considering hematite powder density. It has been modelled as a porous medium, as can be seen in Figure 1a.
- Two cylinders of glass wool hold the powder in the central part. They are 2.5 cm long in each geometry and modelled as a porous medium (Figure 1a).
- The remaining internal part of the pipe is modelled as a fluid (nitrogen) with a velocity in the axial direction; see Figure 1b.
- A, which is the frequency factor, indicates the frequency of collisions between reactant molecules at a standard concentration, and it depends on the temperature and the activation energy. Moreover, it depends on the rate at which molecules collide and on the relative orientation.
- n expresses the dependency over temperature change. It can be set to zero.
- E is the activation energy. It is the minimum amount of energy that must be provided to compounds to result in a chemical reaction [31].
3. Results and Discussion
4. Conclusions
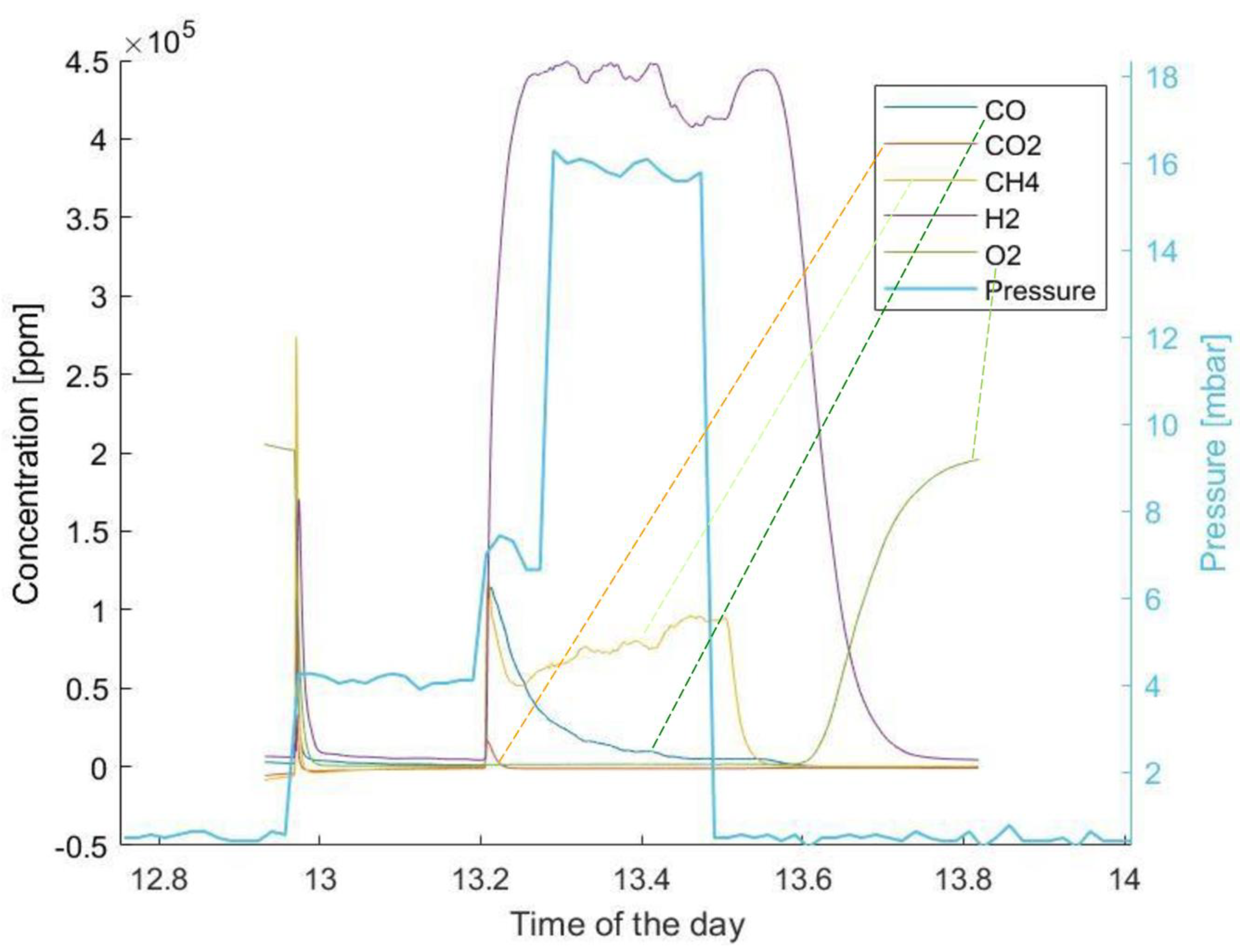
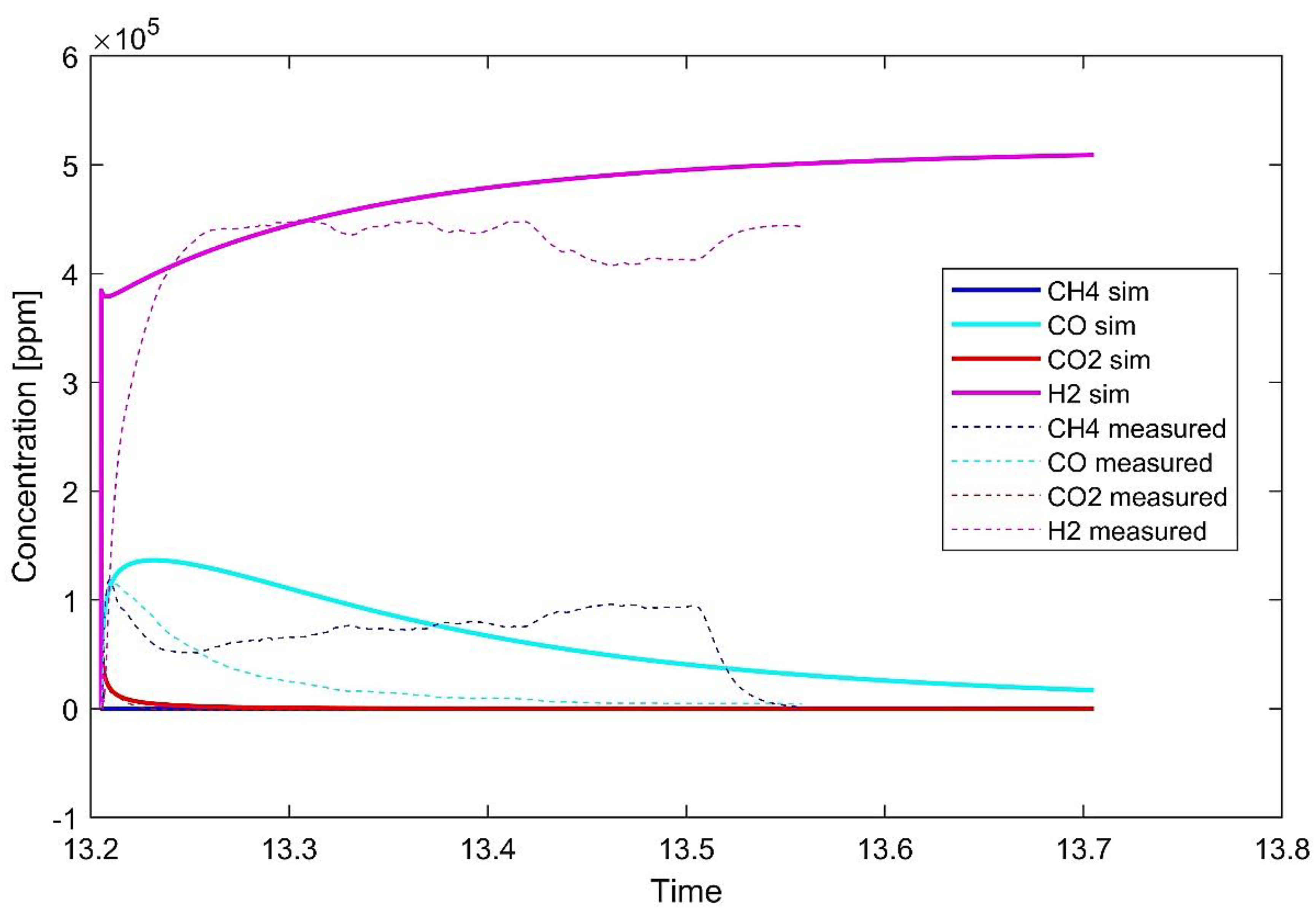
- The production of hydrogen is already relevant in the reduction phase of chemical looping. It might be possible to lower the quantity of unreacted CH4 in real condition experiments by varying the fraction of the gas in the inlet feed or the relative quantity of powder.
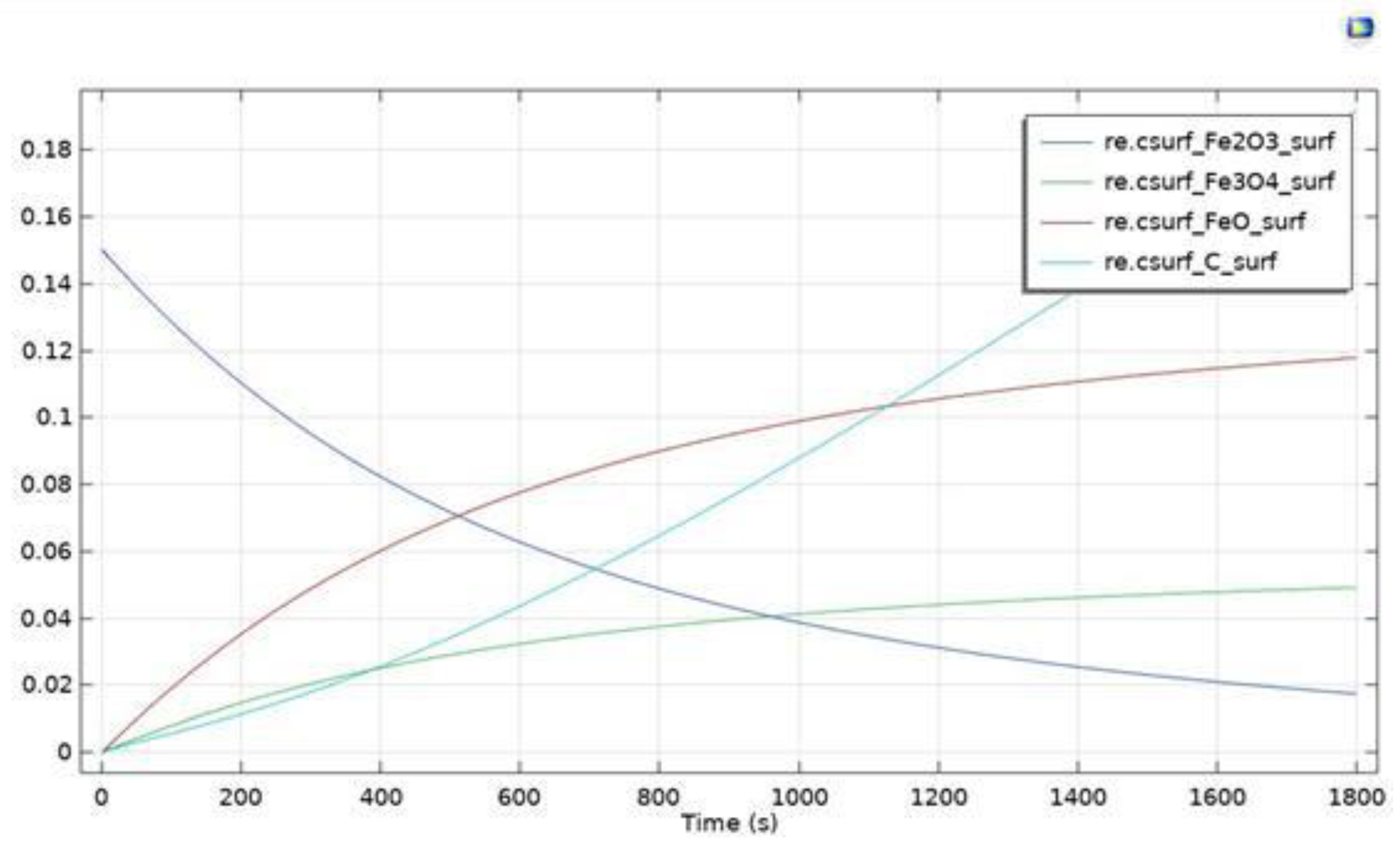
- Flue gases from the experiments highlight that partial oxidation overcame total oxidation, especially as the reaction proceeded. This result is in accordance also with what was found by Monazam et al. [24]. The simulation highlighted the occurence of strong carbon deposition over the carrier. In fact, despite the quantities of the CO and CO2 produced decreasing with the proceeding of the reaction and subsequent exhaustion of hematite, H2 levels were not altered significantly. This might be happening as the molecules of CH4 are cracked due to the suitable temperature range and catalytic action of hematite.
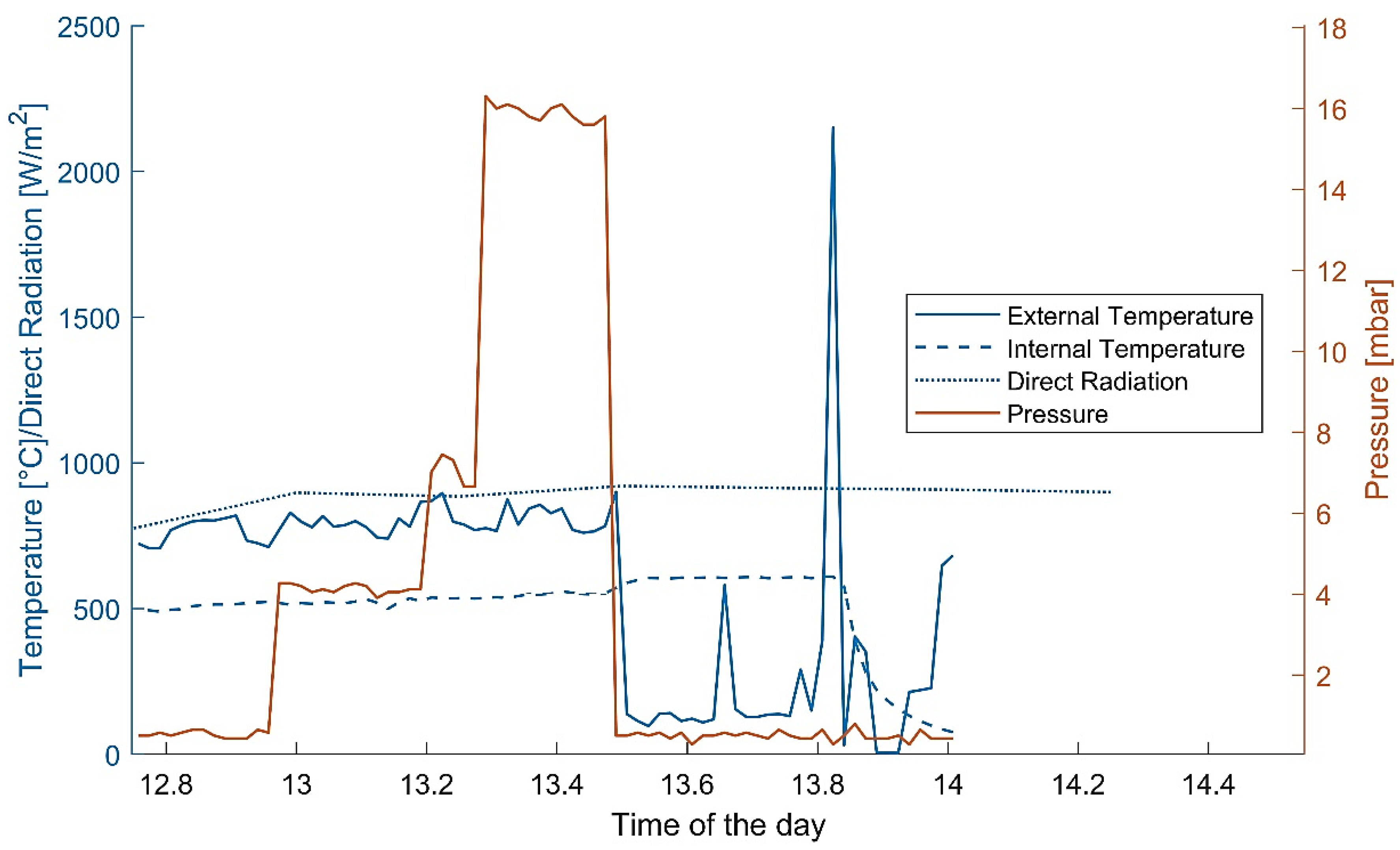
- The concentration of sunbeams on the external surface of a horizontal cylinder poses several threats to the efficacy of the receiver. As the radiation hits the pipe asymmetrically, the material is placed under stress that might hinder its structural properties.
- A solution could be to use a secondary concentrator to catch the light collected by the first reflecting surface and redistribute it.
- On the other hand, if a metallic material is used, an alloy able to operate at extremely high temperature must be selected.
- The extreme variability of the weather can cause a sudden decrease in temperature, even on sunny days. This can not only cause the reaction to stop, but can also cause thermal shocks to the receiver. In the case of wind gusts, the receiver can be cooled down extremely quickly and experience a too-strong quench (if ceramic).
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| effective volumetric heat capacity at constant pressure (kJ/m3/K) | |
| A | Area of the concentrator (m2) |
| CL | Chemical Looping |
| CLC | Chemical Looping Combustion |
| CLPO | Chemical Looping Partial Oxidation |
| CLRM | Chemical Looping Reforming of Methane |
| Co | Optical Concentration ratio |
| CSP | Concentrated Solar Power |
| CSTR | Continuously stirred reactor |
| Dc | Diameter of the dish (mm) |
| df | Diameter of the focal point (mm) |
| f | Focal distance (mm) |
| l | Length of the receiver (mm) |
| OC | Oxygen Carrier |
| P | Power of the concentrator (kW) |
| q | Heat flux generated in the medium due to conduction |
| Q | Incoming solar power (kW) |
| Qted | Heat generated for thermoelastic damping |
| Qvd | Heat generated for viscous dissipation |
| SC | Solar Concentrator |
| u | Velocity (m/s) |
| yR | Depth (mm) |
| ε | Porosity |
| θ | Volume fraction of solid material in porous media |
| φR | Rim angle |
| Density (kg/m3) |
References
- 2030 Climate Target Plan. Available online: https://ec.europa.eu/clima/eu-action/european-green-deal/2030-climate-target-plan_en (accessed on 28 October 2021).
- Stocker, M.; Qin, T.F.; Plattner, D. IPCC (2013). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University: Cambridge, UK; New York, NY, USA, 2013; p. 28. [Google Scholar]
- Intergovernmental Panel on Climate Change Global Warming of 1.5 °C. 2018. Available online: http://www.ipcc.ch/report/sr15/ (accessed on 11 November 2021).
- Tzelepi, V.; Zeneli, M.; Kourkoumpas, D.-S.; Karampinis, E.; Gypakis, A.; Nikolopoulos, N.; Grammelis, P. Biomass Availability in Europe as an Alternative Fuel for Full Conversion of Lignite Power Plants: A Critical Review. Energies 2020, 13, 3390. [Google Scholar] [CrossRef]
- FAQ 1.3—AR4 WGI Chapter 1: Historical Overview of Climate Change Science. Available online: https://archive.ipcc.ch/publications_and_data/ar4/wg1/en/faq-1-3.html (accessed on 11 November 2021).
- Srivastava, R.K.; Shetti, N.P.; Reddy, K.R.; Kwon, E.E.; Nadagouda, M.N.; Aminabhavi, T.M. Biomass utilization and production of biofuels from carbon neutral materials. Environ. Pollut. 2021, 276, 116731. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Luo, S.; Zhang, H.; Ye, J. Toward solar-driven carbon recycling. Joule 2022, 6, 294–314. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, L.; Agrafiotis, C.; Vieten, J.; Roeb, M.; Sattler, C. Solar fuels production: Two-step thermochemical cycles with cerium-based oxides. Prog. Energy Combust. Sci. 2019, 75, 100785. [Google Scholar] [CrossRef]
- Mustafa, A.; Lougou, B.G.; Shuai, Y.; Wang, Z.; Tan, H. Current technology development for CO2 utilization into solar fuels and chemicals: A review. J. Energy Chem. 2020, 49, 96–123. [Google Scholar] [CrossRef]
- Chuayboon, S.; Abanades, S.; Rodat, S. Syngas production via solar-driven chemical looping methane reforming from redox cycling of ceria porous foam in a volumetric solar reactor. Chem. Eng. J. 2019, 356, 756–770. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Hong, H.; Jin, H. Experimental study on honeycomb reactor using methane via chemical looping cycle for solar syngas. Appl. Energy 2020, 268, 114995. [Google Scholar] [CrossRef]
- Cao, Y.; Alsharif, S.; Attia, E.-A.; Shamseldin, M.A.; Ibrahim, B.F. A conceptual process design towards CO2 emission reduction by integration of solar-based hydrogen production and injection into biomass-derived solid oxide fuel cell. Process Saf. Environ. Prot. 2022, 164, 164–176. [Google Scholar] [CrossRef]
- Pan, H.; Li, Y.; Zhu, L.; Lu, Y. Solar-driven H2O/CO2 conversion to fuels via two-step electro-thermochemical cycle in a solid oxide electrochemical cell. Energy Convers. Manag. 2022, 259, 115578. [Google Scholar] [CrossRef]
- Tang, M.; Xu, L.; Fan, M. Progress in oxygen carrier development of methane-based chemical-looping reforming: A review. Appl. Energy 2015, 151, 143–156. [Google Scholar] [CrossRef]
- Abad, A.; Adánez, J.; García-Labiano, F.; de Diego, L.F.; Gayán, P.; Celaya, J. Mapping of the range of operational conditions for Cu-, Fe-, and Ni-based oxygen carriers in chemical-looping combustion. Chem. Eng. Sci. 2007, 62, 533–549. [Google Scholar] [CrossRef]
- Ksepko, E.; Sciazko, M.; Babinski, P. Studies on the redox reaction kinetics of Fe2O3-CuO/Al2O3 and Fe2O3/TiO2 oxygen carriers. Appl. Energy 2014, 115, 374–383. [Google Scholar] [CrossRef]
- Nakamura, T. Hydrogen production from water utilizing solar heat at high temperatures. Sol. Energy 1977, 19, 467–475. [Google Scholar] [CrossRef]
- Tofighi, A.; Sibieude, F. Note on the condensation of the vapor phase above a melt of iron oxide in a solar parabolic concentrator. Int. J. Hydrog. Energy 1980, 5, 375–381. [Google Scholar] [CrossRef]
- Sibieude, F.; Ducarroir, M.; Tofighi, A.; Ambriz, J. High temperature experiments with a solar furnace: The decomposition of Fe3O4, Mn3O4, CdO. Int. J. Hydrog. Energy 1982, 7, 79–88. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Roeb, M.; Sattler, C. A review on solar thermal syngas production via redox pair-based water/carbon dioxide splitting thermochemical cycles. Renew. Sustain. Energy Rev. 2015, 42, 254–285. [Google Scholar] [CrossRef]
- Scheffe, J.R.; Steinfeld, A. Oxygen exchange materials for solar thermochemical splitting of H2O and CO2: A review. Mater. Today 2014, 17, 341–348. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Flamant, G.; Lemort, F. Two-step water splitting thermochemical cycle based on iron oxide redox pair for solar hydrogen production. Energy 2007, 32, 1124–1133. [Google Scholar] [CrossRef]
- Najera, M.; Solunke, R.; Gardner, T.; Veser, G. Carbon capture and utilization via chemical looping dry reforming. Chem. Eng. Res. Des. 2011, 89, 1533–1543. [Google Scholar] [CrossRef]
- Monazam, E.R.; Breault, R.W.; Siriwardane, R.; Richards, G.; Carpenter, S. Kinetics of the reduction of hematite (Fe2O3) by methane (CH4) during chemical looping combustion: A global mechanism. Chem. Eng. J. 2013, 232, 478–487. [Google Scholar] [CrossRef]
- Lu, C.; Li, K.; Wang, H.; Zhu, X.; Wei, Y.; Zheng, M.; Zeng, C. Chemical looping reforming of methane using magnetite as oxygen carrier: Structure evolution and reduction kinetics. Appl. Energy 2018, 211, 1–14. [Google Scholar] [CrossRef]
- El. Ma, MANUALE USO E MANUTENZIONE Concentratore Solare a Disco Matr. 10434 2019. Available online: https://webthesis.biblio.polito.it/19993/1/tesi.pdf (accessed on 30 September 2022).
- Papurello, D.; Bertino, D.; Santarelli, M. CFD Performance Analysis of a Dish-Stirling System for Microgeneration. Processes 2021, 9, 1142. [Google Scholar] [CrossRef]
- DefinerTM 220 Series User Manual. Available online: https://manualzilla.com/doc/6878716/definer%E2%84%A2-220-series-user-manual (accessed on 30 October 2021).
- HeatTransferModuleUsersGuide.pdf. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.heat/HeatTransferModuleUsersGuide.pdf (accessed on 11 November 2021).
- IUPAC—Modified Arrhenius Equation (M03963). Available online: https://goldbook.iupac.org/terms/view/M03963 (accessed on 9 November 2021).
- Laidler, K.J. A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 149–192. [Google Scholar] [CrossRef]
- Slycke, J.T.; Mittemeijer, E.J.; Somers, M.A.J. 1—Thermodynamics and kinetics of gas and gas–solid reactions. In Thermochemical Surface Engineering of Steels; Mittemeijer, E.J., Somers, M.A.J., Eds.; Woodhead Publishing: Oxford, UK, 2015; pp. 3–111. ISBN 978-0-85709-592-3. [Google Scholar]
- Basu, P. Chapter 7—Gasification Theory. In Biomass Gasification, Pyrolysis and Torrefaction, 3rd ed.; Basu, P., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 211–262. ISBN 978-0-12-812992-0. [Google Scholar]
- Neri, M.; Chiavazzo, E.; Mongibello, L. Numerical simulation and validation of commercial hot water tanks integrated with phase change material-based storage units. J. Energy Storage 2020, 32, 101938. [Google Scholar] [CrossRef]
- Nečina, V.; Pabst, W. Influence of the heating rate on grain size of alumina ceramics prepared via spark plasma sintering (SPS). J. Eur. Ceram. Soc. 2020, 40, 3656–3662. [Google Scholar] [CrossRef]
- Ho, C.K. Advances in central receivers for concentrating solar applications. Sol. Energy 2017, 152, 38–56. [Google Scholar] [CrossRef]
- Sarvghad, M.; Delkasar Maher, S.; Collard, D.; Tassan, M.; Will, G.; Steinberg, T.A. Materials compatibility for the next generation of Concentrated Solar Power plants. Energy Storage Mater. 2018, 14, 179–198. [Google Scholar] [CrossRef]
- Cheng, X.; Gu, Z.; Li, F.; Zhu, X.; Wei, Y.; Zheng, M.; Tian, D.; Wang, H.; Li, K. Enhanced resistance to carbon deposition in chemical-looping combustion of methane: Synergistic effect of different oxygen carriers via sequence filling. Chem. Eng. J. 2021, 421, 129776. [Google Scholar] [CrossRef]
- Keller, M.; Matsumura, A.; Sharma, A. Spray-dried Fe/Al2O3 as a carbon carrier for COx-free hydrogen production via methane cracking in a fluidized bed process. Chem. Eng. J. 2020, 398, 125612. [Google Scholar] [CrossRef]
- Keller, M.; Matsuzaki, Y.; Otomo, J. CO2 activation by methane in a dual-bed configuration via methane cracking and iron oxide lattice oxygen transport—Concept and materials development. Chem. Eng. J. 2018, 349, 249–259. [Google Scholar] [CrossRef]
- Sajjadi, B.; Chen, W.-Y.; Fan, M.; Rony, A.; Saxe, J.; Leszczynski, J.; Righetti, T.K. A techno-economic analysis of solar catalytic chemical looping biomass refinery for sustainable production of high purity hydrogen. Energy Convers. Manag. 2021, 243, 114341. [Google Scholar] [CrossRef]
- Bhattacharya, S.P.; Harttig, M. Control of agglomeration and defluidization burning high-alkali, high-sulfur lignites in a small fluidized bed combustor - Effect of additive size and type, and the role of calcium. Energy Fuels 2003, 17, 1014–1021. [Google Scholar] [CrossRef]
- Adanez, J.; Abad, A.; Garcia-Labiano, F.; Gayan, P.; de Diego, L.F. Progress in Chemical-Looping Combustion and Reforming technologies. Prog. Energy Combust. Sci. 2012, 38, 215–282. [Google Scholar] [CrossRef]
- Ruys, A. Processing, structure, and properties of alumina ceramics. In Alumina Ceramics; Ruys, A., Ed.; Woodhead Publishing Series in Biomaterials; Woodhead Publishing: Cambridge, UK, 2019; pp. 71–121. ISBN 978-0-08-102442-3. [Google Scholar]
- Kalogirou, S.A. Chapter 3—Solar Energy Collectors. In Solar Energy Engineering, 2nd ed.; Kalogirou, S.A., Ed.; Academic Press: Boston, MA, USA, 2014; pp. 125–220. ISBN 978-0-12-397270-5. [Google Scholar]
- Miao, Z.; Jiang, E.; Hu, Z. Review of agglomeration in biomass chemical looping technology. Fuel 2022, 309, 122199. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, H.; Tian, X.; Wei, Y.; Rajendran, S.; Zhang, Y.; Bhattacharya, S.; Zheng, C. Chemical looping combustion of coal in a 5kWth interconnected fluidized bed reactor using hematite as oxygen carrier. Appl. Energy 2015, 157, 304–313. [Google Scholar] [CrossRef]
| Symbol | Description | Value | U.m. |
|---|---|---|---|
| Dc | Diameter of the dish | 2370 | mm |
| f | Focal distance | 958 | mm |
| yR | Depth | 370 | mm |
| Rim angle | 61.89 | ° | |
| Co | Optical Concentration ratio | 8013 | - |
| df | Diameter of the focal point | 6.41 | mm |
| l | Length of the receiver | 200 | mm |
| A | Area of the concentrator | 4.5 | |
| P | Power of the concentrator | 2.8 | kW |
| Test | Reactor Material | DI (cm) | Do (cm) | Gas Speed (m/s) |
|---|---|---|---|---|
| #1 | Alumina | 1.402 | 1.806 | 0.045 |
| #2 | Alumina | 1.402 | 1.806 | 0.045 |
| #3 | Steel AISI 316 | 1.537 | 2.120 | 0.037 |
| #4 | Steel AISI 316 | 0.771 | 1.26 | 0.15 |
| #5 | Inconel Hastelloy c-276 | 0.900 | 1.385 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghero, L.; Bressan, M.; Ferrero, D.; Santarelli, M.; Papurello, D. Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study. Catalysts 2022, 12, 1477. https://doi.org/10.3390/catal12111477
Borghero L, Bressan M, Ferrero D, Santarelli M, Papurello D. Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study. Catalysts. 2022; 12(11):1477. https://doi.org/10.3390/catal12111477
Chicago/Turabian StyleBorghero, Luca, Maurizio Bressan, Domenico Ferrero, Massimo Santarelli, and Davide Papurello. 2022. "Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study" Catalysts 12, no. 11: 1477. https://doi.org/10.3390/catal12111477
APA StyleBorghero, L., Bressan, M., Ferrero, D., Santarelli, M., & Papurello, D. (2022). Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study. Catalysts, 12(11), 1477. https://doi.org/10.3390/catal12111477








