Effect of the Heterovalent Doping of TiO2 with Sc3+ and Nb5+ on the Defect Distribution and Photocatalytic Activity
Abstract
:1. Introduction
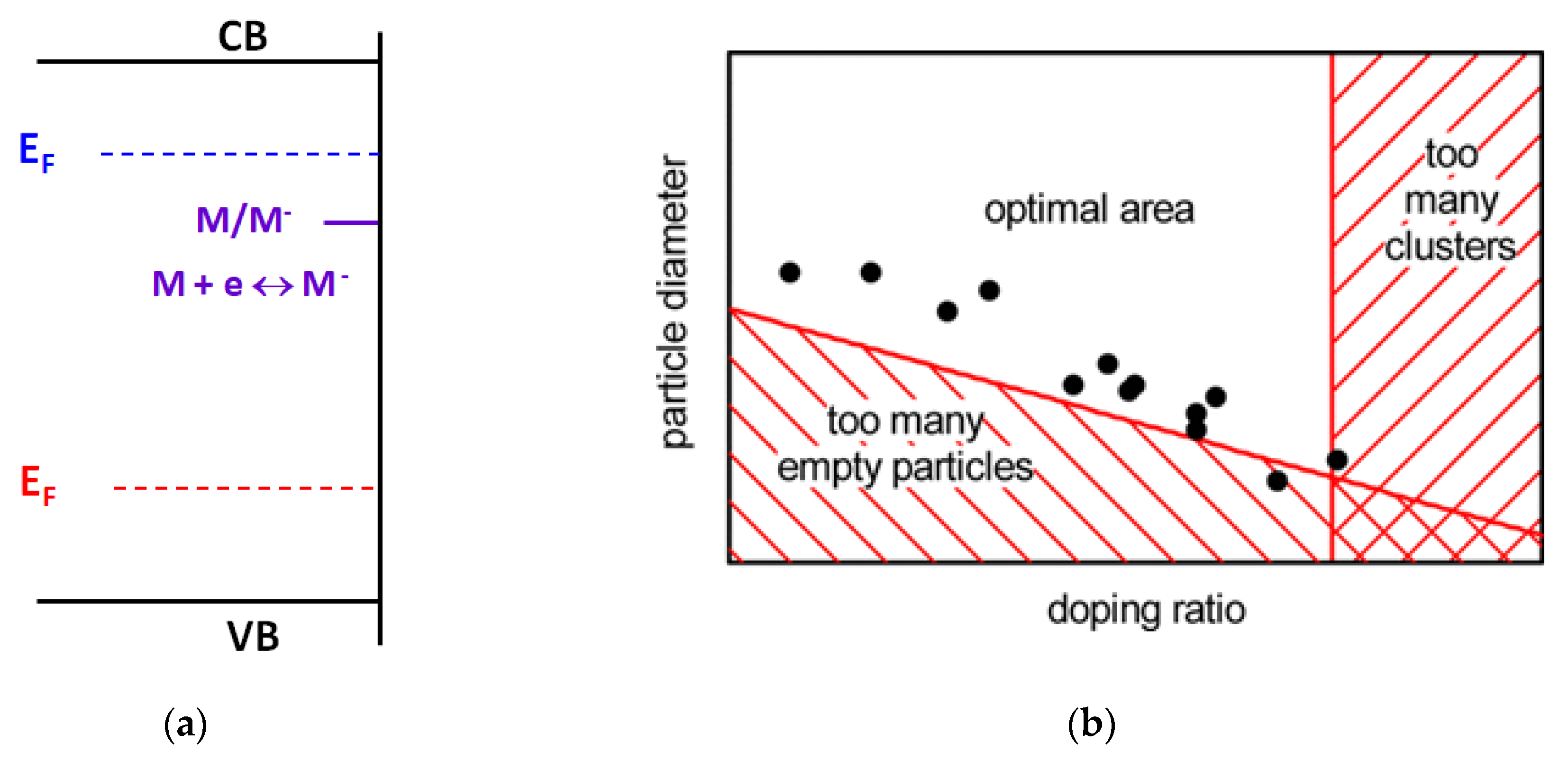
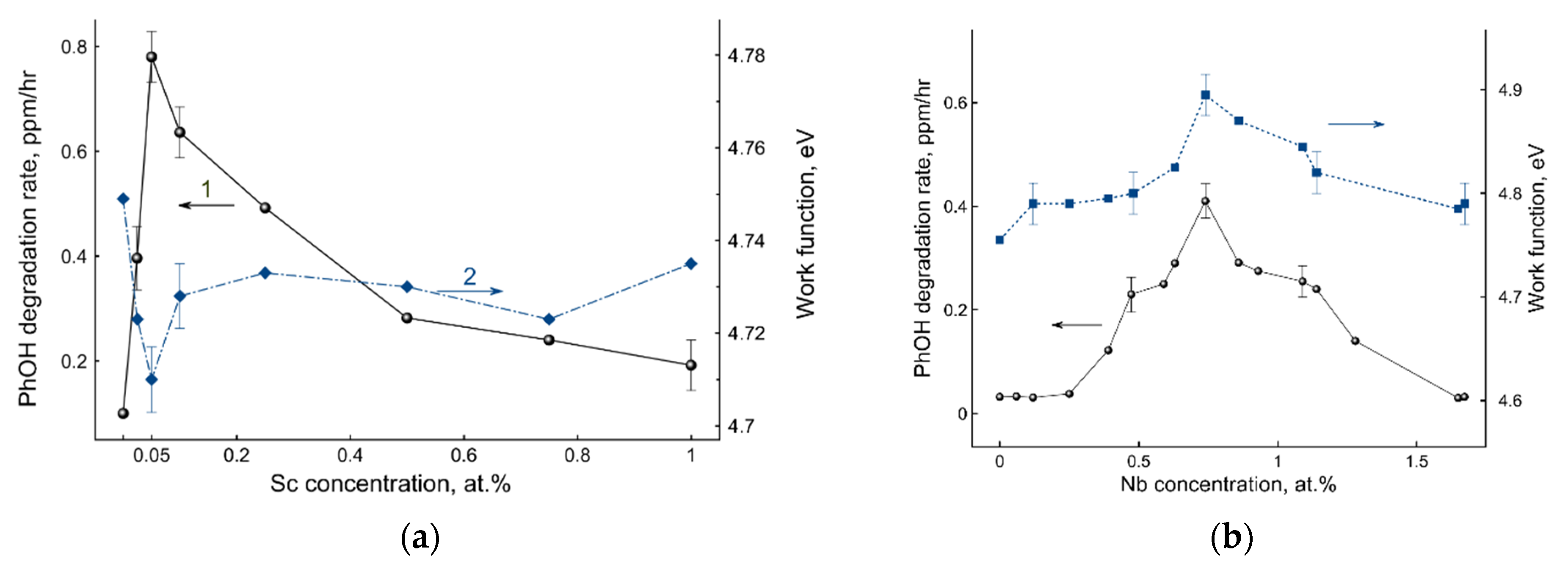
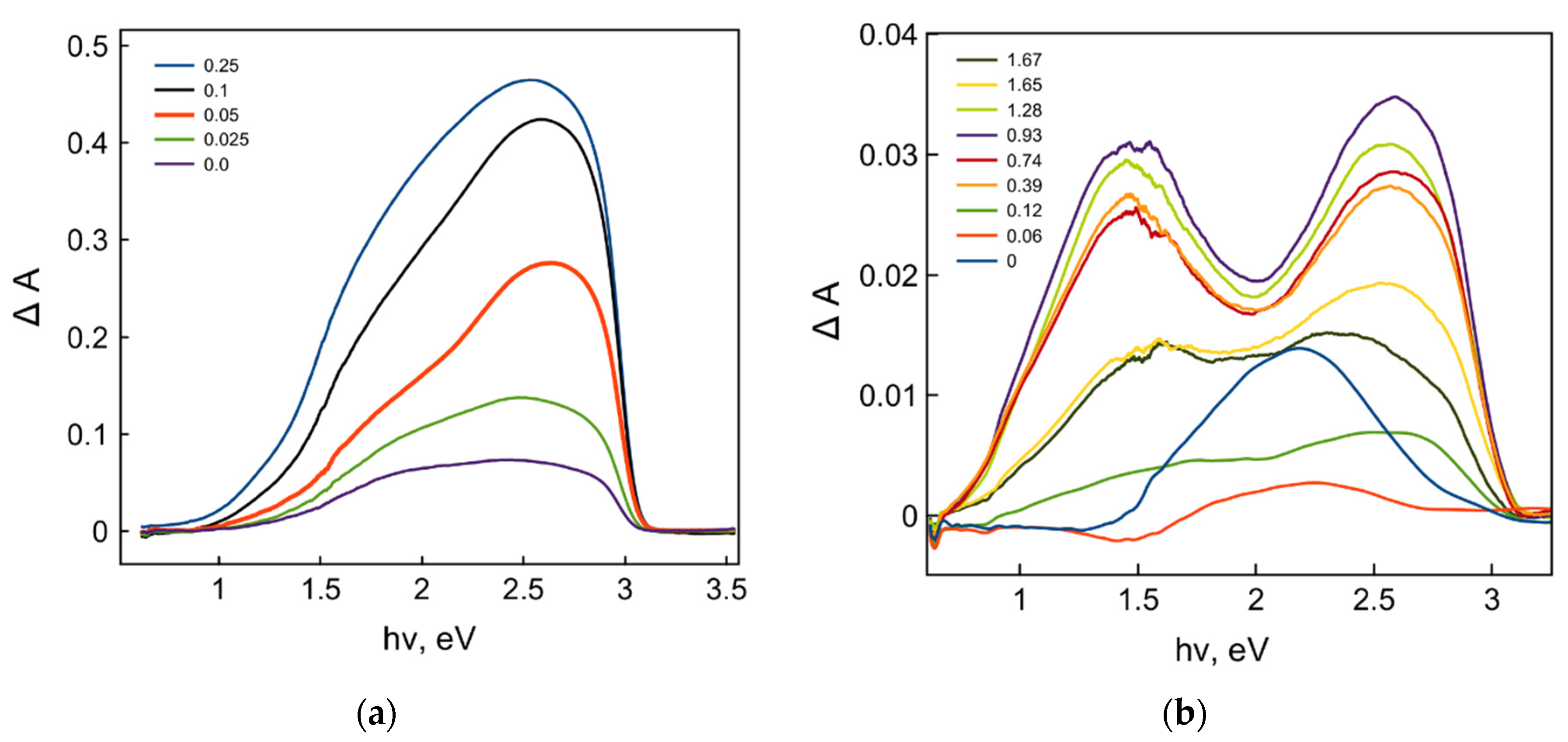
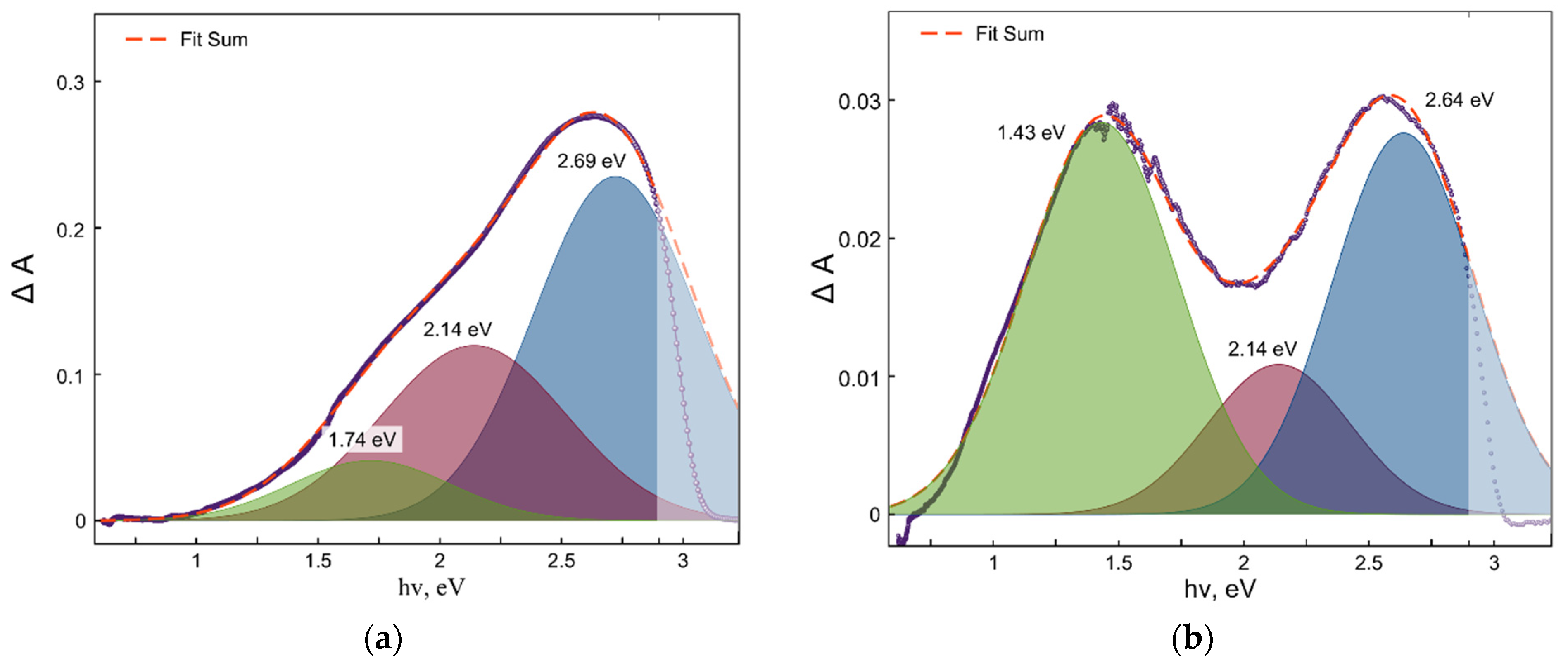
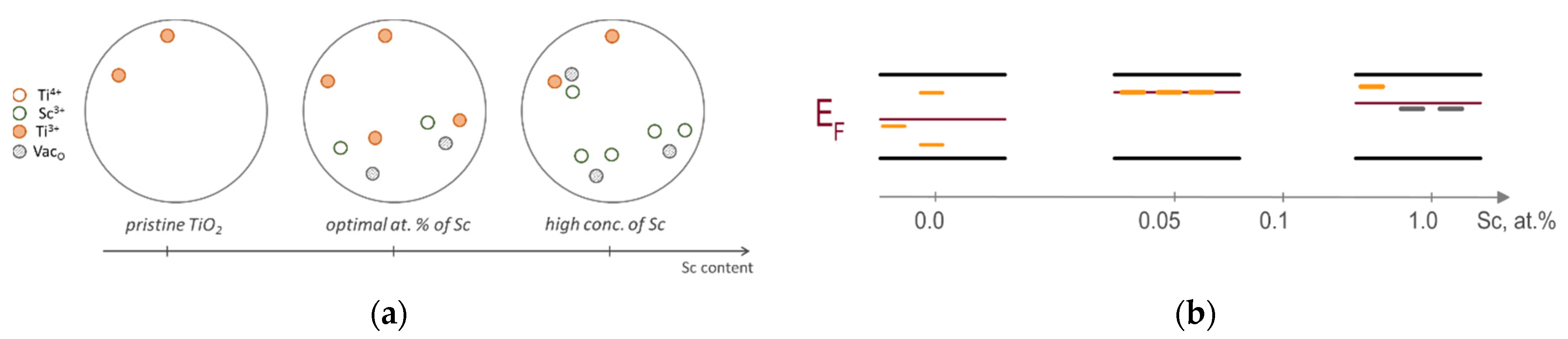
2. Results and Discussion
3. Materials and Methods
3.1. Synthesis and Characterization
3.2. Photocatalytic Measurements
3.3. Work Function Measurements
3.4. Diffuse Reflectance Spectroscopy
3.5. EPR Measurements
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, B.; Lim, T.M.; Subagio, D.P.; Lim, T.T. Zr-doped TiO2 for enhanced photocatalytic degradation of bisphenol A. Appl. Catal. A 2010, 375, 107–115. [Google Scholar] [CrossRef]
- Bigdeli, T.; Moradi Dehaghi, S. The effect of trace amount of Zr-doped TiO2 on photocatalytic activity in degradation of organic waste. Energy Sources A: Recovery Util. Environ. Eff. 2018, 40, 274–281. [Google Scholar] [CrossRef]
- Oropeza, F.E.; Davies, B.; Palgrave, R.G.; Egdell, R.G. Electronic basis of visible region activity in high area Sn-doped rutile TiO2 photocatalysts. Phys. Chem. Chem. Phys. 2011, 13, 7882–7891. [Google Scholar] [CrossRef] [PubMed]
- Byrne, C.; Moran, L.; Hermosilla, D.; Merayo, N.; Blanco, A.; Rhatigan, S.; Hinder, S.; Ganguly, P.; Nolan, M.; Pillai, S.C. Effect of Cu doping on the anatase-to-rutile phase transition in TiO2 photocatalysts: Theory and experiments. Appl. Catal. B Environ. 2019, 246, 266–276. [Google Scholar] [CrossRef]
- Huang, J.Q.; Li, G.J.; Zhou, Z.F.; Jiang, Y.B.; Hu, Q.Q.; Xue, C.B.; Guo, W. Efficient photocatalytic hydrogen production over Rh and Nb codoped TiO2 nanorods. Chem. Eng. J. 2018, 337, 282–289. [Google Scholar] [CrossRef]
- Choi, J.; Park, H.; Hoffmann, M.R. Effects of single metal-ion doping on the visible-light photoreactivity of TiO2. J. Phys. Chem. C 2010, 114, 783–792. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhou, G.; Liu, S.; Ang, H.M.; Tadé, M.O.; Wang, S. Visible light responsive titania photocatalysts codoped by nitrogen and metal (Fe, Ni, Ag, or Pt) for remediation of aqueous pollutants. Chem. Eng. J. 2013, 231, 18–25. [Google Scholar] [CrossRef]
- Murashkina, A.A.; Murzin, P.D.; Rudakova, A.V.; Ryabchuk, V.K.; Emeline, A.V.; Bahnemann, D.W. Influence of the dopant concentration on the photocatalytic activity: Al-doped TiO2. J. Phys. Chem. C 2015, 119, 24695–24703. [Google Scholar] [CrossRef]
- Murashkina, A.A.; Rudakova, A.V.; Ryabchuk, V.K.; Nikitin, K.V.; Mikhailov, R.V.; Emeline, A.V.; Bahnemann, D.W. Influence of the dopant concentration on the photoelectrochemical behavior of Al-doped TiO2. J. Phys. Chem. C 2018, 122, 7975–7981. [Google Scholar] [CrossRef]
- Murzin, P.D.; Murashkina, A.A.; Emeline, A.V.; Bahnemann, D.W. Effect of Sc3+/V5+ co-doping on photocatalytic activity of TiO2. Top. Catal. 2021, 64, 817–823. [Google Scholar] [CrossRef]
- Wolkenstein, T. The Electronic Theory of Catalysis on Semiconductors, 1st ed.; Pergamon Press: Oxford, UK, 1963; 169p. [Google Scholar]
- Wolkenstein, T. The electronic theory of photocatalytic reactions on semiconductors. Adv. Catal. 1973, 23, 157–208. [Google Scholar] [CrossRef]
- Hauffe, K.; Stechemesser, R. Zur Randschicht-Theorie der Adsorption und Katalyse an Halbleiter-Katalysatoren. In Electronic Phenomena in Chemisorption and Catalysis on Semiconductors. Symposium on Electronic Phenomena in Chemisorption and Catalysis on Semiconductors Held in Moscow, July 2–4, 1968, 1st ed.; Hauffe, K., Wolkenstein, T., Eds.; Walter De Gruyter & Co.: Berlin, Germany, 1969; Chapter 1; pp. 1–27. [Google Scholar] [CrossRef]
- Bloh, J.Z.; Dillert, R.; Bahnemann, D.W. Designing optimal metal-doped photocatalysts: Correlation between photocatalytic activity, doping ratio, and particle size. J. Phys. Chem. C 2012, 116, 25558–25562. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, V.; Sachdev, K. Investigation of effect of doping concentration in Nbdoped TiO2 thin films for TCO applications. J. Mater. Sci. 2017, 52, 11580–11591. [Google Scholar] [CrossRef]
- Ratova, M.; Kelly, P.J.; West, G.T.; Iordanova, I. Enhanced properties of magnetron sputtered photocatalytic coatings via transition metal doping. Surf. Coat. Technol. 2013, 228 (Suppl.1), S544–S549. [Google Scholar] [CrossRef]
- Ben Jemaa, I.; Chaabouni, F.; Presmanes, L.; Thimont, Y.; Abaab, M.; Barnabe, A.; Tailhades, P. Structural, optical and electrical investigations on Nb doped TiO2 radiofrequency sputtered thin films from a powder target. J. Mater. Sci. Mater. Electron. 2016, 27, 13242–13248. [Google Scholar] [CrossRef] [Green Version]
- Kaleji, B.K.; Sarraf-Mamoory, R.; Fujishima, A. Influence of Nb dopant on the structural and optical properties of nanocrystalline TiO2 thin films. Mater. Chem. Phys. 2012, 132, 210–215. [Google Scholar] [CrossRef]
- Lee, H.Y.; Robertson, J. Doping and compensation in Nb-doped anatase and rutile TiO2. J. Appl. Phys. 2013, 113, 213706. [Google Scholar] [CrossRef]
- Miyagi, T.; Kamei, M.; Sakaguchi, I.; Mitsuhashi, T.; Yamazaki, A. Photocatalytic property and deep levels of Nb-doped anatase TiO2 film grown by metalorganic chemical vapor deposition. Jpn. J. Appl. Phys. 2004, 43, 775–776. [Google Scholar] [CrossRef]
- Morris, D.; Dou, Y.; Rebane, J.; Mitchell, C.E.J.; Egdell, R.G.; Law, D.S.L.; Vittadini, A.; Casarin, M. Photoemission and STM study of the electronic structure of Nb-doped TiO2. Phys. Rev. B 2000, 61, 13445–13457. [Google Scholar] [CrossRef] [Green Version]
- Nogueira, M.V.; Lustosa, G.M.M.M.; Kobayakawa, Y.; Kogler, W.; Ruiz, M.; Monteiro Filho, E.S.; Zaghete, M.A.; Perazolli, L.A. Nb-doped TiO2 photocatalysts used to reduction of CO2 to methanol. Adv. Mater. Sci. Eng. 2018, 2018, 7326240. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.-C.; Lin, T.-H.; Chih, J.-S.; Hsiao, K.-C.; Wu, P.-Y. Niobium doping induced morphological changes and enhanced photocatalytic performance of anatase TiO2. Jpn. J. Appl. Phys. 2017, 56, 04CP07. [Google Scholar] [CrossRef]
- Mardare, D.; Yildiz, A.; Girtan, M.; Manole, A.; Dobromir, M.; Irimia, M.; Adomnitei, C.; Cornei, N.; Luca, D. Surface wettability of titania thin films with increasing Nb content. J. Appl. Phys. 2012, 112, 073502. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.Y.; Park, J.-H.; Kim, Y.-H.; Lee, M.-H.; Cho, N.-I. Effect of Nb doping on morphology, crystal structure, optical band gap energy of TiO2 thin films. Curr. Appl. Phys. 2014, 14, 421–427. [Google Scholar] [CrossRef]
- Hirano, M.; Date, K. Scandium-doped anatase (TiO2) nanoparticles directly formed by hydrothermal crystallization. J. Am. Ceram. Soc. 2005, 88, 2604–2607. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, T.; Nie, H.; Shen, C. Microstructure and optical properties of scandium doped TiO2 nanoparticles. J. Rare Earths 2006, 24 (Suppl. 3), 72–76. [Google Scholar] [CrossRef]
- Wei, Z.; Mei, W.; Xiyu, S.; Yachao, W.; Zhenyong, L. Electronic and optical properties of the doped TiO2 system. J. Semicond. 2010, 31, 072001. [Google Scholar] [CrossRef]
- Cavalheiro, A.A.; Bruno, J.C.; Saeki, M.J.; Valente, J.P.S.; Florentino, A.O. Effect of scandium on the structural and photocatalytic properties of titanium dioxide thin films. J. Mater. Sci. 2008, 43, 602–608. [Google Scholar] [CrossRef]
- Berglund, S.P.; Hoang, S.; Minter, R.L.; Fullon, R.R.; Mullins, C.B. Investigation of 35 elements as single metal oxides, mixed metal oxides, or dopants for titanium dioxide for dye-sensitized solar cells. J. Phys. Chem. C 2013, 117, 25248–25258. [Google Scholar] [CrossRef]
- Shaitanov, L.; Murashkina, A.; Rudakova, A.; Ryabchuk, V.; Emeline, A.; Artemev, Y.; Kataeva, G.; Serpone, N. UV-induced formation of color centers in dispersed TiO2 particles: Effect of thermal treatment, metal (Al) doping, and adsorption of molecules. J. Photochem. Photobiol. A 2018, 354, 33–46. [Google Scholar] [CrossRef]
- Emeline, A.V.; Rudakova, A.V.; Mikhaylov, R.V.; Ryabchuk, V.K.; Serpone, N. Electron Transfer Processes in Heterostructured Photocatalysts. In Springer Handbook of Inorganic Photochemistry, 1st ed.; Bahnemann, D.W., Patrocinio, A.O.T., Eds.; Springer Nature: Cham, Switzerland, 2022; ISBN 978-3-030-63712-5. [Google Scholar]
- Kuznetsov, V.N.; Serpone, N. Photoinduced coloration and photobleaching of titanium dioxide in TiO2/polymer compositions upon UV- and visible-light excitation of color centers’ absorption bands: Direct experimental evidence negating band-gap narrowing in anion-/cation-doped TiO2s. J. Phys. Chem. C 2007, 111, 15277–15288. [Google Scholar] [CrossRef]
- Kuznetsov, V.N.; Glazkova, N.I.; Mikhaylov, R.V.; Serpone, N. In situ study of photo- and thermo-induced color centers in photochromic rutile TiO2 in the temperature range 90–720 K. Photochem. Photobiol. Sci. 2016, 15, 1289–1298. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, V.N.; Serpone, N. Visible light absorption by various titanium dioxide specimens. J. Phys. Chem. B 2006, 110, 25203–25209. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C.P.; Gopal, N.O.; Wang, T.C.; Wong, M.S.; Ke, S.C. EPR investigation of TiO2 nanoparticles with temperature-dependent properties. J. Phys. Chem. B 2006, 110, 5223–5229. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, I.R.; Rhydderch, S.; Holt, E.; Grant, N.; Storey, J.M.D.; Howe, R.F. EPR studies of electron and hole trapping in titania photocatalysts. Catal. Today 2012, 182, 39–45. [Google Scholar] [CrossRef]
- Iwaszuk, A.; Nolan, M. Charge compensation in trivalent cation doped bulk rutile TiO2. J. Phys. Condens. Matter 2011, 23, 334207. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Carrier Recombination and Noise. In Semiconductor Physics, 1st ed.; Böer, K.W., Pohl, U.W., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–56. [Google Scholar] [CrossRef]
- Gray, T.J.; McCain, C.C.; Masse, N.G. Defect structure and catalysis in the TiO2 system (Semi-conducting and magnetic Properties). J. Phys. Chem. 1959, 63, 472–475. [Google Scholar] [CrossRef]
- O’Shea, K.E.; Cardona, C. The reactivity of phenol in irradiated aqueous suspensions of TiO2. Mechanistic changes as a function of solution pH. J. Photochem. Photobiol. A 1995, 91, 67–72. [Google Scholar] [CrossRef]
- Luttrell, T.; Halpegamage, S.; Tao, J.; Kramer, A.; Sutter, E.; Batzill, M. Why is anatase a better photocatalyst than rutile?—Model studies on epitaxial TiO2 films. Sci. Rep. 2015, 4, 4043. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzin, P.D.; Rudakova, A.V.; Emeline, A.V.; Bahnemann, D.W. Effect of the Heterovalent Doping of TiO2 with Sc3+ and Nb5+ on the Defect Distribution and Photocatalytic Activity. Catalysts 2022, 12, 484. https://doi.org/10.3390/catal12050484
Murzin PD, Rudakova AV, Emeline AV, Bahnemann DW. Effect of the Heterovalent Doping of TiO2 with Sc3+ and Nb5+ on the Defect Distribution and Photocatalytic Activity. Catalysts. 2022; 12(5):484. https://doi.org/10.3390/catal12050484
Chicago/Turabian StyleMurzin, Petr D., Aida V. Rudakova, Alexei V. Emeline, and Detlef W. Bahnemann. 2022. "Effect of the Heterovalent Doping of TiO2 with Sc3+ and Nb5+ on the Defect Distribution and Photocatalytic Activity" Catalysts 12, no. 5: 484. https://doi.org/10.3390/catal12050484
APA StyleMurzin, P. D., Rudakova, A. V., Emeline, A. V., & Bahnemann, D. W. (2022). Effect of the Heterovalent Doping of TiO2 with Sc3+ and Nb5+ on the Defect Distribution and Photocatalytic Activity. Catalysts, 12(5), 484. https://doi.org/10.3390/catal12050484








