Next Article in Journal
Dependence of Photocatalytic Activity on the Morphology of Strontium Titanates
Next Article in Special Issue
Studies on the Selectivity Mechanism of Wild-Type E. coli Thioesterase ‘TesA and Its Mutants for Medium- and Long-Chain Acyl Substrates
Previous Article in Journal
Two-Dimensional Zeolitic Imidazolate Framework ZIF-L: A Promising Catalyst for Polymerization
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 12
Issue 5
10.3390/catal12050522
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Exploration of the Interactions between Maltase–Glucoamylase and Its Potential Peptide Inhibitors by Molecular Dynamics Simulation

by
Shanshan Guan
1,2,*,
Xu Han
1,
Zhan Li
1,
Xifei Xu
1,
Yongran Cui
1,
Zhiwen Chen
1,
Shuming Zhang
1,
Shi Chen
1,
Yaming Shan
3,
Song Wang
4 and
Hao Li
1,2,*
1
College of Biology and Food Engineering, Jilin Engineering Normal University, Changchun 130052, China
2
Key Laboratory of Molecular Nutrition at Universities of Jilin Province, Changchun 130052, China
3
National Engineering Laboratory for AIDS Vaccine, School of Life Sciences, Jilin University, Changchun 130012, China
4
Institute of Theoretical Chemistry, College of Chemistry, Jilin University, Changchun 130023, China
*
Authors to whom correspondence should be addressed.
Catalysts 2022, 12(5), 522; https://doi.org/10.3390/catal12050522
Submission received: 30 March 2022 / Revised: 2 May 2022 / Accepted: 6 May 2022 / Published: 7 May 2022
(This article belongs to the Special Issue Catalytic Reaction Mechanics of Enzymatic Reactions)
Browse Figures
Versions Notes

Abstract

:
Diabetes mellitus, a chronic metabolic disorder, represents a serious threat to human health. The gut enzyme maltase–glucoamylase (MGAM) has attracted considerable attention as a potential therapeutic target for the treatment of type 2 diabetes. Thus, developing novel inhibitors of MGAM holds the promise of improving clinical management. The dipeptides, Thr-Trp (TW) and Trp-Ala (WA), are known inhibitors of MGAM; however, studies on how they interact with MGAM are lacking. The work presented here explored these interactions by utilizing molecular docking and molecular dynamics simulations. Results indicate that the active center of the MGAM could easily accommodate the flexible peptides. Interactions involving hydrogen bonds, cation-π, and hydrophobic interactions are predicted between TW/WA and residues including Tyr1251, Trp1355, Asp1420, Met1421, Glu1423, and Arg1510 within MGAM. The electrostatic energy was recognized as playing a dominant role in both TW-MGAM and WA-MGAM systems. The binding locations of TW/WA are close to the possible acid-base catalytic residue Asp1526 and might be the reason for MGAM inhibition. These findings provide a theoretical structural model for the development of future inhibitors.

1. Introduction

Diabetes mellitus is a chronic metabolic disorder characterized by hyperglycemia caused by insufficient insulin secretion and/or insulin resistance. According to reports by the International Diabetes Federation, nearly 500 million people live with diabetes worldwide [1,2,3]. At present, treatment of type 2 diabetes primarily relies on oral insulin secretion enhancers, insulin secretion pattern regulators, biguanides, and acarbose, to control hyperglycemia [2]. Acarbose is a mature α-glucosidase inhibitor used widely in the treatment of type 2 diabetes [4]. However, long-term oral therapy can produce side effects, highlighting the need to develop novel inhibitors that are safe and effective. Human maltase–glucoamylase (MGAM) is an α-glucosidase that hydrolyzes linear α-1,4-linked oligosaccharide substrates. As such, it plays a key role in releasing glucose from complex carbohydrates in the human small intestine [2,4]. Recently, MGAM has emerged as a potential drug target for the treatment of type 2 diabetes and obesity [5,6,7]. MGAM consists of two domains, the N-domain and C-domain [5], with the C-domain exhibiting higher enzymatic activity [3]. The C-domain of MGAM can be divided into five different structural units, including a trefoil type-P domain, an N-terminal domain, a catalytic domain, a proximal C-terminal domain, and a distal C-terminal domain. The catalytic center domain is composed of residues 1221 to 1632 consisting of a (β/α)8-barrel with two loop inserts [8].
Natural plants are the main sources of α-glucosidase inhibitors [4,9,10]. Several traditional natural compounds have been isolated and studied in order to guide the identification and screening of novel α-glucosidase inhibitors [3,11]. Such inhibitors have been identified from apricot kernels, walnuts, ginkgo, peanut, malt root, and other plants [12]. These inhibitors include polypeptides, phenolic acids, and other compounds [10]. While numerous studies focused on identifying inhibitors, studies on their mechanism of action are lacking. In the study from Gu et al., two kinds of high activity α-glucosidase peptide inhibitors, Thr-Trp (TW) and Trp-Ala (WA), were isolated and purified from apricot kernel protein hydrolysates via ultrafiltration, molecular sieve, and reversed-phase high-performance liquid chromatography. The experimental results showed that TW and WA could inhibit α-glucosidase at IC50 22.93 μmol/L and 23.97 μmol/L in vitro [12]. However, there are few studies on the mechanism of interaction between TW or WA and α-glucosidase. This study explored the potential interaction mechanism between two peptides and the C-domain of MGAM, a representative α-glucosidase subunit [13].
Furthermore, as these peptides are flexible, studying the interactions between any of them and MGAM might be helpful in predicting how the active center of the enzyme accommodates substrates. To explore the mechanisms of MGAM inhibition by these peptides, molecular docking, molecular dynamics simulation, and free-energy calculations were carried out [14,15,16,17,18]. The results of this study might be useful for future exploration of efficient drug targets and provide theoretical insight into a new mechanism of MGAM inhibitors.

2. Results

A series of computational methods were applied in this study. First, molecular docking was carried out to derive the initial MGAM-TW and MGAM-WA complexes. Subsequently, the 200 ns molecular dynamics simulations were performed to explore the detailed binding modes of TW or WA. After obtaining stable simulated trajectories, the binding free energy was calculated to evaluate the binding potential of TW or WA to MGAM. Experimental details are shown in Section 4.

2.1. Validation of the Docking Protocol

In order to validate the docking method, the acarbose was re-docked to the MGAM with Autodock 4. The top scoring pose extracted from docking results was overlapped to the acarbose from the crystal structure. As illustrated in Figure S1, the acarbose could be re-docked to the active center of the MGAM accurately. The root-mean-square deviation (RMSD) between two structures of acarbose was at approximately 3.0 Å. Given the chain flexibility of acarbose, the RMSD value calculated above was considered to be acceptable. Based on the above results, the reliability of the docking method was confirmed. Subsequently, the TW and WA were docked into the active pocket of the MGAM via applying the same procedure. The lowest energy structures were selected from the most clustered class of docking results as the initial structures for molecular dynamics simulations.

2.2. Reliability Considerations and Cluster Analysis of Investigated Complexes

After 200 ns simulations, the radius of gyration (Rg) of the main chain and RMSD of the backbone Cα atoms of the two complexes were calculated to evaluate if these complex systems could reach equilibrium during the simulations [19,20]. As illustrated in Figure 1a, the Rg of the MGAM-TW and MGAM-WA complexes could be stabilized around 2.90~2.93 nm. The results indicated that the volume and shape of the MGAM could be in stable states during the simulations. As shown in Figure 1b, most of the RMSD values in the MGAM-TW and MGAM-WA complexes could be stabilized at around 0.25~0.35 nm. However, the RMSD values of MGAM-WA complexes increased significantly over the time period of 80 ns to 100 ns, indicating that the backbone of MGAM-WA might have been perturbed during this time period. Based on the above results, the structures during 100 to 200 ns stages were considered to analyze the optimal binding configurations between MGAM and the peptides [21].
To identify which conformations could be formed preferentially during 100 to 200 ns, a cluster analysis of MGAM-TW and MGAM-WA complexes was implemented. The cluster analysis was performed using the g_cluster package included in the GROMACS software. The program first calculated the RMSD, measuring the structure difference for each frame, and then applied the specific algorithm and the threshold value to complete the clustering. In this study, the “gromos” method was applied to carry out the cluster analysis and the RMSD cut-off was set to 0.1 nm [22].
Cluster distributions and cluster transitions are shown in Figure 2. The conformations of TW could be classified into three different structural clusters during 100 to 200 ns, with cluster 1 being the most prominent (Figure 2a). During 100 to 200 ns, most conformations of TW tended to fall into cluster 1. Figure 2b shows that the molecular conformations could transfer among cluster 1, cluster 2, and cluster 3. The conformations of WA were classified into 12 different structural clusters as shown in Figure 2c, most of these belonging to cluster 1. During 100 ns and 125 ns, most conformations could be observed in cluster 2, while, after 125 ns, the conformations in cluster 1 were dominated. The transitions of conformations could be observed either between cluster 1, cluster 4, and cluster 5, or between cluster 2, cluster 4, and cluster 6, as shown in Figure 2d.
The representative conformations from the clusters of TW are listed in Table 1, and cluster 1 to cluster 6 of WA are listed in Table 2. The transitions between similar clusters (for example, cluster 1, 2, 3 of TW) could be caused by the deflection of the side chain, and no significant differences could be observed in their backbones. While, in those clusters without transitions, obvious variations could be observed in their backbones and side chains. Detailed information on cluster sizes is listed in Table 1 and Table 2 as well. As shown in Table 1, 9957 possible conformations were settled to cluster 1 of TW, covering 99.56% of potential conformations. The probability of existent conformations in cluster 2 to cluster 3 were all less than 1%. Total 7213 conformations were settled to cluster 1 and 1834 conformations to cluster 2 in Table 2, covering 72.12% and 18.34% of the WA conformations, respectively. The conformation number of WA from cluster 2 to cluster 12 is much less than those from cluster 1, as shown in Table 2 and Table S1, suggesting that the conformations of WA in these clusters could not be attached to the active center of MGAM stably. The diversification of structural clusters could be correlated with the flexibility of peptides.
The conformations of TW and WA from cluster 1 and cluster 2 within the active site of MGAM are shown in Figure 3. The results revealed that TW could be trapped in a pocket located at the catalytic active center of MGAM, as shown in Figure 3a. Evidently, the binding orientations of TW at the active site of MGAM from cluster 1 and cluster 2 are similar. The conformation of TW observed from cluster 2 gave a more extended form compared with that from the cluster 1 structures. Models of the representative structures of the MGAM-WA complex are shown in Figure 3b. These results revealed that WA could also be captured in the pocket located at the catalytic center. The backbone of WA appeared in a significant deflection when the conformations converted from cluster 1 to cluster 2. The above results indicated that TW or WA could regulate their conformation according to the changes in the shape of the active center, ensuring the effective binding. At the same time, it seems that the active center of the MGAM could provide much more freedom for the binding of flexible peptides. Due to the fact that most of the conformations in both complexes could be concentrated in cluster 1, the conformations collected in cluster 1 extracted from the MGAM-TW complex and MGAM-WA complex could be applied for the binding modes analysis.

2.3. Total Binding Free Energy of the Complexes

In this section, the molecular mechanics Poisson–Boltzmann surface area (MMPBSA) method was used to provide approximate estimates and compare the binding potential between the peptides and MGAM. The commonest 200 conformations of cluster 1 from MGAM-TW were collected to calculate the binding energy of the system. The energy distributions of the MGAM-TW complex are shown in Figure S2 and the average energy values are listed in the Table 3. The binding energy of cluster 1 from the MGAM-TW complex was around −229.93 ± 38.66 kJ/mol, indicating that TW could give a strong binding ability with MGAM. As shown in Table 3, the values of electrostatic energy were −495.18 ± 69.46 kJ/mol, suggesting that electrostatic interactions could play a dominant role in total binding energy. Nonetheless, van der Waals energy also contributed to the binding between TW and MGAM. The values for van der Waals energy were −106.66 ± 12.52 kJ/mol. The values for SASA energy were −14.49 ± 0.89 kJ/mol, as shown in Table 3, indicating less contribution to the binding between TW and MGAM.
Similarly, most potential conformations of the MGAM-WA complex were also aggregated in cluster 1. Thus, 200 conformations from these clusters were collected to evaluate the binding energy of the MGAM-WA complex. Energy distributions are shown in Figure S2 and the average energy values are listed in the Table 4. As shown in Figure S2 and Table 4, the binding energy of cluster 1 from the MGAM-WA complex was around −112.53 ± 38.68 kJ/mol, indicating that WA could also provide strong interactions with MGAM. In addition, the values of electrostatic energy were −250.50 ± 55.65 kJ/mol in cluster 1, indicating that electrostatic interactions could provide the dominant energy contribution in the formation of both MGAM-WA and MGAM-TW complexes. Van der Waals interaction also contributed to the binding between WA and MGAM. As shown in Table 4, the van der Waals energy value in cluster 1 was −100.78 ± 10.06 kJ/mol. The values for SASA energy were −13.22 ± 1.04 kJ/mol, as shown in Table 4, indicating less contribution to the binding between WA and MGAM.

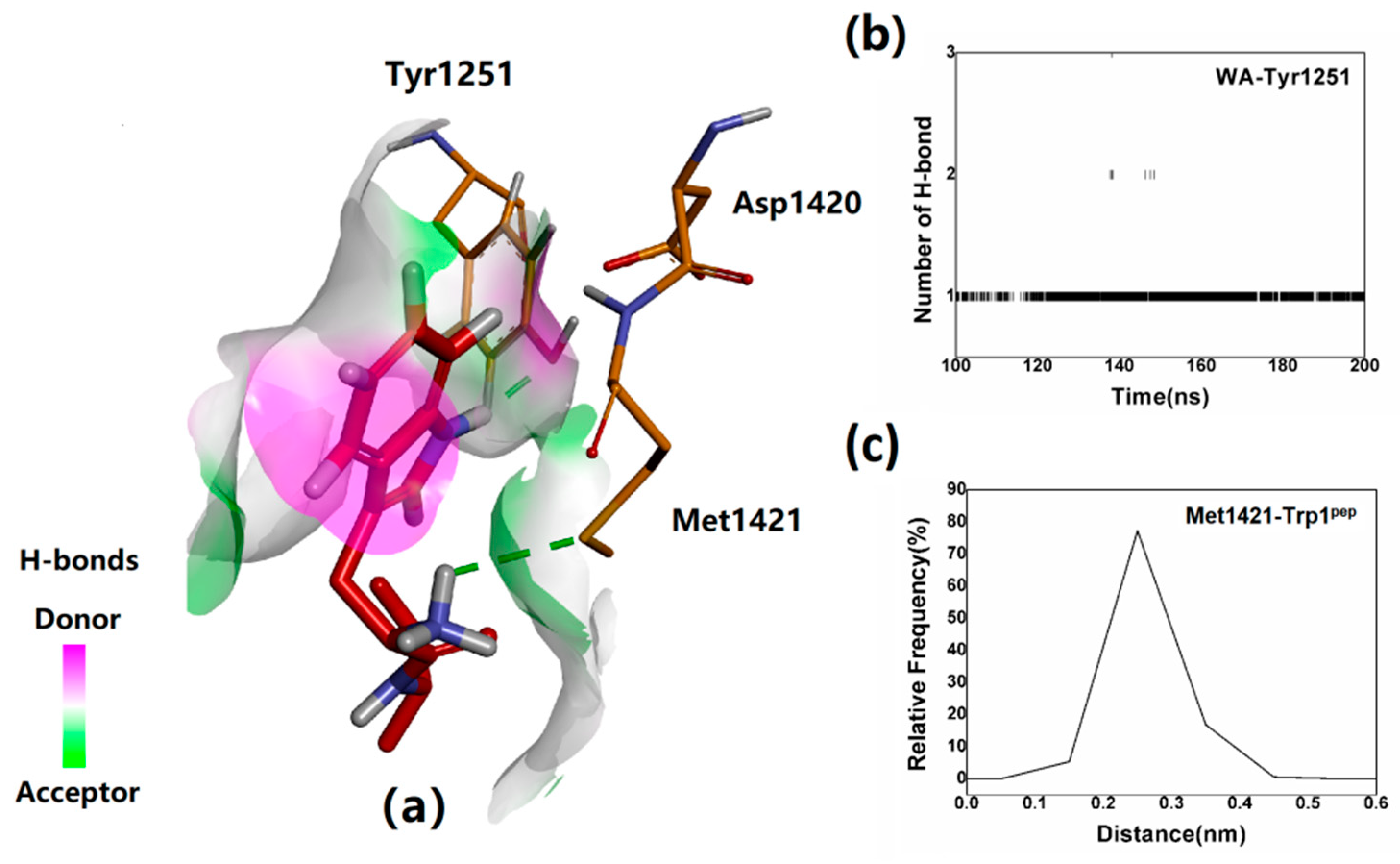
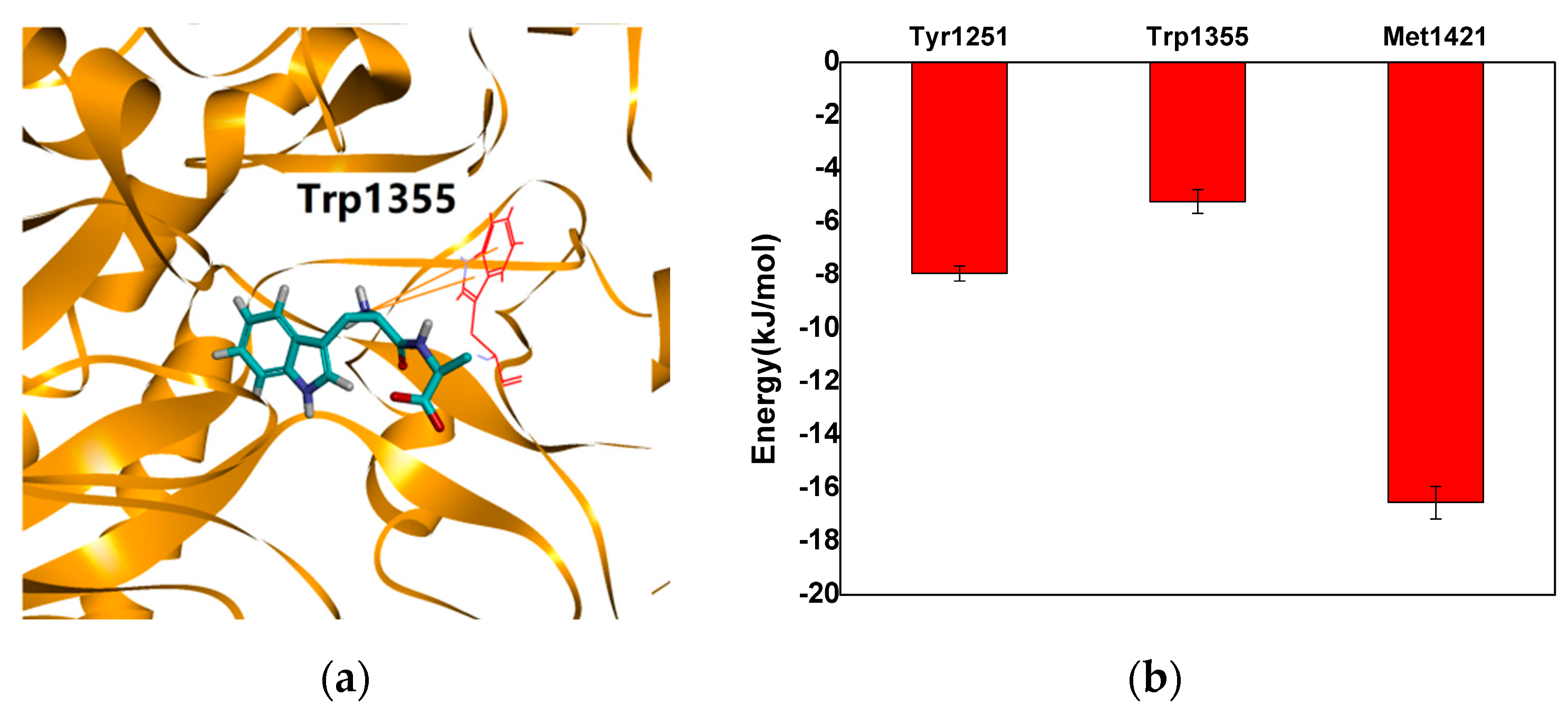
2.4. Verification of the Binding Patterns of Complexes

As the previous results indicate, electrostatic energy provided the dominant contribution in the formation of both MGAM-TW and MGAM-WA complexes; yet, further potential hydrogen bond (H-bond) interactions were explored. The number of H-bond evolutions along the time are illustrated in Figure S3. As shown in Figure S3, the H-bond numbers were 3 ± 2 and 2 ± 1 in the MGAM-TW and MGAM-WA complexes during most of the time. Details of H-bonds from cluster 1 of the MGAM-TW complex are shown in Figure 4 and Table S2. As shown in Figure 4a, two H-bonds could be formed between the carbonyl group of Asp1420 and the amino group of Thr1pep; the probability of these H-bonds was 82.25% (Table S2). Simultaneously, the carboxyl group of Glu1423 could establish a single H-bond with the indole group of Trp2pep; the probability of this H-bond was 95.21% (Table S2). As shown in Figure 4b, H-bonds between TW and Asp1420 and Glu1423 could be in stable states between approximately 100 and 200 ns. Calculated distances between TW and Asp1420 or Glu1423 during the simulations are shown in Figure S4. As shown in Figure S4, the monitored distances could be stabilized at around 0.2 nm during 100 to 200 ns simulation.
In addition to H-bonds, cation-π interactions also played vital roles in maintaining the structures observed in MGAM-TW. As shown in Figure 5a, within structures in MGAM-TW cluster 1, the cation-π interaction could involve Arg1510 and the indole group of Trp2pep. The other cation-π interaction was between the amino group of Thr1pep and the indole group of Trp1355.
To further determine the binding ability between the active-site residues and TW, the energy contributions of the residues mentioned above were calculated. As shown in Figure 5b, the energy contributions of Trp1355, Asp1420, and Glu1423 were −1.95 ± 0.41 kJ/mol, −58.15 ± 0.70 kJ/mol, and −15.32 ± 0.57 kJ/mol in cluster 1 of MGAM-TW, indicating Asp1420 and Glu1423 might be the vital residues for the binding of TW. Notably, the binding energy values of Arg1510 were found to be positive in cluster 1, indicating that the unfavorable energy contributions could be provided by Arg1510, although it could potentially form a cation-π interaction with TW, as shown in Figure 5a.
As shown in Figure 6, the orientation change could be observed on the side chain of Arg1510 during simulation. This change potentially permitted the binding site of MGAM to accommodate an altered conformation of TW. Indeed, an angle deflection could also be observed on the Arg1510 side chain during simulations, as illustrated in Figure S5. During 0 ns to 27 ns, the deflection degree of Arg1510 side chain could reach up to 30° to 70°. According to the further analysis, before 27 ns, Trp2pep could be found in the proximity of the hydrophobic residues, Phe1559 and Phe1560, at the active site, implying that hydrophobic interactions might play a critical role in the peptide binding process, as shown in Figure 6a. However, the amino group of Thr1pep in the current pose was adjacent to the guanidine group of Arg1510, causing the exclusion of positive electric groups. To reduce the binding energy, the TW transferred into another pose after 27 ns, as shown in Figure 6b. The results above indicated that the active center of MGAM could be very permissive towards the binding of flexible peptides.
Subsequently, the binding conformation was also evaluated in cluster 1 of the MGAM-WA complex. As shown in Figure 7a,b, one H-bond was formed between the side chain of Tyr1251 and the indole group of Trp1pep. In addition, a H-bond was also formed between the side chain of Met1421 and the amino group of Trp1pep. It is known that the energy of a H-bond formed with a sulfur atom may be slightly lower; however, even under these circumstances, this H-bond could contribute positively to WA binding. As shown in Figure 7c, the distance between the amino group of Trp1pep and the sulfur atom of Met1421 was approximately 2.60 Å most of the time, which might be advantageous for H-bond formation.
In addition to the H-bonds, cation-π interactions also played a key role in the formation of the MGAM-WA complex. As shown in Figure 8a, a cation-π interaction involving the amino group of Trp1pep and the indole group of Trp1355 was observed in cluster 1. The energy contributions of the residues mentioned above were calculated. As shown in Figure 8b, in cluster 1, the energy contribution of Tyr1251, Trp1355, and Met1421 represented relatively low values at −7.92 ± 0.30 kJ/mol, −5.23 ± 0.44 kJ/mol, and −16.53 ± 0.61 kJ/mol, indicating that the contribution of all the residues mentioned above were positive. Altogether, the free-energy results clearly showed that H-bonds might be much more significant in the formation in MGAM-TW and MGAM-WA complexes.

3. Discussion

The degree of proteolysis is related to the length of the peptide chain. Short peptides are easily absorbed into the metabolic system, and thus their biological activity can be easily maintained [12]. Many short plant peptides have notable hypoglycemic action, due to their ability of α-glucosidase inhibition. Recent work from Gu et al. showed that TW and WA could inhibit α-glucosidase at IC50 22.93 μmol/L and 23.97 μmol/L. α-glucosidase could be a promising target for the development of new therapeutic compounds for the management of diabetes [11]. The C-domain of MGAM is a characteristic α-glucosidase subunit with high enzymatic activity. This study aimed at elucidating the binding interaction between the C-domain of MGAM and two of its natural peptide inhibitors, TW and WA. Exploring the mechanism of how these short peptides interact with the active site of the enzyme is likely to provide valuable clues towards designing new clinically usable inhibitors [12].
The performed structural analysis indicated that the binding of peptide inhibitors at the active site of MGAM might be not rigid absolutely; in particular, the side-chain angle of TW showed a considerable degree of rotation during simulations. Binding energy calculations showed that this rotation could not affect the favorable binding between the peptide and enzyme. The above results indicated that the active center of MGAM might be very permissive to flexible peptides. The two peptides explored in this study have similar structures, with both having large side-chain groups. Although a Trppep is present in both TW and WA, it is located at the opposite terminal of the two peptides. Despite this difference in location, the binding orientation of Trppep remained similar in both complexes.
Acarbose is a pseudo-tetrasaccharide that is composed of an acarviosine group α-(1-4) linked to a maltose. In the crystal structure (PDB ID: 3TOP) [8], the sugar rings 1 and sugar rings 2 of acarbose are the main groups acting with the MGAM. By comparison, the binding positions of the Trppep of TW and WA in the active center were similar to the sugar ring 1 of acarbose in the 3TOP (Figure 9). As shown in Figure 9, the sugar ring 1 of acarbose could bind close to the Asp1526 residue, a previously reported possible acid-base catalytic site [8]. The carboxyl group of Asp1526 could form H-bonds with the -OH and -NH groups of the sugar ring 1 and ring 2. Compared with acarbose, the molecular weights of TW and WA are lower; however, the special binding positions of TW and WA might also give them better inhibitory potentials as shown in Figure 9b,c. As shown in Figure 9b,c, although TW and WA were close to the Asp1526, no significant interactions were found between them and Asp1526. TW and WA have the activity of α-glucosidase inhibition in micromolar range and still need to be optimized to achieve higher inhibitory activity (e.g., in low nanomolar range). The results suggested that a series of derivatives with stronger inhibitory potential based on the dipeptide structures might be designed in future studies. Tryptophane has a unique indole ring structure that possesses more modification sites than other amino acids [23]. For example, based on the structure of WA, the addition of H-bond donors to the indole group of Trp1pep might be benefitial to increase the H-bonds interactions between WA and Asp1526. In addition, following the bioisostere method used in the earlier development of captopril, a marketed inhibitor of the angiotensin-converting enzyme, it could be tried to replace -CH2 of WA-Trp1pep (Figure 9c) with -NH and evaluate the activity of the derivatives in a future study [24].
In the design of future α-glucosidase inhibitors, incorporating aromatic groups and hydrophobic groups may be considered to strengthen the compounds localization at the active site of MGAM. However, the results of binding energy calculations demonstrate that, although aromatic groups may aid the positioning of new inhibitors, H-bonds are likely to remain the most important factor in influencing the affinity of potential drugs to the enzyme. Large numbers of polar residues could be found in the active center of the MGAM. The region consists of H-bond acceptors and donors potentially aiding the binding of ligands. Both the addition of H-bond donors and acceptors should be considered to further stabilize the binding of compounds. More generally, our experience shows that studying binding characteristics between flexible peptides and enzymes may be a helpful tool in predicting how potential ligands may bind to the targeted site of the enzyme.

4. Materials and Methods

4.1. Preparation of Initial Complexes

MGAM was chosen as the preferred model to study the binding conformation of two known inhibitory peptides, TW and WA. The three-dimensional structure of MGAM was obtained from the Research Collaboratory for Structural Bioinformatics Protein Data Bank (RCSB PDB ID: 3top) [8]. All structural elements of the MGAM crystal were retained, but unstructured atoms, molecules, and crystal water were removed for the purposes of the simulations [21]. Peptide sequences were derived from the study of Gu et al. [12].

4.2. Molecular Docking

Flexible docking studies were attempted to explore the binding conformation of peptide inhibitors within the 3D model (PDB ID: 3top) of MGAM using Autodock 4 [25]. Before docking, polar H atoms were added to the MGAM, followed by Gasteiger charge calculation using Autodock tools. The flexible residues were set to contain Asp1157, Tyr1251, Asp1279, Trp1355, Trp1369, Trp1418, Asp1420, Asp1526, Phe1559, Phe1560, and His1584. The PDB file of MGAM was then saved in pdbqt format, ready to be used for docking analysis. TW or WA centered maps were generated using the AutoGrid program with a spacing of 0.375 Å and grid dimensions of 60 × 60 × 60 Å3. Gridbox center was set to coordinates −31.373, 32.061, and 29.534 on the x, y, and z axis respectively. Polar H charges of the Gasteiger-type were assigned, non-polar-H atoms were merged with the carbons, and internal degrees of freedom and torsions were set. For all other parameters, default settings were used [25,26,27]. The lowest energy structure was selected from the most clustered class of docking results as the initial structures for molecular dynamics simulation.

4.3. Molecular Dynamics Simulation

The complex systems were subjected to molecular dynamics simulation in periodic boundary condition using the Gromacs 5.1.4 software package with a SPC (simple point charge) water model [28,29,30]. The simulations were performed under neutral conditions, and the protonation states of the ionizable residues were assigned using the H++ tools [31]. The Gromos 54 A7 force field was applied to describe both the peptides and MGAM [32]. The information on molecule systems is shown in Table S3. To keep the systems at an electrically neutral state, 28 NA+ were added to randomly replace water molecules. First, energies of the complex systems were relaxed with steepest-descent energy minimization to eliminate steric clashes or incorrect geometry. Thereafter, 100 ps NVT (constant number of particles, volume, and temperature) and NPT (constant number of particles, pressure, and temperature) were alternately operated with position restraints on the peptides and MGAM to make the relaxation of the solvent molecules in two phases [33,34]. The solvent molecules were equilibrated with the fixed protein at 310 K, and the initial velocities were chosen from a Maxwellian distribution. Subsequently, MGAM and the peptides were relaxed in a stepwise fashion and heated to 310 K. The long-range electrostatic interactions were described with the particle mesh Ewald algorithm, with an interpolation order of 4, a grid spacing of 0.16 nm, and the Coulomb cutoff distance of 1.0 nm [35]. Temperature and pressure coupling types were set with V-rescale and Parrinello–Rahman, respectively [36]. In the NVT ensemble, the temperature of the systems reached a plateau at the desired value (reference temperature = 310 K; time constant = 0.1 ps). In addition, the equilibration of pressure (reference pressure = 1.0 bar; time constant = 2.0 ps) was performed under the NPT ensemble. The equilibrated ensembles were subjected to molecular dynamics simulations conducted for 200 ns employing the LINear Constraint Solver (LINCS) and SETTLE [37,38] algorithm for bond constraints and geometry of water molecules. The 200 ns molecular dynamics simulations were initiated for collecting data with a time step of 2 fs, and coordinates were saved every 2 ps [39,40].

4.4. Binding Energy Calculations

The molecular mechanics Poisson–Boltzmann surface area method (MM-PBSA) was applied as a scoring function in computational drug design to estimate free energies in biomolecular interactions [41,42,43]. Using the command “gmx mmpbsa,” the binding free energy of a complex was calculated from 200 snapshots extracted from the 200 ns MD trajectory [14,15,44] Furthermore, the binding energy was decomposed on a per-residue basis to analyze the individual energy contributions of each residue to the MGAM-TW/WA interaction.
The binding free energy of a protein–ligand complex in a solvent can be obtained by [21,42]:
ΔGbind = ΔGcomplex − [ΔGprotein + ΔGlig]
In the formula above, the ΔGcomplex is the total free energy of the complex, and the ΔGprotein and ΔGlig represent the energies of the isolate protein and ligand, respectively.
The MM-PBSA method can be conceptually summarized as:
ΔGbind = ΔEgas + ΔGsol = ΔEvdw + ΔEele + ΔGpolar + ΔGnonpolar
∆Egas is the average molecular mechanics potential energy in a vacuum (i.e., gas-phase energy), which includes van der Waals (∆Evdw) and electrostatic (∆Eele) interactions; ∆Gsolv denotes contribution to the solvation free energy that consists of polar solvation (∆Gpolar) and nonpolar solvation (∆Gnonpolar) energies [21,42]. Binding patterns were plotted using Discovery Studio [45].

5. Conclusions

The prevention and treatment of diabetes is a critical area of medical research. As an effective drug target, MGAM provides new opportunities for the treatment of diabetes. This study applied a series of approaches to explore the binding mechanism between MGAM and two of its known inhibitors, TW and WA. The results indicated that TW or WA could regulate their conformation according to the changes in the shape of the active center, ensuring effective binding. It is shown that TW and WA could interact with MGAM through the formation of H-bonds, hydrophobic interactions, and cation-π, with electrostatic interactions providing most of the binding energy. This may be the consequence of the active center of MGAM being rich in amino acid residues with positively charged or cyclic side chains. The binding positions of TW and WA are close to the residue Asp1526, a previously reported possible acid-base catalytic residue, thus this binding may favor the inhibition of the enzyme. It is hoped that the results of the presented work will provide clues in the development of an efficient new MGAM inhibitor.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/catal12050522/s1, Figure S1: The comparison between the re-docked acarbose (blue) and the reference for the crystal structure (yellow). Figure S2: The binding energy distribution of MGAM-TW and MGAM-WA. Figure S3: The number of H-bonds evolution along time (a) MGAM-TW (b) MGAM-WA. Figure S4: The distances between TW and Asp1420/Glu1423 in MGAM-TW complex. Figure S5: The angle deflection of Arg1510 side chain during the simulations in MGAM-TW complex; Table S1: The cluster size of WA in cluster 7 to cluster 12. Table S2: The probability of H-bonds in the MGAM-TW complex. Table S3: Molecular systems.

Author Contributions

Conceptualization, S.G. and Y.S.; data curation, S.G.; formal analysis, S.G. and H.L.; investigation, S.G., X.H., Z.L., X.X., Y.C., Z.C., S.Z., S.C., and H.L.; methodology, S.G. and S.W.; resources, H.L.; writing—original draft, S.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Youth Program of the National Natural Science Foundation of China, grant number 31901062; the National Natural Science Foundation of China, grant number: 31770996; the scientific research planning project of the 13th five-year plan of Jilin Provincial Department of Education, grant number JJKH20200172KJ; Jilin Province Science and Technology Development Projects, grant number 20190303056SF and 20210204197YY; and Changchun City Science and Technology Development Projects, grant number 21ZY15.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cardullo, N.; Muccilli, V.; Pulvirenti, L.; Cornu, A.; Tringali, C. C-glucosidic ellagitannins and galloylated glucoses as potential functional food ingredients with anti-diabetic properties: A study of α-glucosidase and α-amylase inhibition. Food Chem. 2019, 313, 126099. [Google Scholar] [CrossRef] [PubMed]
  2. Lordan, S.; Smyth, T.J.; Soler-Vila, A.; Stanton, C.; Ross, R.P. The α-amylase and α-glucosidase inhibitory effects of Irish seaweed extracts. Food Chem. 2013, 141, 2170–2176. [Google Scholar] [CrossRef] [PubMed]
  3. Etsassala, N.G.E.R.; Badmus, J.A.; Marnewick, J.L.; Iwuoha, E.I.; Nchu, F.; Hussein, A.A. Alpha-Glucosidase and Alpha-Amylase Inhibitory Activities, Molecular Docking, and Antioxidant Capacities of Salvia aurita Constituents. Antioxidants 2020, 9, 1149. [Google Scholar] [CrossRef] [PubMed]
  4. Gong, L.X.; Feng, D.N.; Wang, T.X.; Ren, Y.Q.; Liu, Y.L.; Wang, J. Inhibitors of α-amylase and α-glucosidase: Potential linkage for whole cereal foods on prevention of hyperglycemia. Food Sci. Nutr. 2020, 8, 6320–6337. [Google Scholar] [CrossRef]
  5. Brás, N.; Santos-Martins, D.; Fernandes, P.A.; Ramos, M.J. Mechanistic Pathway on Human α-Glucosidase Maltase-Glucoamylase Unveiled by QM/MM Calculations. J. Phys. Chem. B 2018, 122, 3889–3899. [Google Scholar] [CrossRef]
  6. Kawakami, K.; Li, P.; Uraji, M.; Hatanaka, T.; Ito, H. Inhibitory effects of pomegranate extracts on recombinant human maltase–glucoamylase. J. Food Sci. 2015, 79, H1848–H1853. [Google Scholar] [CrossRef]
  7. Gani, R.S.; Kudva, A.K.; Timanagouda, K.; Raghuveer Raghu, S.V. Synthesis of novel 5-(2,5-bis (2,2,2-trifluoroethoxy) phenyl)-1,3,4-oxadiazole-2-thiol derivatives as potential glucosidase inhibitors. Bioorganic Chem. 2021, 114, 105046. [Google Scholar] [CrossRef]
  8. Ren, L.; Qin, X.; Cao, X.; Wang, L.; Bai, F.; Gang, B.; Shen, Y. Structural insight into substrate specificity of human intestinal maltase-glucoamylase. Protein Cell 2011, 2, 827. [Google Scholar] [CrossRef] [Green Version]
  9. Lankatillake, C.; Luo, S.; Flavel, M.; Lenon, G.B.; Dias, D.A. Screening natural product extracts for potential enzyme inhibitors: Protocols, and the standardisation of the usage of blanks in α-amylase, α-glucosidase and lipase assays. Plant Methods 2021, 17, 3. [Google Scholar] [CrossRef]
  10. Alam, F.; Shafique, Z.; Amjad, S.T.; Hassan, M.H. Enzymes inhibitors from natural sources with antidiabetic activity: A review. Phytother. Res. 2019, 33, 41–54. [Google Scholar] [CrossRef] [Green Version]
  11. Yavari, A.; Mohammadi-Khanaposhtani, M.; Moradi, S.; Bahadorikhalili, S.; Hajimiri, M.H. α-Glucosidase and α-amylase inhibition, molecular modeling and pharmacokinetic studies of new quinazolinone-1,2,3-triazole-acetamide derivatives. Med. Chem. Res. 2021, 30, 702–711. [Google Scholar] [CrossRef]
  12. Gu, X.; Cui, J.; Li, D.; Wang, J.F.; Wang, J.Z. Separation, Purification, and Identification of α-Glucosidase Inhibitory Peptides from Apricot Kernel Protein. J. Chin. Cereals Oils Assoc. 2016, 31, 116–121. [Google Scholar]
  13. Sumaryada, T.; Arwansyah Roslia, A.W.; Ambarsari, L.; Kartono, A. Molecular docking simulation of mangostin derivatives and curcuminoid on maltase-glucoamylase target for searching anti-diabetes drug candidates. In Proceedings of the 2016 1st International Conference on Biomedical Engineering (IBIOMED), Yogyakarta, Indonesia, 5–6 October 2016. [Google Scholar]
  14. Qian, M.; Shan, Y.; Guan, S.; Zhang, H.; Wang, S.; Han, W.W. Structural Basis of Fullerene Derivatives as Novel Potent Inhibitors of Protein Tyrosine Phosphatase 1B: Insight into the Inhibitory Mechanism through Molecular Modeling Studies. J. Chem. Inf. Modeling 2016, 56, 2024–2034. [Google Scholar] [CrossRef] [PubMed]
  15. Sinosh, S.; Dharshini, G.; Shweta, C.; Priya, K.; Akshay, U.; Aditi, G.M.; Vidya, N. Structural and molecular basis of the interaction mechanism of selected drugs towards multiple targets of SARS-CoV-2 by molecular docking and dynamic simulation studies- deciphering the scope of repurposed drugs. Comput. Biol. Med. 2020, 126, 104054. [Google Scholar] [CrossRef]
  16. Saddique, F.A.; Ahmad, M.; Ashfaq, U.A.; Ahmad, M.N.; Aslam, S. Alpha-glucosidase inhibition and molecular docking studies of 1,2-benzothiazine 1,1-dioxide based carbohydrazides. Pak. J. Pharm. Sci. 2019, 32 (Suppl. S6), 2829–2834. [Google Scholar]
  17. Xie, L.; Zhang, T.; Karrar, E.; Zheng, L.; Xie, D.; Jin, J.; Chang, M.; Wang, X.; Jin, Q. Insights into an α-glucosidase inhibitory profile of 4,4-dimethylsterols by multispectral techniques and molecular docking. J. Agric. Food Chem. 2021, 69, 15252–15260. [Google Scholar] [CrossRef]
  18. Kiruthiga, N.; Alagumuthu, M.; Selvinthanuja, C.; Srinivasan, K.; Sivakumar, T. Molecular Modelling, Synthesis and Evaluation of Flavone and Flavanone Scaffolds as Anti-inflammatory Agents. Anti-Inflamm. Anti-Allergy Agents Med. Chem. 2021, 20, 20–38. [Google Scholar] [CrossRef]
  19. Zeb, A.; Ali, S.S.; Azad, A.K.; Safdar, M.; Wei, D. Genome-wide screening of vaccine targets prioritization and reverse vaccinology aided design of peptides vaccine to enforce humoral immune response against Campylobacter jejuni. Comput. Biol. Med. 2021, 133, 104412. [Google Scholar] [CrossRef]
  20. Yang, Y.; Wang, X.; Gao, Y.; Niu, X. Insight into the Dual Inhibition Mechanism of Corilagin against MRSA Serine/Threonine Phosphatase (Stp1) by Molecular Modeling. ACS Omega 2020, 5, 32959–32968. [Google Scholar] [CrossRef]
  21. Guan, S.S.; Zhu, K.T.; Dong, Y.J.; Li, H.; Shan, Y.M. Exploration of Binding Mechanism of a Potential Streptococcus pneumoniae Neuraminidase Inhibitor from Herbaceous Plants by Molecular Simulation. Int. J. Mol. Sci. 2020, 21, 1003. [Google Scholar] [CrossRef] [Green Version]
  22. Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; Van Gunsteren, W.F.; Mark, A.E. Peptide Folding: When Simulation Meets Experiment. Angenw. Chem. Int. Ed. 2010, 38, 236–240. [Google Scholar] [CrossRef]
  23. Xu, F.; Deng, Z.X.; Lin, S.J. Tryptophan, an important starting material in biosynthesis of microbial natural products. Microbiol. China 2013, 40, 1796–1809. [Google Scholar]
  24. Patchett, A.A.; Harris, E.; Tristram, E.W.; Wyvratt, M.J.; Wu, M.T.; Taub, D.; Peterson, E.R.; Ikeler, T.J.; ten Broeke, T.; Payne, L.G.; et al. A new class of angiotensin-converting enzyme inhibitors. Nature 1980, 288, 280–283. [Google Scholar] [CrossRef] [PubMed]
  25. Morris, G. Automated docking using a Lamarckian genetic algorithm and empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. [Google Scholar] [CrossRef] [Green Version]
  26. Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [Green Version]
  27. Mothay, D.; Ramesh, K.V. Binding site analysis of potential protease inhibitors of COVID-19 using AutoDock. VirusDisease 2020, 31, 194–199. [Google Scholar] [CrossRef]
  28. Hess, B.; Van, D. Hydration thermodynamic properties of amino acid analogues: A systematic comparison of biomolecular force fields and water models. J. Phys. Chem. B 2006, 110, 17616–17626. [Google Scholar] [CrossRef]
  29. Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
  30. Safarizadeh, H.; Garkani-Nejad, Z. Molecular docking, molecular dynamics simulations and QSAR studies on some of 2-arylethenylquinoline derivatives for inhibition of Alzheimer’s amyloid-beta aggregation: Insight into mechanism of interactions and parameters for design of new inhibitors. J. Mol. Graph. Model. 2019, 87, 129–143. [Google Scholar] [CrossRef]
  31. Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulation. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [Green Version]
  32. Bachmann, S.J.; Van Gunsteren, W.F. Structural and energetic effects of the use of polarisable water to solvate proteins. Mol. Phys. 2015, 113, 2815–2828. [Google Scholar] [CrossRef]
  33. Pan, Y.; Lu, Z.; Li, C.; Qi, R.; Han, W. Molecular Dockings and Molecular Dynamics Simulations Reveal the Potency of Different Inhibitors against Xanthine Oxidase. ACS Omega 2021, 6, 11639–11649. [Google Scholar] [CrossRef]
  34. Jingwen, E.; Liu, Y.; Guan, S.; Luo, Z.; Han, F.; Han, W.; Wang, S.; Zhang, H. How Different Substitution Positions of F, Cl Atoms in Benzene Ring of 5-Methylpyrimidine Pyridine Derivatives Affect the Inhibition Ability of EGFRL858R/T790M/C797S Inhibitors: A Molecular Dynamics Simulation Study. Molecules 2020, 25, 895. [Google Scholar]
  35. Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
  36. Berendsen, H.J.C.P.; Postma, J.; Gunsteren, W.; Dinola, A.D.; Haak, J.R. Molecular-Dynamics with Coupling to An External Bath. J. Chem. Phys. 1984, 81, 3684. [Google Scholar] [CrossRef] [Green Version]
  37. Rampogu, S.; Baek, A.; Park, C.; Son, M.; Parate, S.; Parameswaran, S.; Park, Y.; Shaik, B.; Kim, J.H.; Park, S.J.; et al. Discovery of Small Molecules That Target Vascular Endothelial Growth Factor Receptor-2 Signalling Pathway Employing Molecular Modelling Studies. Cells 2019, 8, 269. [Google Scholar] [CrossRef] [Green Version]
  38. Pei, P.; Qin, H.; Chen, J.; Wang, F.; He, C.; He, S.; Hong, B.; Liu, K.; Qiao, R.; Fan, H.; et al. Computational design of ultrashort peptide inhibitors of the receptor-binding domain of the SARS-CoV-2 S protein. Brief. Bioinform. 2021, 22, bbab243. [Google Scholar] [CrossRef]
  39. Sadr, A.S.; Eslahchi, C.; Ghassempour, A.; Kiaei, M. In silico studies reveal structural deviations of mutant profilin-1 and interaction with riluzole and edaravone in amyotrophic lateral sclerosis. Sci. Rep. 2021, 11, 6849. [Google Scholar] [CrossRef]
  40. Qian, M.; Guan, S.; Shan, Y.; Zhang, H.; Wang, S. Structural and molecular basis of cellulase Cel48F by computational modeling: Insight into catalytic and product release mechanism. J. Struct. Biol. 2016, 194, 347–356. [Google Scholar] [CrossRef]
  41. Wang, M.; Wong, C.F. Rank-ordering protein-ligand binding affinity by a quantum mechanics/molecular mechanics/Poisson-Boltzmann-surface area model. J. Chem. Phys. 2007, 126, 01B801. [Google Scholar] [CrossRef]
  42. Kumari, R.; Kumar, R.; Lynn, A. g_mmpbsa—A GROMACS tool for high-throughput MM-PBSA calculations. J. Chem. Inf. Modeling 2014, 54, 1951–1962. [Google Scholar] [CrossRef]
  43. Tian, Y.; Shen, S.; Gu, L.; Zhou, J.; Zheng, X. Computer-Aided Design of Glucoside Brain-Targeted Molecules Based on 4PYP. J. Mol. Graph. Model. 2020, 103, 107819. [Google Scholar] [CrossRef]
  44. Adelusi, T.I.; Abdul-Hammed, M.; Idris, M.O.; Kehinde, O.Q.; Kolawole, O.E. Exploring the inhibitory potentials of Momordica charantia bioactive compounds against Keap1-Kelch protein using computational approaches. Silico Pharmacol. 2021, 9, 39. [Google Scholar] [CrossRef]
  45. Discovery Studio; Release 2020; Accelrys Inc.[Z.]: San Diego, CA, USA, 2020.
Catalysts 12 00522 g001 550
Figure 1. (a) Rg plots and (b) RMSD plots of MGAM-TW and MGAM-WA complexes during 200 ns molecular dynamics simulations.
Figure 1. (a) Rg plots and (b) RMSD plots of MGAM-TW and MGAM-WA complexes during 200 ns molecular dynamics simulations.
Catalysts 12 00522 g001
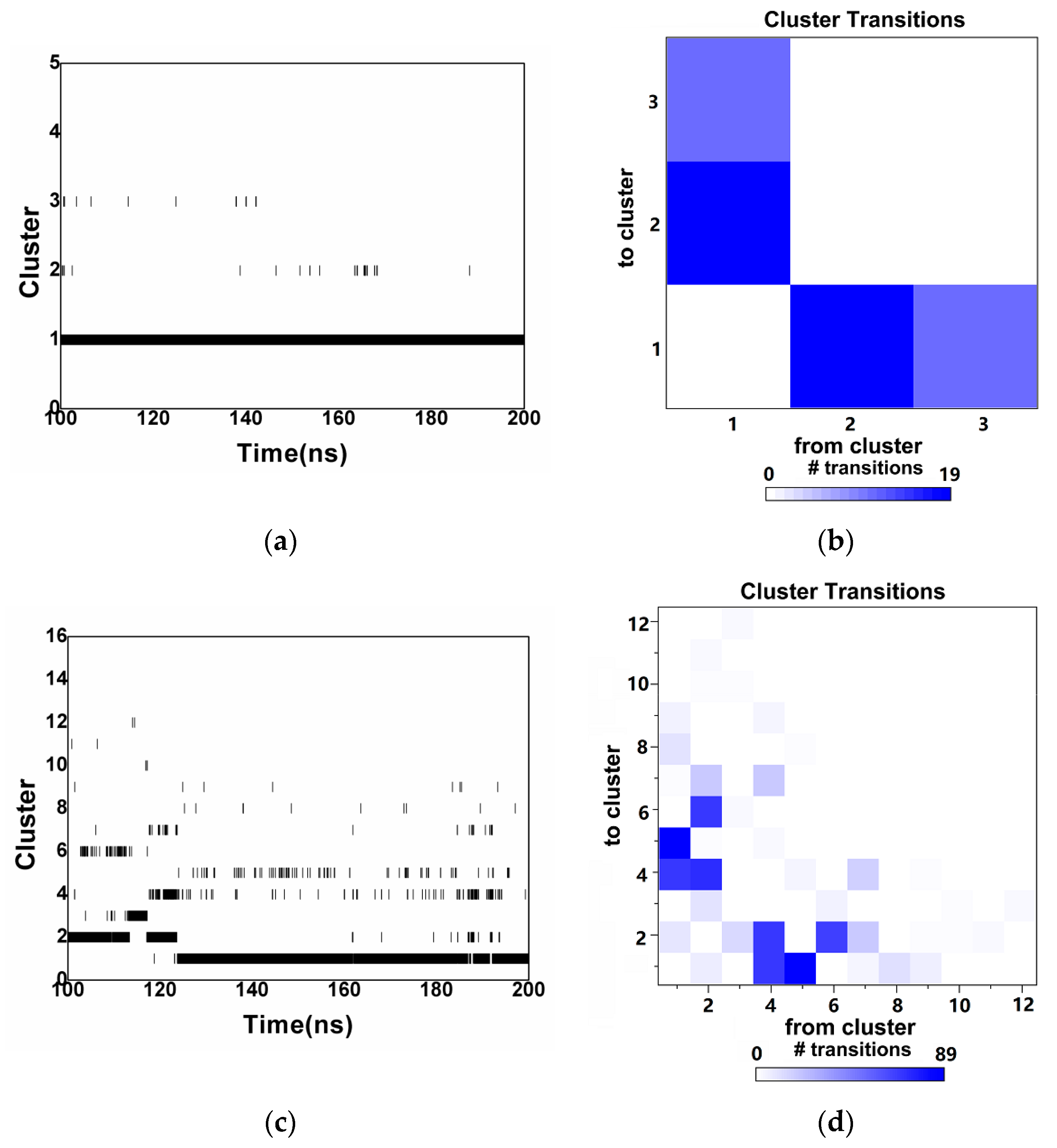
Catalysts 12 00522 g002 550
Figure 2. (a) The cluster distributions of MGAM-TW, (b) the cluster transitions of MGAM-TW, (c) the cluster distributions of MGAM-WA, and (d) the cluster transitions of MGAM-WA.
Figure 2. (a) The cluster distributions of MGAM-TW, (b) the cluster transitions of MGAM-TW, (c) the cluster distributions of MGAM-WA, and (d) the cluster transitions of MGAM-WA.
Catalysts 12 00522 g002
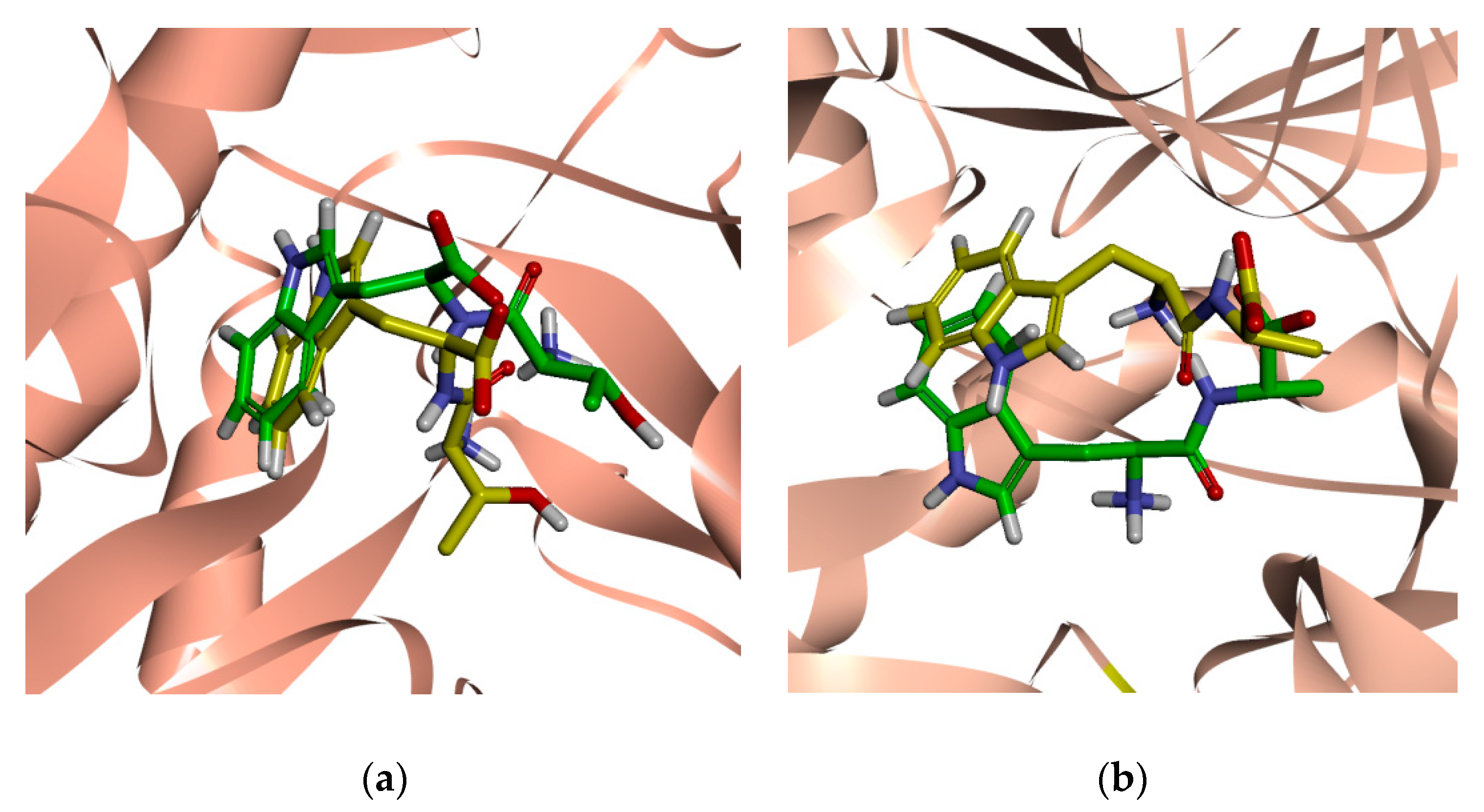
Catalysts 12 00522 g003 550
Figure 3. (a) The cartoon mode of the representative structure of cluster 1 (yellow) and cluster 2 (green) from MGAM-TW complex and (b) the cartoon mode of the representative structure of cluster 1 (yellow) and cluster 2 (green) from MGAM-WA complex.
Figure 3. (a) The cartoon mode of the representative structure of cluster 1 (yellow) and cluster 2 (green) from MGAM-TW complex and (b) the cartoon mode of the representative structure of cluster 1 (yellow) and cluster 2 (green) from MGAM-WA complex.
Catalysts 12 00522 g003
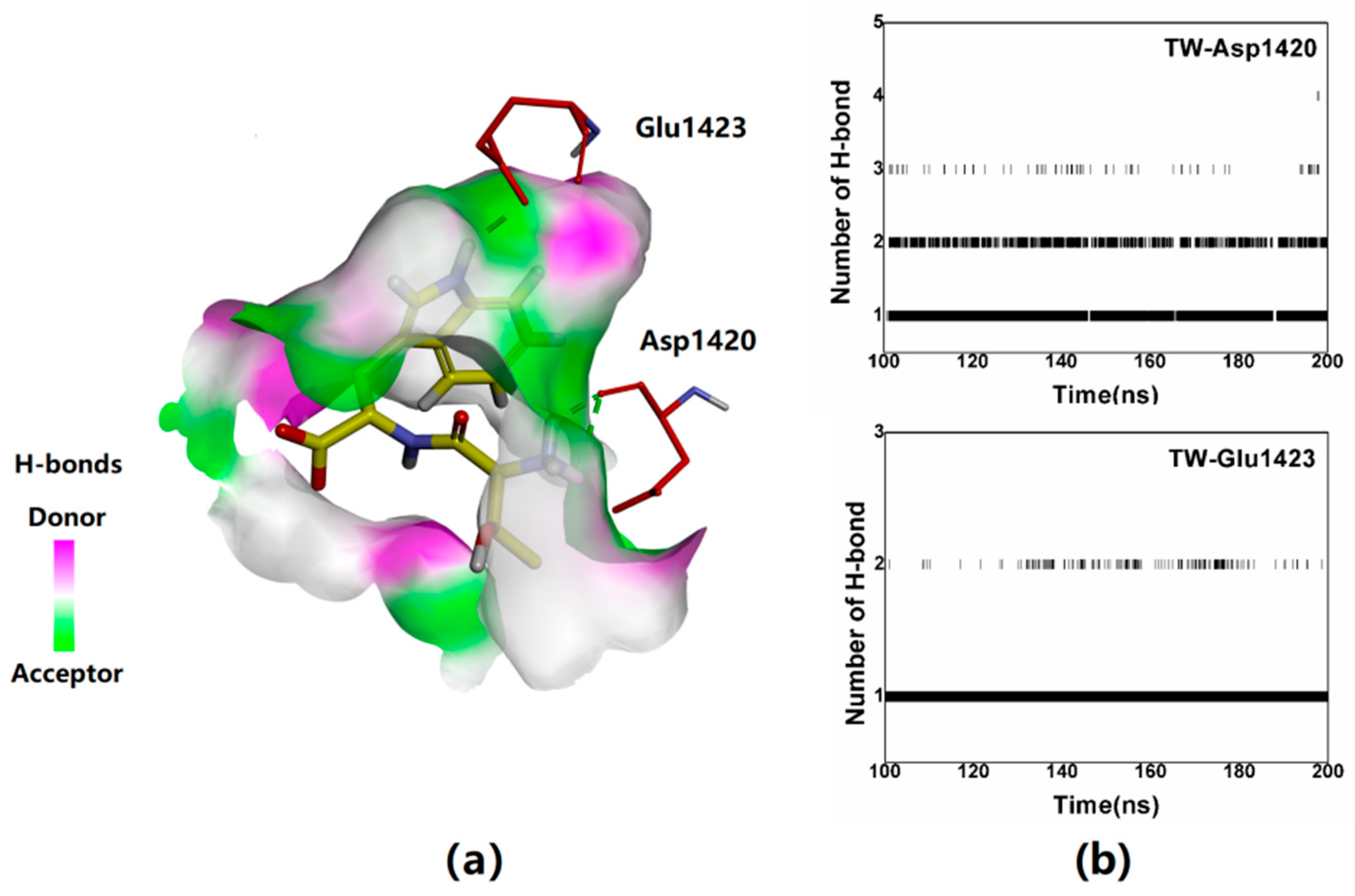
Catalysts 12 00522 g004 550
Figure 4. (a) Predicted detailed binding modes of MGAM-TW complex from cluster 1 and (b) the number of H-bonds between TW and Asp1420/Glu1423 during 100~200 ns simulation.
Figure 4. (a) Predicted detailed binding modes of MGAM-TW complex from cluster 1 and (b) the number of H-bonds between TW and Asp1420/Glu1423 during 100~200 ns simulation.
Catalysts 12 00522 g004
Catalysts 12 00522 g005 550
Figure 5. (a) The cation-π interaction of cluster 1 from MGAM-TW and (b) the energy contributions of the vital residues of cluster 1 from MGAM-TW. The errors marked on the graph represent the absolute errors of the data.
Figure 5. (a) The cation-π interaction of cluster 1 from MGAM-TW and (b) the energy contributions of the vital residues of cluster 1 from MGAM-TW. The errors marked on the graph represent the absolute errors of the data.
Catalysts 12 00522 g005
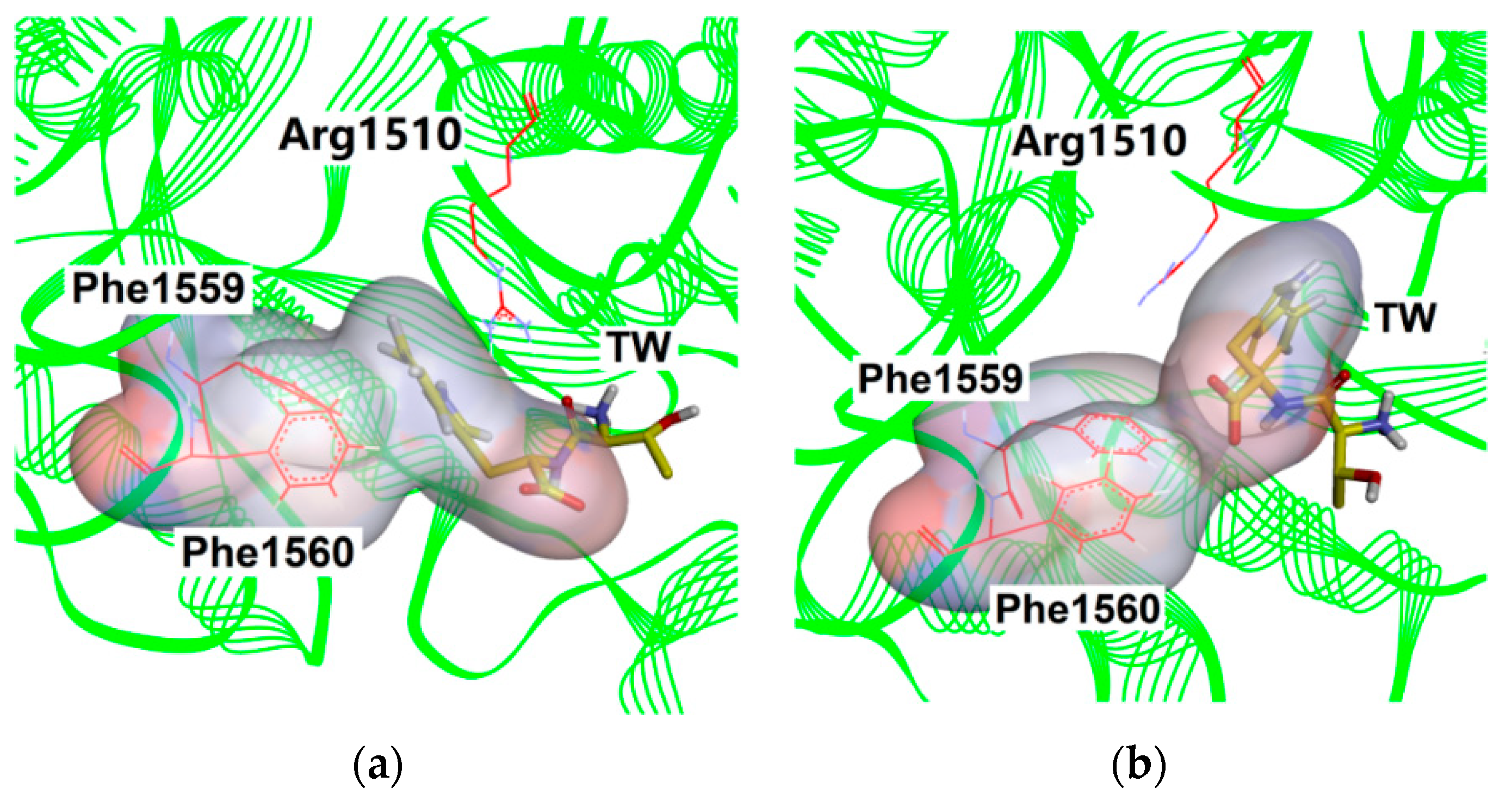
Catalysts 12 00522 g006 550
Figure 6. (a) Schematic diagram of the hydrophobic regions of MGAM-TW before 27 ns and (b) schematic diagram of the hydrophobic regions of MGAM-TW after 27 ns.
Figure 6. (a) Schematic diagram of the hydrophobic regions of MGAM-TW before 27 ns and (b) schematic diagram of the hydrophobic regions of MGAM-TW after 27 ns.
Catalysts 12 00522 g006
Catalysts 12 00522 g007 550
Figure 7. (a) The H-bonds mode of MGAM-WA from cluster 1, (b) the number of H-bonds between WA and Asp1420, and (c) the distance distribution between the amino group of Trp1pep and the sulfur atoms of Met1421.
Figure 7. (a) The H-bonds mode of MGAM-WA from cluster 1, (b) the number of H-bonds between WA and Asp1420, and (c) the distance distribution between the amino group of Trp1pep and the sulfur atoms of Met1421.
Catalysts 12 00522 g007
Catalysts 12 00522 g008 550
Figure 8. (a) The cation-π interaction of cluster 1 from MGAM-WA and (b) the energy contributions of the vital residues of cluster 1 from MGAM-WA.
Figure 8. (a) The cation-π interaction of cluster 1 from MGAM-WA and (b) the energy contributions of the vital residues of cluster 1 from MGAM-WA.
Catalysts 12 00522 g008
Catalysts 12 00522 g009 550
Figure 9. (a) The binding pose of acarbose at the active site of MGAM (blue: sugar ring 1 and ring 2; yellow: sugar ring 3 and ring 4), (b) the binding pose of TW at the active site of MGAM and (c) the binding pose of WA at the active site of MGAM.
Figure 9. (a) The binding pose of acarbose at the active site of MGAM (blue: sugar ring 1 and ring 2; yellow: sugar ring 3 and ring 4), (b) the binding pose of TW at the active site of MGAM and (c) the binding pose of WA at the active site of MGAM.
Catalysts 12 00522 g009
Table
Table 1. The cluster size and the representative conformations of TW.
Table 1. The cluster size and the representative conformations of TW.
ClusterSizePercentageConformation
1995799.56% Catalysts 12 00522 i001
2320.32% Catalysts 12 00522 i002
3120.12% Catalysts 12 00522 i003
Table
Table 2. The cluster size and the representative conformations of WA collected in the first six clusters.
Table 2. The cluster size and the representative conformations of WA collected in the first six clusters.
ClusterSizePercentageConformation
1721372.12% Catalysts 12 00522 i004
2183418.34% 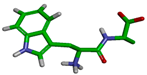Catalysts 12 00522 i005
33963.96% 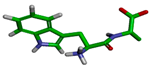Catalysts 12 00522 i006
42552.55% 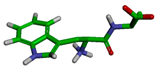Catalysts 12 00522 i007
51071.07% 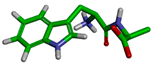Catalysts 12 00522 i008
61051.05% Catalysts 12 00522 i009
Table
Table 3. Energy components of the MGAM-TW complex.
Table 3. Energy components of the MGAM-TW complex.
Energy ComponentsEnergy of Cluster 1 (kJ/mol)
Van der Waals energy−106.66 ± 12.52
Electrostatic energy−495.18 ± 69.46
Polar solvation energy386.41 ± 42.82
SASA energy−14.49 ± 0.89
Binding energy−229.93 ± 38.66
Table
Table 4. Energy components of the MGAM-WA complex.
Table 4. Energy components of the MGAM-WA complex.
Energy ComponentsEnergy of Cluster 1 (kJ/mol)
Van der Waals energy−100.78 ± 10.06
Electrostatic energy−250.50 ± 55.65
Polar solvation energy251.95 ± 35.69
SASA energy−13.22 ± 1.04
Binding energy−112.53 ± 38.68
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Guan, S.; Han, X.; Li, Z.; Xu, X.; Cui, Y.; Chen, Z.; Zhang, S.; Chen, S.; Shan, Y.; Wang, S.; et al. Exploration of the Interactions between Maltase–Glucoamylase and Its Potential Peptide Inhibitors by Molecular Dynamics Simulation. Catalysts 2022, 12, 522. https://doi.org/10.3390/catal12050522

AMA Style

Guan S, Han X, Li Z, Xu X, Cui Y, Chen Z, Zhang S, Chen S, Shan Y, Wang S, et al. Exploration of the Interactions between Maltase–Glucoamylase and Its Potential Peptide Inhibitors by Molecular Dynamics Simulation. Catalysts. 2022; 12(5):522. https://doi.org/10.3390/catal12050522

Chicago/Turabian Style

Guan, Shanshan, Xu Han, Zhan Li, Xifei Xu, Yongran Cui, Zhiwen Chen, Shuming Zhang, Shi Chen, Yaming Shan, Song Wang, and et al. 2022. "Exploration of the Interactions between Maltase–Glucoamylase and Its Potential Peptide Inhibitors by Molecular Dynamics Simulation" Catalysts 12, no. 5: 522. https://doi.org/10.3390/catal12050522

APA Style

Guan, S., Han, X., Li, Z., Xu, X., Cui, Y., Chen, Z., Zhang, S., Chen, S., Shan, Y., Wang, S., & Li, H. (2022). Exploration of the Interactions between Maltase–Glucoamylase and Its Potential Peptide Inhibitors by Molecular Dynamics Simulation. Catalysts, 12(5), 522. https://doi.org/10.3390/catal12050522

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop