Next Article in Journal
An In-Depth Exploration of the Electrochemical Oxygen Reduction Reaction (ORR) Phenomenon on Carbon-Based Catalysts in Alkaline and Acidic Mediums
Next Article in Special Issue
Revealing the Synergetic Effects between Reactants in Oxidative Coupling of Methane on Stepped MgO(100) Catalyst
Previous Article in Journal
Mechanistic Details of the Sharpless Epoxidation of Allylic Alcohols—A Combined URVA and Local Mode Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 12
Issue 7
10.3390/catal12070790
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

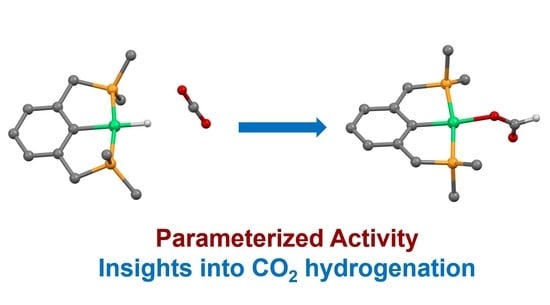
Insights into the Capture of CO2 by Nickel Hydride Complexes

by
Min Zhang
1,
Xiaoqing Liang
1,
Yaozheng Wang
2,
Hongyu Yang
3 and
Guangchao Liang
3,*
1
Department of Pharmacy, School of Medicine, Xi’an International University, Xi’an 710077, China
2
College of Information Management, Minnan University of Science and Technology, Quanzhou 362700, China
3
Academy of Advanced Interdisciplinary Research, Xidian University, Xi’an 710071, China
*
Author to whom correspondence should be addressed.
Catalysts 2022, 12(7), 790; https://doi.org/10.3390/catal12070790
Submission received: 24 June 2022 / Revised: 13 July 2022 / Accepted: 14 July 2022 / Published: 19 July 2022
(This article belongs to the Special Issue Computational Insights into Small Molecule Activation)
Browse Figures
Versions Notes

Abstract

:
As a desired feedstock for sustainable energy source and for chemical synthesis, the capture and utilization of CO2 have attracted chemists’ continuous efforts. The homogeneous CO2 insertion into a nickel hydride complex to generate formate provides insight into the role of hydrogen as an active hydride form in the hydrogenation of CO2, which serves as a practicable approach for CO2 utilization. To parameterize the activities and to model the structure–activity relationship in the CO2 insertion into nickel hydride, the comprehensive mechanism of CO2 insertion into a series of square planar transition metal hydride (TM–H, TM = Ni, Pd, and Co) complexes was investigated using density functional theory (DFT) computations. The stepwise pathway with the TM-(H)-formate intermediate for the CO2 insertion into all seven square planar transition metal hydride (TM–H) complexes was observed. The overall rate-determining step (RDS) was the nucleophilic attraction of the terminal O atom on the Ni center in Ni-(H)-formate to form Ni-(O)-(exo)formate. The charge of the Ni atom in the axially vacant [Ni]+ complex was demonstrated as the dominant factor in CO2 insertion, which had an excellent linear correction (R2 = 0.967) with the Gibbs barrier (ΔG‡) of the RDS. The parameterized activities and modeled structure–activity relationship provided here light the way to the design of a more efficient Ni–H complex in the capture and utilization of CO2.

Graphical Abstract

1. Introduction

The utilization of CO2 as the sustainable carbon feedstock for energy source and for chemical synthesis has been demonstrated as a promising strategy in solving the environmental crisis caused by the consumption of fossil fuels [1,2,3,4]. The well-developed approaches for the capture and utilization of CO2 including the reduction of CO2 [5,6] and hydrogenation of CO2 [7,8,9] have been established. The transition metal (TM) complex-catalyzed homogeneous hydrogenation of CO2 to formate usually involves (1) activation of a H2 molecule to form the hydride species, (2) CO2 insertion into the TM–H bond, and (3) the release of formate and regeneration of the catalyst. As a critical step in the catalytic hydrogenation of CO2 to formate, the capture of CO2 by transition metal hydride complex (TM–H) via the CO2 insertion into the transition metal hydride bond (TM–H bond) has attracted chemists’ continued attention, and studies on the CO2 insertion into the TM–H bond have served as a model to understand the role of hydrogen activated as hydride in the hydrogenation of CO2 [9,10].
Hazari and co-workers showed that CO2 reacted with tBu2(PCP)Ni–H (PCP = 2,6-bis((phosphaneyl)methyl)phenyl) within minutes at room temperature forming the tBu2(PCP)Ni-(O)-formate, which was characterized by X-ray crystallography (CSD entry: UMAPAA) [11]. The 13CO2 labeling showed that the insertion of CO2 into tBu2(PCP)Ni–H is reversible, and the barrier for insertion of CO2 determined by the experimental Eyring plot was 16.3 kcal mol−1 (Figure 1) [11,12]. The solvent effect on the reaction rate with an order of THF (6.8 ± 0.7 M−1 s−1) < benzene (15 ± 2 M−1 s−1) < acetone (51 ± 5 M−1 s−1) < pyridine (130 ± 1 M−1 s−1) < MeCN (220 ± 2 M−1 s−1) was observed for the insertion of CO2, and this order agrees with the order of the relative Lewis acidities of the above solvents [12].
Three major steps for the CO2 insertion into Ni–H to form Ni-(O)-formate are proposed, including (1) the hydride transfer to the Ni-(H)-formate, (2) the rearrangement of the Ni-(H)-formate to form Ni-(O)-formate, and (3) the isomerization of the Ni-(O)-formate (Scheme 1) [12,13]. The stepwise pathway (1 → 2 → TS-2-3 → 3 → TS-3-4i → 4i → TS-4i-4 → 4, Scheme 1) and concerted pathway (1 → 2 → TS-3-4i → 4i →TS-4i-4 → 4, Scheme 1) have been proposed for the CO2 insertion into transition metal hydride (TM–H) complexes. tBu2(PCP)Ni–H (PCP = 2,6-bis((phosphaneyl)methyl)phenyl) and its substituted analogs usually follow the stepwise pathway, and it is also true for the cis-Co(dmpe)2H (dmpe = 1,2-bis(dimethylphosphaneyl)ethane) [14]. However, CO2 insertion into the Ir–H complexes (Cp*(6,6′-dhbp)Ir–H)[OTf] and (Cp*(6,6′-dmbp)Ir–H)[OTf] (6,6′-dhbp = 6,6′-dihydroxybipyridine, 6,6′-dmbp = 6,6′-dimethoxybipyridine) [15], cis-Ru(dmpe)2H2 (dmpe = 1,2-bis(dimethylphosphaneyl)ethane) [16], and (CNN)(dppb)Ru–H (CNN = 2-aminomethyl-6-tolylpyridine, dppb = 1,4-bis-(diphenylphosphino)butane) [17] follows the concerted pathway without the observation of TM-(H)-formate. These different pathways raise the concern of whether the palladium analog, tBu2(PCP)Pd–H, and the cobalt analog, tBu2(PNP)Co–H (PNP = 2,6-bis((phosphaneyl)methyl)pyridyl), also follow the same stepwise pathway in the CO2 insertion as tBu2(PCP)Ni–H. The four-centered transition state (TS-3-4i in Scheme 1) is suggested as the rate-determining transition state, and the rearrangement of the Ni-(H)-formate to form Ni-(O)-formate (3 → TS-3-4i → 4i, Scheme 1) is shown as the overall rate-determining step (RDS) [12,18]. However, the structure and its electronic characterization of Ni-(H)-formate are not fully determined, which needs further comprehensive investigations.
In this contribution, to understand the role of hydrogen, activated as a hydride form, in the hydrogenation of CO2, the detailed reaction mechanism of CO2 insertion into nickel hydride was investigated by density functional theory (DFT) computations. With the obtained rate-determining step (RDS), a series of square planar transition metal hydride (TM–H, TM = Ni, Pd, and Co) complexes (Figure 2) with various steric and electronic effects were studied for the insertion of CO2 into the transition metal hydride (TM–H) bond. The activities of TM–H complexes in the reaction of CO2 insertion were then parameterized, and the possible structure–activity relationship was also modeled, which light the way to the design of a more efficient Ni–H complex in the conversion of CO2 to formate.

2. Computational Methods

Gas-phase geometry optimizations were carried out with B3LYP/BS1 [19,20,21,22] using Gaussian 16 (Revision C 01) [23]. In basis set 1 (BS1), the modified-LANL2DZ [24,25] basis set and LANL2DZ ECP were used for Ni, Co, and Pd; the LANL2DZ(d,p) [24,26] basis set and LANL2DZ ECP were used for P and I; the 6-31G(d′) [27,28,29,30] basis sets were used for all other atoms (C, O, N, and H). The self-consistent reaction field (SCRF) single-point computations in tetrahydrofuran (THF) were performed with the solvation model based on density (SMD) [31] and the Ahlrichs redefined Def2-TZVP [32,33] basis sets (H, C, O, N, P, I, Ni, Co, and Pd) with the energy-adjusted pseudopotential [33] for Pd (BS2). The hydricity (ΔGH−) of each metal hydride was calculated using the equation presented in Scheme S1 [34,35,36]. Grimme’s D3 [37] dispersion with Becke–Johnson damping [D3(BJ)] [38] and the automatic density fitting approximation [39,40] with pure spherical harmonic 5d and 7f functions were utilized for all computations. All located minima were verified by vibrational frequency computations with no imaginary frequency, and all located transition states were obtained with only one imaginary frequency. The IRC (intrinsic reaction coordinate) computations from the located transition states were performed, and both directions of the reaction path following the transition state were computed [41]. The Gaussian 16 default ultrafine integration grid, 2-electron integral accuracy of 10−12, and SCF convergence criterion of 10−8 were used for all computations. All computations were performed at 1 atm and 298.15 K. The electron density of the bond critical point [r(BCP)] based on Bader’s theory of atoms-in-molecules (AIMs) [42,43,44] and the natural adaptive orbital (NAdO) [45] were calculated by the Multiwfn package (version 3.8) [46,47] and were visualized by the VMD package (version 1.9.3) [48,49]. The SambVca (version 2.1) [50,51,52] web application was used to illuminate the steric hindrance of the ligand with parameters of percentages of buried volume (%VBur) [53] and the steric map (Table S4) [54]. Gibbs free energies from SMD(THF)-B3LYP-D3(BJ)/BS2//B3LYP-D3(BJ)/BS1 computations are reported in the main text and are given in kcal mol−1.

3. Results and Discussion

The DFT-optimized structures of nickel hydride (Ni–H) complex tBu2(PCP)Ni–H (PCP = 2,6-bis((phosphaneyl)methyl)phenyl) and its [NiII]-(O)-formate were matched with the reported X-ray crystal structures (CSD entries: SURZIP and UMAPAA). Relatively small root-mean-square deviations (RMSDs, in Å) of 0.1680 and 0.1240 were obtained (Table S1), which demonstrated the good reliability and accuracy of the optimization methodology [55]. For comparison, the optimizations of tBu2(PCP)Ni–H and its [NiII]-(O)-formate complex were also performed with SMD(THF)-B3LYP-D3(BJ)/BS2, and the RMSD values (in Å) for SMD(THF)-B3LYP-D3(BJ)/BS2 optimized structures were 0.092 and 0.0886, respectively (Table S1). The relatively small differences in the RMSD values between the B3LYP-D3(BJ)/BS1 optimization and the SMD(THF)-B3LYP-D3(BJ)/BS2 optimization demonstrate the good reliability and accuracy of B3LYP-D3(BJ)/BS1 [56,57,58].
To investigate the CO2 insertion into nickel hydride complexes, the following three sections are discussed, including the (1) mechanism of CO2 insertion into the Ni–H bond of tBu2(PCP)Ni–H; (2) analysis of Ni-(H)-formate intermediate 3, and (3) parameterized activity and modeling of Ni–H complexes for CO2 insertion.

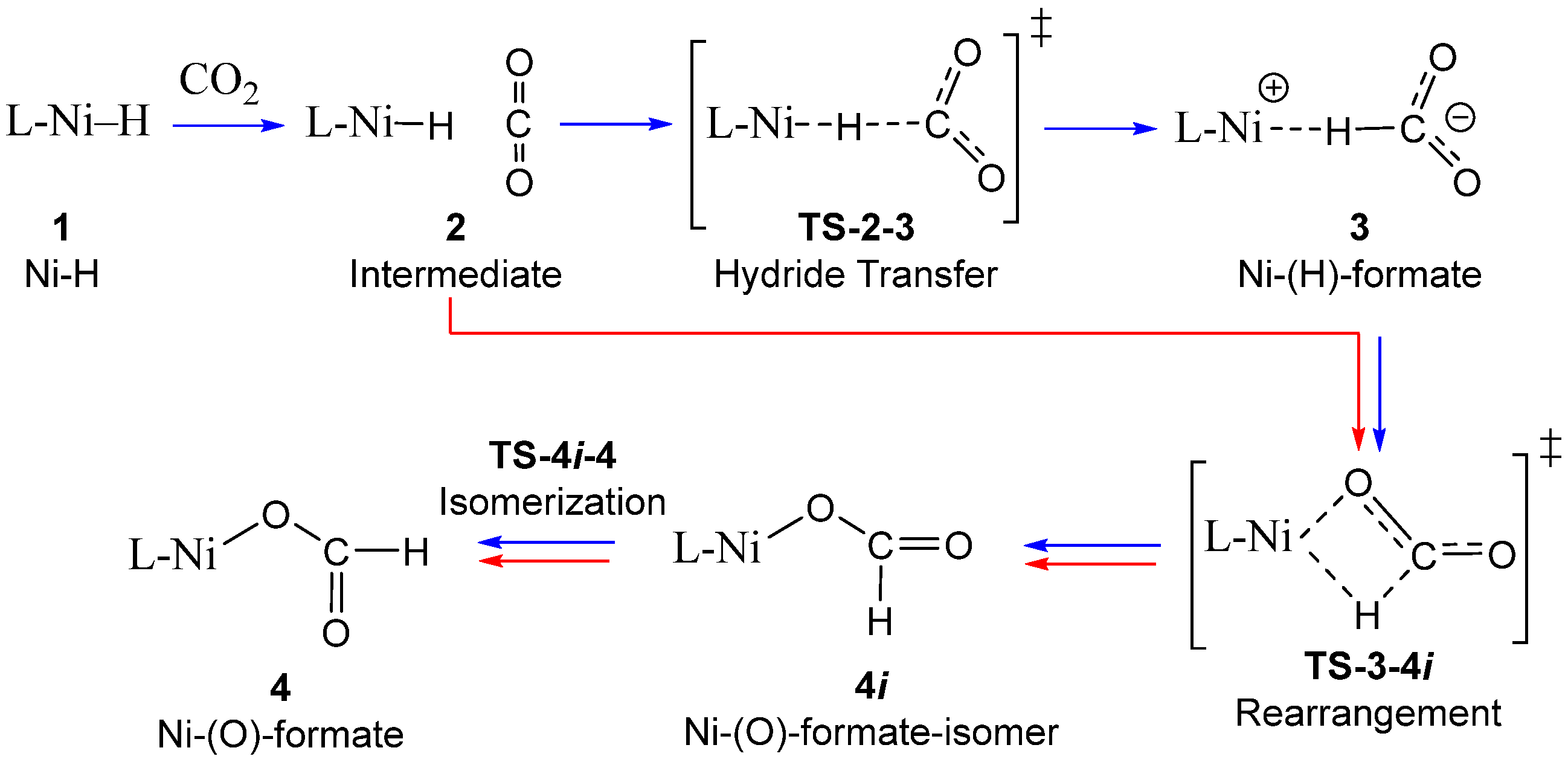
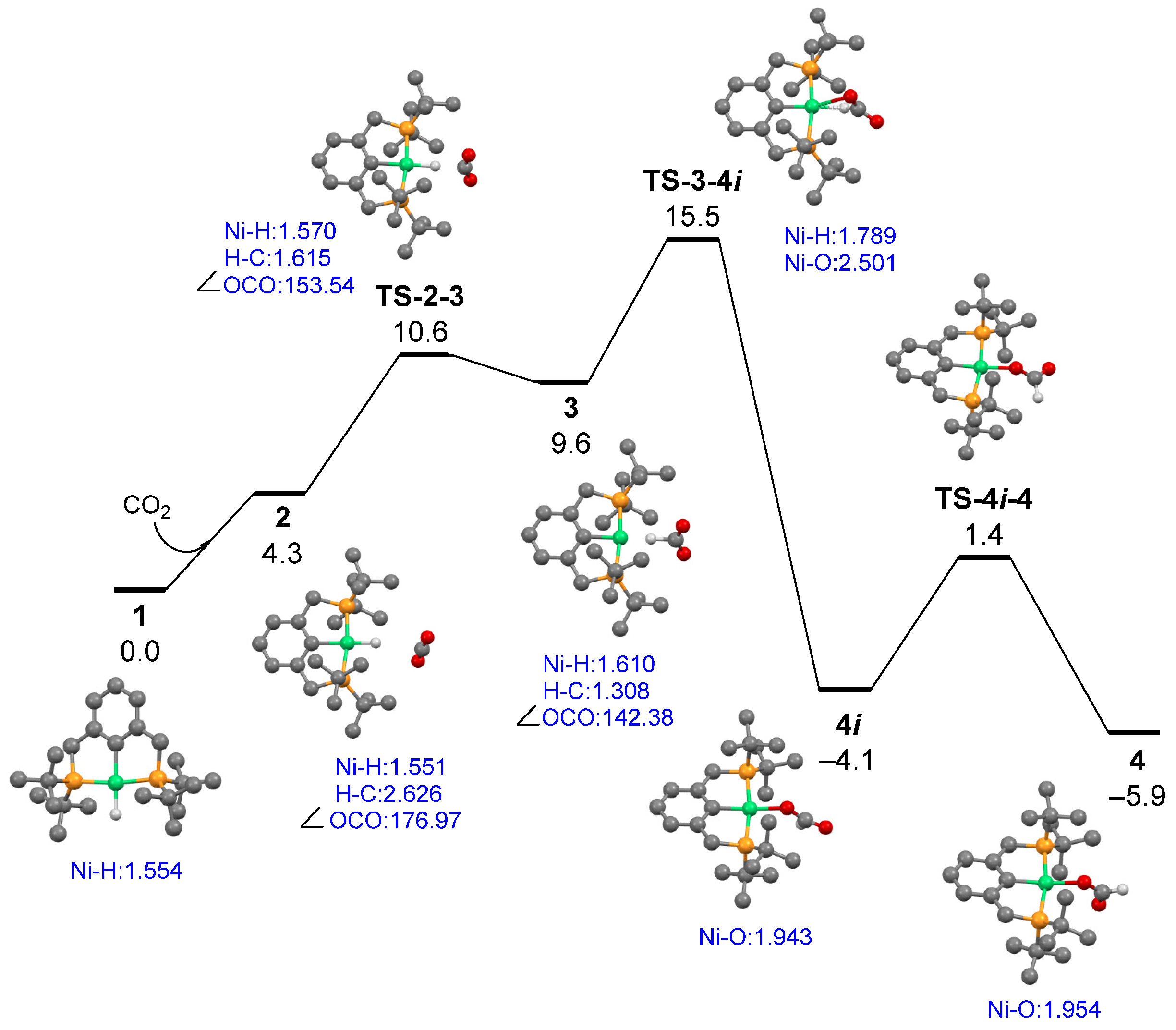
3.1. Mechanism of CO2 Insertion into Ni–H Bond of tBu2(PCP)Ni–H

As presented in Scheme 1, three major steps including (1) the hydride transfer to form the Ni-(H)-formate 3 (1 → 3, Figure 3), (2) rearrangement of the Ni-(H)-formate to form Ni-(O)-formate (3 → 4i, Figure 3), and (3) isomerization of the Ni-(O)-formate (4i → 4, exo→endo, Figure 3) are investigated for the CO2 insertion reaction. First, a direct hydride transfer from the tBu2(PCP)Ni–H structure 1 to the CO2 (Ni–H…CO2 adduct 2) generates the Ni-(H)-formate intermediate 3 (9.6 kcal mol−1, Figure 3) with a Gibbs free energy of activation (ΔG‡) of 10.6 kcal mol−1. The Ni…H atom distance in Ni-(H)-formate intermediate 3 is 1.610 Å, which is longer than that in Ni–H complex 1 (1.551 Å). A linear Ni-H-C(CO2) bond angle (197.97°) in Ni-(H)-formate intermediate 3 is observed, which shows the existence of electrostatic attraction between the Ni center and the H atom in 3 Ni-(H)-formate (see further discussions below on intermediate 3). It is also noted that the formation of the Ni-(H)-formate intermediate 3 from the Ni–H…CO2 adduct 2 is endergonic, and the relative Gibbs free energies for 3 Ni-(H)-formate and 2 Ni–H…CO2 adduct are 9.6 and 4.3 kcal mol−1, respectively. The possible direct proton transfer from the Ni–H to the CO2 in Ni–H…CO2 adduct 2 is also modeled (1 → 2 → TS-2-5 → 5, Figure S2), and a Ni-(O)-hydroxy(oxo)methanide intermediate 5 with a Gibbs free energy of 36.7 kcal mol−1 is located. This direct proton transfer has a Gibbs free energy of activation of 57.3 kcal mol−1 (TS-2-5, Figure S2), which is significantly unfavorable compared to the direct hydride transfer in Ni–H…CO2 adduct 2 to form Ni-(H)-formate 3 (10.6 kcal mol−1, Figure 3) and is excluded for the pathway of CO2 insertion into nickel hydride [36]. Another unfavorable CO pathway is also explored (1 → 2 → 3i → TS-3i-6 → 6→ 7, Figure S3). The proposed CO pathway starts with a Ni-(H)-formate isomer 3i, which has a nonlinear Ni-H-C bond angle of 160.30° instead of the linear Ni-H-C bond angle of 179.97° in Ni-(H)-formate 3. The following transition state TS-3i-6 from 3i forms the Ni-carboxylic acid intermediate 6 with a Gibbs free energy of activation of 49.8 kcal mol−1, which is the overall rate-determining step (RDS) in the proposed CO pathway. The final Ni-carbonyl intermediate 7 was generated via the dissociation of the hydroxyl group from the Ni-carboxylic acid intermediate 6, and a relatively high Gibbs free energy of 32.3 kcal mol−1 for intermediate 7 was obtained. The significantly high Gibbs free energy of activation of 49.8 kcal mol−1 from the located RDS (TS-3i-6, Figure S3) limits the possibility of the CO pathway.
Once the Ni-(H)-formate intermediate 3 is formed, the following rearrangement caused by the nucleophilic attraction of one terminal O atom on the Ni center forms the Ni-(O)-(exo)formate 4i (3→4i, Figure 3) with a Gibbs free energy of activation of 15.5 kcal mol−1. A bent Ni-O-C bond angle (131.23°) is shown in Ni-(O)-(exo)formate 4i with an exo formate fragment. The formation of 4i Ni-(O)-(exo)formate is exergonic, and the relative Gibbs free energy for 4i Ni-(O)-(exo)formate is –4.1 kcal mol−1. The isomerization of 4i Ni-(O)-(exo)formate forms the final product 4 Ni-(O)-(endo)formate (4i→4, exo→endo, Figure 3) with a Gibbs free energy of activation (ΔG‡) of 1.4 kcal mol−1. The DFT-optimized structure of final product 4 Ni-(O)-(endo)formate matches well with its reported X-ray crystal structures (CSD entry: UMAPAA) with an RMSD value (in Å) of 0.1240 (Table S1). The overall stepwise pathway for the capture of CO2 by tBu2(PCP)Ni–H 1 to form 4 Ni-(O)-(endo)formate (1 → 4, Figure 3) is favorable at –5.9 kcal mol−1 from the computations of SMD(THF)-B3LYP-D3(BJ)/BS2//B3LYP-D3(BJ)/BS1, which is consistent with the SMD(THF)-B3LYP-D3(BJ)/BS2 computed value of –5.2 kcal mol−1. The computed Gibbs barrier for the overall rate-determining step (RDS) based on the energetic span/transition state theory is determined as 15.5 kcal mol−1 (TS-3-4i, Figure 3), which agrees with the experimental value of 16.3 kcal mol−1 determined by the Eyring plot [12].
With the established pathway of CO2 insertion into tBu2(PCP)Ni–H (PCP = 2,6-bis((phosphaneyl)methyl)phenyl) (Figure 3), the catalytic activities of a series of square planar transition metal hydride complexes (I to VII, Figure 2) for CO2 insertion are investigated. The parent tBu2(PCP)Ni–H complex (I) is modified by the introduced electron-donating (p-OMe, tBu2(p-MeO-PCP)Ni–H, II) and electron-withdrawing groups (p-iodo, tBu2(p-I-PCP)Ni–H, III) on the para position of the phenyl fragment. To evaluate the steric effect in the CO2 insertion, two tert-butyl groups (tBu2) in tBu2(PCP)Ni–H complex (I) are replaced by two isopropyl groups (iPr2), forming iPr2(PCP)Ni–H (IV). To address the electronic effect, the phenyl group in tBu2(PCP)Ni–H complex (I) is changed to a cyclohexyl group (Cy), forming tBu2(PCyP)Ni–H (V) (PCyP = 2,6-bis((phosphaneyl)methyl)cyclohexyl). To further confirm the established stepwise pathway (1 → 2 → TS-2-3 → 3 → TS-3-4i → 4i → TS-4i-4 → 4, Scheme 1 and Figure 3) of CO2 insertion into TM–H complexes, the structural analogs tBu2(PCP)Pd–H (VI) and tBu2(PNP)Co–H (VII) (PNP = 2,6-bis((phosphaneyl)methyl)pyridyl) are also computationally modeled for the CO2 insertion into the Pd–H bond and Co–H bond, respectively.
The computed hydricities and Gibbs free energies of activation for these seven square planar transition metal hydride complexes (TM–H, TM = Ni, Pd, and Co) (I to VII, Figure 2) for CO2 insertion are summarized in Table 1. The APT charge of the transition metal atom in the axially vacant [TM]+ and the percentages of buried volume in the axially vacant [TM]+ are also included in Table 1. The Gibbs free energies of other intermediates on the computed pathway are presented in Figure S4. It is worth noting that the TM-(H)-formate intermediate for the CO2 insertion into all seven square planar transition metal hydride (TM–H) complexes (I to VII) were located. As one major difference between the stepwise pathway and concerted pathway in the CO2 insertion, the TM-(H)-formate intermediate could only be observed in the stepwise pathway, as pointed out by Hazari and co-workers [12,59]. In this study, the TM-(H)-formate intermediates for all seven square planar transition metal hydride (TM–H, TM = Ni, Pd, and Co) complexes were successfully located, and no direct conversion from the TM–H…CO2 adduct and TM-(O)-formate could be established. This suggests that no reasonable concerted pathway in the CO2 insertion for the seven square planar TM–H complexes (TM = Ni, Pd, and Co) could be obtained. Compared to the linear Ni-H-C bond angle (179.97°) in Ni-(H)-formate intermediate 3 of Ni–H complex I, the nonlinear Pd-H-C bond angle (152.45°) in the Pd-(H)-formate intermediate of Pd–H complex VI and the nonlinear Co-H-C bond angle (133.27°) in the Co-(H)-formate intermediate of Co–H complex VII were observed, which affected the electron densities of TM…H bond critical points and C(formate)-H bond critical points, leading to various Gibbs barriers for the RDS (Table 1), but did not change the stepwise pathway. The geometrical commonality of the square planar structure could be used to explain the comparable stepwise pathway for the CO2 insertion into all seven TM–H complexes (TM = Ni, Pd, and Co).
Comparisons of the computed ΔG‡ of the RDS (TS-3-4i) of tBu2(PCP)Ni–H (I), tBu2(p-MeO-PCP)Ni–H (II), and tBu2(p-I-PCP)Ni–H (III) show that the introduced electron-withdrawing group (p-iodo) decreases the catalytic activity with the highest ΔG‡ of 15.9 kcal mol−1 and the introduced electron-donating group (p-OMe) increases the catalytic activity with the lowest ΔG‡ of 15.3 kcal mol−1. This computed order of ΔG‡ of the RDS (III > I > II) is consistent with the experimentally determined reaction rate (k) (1.6 ± 0.2 for III, 6.8 ± 0.7 for I, and 11.7 ± 1 M−1 s−1 for II). The computed hydricities of tBu2(p-I-PCP)Ni–H (III), tBu2(PCP)Ni–H (I), and tBu2(p-MeO-PCP)Ni–H (II) are 52.3, 50.6, and 50.1 kcal mol−1, respectively, and an order for Ni–H bond strength of III > I > II is concluded. The RDS (TS-3-4i) is the nucleophilic attraction of the terminal O atom on the Ni center in 3 Ni-(H)-formate, forming the 4i Ni-(O)-(exo)formate, and the effect of the APT charge of the transition metal atom in the axially vacant [TM]+ and the effect of the percentages of buried volume in the axially vacant [TM]+ on the CO2 insertion into all seven TM–H complexes are also evaluated. Identical values of %VBur in the axially vacant [TM]+ complexes I, II, and III are obtained (81.4, Table 1), which suggest that the introduced para group has a negligible effect on the rigid PCP structure and on the geometry of the two tert-butyl groups (tBu2). However, the %VBur decreases from 81.4 to 77.4 for iPr2(PCP)Ni–H (IV) when the two tert-butyl groups (tBu2) in tBu2(PCP)Ni–H complex (I) are replaced by two isopropyl groups (iPr2). The computed ΔG‡ of the RDS (TS-3-4i) for iPr2(PCP)Ni–H (IV) is 14.7 kcal mol−1, which is also lower than those for tBu2(p-I-PCP)Ni–H (III), tBu2(PCP)Ni–H (I), and tBu2(p-MeO-PCP)Ni–H (II), leading to a faster reaction rate (k) of 4400 M−1 s−1. Computational results show that tBu2(PCyP)Ni–H (V) has the lowest ΔG‡ of the RDS among all the five Ni–H species (I to V) for the CO2 insertion (10.8 kcal mol−1) and the lowest hydricity (43.3) among all the five Ni–H species, but the highest buried volume in the axially vacant [Ni]+ (83.4). This inconsistent observation suggests that the steric effect of CO2 is less important than the electronic effect of the Ni–H complexes in the CO2 insertion. Compared to Bu2(PCP)Ni–H complex (I), the structural analog tBu2(PCP)Pd–H (VI) presents a similar stepwise pathway for the CO2 insertion with a Pd-(H)-formate intermediate, and a slightly lower ΔG‡ of the RDS (15.1 kcal mol−1) for tBu2(PCP)Pd–H (VI) is obtained. It is an interesting finding that the cobalt analog, tBu2(PNP)Co–H (VII) (PNP = 2,6-bis((phosphaneyl)methyl)pyridyl), shows the lowest ΔG‡ of the RDS (8.9 kcal mol−1) among all seven square planar TM–H complexes (I to VII), presents the lowest hydricity of 41.2 kcal mol−1, and also has the smallest buried volume in the axially vacant [Co]+ (77.7) among all six tert-butyl substituent (tBu2) hydride complexes (I to III and V to VII). Compared to the anionic phenyl group and Ni(II) atom in tBu2(PCP)Ni–H complex (I), the neutral pyridyl group and the Co(I) atom in tBu2(PNP)Co–H (VII) produce an electron-rich Co center, leading to a weaker Co–H bond and a lower value of ΔG‡ for the RDS.

3.2. Analysis of Ni-(H)-Formate Intermidiate 3

To further illustrate the electrostatic attraction between the Ni center and the H atom in 3 Ni-(H)-formate, atoms-in-molecules (AIMs) analysis and the natural adaptive orbital (NadO) of Ni-(H)-formate complexes are performed (Figure 4 and Figure 5, Tables S2 and S3). A nonnegligible electron density of a Ni…H bond critical point [r(BCP)] from AIM analysis is observed, and the r(BCP) for the Ni…H bond in the Ni-(H)-formate complexes I, II, and III are 0.0786, 0.0782, and 0.0801, respectively (Figure 4). For comparisons, the r(BCP) for the C(formate)-H bond in Ni-(H)-formate complexes I, II, and III are 0.1527, 0.1549, and 0.1473, respectively. The order of the relative strength of the Ni…H interaction in Ni-(H)-formate is III > I > II, which is consistent with the value of positive charge of the Ni atom in complexes III, I, and II introduced by the electron-withdrawing group (p-iodo) and electron-donating group (p-OMe). The r(BCP) for Ni…H interaction in Ni-(H)-formate complexes IV and V are 0.0800 and 0.0730, respectively, and the r(BCP) for the C(formate)-H bond in Ni-(H)-formate complexes IV and V are 0.1464 and 0.1673, respectively (Table S2). The Ni-(H)-formate complex V with the nonplanar and nonaromatic cyclohexyl ligand presents the smallest r(BCP) for the Ni…H bond (0.0730) and the biggest r(BCP) for the C(formate)-H bond (0.1673) in Ni-(H)-formate among all five Ni complexes. As the electron delocalization in Ni-(H)-formate complex V is limited by the nonplanar and nonaromatic cyclohexyl ligand compared to the aromatic phenyl and substituted phenyl groups in Ni-(H)-formate complexes I, II, III, and IV, the weakest Ni…H interaction in Ni-(H)-formate complex V is expected and also verified. Compared to the electron density of Ni…H in Ni-(H)-formate complexes I, II, and III (0.0786, 0.0782, and 0.0801, respectively), the electron density of the Co…H bond critical point [r(BCP)] is quite small for VII (0.0698, Figure 4), which shows that the Co…H bond interaction is much weaker than the Ni…H ones. Not surprisingly, the strongest C(formate)-H bond with an r(BCP) of 0.1838 for Co-(H)-formate (VII) among all the TM-(H)-formate intermediates was observed. As the overall rate-determining step (RDS) is the nucleophilic attraction of the terminal O atom on the TM center in TM-(H)-formate to form TM-(O)-(exo)formate (TS-3-4i), a lower Gibbs barrier for this conversion induced by the weaker TM…H bond is anticipated. The cobalt pyridine intermediate Co-(H)-formate (VII) with the weakest TM…H bond has the lowest Gibbs barrier for the RDS among all the TM–H complexes (8.9 kcal mol−1, Table 1).
The Ni-H-C interaction in the Ni-(H)-formate complexes is also investigated by the natural adaptive orbitals (NAdOs), and comparable NAdO compositions in complexes I, II, and III are obtained (Figure 5). A slightly higher contribution of the 3d orbital from the Ni atom for the NAdO in Ni-(H)-formate complex III (18.5%) compared to those in Ni-(H)-formate complexes I (18.2%) and II (18.2%) is observed, which is caused by the introduced electron-withdrawing group (p-iodo), demonstrating the stronger Ni…H interaction in Ni-(H)-formate complex III. Compared to the NAdO orbital contributions in the Ni-(H)-formate complexes I, II, and III, a noticeably higher contribution from the 2p orbital of the C atom (13.5%) and a lower contribution from the 3d orbital of the Co atom (15.9%) for the Co-H-C NAdO in the Co-(H)-formate complex VII were observed. The non-linear Co-H-C bond angle (133.27°) in Co-(H)-formate complex VII compared to the linear Ni-H-C bond angle (179.97°) in Ni-(H)-formate complex I may cause the different NAdO orbital contributions.

3.3. Parameterized Activity and Modeling of Ni–H Complexes for CO2 Insertion

The nucleophilic attraction of the terminal O atom on the Ni center in 3 Ni-(H)-formate to form 4i Ni-(O)-(exo)formate (3 → TS-3-4i → 4i, Figure 3 and Table 1) is demonstrated as the overall RDS for CO2 insertion into nickel hydride, and the effect of the APT charge of the Ni atom in the axially vacant [Ni]+ complexes on CO2 insertion is confirmed. An excellent linear fitting (R2 = 0.967) between the ΔG‡ of the RDS for Ni–H complexes I to V and the APT charges of Ni atoms in the related axially vacant [Ni]+ complexes is observed (Figure 6). An acceptable linear fitting (R2 = 0.8002) between the ΔG‡ of the RDS for all seven transition metal hydride complexes (I to VII) and the APT charges of transition metals in the related axially vacant [TM]+ complexes is also obtained (Figure S6).
In an attempt to achieve a structure–activity relationship in the capture of CO2 by transition metal hydride complexes (TM–H), the correlation between the ΔG‡ of the RDS for Ni–H complexes I to V and the computed hydricities is fitted (Figure 7). An appropriate linear fitting (R2 = 0.8164) between the ΔG‡ of the RDS for Ni–H complexes I to V and the computed hydricities is achieved, but the second-order polynomial fitting provides a better accuracy (R2 = 0.973) (Figure 7). An improved second-order polynomial fitting between the ΔG‡ of the RDS and the computed hydricities for all seven TM–H complexes (I to VII) is also observed (R2 = 0.9832) (Figure S7). The above discussed second-order polynomial fittings suggest the existence of the optimal value of hydricity for the reaction of CO2 insertion and also indicate that a single-parameter model is not adequate to present a convincing structure–activity relationship in the capture of CO2 by TM–H complexes. With the obtained RDS for CO2 insertion into nickel hydride (3 → TS-3-4i → 4i, Figure 3 and Table 1), the multi-parameter models (Scheme 2) including the APT charge of Ni atoms in the axially vacant [Ni]+ complexes, the buried volume (%VBur) in the axially vacant [Ni]+ complexes, and the computed hydricities of Ni–H complexes are investigated. An excellent two-parameter model (R2 = 0.9872, Equation (1), Scheme 2) and a three-parameter model (R2 = 0.9967, Equation (2), Scheme 2) to quantitatively describe the overall ΔG‡ of the RDS for CO2 insertion into nickel hydride are established, which also demonstrate the dominant factor of the APT charge of Ni atoms in the axially vacant [Ni]+ complexes for the reaction of CO2 insertion, as illustrated in Figure 6.

4. Conclusions

To convert CO2 into the useful chemical feedstock and to achieve the target of carbon neutrality, the capture and utilization of CO2 by transition metal hydride complexes (TM–H) via the homogeneous hydrogenation of CO2 are desired. Theoretical insights into the hydrogenation of CO2 have been benefited from the computational modeling. The activation of an H2 molecule to form the hydride species, the following CO2 insertion into the TM–H bond, and the release of formate are the key steps in the hydrogenation of CO2 to generate formate. The computational investigations for the homogeneous CO2 insertion into tBu2(PCP)Ni–H (PCP = 2,6-bis((phosphaneyl)methyl)phenyl) are performed in this study. The reaction of CO2 insertion into Ni–H is followed by a stepwise pathway, and the rearrangement of the Ni-(H)-formate to form Ni-(O)-formate is the overall rate-determining step (RDS, ΔG‡ = 15.5 kcal mol−1 for tBu2(PCP)Ni–H). The complexes with improved hydride donor abilities have promote the activities of CO2 insertion with lower ΔG‡ (15.5 kcal mol−1 for tBu2(PCP)Ni–H, 15.3 kcal mol−1 for tBu2(p-MeO-PCP)Ni–H, and 10.8 kcal mol−1 for tBu2(PCyP)Ni–H). The structure–activity relationship of homogeneous CO2 insertion with a series of square planar transition metal hydride complexes (TM–H) is evaluated. The single-parameter and multi-parameter models show that the charge of the Ni atom in the axially vacant [Ni]+ complexes is the dominant factor on CO2 insertion with an excellent linear fitting (R2 = 0.967). The parameterized activities and modeled structure–activity relationship provided here are the helpful references to the design of a more efficient Ni–H complex in the homogeneous hydrogenation of CO2 to formate.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal12070790/s1, Table S1: The matched structures; Table S2: The AIM analysis; Table S3: The first three NAdOs; Table S4: The steric map of optimized TM–H; Table S5: DFT-computed energies for species; Table S6: Cartesian coordinates; Scheme S1: Equation used to calculate the hydricity; Scheme S2: The multi-parameter models; Figure S1: Free energy diagram for CO2 insertion into tBu2(PCP)Ni–H; Figure S2: Free energy diagram for proton transfer; Figure S3: Free energy diagram for formate pathway and CO pathway; Figure S4: Free energy diagram for CO2 insertion into TM–H; Figure S5: The representations of 3D and 2D steric maps; Figures S6 and S7: The linear fitting; Figures S8–S11: IRC plots.

Author Contributions

M.Z.: conceptualization, investigation, formal analysis, writing—original draft; X.L.: investigation, formal analysis; Y.W.: visualization, formal analysis; H.Y.: data curation, formal analysis; G.L.: conceptualization, formal analysis, methodology, writing—review and editing, funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by start-up funds from Xidian University (1018/10251210050).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We are grateful for the financial support from Xi’an International University and the start-up funds from Xidian University (1018/10251210050), and we thank the high-performance computing platform of Xidian University (XDHCPP) for computing support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hasan, M.M.F.; Rossi, L.M.; Debecker, D.P.; Leonard, K.C.; Li, Z.; Makhubela, B.C.E.; Zhao, C.; Kleij, A. Can CO2 and Renewable Carbon Be Primary Resources for Sustainable Fuels and Chemicals? ACS Sustain. Chem. Eng. 2021, 9, 12427–12430. [Google Scholar] [CrossRef]
  2. Saravanan, A.; Kumar, P.S.; Vo, D.-V.N.; Jeevanantham, S.; Bhuvaneswari, V.; Narayanan, V.A.; Yaashikaa, P.R.; Swetha, S.; Reshma, B. A comprehensive review on different approaches for CO2 utilization and conversion pathways. Chem. Eng. Sci. 2021, 236, 116515. [Google Scholar] [CrossRef]
  3. Valluri, S.; Claremboux, V.; Kawatra, S. Opportunities and challenges in CO2 utilization. J. Environ. Sci. 2022, 113, 322–344. [Google Scholar] [CrossRef]
  4. Kinzel, N.W.; Werlé, C.; Leitner, W. Transition Metal Complexes as Catalysts for the Electroconversion of CO2: An Organometallic Perspective. Angew. Chem. Int. Ed. 2021, 60, 11628–11686. [Google Scholar] [CrossRef]
  5. Navarro-Jaén, S.; Virginie, M.; Bonin, J.; Robert, M.; Wojcieszak, R.; Khodakov, A.Y. Highlights and challenges in the selective reduction of carbon dioxide to methanol. Nat. Rev. Chem. 2021, 5, 564–579. [Google Scholar] [CrossRef]
  6. Zhang, S.; Fan, Q.; Xia, R.; Meyer, T.J. CO2 Reduction: From Homogeneous to Heterogeneous Electrocatalysis. Acc. Chem. Res. 2020, 53, 255–264. [Google Scholar] [CrossRef]
  7. Kostera, S.; Peruzzini, M.; Gonsalvi, L. Recent Advances in Metal Catalyst Design for CO2 Hydroboration to C1 Derivatives. Catalysts 2021, 11, 58. [Google Scholar] [CrossRef]
  8. Bai, S.-T.; De Smet, G.; Liao, Y.; Sun, R.; Zhou, C.; Beller, M.; Maes, B.U.W.; Sels, B.F. Homogeneous and heterogeneous catalysts for hydrogenation of CO2 to methanol under mild conditions. Chem. Soc. Rev. 2021, 50, 4259–4298. [Google Scholar] [CrossRef] [PubMed]
  9. Wang, W.-H.; Himeda, Y.; Muckerman, J.T.; Manbeck, G.F.; Fujita, E. CO2 Hydrogenation to Formate and Methanol as an Alternative to Photo- and Electrochemical CO2 Reduction. Chem. Rev. 2015, 115, 12936–12973. [Google Scholar] [CrossRef]
  10. Jessop, P.G.; Joó, F.; Tai, C.-C. Recent advances in the homogeneous hydrogenation of carbon dioxide. Coord. Chem. Rev. 2004, 248, 2425–2442. [Google Scholar] [CrossRef]
  11. Schmeier, T.J.; Hazari, N.; Incarvito, C.D.; Raskatov, J.A. Exploring the reactions of CO2 with PCP supported nickel complexes. Chem. Commun. 2011, 47, 1824–1826. [Google Scholar] [CrossRef] [PubMed]
  12. Heimann, J.E.; Bernskoetter, W.H.; Hazari, N.; Mayer, J.M. Acceleration of CO2 insertion into metal hydrides: Ligand, Lewis acid, and solvent effects on reaction kinetics. Chem. Sci. 2018, 9, 6629–6638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Heimann, J.E.; Bernskoetter, W.H.; Hazari, N. Understanding the Individual and Combined Effects of Solvent and Lewis Acid on CO2 Insertion into a Metal Hydride. J. Am. Chem. Soc. 2019, 141, 10520–10529. [Google Scholar] [CrossRef] [PubMed]
  14. Kumar, N.; Camaioni, D.M.; Dupuis, M.; Raugei, S.; Appel, A.M. Mechanistic insights into hydride transfer for catalytic hydrogenation of CO2 with cobalt complexes. Dalton Trans. 2014, 43, 11803–11806. [Google Scholar] [CrossRef]
  15. Siek, S.; Burks, D.B.; Gerlach, D.L.; Liang, G.; Tesh, J.M.; Thompson, C.R.; Qu, F.; Shankwitz, J.E.; Vasquez, R.M.; Chambers, N.; et al. Iridium and Ruthenium Complexes of N-Heterocyclic Carbene- and Pyridinol-Derived Chelates as Catalysts for Aqueous Carbon Dioxide Hydrogenation and Formic Acid Dehydrogenation: The Role of the Alkali Metal. Organometallics 2017, 36, 1091–1106. [Google Scholar] [CrossRef]
  16. Whittlesey, M.K.; Perutz, R.N.; Moore, M.H. Facile insertion of CO2 into the Ru-H bonds of Ru(dmpe)2H2 (dmpe = Me2PCH2CH2PMe2): Identification of three ruthenium formate complexes. Organometallics 1996, 15, 5166–5169. [Google Scholar] [CrossRef]
  17. Ramakrishnan, S.; Waldie, K.M.; Warnke, I.; De Crisci, A.G.; Batista, V.S.; Waymouth, R.M.; Chidsey, C.E.D. Experimental and Theoretical Study of CO2 Insertion into Ruthenium Hydride Complexes. Inorg. Chem. 2016, 55, 1623–1632. [Google Scholar] [CrossRef]
  18. Suh, H.-W.; Schmeier, T.J.; Hazari, N.; Kemp, R.A.; Takase, M.K. Experimental and Computational Studies of the Reaction of Carbon Dioxide with Pincer-Supported Nickel and Palladium Hydrides. Organometallics 2012, 31, 8225–8236. [Google Scholar] [CrossRef]
  19. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  20. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  21. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained With The Correlation Energy Density Functionals Of Becke And Lee, Yang And Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
  23. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
  24. Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
  25. Couty, M.; Hall, M.B. Basis sets for transition metals: Optimized outer p functions. J. Comput. Chem. 1996, 17, 1359–1370. [Google Scholar] [CrossRef]
  26. Check, C.E.; Faust, T.O.; Bailey, J.M.; Wright, B.J.; Gilbert, T.M.; Sunderlin, L.S. Addition of polarization and diffuse functions to the LANL2DZ basis set for p-block elements. J. Phys. Chem. A 2001, 105, 8111–8116. [Google Scholar] [CrossRef]
  27. Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular-Orbital Studies of Organic-Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
  28. Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular-Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
  29. Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B Condens. Matter 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  30. Foresman, J.B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods, 2nd ed.; Gaussian, Inc.: Pittsburgh, PA, USA, 1996. [Google Scholar]
  31. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
  32. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  33. Andrae, D.; Häusermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
  34. Wiedner, E.S.; Chambers, M.B.; Pitman, C.L.; Bullock, R.M.; Miller, A.J.M.; Appel, A.M. Thermodynamic hydricity of transition metal hydrides. Chem. Rev. 2016, 116, 8655–8692. [Google Scholar] [CrossRef] [PubMed]
  35. Ilic, S.; Alherz, A.; Musgrave, C.B.; Glusac, K.D. Thermodynamic and kinetic hydricities of metal-free hydrides. Chem. Soc. Rev. 2018, 47, 2809–2836. [Google Scholar] [CrossRef] [PubMed]
  36. Liang, G.; Zhang, M.; Webster, C.E. Mechanistic Studies of Oxygen-Atom Transfer (OAT) in the Homogeneous Conversion of N2O by Ru Pincer Complexes. Inorganics 2022, 10, 69. [Google Scholar] [CrossRef]
  37. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
  38. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  39. Dunlap, B.I. Fitting the Coulomb potential variationally in Xα molecular calculations. J. Chem. Phys. 1983, 78, 3140–3142. [Google Scholar] [CrossRef]
  40. Dunlap, B.I. Robust and variational fitting: Removing the four-center integrals from center stage in quantum chemistry. J. Mol. Struct. THEOCHEM 2000, 529, 37–40. [Google Scholar] [CrossRef]
  41. Zhang, M.; Liang, G. Understanding the Sigmatropic Shifts of Cyclopenta-2,4-dien-1-yltrimethylsilane in its Diels—Alder Addition. Org. Biomol. Chem. 2021, 19, 1732–1737. [Google Scholar] [CrossRef]
  42. Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
  43. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  44. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  45. Casals-Sainz, J.L.; Fernández-Alarcón, A.; Francisco, E.; Costales, A.; Pendás, Á.M. Bond Order Densities in Real Space. J. Phys. Chem. A 2020, 124, 339–352. [Google Scholar] [CrossRef] [PubMed]
  46. Multiwfn, Version 3.8; 2021. Available online: http://sobereva.com/multiwfn/ (accessed on 2 December 2021).
  47. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  48. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  49. VMD, Version 1.9.3; 2016. Available online: http://www.ks.uiuc.edu/Research/vmd/ (accessed on 4 December 2021).
  50. Falivene, L.; Credendino, R.; Poater, A.; Petta, A.; Serra, L.; Oliva, R.; Scarano, V.; Cavallo, L. SambVca 2. A Web Tool for Analyzing Catalytic Pockets with Topographic Steric Maps. Organometallics 2016, 35, 2286–2293. [Google Scholar] [CrossRef] [Green Version]
  51. SambVca, Version 2.1; 2019. Available online: https://www.molnac.unisa.it/OMtools/sambvca2.1/index.html (accessed on 12 November 2021).
  52. Falivene, L.; Cao, Z.; Petta, A.; Serra, L.; Poater, A.; Oliva, R.; Scarano, V.; Cavallo, L. Towards the online computer-aided design of catalytic pockets. Nat. Chem. 2019, 11, 872–879. [Google Scholar] [CrossRef] [Green Version]
  53. Poater, A.; Ragone, F.; Giudice, S.; Costabile, C.; Dorta, R.; Nolan, S.P.; Cavallo, L. Thermodynamics of N-Heterocyclic Carbene Dimerization: The Balance of Sterics and Electronics. Organometallics 2008, 27, 2679–2681. [Google Scholar] [CrossRef]
  54. Poater, A.; Ragone, F.; Mariz, R.; Dorta, R.; Cavallo, L. Comparing the Enantioselective Power of Steric and Electrostatic Effects in Transition-Metal-Catalyzed Asymmetric Synthesis. Chem. Eur. J. 2010, 16, 14348–14353. [Google Scholar] [CrossRef]
  55. Zhang, M.; Liang, G.; Xing, M. Theoretical Investigation of Hydrogen Bonds Assisted Tetradentate N4 Copper(I) Chloride and trans-1,2-Peroxodicopper Complexes. Eur. J. Inorg. Chem. 2021, 2021, 2194–2200. [Google Scholar] [CrossRef]
  56. Witte, J.; Mardirossian, N.; Neaton, J.B.; Head-Gordon, M. Assessing DFT-D3 Damping Functions Across Widely Used Density Functionals: Can We Do Better? J. Chem. Theory Comput. 2017, 13, 2043–2052. [Google Scholar] [CrossRef] [Green Version]
  57. Zhang, L.; An, K.; Wang, Y.; Wu, Y.-D.; Zhang, X.; Yu, Z.-X.; He, W. A Combined Computational and Experimental Study of Rh-Catalyzed C–H Silylation with Silacyclobutanes: Insights Leading to a More Efficient Catalyst System. J. Am. Chem. Soc. 2021, 143, 3571–3582. [Google Scholar] [CrossRef] [PubMed]
  58. Zheng, D.; Wang, F. Performing Molecular Dynamics Simulations and Computing Hydration Free Energies on the B3LYP-D3(BJ) Potential Energy Surface with Adaptive Force Matching: A Benchmark Study with Seven Alcohols and One Amine. ACS Phys. Chem. Au 2021, 1, 14–24. [Google Scholar] [CrossRef] [PubMed]
  59. Hazari, N.; Heimann, J.E. Carbon Dioxide Insertion into Group 9 and 10 Metal–Element σ Bonds. Inorg. Chem. 2017, 56, 13655–13678. [Google Scholar] [CrossRef] [PubMed]
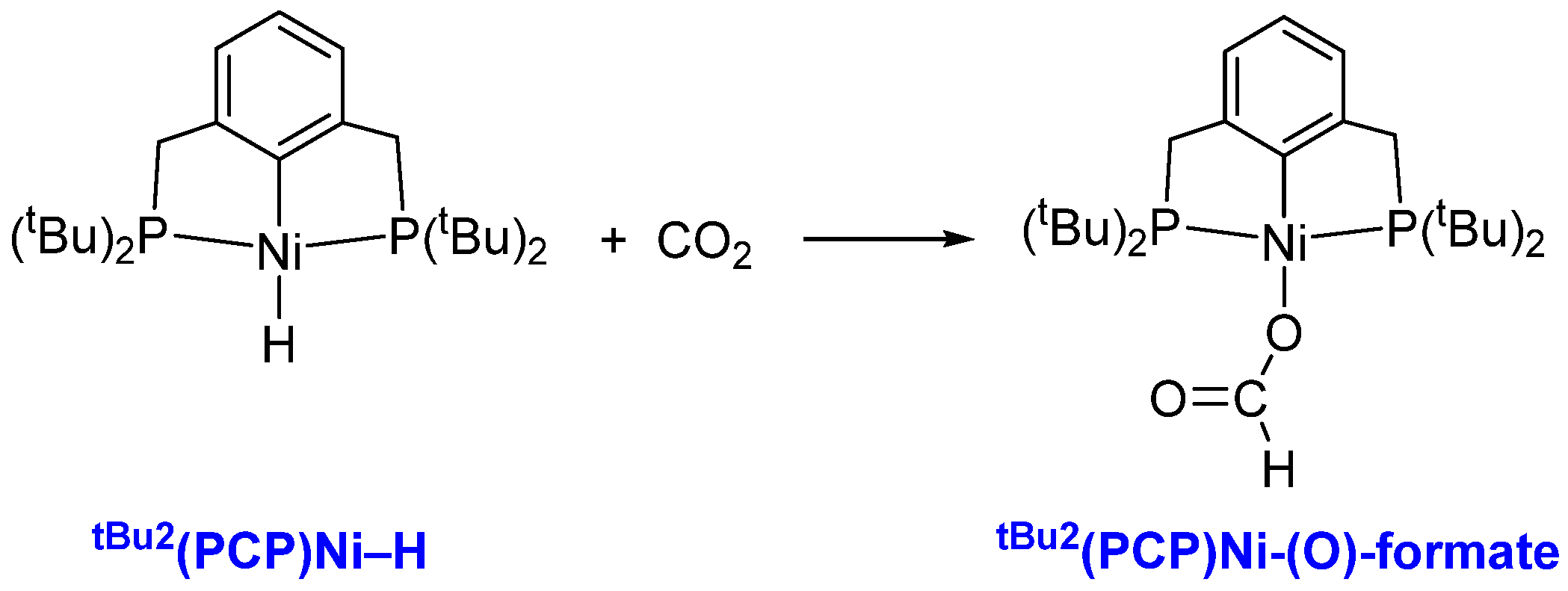
Catalysts 12 00790 g001 550
Figure 1. Reaction of CO2 with tBu2(PCP)Ni-H.
Figure 1. Reaction of CO2 with tBu2(PCP)Ni-H.
Catalysts 12 00790 g001
Catalysts 12 00790 sch001 550
Scheme 1. Proposed pathway for the CO2 insertion into nickel hydride complex.
Scheme 1. Proposed pathway for the CO2 insertion into nickel hydride complex.
Catalysts 12 00790 sch001
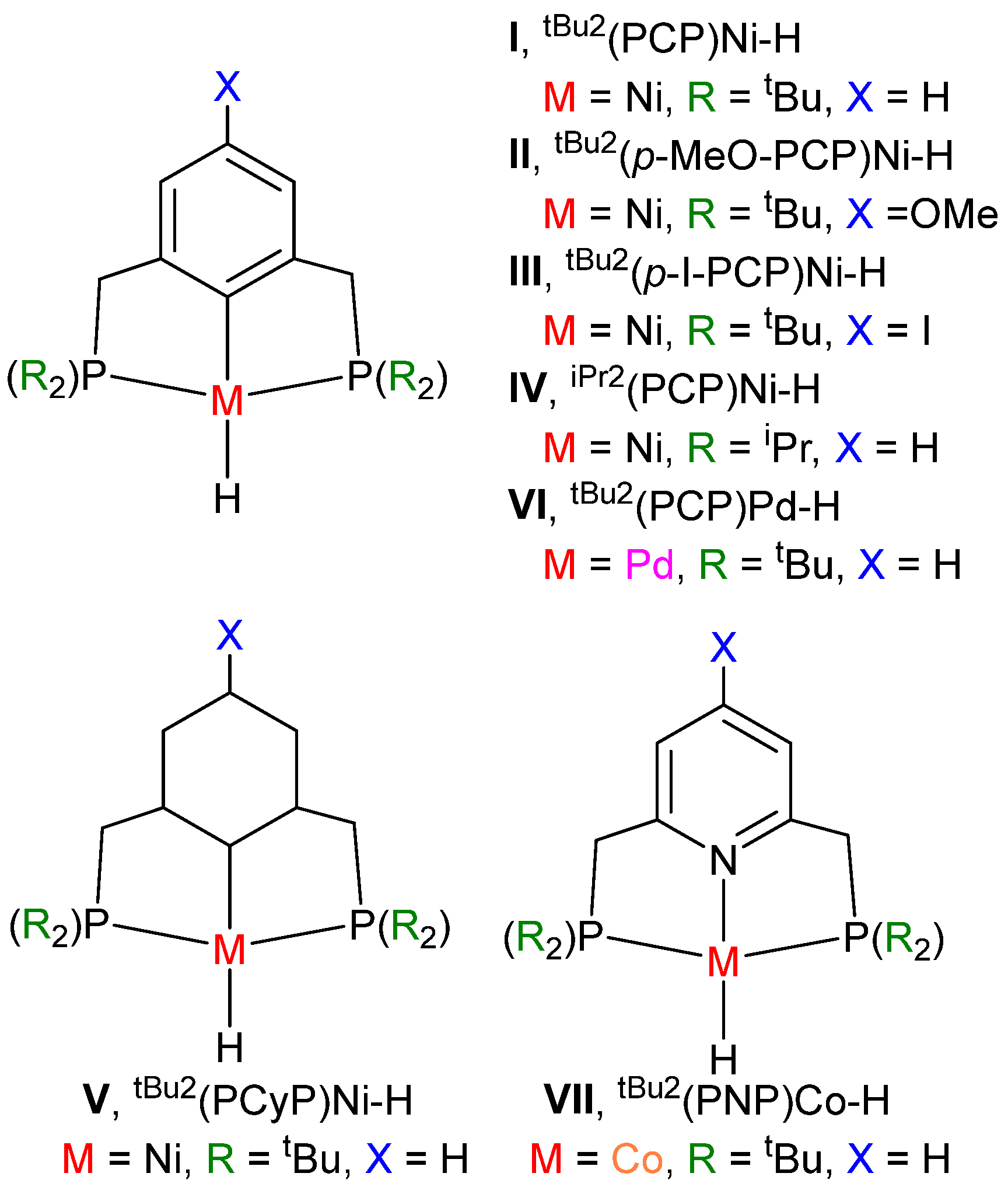
Catalysts 12 00790 g002 550
Figure 2. Studied transition metal hydride (TM–H) complexes I to VII for CO2 insertion.
Figure 2. Studied transition metal hydride (TM–H) complexes I to VII for CO2 insertion.
Catalysts 12 00790 g002
Catalysts 12 00790 g003 550
Figure 3. Free energy diagram for CO2 insertion into I, tBu2(PCP)Ni–H. Selected atom distances are given in Å, selected bond angles are given in degrees, and ΔG°/ΔG‡ are in kcal mol−1. Hydrogen atoms except the hydride are omitted for clarity. Color code: green, Ni; yellow, P; gray, C; red, O; white, H.
Figure 3. Free energy diagram for CO2 insertion into I, tBu2(PCP)Ni–H. Selected atom distances are given in Å, selected bond angles are given in degrees, and ΔG°/ΔG‡ are in kcal mol−1. Hydrogen atoms except the hydride are omitted for clarity. Color code: green, Ni; yellow, P; gray, C; red, O; white, H.
Catalysts 12 00790 g003
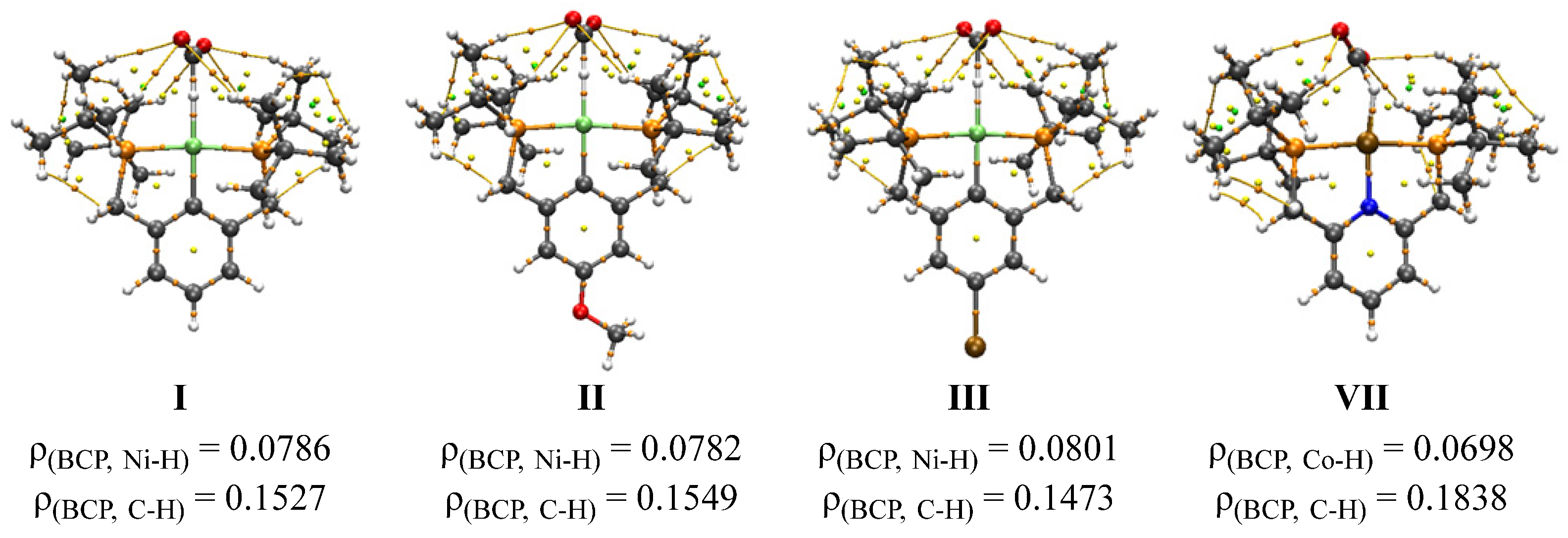
Catalysts 12 00790 g004 550
Figure 4. The critical points from atoms-in-molecules (AIMs) analysis of TM-(H)-formate complexes I, II, III, and VII. The orange balls represent the BCP (bond critical point), the yellow balls represent the ring critical point (RCP), and the bond paths for hydrogen bonds are shown in orange.
Figure 4. The critical points from atoms-in-molecules (AIMs) analysis of TM-(H)-formate complexes I, II, III, and VII. The orange balls represent the BCP (bond critical point), the yellow balls represent the ring critical point (RCP), and the bond paths for hydrogen bonds are shown in orange.
Catalysts 12 00790 g004
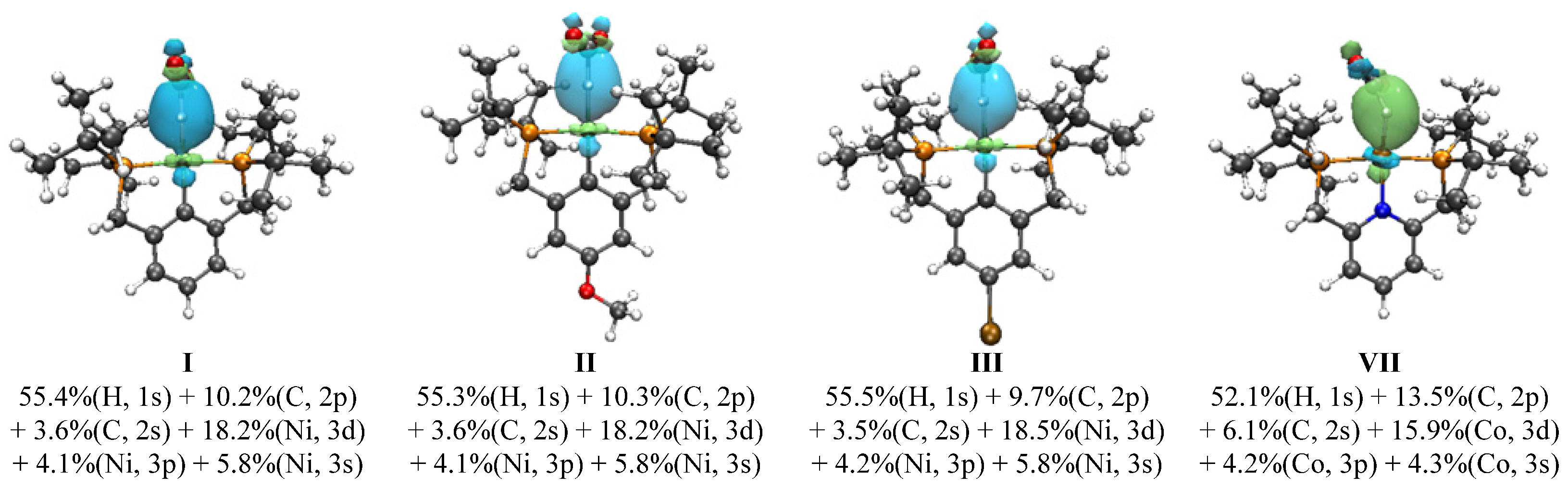
Catalysts 12 00790 g005 550
Figure 5. The natural adaptive orbitals (NAdOs) with their eigenvalues for the TM-H-C interaction in the TM-(H)-formate complexes I, II, III, and VII. Only the first NAdOs with the isovalue of 0.05 are presented in the main text.
Figure 5. The natural adaptive orbitals (NAdOs) with their eigenvalues for the TM-H-C interaction in the TM-(H)-formate complexes I, II, III, and VII. Only the first NAdOs with the isovalue of 0.05 are presented in the main text.
Catalysts 12 00790 g005
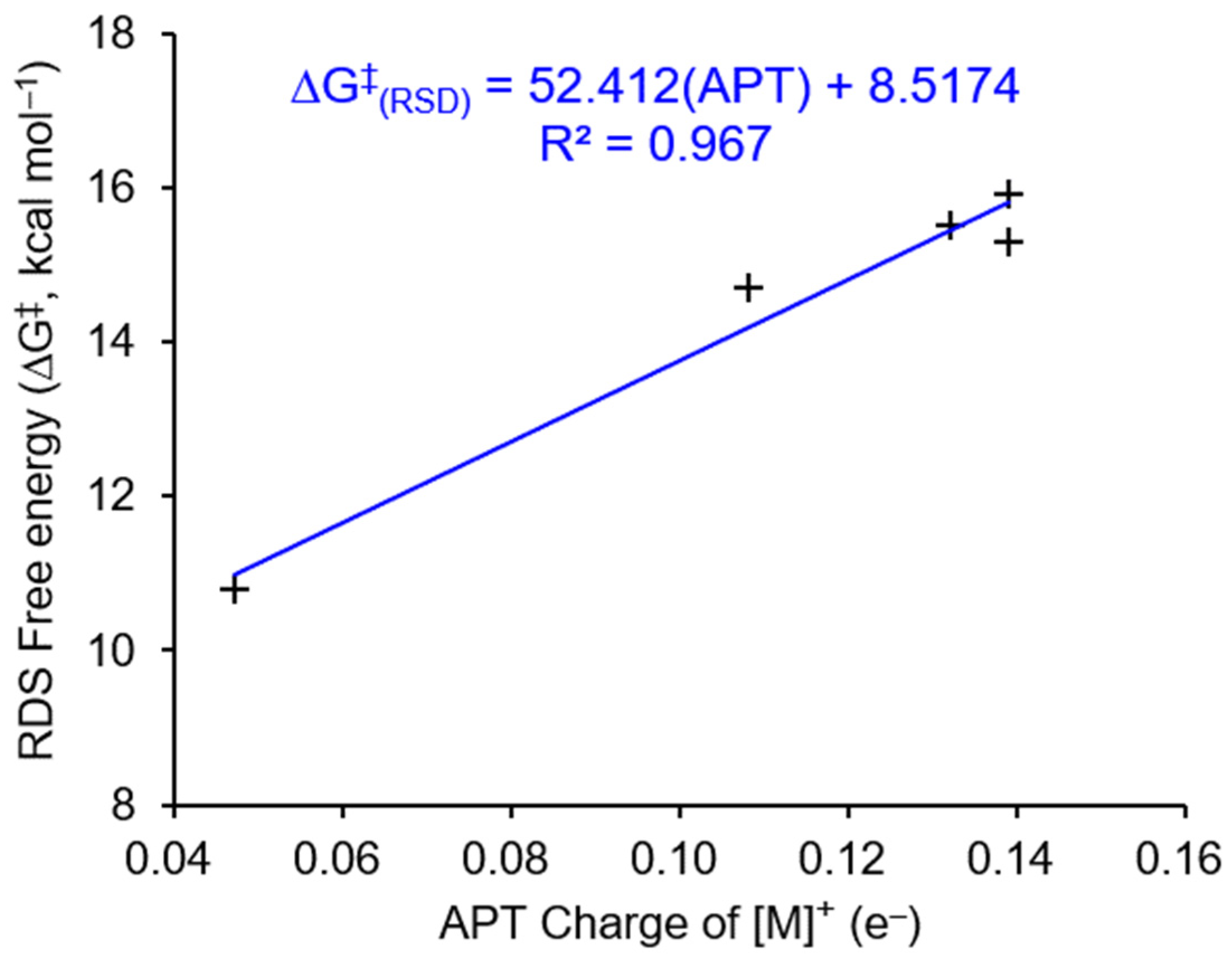
Catalysts 12 00790 g006 550
Figure 6. The linear fitting between the ΔG‡ of RDS for Ni–H complexes I to V and the APT charges of Ni atoms in the related [Ni]+.
Figure 6. The linear fitting between the ΔG‡ of RDS for Ni–H complexes I to V and the APT charges of Ni atoms in the related [Ni]+.
Catalysts 12 00790 g006
Catalysts 12 00790 g007 550
Figure 7. The fitting between the ΔG‡ of RDS for Ni–H complexes I to V and the computed hydricities. The blue line represents the second-order polynomial fitting and the red line represents the linear fitting.
Figure 7. The fitting between the ΔG‡ of RDS for Ni–H complexes I to V and the computed hydricities. The blue line represents the second-order polynomial fitting and the red line represents the linear fitting.
Catalysts 12 00790 g007
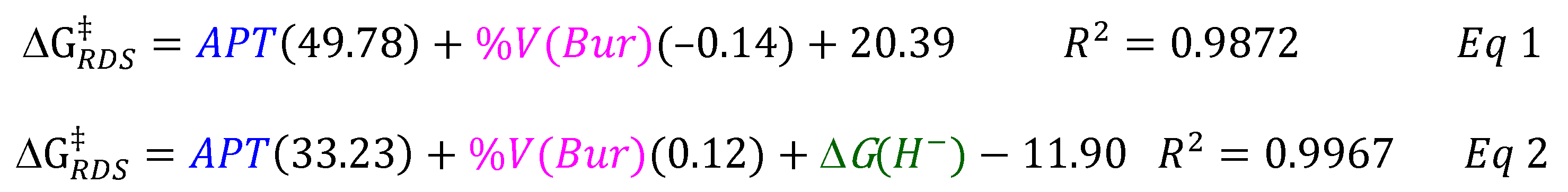
Catalysts 12 00790 sch002 550
Scheme 2. The multi-parameter models for the ΔG‡ of RDS for Ni–H complexes I to V. In Equations (1) and (2), APT is the APT charge of Ni atom in the axially vacant [Ni]+; %VBur is the percentages of buried volume in the axially vacant [Ni]+.
Scheme 2. The multi-parameter models for the ΔG‡ of RDS for Ni–H complexes I to V. In Equations (1) and (2), APT is the APT charge of Ni atom in the axially vacant [Ni]+; %VBur is the percentages of buried volume in the axially vacant [Ni]+.
Catalysts 12 00790 sch002
Table
Table 1. Computed hydricity, %VBur, and ΔG‡ for TM–H complexes I to VII.
Table 1. Computed hydricity, %VBur, and ΔG‡ for TM–H complexes I to VII.
SpeciesHydricityTS-2-3TS-3-4iAPT%VBurk (M−1 s−1)
I, tBu2(PCP)Ni–H50.610.615.50.13281.46.8 ± 0.7
II, tBu2(p-MeO-PCP)Ni–H50.110.715.30.13981.411.7 ± 1
III, tBu2(p-I-PCP)Ni–H52.311.115.90.13981.41.6 ± 0.2
IV, iPr2(PCP)Ni–H53.211.514.70.10877.44400
V, tBu2(PCyP)Ni–H43.310.410.80.04783.4-
VI, tBu2(PCP)Pd–H48.710.515.10.05281.3-
VII, tBu2(PNP)Co–H41.28.48.9−0.11677.7-
Note: APT is the APT charge of transition metal atom in the axially vacant [TM]+, %VBur is the percentage of buried volume in the axially vacant [TM]+. Reaction rate (k) is experimentally determined at 298 K in THF.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhang, M.; Liang, X.; Wang, Y.; Yang, H.; Liang, G. Insights into the Capture of CO2 by Nickel Hydride Complexes. Catalysts 2022, 12, 790. https://doi.org/10.3390/catal12070790

AMA Style

Zhang M, Liang X, Wang Y, Yang H, Liang G. Insights into the Capture of CO2 by Nickel Hydride Complexes. Catalysts. 2022; 12(7):790. https://doi.org/10.3390/catal12070790

Chicago/Turabian Style

Zhang, Min, Xiaoqing Liang, Yaozheng Wang, Hongyu Yang, and Guangchao Liang. 2022. "Insights into the Capture of CO2 by Nickel Hydride Complexes" Catalysts 12, no. 7: 790. https://doi.org/10.3390/catal12070790

APA Style

Zhang, M., Liang, X., Wang, Y., Yang, H., & Liang, G. (2022). Insights into the Capture of CO2 by Nickel Hydride Complexes. Catalysts, 12(7), 790. https://doi.org/10.3390/catal12070790

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop