Development of an Improved Kinetic Model for CO2 Hydrogenation to Methanol
Abstract
:1. Introduction
Statement of Originality
2. Literature Review and Theory
3. Results and Discussion
3.1. Diffusion Limitation Tests
3.2. Comparison of Models
3.2.1. Model of van den Bussche and Froment (VBF)
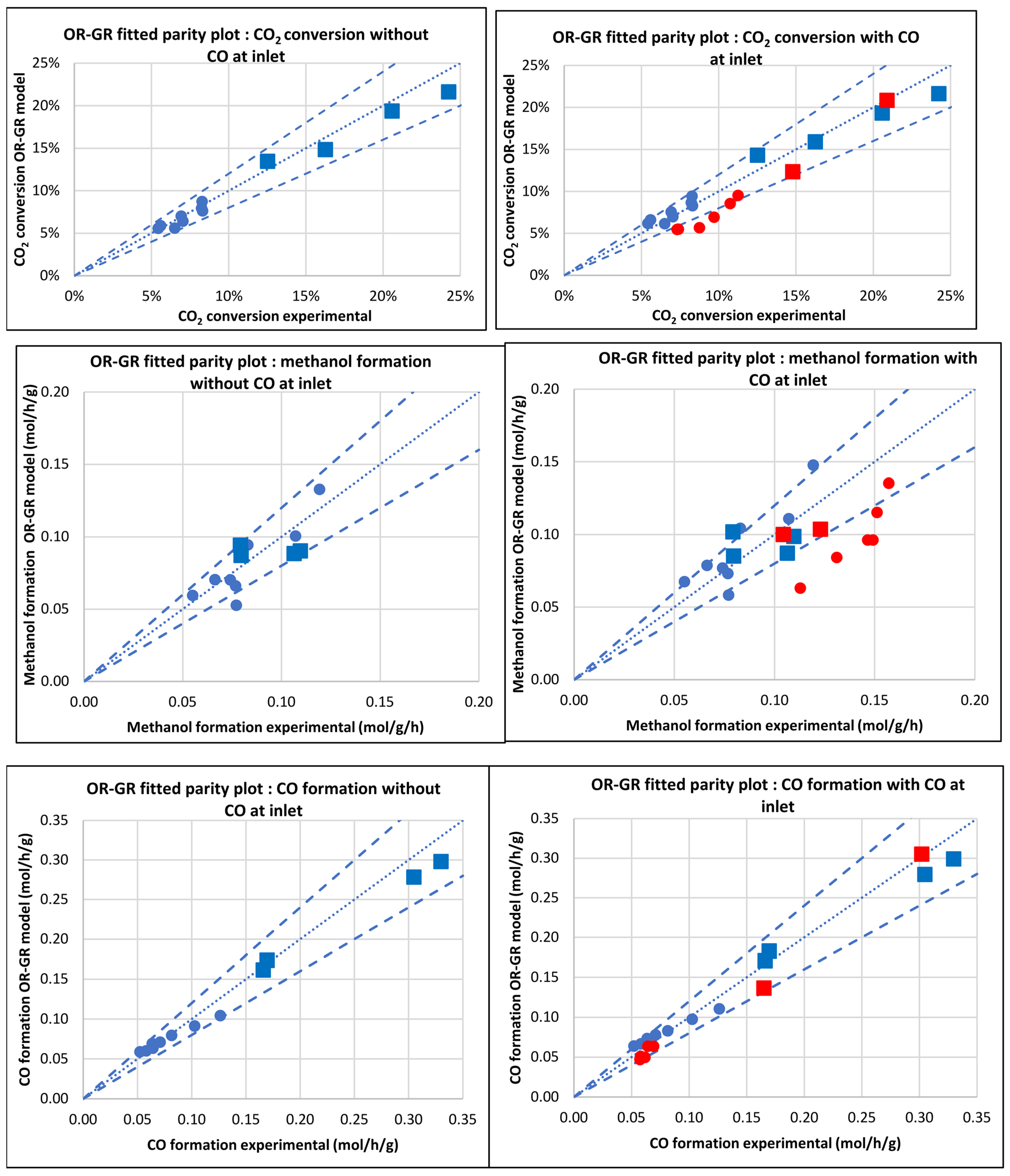
3.2.2. Model of Graaf et al. [12] (OR-GR)
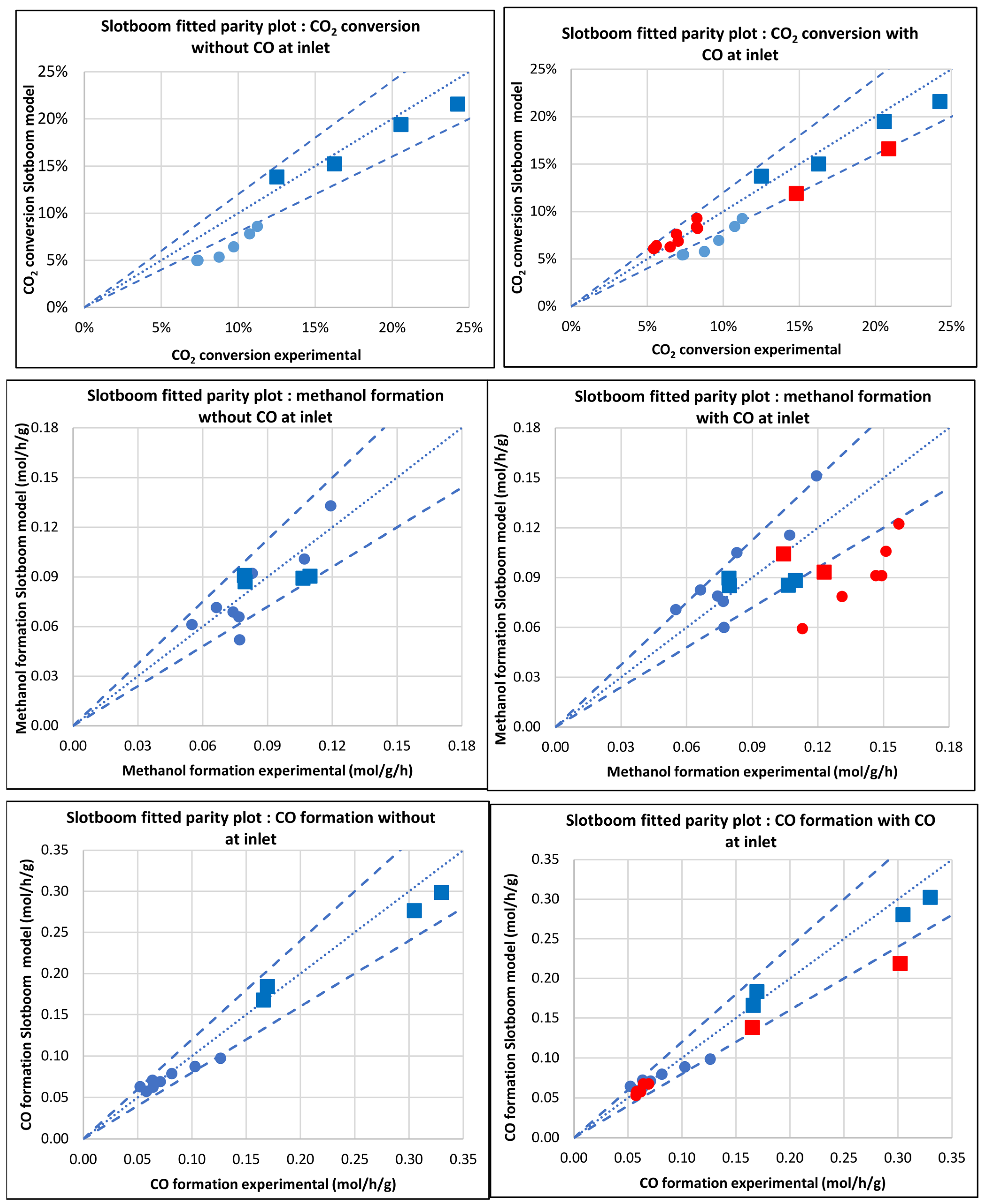
3.2.3. Model of Slotboom et al. [8] (Slotboom)
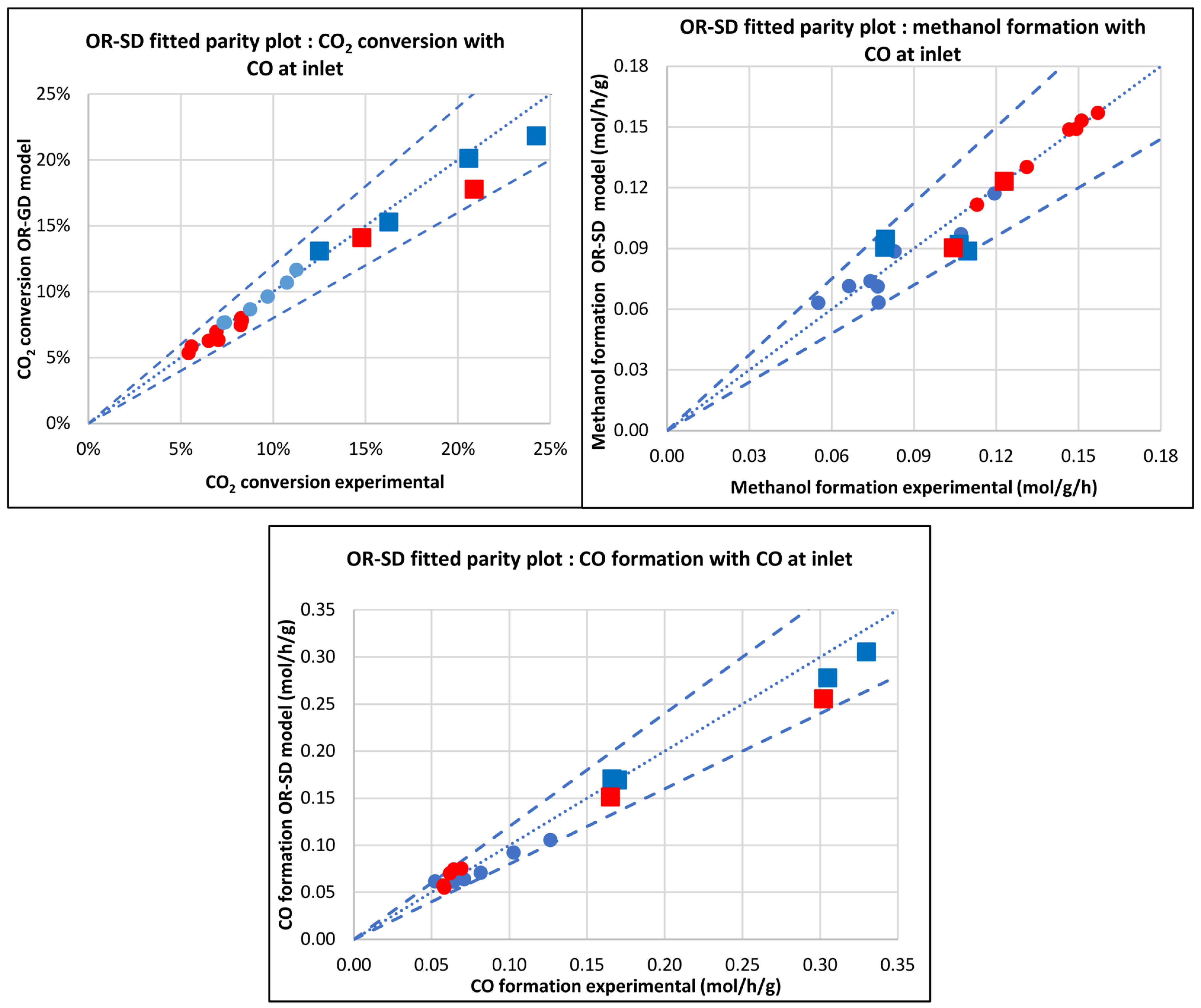
3.2.4. Original Siedel et al. [43] Model (OR-SD)
3.2.5. Modified Model (MOD)
3.3. Kinetic and Statistical Parameters
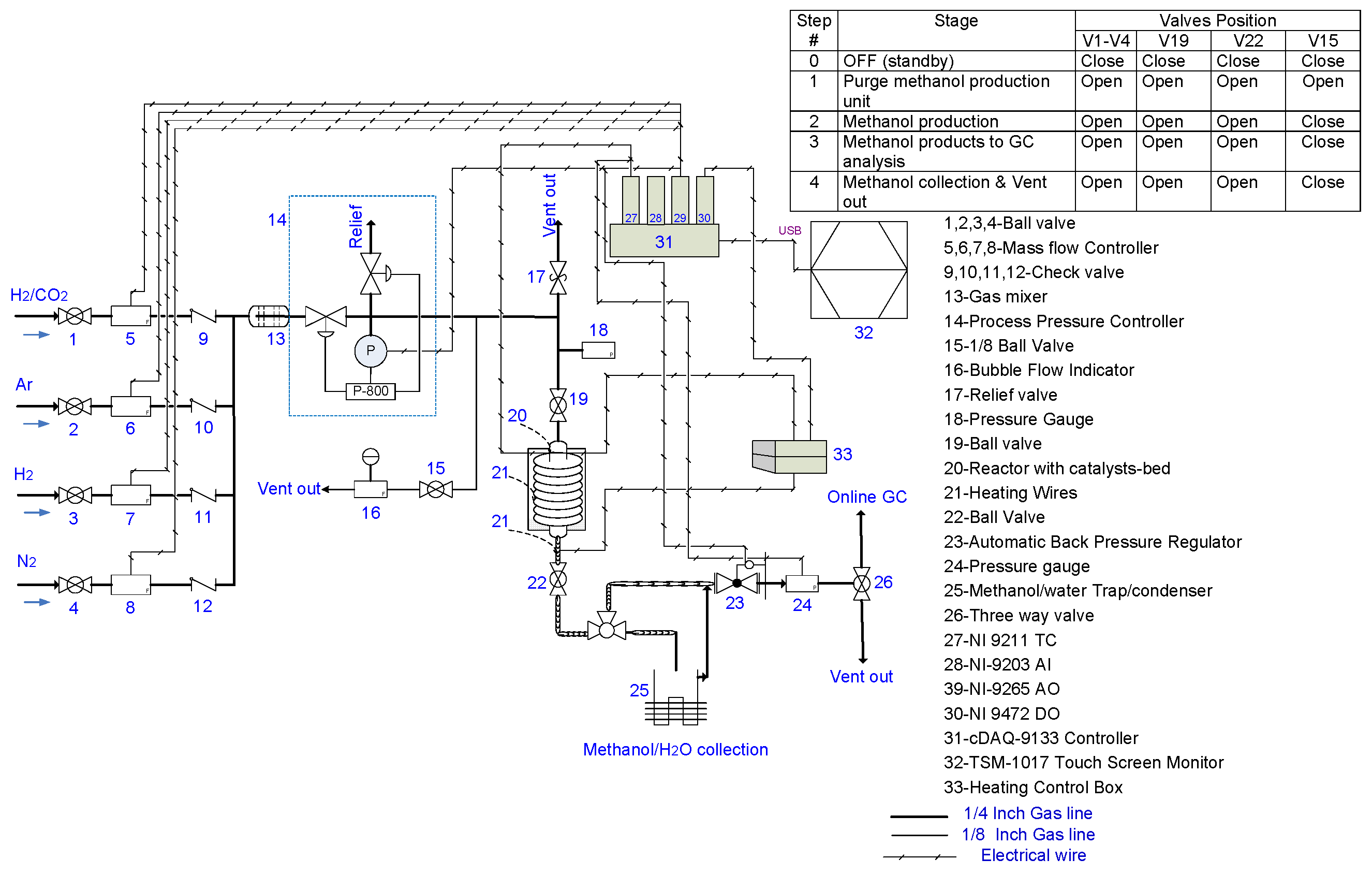
4. Experimental Procedure and Apparatus
5. Parameter Estimation
- -
- Rule 1: k > 0 imposed by logarithmic Arrhenius form.
- -
- Rule 2: Ea > 0 or bi > 0, imposed by bounds.
- -
- Rule 3: ΔH°ads < 0, imposed by bounds.
- -
- Rule 4: 0 < –ΔS°ads < S°gas.
Regression Method
6. Conclusions and Recommendations for Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation/Symbol | Meaning (Unit) |
| Ar | Area of the fixed bed reactor (m2) |
| bi | Logarithmic Arrhenius constants(–) |
| ΔG | Gibbs free energy (J mol−1) |
| ΔHr | Heat of reaction (kJ mol−1) |
| COR | Carbon oxide ratio (–) |
| GHSV0 | Gas hourly space velocity at nominal standard conditions (h−1) |
| GHSV | Gas hourly space velocity (NL.h−1.gcat−1) |
| Kpj° (T) | Temperature dependent equilibrium constant (–) |
| kj | Reaction rate constant (–) |
| Ki | Adsorption constant (–) |
| Molecular weight (kg mol−1) | |
| mc | Mass of the catalyst (kg) |
| mi | Mass of component (kg) |
| Npoints | Number of experimental points (–) |
| Np | Number of parameters (–) |
| Qv,0 | Standard volume flow (293 K and 1·105 Pa) (NmL min−1) |
| R | Ideal gas constant (J mol−1K−1) |
| RMSEi | root mean square error of molar fractions for component i (–) |
| rj | Reaction rate (mol/kgcat/s) |
| Mass flowrate (kg/s), | |
| SN | Stoichiometric number (–) |
| T | Temperature (K) |
| νi,j | Stoichiometric reaction rate constant (–) |
| x | Axial distance in the reactor (m) |
| wi | Weight fraction (–) |
| yi | Mole fraction (–) |
| Fixed bed porosity (–) | |
| ∗γ, γ0 | Relative surface contact free energy (–) |
| Θi | Fraction of free surface centers (–) |
| ρcat | Catalyst density (kg m−3) |
| Total amount of relative reduced surface centers (–) | |
| γ | Volume flow contraction (–) |
Appendix A. Experimental Data
| Partial Pressures Inlet (bar) | Outlet (mol/h/gcat) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Experiment | GHSV0 (h−1) | Pressure (bar) | T (°C) | H2 | CO2 | CO | Ar | CO2 Conversion (%) | H2/CO2 Ratio | CO | CH3OH |
| 1 | 774,000 | 50 | 210 | 35.9 | 10.1 | 0.0 | 4.0 | 5.4 | 3.6 | 7.1 × 10−2 | 6.6 × 10−2 |
| 2 | 774,000 | 50 | 210 | 35.9 | 8.1 | 0.0 | 6.0 | 5.9 | 4.4 | 5.8 × 10−2 | 5.5 × 10−2 |
| 3 | 774,000 | 60 | 210 | 43.3 | 14.3 | 0.0 | 2.3 | 7.0 | 3.0 | 1.0 × 10−1 | 1.1 × 10−1 |
| 4 | 774,000 | 77 | 210 | 55.6 | 18.4 | 0.0 | 3.0 | 8.2 | 3.0 | 1.3 × 10−1 | 1.2 × 10−1 |
| 5 | 774,000 | 50 | 210 | 35.4 | 11.7 | 1.0 | 1.9 | 7.4 | 3.0 | 6.9 × 10−2 | 1.5 × 10−1 |
| 6 | 774,000 | 50 | 210 | 35.4 | 11.7 | 1.0 | 1.9 | 7.1 | 3.0 | 6.4 × 10−2 | 1.5 × 10−1 |
| 7 | 516,000 | 50 | 210 | 36.1 | 11.9 | 0.0 | 2.0 | 6.9 | 3.0 | 5.2 × 10−2 | 7.7 × 10−2 |
| 8 | 516,000 | 50 | 235 | 36.1 | 11.9 | 0.0 | 2.0 | 12.5 | 3.0 | 8.2 × 10−2 | 8.3 × 10−2 |
| 9 | 516,000 | 50 | 260 | 36.1 | 11.9 | 0.0 | 2.0 | 20.6 | 3.8 | 5.8 × 10−2 | 1.1 × 10−1 |
| 10 | 516,000 | 50 | 210 | 38.2 | 10.2 | 0.0 | 1.6 | 8.3 | 3.8 | 5.8 × 10−2 | 1.5 × 10−1 |
| 11 | 516,000 | 50 | 235 | 38.2 | 10.2 | 0.0 | 1.6 | 16.3 | 3.8 | 6.2 × 10−2 | 1.6 × 10−1 |
| 12 | 516,000 | 50 | 260 | 38.2 | 10.2 | 0.0 | 1.6 | 24.3 | 3.8 | 6.4 × 10−2 | 7.4 × 10−2 |
| 13 | 516,000 | 50 | 210 | 35.4 | 11.7 | 1.0 | 1.9 | 9.7 | 3.0 | 1.7 × 10−1 | 7.9 × 10−2 |
| 14 | 516,000 | 50 | 235 | 35.4 | 11.7 | 1.0 | 1.9 | 14.8 | 3.0 | 3.3 × 10−1 | 8.0 × 10−2 |
| 15 | 516,000 | 50 | 260 | 35.4 | 11.7 | 1.0 | 1.9 | 20.9 | 3.0 | 6.4 × 10−2 | 7.7 × 10−2 |
| 16 | 516,000 | 40 | 210 | 28.9 | 9.6 | 0.0 | 1.5 | 6.5 | 3.0 | 1.7 × 10−1 | 1.1 × 10−1 |
| 17 | 516,000 | 65 | 210 | 46.9 | 15.6 | 0.0 | 2.5 | 8.3 | 3.0 | 3.1 × 10−1 | 1.1 × 10−1 |
| 18 | 516,000 | 40 | 210 | 28.4 | 9.3 | 0.8 | 1.5 | 8.7 | 3.0 | 5.8 × 10−2 | 1.3 × 10−1 |
| 19 | 516,000 | 65 | 210 | 46.0 | 15.2 | 1.3 | 2.5 | 10.7 | 3.0 | 1.7 × 10−1 | 1.2 × 10−1 |
| 20 | 516,000 | 75 | 210 | 53.1 | 17.5 | 1.5 | 2.9 | 11.2 | 3.0 | 3.0 × 10−1 | 1.0 × 10−1 |
References
- Kobl, K.; Thomas, S.; Zimmermann, Y.; Parkhomenko, K.; Roger, A.-C. Power-law kinetics of methanol synthesis from carbon dioxide and hydrogen on copper–zinc oxide catalysts with alumina or zirconia supports. Catal. Today 2016, 270, 31–42. [Google Scholar] [CrossRef]
- Kyrimis, S.; Potter, M.E.; Raja, R.; Armstrong, L.-M. Understanding catalytic CO2 and CO conversion into methanol using computational fluid dynamics. Faraday Discuss. 2021, 230, 100–123. [Google Scholar] [CrossRef] [PubMed]
- Prakash, G.K.S.; Olah, G.; Goeppert, A. Beyond Oil and Gas: The Methanol Economy, 3rd Updated and Enlarged ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Peter, M. Mechanistic Modeling of Reaction Kinetics and Dynamic Changes in Catalyst Morphology on a Mesoscopic scale. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2012. Available online: http://nbn-resolving.de/urn/resolver.pl?urn:nbn:de:bvb:91-diss-20120712-1095829-1-3 (accessed on 1 September 2023).
- Tarasov, A.V.; Seitz, F.; Schlögl, R.; Frei, E. In Situ Quantification of Reaction Adsorbates in Low-Temperature Methanol Synthesis on a High-Performance Cu/ZnO:Al Catalyst. ACS Catal. 2019, 9, 5537–5544. [Google Scholar] [CrossRef]
- Bisotti, F.; Fedeli, M.; Prifti, K.; Galeazzi, A.; Dell’angelo, A.; Manenti, F. Impact of Kinetic Models on Methanol Synthesis Reactor Predictions: In Silico Assessment and Comparison with Industrial Data. Ind. Eng. Chem. Res. 2022, 61, 2206–2226. [Google Scholar] [CrossRef]
- Bisotti, F.; Fedeli, M.; Prifti, K.; Galeazzi, A.; Dell’angelo, A.; Barbieri, M.; Pirola, C.; Bozzano, G.; Manenti, F. Century of Technology Trends in Methanol Synthesis: Any Need for Kinetics Refitting? Ind. Eng. Chem. Res. 2021, 60, 16032–16053. [Google Scholar] [CrossRef]
- Slotboom, Y.; Bos, M.; Pieper, J.; Vrieswijk, V.; Likozar, B.; Kersten, S.; Brilman, D. Critical assessment of steady-state kinetic models for the synthesis of methanol over an industrial Cu/ZnO/Al2O3 catalyst. Chem. Eng. J. 2020, 389, 124181. [Google Scholar] [CrossRef]
- Nestler, F.; Müller, V.P.; Ouda, M.; Hadrich, M.J.; Schaadt, A.; Bajohr, S.; Kolb, T. A novel approach for kinetic measurements in exothermic fixed bed reactors: Advancements in non-isothermal bed conditions demonstrated for methanol synthesis. React. Chem. Eng. 2021, 6, 1092–1107. [Google Scholar] [CrossRef]
- Nestler, F.; Schütze, A.; Ouda, M.; Hadrich, M.; Schaadt, A.; Bajohr, S.; Kolb, T. Kinetic modelling of methanol synthesis over commercial catalysts: A critical assessment. Chem. Eng. J. 2020, 394, 124881. [Google Scholar] [CrossRef]
- Votsmeier, M. Efficient implementation of detailed surface chemistry into reactor models using mapped rate data. Chem. Eng. Sci. 2009, 64, 1384–1389. [Google Scholar] [CrossRef]
- Klingenberger, M.; Hirsch, O.; Votsmeier, M. Efficient interpolation of precomputed kinetic data employing reduced multivariate Hermite Splines. Comput. Chem. Eng. 2017, 98, 21–30. [Google Scholar] [CrossRef]
- Seidel, C.; Jörke, A.; Vollbrecht, B.; Seidel-Morgenstern, A.; Kienle, A. Kinetic modeling of methanol synthesis from renewable resources. Chem. Eng. Sci. 2018, 175, 130–138, Erratum in Chem. Eng. Sci. 2020, 223, 115724. [Google Scholar] [CrossRef]
- Seidel, C.; Nikolic, D.; Felischak, M.; Petkovska, M.; Seidel-Morgenstern, A.; Kienle, A. Optimization of Methanol Synthesisunder Forced Periodic Operation. Processes 2021, 9, 872. [Google Scholar] [CrossRef]
- Skrzypek, J.; Lachowska, M.; Moroz, H. Kinetics of methanol synthesis over commercial copper/zinc oxide/alumina catalysts. Chem. Eng. Sci. 1991, 46, 2809–2813. [Google Scholar] [CrossRef]
- Kubota, T.; Hayakawa, I.; Mabuse, H.; Mori, K.; Ushikoshi, K.; Watanabe, T.; Saito, M. Kinetic study of methanol synthesis from carbon dioxide and hydrogen. Appl. Organomet. Chem. 2001, 15, 121–126. [Google Scholar] [CrossRef]
- van den Bussche, K.M.; Froment, G.F. A steady-state kinetic model for methanol synthesis and the water gas shift reaction on a commercial Cu/ZnO/Al2O3 catalyst. J. Catal. 1996, 161, 1–10. [Google Scholar] [CrossRef]
- de Oliveira Campos, B.L.; Herrera Delgado, K.; Wild, S.; Studt, F.; Pitter, S.; Sauer, J. Surface reaction kinetics of the methanol synthesis and the water gas shift reaction on Cu/ZnO/Al2O3. React. Chem. Eng. 2021, 6, 1483–1486. [Google Scholar] [CrossRef]
- de Oliveira Campos, B.L.; Herrera Delgado, K.; Pitter, S.; Sauer, J. Development of consistent kinetic models derived from a microkinetic model of the methanol synthesis. Ind. Eng. Chem. Res. 2021, 60, 15074–15086. [Google Scholar] [CrossRef]
- Bozzano, G.; Manenti, F. Efficient methanol synthesis: Perspectives, technologies and optimization strategies. Prog. Energy Combust. Sci. 2016, 56, 71–105. [Google Scholar] [CrossRef]
- Angelo, L.; Kobl, K.; Tejada, L.M.M.; Zimmermann, Y.; Parkhomenko, K.; Roger, A.-C. Study of CuZnMOx oxides (M = Al, Zr, Ce, CeZr) for the catalytic hydrogenation of CO2 into methanol. Comptes Rendus Chim. 2015, 18, 250–260. [Google Scholar] [CrossRef]
- Ruland, H.; Song, H.; Laudenschleger, D.; Stürmer, S.; Schmidt, S.; He, J.; Kähler, K.; Muhler, M.; Schlögl, R. CO2 Hydrogenation with Cu/ZnO/Al2O3: A Benchmark Study. ChemCatChem 2020, 12, 3216–3222. [Google Scholar] [CrossRef]
- Park, N.; Park, M.-J.; Lee, Y.-J.; Ha, K.-S.; Jun, K.-W. Kinetic modeling of methanol synthesis over commercial catalysts based on three-site adsorption. Fuel Process. Technol. 2014, 125, 139–147. [Google Scholar] [CrossRef]
- Graaf, G.; Stamhuis, E.; Beenackers, A. Kinetics of low-pressure methanol synthesis. Chem. Eng. Sci. 1988, 43, 3185–3195. [Google Scholar] [CrossRef]
- Díez-Ramírez, J.; Díaz, J.; Dorado, F.; Sánchez, P. Kinetics of the hydrogenation of CO2 to methanol at atmospheric pressure using a Pd-Cu-Zn/SiC catalyst. Fuel Process. Technol. 2018, 173, 173–181. [Google Scholar] [CrossRef]
- Ovesen, C.; Clausen, B.; Schiøtz, J.; Stoltze, P.; Topsøe, H.; Nørskov, J. Kinetic Implications of Dynamical Changes in Catalyst Morphology during Methanol Synthesis over Cu/ZnO Catalysts. J. Catal. 1997, 168, 133–142. [Google Scholar] [CrossRef]
- Choi, Y.; Futagami, K.; Fujitani, T.; Nakamura, J. The difference in the active sites for CO2 and CO hydrogenations on Cu/ZnO-based methanol synthesis catalysts. Catal. Lett. 2001, 73, 27–31. [Google Scholar] [CrossRef]
- Kamsuwan, T.; Guntida, A.; Praserthdam, P.; Jongsomjit, B. Differences in Deterioration Behaviors of Cu/ZnO/Al2O3 Catalysts with Different Cu Contents toward Hydrogenation of CO and CO2. ACS Omega 2022, 7, 25783–25797. [Google Scholar] [CrossRef]
- Shi, Y.-F.; Kang, P.-L.; Shang, C.; Liu, Z.-P. Methanol Synthesis from CO2/CO Mixture on Cu–Zn Catalysts from Microkinetics-Guided Machine Learning Pathway Search. J. Am. Chem. Soc. 2022, 144, 13401–13414. [Google Scholar] [CrossRef]
- Hoang, T.T.N.; Tsai, D.-H. Low-temperature methanol synthesis via (CO2 + CO) combined hydrogenation using Cu-ZnO/Al2O3 hybrid nanoparticle cluster. Appl. Catal. A Gen. 2022, 645, 118844. [Google Scholar] [CrossRef]
- Grunwaldt, J.-D.; Molenbroek, A.; Topsøe, N.-Y.; Topsøe, H.; Clausen, B. In Situ Investigations of Structural Changes in Cu/ZnO Catalysts. J. Catal. 2000, 194, 452–460. [Google Scholar] [CrossRef]
- Li, H.-X.; Yang, L.-Q.; Chi, Z.-Y.; Zhang, Y.-L.; Li, X.-G.; He, Y.-L.; Reina, T.R.; Xiao, W.-D. CO2 Hydrogenation to Methanol Over Cu/ZnO/Al2O3 Catalyst: Kinetic Modeling Based on Either Single- or Dual-Active Site Mechanism. Catal. Lett. 2022, 152, 3110–3124. [Google Scholar] [CrossRef]
- Nielsen, N.D.; Jensen, A.D.; Christensen, J.M. The roles of CO and CO2 in high pressure methanol synthesis over Cu-based catalysts. J. Catal. 2021, 393, 324–334. [Google Scholar] [CrossRef]
- Grabow, L.C.; Mavrikakis, M. Mechanism of methanol synthesis on Cu through CO2 and CO hydrogenation. ACS Catal. 2011, 1, 365–384. [Google Scholar] [CrossRef]
- Guo, S.-J.; Wang, H.; Qin, Z.-F.; Li, Z.-K.; Wang, G.-F.; Dong, M.; Fan, W.-B.; Wang, J.-G. Conversion of the CO and CO2 mixture to alcohols and hydrocarbons by hydrogenation under the influence of the water-gas shift reaction, a thermodynamic consideration. J. Fuel Chem. Technol. 2023, 51, 482–491. [Google Scholar] [CrossRef]
- Guo, S.; Wang, H.; Qin, Z.; Li, Z.; Wang, G.; Dong, M.; Fan, W.; Wang, J. Feasibility, Limit, and Suitable Reaction Conditions for the Production of Alcohols and Hydrocarbons from CO and CO2 through Hydrogenation, a Thermodynamic Consideration. Ind. Eng. Chem. Res. 2022, 61, 17027–17038. [Google Scholar] [CrossRef]
- Wilkinson, S.; van de Water, L.; Miller, B.; Simmons, M.; Stitt, E.; Watson, M. Understanding the generation of methanol synthesis and water gas shift activity over copper-based catalysts—A spatially resolved experimental kinetic study using steady and non-steady state operation under CO/CO2/H2 feeds. J. Catal. 2016, 337, 208–220. [Google Scholar] [CrossRef]
- Skrzypek, J.; Lachowska, M.; Grzesik, M.; Słoczyński, J.; Nowak, P. Thermodynamics and kinetics of low pressure methanol synthesis. Chem. Eng. J. Biochem. Eng. J. 1995, 58, 101–108. [Google Scholar] [CrossRef]
- Bernardi, A.; Gomoescu, L.; Wang, J.; Pantelides, C.C.; Chadwick, D.; Chachuat, B. Kinetic Model Discrimination for Methanol and DME Synthesis using Bayesian Estimation. IFAC-PapersOnLine 2019, 52, 335–340. [Google Scholar] [CrossRef]
- Bukhtiyarova, M.; Lunkenbein, T.; Kähler, K.; Schlögl, R. Methanol Synthesis from Industrial CO2 Sources: A Contribution to Chemical Energy Conversion. Catal. Lett. 2017, 147, 416–427. [Google Scholar] [CrossRef]
- Henkel, T. Modellierung von Reaktion und Stofftransport in geformten Katalysatoren am Beispiel der Methanolsynthese. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2011. [Google Scholar]
- Wang, X.; Zhang, H. Kinetically relevant variation triggered by hydrogen pressure: A mechanistic case study of CO2 hydrogenation to methanol over Cu/ZnO. J. Catal. 2022, 406, 145–156. [Google Scholar] [CrossRef]
- Vollbrecht, B. Zur Kinetik der Methanolsynthese an einem technischen Cu/ZnO/Al2O3 Katalysator. Ph.D. Thesis, Universität Magdeburg, Magdeburg, Germany, 2007. [Google Scholar]
- Kunkes, E.L.; Studt, F.; Abild-Pedersen, F.; Schlögl, R.; Behrens, M. Hydrogenation of CO2 to methanol and CO on Cu/ZnO/Al2O3: Is there a common intermediate or not? J. Catal. 2015, 328, 43–48. [Google Scholar] [CrossRef]
- Delgado, J.M.P.Q. A critical review of dispersion in packed beds. Heat Mass Transf. 2006, 42, 279–310. [Google Scholar] [CrossRef]
- Ertl, G.; Knözinger, H.; Weitkamp, J. (Eds.) Handbook of Heterogeneous Catalysis; Wiley-VCH: New York, NY, USA, 1997. [Google Scholar]

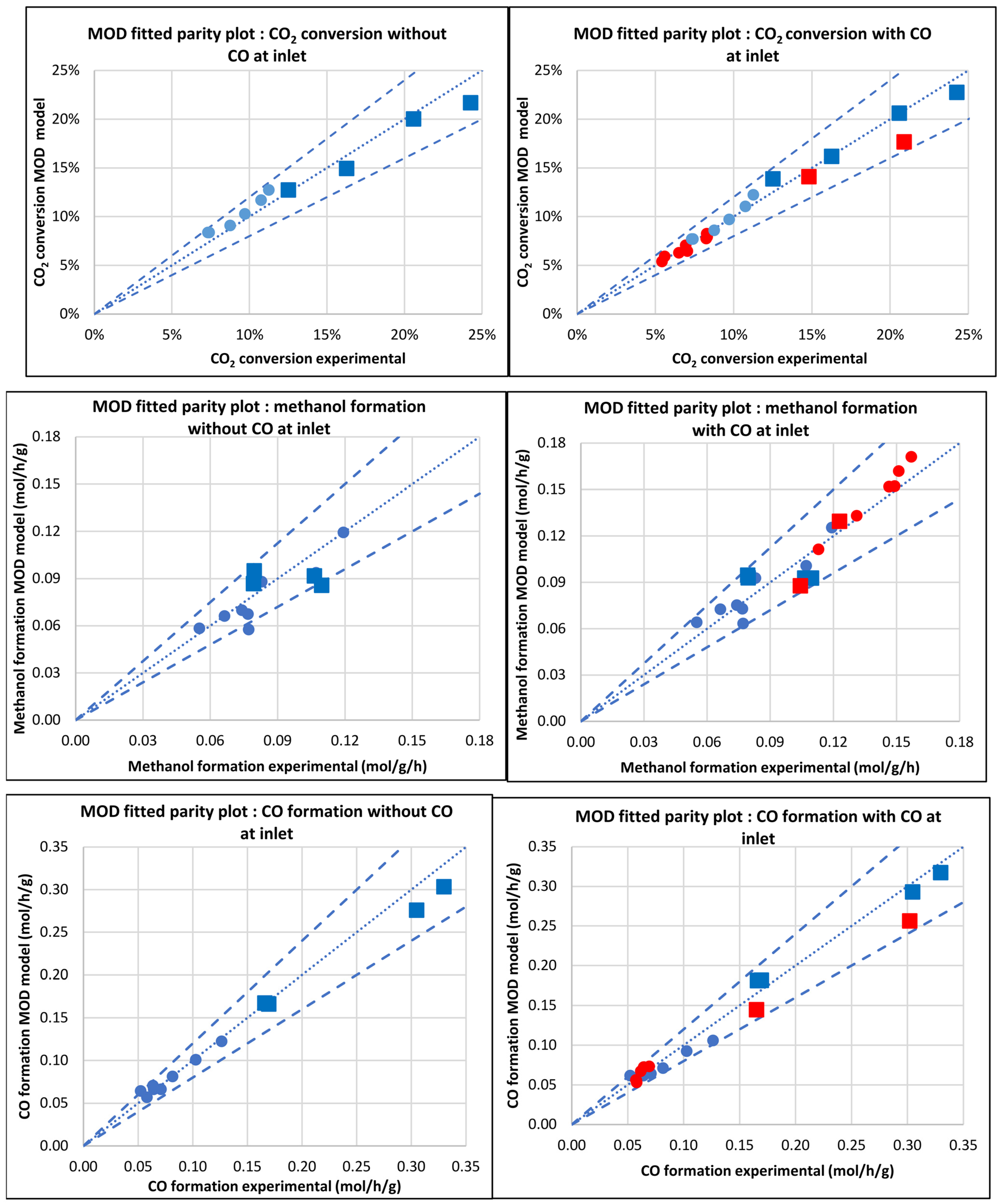
| Database/Author | No of Exper. Points | Reactor | Press. (bar) | Temp. (°C) | GHSV (NL.h−1.gcat−1) | H2 Feed (%v/v) | CO2 Feed (%v/v) | CO Feed (%v/v) | Inert Feed (%v/v) | COx Convers. (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| OR-GR | 89 | SBR 1 | 15–50 | 210–245 | 0.36–25.2 | 63–89 | 2.1–26 | 0–22 | - | - |
| VBF | 276 | PFFR 2 | 15–51 | 180–280 | - | - | - | - | - | - |
| de Oliveira Campos et al. [18] | 359 | PFFR | 40–60 | 210–260 | 24–40 | 35–60 | 0–20 | 3–30 | 20–50 | 0.9–30.9 |
| Slotboom et al. [8] | 234 | PFFR | 20–70 | 178–260 | 1.3–6.5 | 66–80 | 12–25 | - | 0–11 | 0.4–9.6 |
| Seidel et al. [13,14] | 139 | CSTR 3 | 30–70 | 230–260 | 3.6 | 60–76 | 0–13 | 0–21 | 15–16 | 2.9–52.6 |
| Park et al. [23] | 98 | PFFR | 50–90 | 230–340 | 8–40 | 50–83 | 2–16 | 7–29 | 0–28 | 5.1–56 |
| Internal Diffusion Limitation | External Diffusion Limitation | ||||
|---|---|---|---|---|---|
| Test 3 | Test 4 | Test 5 | Test 1 | Test 2 | |
| Parameter | Grain size: 40–63 µm | Grain size: 63–125 µm | Grain size: 125–250 µm | Flow: 28.5 mL/min | Flow: 57.0 mL/min |
| CO2 conversion (%) | 16.1 | 15.5 | 10.4 | 15.5 | 15.0 |
| Reaction | Rate Constant | Units | Experiments | |
|---|---|---|---|---|
| All with CO in Feed | ||||
| 1 | ||||
| 2 | ||||
| Reaction | Rate Constant | Units | Experiments | |
|---|---|---|---|---|
| All with CO in Feed | ||||
| 1 | 2.88 | |||
| 2 | 1.78 | |||
| 3 | 0.00 | 5.19 | ||
| Reaction | Reaction Rate Constant | Units | Experiments | |
|---|---|---|---|---|
| All with CO in Feed | ||||
| 1 | ||||
| 2 | ||||
| Reaction | Rate Constant | Units | For All Experiments, Including Those with CO in Feed |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | 9.97 |
| Reaction | Rate Constant | Units | Experiments: | |
|---|---|---|---|---|
| With CO in Feed | ||||
| 1 | ||||
| 2 | ||||
| Parameters | Units | MOD | OR-SD |
|---|---|---|---|
| ER1 | kJ.mol−1 | 25.0 | 5.4 |
| ER2 | kJ.mol−1 | 98.2 | 76.4 |
| ER3 | kJ.mol–1 | - | 12 |
| k1 | mol/h/g/bar2 | 7.45 × 10−1 | 2.377 × 10−1 |
| k2 | mol/h/g/bar2 | 8.62 × 10−3 | 8.56 × 10−3 |
| k3 | mol/h/g/bar2 | - | 9.97 × 10−4 |
| b-CO | bar−1 | 0.743 | 0.147 |
| b-H2O | bar−1 | 0.058 | 0.030 |
| b-H2 | - | 3786 bar−0.5 | 1361 bar−1 |
| b-O | - | 178 | 1600 |
| b-CO2 | bar−1 | 0 | 0 |
| Model | Sumres (%) | No of Parameters |
|---|---|---|
| VBF | 7 | 10 |
| OR-GR | 8.2 | 12 |
| Slotboom | 9 | 6 |
| OR-SD | 1.7 | 12 |
| MOD | 1.7 | 9 |
| Parameters | Units | Test 1 | Test 2 |
|---|---|---|---|
| Mass of catalyst | mg | 4.0 | 8.0 |
| Q | Nml/min | 28.5 | 57.0 |
| Temperature | °C | 260 | 260 |
| Pressure | bar | 50 | 50 |
| Sample size | µm | 63–125 | 63–125 |
| Parameters | Units | Test 3 | Test 4 | Test 5 |
|---|---|---|---|---|
| Particle size | µm | S1 = 40–63 | S2 = 63–125 | S3 = 125–250 |
| mc | mg | 8.0 | 8.0 | 8.0 |
| Q | Nml/min | 57 | 57 | 57 |
| Temperature | °C | 260 | 260 | 260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbatha, S.; Thomas, S.; Parkhomenko, K.; Roger, A.-C.; Louis, B.; Cui, X.; Everson, R.; Langmi, H.; Musyoka, N.; Ren, J. Development of an Improved Kinetic Model for CO2 Hydrogenation to Methanol. Catalysts 2023, 13, 1349. https://doi.org/10.3390/catal13101349
Mbatha S, Thomas S, Parkhomenko K, Roger A-C, Louis B, Cui X, Everson R, Langmi H, Musyoka N, Ren J. Development of an Improved Kinetic Model for CO2 Hydrogenation to Methanol. Catalysts. 2023; 13(10):1349. https://doi.org/10.3390/catal13101349
Chicago/Turabian StyleMbatha, Siphesihle, Sébastien Thomas, Ksenia Parkhomenko, Anne-Cécile Roger, Benoit Louis, Xiaoti Cui, Ray Everson, Henrietta Langmi, Nicholas Musyoka, and Jianwei Ren. 2023. "Development of an Improved Kinetic Model for CO2 Hydrogenation to Methanol" Catalysts 13, no. 10: 1349. https://doi.org/10.3390/catal13101349
APA StyleMbatha, S., Thomas, S., Parkhomenko, K., Roger, A.-C., Louis, B., Cui, X., Everson, R., Langmi, H., Musyoka, N., & Ren, J. (2023). Development of an Improved Kinetic Model for CO2 Hydrogenation to Methanol. Catalysts, 13(10), 1349. https://doi.org/10.3390/catal13101349