Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst
Abstract
:1. Introduction
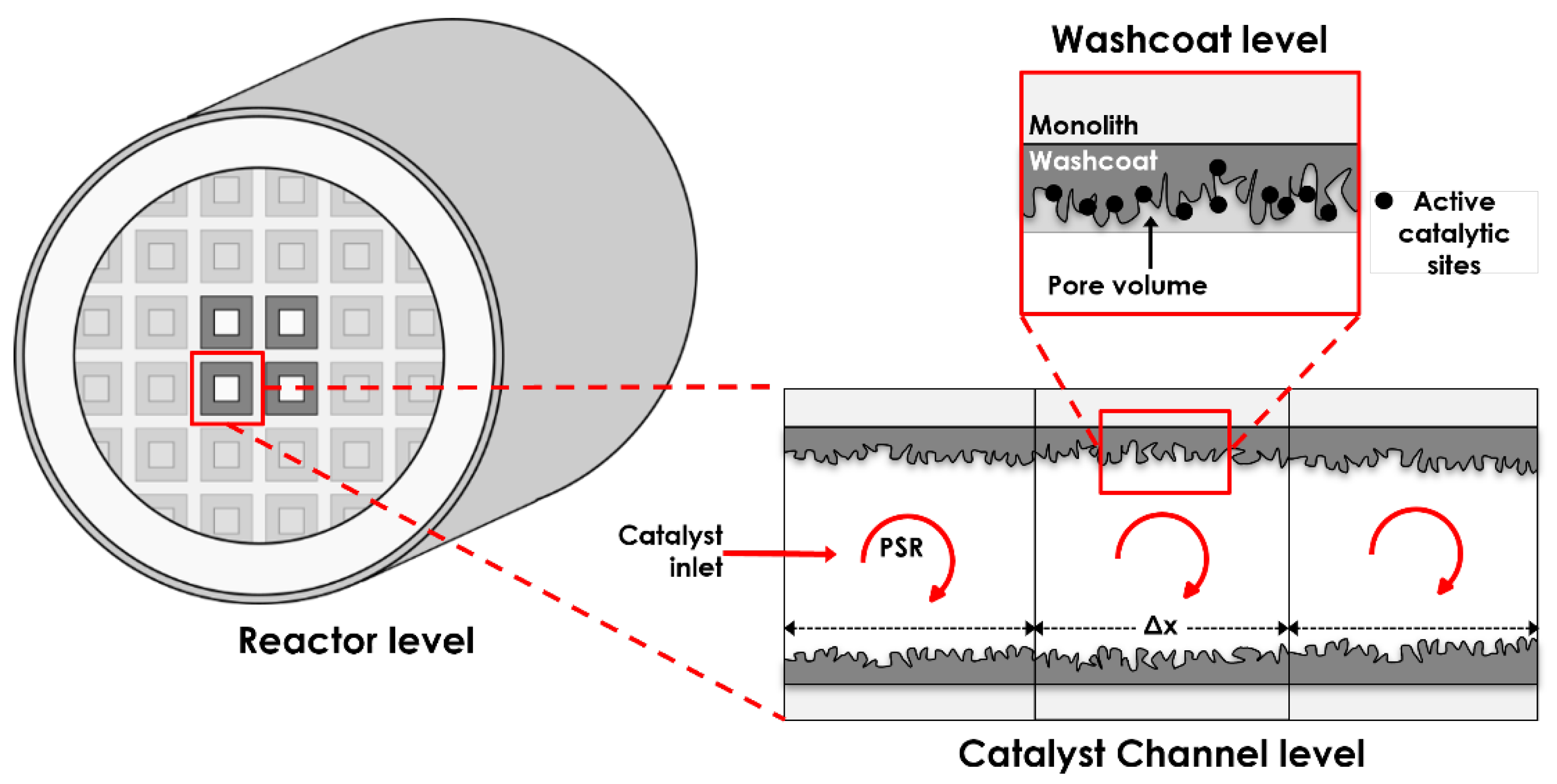
2. Model Description
2.1. Conservation Equations
2.2. Flow Equations
3. Experiments
3.1. Fixed-Bed Reactor Experiment
3.1.1. Setup
3.1.2. Catalyst and Characterization
3.1.3. Experimental Procedure
3.2. Monolith Experiment from Literature
4. 1D Simulations Setup
5. Surface Chemistry Description and Development
6. Results and Discussion
6.1. Fixed-Bed Reactor Experiments
6.2. Monolith Experiments from the Literature
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman letters | |
| A | Cross-sectional channel area (m) |
| Catalytic surface area in current cell (m) | |
| Geometric surface area of the wall in the cell (m) | |
| Specific heat capacity at constant pressure (J/(kg*K)) | |
| Concentration of species i in the bulk gas (mol/m) | |
| Concentration of species i in the thin-film layer (mol/m) | |
| Hydraulic diameter of the channel (m) | |
| Horizontal distance between representative channels (m) | |
| Diffusion coefficient of species i (m/s) | |
| Thermal diffusion coefficient (m/s) | |
| Friction factor (:) | |
| Mean specific enthalpy of bulk gas (J/kg) | |
| Specific enthalpy of species j transported between bulk gas | |
| and thin-film layer. If the species is transported from the bulk gas, | |
| the bulk gas enthalpy is used; if it is transported to the bulk gas, | |
| the thin-film layer enthalpy is used (J/kg) | |
| Specific enthalpy of species j in surface phase m (J/kg) | |
| Heat transfer coefficient (W/(m*K)) | |
| Thermal conductivity (W/(m*K)) | |
| Mass transfer coefficient of species i (m/s) | |
| Thermal conductivity (W/(m*K)) | |
| Overall effectiveness factor (:) | |
| Overall heat transfer factor (:) | |
| Overall mass transfer factor (:) | |
| Horizontal heat conductivity (W/(m*K)) | |
| Vertical heat conductivity (W/(m*K)) | |
| Gas mass in cell (kg) | |
| Number of gas phase species | |
| Number of surface phases | |
| Number of species in surface phase m | |
| Nusselt number (:) | |
| Asymptotic Nusselt number for constant flux boundary condition (:) | |
| p | Pressure (Pa) |
| P | Geometric wetted perimeter of the channel (m) |
| Prandtl number (:) | |
| Reynolds number (:) | |
| Schmidt number of species i (:) | |
| Sherwood number for species i (:) | |
| Asymptotic Sherwood number for constant flux boundary condition (:) | |
| t | Time (s) |
| Ambient temperature (K) | |
| Gas temperature (K) | |
| Temperature of the wall and thin-film layer (K) | |
| v | Fluid velocity along the channel (m/s) |
| Volume of the thin-film layer gas in the current cell (m) | |
| Volume of the solid wall material (substrate) in the current cell (m) | |
| w | Radial distance through the washcoat (m) |
| Molecular weight of species i (kg/mol) | |
| Mass fraction of species i (:) | |
| Greek letters | |
| site density of surface phase n (mol/m) | |
| length of cell (m) | |
| site fraction of species i (:) | |
| Planck mean absorption coefficient for species i (1/(m*Pa)) | |
| dynamic viscosity (kg/(m*s)) | |
| dynamic viscosity of species i (kg/(m*s)) | |
| gas density (kg/m) | |
| Boltzmann constant ((m*kg)/(s*K)) | |
| site occupancy number of species i at site n (:) | |
| species production rate from reactions in given phase, | |
| (mole/m) for gas phase, (mole/m) for surface phase | |
| Subscripts | |
| g | Bulk gas |
| Inlet flow to the cell | |
| i | Species i |
| j | Species j |
| l | Current washcoat layer |
| p | Thin-film layer gas |
| s | Substrate material |
| Negative horizontal direction | |
| Positive horizontal direction | |
| Negative vertical direction | |
| Positive vertical direction | |
| Abbreviations | |
| GHSV | Gas hourly space velocity |
| MGT | Micro gas turbine |
| MSR | Methane steam reforming |
| SOFC | Solid oxide fuel cell |
References
- Yusaf, T.; Fernandes, L.; Abu Talib, A.; Altarazi, Y.; Alrefae, W.; Kadirgama, K.; Ramasamy, D.; Jayasuriya, A.; Brown, G.; Mamat, R.; et al. Sustainable Aviation—Hydrogen Is the Future. Sustainability 2022, 14, 548. [Google Scholar] [CrossRef]
- Jain, I. Hydrogen the fuel for 21st century. Int. J. Hydrogen Energy 2009, 34, 7368–7378. [Google Scholar] [CrossRef]
- Zuben, T.; Moreira, D.; Germscheidt, R.; Yoshimura, R.; Dorretto, D.; Araujo, A.; Salles, A., Jr.; Bonacin, J. Is hydrogen indispensable for a sustainable world? A review of H2 applications and perspectives for the next years. J. Braz. Chem. Soc. 2022, 33, 824–843. [Google Scholar] [CrossRef]
- European Commission. The European Green Deal; European Commission: Brussels, Belgium, 2019; Volume 53, p. 24. [Google Scholar]
- Cuevas, F.; Zhang, J.; Latroche, M. The vision of France, Germany, and the European Union on future hydrogen energy research and innovation. Engineering 2021, 7, 715–718. [Google Scholar] [CrossRef]
- Felseghi, R.; Carcadea, E.; Raboaca, M.; Trufin, C.; Filote, C. Hydrogen fuel cell technology for the sustainable future of stationary applications. Energies 2019, 12, 4593. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Safari, A. Comparative study of different fuel cell technologies. Renew. Sustain. Energy Rev. 2021, 16, 981–989. [Google Scholar] [CrossRef]
- Berg, H.; Himmelberg, A.; Lehmann, M.; Dückershoff, R.; Neumann, M. The Turbo-Fuel-Cell 1.0–family concept. IOP Conf. Ser. Mater. Sci. Eng. 2018, 297, 012004. [Google Scholar] [CrossRef]
- Herrera Delgado, K. Surface Reaction Kinetics for Oxidation and Reforming of H2, CO, and CH4 over Nickel-Based Catalysts; Karlsruher Institut für Technologie (KIT): Karlsruhe, Germany, 2014. [Google Scholar]
- Younas, M.; Shafique, S.; Hafeez, A.; Javed, F.; Rehman, F. An overview of hydrogen production: Current status, potential, and challenges. Fuel 2022, 316, 123317. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J. Production of synthesis gas. Catal. Today 1993, 18, 305–324. [Google Scholar] [CrossRef]
- Angeli, S.; Monteleone, G.; Giaconia, A.; Lemonidou, A. State-of-the-art catalysts for CH4 steam reforming at low temperature. Int. J. Hydrogen Energy 2014, 39, 1979–1997. [Google Scholar] [CrossRef]
- Meloni, E.; Martino, M.; Palma, V. A short review on Ni based catalysts and related engineering issues for methane steam reforming. Catalysts 2020, 10, 352. [Google Scholar] [CrossRef]
- Sá, S.; Silva, H.; Brandão, L.; Sousa, J.; Mendes, A. Catalysts for methanol steam reforming—A review. Appl. Catal. Environ. 2010, 99, 43–57. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J. Coking on nickel catalysts for steam reforming of hydrocarbons. J. Catal. 1974, 33, 184–201. [Google Scholar] [CrossRef]
- Pashchenko, D.; Makarov, I. Carbon deposition in steam methane reforming over a Ni-based catalyst: Experimental and thermodynamic analysis. Energy 2021, 222, 119993. [Google Scholar] [CrossRef]
- Trimm, D. Coke formation and minimisation during steam reforming reactions. Catal. Today 1997, 37, 233–238. [Google Scholar] [CrossRef]
- Laidler, K.; Meiser, J. Physical Chemistry; Benjamin-Cummings Publishing Co., Subs. of Addison Wesley Longman, University of Michigan: Ann Arbor, MI, USA, 1982; Volume 1. [Google Scholar]
- Baxter, R.; Hu, P. Insight into why the Langmuir–Hinshelwood mechanism is generally preferred. J. Chem. Phys. 2002, 116, 4379–4381. [Google Scholar] [CrossRef]
- Bowen, J.; Acrivos, A.; Oppenheim, A. Singular perturbation refinement to quasi-steady state approximation in chemical kinetics. Chem. Eng. Sci. 1963, 18, 177–188. [Google Scholar] [CrossRef]
- Salciccioli, M.; Stamatakis, M.; Caratzoulas, S.; Vlachos, D. A review of multiscale modeling of metal-catalyzed reactions: Mechanism development for complexity and emergent behavior. Chem. Eng. Sci. 2011, 66, 4319–4355. [Google Scholar] [CrossRef]
- Quirino, P.; Amaral, A.; Pontes, K.; Rossi, F.; Manenti, F. Impact of kinetic models in the prediction accuracy of an industrial steam methane reforming unit. Comput. Chem. Eng. 2021, 152, 107379. [Google Scholar] [CrossRef]
- Singh, C.; Saraf, D. Simulation of side fired steam-hydrocarbon reformers. Ind. Eng. Chem. Process. Des. Dev. 1979, 18, 1–7. [Google Scholar] [CrossRef]
- Hou, K.; Hughes, R. The kinetics of methane steam reforming over a Ni/α-Al2O catalyst. Chem. Eng. J. 2001, 82, 311–328. [Google Scholar] [CrossRef]
- Numaguchi, T.; Kikuchi, K. Intrinsic kinetics and design simulation in a complex reaction network; steam-methane reforming. Chem. Eng. Sci. 1988, 43, 2295–2301. [Google Scholar] [CrossRef]
- Xu, J.; Froment, G. Methane steam reforming, methanation and water-gas shift: I. Intrinsic kinetics. AIChE J. 1989, 35, 88–96. [Google Scholar] [CrossRef]
- Maier, L.; Schädel, B.; Herrera Delgado, K.; Tischer, S.; Deutschmann, O. Steam reforming of methane over nickel: Development of a multi-step surface reaction mechanism. Top. Catal. 2011, 54, 845–858. [Google Scholar] [CrossRef]
- Matera, S.; Schneider, W.; Heyden, A.; Savara, A. Progress in accurate chemical kinetic modeling, simulations, and parameter estimation for heterogeneous catalysis. ACS Catal. 2019, 9, 6624–6647. [Google Scholar] [CrossRef]
- Loge AB©. 2022. Available online: http://logesoft.com/loge-software/ (accessed on 3 March 2022).
- Fröjd, K.; Mauss, F. A three-parameter transient 1D catalyst model. SAE Int. J. Engines 2011, 4, 1747–1763. [Google Scholar] [CrossRef]
- Aslanjan, J.; Klauer, C.; Perlman, C.; Günther, V.; Mauss, F. Simulation of a Three-Way Catalyst Using Transient Single and Multi-Channel Models; SAE Technical Paper; SAE: Detroit, MI, USA, 2017. [Google Scholar]
- Richter, J.; Günther, V.; Mauss, F. Reaction mechanism development and investigation on the convergence influence in a 1D catalyst model for a γ-alumina stabilized three-way catalyst. In Proceedings of the International Symposium on Diagnostics and Modeling of Combustion in Internal Combustion Engines, Sapporo, Japan, 28–31 July 2022; p. A10-3. [Google Scholar]
- Rakhi, G.V.; Richter, J.; Mauss, F. Steam reforming of methane over nickel catalyst using a one-dimensional model. Int. J. Environ. Sci. 2022, 5, 1–32. [Google Scholar] [CrossRef]
- Seidel, L. Development and Reduction of a Multicomponent Reference Fuel for Gasoline; BTU Cottbus-Senftenberg: Cottbus, Germany, 2017. [Google Scholar]
- Incropera, F.; DeWitt, D.; Bergman, T.; Lavine, A. Fundamentals of Heat and Mass Transfer 6E; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Ramanathan, K.; Balakotaiah, V.; West, D. Light-off criterion and transient analysis of catalytic monoliths. Chem. Eng. Sci. 2003, 58, 1381–1405. [Google Scholar] [CrossRef]
- Santos, H.; Costa, M. Modelling transport phenomena and chemical reactions in automotive three-way catalytic converters. Chem. Eng. J. 2009, 148, 173–183. [Google Scholar] [CrossRef]
- DETCHEM Detailed Chemistry in CFD|Simulate Reacting Flows. 2022. Available online: https://www.detchem.com/mechanisms (accessed on 3 March 2022).









| Parameter | Unit | Fixed-Bed Reactor Experiment (with Increasing GHSV) | Monolith Experiment from [27] |
|---|---|---|---|
| Inlet gas composition | Mole fraction (-) | CH: 0.33; HO: 0.67 | CH: 0.07; HO: 0.18; Ar: 0.75 |
| Inlet gas temperature | K | 1013.25 | 573.15 |
| Initial catalyst surface temperature | K | 998.95, 974.85, 954.2, 939.3, 934.0, 928.50 | 922.89, 1020.28, 1119.93, 1215.35 |
| Ambient (oven) temperature | K | 1012.00, 1005.10, 997.50, 992.50, 989.30, 987.50 | 922.89, 1020.28,1119.93, 1215.35 |
| Inlet gas pressure | 10 Pa | 1.02, 1.02, 1.02, 1.03, 1.03, 1.03 | 1.01 |
| Inlet mass flow | 10 kg/s | 3.30, 6.60, 9.90, 13.20, 16.5, 19.8 | - |
| Inlet velocity | m/s | - | 0.056 |
| Parameter | Unit | Fixed-Bed Reactor Experiment | Monolith Experiment from [27] |
|---|---|---|---|
| Catalyst outer geometry | - | Circular | Circular |
| Channel geometry | - | Quadratic | Quadratic |
| Number of cell | - | 25 | 25 |
| Channel density | 10 1/m | 9.30 | 5.04 |
| Axial heat conductivity | W/mK | 1.00 × 10 | 85.0 |
| Catalyst length | m | 2.5 × 10 | 3.00 × 10 |
| Catalyst radius | m | 4.85 | 7.5 |
| Hydraulic diameter | m | 9.72 × 10 | 1.13 × 10 |
| Surface area per catalyst length | m/m | 1.00 × 10 | 1.00 × 10 |
| Reaction | A (cm, mol, s) | (-) | E (kJ/mol) | Revision | |
|---|---|---|---|---|---|
| R1 | H + 2Ni(s) → 2H(s) | 1.000 × 10 | 0.00 | s.c. | |
| R2 | 2H(s) → 2Ni(s) + H | 2.545 × 10 | 0.00 | 81.21 | This work |
| R3 | O + 2Ni(s) → 2O(s) | 1.000 × 10 | 0.00 | s.c. | |
| R4 | 2O(s) → 2Ni(s) + O | 4.283 × 10 | 0.00 | 474.95 | |
| R5 | CH + Ni(s) → CH(s) | 8.000 × 10 | 0.00 | s.c. | |
| R6 | CH(s) → CH + Ni(s) | 8.705 × 10 | 0.00 | 37.55 | |
| R7 | HO + Ni(s) → HO(s) | 1.000 × 10 | 0.00 | s.c. | |
| R8 | HO(s) → HO + Ni(s) | 3.732 × 10 | 0.00 | 60.79 | |
| R9 | CO + Ni(s) → CO(s) | 1.000 × 10 | 0.00 | s.c. | |
| R10 | CO(s) → CO + Ni(s) | 6.447 × 10 | 0.00 | 25.98 | |
| R11 | CO + Ni(s) → CO(s) | 5.000 × 10 | 0.00 | s.c. | |
| R12 | CO(s) → CO + Ni(s) | 5.660 × 10 | 0.70 | 111.00 | This work |
| Coverage /CO(s) | 0.00 | 0.00 | −50.00 | ||
| R13 | CH(s) + Ni(s) → CH(s) + H(s) | 4.440 × 10 | 0.00 | 40.40 | This work |
| R14 | CH(s) + H(s) → CH(s) + Ni(s) | 6.034 × 10 | 0.00 | 61.58 | |
| R15 | CH(s) + Ni(s) → CH(s) + H(s) | 3.700 × 10 | 0.00 | 100.00 | |
| R16 | CH(s) + H(s) → CH(s) + Ni(s) | 1.293 × 10 | 0.00 | 55.33 | |
| R17 | CH(s) + Ni(s) → CH(s) + H(s) | 3.700 × 10 | 0.00 | 97.10 | |
| R18 | CH(s) + H(s) → CH(s) + Ni(s) | 4.089 × 10 | 0.00 | 79.18 | |
| R19 | CH(s) + Ni(s) → C(s) + H(s) | 3.700 × 10 | 0.00 | 18.80 | |
| R20 | C(s) + H(s) → CH(s) + Ni(s) | 4.562 × 10 | 0.00 | 161.11 | |
| R21 | CH(s) + O(s) → CH(s) + OH(s) | 1.700 × 10 | 0.00 | 88.30 | |
| R22 | CH(s) + OH(s) → CH(s) + O(s) | 9.876 × 10 | 0.00 | 30.37 | |
| R23 | CH(s) + O(s) → CH(s) + OH(s) | 3.700 × 10 | 0.00 | 130.10 | |
| R24 | CH(s) + OH(s) → CH(s) + O(s) | 4.607 × 10 | 0.00 | 23.62 | |
| R25 | CH(s) + O(s) → CH(s) + OH(s) | 3.700 × 10 | 0.00 | 126.80 | |
| R26 | CH(s) + OH(s) → CH(s) + O(s) | 1.457 × 10 | 0.00 | 47.07 | |
| R27 | CH(s) + O(s) → C(s) + OH(s) | 3.700 × 10 | 0.00 | 48.10 | |
| R28 | C(s) + OH(s) → CH(s) + O(s) | 1.625 × 10 | 0.00 | 128.61 | |
| R29 | H(s) + O(s) → OH(s) + Ni(s) | 5.000 × 10 | 0.00 | 97.90 | |
| R30 | OH(s) + Ni(s) → H(s) + O(s) | 1.781 × 10 | 0.00 | 36.09 | |
| R31 | H(s) + OH(s) → HO(s) + Ni(s) | 3.000 × 10 | 0.00 | 42.70 | |
| R32 | HO(s) + Ni(s) → H(s) + OH(s) | 2.271 × 10 | 0.00 | 91.76 | |
| R33 | OH(s) + OH(s) → HO(s) + O(s) | 3.000 × 10 | 0.00 | 100.00 | |
| R34 | HO(s) + O(s) → OH(s) + OH(s) | 6.373 × 10 | 0.00 | 210.86 | |
| R35 | C(s) + O(s) → CO(s) + Ni(s) | 5.200 × 10 | 0.00 | 148.10 | |
| R36 | CO(s) + Ni(s) → C(s) + O(s) | 1.354 × 10 | −3.00 | 116.12 | |
| Coverage /CO(s) | 0.00 | 0.00 | −50.00 | ||
| R37 | CO(s) + O(s) → CO(s) + Ni(s) | 2.000 × 10 | 0.00 | 123.60 | |
| Coverage /CO(s) | 0.00 | 0.00 | −50.00 | ||
| R38 | CO(s) + Ni(s) → CO(s) + O(s) | 4.653 × 10 | −1.00 | 89.32 | |
| R39 | CO(s) + H(s) → HCO(s) + Ni(s) | 4.019 × 10 | −1.00 | 132.23 | |
| R40 | HCO(s) + Ni(s) → CO(s) + H(s) | 3.700 × 10 | 0.00 | 0.00 | |
| Coverage /CO(s) | 0.00 | 0.00 | −50.00 | ||
| R41 | HCO(s) + Ni(s) → CH(s) + O(s) | 3.700 × 10 | −3.00 | 95.80 | |
| R42 | CH(s) + O(s) → HCO(s) + Ni(s) | 4.604 × 10 | 0.00 | 109.97 |
| Parameter | Unit | Fixed-Bed Reactor Experiment (with Increasing GHSV) | Monolith Experiment from [27] |
|---|---|---|---|
| S/C ratio | (-) | 2.00 | 2.70 |
| Temperature | K | 1012.00, 1005.10, 997.50, 992.50, 989.30, 987.50 | 922.89, 1020.28,1119.93, 1215.35 |
| Pressure | Pa | 1.02, 1.02, 1.02, 1.03, 1.03, 1.03 | 1.01 |
| GHSV | 1/h | 1000, 2000, 3000, 4000, 5000, 6000 | 9000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richter, J.; Rachow, F.; Israel, J.; Roth, N.; Charlafti, E.; Günther, V.; Flege, J.I.; Mauss, F. Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst. Catalysts 2023, 13, 884. https://doi.org/10.3390/catal13050884
Richter J, Rachow F, Israel J, Roth N, Charlafti E, Günther V, Flege JI, Mauss F. Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst. Catalysts. 2023; 13(5):884. https://doi.org/10.3390/catal13050884
Chicago/Turabian StyleRichter, Jana, Fabian Rachow, Johannes Israel, Norbert Roth, Evgenia Charlafti, Vivien Günther, Jan Ingo Flege, and Fabian Mauss. 2023. "Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst" Catalysts 13, no. 5: 884. https://doi.org/10.3390/catal13050884
APA StyleRichter, J., Rachow, F., Israel, J., Roth, N., Charlafti, E., Günther, V., Flege, J. I., & Mauss, F. (2023). Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst. Catalysts, 13(5), 884. https://doi.org/10.3390/catal13050884








