Theoretical Study on the Mechanism of CO* Electrochemical Reduction on Cu(111) under Constant Potential
Abstract
:1. Introduction
2. Results and Discussion
2.1. The CHO* Path
2.2. The COH* Path
2.3. CO Poisoning
3. Computational Methods
3.1. Constant Potential Model
3.2. Electronic Structure Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olah, G.A.; Prakash, G.S.; Goeppert, A. Anthropogenic chemical carbon cycle for a sustainable future. J. Am. Chem. Soc. 2011, 133, 12881–12898. [Google Scholar] [CrossRef] [PubMed]
- Hori, Y.; Murata, A.; Takahashi, R. Formation of hydrocarbons in the electrochemical reduction of carbon dioxide at a copper electrode in aqueous solution. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1989, 85, 2309–2326. [Google Scholar] [CrossRef]
- Hori, Y.; Takahashi, R.; Yoshinami, Y.; Murata, A. Electrochemical reduction of CO at a copper electrode. J. Phys. Chem. B 1997, 101, 7075–7081. [Google Scholar] [CrossRef]
- Hori, Y.I. Electrochemical CO2 reduction on metal electrodes. In Modern Aspects of Electrochemistry; Springer: Berlin/Heidelberg, Germany, 2008; pp. 89–189. [Google Scholar]
- Bagger, A.; Ju, W.; Varela, A.S.; Strasser, P.; Rossmeisl, J. Electrochemical CO2 reduction: A classification problem. ChemPhysChem 2017, 18, 3266–3273. [Google Scholar] [CrossRef] [PubMed]
- Peterson, A.A.; Abild-Pedersen, F.; Studt, F.; Rossmeisl, J.; Nørskov, J.K. How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 2010, 3, 1311–1315. [Google Scholar] [CrossRef]
- Nie, X.; Esopi, M.R.; Janik, M.J.; Asthagiri, A. Selectivity of CO2 reduction on copper electrodes: The role of the kinetics of elementary steps. Angew. Chem. 2013, 125, 2519–2522. [Google Scholar] [CrossRef]
- Zhao, Q.; Carter, E.A. Revisiting competing paths in electrochemical CO2 reduction on copper via embedded correlated wavefunction theory. J. Chem. Theory Comput. 2020, 16, 6528–6538. [Google Scholar] [CrossRef]
- Xiao, H.; Cheng, T.; Goddard, W.A., III; Sundararaman, R. Mechanistic explanation of the pH dependence and onset potentials for hydrocarbon products from electrochemical reduction of CO on Cu (111). J. Am. Chem. Soc. 2016, 138, 483–486. [Google Scholar] [CrossRef]
- Sundararaman, R.; Goddard, W.A., III; Arias, T.A. Grand canonical electronic density-functional theory: Algorithms and applications to electrochemistry. J. Chem. Phys. 2017, 146, 114104. [Google Scholar] [CrossRef]
- Taylor, C.D.; Wasileski, S.A.; Filhol, J.S.; Neurock, M. First principles reaction modeling of the electrochemical interface: Consideration and calculation of a tunable surface potential from atomic and electronic structure. Phys. Rev. B 2006, 73, 165402. [Google Scholar] [CrossRef]
- Duan, Z.; Xiao, P. Simulation of Potential-Dependent Activation Energies in Electrocatalysis: Mechanism of O–O Bond Formation on RuO2. J. Phys. Chem. C 2021, 125, 15243–15250. [Google Scholar] [CrossRef]
- Nie, X.; Luo, W.; Janik, M.J.; Asthagiri, A. Reaction mechanisms of CO2 electrochemical reduction on Cu (111) determined with density functional theory. J. Catal. 2014, 312, 108–122. [Google Scholar] [CrossRef]
- Zhao, Q.; Martirez, J.M.P.; Carter, E.A. Revisiting understanding of electrochemical CO2 reduction on Cu (111): Competing proton-coupled electron transfer reaction mechanisms revealed by embedded correlated wavefunction theory. J. Am. Chem. Soc. 2021, 143, 6152–6164. [Google Scholar] [CrossRef]
- Trasatti, S. Structure of the metal/electrolyte solution interface: New data for theory. Electrochim. Acta 1991, 36, 1659–1667. [Google Scholar] [CrossRef]
- Donald, W.; Leib, R.; O’Brien, J.; Williams, E. Directly Relating Gas-Phase Cluster Measurements to Solution-Phase Hydrolysis, the Absolute Standard Hydrogen Electrode Potential, and the Absolute Proton Solvation Energy. Chem. Eur. J. 2010, 15, 5926–5934. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Mathew, K.; Kolluru, V.S.C.; Hennig, R.G. VASPsol: Implicit Solvation and Electrolyte Model for Density-Functional Theory. 2018. Available online: https://github.com/henniggroup/VASPsol (accessed on 9 July 2022).
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Mathew, K.; Kolluru, V.C.; Mula, S.; Steinmann, S.N.; Hennig, R.G. Implicit self-consistent electrolyte model in plane-wave density-functional theory. J. Chem. Phys. 2019, 151, 234101. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
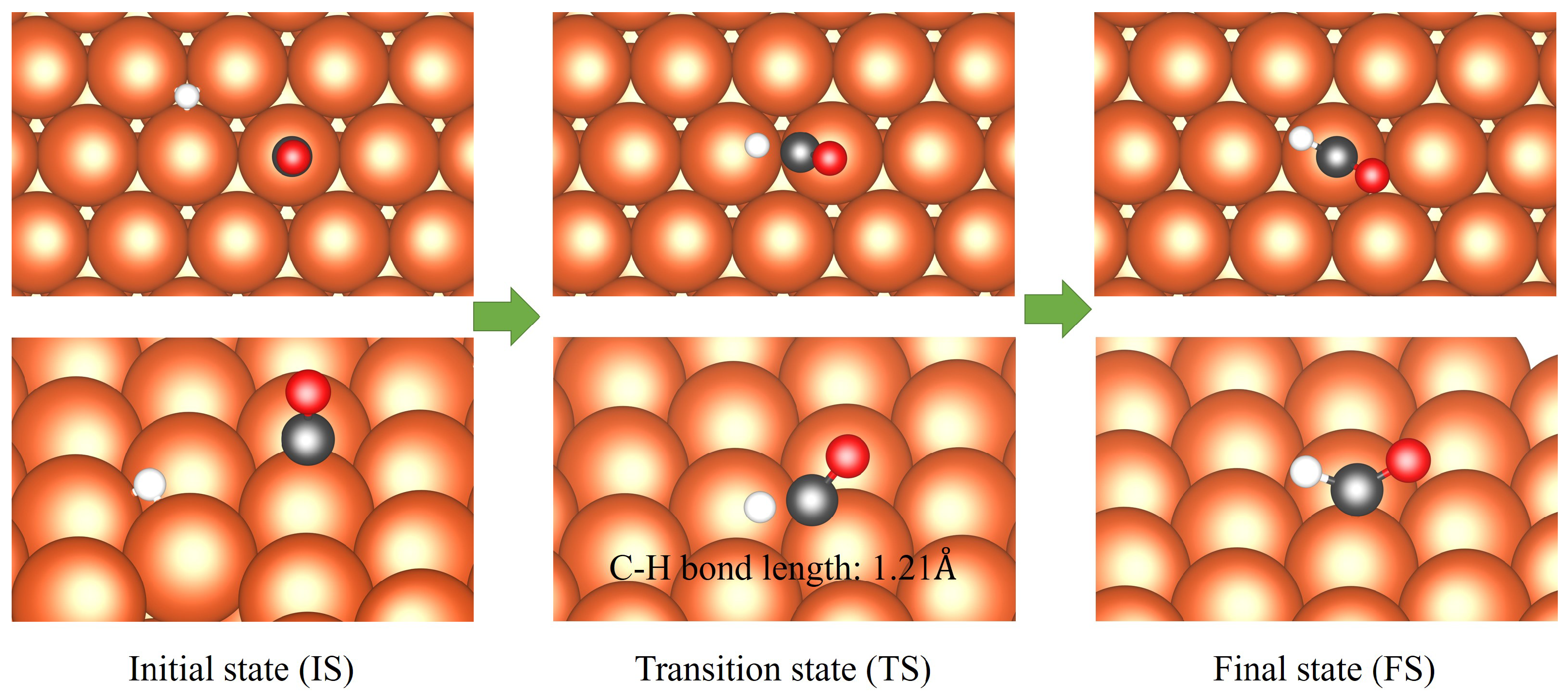

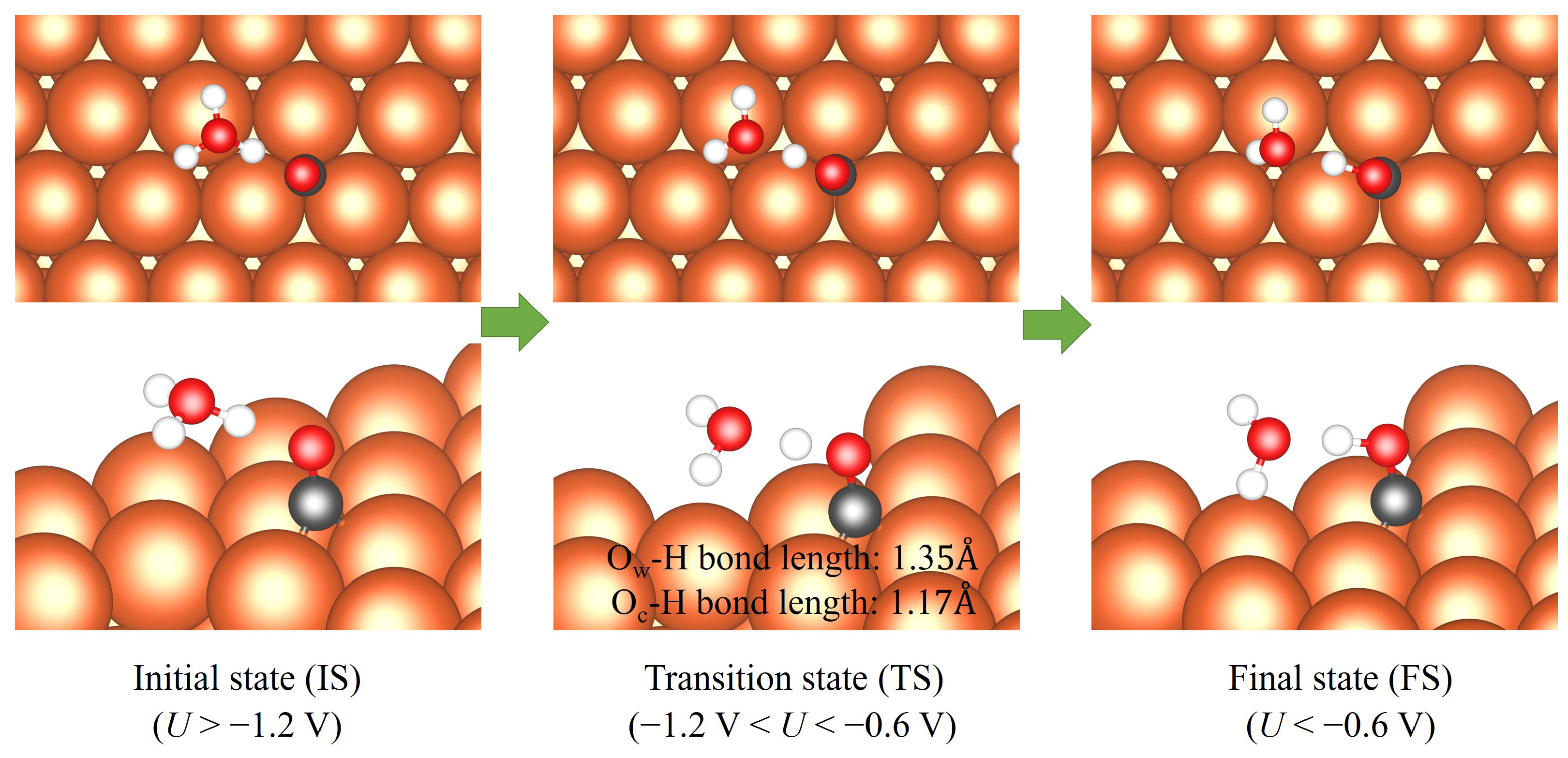
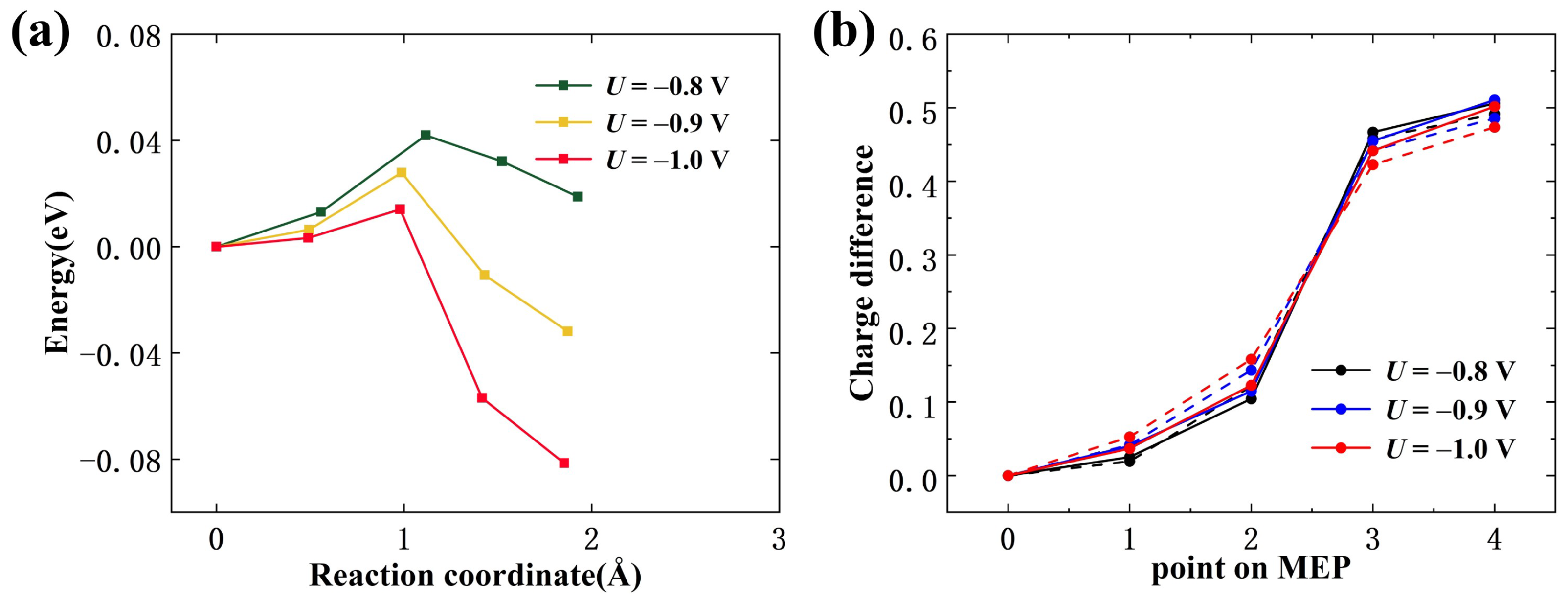


| Potential | Atom or Fragment | Strctures along the MEP | |||||
|---|---|---|---|---|---|---|---|
| IS | 1 | 2 | 3 | MS | FS | ||
| 0.0 V | Cu 1 | 0.100 | 0.119 | 0.091 | 0.096 | 0.113 | 0.051 |
| C | 0.935 | 0.871 | 0.673 | 0.628 | 0.605 | 0.709 | |
| O | −1.062 | −1.021 | −1.042 | −1.039 | −1.060 | −1.050 | |
| H | −0.261 | −0.203 | 0.089 | 0.064 | 0.052 | 0.173 | |
| −0.4 V | Cu | 0.085 | 0.114 | 0.080 | 0.087 | 0.112 | 0.042 |
| C | 0.904 | 0.853 | 0.653 | 0.616 | 0.588 | 0.710 | |
| O | −1.057 | −1.037 | −1.065 | −1.063 | −1.074 | −1.079 | |
| H | −0.265 | −0.215 | 0.068 | 0.054 | 0.046 | 0.140 | |
| −0.8 V | Cu | 0.088 | 0.114 | 0.074 | 0.088 | 0.109 | 0.050 |
| C | 0.870 | 0.847 | 0.640 | 0.579 | 0.590 | 0.724 | |
| O | −1.070 | −1.071 | −1.096 | −1.081 | −1.095 | −1.119 | |
| H | −0.271 | −0.237 | 0.041 | −0.039 | 0.001 | 0.067 | |
| −1.2 V | Cu | 0.090 | 0.133 | 0.065 | 0.071 | 0.093 | 0.072 |
| C | 0.843 | 0.838 | 0.638 | 0.644 | 0.608 | 0.685 | |
| O | −1.089 | −1.111 | −1.127 | −1.126 | −1.133 | −1.160 | |
| H | −0.288 | −0.250 | −0.007 | −0.042 | −0.026 | 0.035 | |
| Potential | Atom or Fragment | Structures along the MEP | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| −0.8 V | Cu 1 | 0.268 | 0.261 | 0.271 | 0.277 | 0.281 |
| C | 0.403 | 0.405 | 0.449 | 0.249 | 0.225 | |
| O | −1.057 | −1.069 | −1.137 | −1.177 | −1.152 | |
| H | 0.713 | 0.706 | 0.685 | 0.670 | 0.656 | |
| 0.196 | 0.188 | 0.154 | 0.047 | 0.020 | ||
| −0.9 V | Cu | 0.271 | 0.267 | 0.278 | 0.283 | 0.279 |
| C | 0.389 | 0.444 | 0.417 | 0.250 | 0.210 | |
| O | −1.064 | −1.140 | −1.142 | −1.188 | −1.182 | |
| H | 0.701 | 0.692 | 0.679 | 0.663 | 0.680 | |
| 0.202 | 0.192 | 0.104 | 0.056 | 0.009 | ||
| −1.0 V | Cu | 0.273 | 0.264 | 0.262 | 0.268 | 0.274 |
| C | 0.367 | 0.365 | 0.380 | 0.246 | 0.198 | |
| O | −1.072 | −1.087 | −1.138 | −1.203 | −1.198 | |
| H | 0.707 | 0.680 | 0.671 | 0.665 | 0.686 | |
| 0.185 | 0.193 | 0.151 | 0.037 | −0.001 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, S.; Liang, W. Theoretical Study on the Mechanism of CO* Electrochemical Reduction on Cu(111) under Constant Potential. Catalysts 2023, 13, 960. https://doi.org/10.3390/catal13060960
Mei S, Liang W. Theoretical Study on the Mechanism of CO* Electrochemical Reduction on Cu(111) under Constant Potential. Catalysts. 2023; 13(6):960. https://doi.org/10.3390/catal13060960
Chicago/Turabian StyleMei, Shange, and Wanzhen Liang. 2023. "Theoretical Study on the Mechanism of CO* Electrochemical Reduction on Cu(111) under Constant Potential" Catalysts 13, no. 6: 960. https://doi.org/10.3390/catal13060960
APA StyleMei, S., & Liang, W. (2023). Theoretical Study on the Mechanism of CO* Electrochemical Reduction on Cu(111) under Constant Potential. Catalysts, 13(6), 960. https://doi.org/10.3390/catal13060960





