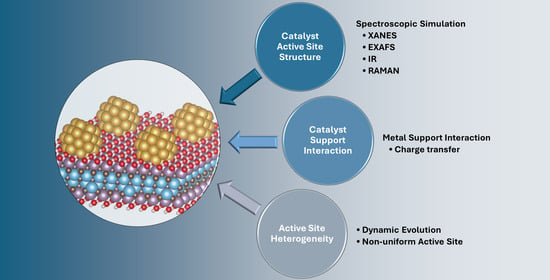
Recent Advances on Computational Modeling of Supported Single-Atom and Cluster Catalysts: Characterization, Catalyst–Support Interaction, and Active Site Heterogeneity

Abstract

To satisfy the need for catalyst materials with high activity, selectivity, and stability for energy conversion, material design and discovery guided by theoretical insights are a necessity. In the past decades, the rise in theoretical investigations into the properties of catalyst materials, reaction mechanisms, and catalyst design principles has shed light on the catalysis field. Quantitative structure–activity relationships have been developed through incorporating spectroscopic simulations, electronic structure calculations, and reaction mechanistic studies. In this review, we report the state-of-the-art computational approaches to catalyst materials characterization for supported single-atom and cluster catalysts utilizing spectroscopic simulations, i.e., XANES simulation, and material properties investigation via electronic-structure calculations. Furthermore, approaches regarding reaction mechanisms, focusing on active site heterogeneity, are also discussed.

1. Introduction

The chemical challenges in energy and the environment are driving the scientific community to find alternative catalytic solutions. Fundamental reactions associated with energy conversion, such as olefin oligomerization, metathesis, hydrofunctionalization, oxygen reduction (ORR), CO₂ reduction, etc., are of interest in catalysis research. Supported catalysts, spanning from single atoms to nanoparticles, are extensively used in industry for these reactions and have shown great advantages compared to conventional heterogeneous catalysts. For example, Pt/C has been used for ORR in fuel cell applications [1], and Pt supported by A-type zeolite is employed for CO oxidation in H₂-rich streams [2]. In addition, CrO_x supported by Al₂O₃ catalyzes direct ethane dehydrogenation [3], and am Al₂O₃-supported Cu-ZnO_x catalyst has been used for the steam reforming of methanol [4]. To satisfy the need for a new generation of catalyst materials that are more active, more selective, and made from earth-abundant elements, continuous efforts are required for catalyst material discoveries and developments [5]. However, a typical trial-and-error approach for catalyst design and discovery is a long, expensive, and tedious process [6]. In recent decades, computational catalysis utilizing quantum mechanical simulations, such as density functional theory (DFT), has been playing a critical role in the rational design of novel catalyst materials [5,6,7,8,9,10,11,12,13,14]. The basic strategy is to design catalysts based on a fundamental understanding of key descriptors that determine the catalytic activities. In principle, the electronic structures are the determining factor of the catalytic activity [5,15,16,17,18,19]. By engineering electronic structures via modulating atomic compositions and molecular structures, catalytic activity tuning can be achieved [20,21,22,23,24,25].

For a typical computational catalyst design approach, as illustrated in Figure 1, it starts with building molecular models to well represent a catalyst system, followed by studying the catalytic reaction mechanisms. In these two steps, theories can provide an understanding of the catalyst structures and reaction mechanisms, and experimental testing can validate theoretical predictions. For example, spectroscopic characterization techniques, such as X-ray absorption spectroscopy (XAS) (including X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS)), X-ray photoelectron spectroscopy (XPS), X-ray diffraction (XRD), nuclear magnetic resonance (NMR), infrared (IR) spectroscopy, etc., can provide experimental references for establishing the molecular structures of the catalyst. Thanks to the recent advancements in spectroscopic simulation techniques, XANES, EXAFS, NMR, and IR can be simulated based on established molecular models and compared directly with experimental spectra to validate the computational models. Similarly, experimental analysis of catalytic reactions can also provide information on reaction intermediates to aid theoretical investigation of reaction mechanisms. By generating free energy diagrams (FED), both reaction thermodynamics and kinetic barriers can be revealed, along with the most favorable reaction pathways. Furthermore, the electronic properties, i.e., molecular orbitals, density of states, Bader charge, etc., are often calculated to aid the understanding of the physical and chemical properties of the catalyst. Also, the adsorption energies of the reaction intermediates often correlate with the physical properties of the catalyst materials, e.g., electronic structure [24,25], d-band center [5,15,16,17,18], charge density [26,27,28], or spin density [29,30,31]. These intercorrelations between binding energies and physical properties are called structure–activity correlations, which are often used to derive catalyst design principles. Therefore, adsorption energies and physical properties are commonly used as descriptors for a particular reaction system. By carrying out catalyst material screening based on the selected descriptors, predictions can be made on new catalyst materials with better theoretical activity and aid experimental catalyst material design and development.

Despite the great advancement in computational catalysis, where the knowledge-based improvement and design of new catalysts is supported and led by quantum chemical calculations, there are still challenges that need to be carefully addressed. For instance, supported catalysts commonly experience dynamic restructuring or interconversion among different catalyst sites, also known as the dynamic evolution of the catalytic sites, during chemical reactions [32,33,34,35,36,37]. Such phenomena can make catalyst characterization more challenging, experimentally requiring in situ spectroscopic techniques. In the meantime, another complexity of heterogeneous catalysts is the nonuniformity of the catalytic sites, known as active site heterogeneity. Synthesized nanocluster/nanoparticle catalysts often have a dispersive distribution of particle size, and supported single-site catalysts consist of a variety of catalytic sites with different local coordination environments. The heterogeneity of the catalytic sites leads to different catalytic activities. Dynamic evolution of the catalyst under reaction conditions can further increase the active site heterogeneity [32,38]. Interpreting the characterization spectroscopy (e.g., XAS) of the catalysts with high site heterogeneity is particularly difficult. This is because XAS measures all the catalytic sites, and the response from this technique is dominated by the sites with the highest volumetric density. However, the overall activity is dominated by the sites with the highest turnover frequencies, not necessarily those with the highest density. Therefore, a comprehensive study combining catalyst structure characterization with mechanistic studies is required to identify the catalyst active site. Another aspect is that for supported catalyst systems, understanding the interactions between supported active sites and catalyst support can sometimes be challenging. Catalyst supports, such as TiO₂, LiTiO₂, CeO₂, LiMnO₂, etc., have shown electronic interactions with supported active sites [39,40,41,42]. For some supported catalysts (particles), the active sites are located at the interface between the catalyst and the support; the high activity of the interface could potentially result from the electronic communication between the catalyst support and supported site, a better stabilized facet due to the support effect, or a newly formed structure due to skin and strain effects [43]. Thus, accurately capturing the electronic communication between the catalyst sites and support and their electronic structures is crucial.

In this review, we focus on the general computational strategies and best practices for studying supported single atoms and small clusters/particles as heterogeneous catalysts, including thermal- and electrocatalytic systems. The computational strategies of ab initio spectroscopic simulations, reaction mechanistic studies, and electronic property investigations are discussed, as are the critical challenges and best practices in thermal and electrocatalytic systems.

2. General Approach

2.1. Catalyst Active Site Characterization

Identifying the structure of the catalyst is key to rational catalyst design. Characterization techniques such as XAS are powerful tools to reveal the catalyst site structure for supported single-atom catalysts, metal clusters, and nanoparticles. XAS can qualitatively reveal the catalyst oxidation states, bond lengths, symmetry, and coordination environments of the absorbing elements. Nevertheless, the catalyst structures still cannot be explicitly well understood solely based on experimental spectra, due to the potential dynamic evolution and heterogeneity of the active sites. An integrated experimental and computational XAS analysis is needed to enable the comprehensive characterization of these structural features. Computational spectroscopy simulations, e.g., XANES simulations, offer a powerful technique for interpreting experimental spectra, providing a one-to-one correspondence between molecular structures and spectral features. There are two regions of XAS spectra, including XANES (lower energy region) and EXAFS (higher energy region), with the former being information richer and more challenging to simulate. XANES simulations in catalysis have attracted increasing attention, and thus, in this review, we specifically focus on the discussion of XANES simulations. The common methods used to simulate electron excitations for XANES spectra include time-dependent density functional theory (TDDFT) [44,45,46,47], Green’s function approximation [48], and the finite-difference method [48,49]. Nowadays, reliable program packages, i.e., FDMNES [48,49,50,51], FEFF [52], Wien2k [53], ADF [54], ORCA [55,56,57,58,59], and XSPECTRA [60,61,62,63], implement ab initio approaches to calculate the XANES of particular given atomic configurations. By comparing the theoretical XANES spectra based on a series of possible structures with the experimentally measured XANES spectra, the structure of the catalyst can be identified.

However, some of the catalyst structures are not stable during the reaction, especially for the atomically dispersed single-atom catalysts (SAC), supported clusters, and particles, whose structures could undergo dynamic change during reactions [32,33,34,35,36,37]. By only performing XANES analysis on the as-prepared catalyst, the active site structure may not be accurately captured. To further understand this phenomenon, in situ XANES measurements are needed. By coupling in situ measurements with XANES simulation, the structural evolution of the active sites can be better understood. On the other hand, active site heterogeneity introduces more complexity in the interpretation of the XANES spectra, as XANES measures all the catalytic sites in the system. One approach is to perform linear combination fitting (LCF) over the simulated XANES spectra of all the candidate structures, where the qualitative fundamental information regarding active site structures could be qualitatively retrieved.

2.2. Reaction Thermodynamics and Kinetics

Catalytic reaction pathways are calculated (often using first-principles DFT) to obtain information regarding the catalytic activity and to explore the reaction mechanism and product selectivity. The Gibbs free energy of each reaction intermediate can be calculated using the total free energy of the products minus the total free energy of the reactants. The total energies can be obtained directly by DFT, while, the zero-point energy and entropy are calculated using statistical mechanics [8].

In electrocatalysis, such as oxygen reduction reactions (ORRs), oxygen evolution reactions (OERs), CO₂ reduction reactions (CO2RRs), etc., each reaction involves multiple charge transfer steps at the catalyst surface. One of the most popular approaches to treating electron transfer is the computational hydrogen electrode (CHE) model, proposed by Nørskov et al. [64] The CHE model accounts for the energy of proton-electron pairs using half of the chemical potential of H₂ in the gas phase, (i.e., $\frac{1}{2}\mu \left(H_2\right(g\left)\right)$, Equation (1), where U is the applied potential bias. Furthermore, to account for the free energy of the pH, Equation (1) is used, where $k_B$ is the Boltzmann constant and T is temperature. As a result, the free energy of an elementary reaction step can be calculated by Equation (3).

$$\mu \left(H^{+}+e^{-}\right)=\frac{1}{2}\mu \left(H_2\left(g\right)\right)-eU$$

(1)

$$∆G_{pH}=(-k_{B}Tln10)\times pH$$

(2)

$$∆G_{rxn}=∆G+neU+∆G_{pH}$$

(3)

With the calculated adsorption and reaction free energies, free energy diagrams are constructed to directly reveal the reaction thermodynamics of each elementary reaction step. Based on the reaction thermodynamics presented by free energy diagrams, the catalytic activity of different catalyst materials can be compared, and the preferred byproduct of a chemical reaction can be identified.

Furthermore, in the electrocatalysis system, since the calculated reaction free energy involves the potential bias term, Equations (1) and (3), the applied potential is added to calculate the reaction energy at a particular potential bias. To assess the electrocatalytic performance, the limiting potential, $U_{lim}$, which is also known as working potential [65,66,67] or onset potential [68,69], is employed. $U_{lim}$ is defined as the highest applied potential that keeps the reaction exothermic [65,66,67,68,69,70,71,72,73]. As indicated by Equation (4), $U_{lim}$ is calculated by dividing the $∆G_{rxn}$ of the most endothermic step by the number of charges being transferred during that elementary step. Furthermore, the overpotential, ${\eta }_{lim}$, can be calculated using Equation (5), where $E_{eq}$ is the equilibrium potential of the electrochemical reaction. In general, the higher the $U_{lim}$, the lower the ${\eta }_{lim}$, and therefore the better the electrocatalytic activity. The CHE model is sufficient for providing information regarding the reaction mechanism and the qualitative adsorption trend; however, it does not account for any solvation effects or an electrified surface [74,75].

$$U_{lim}=-\frac{\max \left[{∆G}_1,∆G_2,{∆G}_3,∆G_4,\dots \right]}{ne}$$

(4)

$${\eta }_{lim}=E_{eq}-U_{lim}$$

(5)

More importantly, for a catalytic reaction, the reaction kinetics is also critical; therefore, calculating the transition state energy and obtaining the reaction barrier are crucial. The nudged elastic band (NEB) method [76] is often used to search for the transition state structure. This method optimizes a string of geometries between the reactant and product and then relaxes this series of structures to find the real minimum energy pathways and converge the structures to the saddle point (transition state). The climbing image (CI)-NEB method [77] constitutes a small feature; that is, during the geometry optimization, CI-NEB can shift the structure with the highest energy towards the energy uphill with the tangential forces turned off. As a result, the structure with the highest energy maximizes its energy along the tangential direction of the band while minimizing the energies in other directions. As the CI-NEB calculation converges, the transition state converges to the saddle point. However, the CI-NEB method can be computationally intensive, especially for periodic models. Therefore, this method is sometimes used to perform transition state searches to locate the estimated transition state structure, and then the DIMER method [78] will be used to obtain the transition state energy. This method only requires two structures of the system (or a ‘dimer’), which is developed based on the eigenvector-following theory, while using only the first derivatives of the potential energy. Therefore, the DIMER method provides a convenient solution to obtain the minimum energy pathway and transition state energy. Thus, the coupled CI-NEB and DIMER method has become a more efficient approach for transition state searches of supported transition metal catalysts [8,30,32,79,80,81,82].

More interestingly, an empirical scaling relationship was found in a number of transition metal catalysts between reaction energies and the energy barriers, which is known as the Brønsted–Evans–Polanyi (BEP) relationship [83,84,85,86]. Nørskov et al. [85] suggested that the transition state structure has lost its molecular identity and that the variations in the transition state energy should follow that of the final state energy, which results in a linear correlation with a slope close to one. Such BEP relationships have been extremely useful in terms of providing data for kinetic models and an empirical approach to estimating the energy barrier without performing transition state searches. Catmap [87] and Cantera [88] can adapt BEP correlation to perform microkinetic modeling.

2.3. Chemical and Physical Properties of the Materials

The electronic structure of the catalyst active sites plays an important role when studying chemisorption and catalytic activity. Nilsson et al. [17] discussed that during chemisorption over metal catalysts, the valence band will inevitably couple with the s states of the metal surface; thus, the different catalytic functions will only rely on the d states. This coupling leads to the formation of bonding and antibonding states between the electronic states of the adsorbates and a narrow distribution of the d-states of metal catalysts. When chemisorption takes place over metal surfaces, the occupancy of d-states is full, therefore, the binding strength will depend on the filling of the antibonding states, which varies with the metal in question [15,17]. Since the antibonding states are always higher than the d-states, the energy of the d-states relative to the Fermi level can also be used as a matrix to indicate the binding strength. Since the chemisorption trend has been established based on the d-band theory, as the d-band center shifts closer to the Fermi level, a stronger adsorption energy is expected, and vice versa. This theory works particularly well for transition metal and bimetallic systems in predicting adsorption energies, catalytic activity, and catalyst material design [89,90,91,92,93].

The charge redistribution in the local environment of the active site can greatly influence the catalytic activity. Therefore, computational charge density analysis, i.e., Bader charge [94,95,96], natural bond orbital (NBO) [97,98,99], etc., has been used to reveal the charge redistribution or charge transfer over a catalyst material. For example, Bader charge analysis can approximate the electronic charge density by dividing space within molecular systems into atomic volumes using charge density. The electronic charge density can be used to partition a molecular system into different sections based on zero flux surfaces, which are 2-d surfaces with a minimum charge density that is normal to the surface; therefore, the volume of each section is the occupation volume of each corresponding atomic species. This approach can reveal the charges carried at the active site and the interactions with its surrounding local environment. NBO, on the other hand, also operates on electron density; however, it uses localized atomic orbitals to describe the electron density, which usually works very well for Lewis structures. Crystal Orbital Hamilton Population (COHP) [100,101] can also be employed to study the interaction between catalyst active sites and reaction intermediates. It partitions the band structure into orbital-pair interactions, which is a “bond-weighted” density of states (DOS) between two adjacent atoms. The band-structure energy is analyzed by the COHP diagram, which explicitly shows the bonding and antibonding contributions. An energy integral of the COHP indicates the bonding strength.

By exploring the electronic structures of the catalyst materials, the physical/chemical properties that are related to the catalytic activities can be revealed. These properties may also be used as descriptors for future catalyst screening and design purposes.

3. Best Practices

In recent years, efforts have been made to establish quantitative structure–activity relationships (QSAR), which is a critical concept in rational catalyst design [102,103,104]. Such a correlation allows effective prediction of novel catalytic materials. For this reason, gaining a better understanding of the catalyst structures of the synthesized materials via characterization techniques is very important. By coupling the experimental characterization and the spectroscopic simulations, one can reveal the catalytic active site information, i.e., the molecular structure, oxidation state, available facets, etc. Based on the optimized catalyst active site structures, DFT calculations are performed to obtain chemical and physical properties and investigate the reaction mechanisms. This valuable information from spectroscopic simulation and reaction mechanistic investigation can then be utilized to establish QSAR for catalyst material design.

3.1. Characterization

In catalyst design, one frequently asked question is, “what is the true active site?”. Experimentally, characterization techniques can reveal information such as coordination environment, oxidation states, available facets, particle sizes, and so on, but it is challenging to reveal the true identity of the catalytic active site structures. Encouragingly, by coupling characterization techniques with spectroscopic simulations, i.e., IR [105,106,107,108], XPS [109,110,111], EXAFS [112,113,114,115], etc., a clearer image of the catalyst active site can be drawn. Due to recent advancements in XAS techniques for supported catalysts, this section is primarily focused on XANES simulations.

XANES is a particularly powerful technique for determining the key electronic properties and local bonding environment of transition metal-containing catalysts, ranging from discrete molecular complexes to supported single-site catalysts and nanoparticles. Compared to EXAFS, which reflects bond lengths and neighboring atom types, XANES also contains data in composite form about local geometric and electronic structures [44,116,117]. Due to this complexity, XANES can also be more challenging to analyze. While some key characteristics of the metal centers and their coordination environment can be directly extracted from the experimental XANES and EXAFS, such as average oxidation state and coordination number, certain bonding interactions that are crucial to catalytic processes, such as metal-hydride and second-shell coordination interactions, are often only present as subtle features in XANES, making the experimental spectra challenging to interpret directly [118,119,120,121,122]. As shown in Figure 2, Cr-containing XANES have all shown different XANES features based on their coordination environment and oxidation state.

In recent years, XANES simulations have been utilized to reveal catalyst structures. For example, Zitolo et al. [123] synthesized the Fe-N-C moiety via the pyrolysis approach; however, the active site structure remains elusive. By carrying out XANES simulations on proposed structures and comparing them with experimental XANES measurements, the active center is revealed to be an FeN₄ structure with two or one molecular O₂ adsorbed in end-on or side-on modes (Figure 3a,b). Jia et al. [124] also carried out XANES simulation to demonstrate the XANES feature evolution as a function of FeN₄ structure distortion. As indicated by Figure 3c, as Fe-N bond distances increase, peak B in the rising edge region diminishes, edge peak C becomes more intense, and curve pit E shifts to higher energy. Such an interesting trend could provide valuable insight into understanding Fe-N-C structural evolution under the ORR condition. Zhang et al. [119] have employed XANES simulation to reveal the active site structures, FeN₄ and FeN₅, for CO₂-CO conversion. According to the XANES simulation, the pre-edge, edge, and post-edge features matched well with experimentally measured XANES, which confirmed the existence of atomically dispersed FeN₄ and FeN₅ active sites (Figure 3d). Wang et al. [118] synthesized Fe-Co dual sites embedded in porphyrin-like C structures, which showed comparable ORR activity vs. Pt/C. To reveal the active site structure, a series of Fe-Co dual site structures stabilized by various numbers of N atoms in graphene were considered. By performing XANES and EXAFS simulations on these proposed structures and comparing them with experimentally measured XANES (Figure 3e), the active site structure was revealed to be the Fe-Co dual sites coordinated with six pyridinic N atoms, and the mechanistic study was then done to further validate the ORR activity. Xu et al. carried out XANES simulations to study the Ni site structure and coordination environment of a Ni single-atom site supported by Li_xMn₂O₄ (x = 1 or 2) synthesized by oxidative grafting. By comparing simulated and experimentally measured XANES, (Figure 4a,b), it was concluded that Ni sites prefer to stay in the Li channel and form an octahedral structure. In another example, Zandkarimi et al. [120] have investigated Cu catalyst oxidation states and structural changes throughout the oxidative dehydrogenation of alkanes via XANES simulation. They found that the Cu cluster size and presence of isomers can impact simulated XANES spectra due to different electronic configurations. Similarly, in homogenous systems, Chen and coworkers [125] confirmed the D_3h structure of iron pentacarbonyl (Fe(CO)₅) by XANES simulation and EXAFS characterization. Time-dependent DFT calculations were performed to investigate the molecular orbitals between Fe and CO that describe the pre-edge peak. By comparing the intensities of two pre-edge peaks between the D_3h and C_4v structures, one of the pre-edge peaks on the C_4v symmetry decreased due to the nonbonding interaction between Fe and the ligands. Since XANES indicates the geometry sensitivity of the π bonding interaction between Fe and CO, XANES simulations provide the geometry of the molecular system. Furthermore, XANES simulation serves as a valuable tool for the examination of electronic structures. For instance, Ganguly and colleagues employed DFT calculations to model XANES spectra for manganese corroles [126]. Computational simulations elucidated the blue shift and increased intensity observed in the Mn pre-edge peak of Mn[TpCF₃PC]Ph (TpCF₃PC = meso-tris(p-CF₃-phenyl)corrole), attributing it to significant $3{\mathrm{d}}_{{\mathrm{z}}^2}-4{\mathrm{p}}_{\mathrm{z}}$ mixing.

Almost without exception, supported catalysts experience dynamic restructuring under reaction conditions that is ultimately responsible for their catalytic activity and longevity. Understanding the origins and consequences of dynamic catalyst behavior at an atomistic level is therefore key to synthesizing novel catalysts that can readily form and maintain desired active site structures as catalytic reactions proceed. By performing in situ XANES measurements, the dynamic evolution of catalyst structures can be realized. Xu et al. [32] examined the dynamic evolution of a Cu catalyst for the electrochemical reduction of CO₂ to ethanol. Ab initio XANES spectra were used to characterize the reaction at all stages of catalysis using the FDMNES code to then compare with in situ XANES for Cu. To properly describe the key peaks in the pre-edge, rising edge, and post-edge regions of the XANES, a linear combination of the computed XANES spectra of various clusters and slabs, i.e., Cu₃, Cu₅₅, and Cu (111), Figure 4c, was needed. In a qualitative sense, this analysis showed that at least a small percentage of the Cu sites come from small Cu clusters that are responsible for C-C bond formation and producing ethanol due to this linear combination technique not representing quantitative information about particle size ratios. Another study by Poths et al. [128] also focused on the dynamic changes in the Cu₄ clusters and Cu₃Pd clusters supported on alumina during the temperature-programmed reaction of the oxidative dehydrogenation of propane. They reported that the operando XANES spectra can be more accurately fitted when using both bulk and cluster standards during LCF, and these mixed standards can not only track the changes in cluster sizes (due to cluster sintering) but also in oxidation states. Based on LCF, they also found that the clusters were reduced and partially re-oxidized as the temperature increased and then decreased. In addition, it was also evident that the fraction of the bulk standard irreversibly grew due to the temperature-programmed reaction causing irreversible sintering.

To identify the catalyst structures that are responsible for the experimentally measured XANES spectra, simulations of the various structures of interest need to be carried out and fitted with the experimental data. However, such trial-and-error procedures, especially for complex and/or dynamic systems, are very expensive and time-consuming. In recent years, the development of big data driven approaches has attracted attention. By employing machine learning (ML) techniques, one can overcome the limitations of manual multidimensional big data analysis. Such a data-driven approach can accelerate the discovery of the desired catalyst structures with minimal computation. However, the machine learning-driven approach needs a large database to accurately obtain the correlation between the structural features, i.e., bond distance, bond angle, coordination number, etc., and XANES features, i.e., pre-edge, energy, edge energy, peak intensities, etc. Guda et al. [129] carried out high throughput calculations to simulate XANES spectra for Fe oxide clusters by modulating the structure parameters (Figure 5a–c). They have reported the correlations within coordination number, edge energy, white line curvature, and pit energy, the correlations within Fe-O bond distance, pit energy, and edge energy, and the correlations within Fe valance, white line energy, and the energy difference between white line and the pit of XANES spectra (Figure 5d–i). In addition, mathematical relations were generated to provide a simple and fast tool to extract structural information from spectral shapes. Such a methodology was successful in predicting a multicomponent Fe:SiO₂ system. Liu et al. [130] also performed ML to build the relationship between XANES spectra and structural parameters for simple copper oxide cluster systems utilizing a neural network approach. This approach enabled the determination of the average particle size and the oxidation state of the metal clusters. However, as this system is designed for an idealized, pure metal oxide phase, it does not apply to the supported metal oxide cluster systems. Mizoguchi et al. [131] employed an ML approach utilizing hierarchical clustering and a decision tree to interpret and predict ELNES/XANES spectra. Such an approach not only allows one to extract chemical, elemental, and geometric information from experimental spectra, but also provides means to predict the spectral features from the material information. Their work was also extended to predicting the geometrical properties, i.e., average bond lengths, bond angles, and Voronoi volume, and bonding properties, i.e., bond overlap population, Mulliken charge, and transition energy, from core-loss spectra using a feedforward neural network approach.

3.2. Catalyst–Support Interaction

In rational catalyst design, the catalytic properties are often used as descriptors to perform catalyst material searches. Electronic structures, i.e., density of states (DOS), d-band centers, charge densities, spin densities, etc., have drawn close attention from researchers, and therefore, electronic structure engineering has become one of the main strategies to achieve future catalyst design and activity tuning. There are many approaches to modulating the electronic structures of catalyst active sites, e.g., controlling the coordination environment [25,26,28,73,132], interfacial engineering [70,133,134,135], or defect engineering [136,137,138,139,140]. However, in this section, we would like to focus on the catalyst–support interaction.

Transition metals are commonly employed as the metal centers in single atom catalysts (SACs) due to their high catalytic performance because of the unsaturated coordination of metal atoms [141]. The most common types of SACs include graphene-supported single atoms, e.g., FeN₄, CoN₄, supported organometallic and metal hydrides via surface organometallic chemistry, and doped metal atoms in metal and metal oxide supports. However, these SACs all feature properties such as a low-coordination environment of metal centers, quantum size effects, and metal-support interactions, which make them a unique type of catalyst with high tunability [142,143,144,145]. With the increasing interest in SACs due to their high catalytic performance in various reactions, there is a growing need for a comprehensive understanding of the electronic structures of the catalyst active site. However, the complexity arising out of the coordination environment of a single metal atom and its interaction with the supporting materials makes achieving a deeper understanding challenging. Thus, computational studies are a powerful tool for screening different metal atoms and investigating catalyst electronic structures.

In homogeneous catalysis, redox non-innocent ligands are often introduced to the metal center to fine-tune the catalytic activity via electronic structure modulation. These types of ligands can act like an “electron-reservoir”, where the synergistic interplay between the ligands and metal center can facilitate chemical reactions. In heterogeneous catalysis, electronic metal support interaction (EMSI), a form of strong metal support interaction (SMSI) that results from the dynamic interplay between the electronic structure of the metal oxide support and the supported catalysts, can also be utilized to achieve catalyst activity tuning via electronic structure modulation [146,147,148,149,150]. Organometallic molecules can be grafted onto a catalyst support via surface organometallic chemistry (SOMC), which is a powerful strategy for the synthesis of well-defined, homogenous-in-function, heterogeneous catalysts [39]. When single-atom catalysts are grafted onto redox-non-innocent catalyst supports, such as lithium manganese oxide (LMO, Li_xMnO₂) and lithium titanium oxide (LTO, Li_xTiO₂), with the ability to tune surface potential as a function of lithium intercalation, active site electronic structure modulation can be achieved. Chapovetsky et al. [39] have demonstrated the oxidative grafting of Ni single atoms onto LiMn₂O₄ supports for cyclohexene hydrogenation reactions. They have found that Ni/LiMn₂O₄ is not active. However, further intercalation of lithium into catalyst support, Ni/Li₂Mn₂O₄, showed almost 100% conversion at room temperature under 95 PSI H₂ in toluene. With DFT calculations, the magnetization of Ni on LiMn₂O₄ was found to be 1.76, suggesting that Ni(II) was formed after an oxidative grafting reaction. Further lithium intercalation caused the Ni magnetization to decrease to 0.46, indicating the formation of Ni(I). Hence, the reduction of Ni(II) must be due to the additional lithium interaction in the catalyst support, which donates extra electrons to reduce Ni(II) to Ni(I) and facilitate the hydrogenation reaction. Based on the mechanistic study, Ni/Li₂Mn₂O₄ showed much lower reaction energies compared with Ni/LiMn₂O₄, which validated the experimental observation. The follow-up study [127] demonstrated the reduction of supported single-atom sites (Fe, Co, Ni, and Cu) over Li₂Mn₂O₄ via Li intercalation into catalyst support utilizing Bader charge analysis. Furthermore, based on the reaction mechanism study, the considered active sites are more active towards cyclohexene hydrogenation than the reduced support, Li₂Mn₂O₄, with low reaction thermodynamics and kinetic barriers. It was concluded that the improved catalytic activity is due to (1) the reduction at the active sites, which provides more change density to promote the reaction with a lower kinetic barrier, and (2) the reduced catalyst support can better stabilize low-coordinated ions, which allows the single-atom sites to diffuse in and out of the catalyst surface to better stabilize reaction intermediates. Another example that utilizes EMSI to facilitate chemical reactions is ethylene hydrogenation over Pt/TiO₂ by Gunasooriya et al. [40], which reported that the charges injecting into Pt nanoparticles from TiO₂ anatase support can decrease the adsorption energies of both C₂H₄ and C₂H₃ and facilitate hydrogenations reactions based on DFT investigation. They also concluded that the activity of the supported metal catalysts can be controlled by tuning the electronic properties of the semiconducting catalyst support. Wan et al. [151] demonstrated that the spillover of hydrogen over Au/anatase-TiO₂ is not only affected by cluster size but also by EMSIF. In this study, Au particles with various cluster sizes are considered over TiO₂ (101) and (001) catalysts. Over stoichiometric surfaces, H-H bond activation energy decreases as the particle size increases. In addition, electronic communication between Au clusters and TiO₂ (101) and (001) surfaces were found (Figure 6a). When considering surface O defects, reduced surfaces accumulate more charges on the supported Au clusters, improve thermal stability, and facilitate H₂ adsorption; however, the impact on H-H activation is insubstantial. In a recent study, Prats et al. [152] carried out high-throughput screening and evaluated metal cluster interactions with transition metal carbides (TMC). The metal cluster adsorption energies per atom are quite high, −2 to −3 eV over cubic TMC (001) facets and −3 to −5 eV over hexagonal TMC (001) facets. The strong interaction is mainly due to EMSI (Figure 6b), which makes supported clusters resistant to aggregation/sintering. Prediction was also made that Pt, Pd, and Rh clusters on hexagonal TMC (001) facets are good candidates with the highest potential catalytic activity due to the significant polarization of cluster electron density and high stability. Han et al. [153] also investigated the hydrogenation of the ethylene reaction of the Ni₄ cluster over redox-active supports, such as TiO₂, CeO₂, and BNO. Bader charge analysis indicates that the Ni₄ cluster has a higher charge density over a BNO support compared with CeO_2, followed by TiO₂ (Figure 6c). With the highest charge density of Ni₄/BNO, the catalytic activity is the highest among the three considered supports with the lowest reaction kinetic barriers, while Ni₄/TiO₂ and CeO₂ with a lower charge density exhibit higher energy barriers (Figure 6d).

Introducing dopants into a catalyst support can also affect the catalytic activity by modifying the electronic structures of the supported catalyst. Studies by Elangovan et al. reported that the small Pt nanoparticles (~1 nm) can be stabilized by vertically aligned carbon nanofibers (VANCF) for ORR. However, with N dopants being introduced into the VACNF support, according to DFT calculations, the electrons were transferred from Pt to N dopants, causing the d-band center to shift closer to the Fermi level and promoting binding to OH, which made the Pt/VACNF more resistant to CO poisoning. Chen et al. [28] demonstrated that by incorporating P and S into the carbon framework, the Fe electronic structure can be tuned, as shown in Figure 7a–c, hence the electrocatalytic activity for ORR. Furthermore, the linear correlation between the Bader charge at the Fe center and OH binding energy was also found (Figure 7d). Similarly, such a linear correlation was also reported by Xu et al. on the dual metal center embedded in a graphene framework (Figure 7e) [71]. Mun et al. [26] also introduced electron withdrawing -SO₂ and electron donating -S to the carbon basal plane and tested the ORR activity of the Fe-N-C active center (Figure 7f). They reported that the electron withdrawing -SO₂ caused the Fe-N-C d-band center to shift to lower energy, weaken the binding to ORR intermediates, and enhance ORR activity (Figure 7g,h).

With the great achievements in understanding and modulating the electronic structures in catalytic systems to enhance catalytic activity, the mathematical correlations between the electronic structures and reaction intermediate adsorption energies have also been demonstrated in recent years. The linear correlation between the d-band center and adsorption energies has already been found by many groups over pure metallic and metal alloy surfaces [154]. Similarly, over the single atom catalyst, the correlations between Bader charge and binding energy were also reported in the literature [28,71,155]. In recent years, the concept of COHP has attracted attention, especially for the metal oxide and nitride systems. Qian et al. have reported a linear correlation between integrated COHP (ICOHP) vs. H adsorption and C₂H₄ adsorption energy. Comer et al. [156] also reported a mathematical correlation between ICOHP and O* and OH* adsorption energies over 3d, 4d, and 5d transition metal oxide surfaces and bulk systems. They have concluded that the ICOHP can be used as a descriptor to predict O* and OH* bonding strengths, which can be relevant in building machine learning models for surface adsorption. Shan et al. [157] also derived covalency from COHP calculations and demonstrated the linear correlation between covalency and N binding energies over metal nitride systems. As shown in these examples, there are certainly empirical mathematical correlations between electronic structure descriptors and the adsorption energies of reaction intermediates. Therefore, by modulating these electronic properties of the catalyst materials utilizing catalyst–support interactions, one can design a better catalyst via descriptor-based material screening or a machine learning approach.

3.3. Active Site Heterogeneity

In catalysis research, reaction mechanism studies can reveal the most thermodynamically and kinetically favored pathway. By performing DFT simulations, one can construct the reaction network and by comparing reaction energetics and kinetic barriers, the optimal pathway can be drawn. In addition, empirical correlations within adsorption energies and correlations between reaction energy and reaction kinetic barriers, i.e., a BEP relationship, can be derived for microkinetic modeling and the development of catalyst design principles. However, there are still challenges in reaction mechanism modeling. In this section, we will focus on discussing catalyst active site heterogeneity.

SACs are typically atomically dispersed on support materials; their structures can vary due to the influence of high surface free energy. This means that after the synthesis of SACs, the active site structure distortion, defects, and active site structure evolution should be considered, which is known as a heterogeneity issue in the catalysis field. Consequently, computational chemistry has been employed to explore catalytic mechanisms and atomic-scale geometries at active sites in SACs [5,158,159,160,161,162,163]. The utilization of theoretical studies not only aids in understanding mechanisms but also in suggesting newly designed catalysts [161,164]. For example, Yang et al. [164] investigated the electrochemical reaction mechanisms of CO₂ reduction on nitrogen-doped graphene for Fe, Co, and Ni by DFT calculations. They revealed that different products are formed depending on the transition metal type, and the coordination environment plays an important role in the catalytic effects. Their work also shows the possibility of a single non-noble atom catalyst for CO₂ reduction computationally. Xu et al. [32] have studied the dynamic evolution of atomically dispersed Cu catalysts that form Cu particles of different sizes during electrocatalysis. By carefully examining the CO₂ reduction activity on Cu₃ clusters, Cu₅₅ particles, and Cu (111) surfaces, which represent small clusters, 1 nm particles, and larger particles with well-defined facets, they found that the smaller particles are responsible for ethanol formation with a low C-C bond energy barrier, while the larger particles and periodic surface are responsible for HCOOH and CH₄ formation. A study by Peters et al. [165,166,167,168] illustrates how machine learning and importance learning techniques can be used to predict site-averaged activation barriers using quenched-disorder amorphous silica models. These models initially started as a simple two-dimensional lattice with quenched disorder that was parameterized accordingly with silanol (Si-OH), silanolate (Si-O-M), siloxane (Si-O-Si), and a grafted metal atom (M) to simulate tens of thousands of potential grafting sites [165,166]. Using around 40–50 of these sites as a training set, importance learning models (sampling techniques), which work as an efficient sampling technique and machine learning model, were used to predict the site-averaged kinetics. Evolutions of this method utilize smaller 3D cluster models and amorphous silica slab models using a reactive force field (ReaxFF) in LAMMPS to generate the distribution of vicinal silanol angles and other descriptors needed to feed into the importance learning algorithm to describe site-averaged kinetics of grafting TiCl₄ as well as a multistep reaction (Figure 8a,b) [167,168]. Coupled with the generation of more realistic catalytic models, these important learning techniques can enhance the computational design of catalysts but would require knowledge of possible pathways beforehand to efficiently use machine learning to train an accurate kinetic model.

Another aspect of computational design for active site heterogeneity showcases how active site heterogeneity affects thermodynamic, kinetic, and spectroscopic measurements for single site catalysts [32,44,163,169,170,171]. Previous work by our group in this area focuses on the a-SiO₂-supported tripodal organovanadium (III) complex [SiO₂V^III(Mes)(THF)], which was previously reported to catalyze olefin hydrogenation efficiently [172]. To model these catalysts, constrained silsesquioxane cages were built to simulate the nonuniformity of a-SiO₂, as these cluster models have been shown to be effective models for a-SiO₂ [173,174,175,176,177]. Using these cages works for materials like silica where the electron density is localized within the active site and not delocalized on the surface, e.g., 3d transition metal oxides. From a thermodynamic perspective on the mechanism of styrene hydrogenation through heterolytic bond activation, the stability of the active sites and their respective hydrides was directly impacted by the elongation of the bond between V and a donor siloxane, V-O(siloxane). To verify the experimental kinetic profile for the styrene hydrogenation using [SiO₂V^III(Mes)(THF)], kinetic Monte Carlo (kMC) studies were performed to compare simulated distributions of the various catalytic models to experimental kinetic profiles (Figure 8c) [163,169,170,171]. Follow up studies showed how the overall kinetics can be predicted with transition state theory and an optimal catalytic site can be generated within a multidimensional grid search using the local environment around the grafting site (Figure 8d). For a 2D scan of the free energy surface (Figure 8e), the dimensions were the V-O (siloxane) bond distance and the Euclidean distance between the two O atoms on the silica surface bound to the metal (O-O distance); for a 3D scan of the free energy surface (Figure 8f), the three dimensions were the Euclidean distance between the three O atoms that form the tripodal site. With these multidimensional parameters, optimal local environments were derived through a nonlinear optimization method, which can then be used to locate activity hotspots on a catalytic surface that can guide both computational and synthetic catalyst design.

4. Conclusions and Outlook

As discussed in this review, computational catalysis can be employed to effectively develop the structure–activity correlation, which can guide future catalyst material design and development. Spectroscopic simulations can provide structural information about the active site and structural evolution during catalysis. The physical and chemical properties of the active site can also be reflected by performing electronic structure calculations. By carrying out reaction-mechanistic studies, the optimal reaction pathway can be identified. However, to accurately obtain the reaction energetics and kinetics, the active site heterogeneity and solvation effect with an electrified surface should be treated in an appropriate manner. XANES simulation can provide critical information regarding the catalyst active site structure and reveal physical and chemical properties. These insights can assist one in building more realistic models to understand the reaction mechanism and catalyst active site evolution during catalysis. Furthermore, catalyst–support interaction has been extensively studied for catalyst activity tuning. The empirical correlations within adsorption energies, electronic structures, and energy barriers are realized to generate structure–activity correlations to guide future catalyst material design and discovery. Despite that, active site heterogeneity should also be considered when exploring the reaction mechanism and deriving the structure–activity correlation. A few methods for investigating this issue have been reviewed in this paper. To achieve a better understanding of catalyst activity, different particle sizes, bond lengths, and even possible ligands should be taken into consideration. All in all, this valuable information extracted from computational catalysis can be used for future catalyst design and discovery.