1. Introduction
Economical water splitting technology for the development of low-cost and efficient fuels motivates research in many fields. This particular application of the conversion of solar energy into chemical reaction can be accomplished using a catalytic site mounted on a substrate. The periodic pore system that is characteristic of silica substrates is considered to be one of the best options for use in heterogeneous catalysis research, mostly due to its high surface-to-volume ratio [
1]. Micro- and mesoporous materials have a wide range of functionality, some of which are still being discovered [
2]. Solar energy conversion [
3], energy storage, and photodynamic therapy [
4] are just a few areas in which these materials have found wide-spread utility.
The addition of titanium atoms to the inner surface of the silica pore walls provides a photoactive material [
5] and introduces numerous charge transfer states, which can be analyzed by atomistic computational modeling [
6,
7,
8]. It has been known since the 1970s that titanium dioxide (TiO
2) can be used in water-splitting applications [
9]. Since then, numerous researchers have been trying to improve conditions for photocatalysis using TiO
2 in conjunction with various substrates [
10,
11], dopants [
12,
13,
14], dyes [
15,
16],
etc. Titanium’s distribution onto a periodic and porous substrate has been shown to increase the effectiveness of hydrogen evolution when compared to bulk TiO
2 [
17]. Evaluation of these parameters is, by no means, a simple task. It is a goal of this research to evaluate one of these parameters and its role in catalysis: a silica substrate. At present, many materials have been reported as photocatalysts for water splitting. However, titanium-doped microporous silica demonstrates H
2 production reaction using sacrificial reagents such as triethanolamine (TEOA) or methanol. This material, thus, is able to perform a significant part of the water-splitting mechanism. By simulation of this model, we learn more details of the role of charge transfer for photocatalysis. Additionally, while it is important to evaluate the other aspects of catalysis, which are known to improve photocatalytic efficiency (
i.e., co-catalysts, alternative dopants, dyes, and the use of sacrificial agents), we ventured to simplify the model in order to eliminate parameters that might obscure the role of the silica substrate.
Charge transfer dynamics that occur prior to the dissociation of water molecules near the titanium atoms can be scrutinized using non-adiabatic molecular dynamics [
18]. In order to further understand the process by which charge transfer favors water-splitting, electron dynamics may be employed. Ideally, one would analyze bandgap excitation, electron relaxation and dynamics of ions all at once. Since this is not possible with current molecular simulation techniques, a separation of the governing aspects of the reaction must occur. To make this investigation more practical, ground state electronic structure is explored first. This information helps to identify orbital transitions due to excitations, which are of interest. Molecular dynamics [
19] are simulated, which leads to couplings [
20] and eventually to electron dynamics of photoexcitation [
21] that then provides excitation lifetimes [
22] and details of the charge transfer meachanism [
6,
7,
8]. These lifetimes are an integral part of making conclusions about a material and its photocatalytic properties. If electron relaxation rates are low enough, catalytic reactions may occur.
The ability to use photoexcitations as initial conditions for electron dynamics allows for investigations into the dynamics of the formation of possible charge transfer states, which could lead to chemical reactions. A range of the most important orbitals can be narrowed down by visualizing them and identifying orbitals of interest based on their locations on the model. These orbitals can be used as an input to electron dynamics to compute relaxation dynamics and rates for electrons and holes. These data (on dynamics and rates) allow for the identification of so-called “trap states” [
23]. A trap state is defined as an energy state in which the electron or hole becomes trapped for a relatively long time when compared to the overall time of relaxation. The basic idea is that the existence of trapping states could facilitate charge transfer because it encourages charge separation, which can then induce a chemical reaction.
2. Results and Discussion
An alpha-quartz silica slab, of the dimensions 5.4 × 14.7 × 17.0 Å
3 (cubic Angstroms) and composition Si
36O
72, was the basis for this model. Atoms were systematically removed until a ~1 nm cylindrical pore was created, leading to a modified composition of Si
24O
48. A tetrahedrally-coordinated Ti atom was added to the inner surface of the pore wall and capped, as well as the addition of H caps onto the exposed O atoms. Water molecules were added to the inside of the pore, giving an overall chemical composition of Si
24O
48 + TiO
2H
2 + 11H
2O. A fraction of water molecules dissociate and adsorb onto uncoordinated ions from the inner surface of the pore: H
+ to uncoordinated O, and OH
− to uncoordinated Si or Ti atoms. Thus, the model contains intact and dissociated water molecules.
Figure 1 displays a diagram of the model, indicating the position of the Ti atom in relation to the placement of water molecules within the pore. Oxygen atoms represent the inner surface of the pore. Utilizing periodic boundary conditions in three dimensions, this model simulates a periodic and tubular pore system, which is similar to forms of silica substrates used in experimental photocatalysis research. We compare four models: silica slab with an empty pore, water alone (single and multiple molecules), silica with Ti and a water-filled pore.
In catalytic simulations, it is important to investigate basic electronic properties as a starting point for further inquiries into charge transfer and molecular dynamics. In
Figure 2, densities of states and absorbance spectra are computed according to Equations (5)–(8), which are simple ways to visualize observables related to basic electronic properties. Comparing the isolated water molecule and a cluster of H
2O in
Figure 2A,B, it is seen that a cluster of H
2O molecules provides an occupied orbital in the valence band that does not exist in a single water molecule. Perhaps this is indicative of water’s ability to ionize
. A close comparison of the densities of states of all models under consideration (top row,
Figure 2) reveals similarities. One notable similarity can be seen between the silica slab only (
Figure 2C) and the Ti-functionalized pore (
Figure 2D). There is a similar pattern in the valence bands from −10 to ~0 eV and conduction band in the range of 0 to 10 eV in these two models. However, the addition of a Ti atom provides more states in the ~0 to 4 eV range in
Figure 2D. We expect this to occur with the addition of a transition metal, as these states are Ti
d-orbitals. The density of states for this primary model (
Figure 2D) shows a small band gap of ~0.032 eV. Additionally, one can see electron occupation in the valance band of the water cluster, in the water-filled pore, and also in the Ti-functionalized pore (see
Figure 2B–D), potentially indicating a more facile charge transfer.
Absorbance spectra were analyzed with two main goals in mind: first, to gain an understanding of the basic electronic properties of the model, and, second, to obtain the initial conditions for future electron dynamics simulations. With the first goal in mind, the components of the system are investigated separately in order to determine how each contributes to the overall character. The multi-molecular water (
Figure 2F) shows an absorbance peak at about 380 nm, which is outside of the visible spectrum. A comparison of the absorbance spectra is made between the components of the model (as displayed in
Figure 2E–G), and the complete model’s absorbance spectrum (
Figure 2H). The complete model has its peaks labeled based on the analysis of orbital transitions and comparison to the spectra of the components of the model. The model absorbs in the UV region of the electromagnetic spectrum, which is consistent with known absorption of silica.
The inclusion of a Ti atom on the inner pore wall has contributed transition metal
d-orbitals to the electronic structure of the model. The titanium exists in a +4 oxidation state, which means all of its
d-orbitals are empty, with an electron configuration of [Ar] 3d
0 4s
0. Since the Ti is tetrahedrally-coordinated, it is expected to see tetrahedral crystal field splitting among the orbital energies,
[
24,
25]. In fact, this was found as one of the results of this research. These orbitals were characterized as
d-orbitals by plotting isosurfaces and identifying the characteristic shapes of
d-orbitals. LU+5 and LU+4 orbitals have
d-character with some
p-orbital shape contribution, which is why there are six
d-orbitals reported, instead of five. In
Figure 3, there exists a gap between the two lowest-energy
d-orbitals and the energies of the remaining
d-orbitals. Tetrahedral crystal field splitting of Ti’s
d-orbitals exists within a reasonably-sized sub-gap of energy between energies of the two groups of nearly-degenerate orbitals. This sub-gap energy is about 1.2 eV, which is of realistic magnitude to confirm the accuracy of the model.
The model can exist in several excited states. Some of the excitations have neutral character, others exhibit charge transfer character. These charge transfer states have been included due to the trapping states that are contained in each of them. Furthermore, HO-11, HO-6, LU+7, and LU+8 orbitals exist on water molecules within the pore, as displayed in
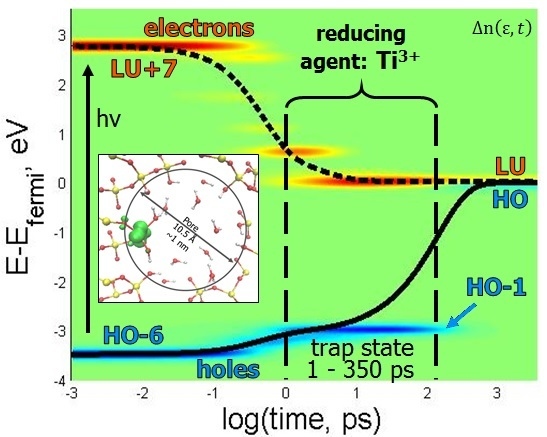
Figure 4. In a photoexcited state, one can observe the non-radiative transition from one excitation to another due to non-adiabatic couplings. If there is a possibility of a chemical reaction occurring, the focus should be on those molecules and orbitals involved in such a reaction. In this model, the dynamics of charge transfer states formation have been identified. The dynamics of charge transfer are triggered by the photoexcitation to a neutral state (HO-6, LU+7) and (HO-11, LU+8). The dynamics induced by different photoexcitations are compared in
Figure 5.
The pathways of occupation dynamics are determined by the initial excitation A → B, see Equation (14). Solutions of Equations (13)–(16) first provide occupations as functions of time,
, which are displayed in
Figure 5A,B, for one excitation and another in
Figure 5D,E. In
Figure 5A, electron occupation relaxes from LU+7, but not before transitioning through several short-lived states and one longer-lived state at LU+2, which exists on the Ti atom (
Figure 4D). LU+2 behaves as an electron trap, which slows its relaxation rate. Ultimately, LU+7 → LU relaxation occurs at a rate of 0.8141 ps
−1, which is computed according to Equation (22). A summary of relaxation rates can be found in
Table 1. In contrast, the HO-6 → HO relaxation (
Figure 5B) occurs at a much slower rate of 0.0301 ps
−1. This slower rate is due to stable hole trapping states, which occur at HO-3 and HO-1 and are located within the silica substrate (
Figure 4H,I). Viewing the larger peaks contained in
Figure 5A helps to identify more influential trap states. The observation that LU+6 and LU+2 peaks have higher amplitude than other states indicates that more time is spent in those states. The same can be said for
Figure 5B, containing larger peaks at HO-3 and HO-1. These states are occupied for a longer time. All of the above information can be included in one figure (
Figure 5C and are derived using Equations (17) and (18)).
Figure 5C,F is helpful in visualizing the movement of electrons and holes in both orbitals and energy over time.
Figure 5D,E tells similar stories, with meta-stable electron traps occurring at LU+7 and LU+2. The rate of electron relaxation is calculated to be 0.7919 ps
−1. A stable hole trap exists at HO-1, which lengthens the hole’s relaxation rate compared to the electron, and can be visualized more clearly in
Figure 5E. The more interesting aspect of this story is that the hole traps exist on Si orbitals, which could be a testament to why silica is such an effective substrate for heterogeneous catalysis, as it facilitates charge separation. Until the hole relaxes, the model resides in the oxidation state O
− + Ti
3+. The lowest occupied orbital is located on Ti and is occupied by the electron, which means that the titanium is in the Ti
3+ state rather than Ti
4+, which is specific for the ground state. The titanium in a photo-induced metastable Ti
3+ state is expected to be a strong reducing agent. Thus, in this excited state, Ti
3+ is able to promote reducing half reactions 2H
+ + 2Ti
3+ → H
2 + 2Ti
4+ contributing to water splitting and hydrogen evolution. Additionally, the hole trap occurring at HO-1 is a consequence of the energy gap law [
26], because there is a sizable energy gap between HO and HO-1 (~3 eV), which makes it difficult for the energy to dissipate into vibrations during the relaxation process, as all vibrational frequencies are below this sub-gap.
The electron traps for both excitations are located on one of the Ti atom’s orbitals, which seems logical since the Ti is known to be the catalytic site of the water-splitting reaction. The rates of electron relaxation differ by 0.0222 ps−1. The difference of the rates of hole relaxation, however, is only 0.0040 ps−1. The hole relaxation rates are less dependent upon initial excitation than the electrons. The excitations of HO-6 → LU+7 and HO-11 → LU+8 have features in common, such as the existence of the same electron trap state of LU+2 and hole trap state HO-1. This indicates that these two trap states exist, independent of the excitation. Additionally, the rates of hole relaxation are very similar, indicating that the existence of the hole trap is the determining factor in the magnitude of the rate. This feature of dynamics is dictated by electronic structure with an occupied orbital in the middle of the gap.
3. Experimental Section
Atomic structure determines initial positions of each ion,
, in the model. Density-Functional Theory (DFT) was chosen because it allows one to analyze electronic structure and spectra [
27]. The Vienna
Ab-Initio Simulation Package (VASP v5.4, Computational Materials Physics, Vienna, Austria, 2015) was used for calculations, with Projector Augmented Wave (PAW) pseudopotentials and Generalized Gradient Approximation (GGA) Perdew-Burke-Ernzerhof (PBE) functionals [
28]. Periodic boundary conditions are used in order to simulate the periodicity of typical silica substrate material.
Figure 1A provides a visualization of the model as a unit cell. As portrayed in
Figure 1B, the unit cell may be replicated and then translated in the
x,
y, or
z directions. The potential is not affected by this replication and subsequent movement along a translation vector,
, and therefore, the potential experienced by the electrons [
29,
30] of the original unit cell is equivalent to any replica as given by Equation (1)
with component vectors
,
, and
, and integers
k,
l, and
m.
The Kohn-Sham equation is the Schrödinger equation of a fictional system of particles which do not interact and that generate the same density as any system of interacting particles. This is given by Equation (2)
where the first term corresponds to kinetic energy,
T, and includes a symbol for the gradient
. In solving Equation (1), a set of single-electron orbitals
and their energies
is determined. These orbitals are then combined with an orbital occupation function,
, for assembling the overall density of electrons, as given by Equation (3)
In addition, the total density defines the potential, is defined by Equation (4)
which is defined as functional derivative of the total energy with respect to variation of the total density and includes the interactions of electrons with ions, and three electron iterations: Coulomb, correlation, and exchange. Rectangular brackets symbolize a functional. Equations (2)–(4) are solved in a self-consistent and iterative fashion. Electrostatic potential introduced in Equation (4) demonstrates the interaction of a valence electron with the remaining charge of electrons and ions. This electrostatic potential is a consequence computed in DFT.
The electronic density of state (DOS) is defined as the number of states per interval of energy that are capable of electron population [
29]. DOS are used to describe electronic structure of the model. DOS is given by Equation (5)
where the index,
i, runs over all orbitals calculated and
is the energy of a given orbital (calculated using DFT). The Dirac delta function is approximated by a finite width Gaussian function.
The optical absorption spectrum is computed based on the transition dipole moment, by Equation (6)
which calculates transition dipoles from initial
to final
and is directly related to the oscillator strength, which is then given by Equation (7)
Here,
is the angular frequency of the excitation from state
i to state
j,
is the transition dipole from state
i to state
j, with
and
e as fundamental constants. The oscillator strength contributes a weight in the absorption spectrum, leading to Equation (8)
in order to apply intensities to the Eigen energy differences which are most probable to absorb light in specific energy ranges.
Molecular dynamics (MD) [
30] was used to simulate the change of the positions of the atoms after the cluster is “heated” at a given temperature for a given amount of time. The kinetic energy of the model should remain constant, so the velocities of all the atoms were rescaled to mimic a constant temperature during the MD process according to Equation (9), where M
I and
denote the mass and initial velocity of I
th nucleus, respectively, N is the number of nuclei, k
B is the Boltzmann constant, and T is the temperature. The Hellman-Feynman forces,
, act on each atom to determine the acceleration that is to be used in the Newton equation of motion, Equation (10),
by iterative solving of the Kohn–Sham equation and then updating the ionic positions to generate a single example of nuclear positions trajectory
for a micro-canonical ensemble. The time dependent adjustments of KS orbitals
and orbital energies
can also be monitored as a function of time. On-the-fly non-adiabatic couplings [
20,
31] were computed along the nuclear trajectory
by Equation (11).
Next, the autocorrelation functions of these couplings were processed with Equation (12).
According to Redfield theory [
32], the Fourier transform of
M(τ) provides parameters
for the equation of motion of electronic degrees of freedom, as per Equation (13)
where
and
represent the Liouville and Redfield superoperators acting on the density operator.
The initial values of the density matrix at time t = 0, were symbolized by and served as the initial condition for a system of differential equations, as per Equation (14).
Here, indices A and B label specific initial conditions, the Dirac delta function reflects the fact that off-diagonal elements are set to zero, stands for the initial occupation of ith Kohn–Sham orbital so that and . A Dirac delta with a negative sign corresponds to the removal of an electron from the Ath Kohn–Sham orbital, Dirac delta with a positive sign corresponds to the addition of an electron to the Bth Kohn–Sham orbital. Equation (14) summarizes the following situation: an electron-hole pair A → B is excited, with A and B being indices of orbitals corresponding to the valence band, where an electron is promoted from, and the conduction band, where the electron is promoted to. The pairs of orbitals, (A,B), were chosen according the maximum values of oscillator strengths for the corresponding excitation .
The time evolution of the electronic state was calculated by solving the equation of motion as follows:
First, Liouville–Redfield superopertor is diagonalized, providing a set of eigenvalues
and eigenvectors,
, according to Equation (15)
Here solutions of Equation 15 are labeled by index
. Then, the superposition of eigenvectors, given by Equation (16),
were used to compose the density matrix for each instant of time in such a way that it matches the initial conditions Equation (14) [
6,
7,
8,
22]. The electron in the conduction band and the hole in the valence band are indicated by e and h, respectively. In addition, index e was used with the appreciation that equations for holes are the same as for electrons.
Utilizing the above information, the charge density distribution, rate of energy dissipation, and rate of charge transfer were calculated as follows [
6,
7,
8,
22,
33].
The distribution of a carrier (electron or hole) in space Equation (17) and in energy Equation (18) are as follows:
Here,
represents the occupation of the i
th orbital,
. The expectation value of energy of a carrier is given by Equation (19)
Equation (18) can be rewritten to have a dimensionless energy in this manner:
If one assumes a single exponential fit of the carrier energy dissipation, then as per Equation (21)
then the energy dissipation rate can be expressed by Equation (22):
The constant represents the average relaxation time for the electron (or hole), and therefore the dynamics of the electronic relaxation.
A photoexcitation from ground state to excited state (A,B) results in a sequence of elementary relaxation events (refer to
Scheme 1) with the electron and hole subsequently moving one step towards lower excitation, however, the time needed for each step is different, this relaxation dynamics may often exhibit so-called “trapping” when a charge carrier gets trapped in a specific orbital and requires substantial time for the next relaxation step.
4. Conclusions
Heterogeneous catalysis, as modeled here, with a silica substrate and titanium atom, has been evaluated using DFT. Since the formation of charge transfer states is a prerequisite for a chemical reaction, it was necessary to identify such states in this model, which was accomplished in this work. This is another successful application of the density matrix method for electron dynamics. A survey of DOS and absorbance spectra of individual components and of the whole system concludes that a composite of the individual components of the system combine to form the whole density of states.
The calculated data reveal a much longer relaxation time for holes relative to that for electrons, which is dictated by energy offsets. It may seem intuitive that only electron trap states would facilitate a catalytic reaction, but hole trap states would also, as this study demonstrates: either would prevent recombination of the electron–hole pair. Holes affect electrons insofar as that the electron cannot recombine if the hole is still in an excited state. In fact, a prolonged separation of charge was found, which may indicate a higher probability of reaction since there is more electron movement within the system’s components. In order for water splitting to occur, the reaction must happen while the charge transfer state exists, before it recombines. Interestingly, an important trap state was found to be located within the silica substrate. This trap state prolongs relaxation, widening the window available for a chemical reaction to occur.
The presence and location of the trap state indicates that such heterogeneous substrates may play a greater role in catalysis than previously envisaged. This allows one to modify the system to provide better electronic characteristics for more efficient water-splitting, i.e., tuning the band-gap. In other words, in the future, one may be able to choose substrates and catalytic sites to correspond to desired electronic properties in order to optimize catalytic reactions. This research will continue by applying this methodology to different situations (such as introduction of oxygen vacancy and other metal oxide materials) to clarify the charge transfer mechanism in various photocatalytic materials.