Water–Gas Shift Reaction over Ni/CeO2 Catalysts
Abstract
:1. Introduction
2. Results
2.1. Ni/CeO2 Catalyst Characterization
2.2. Kinetic Behavior on the WGS Reaction in the Fixed-Bed Reactor Configuration
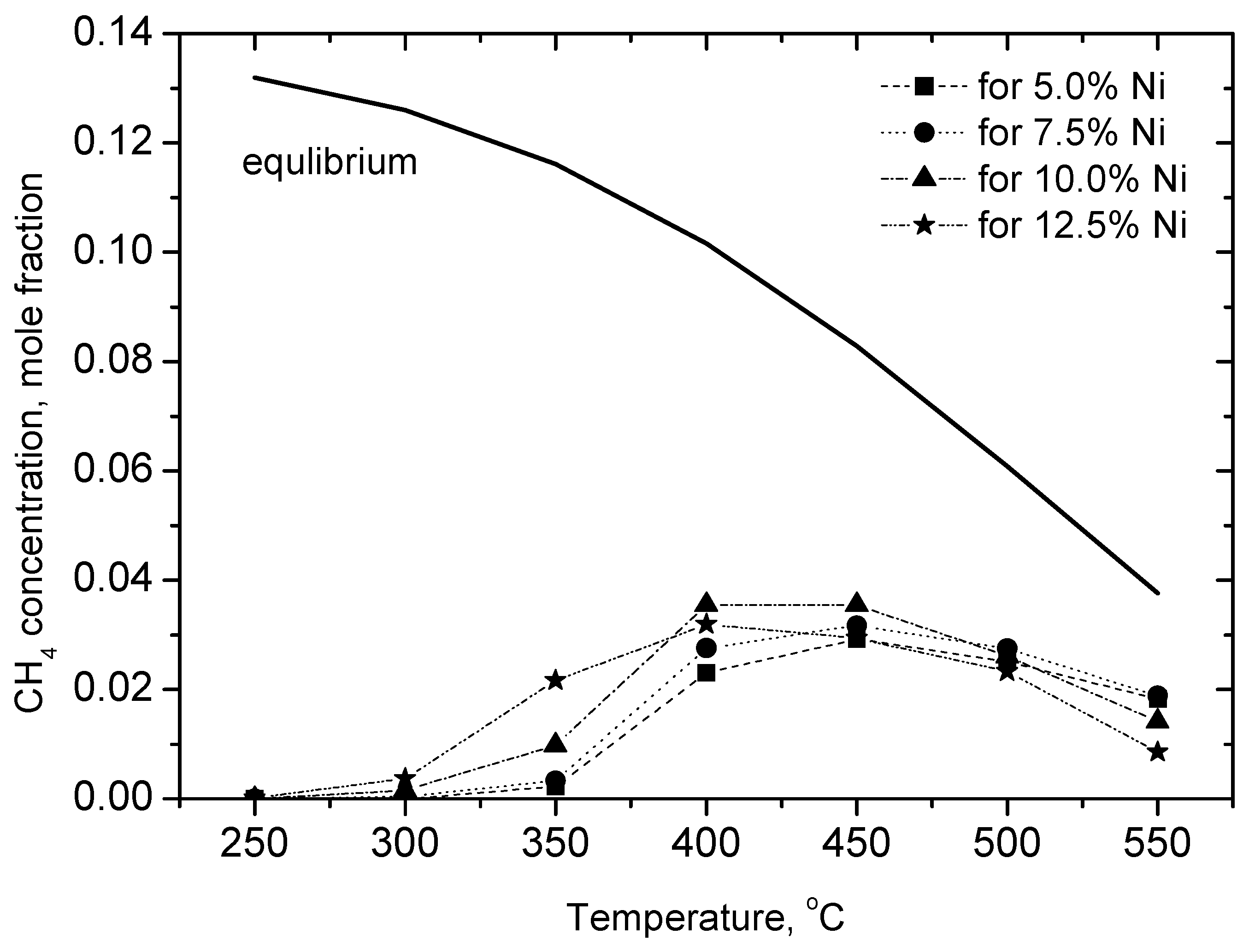
2.2.1. Experimental Observation
2.2.2. Kinetic Modeling
2.3. Kinetic Behavior of the WGS Reaction in a Microchannel Reactor Configuration
2.3.1. Experimental Data
2.3.2. Kinetic Assessment
Effect of the Resistance to Mass Transfer
Kinetic Modeling
2.3.3. Microreactor Simulations
- ygi—concentrations in gas phase, mole fraction;
- ysi—concentrations in solid phase, mole fraction;
- u—velocity of gas, m/s;
- ɛ—catalyst fraction;
- Sv—the specific surface-to-volume ratio in the channel, m−1,
- β—mass transfer coefficient, m/s;
- cp—gas heat capacity, J m−3 K−1;
- cs—catalyst heat capacity, J m−3 K−1;
- Tg—gas phase temperature, К;
- Ts—solid phase temperature, К;
- α—mass transfer coefficient, m/s;
- Tfurnace—temperature in the furnace, К;
- λ—thermal conductivity of the catalyst;
- L—reactor length;
- Vm—molar volume, m3 mol−1.
3. Materials and Methods
3.1. Ni/CeO2 Catalysts Preparation and Characterization
3.2. Catalyst Testing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ledjeff-Hey, K.; Roes, J.; Wolters, R. CO2-scrubbing and methanation as purification system for PEFC. J. Power Sources 2000, 86, 556–561. [Google Scholar] [CrossRef]
- Minyukova, T.P.; Itenberg, I.S.; Khassin, A.A.; Sipatrov, A.G.; Dokuchits, E.V.; Terent’ev, V.Y.; Khristolyubov, A.P.; Brizitskii, O.F.; Yurieva, T.M. Permeable composite material for compact apparatus for hydrogen-rich gases deep cleaning from CO. Chem. Eng. J. 2007, 134, 235–238. [Google Scholar] [CrossRef]
- Stankiewicz, A.I.; Moulijn, J.A. Process intensification: Transforming chemical engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
- Ehrfeld, W.; Hessel, V.; Löwe, H.B. State of the Art of Microreaction Technology. In Microreactors: New Technology for Modern Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2000; ISBN 9783527295906. [Google Scholar]
- Smith, R.J.; Loganathan, M.; Shantha, M.S. A review of the water gas shift reaction kinetics. Int. J. Chem. React. Eng. 2010, 8. [Google Scholar] [CrossRef]
- Membrane Reactors for Energy Applications and Basic Chemical Production. In Woodhead Publishing in Energy; Basile, A.; Di Paola, L.; Hai, F.; Piemonte, V. (Eds.) Elsevier Ltd.: Cambridge, UK, 2010; Volume 76, ISBN 978-1-78242-223-5. [Google Scholar]
- Schumacher, N.; Boisen, A.; Dahl, S.; Gokhale, A.A.; Kandoi, S.; Grabow, L.C.; Dumesic, J.A.; Mavrikakis, M.; Chorkendorff, I. Trends in low-temperature water-gas shift reactivity on transition metals. J. Catal. 2005, 229, 265–275. [Google Scholar] [CrossRef]
- Pinaeva, L.G.; Sadovskaya, E.M.; Ivanova, Y.A.; Kuznetsova, T.G.; Prosvirin, I.P.; Sadykov, V.A.; Schuurman, Y.; van Veen, A.C.; Mirodatos, C. Water gas shift and partial oxidation of CH4 over CeO2–ZrO2 (–La2O) and Pt/CeO2–ZrO2 (–La2O3): Performance under transient conditions. Chem. Eng. J. 2014, 257, 281–291. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Q.; Flytzani-Stephanopoulos, M. Low-temperature water-gas shift reaction over Cu- and Ni-loaded cerium oxide catalysts. Appl. Catal. B Environ. 2000, 27, 179–191. [Google Scholar] [CrossRef]
- Jacobs, G.; Chenu, E.; Patterson, P.M.; Williams, L.; Sparks, D.; Thomas, G.; Davis, B.H. Water-Gas Shift: Comparative Screening of Metal Promoters for Metal/Ceria Systems and Role of the Metal. Appl. Catal. A Gen. 2004, 258, 203–214. [Google Scholar] [CrossRef]
- Czekaj, I.; Loviat, F.; Raimondi, F.; Wambach, J.; Biollaz, S.; Wokaun, A. Characterization of surface processes at the Ni-based catalyst during the methanation of biomass-derived synthesis gas: X-ray photoelectron spectroscopy (XPS). Appl. Catal. A Gen. 2007, 329, 68–78. [Google Scholar] [CrossRef]
- Haryanto, A.; Fernando, S.D.; Filip To, S.D.; Steele, P.H.; Pordesimo, L.; Adhikari, S. High Temperature Water Gas Shift Reaction over Nickel Catalysts for Hydrogen Production: Effect of Supports, GHSV, Metal Loading, and Dopant Materials. J. Thermodyn. Catal. 2011, 2, 106. [Google Scholar] [CrossRef]
- Pastor-Pérez, L.; Reina, T.R.; Ivanova, S.; Centeno, M.A.; Odriozola, J.A.; Sepúlveda-Escribano, A. Ni-CeO2/C Catalysts with enhanced OSC for the WGS reaction. Catalysts 2015, 5, 298–309. [Google Scholar] [CrossRef] [Green Version]
- Barrio, L.; Kubacka, A.; Zhou, G.; Estrella, M.; Martínez-Arias, A.; Hanson, J.C.; Fernández-García, M.; Rodriguez, J.A. Unusual physical and chemical properties of Ni in Ce1−xNixO2−y oxides: Structural characterization and catalytic activity for the water gas shift reaction. J. Phys. Chem. C 2010, 114, 12689–12697. [Google Scholar] [CrossRef]
- Pastor-Pérez, L.; Buitrago-Sierra, R.; Sepúlveda-Escribano, A. CeO2-promoted Ni/activated carbon catalysts for the water–gas shift (WGS) reaction. Int. J. Hydrogen Energy 2014, 39, 17589–17599. [Google Scholar] [CrossRef]
- Tang, K.; Liu, W.; Li, J.; Guo, J.; Zhang, J.; Wang, S.; Niu, S.; Yang, Y. The Effect of Exposed Facets of Ceria to the Nickel Species in Nickel-Ceria Catalysts and Their Performance in a NO + CO Reaction. ACS Appl. Mater. Interfaces 2015, 7, 26839–26849. [Google Scholar] [CrossRef] [PubMed]
- Zyryanova, M.M.; Snytnikov, P.V.; Amosov, Y.I.; Ven’yaminov, S.A.; Golosman, E.Z.; Sobyanin, V.A. Selective Methanation of CO in the Presence of CO2 in Hydrogen-Containing Mixtures on Nickel Catalysts. Kinet. Catal. 2010, 51, 907–913. [Google Scholar] [CrossRef]
- Zyryanova, M.M.; Snytnikov, P.V.; Gulyaev, R.V.; Amosov, Y.I.; Boronin, A.I.; Sobyanin, V.A. Performance of Ni/CeO2 Catalysts for Selective CO Methanation in Hydrogen-Rich Gas. Chem. Eng. J. 2014, 238, 189–197. [Google Scholar] [CrossRef]
- Konishcheva, M.V.; Potemkin, D.I.; Snytnikov, P.V.; Zyryanova, M.M.; Pakharukova, V.P.; Simonov, P.A.; Sobyanin, V.A. Selective CO Methanation in H2-Rich Stream over Ni–, Co– and Fe/CeO2: Effect of Metal and Precursor Nature. Int. J. Hydrogen Energy 2015, 40, 14058–14063. [Google Scholar] [CrossRef]
- Alstrup, I. On the Kinetics of Co Methanation on Nickel Surfaces. J. Catal. 1995, 151, 216–225. [Google Scholar] [CrossRef]
- Yadav, R.; Rinker, R.G. Step-Response Kinetics of Methanation over a Ni/Al2O3 Catalyst. Ind. Eng. Chem. Res. 1992, 31, 502–508. [Google Scholar] [CrossRef]
- Ramaroson, E.; Tempere, J.F.; Guilleux, M.F. Spectroscopic characterization and reactivity study of ceria-supported nickel catalysts. J. Chem. Soc. Faraday Trans. 1992, 88, 1211–1218. [Google Scholar] [CrossRef]
- Herrmann, J.M.; Ramaroson, E.; Tempere, J.F.; Guilleux, M.F. Semiconductivity study of ceria-supported nickel related to its methanation catalytic activity. Appl. Catal. 1989, 53, 117–134. [Google Scholar] [CrossRef]
- Andersson, M.P.; Abild-Pedersen, F.; Remediakis, I.N.; Bligaard, T.; Jones, G.; Engbæk, J.; Lytken, O.; Horch, S.; Nielsen, J.H.; Sehested, J.; et al. Structure sensitivity of the methanation reaction: H2-induced CO dissociation on nickel surfaces. J. Catal. 2008, 255, 6–19. [Google Scholar] [CrossRef]
- Ermakova, A. Methods of Applied Thermodynamics, Employed for Mathematical Simulation of Chemical Processes and Reactors; Teaching medium; Boreskov Institute of Catalysis, Siberian Branch of the Russian Academy of Sciences: Novosibirsk, Russia, 2002. (In Russian) [Google Scholar]
- Fadeev, S.I.; Ermakova, A.; Ivanov, E.A.; Gudkov, A.V. The calculation of thermodynamic equilibrium of gas phase processes by parameter marching method. Theor. Found. Chem. Technol. 1997, 31, 62–67. (In Russian) [Google Scholar]
- Ermakova, A. Macrokinetic models of complex reactions. In Industrial Catalysis in Lectures; Noskov, A.S., Ed.; Kalvis: Moscow, Russia, 2006; Volume 4, pp. 67–114. ISBN 5895300049. (In Russian) [Google Scholar]
- Ermakova, A. Macrokinetic models of complex reactions. In Investigation Methods of Chemical Reactions Kinetics; Parmon, V.N., Ed.; Boreskov Institute of Catalysis: Novosibirsk, Russia, 2000; pp. 5–52. (In Russian) [Google Scholar]
- Ermakova, A. Macrokinetics Methods Used in Mathematical Modeling of Chemical Processes and Reactors; Institut Kataliza SO RAN im. G.K. Boreskova: Novosibirsk, Russia, 2001. (In Russian) [Google Scholar]
- Shekhawat, D.; Spivey, J.J.; Berry, D.A. Fuel Cells: Technologies for Fuel Processing; Elsevier: Oxford, UK, 2011; ISBN 978-0-444-53563-4. [Google Scholar]
- Goerke, O.; Pfeifer, P.; Schubert, K. Water gas shift reaction and selective oxidation of CO in microstructures. Appl. Catal. A Gen. 2004, 263, 11–18. [Google Scholar] [CrossRef]
- Carrasco, J.; López-Durán, D.; Liu, Z.; Duchoň, T.; Evans, J.; Senanayake, S.D.; Crumlin, E.J.; Matolín, V.; Rodríguez, J.A.; Ganduglia-Pirovano, M.V. In situ and theoretical studies for the dissociation of water on an active Ni/CeO2 catalyst: Importance of strong metal-support interactions for the cleavage of O-H bonds. Angew. Chem. Int. Ed. 2015, 54, 3917–3921. [Google Scholar] [CrossRef] [PubMed]
- Kolb, G.; Baier, T.; Schürer, J.; Tiemann, D.; Ziogas, A.; Specchia, S.; Galletti, C.; Germani, G.; Schuurman, Y. A micro-structured 5 kW complete fuel processor for iso-octane as hydrogen supply system for mobile auxiliary power units. Part II—Development of water–gas shift and preferential oxidation catalysts reactors and assembly of the fuel processor. Chem. Eng. J. 2008, 138, 474–489. [Google Scholar] [CrossRef]
- Tonkovich, A.Y.; Zilka, J.L.; LaMont, M.J.; Wang, Y.; Wegeng, R.S. Microchannel reactors for fuel processing applications. I. Water gas shift reactor. Chem. Eng. Sci. 1999, 54, 2947–2951. [Google Scholar] [CrossRef]
- Germani, G.; Alphonse, P.; Courty, M.; Schuurman, Y.; Mirodatos, C. Platinum/ceria/alumina catalysts on microstructures for carbon monoxide conversion. Catal. Today 2010, 110, 114–120. [Google Scholar] [CrossRef] [Green Version]
- Adachi, H.; Ahmed, S.; Lee, S.H.D.; Papadias, D.; Ahluwalia, R.K.; Bendert, J.C.; Kanner, S.A.; Yamazaki, Y. A natural-gas fuel processor for a residential fuel cell system. J. Power Sources 2009, 188, 244–255. [Google Scholar] [CrossRef]
- Groppi, G.; Ibashi, W.; Tronconi, E.; Forzatti, P. Structured reactors for kinetic measurements in catalytic combustion. Chem. Eng. J. 2001, 82, 57–71. [Google Scholar] [CrossRef]
- Groppi, G.; Ibashi, W.; Tronconi, E.; Forzatti, P. Structured reactors for kinetic measurements under severe conditions in catalytic combustion over palladium supported systems. Catal. Today 2001, 69, 399–408. [Google Scholar] [CrossRef]
- Aris, R. The Mathematical Theory of Diffusion and Reaction in Permeable Catalyst; Clarendon Press: Oxford, UK, 1975; ISBN 0198519311. [Google Scholar]
- Hill, C.G. An Introduction to Chemical Engineering Kinetics and Reactor Design; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Schmidt, D. The Engineering of Chemical Reactions, 2nd ed.; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 3rd ed.; Prentice-Hall International, Inc.: Upper Saddle River, NJ, USA, 2009; ISBN 013-9-73-785-5. [Google Scholar]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Groppi, G.; Belloli, A.; Tronconi, E.; Forzatti, P. A comparison of lumped and distributed models of monolith catalytic combustors. Chem. Eng. Sci. 1995, 50, 2705–2715. [Google Scholar] [CrossRef]
- Dooling, D.J.; Rekoske, J.E.; Broadbelt, L.J. Microkinetic Models of Catalytic Reactions on Nonuniform Surfaces: Application to Model and Real Systems. Langmuir 1999, 15, 5846–5856. [Google Scholar] [CrossRef]
- Kelley, R.D.; Goodman, D.W. The Chemical Physics of Solid Surfaces and Heterogeneous Catalysis; King, D.A., Woodruff, D.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1982; Volume 4, pp. 427–454. [Google Scholar]
- Kim, S.H.; Nam, S.-W.; Lim, T.-H.; Lee, H.-I. Effect of pretreatment on the activity of Ni catalyst for CO removal reaction by water–gas shift and methanation. Appl. Catal. B Environ. 2008, 81, 97–104. [Google Scholar] [CrossRef]
- Delgado, K.H.; Maier, L.; Tischer, S.; Zellner, A.; Stotz, H.; Deutschmann, O. Surface Reaction Kinetics for Oxidation and Reforming of H2, CO, and CH4 over Nickel-based Catalysts. Catalysts 2015, 5, 871–904. [Google Scholar] [CrossRef]
- Safronovich, E.S.; Gribovskii, A.G.; Vernikovskaya, N.V.; Ovchinnikova, E.V.; Makarshin, L.L.; Chumachenko, V.A. Realization of Highly Exothermal Processes in Micro-Channel Reactors: Experimental Studies and Mathematical Modeling. In Proceedings of the IV International Scientific School-Conference for Young Scientists in Memory of Professor L.N. Kurina “Catalysis: From Science to Industry”, Tomsk, Russia, 23–27 October 2016; Ivan Fedorov: Tomsk, Russia, 2016; p. 120. [Google Scholar]
- Sadykov, V.A.; Kuznetsova, T.G.; Frolova-Borchert, Y.V.; Alikina, G.M.; Lukashevich, A.I.; Rogov, V.A.; Muzykantov, V.S.; Pinaeva, L.G.; Sadovskaya, E.M.; Ivanova, Y.A.; et al. Fuel-rich methane combustion: Role of the Pt dispersion and oxygen mobility in a fluorite-like complex oxide support. Catal. Today 2006, 117, 475–483. [Google Scholar] [CrossRef]
- Kuznetsova, T.G.; Sadykov, V.A.; Moroz, E.M.; Trukhan, S.N.; Paukshtis, E.A.; Kolomiichuk, V.N.; Burgina, E.B.; Zaikovskii, V.I.; Fedotov, M.A.; Lunin, V.V.; et al. Preparation of Ce-Zr-O composites by a polymerized complex method. Stud. Surf. Sci. Catal. 2002, 143, 659–667. [Google Scholar] [CrossRef]
- Makarshin, L.L.; Gribovskij, A.G.; Andreev, D.V.; Parmon, V.N. Catalytic Micro-Passage Plates and Method of Their Making. Patent RU232,304,7, 27 April 2008. [Google Scholar]
- Makarshin, L.L.; Andreev, D.V.; Gribovskii, A.G.; Dutov, P.M.; Khantakov, R.M.; Parmon, V.N. Effect of the microchannel plate design on the capacity of methanol steam reformers. Kinet. Catal. 2007, 48, 765–771. [Google Scholar] [CrossRef]





















| No. | Chemical Composition | Specific Surface Area, m2·g−1 |
|---|---|---|
| 1 | 5% Ni/CeO2 | 82 |
| 2 | 7.5% Ni/CeO2 | 80 |
| 3 | 10% Ni/CeO2 | 75 |
| 4 | 12.5% Ni/CeO2 | 69 |
| Sample | Phase Composition | Cell Parameter, Å | X-ray Particle Size D, Å |
|---|---|---|---|
| 5% Ni/CeO2 | CeO2 | 5.407 | 135 |
| NiO | 4.178 | 115 | |
| 10% Ni/CeO2 | CeO2 | 5.406 | 125 |
| NiO | - | 180 |
| Reaction | ln k0 | Е, kJ/mol |
|---|---|---|
| CO + H2O → CO2 + H2 | 23.53 (+/−) 3.12 | 108 (+/−) 14.1 |
| Inlet | H2 | N2 | CO | H2O | GHSV, h−1 |
|---|---|---|---|---|---|
| Q, cm3/s | 2.8 | 2.8 | 1.4 | 2.8 | 17,640 |
| 5.6 | 5.6 | 2.8 | 5.6 | 35,280 | |
| 8.4 | 8.4 | 4.2 | 8.4 | 52,920 | |
| y0,i, mol/mol | 0.2864 | 0.2864 | 0.1429 | 0.2864 | |
| C0,i, mol/m3 | 12.75 | 12.75 | 6.38 | 12.75 |
| Ni Loading on CeO2 (wt %) | CO Concentration, (%, Dry Basis) | |||
|---|---|---|---|---|
| GHSV = 17,640 h−1 | GHSV = 35,280 h−1 | GHSV = 52,920 h−1 | ||
| 400 °С | 450 °С | 400 °С | ||
| 5 | 3.43 | 2.84 | 8.10 | 9.47 |
| 7.5 | 2.85 | 1.99 | 6.59 | 8.41 |
| 10 | 0.34 | 1.05 | 3.70 | 5.75 |
| 12.5 | 0.54 | 0.81 | 3.52 | 5.88 |
| Reaction | K0i | lnK0i | Еeqi, kJ/mol |
|---|---|---|---|
| CO + H2O → CO2 + H2 | 1.350 × 10−2 | −4.30502 | 38.038 |
| CO + 3H2 → CH4 + H2O | 2.741 × 10−13 | −28.92531 | 216.808 |
| No | Reaction | Ni Content | ln k0i | Ei, kJ/mol |
|---|---|---|---|---|
| 1 | CO + H2O | 5% | 7.109 ± 3.1 | 51.23 ± 16.5 |
| 2 | CO + 3 H2 | 5% | 5.206 ± 2.8 | 37.70 ± 16.8 |
| 1 | CO + H2O | 7.5% | 5.113 ± 2.8 | 42.13 ± 14.5 |
| 2 | CO +3 H2 | 7.5% | 3.760 ± 2.9 | 32.29 ± 17.3 |
| 1 | CO + H2O | 10% | 6.361 ± 4.5 | 47.37 ± 22.2 |
| 2 | CO +3 H2 | 10% | 1.788 ± 3.0 | 21.56 ± 17.3 |
| 1 | CO + H2O | 12.5% | 6.187 ± 3.6 | 47.86 ± 17.9 |
| 2 | CO + 3 H2 | 12.5% | 0.00056 ± 3.1 | 16.09 ± 17.8 |
| No | Reaction | Ni content | ln k0i | Ei, kJ/mol |
|---|---|---|---|---|
| 1 | CO + H2O | 5%–12.5% | 5.241 ± 1.6 | 42.51 ± 7.9 |
| 2 | CO + 3 H2 | 5%–12.5% | 1.957 ± 1.5 | 23.33 ± 9.0 |
| Cell | Dimensions |
|---|---|
 | Length—1.5 mm Height—0.5 mm Sv = 186.67 m−1 K1 = 1.95 × 1011 × exp(-E1/(R × Tc)) mol·m−3·s−1 E1 = 109,600 J·mol−1 K2 = 0.856 × 104 × exp(-E2/(R × Tc)) mol·m−3·s−1 E2 = 16,000 J·mol−1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobrova, L.; Andreev, D.; Ivanov, E.; Mezentseva, N.; Simonov, M.; Makarshin, L.; Gribovskii, A.; Sadykov, V. Water–Gas Shift Reaction over Ni/CeO2 Catalysts. Catalysts 2017, 7, 310. https://doi.org/10.3390/catal7100310
Bobrova L, Andreev D, Ivanov E, Mezentseva N, Simonov M, Makarshin L, Gribovskii A, Sadykov V. Water–Gas Shift Reaction over Ni/CeO2 Catalysts. Catalysts. 2017; 7(10):310. https://doi.org/10.3390/catal7100310
Chicago/Turabian StyleBobrova, Ludmilla, Dmitry Andreev, Eugene Ivanov, Natalia Mezentseva, Mikhail Simonov, Lev Makarshin, Alexander Gribovskii, and Vladislav Sadykov. 2017. "Water–Gas Shift Reaction over Ni/CeO2 Catalysts" Catalysts 7, no. 10: 310. https://doi.org/10.3390/catal7100310
APA StyleBobrova, L., Andreev, D., Ivanov, E., Mezentseva, N., Simonov, M., Makarshin, L., Gribovskii, A., & Sadykov, V. (2017). Water–Gas Shift Reaction over Ni/CeO2 Catalysts. Catalysts, 7(10), 310. https://doi.org/10.3390/catal7100310







