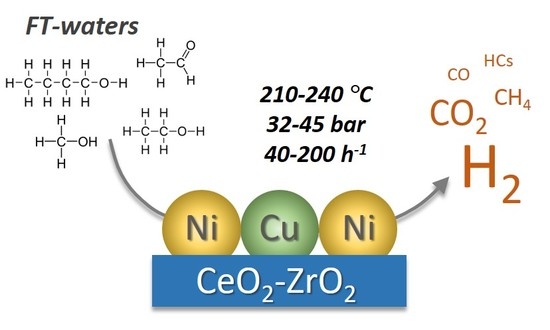
Kinetic Modelling of the Aqueous-Phase Reforming of Fischer-Tropsch Water over Ceria-Zirconia Supported Nickel-Copper Catalyst
Abstract
:1. Introduction
2. Results and Discussion
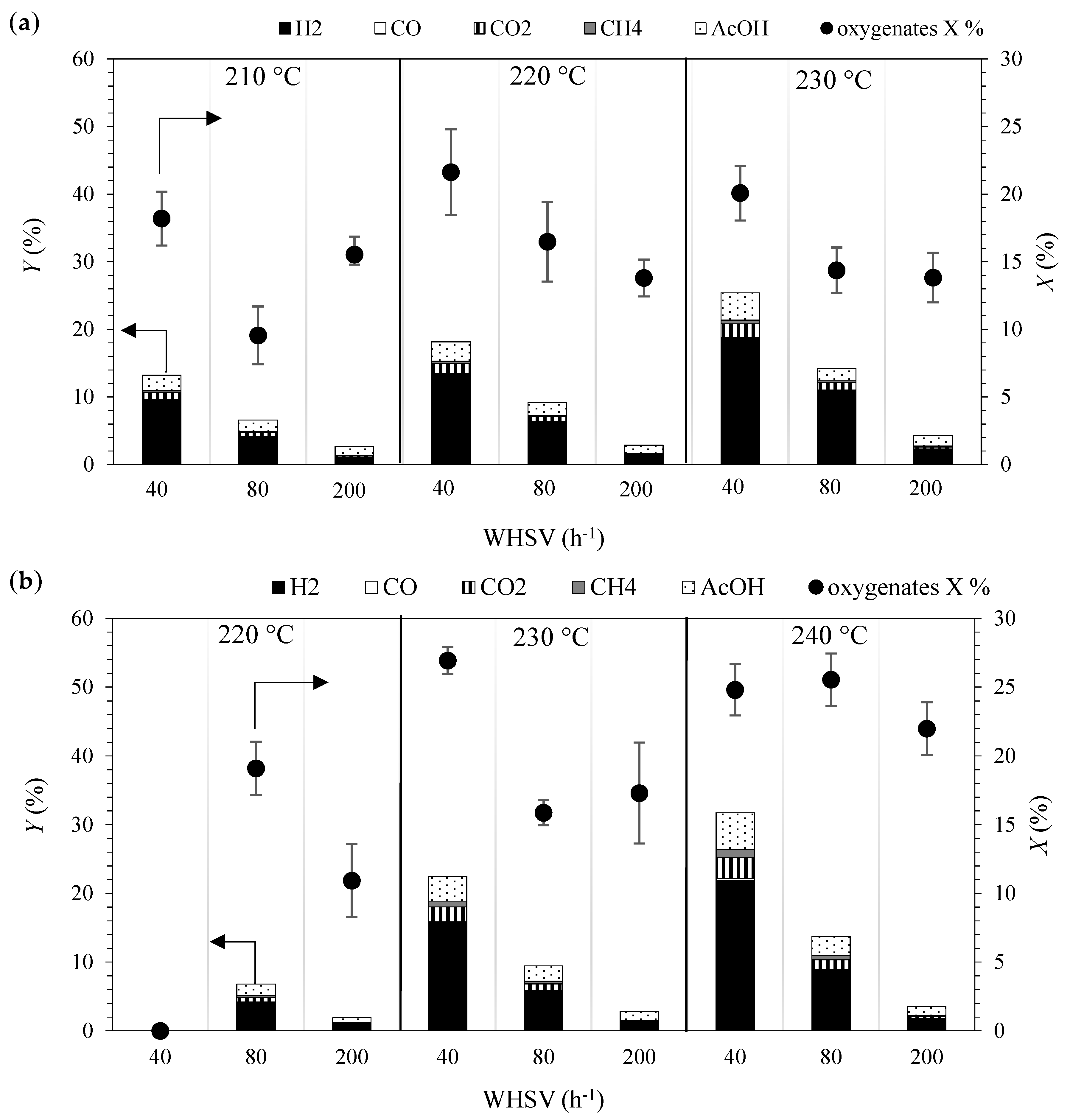
2.1. Kinetic Experiments
2.2. Evaluation of Mass Transfer Resistances
2.3. Selection of Reactions for the Kinetic Model
2.4. Kinetic Model
2.5. Parameter Estimation
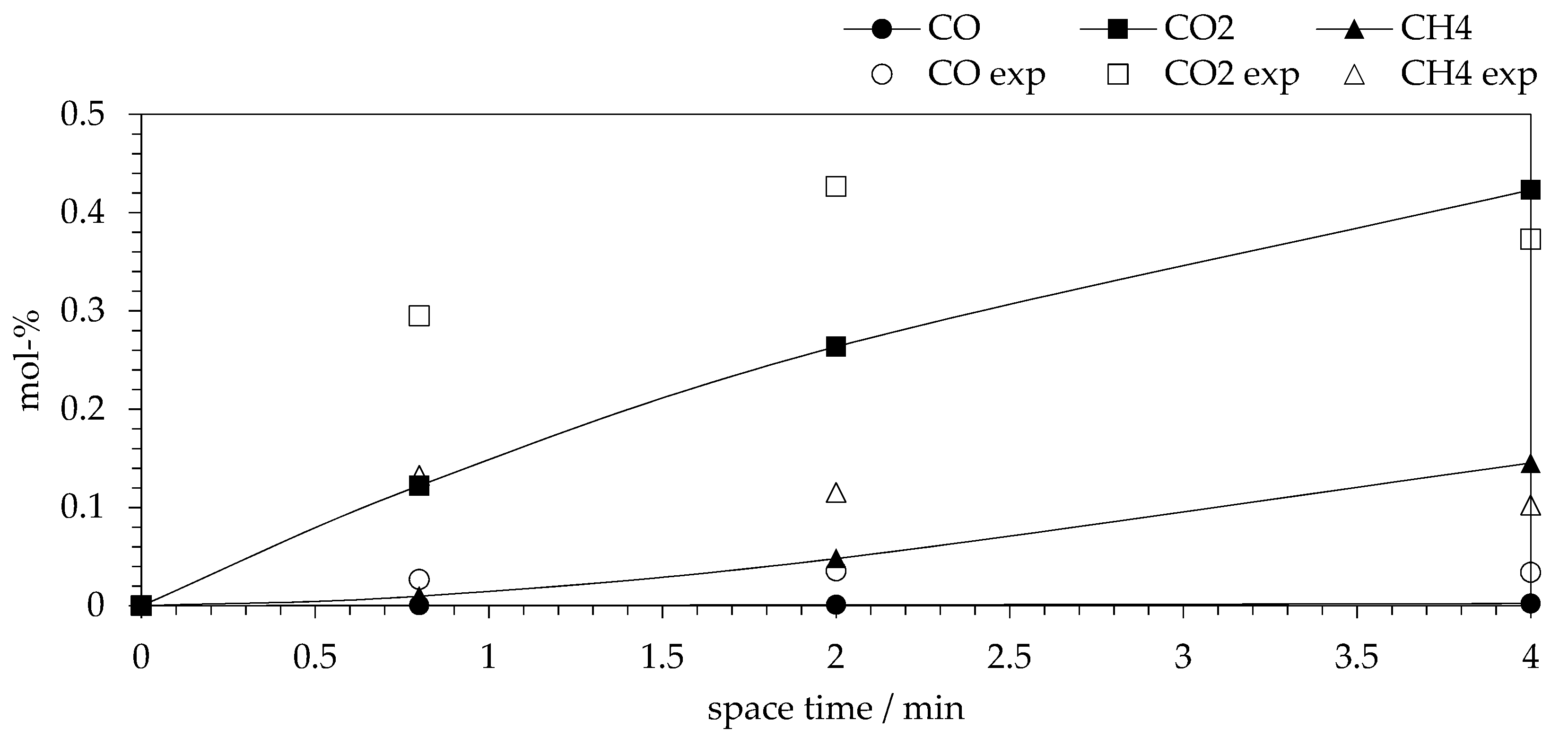
2.6. Comparison of Experimental and Model Data
3. Materials and Methods
3.1. Catalyst Preparation
3.2. Feedstock
3.3. APR of FT Water
3.4. Evaluation of Mass Transfer Resistances
3.5. Selection of Reactor Model
3.6. Gas–Liquid Solubility
3.7. Kinetic Parameter Estimation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nel, R.J.J.; De Klerk, A. Fischer-Tropsch aqueous phase refining by catalytic alcohol dehydration. Ind. Eng. Chem. Res. 2007, 46, 3558–3565. [Google Scholar] [CrossRef]
- Clur, D.J.; Shaw, G.D.H. Recovery of Water Originating From Low Temperature Fischer-Tropsch Synthesis Processes. WO 2005/113426 A1, 12 May 2005. [Google Scholar]
- Dancuart Kohler, L.P.F.; Du Plessis, G.H.; Du Toit, F.J.; Koper, E.L.; Phillips, T.D.; Van Der Walt, J. Method of Purifying Fischer-Tropsch Derived Water. WO 03/106349 A1, 19 December 2006. [Google Scholar]
- Cortright, R.D.; Davda, R.R.; Dumesic, J.A. Hydrogen from catalytic reforming of biomass-derived hydrocarbons in liquid water. Nature 2002, 418, 964–967. [Google Scholar] [CrossRef] [PubMed]
- Ciftci, A.; Ligthart, D.A.J.M.; Sen, A.O.; Van Hoof, A.J.F.; Friedrich, H.; Hensen, E.J.M. Pt-Re synergy in aqueous-phase reforming of glycerol and the water-gas shift reaction. J. Catal. 2014, 311, 88–101. [Google Scholar] [CrossRef]
- Coronado, I.; Stekrova, M.; García Moreno, L.; Reinikainen, M.; Simell, P.; Karinen, R.; Lehtonen, J. Aqueous-phase reforming of methanol over nickel-based catalysts for hydrogen production. Biomass Bioenergy 2017, 106, 29–37. [Google Scholar] [CrossRef]
- Davda, R.R.; Shabaker, J.W.; Huber, G.W.; Cortright, R.D.; Dumesic, J.A. Aqueous-phase reforming of ethylene glycol on silica-supported metal catalysts. Appl. Catal. B Environ. 2003, 43, 13–26. [Google Scholar] [CrossRef]
- Dietrich, P.J.; Lobo-Lapidus, R.J.; Wu, T.; Sumer, A.; Akatay, M.C.; Fingland, B.R.; Guo, N.; Dumesic, J.A.; Marshall, C.L.; Stach, E.; et al. Aqueous phase glycerol reforming by PtMo bimetallic nano-particle catalyst: Product selectivity and structural characterization. Top. Catal. 2012, 55, 53–69. [Google Scholar] [CrossRef]
- El Doukkali, M.; Iriondo, A.; Arias, P.L.; Requies, J.; Gandarías, I.; Jalowiecki-Duhamel, L.; Dumeignil, F. A comparison of sol-gel and impregnated Pt or/and Ni based γ-alumina catalysts for bioglycerol aqueous phase reforming. Appl. Catal. B Environ. 2012, 125, 516–529. [Google Scholar] [CrossRef]
- Kirilin, A.V.; Tokarev, A.V.; Kustov, L.M.; Salmi, T.; Mikkola, J.P.; Murzin, D.Y. Aqueous phase reforming of xylitol and sorbitol: Comparison and influence of substrate structure. Appl. Catal. A Gen. 2012, 435–436, 172–180. [Google Scholar] [CrossRef]
- Koichumanova, K.; Vikla, A.K.K.; De Vlieger, D.J.M.; Seshan, K.; Mojet, B.L.; Lefferts, L. Towards stable catalysts for aqueous phase conversion of ethylene glycol for renewable hydrogen. ChemSusChem 2013, 6, 1717–1723. [Google Scholar] [CrossRef]
- Manfro, R.L.; Da Costa, A.F.; Ribeiro, N.F.P.; Souza, M.M.V.M. Hydrogen production by aqueous-phase reforming of glycerol over nickel catalysts supported on CeO2. Fuel Process. Technol. 2011, 92, 330–335. [Google Scholar] [CrossRef]
- Stekrova, M.; Rinta-Paavola, A.; Karinen, R. Hydrogen production via aqueous-phase reforming of methanol over nickel modified Ce, Zr and La oxide supports. Catal. Today 2018, 304, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Tanksale, A.; Wong, Y.; Beltramini, J.N.; Lu, G.Q. Hydrogen generation from liquid phase catalytic reforming of sugar solutions using metal-supported catalysts. Int. J. Hydrogen Energy 2007, 32, 717–724. [Google Scholar] [CrossRef]
- Remón, J.; Bimbela, F.; Oliva, M.; Ruiz, J.; García, L. Aqueous phase reforming of crude glycerol from biodiesel production: Influence of glycerol concentration. In Proceedings of the 20th Europen Biomass Conference and Exhibition, Milan, Italy, 18–22 June 2012; pp. 1169–1173. [Google Scholar]
- Vispute, T.P.; Huber, G.W. Production of hydrogen, alkanes and polyols by aqueous phase processing of wood-derived pyrolysis oils. Green Chem. 2009, 11, 1433–1445. [Google Scholar] [CrossRef] [Green Version]
- Coronado, I.; Stekrova, M.; Reinikainen, M.; Simell, P.; Lefferts, L.; Lehtonen, J. A review of catalytic aqueous-phase reforming of oxygenated hydrocarbons derived from biorefinery water fractions. Int. J. Hydrog. Energy 2016, 41, 11003–11032. [Google Scholar] [CrossRef]
- Shabaker, J.W.; Davda, R.R.; Huber, G.W.; Cortright, R.D.; Dumesic, J.A. Aqueous-phase reforming of methanol and ethylene glycol over alumina-supported platinum catalysts. J. Catal. 2003, 215, 344–352. [Google Scholar] [CrossRef]
- Shabaker, J.W.; Dumesic, J.A. Kinetics of Aqueous-Phase Reforming of Oxygenated Hydrocarbons: Pt/Al2O3 and Sn-Modified Ni Catalysts. Ind. Eng. Chem. 2004, 43, 3105–3112. [Google Scholar] [CrossRef]
- Aiouache, F.; McAleer, L.; Gan, Q.; Al-Muhtaseb, A.H.; Ahmad, M.N. Path lumping kinetic model for aqueous phase reforming of sorbitol. Appl. Catal. A Gen. 2013, 466, 240–255. [Google Scholar] [CrossRef]
- Kirilin, A.; Wa, J.; Tokarev, A.; Murzin, D.Y. Kinetic Modeling of Sorbitol Aqueous-Phase Reforming over Pt/Al2O3. Ind. Eng. Chem. Res. 2014, 53, 4580–4588. [Google Scholar] [CrossRef]
- Neira D’Angelo, M.F.; Schouten, J.C.; Van Der Schaaf, J.; Nijhuis, T.A. Three-phase reactor model for the aqueous phase reforming of ethylene glycol. Ind. Eng. Chem. Res. 2014, 53, 13892–13902. [Google Scholar] [CrossRef]
- Murzin, D.Y.; Garcia, S.; Russo, V.; Kilpiö, T.; Godina, L.I.; Tokarev, A.V.; Kirilin, A.V.; Simakova, I.L.; Poulston, S.; Sladkovskiy, D.A.; et al. Kinetics, Modeling, and Process Design of Hydrogen Production by Aqueous Phase Reforming of Xylitol. Ind. Eng. Chem. Res. 2017, 56, 13240–13253. [Google Scholar] [CrossRef]
- Coronado, I.; Pitínová, M.; Karinen, R.; Reinikainen, M.; Puurunen, R.L.; Lehtonen, J. Aqueous-phase reforming of Fischer-Tropsch alcohols over nickel-based catalysts to produce hydrogen: Product distribution and reaction pathways. Appl. Catal. A Gen. 2018, 567, 112–121. [Google Scholar] [CrossRef]
- Arandia, A.; Coronado, I.; Remiro, A.; Gayubo, A.; Reinikainen, M. Aqueous-phase reforming of bio-oil aqueous fraction over nickelbased catalysts. Int. J. Hydrog. Energy 2019, 44, 13157–13168. [Google Scholar] [CrossRef]
- Neira D’Angelo, M.F.; Ordomsky, V.; Van der Schaaf, J.; Schouten, J.C.; Nijhuis, T.A. Aqueous phase reforming in a microchannel reactor: The effect of mass transfer on hydrogen selectivity. Catal. Sci. Technol. 2013, 3, 2834. [Google Scholar] [CrossRef]
- Davda, R.R.; Shabaker, J.W.; Huber, G.W.; Cortright, R.D.; Dumesic, J.A. A review of catalytic issues and process conditions for renewable hydrogen and alkanes by aqueous-phase reforming of oxygenated hydrocarbons over supported metal catalysts. Appl. Catal. B Environ. 2005, 56, 171–186. [Google Scholar] [CrossRef]
- Scott Fogler, H. Elements of Chemical Reaction Engineering, 4th ed.; Pearson Education: Beijing, China, 2006. [Google Scholar]
- Chu, X.; Liu, J.; Sun, B.; Dai, R.; Pei, Y.; Qiao, M.; Fan, K. Aqueous-phase reforming of ethylene glycol on Co/ZnO catalysts prepared by the coprecipitation method. J. Mol. Catal. A Chem. 2011, 335, 129–135. [Google Scholar] [CrossRef]
- Nozawa, T.; Mizukoshi, Y.; Yoshida, A.; Naito, S. Aqueous phase reforming of ethanol and acetic acid over TiO2 supported Ru catalysts. Appl. Catal. B Environ. 2014, 146, 221–226. [Google Scholar] [CrossRef]
- Liu, T.; Chiu, S. Promoting effect of tin on Ni/C catalyst for methanol carbonylation. Ind. Eng. Chem. 1994, 33, 488–492. [Google Scholar] [CrossRef]
- Wheeler, C.; Jhalani, A.; Klein, E.J.; Tummala, S.; Schmidt, L.D. The water-gas-shift reaction at short contact times. J. Catal. 2004, 223, 191–199. [Google Scholar] [CrossRef]
- Swickrath, M.; Anderson, M. The Development of Models for Carbon Dioxide Reduction Technologies for Spacecraft Air Revitalization. In Proceedings of the 42nd International Conference on Environmental Systems, San Diego, CA, USA, 15–19 July 2012. [Google Scholar]
- Chiang, J.H.; Hopper, J.R. 1983 Kinetics of the hydrogenation of carbon dioxide over supported nickel. Ind. Eng. Chem. Prod. Res. Dev. 1983, 22, 225–228. [Google Scholar] [CrossRef]
- Koschany, F.; Schlereth, D.; Hinrichsen, O. On the kinetics of the methanation of carbon dioxide on coprecipitated NiAl(O)x. Appl. Catal. B Environ. 2016, 181, 504–516. [Google Scholar] [CrossRef]
- Tu, Y.-J.; Li, C.; Yu-Wen, C. Effect of chromium promoter on copper catalysts in ethanol dehydrogenation. Chem. Technol. Biotechnol. 1994, 59, 141–147. [Google Scholar] [CrossRef]
- Vidal, F.; Koponen, J.; Ruuskanen, V.; Bajamundi, C.; Kosonen, A.; Simell, P.; Ahola, J.; Frilund, C.; Elfving, J.; Reinikainen, M.; et al. Power-to-X technology using renewable electricity and carbon dioxide from ambient air: SOLETAIR proof-of-concept and improved process concept. J. CO2 Util. 2018, 28, 235–246. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill Companies Inc.: New York, NY, USA, 2007. [Google Scholar]
- Whitman, W.G. The Two-Film Theory of Gas Absorption It Seems to Explain Satisfactorily the Well-Recognized Differences of Absorption Rate for Varying Concentrations. Chem. Metall. Eng. 1923, 29, 146–148. [Google Scholar]
- Geankoplis, C.J. Transport Processes and Separation Processes Principles, 4th ed.; Pearson Education: Beijing, China, 2003. [Google Scholar]



| Model A | Model B | Model C | ||||
|---|---|---|---|---|---|---|
| Parameter/unit | Value | Variance | Value | Variance | Value | Variance |
| k1,mean/(m3)m kgcat−1 molm−1·s−1 | 1.17·10−7 | 4.89·10−7 | 2.52·10−7 | 6.35·10−7 | 8.32·10−8 | 1.05·10−7 |
| k2,mean/(m3)m kgcat−1 molm−1·s−1 | 1.88·10−7 | 7.82·10−7 | 6.33·10−7 | 1.07·10−6 | 2.01·10−7 | 4.29·10−8 |
| k5, mean/(m3)2·kgcat−1·mol−1·s−1 | 2.35·10−8 | 4.66·10−7 | 2.31·10−7 | 4.39·10−5 | 8.69·10−8 | 5.57·10−6 |
| k6, mean/m3·kgcat−1·s−1 | 1.75·10−7 | 4.75·10−8 | 1.70·10−7 | 5.06·10−8 | 1.56·10−7 | 4.91·10−8 |
| k7, mean/mol0.13·(m3)0.87·kgcat−1·s−1 | 1.29·10−6 | 3.38·10−7 | 1.30·10−6 | 3.23·10−7 | 1.27·10−6 | 3.44·10−7 |
| Ea,1/J·mol−1 | 40,999 | 142,186 | 124,422 | 215,465 | 108,516 | 170,804 |
| Ea,2/J·mol−1 | 88,861 | 34,716 | 75,293 | 30,772 | 77,529 | 30,518 |
| Ea,5/J·mol−1 | 1341 | 49,411 | 38,686 | 46,518 | 35,743 | 52,077 |
| Kalcohol/m3·mol−1 | 5.48·10−5 | 8.69·10−3 | ||||
| m/- | 0.73 | 0.37 | ||||
| Residual Sum of Squares | 3.04·10−5 | 2.95·10−5 | 2.99·10−5 | |||
| Compound | ID | Wt.% * | Oxygenates Distribution wt.% |
|---|---|---|---|
| Ethanal | MeCHO | 0.10 ± 0.01 | 3.9 |
| Propanal | EtCHO | 0.01 ± 0.00 | 0.5 |
| Propan-2-one | Ace | 0.03 ± 0.02 | 1.1 |
| Methanol | MeOH | 0.70 ± 0.02 | 26.4 |
| Ethanol | EtOH | 1.00 ± 0.04 | 38.0 |
| Propan-1-ol | PrOH | 0.25 ± 0.02 | 9.5 |
| Butan-1-ol | BuOH | 0.28 ± 0.02 | 10.4 |
| Pentan-1-ol | PeOH | 0.16 ± 0.01 | 6.0 |
| Hexan-1-ol | HexOH | 0.04 ± 0.00 | 1.5 |
| Heptan-1-ol | HepOH | 0.05 ± 0.01 | 2.0 |
| Acetic acid | AcOH | 0.02 ± 0.00 | 0.7 |
| Oxygenates | 2.6 | 100.0 | |
| Water | 97.4 | - |
| T (°C) | H (atm/mol Fraction) | ||||
|---|---|---|---|---|---|
| N2 | H2 | CO2 | CO | CH4 | |
| 210 | 322,120 | 197,578 | 18,764 | 217,460 | 153,022 |
| 220 | 334,900 | 204,233 | 20,214 | 226,120 | 157,674 |
| 230 | 347,680 | 210,889 | 21,718 | 234,780 | 162,184 |
| 240 | 360,460 | 217,545 | 23,275 | 243,440 | 166,551 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado, I.; Arandia, A.; Reinikainen, M.; Karinen, R.; Puurunen, R.L.; Lehtonen, J. Kinetic Modelling of the Aqueous-Phase Reforming of Fischer-Tropsch Water over Ceria-Zirconia Supported Nickel-Copper Catalyst. Catalysts 2019, 9, 936. https://doi.org/10.3390/catal9110936
Coronado I, Arandia A, Reinikainen M, Karinen R, Puurunen RL, Lehtonen J. Kinetic Modelling of the Aqueous-Phase Reforming of Fischer-Tropsch Water over Ceria-Zirconia Supported Nickel-Copper Catalyst. Catalysts. 2019; 9(11):936. https://doi.org/10.3390/catal9110936
Chicago/Turabian StyleCoronado, Irene, Aitor Arandia, Matti Reinikainen, Reetta Karinen, Riikka L. Puurunen, and Juha Lehtonen. 2019. "Kinetic Modelling of the Aqueous-Phase Reforming of Fischer-Tropsch Water over Ceria-Zirconia Supported Nickel-Copper Catalyst" Catalysts 9, no. 11: 936. https://doi.org/10.3390/catal9110936
APA StyleCoronado, I., Arandia, A., Reinikainen, M., Karinen, R., Puurunen, R. L., & Lehtonen, J. (2019). Kinetic Modelling of the Aqueous-Phase Reforming of Fischer-Tropsch Water over Ceria-Zirconia Supported Nickel-Copper Catalyst. Catalysts, 9(11), 936. https://doi.org/10.3390/catal9110936