1. Introduction
Fuel cells are electrochemical devices used to convert the chemical energy of a fuel, usually hydrogen, to the electricity directly. Among the fuel cells, the solid oxide fuel cells (SOFCs) are an attractive solution for the future of electric power generation systems in almost all system scales, from small domestic to large industrial generators. Therefore, SOFCs gain more and more attraction in the scientific community. Solid oxide fuel cells utilize good oxygen anions mobility in the elevated temperature (up to 1000
) [
1]. The high temperature enables fast electrochemical kinetics without a need to use expensive precious metal catalysts, which is the case of low-temperature fuel cells [
2,
3]. The high quality of the waste heat makes it possible to install SOFCs in combined heat and power systems. The high operating temperature also allows for converting electrochemically the carbon monoxide or even to conduct the in-stack internal reforming process, which leads to wide fuel flexibility—the variety of reformed hydrocarbons may be used as a fuel for the SOFC [
4,
5,
6]. Among other advantages there are: low emissions of the greenhouse gases (for the hydrogen-fueled fuel cells virtually there is no emissions) and no emissions of the toxic compounds, relatively high tolerance to fuel impurities [
7] and outstanding energy conversion efficiency [
2]. However, the high operating temperature creates also several problems, especially with the degradation of the materials, corrosion and sealing [
1]. This leads to the concept of intermediate temperature solid oxide fuel cells (IT-SOFCs), which work in the temperature range 550
–800
[
8].
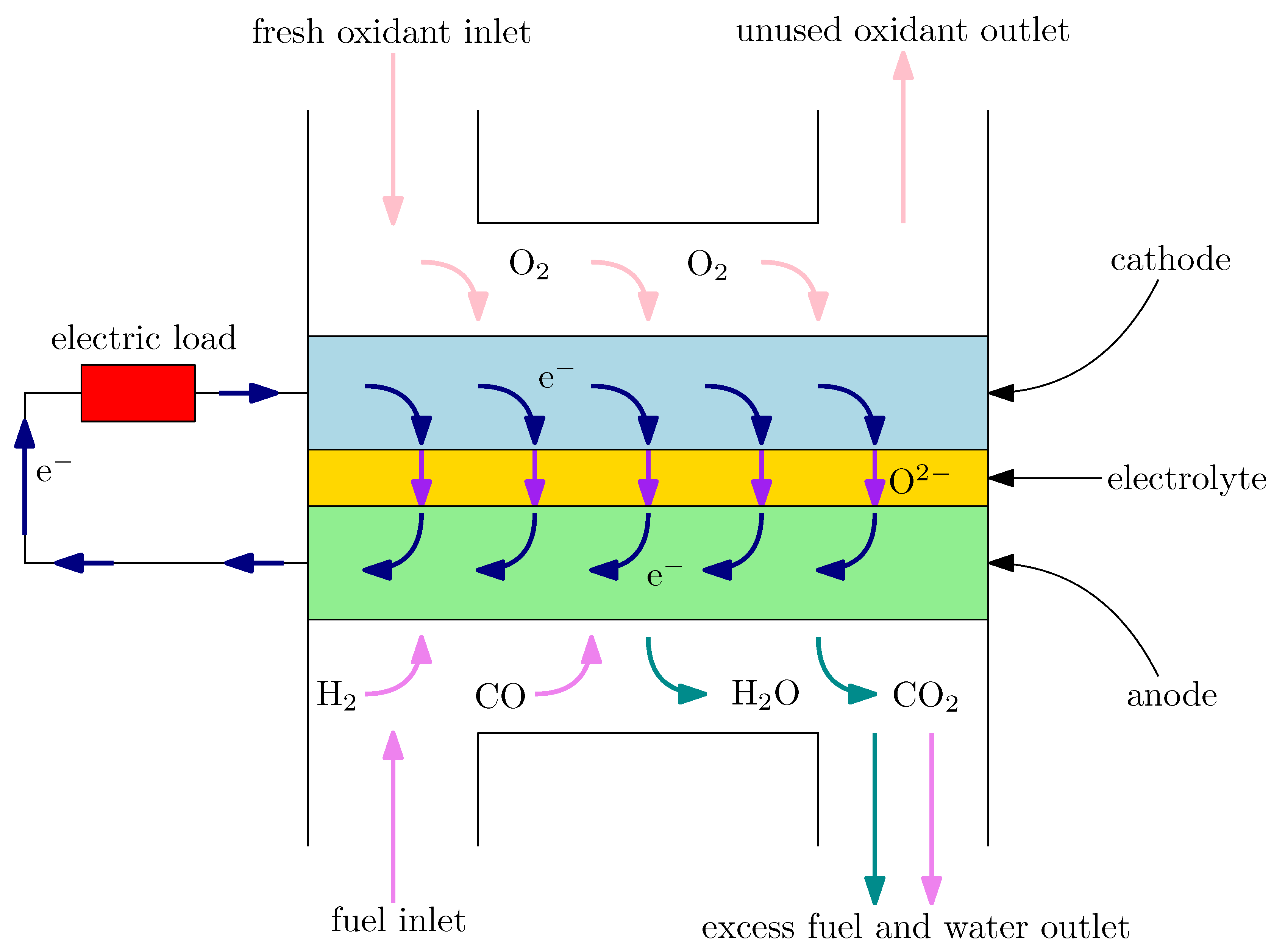
A typical solid oxide fuel cell contains two porous electrodes (an anode and a cathode) and a ceramic solid electrolyte, which separates the electrodes. The schematic diagram of a SOFC is shown in
Figure 1. On the anode, the fuel is provided and oxidized according to the following reactions:
The produced electrons are transported through the external circuit to the cathode. On the cathode, the electrons take part in the oxygen reduction reaction:
O
2 + 2 e
− → O
2−. The oxygen ions are then conducted to the anode through the electrolyte to oxidize the fuel, which closes the process. The electrodes are characterized by the complex microstructure. For example, the electrochemical reactions can occur only on the sites, where the electron conductor, ion conductor and pore (i.e., “gas conductor”) are in contact. These places are called triple-phase boundaries (TPBs) or—in the case of an electrode material with mixed conductivity (e.g., lanthanum strontium cobalt ferrite (LSCF))—double-phase boundaries (DPBs). The microstructure is a key factor which allows the control of the SOFC performance [
9].
Since the construction and testing of novel inventions in the IT-SOFC technology are time-consuming and rather expensive, progress in computational technology and in the methods of mathematical and numerical modeling of solid oxide fuel cells are more and more important. Moreover, the results of numerical models lead to deeper insight into the processes occurring within the SOFC. To analyze the behavior of the SOFCs, usually two classes of the mathematical models are in use. The macroscale models primarily utilize the mass and energy balances or the computational fluid dynamics (CFD) methods to analyze the behavior of the SOFC-based systems [
10,
11,
12], stacks [
13,
14,
15,
16] or single cells [
17,
18,
19,
20,
21]. Moreover, methods such as the finite element (FEM) analysis of thermal stresses [
22] or the artificial neural networks [
23] are employed. The macroscale models are characterized by the low level of modeling details and usually simplified electrochemistry. This approach allows for representing large-scale systems and to analyze the thermo-fluid behavior of the gases inside the cell. On the other hand, the microscale models focus mainly on the analyses of the mass and charge transport within the single electrode or within the PEN (positive electrode–electrolyte–negative electrode) assembly. The microscale models employ a variety of methods, such as the models based on the finite volume solution of partial differential equations [
24,
25,
26], the models which implement the Lattice–Boltzmann method (LBM) [
27,
28,
29], the sub-grid scale models [
30], the random resistor network models [
31] or the kinetic Monte Carlo models [
32]. A greater amount of modeling details allows for describing the behavior of the electrode very accurately. However, because of the large computational cost, the simulation of the whole cell is a difficult task. Moreover, microscale models usually do not include energy transport.
It is possible to combine the macro- and microscale approach and to form a hybrid multiscale model [
33], which focuses on the interaction between unit performance and the microstructure of the electrodes. Multiscale models allow for simulating the cell behavior very accurately and to observe the impact of the microstructure on a cell or even a SOFC stack performance. Because of the large complexity and high computational cost, there have been a few attempts to develop the multiscale model. For example, Ho et al. prepared the multiscale model in STAR-CD software (version 3.24, CD-Adapco Group, Melville, NY, USA) [
34]. The authors did not mention, from where they took the microstructural data. Moreover, they state that the amount of experimental data needed to confirm the numerical models of the SOFCs are rare in the literature. Sohn et al. published a two-dimensional multiscale model of an anode-supported SOFC [
35]. The synthetic microstructure is constructed using the random binary packing algorithm and only the electrochemical model is verified with the experimental data. Both models are not used to check the impact of the different microstructure. Brus et al. presented a two-dimensional isothermal model of the PEN [
36]. The averaged electrodes’ microstructure parameters were taken from thefocused ion beam/scanning electron microscopy (FIB-SEM) measurements, and the set of the experimental results from the short stack is presented. The model does not take into account the flow in the gas channels.
As can be seen from the literature review, complex multiscale models are rare and these models are significantly simplified. According to the knowledge of the authors, there is no experimentally confirmed non-isothermal multiscale model, which use a real microstructure data. In this work, we want to develop and to make an attempt to falsify the non-isothermal multiscale model of a single planar SOFC. A mathematical model cannot be proved to be true; however, if the experimental and numerical data are in agreement, the model may be accepted as a verified, which is a goal of the falsification procedure [
37]. To reach this aim, we performed the electrochemical tests of the short stack of solid oxide fuel cells to gain a unique set of data. Next, the samples of the analyzed cells’ electrodes were observed in three dimensions using the FIB-SEM technique. Collected images are used for the quantification of microstructural parameters, which are implemented into the numerical model. The numerical results from the proposed model are compared with the experimental data. On the basis of the numerical results, we discuss the power generation process in order to achieve a better understanding of the SOFC physics. To demonstrate the importance of the microstructure, the simulation with the different microstructure is provided. We also believe that the experimental and microstructural data presented in this work help to form the benchmark for future numerical simulations of the SOFCs.
3. Microstructure Analysis and Quantification
The dual beam microtomography based on the focused ion beam and scanning electron microscopy (FIB-SEM) is a technique, which can be used to examine the complex microstructure of the porous materials, for example electrodes of a solid oxide fuel cell. The first FIB-SEM three-dimensional reconstruction of the SOFC anode was reported by Wilson et al. in 2006 [
38], since this year the number of scientific papers which focus on the FIB-SEM observation of the SOFC’s electrodes increase [
28,
36,
39,
40,
41]. To gain unique data about the microstructure of the cells investigated empirically (see
Section 2.2), the FIB-SEM method is used here.
3.1. Sample Preparation and FIB-SEM Observation
The representative samples of the anode and the cathode functional layer were taken from the investigated short stack (see
Section 2). Since the structure of the electrodes is porous, the pores were impregnated with EpoFix resin (Struers) under vacuum conditions, in order to achieve the recognition of the pores on the SEM images. Next, the samples were cut and polished with sand paper and diamond paste.
The observation of the electrodes’ microstructure was conducted on the FEI Versa 3D Dual Beam FIB-SEM apparatus, located in Academic Centre for Materials and Nanotechnology, AGH University of Science and Technology, Krakow, Poland.
Figure 4 shows the scheme of the FIB-SEM setup. The “cut-and-see” observation procedure is as follows:
A trench is prepared by the focused beam of Ga+ ions (FIB).
The intersection of an electrode is photographed with the SEM.
The FIB mills the thin layer of the electrode and exposes the next intersection.
The procedure is continued until the whole volume of interest is imaged.
As a result, the set of 2D SEM images is acquired. The 3D reconstruction of the electrodes is obtained by the resampling, cropping, aligning and stacking of the images in the 3D space.
3.2. Segmentation of the Microstructure
The SEM images were resampled, cropped, stacked and aligned in the Avizo 3D analysis software (version 9.2.0, FEI, Hillsboro, OR, USA). However, the result is a set of raw images, with no information about the phases. Therefore, the segmentation procedure is required. The segmentation is a process of assigning every one of the voxels from the images stack to one of the electrodes’ structural phases.
The segmentation is often done manually. This is a difficult and time-consuming task. Therefore, we want to propose a simple framework for the semi-automatic segmentation procedure. The Fiji distribution of the open source image analysis software ImageJ (version 1.52i, National Institutes of Health, Bethesda, MD, USA) [
42,
43] is primarily used to perform this task, together with the several in-home scripts in the Python programming language, with an extensive use of the scikit-image image processing library [
44]. The procedure is illustrated in
Figure 5 on an example of the cathode segmentation. The semi-automatic segmentation algorithm, shown in
Figure 5, may be summarized as follows:
The homomorphic filter [
45] with the high- and low-frequency filters (
,
) and the Gaussian filter (
) is applied in order to equalize the brightness of the images (in-house script).
The enhance contrast tool (with options: normalize, equalize histogram, use stack histogram) is used to underline the differences between the phases (Fiji).
The unsharp masking (, mask weight 0.6) is utilized to sharpen the image (Fiji).
The Gaussian blur () is used in order to remove the artifacts, which appear at the phase boundaries (Fiji).
The Kuwahara filter (sampling window 5) is exploited to smooth the images and to remove further artifacts (Fiji).
The statistical region merging algorithm (
) [
46] is used for the initial recognition of the phases (Fiji).
The unsharp masking and the Kuwahara filter with parameters the same as the above are applied to the images (Fiji).
The Trainable Weka Segmentation tool (version 3.2.32, see Reference [
47] for further details), which utilize the artificial neural networks and machine learning algorithms to automatically segment the images, is used to recognize the phases (Fiji). The following training features were chosen: Gaussian blur (
,
), Laplacian, Hessian, Structure, and Edges. The fast version of the random forests machine learning algorithm is utilized to recognize the phases. The Weka software requires some training data, therefore a few images were segmented manually.
The Kuwahara filter is applied again (Fiji).
The image is recolored (the following color levels in the grayscale are required for the quantification algorithms: anode—pore 0, YSZ 127, Ni 256; cathode—pore 0, GDC 127, LSCF 256) and the bad pixels are removed (in-house script).
The samples of the raw FIB-SEM images and the segmented images are presented in
Figure 6. The result images were visually compared with the raw SEM photographs and good agreement was found.
3.3. Quantification of the Microstructure
Based on the obtained set of the segmented images, the three-dimensional digital representations of the electrodes’ microstructure were prepared in the Avizo 3D software. Three-dimensional representations of the microstructure of the anode and cathode are presented in
Figure 7.
Table 4 shows the volume of the reconstructed samples and the voxel sizes. Based on the segmented images, the averaged microstructural parameters are derived.
3.3.1. Volume Fraction and Mean Particle Diameter
The volume fraction
was calculated by counting off the voxels which belong to each phase. The percentage of the voxels which belong to the phase of interest to the total number of voxels was computed [
36,
41]. The mean diameters of the solid particles and pores
were evaluated using the three-dimensional version of the line intercept method (see [
48] for the details of the procedure). The results are shown in
Table 5.
3.3.2. Tortuosity Factors
The tortuosity factors
are calculated using the random walking algorithm. The computations are based on the fact, that the mean square displacements of the random walkers and—what follows—the diffusion coefficients are lower in the porous structure than in the void space. The degree of the reduction of the diffusion coefficients is interpreted as the tortuosity factors. The details of the algorithm can be found in [
41,
49]. The calculated tortuosity factors are shown in
Table 6.
3.3.3. Phase Boundaries’ Densities
The computation of the phase boundaries’ densities was performed in the Avizo software. The results are shown in
Table 7.
4. Mathematical Model
The steady mathematical model is based on the set of partial differential equations and the Butler–Volmer electrochemical model, with the inclusion of the averaged microstructure parameters (see
Section 3). The computational domain is shown on
Figure 8. In this model, it is assumed that the computational domain is divided into five subdomains: the cathode and anode channels, the cathode, the electrolyte and the anode. The dimensions of the subdomains are the same as for the cells investigated experimentally (see
Table 1). The porous anode is fabricated from the Ni/YSZ and the solid electrolyte is made from the YSZ. The layered structure of the cathode is neglected and it is assumed that the cathode is made from the pure LSCF. Because the GDC is not introduced in the model, the microstructure was recalculated for the pure LSCF cathode (for the recalculation, it was assumed that the analyzed cathode, shown in
Figure 7b, is composed of the single LSCF phase). Such an assumption leads to an unavoidable error in the numerical results. Having said that, the cathodic voltage losses are usually lower than the anodic polarization losses [
36]. Moreover, at the elevated temperature (>
), the LSCF/GDC behavior is similar to the pure LSCF performance [
50]. The results are presented in
Table 8.
The gases in the system are treated as the Newtonian ideal gases, and the radiation heat transfer, viscous dissipation, gravity and other body forces are neglected. It is also assumed that, at the anode inlet, only hydrogen, water vapor and nitrogen are present, whereas, in the cathode inlet, air containing 21% of the oxygen and 79% of the nitrogen is provided. Please note that the model presented here is based on our previous isothermal model of the PEN [
36].
4.1. Thermo-Electric Model
The thermo-electric model describes the thermodynamics and the electrochemistry of the SOFC. The hydrogen-fueled SOFC realizes the following reactions:
the anodic reaction—hydrogen oxidation: H2 + O2− → H2O + 2 e−;
the cathodic reaction—oxygen reduction: O2 + 2 e− → O2−;
the overall cell reaction: H2 + O2 → H2O.
These reactions may occur only at the sites, where the constant supply and drain of the reactants and products are possible. These reaction sites are called the triple phase boundaries (TPBs) on the anode and the double phase boundaries (DPBs) on the cathode. Please mind that the cathodic TPB is neglected in this model.
The open circuit voltage of such a cell may be described by the Nernst equation. For the cell working in any temperature and pressure, the Nernst equation may be written as [
3]:
where
(
) is the open circuit voltage of the SOFC,
(
) is the specific molar Gibbs free energy of the water formation in the standard state (here, the standard state temperature is
and the standard state pressure is
= 101,325 Pa = 1 atm),
(
) is the change of the specific molar entropy associated with the water formation reaction,
T (
) is the temperature and
(
) stands for the partial pressure of species
i.
F is the Faraday constant (
F = 96,485.32289 C mol
) and
R is the universal gas constant (
).
To calculate the volumic current density, generated at the triple phase boundaries (on the anode) () and the double phase boundaries (on the cathode) (), the Butler–Volmer equations are utilized:
anode:
cathode:
Here,
(
) is the exchange current density per unit length of the TPB and
(
) is the exchange current density per unit area of the DPB;
(
) is the TPB length density and
(
) is the DPB area density. The anodic and cathodic charge-transfer coefficients are taken from the porous Ni/YSZ anode measurements of de Boer [
51] and from the LSCF cathode investigation of Fleig et al. [
52]. The activation overpotentials
(
) are calculated as follows:
anode:
cathode:
In Equations (
4a) and (
4b), the symbols
(
) are the electric potentials of the electronic and ionic conducting phases,
(
) means the partial pressure of species
i, and the superscript
indicates that the partial pressure value is the bulk inlet partial pressure.
The exchange current densities per unit length of the TPB/unit area of the DPB are formulated in accordance with the literature data [
51,
53]. The pre-exponential factors are the fitting parameters, proposed by Suzue et al. (for the andoe) [
27] and Matsuzaki et al. (for the cathode) [
28]. The exchange current densities are calculated as:
anode:
cathode:
where the partial pressures
are taken in pascals.
4.2. Transport Model
The transport model is based on the set of the partial differential equations, which describe species, energy and charge conservation. In addition, the equation of the state—here the ideal gas law—is used:
where
P (
) is the total pressure,
v (
) is the specific volume,
M (
) is the molar mass and
T (
) is the temperature.
The velocity
inside the gas channels is described by the following form of the Darcy–Brinkmann equation [
54], obtained for the fully-developed, one-dimensional, axial, incompressible flow:
This partial differential equation is possible to be solved analytically with the no-slip boundary conditions. Moreover, the pressure gradient may be replaced by the mass flow rate, defined as
. The velocity profile is then described by:
The function
in Equation (
8) is given by:
and the constant
C, which appears in Equation (
8), is evaluated as follows:
In the above equations,
(
) is the mass flow rate,
is the averaged cross-sectional density, calculated with the ideal gas law (Equation (
6)),
W and
H (
) stand for the width and height of the channels, respectively.
K (
) is the permeability of a porous medium, calculated with the Kozeny–Carman model [
55]:
The porosity of the gas channels
is 0.55 and the mean pore diameters are:
for the anode channel and
for the cathode channel.
4.2.1. Species Conservation
The species transport is based on the Fick model of diffusion. In terms of the mass fractions, the species conservation equation is written as:
where
is the mass fraction of the species
i,
(
) is the density of the mixture of gases,
is the porosity,
(
) is the velocity vector,
(
) is the effective diffusion coefficient for species
i and
(
) stands for the mass source. Utilizing the fact that, for the ideal gases, the mass fraction may be written as:
and using the ideal gas law Equations (
6) and (
12) may be reformulated as:
The effective diffusion coefficient is microstructure-dependent and may be computed as:
where
(
) is the bulk diffusion coefficient of species
i, calculated with the Bosanquet formula [
56]:
Here,
(
) is the diffusion coefficient of species
i in the mixture of gases and it is calculated using modified Blanc’s law [
57,
58]:
and the binary diffusion coefficient
(
) is computed using the Fuller, Shettler and Giddings method for gas mixture at low pressure [
58,
59]:
The atomic diffusion volumes
may be found in Ref. [
58].
In the Bosanquet equation, Equation (
15),
(
) stands for the Knudsen diffusion coefficient [
57]:
where
(
) is the average pore radius and it comes from the microstructure quantification (see
Section 3).
The mass sources
in Equation (
13) describe the amount of species produced during the electrochemical reactions and they are calculated using Faraday’s laws of electrolysis. The summary of the mass sources is presented in
Table 9.
4.2.2. Energy Conservation
The energy conservation equation is based on the local thermal equilibrium approach, i.e., it is assumed that, in the domains filled with porous media (anode and cathode), the fluid and solid are always in the thermal equilibrium. Therefore, the energy conservation can be written mathematically as:
where
(
) is the constant pressure specific heat of the gas mixture (see [
60] for the polynomial formulas),
(
) stands for the effective thermal conductivity and
(
) is the heat source.
The effective thermal conductivity depends on the microstructure and it is computed as [
54]:
where subscripts
and
stands for the value for the gas mixture and the solid particles, respectively. The thermal conductivities of the solids are shown in
Table 10,
where
(
) is the thermal conductivity of a pure gas
i, calculated using the Todd and Young data [
60]. The function
is calculated using the data of Mason and Saxena [
61] as well as the Roy and Todos method of estimating the thermal conductivities at low pressure [
62,
63]. The heat is produced within the SOFC in three ways:
the Joule heat , produced because of the resistance for the electronic or ionic charge flow,
the activation heat , the result of the irreversible activation barrier,
and the water formation heat , the heat formed when a molecule of water is created.
All of these contributions to the total heat source are generated in the different elements of the PEN. The summary of the heat sources is shown in
Table 11.
4.2.3. Charge Conservation
The charge conservation is based on the Ohm’s law and may be formulated as:
where
(
) is the electric potential of the appropriate phase
i,
(
) stands for the effective electronic or ionic conductivity of phase
i and
(
) is the source term.
The effective conductivities are microstructure-relative and they are computed with the following formula:
The bulk conductivities
(
) are calculated from the curve fit to the data published in the open literature [
28,
68,
69,
70]:
In Equation (
24d),
stands for the specific molar volume of the LSCF,
= 28,170 mol m
. The constant
C is calculated using the following formula [
28]:
It is assumed that the potential of the phase is changed by the electrochemical reactions, therefore the change is proportional to the current calculated by the Butler–Volmer equation (Equations (3)). The summary of the sources of the electric potential is shown in
Table 12.
The equation for the electronic phase potential is required to be solved within the anode and cathode and the equation for the ionic phase potential should be solved in all of the elements of the PEN.
4.3. Boundary Conditions
To close the mathematical mode, the boundary conditions are required. In this model, every one of the subdomains is treated separately and the transmission conditions at the interfaces between the subdomains are used.
At the cathode channel inlet and the anode channel inlet:
for Equation (
13): the given inlet composition—
and
(cathode), and
,
and
(anode);
for Equation (
19): the given inlet temperature—
.
At the cathode channel outlet and the anode channel outlet:
for Equation (
13): the outflow condition—
;
for Equation (
19): the outflow condition—
.
At the walls:
for Equation (
13): walls impermeable for mass transport—
;
for Equation (
19): the constant temperature—
.
At the cathode surface:
for Equation (
13): the transmission condition—
,
;
for Equation (
19): the transmission condition—
,
;
for Equation (
22) for the electrons: the potential equals the terminal voltage—
;
for Equation (
22) for the ions: no current flow—
.
At the anode surface:
for Equation (
13): the transmission condition—
,
;
for Equation (
19): the transmission condition—
,
;
for Equation (
22) for the electrons: the potential equals the open circuit voltage
;
for Equation (
22) for the ions: no current flow—
.
Between the cathode and the electrolyte:
for Equation (
13): electrolyte impermeable for mass transport—
;
for Equation (
19): the transmission condition—
,
;
for Equation (
22) for the electrons: electrolyte impermeable—
;
for Equation (
22) for the ions: the transmission condition—
,
.
Between the anode and the electrolyte
for Equation (
13): electrolyte impermeable for mass transport—
;
for Equation (
19): the transmission condition—
,
;
for Equation (
22) for the electrons: electrolyte impermeable—
;
for Equation (
22) for the ions: the transmission condition—
,
.
At the other boundaries, it is assumed that no flux crosses these boundaries or .
4.4. Numerical Method
The in-house numerical code written in C++ and Python programming languages with the use of the SciPy numerical library [
71] is utilized to calculate the results. The partial differential equations are discretized using the finite volume method. The discussion of the finite volume method is omitted here, since many excellent textbooks which describe the method in detail are available [
72,
73]. The systems of linear algebraic equations, the result of the discretization procedure, are solved iteratively using the SciPy implementation of the bi-conjugate gradients stabilized method of van der Vorst [
74] with the tolerance 10
−8.
The developed FVM solver was tested using the method of manufactured solutions (MMS) [
75]. The following benchmark equation has been used:
The values of the constants were assumed as
,
. It was found that the relative percent error of the numerical solution is always less than
% for the tests that mimic the simulated system. Based on the results of the MMS, the grid resolution was chosen as follows: in the
x-direction, there are 80 control volumes (CVs) and, in the
y-direction, there are 60 CVs for the cathode channel, 25 CVs for the cathode, five CVs for the electrolyte, 60 CVs for the anode and 30 CVs for the anode channel.The grid system is shown in
Figure 9.
The stop conditions were chosen as follows: for the species transport, the absolute change of the partial pressures between two subsequent iterations should be less than ; for the energy transport, the absolute change of the temperature between two subsequent iterations should be less than and, for the charge transport, the absolute change of the potential between two subsequent iterations should be less than . In addition, the relative change of the values of the volumic current density, calculated using the Butler–Volmer model, should be less than 10−4.
The numerical computations made use of the Prometheus computing cluster, located at AGH University of Science and Technology, Krakow, Poland [
76]. A single computational node of the cluster, HP ProLiant XL730f Gen 9 (Hewlett Packard Enterprise, Palo Alto, CA, USA), contains of two
Intel Xeon E5-2680v3 processors (Santa Clara, CA, USA) with 24 cores in total and 128 GB of the RAM memory. The computations were performed on a single node and the time of the computation for a chosen operating voltage was approximately 20 h.
6. Conclusions
This work shows a multiscale mathematical model of the solid oxide fuel cell. To build the model properly and to gain a set of benchmark data, the experimental investigation of the SOFC short stack and the direct FIB-SEM observation of the porous electrodes have been performed. For the FIB-SEM images segmentation, the semi-automatic algorithm is proposed. Based on the mathematical model, the finite volume numerical model was prepared.
The calculated current–voltage characteristics have been compared to the one obtained from the experiment and a fair agreement was found between the empirical and numerical data. This indicates that the proposed multiscale model can properly predict the electric behavior of a SOFC. The analysis of the current generation inside the cell shows that the current is produced inside the cell primarily near the electrolyte. This effect is connected with a low mobility of the oxygen anions. Furthermore, the simulation of the cell enclosed in a constant temperature furnace, which is represented by the Dirichlet boundary conditions, demonstrates that the SOFC in this case is almost an isothermal system. Calculations with the averaged microstructure parameters adopted from the literature lead to a visible and significant discrepancy between the numerical and experimental data. This confirms that the microstructure has a non-negligible impact on the numerical calculations and should be introduced into the mathematical models of SOFCs.