Review on the Macro-Transport Processes Theory for Irregular Pores able to Perform Catalytic Reactions
Abstract
:1. Introduction
2. A Generalized Macrotransport Process Theory for Irregular Domains
2.1. Contraction of the Description for Diffusion Processes
2.2. The Diffusion Coefficient in the Contracted Description
3. Adsorption–Desorption Kinetics in Macrotransport Process Theory for Irregular Domains
3.1. The Thiele Modulus
3.2. An Application: Conic Pores
4. Effect of Diffusion of the Adsorbed Phase over the Internal Pore Surface
5. Heterogeneous Catalysis
5.1. An Example: The Isomerization Reaction
6. The Effective Diffusion Coefficient of Adsorbent and Non-Adsorbent Membranes
Adsorbent Membranes
7. How to Use This Theory in Uptake Experiments
7.1. Breakthrough Curve and Internal Pore Geometry
7.2. Effective Diffusivity of the Membrane as a Function of the Average Load
8. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
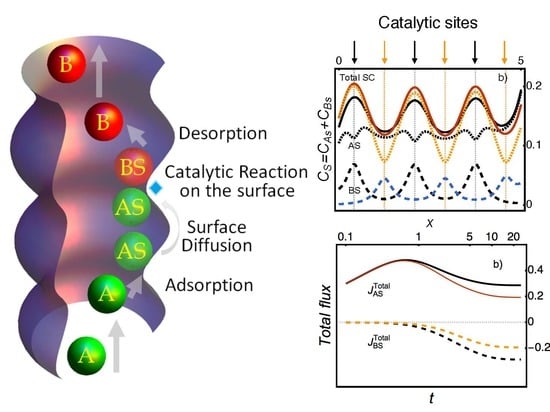
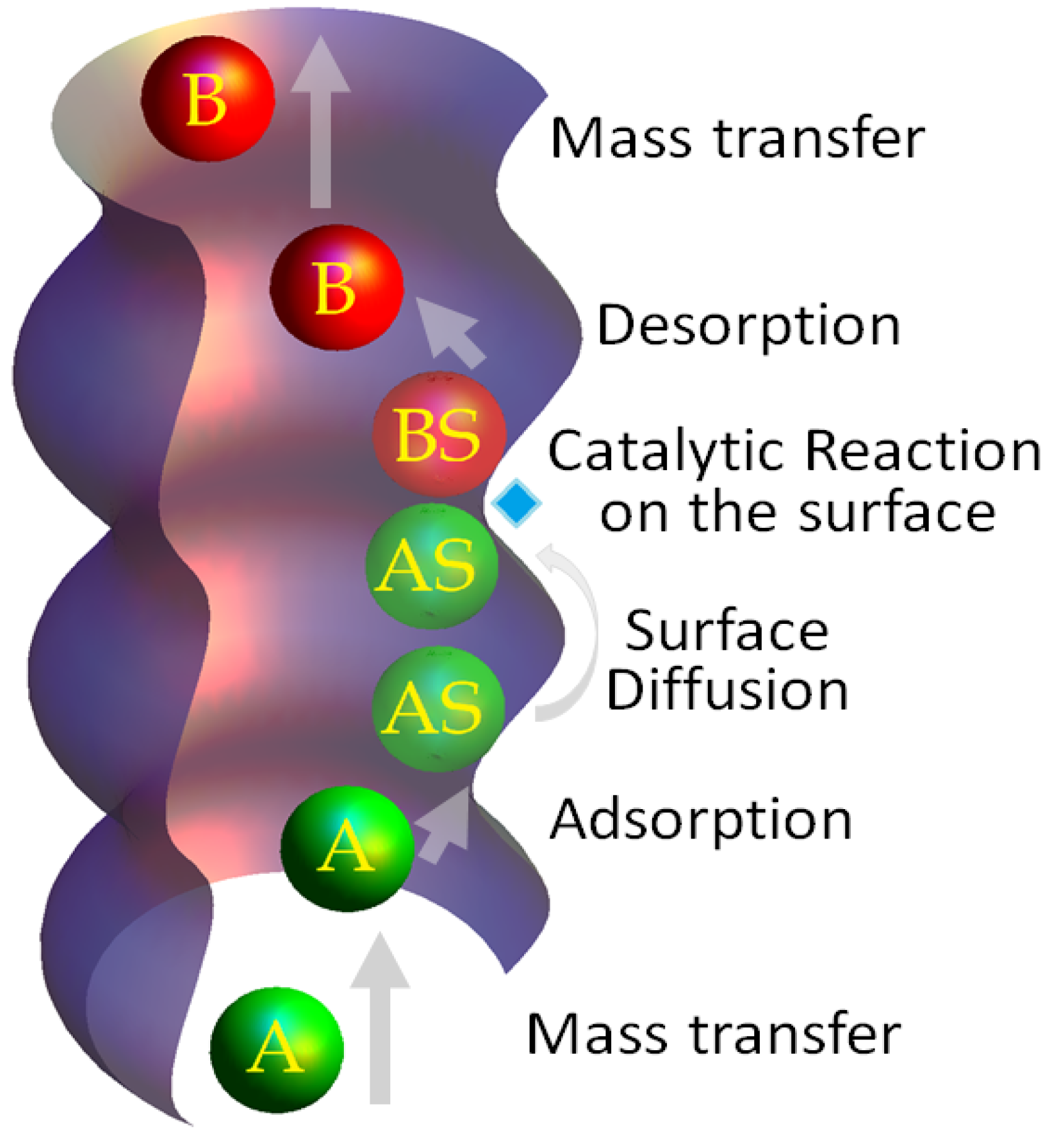
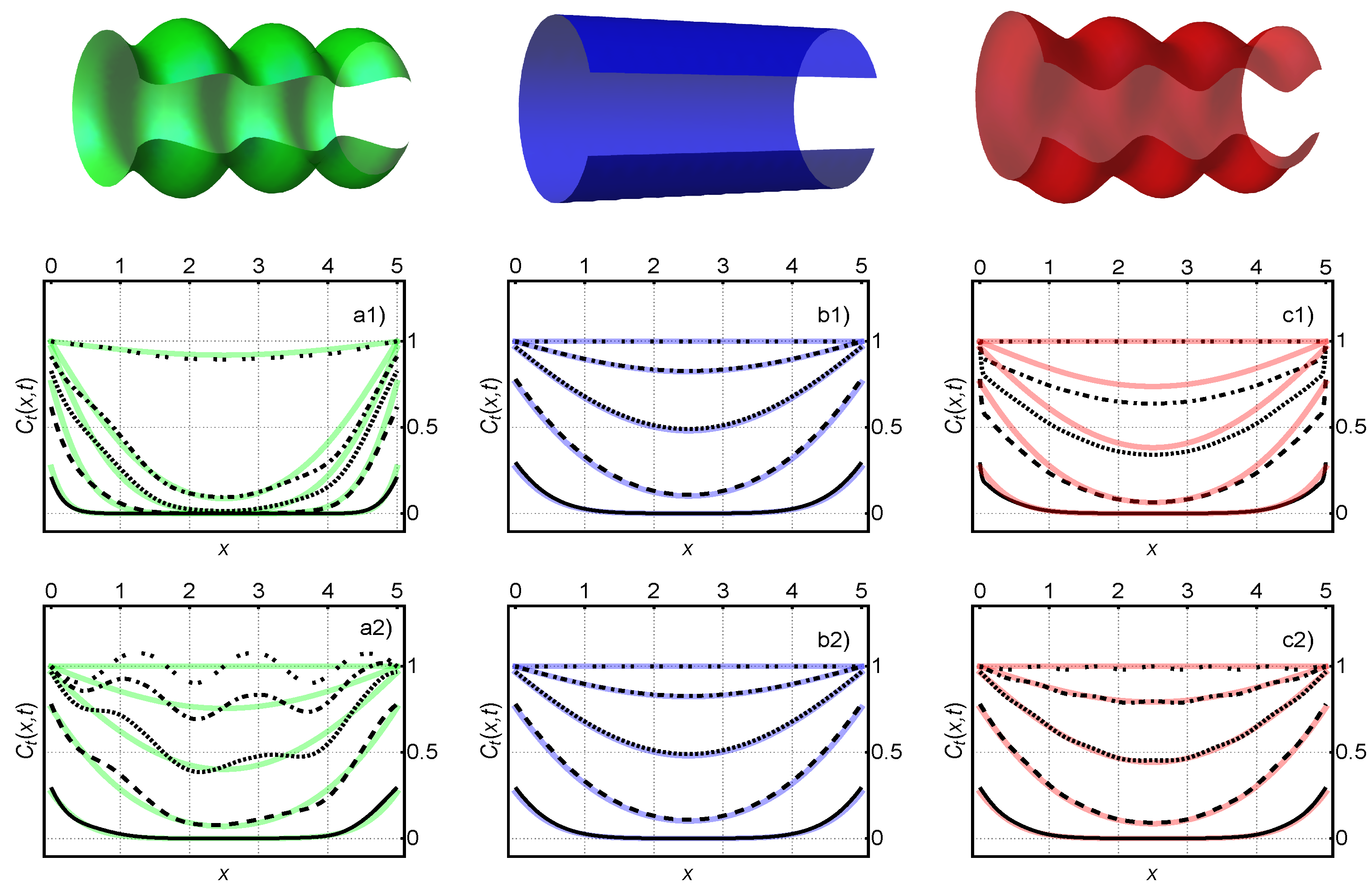
Appendix A.1. Figure 1
| Label | w1 (z) | w2 (z) |
|---|---|---|
| Tortuous | ||
| Winding | ||
| Straight | 0 | 1 |
| Conical | −m z | 1 + m z |
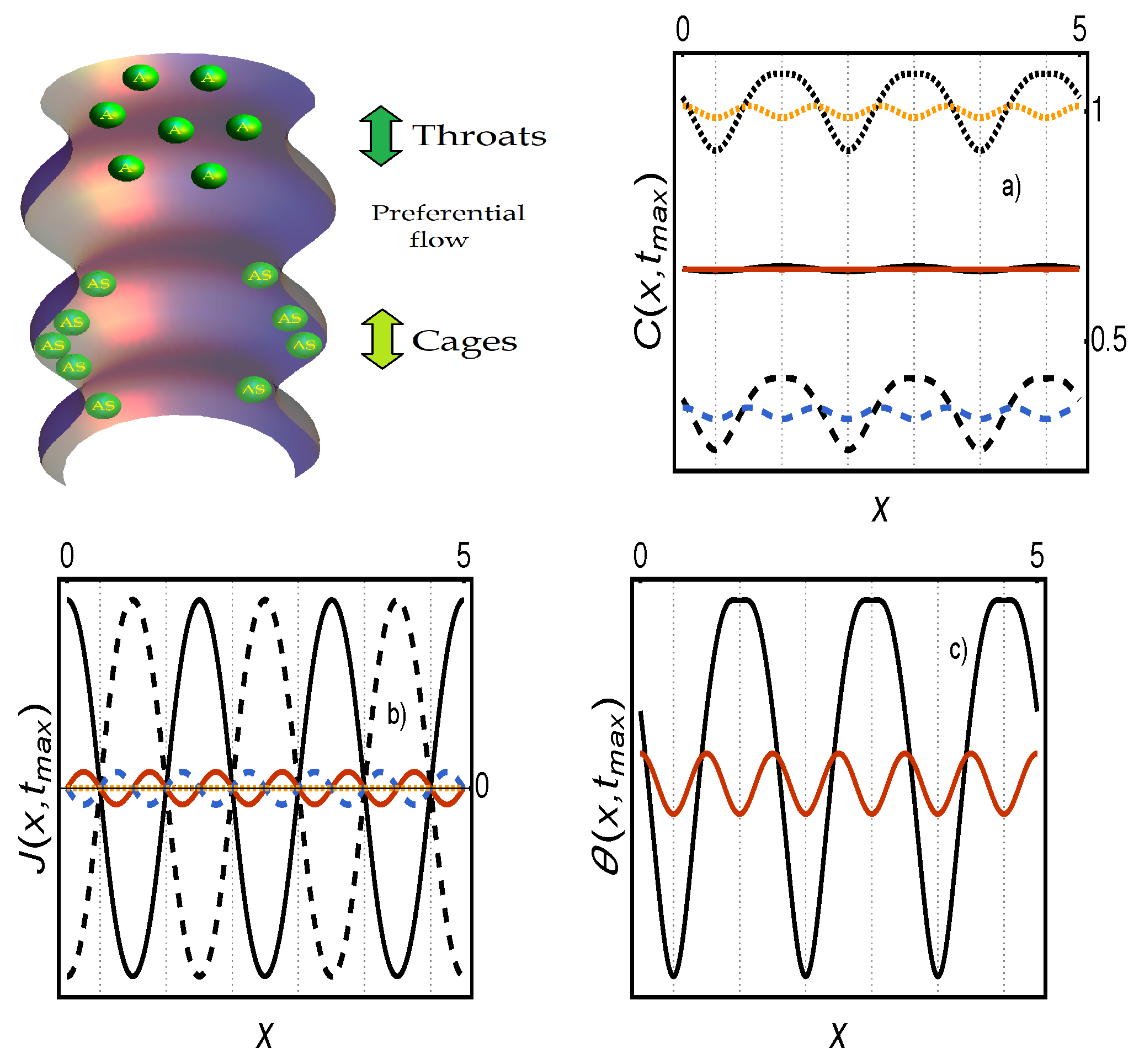
Appendix A.2. Figure 2
Appendix A.3. Figure 3
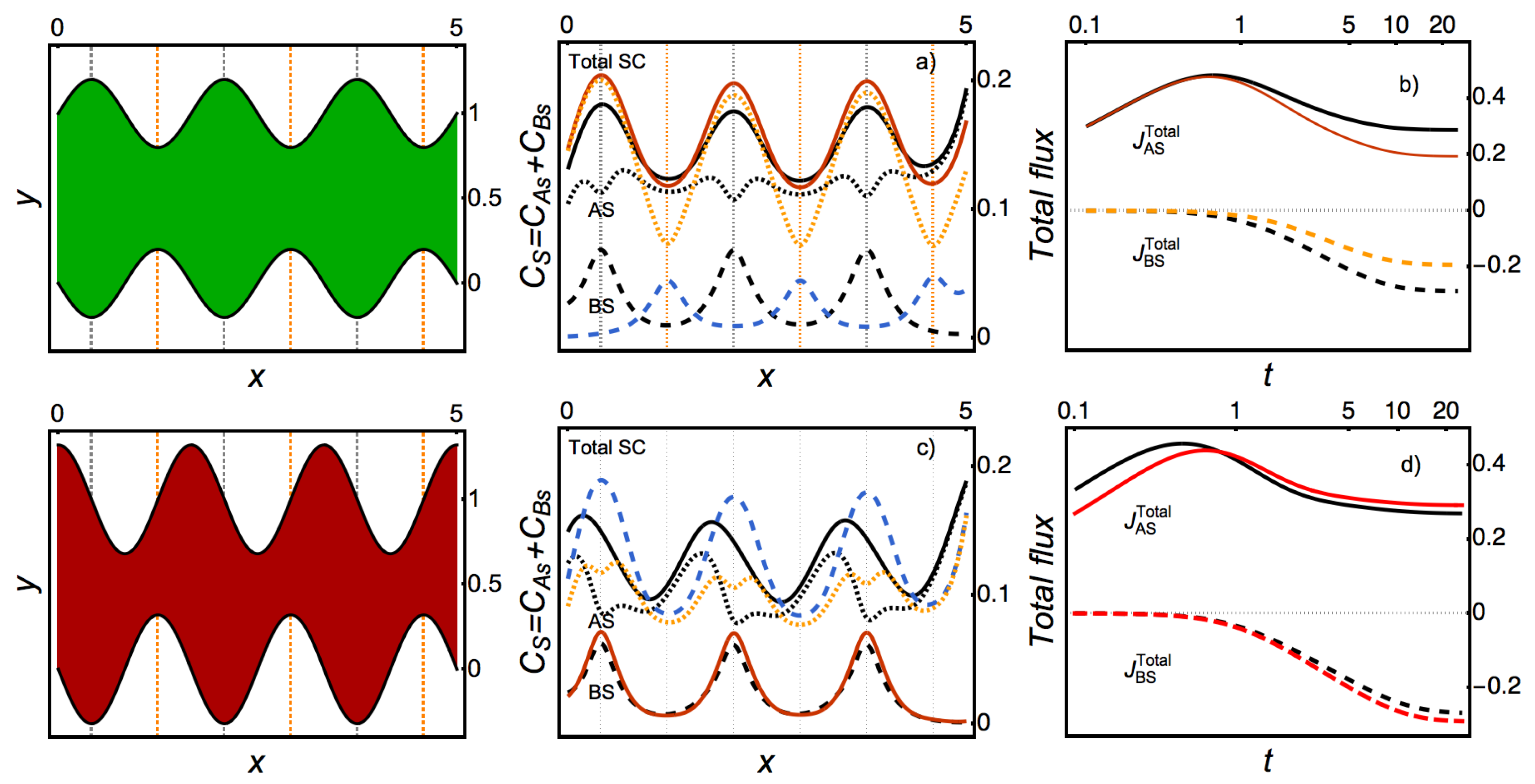
Appendix A.4. Figure 5
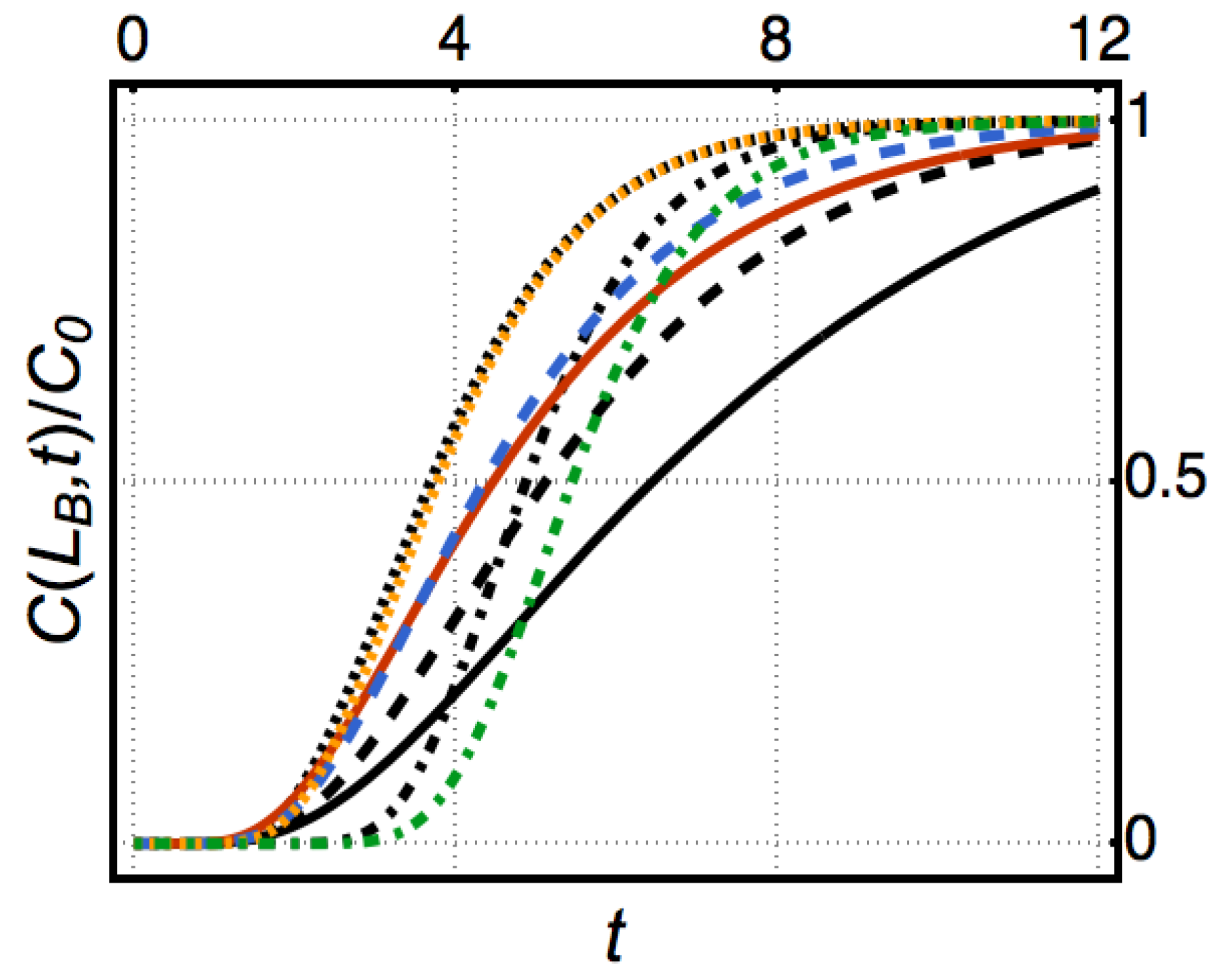
Appendix A.5. Figure 7
Appendix A.6. Figure 8
Appendix A.7. Figure 9
Appendix A.8. Figure 10
References
- Taylor, G.I. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1953, 219, 186–203. [Google Scholar]
- Aris, R. On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 235, 67–77. [Google Scholar]
- Brenner, H. Macrotransport Processess; Butterworth-Heinemann: Boston, MA, USA, 1993. [Google Scholar]
- Ibrahim, H.; Hassan, H.; Mekhamer, H.; Kenawy, S. Diffusion and sorption of Cs+ and Sr 2+ ions onto synthetic mullite powder. J. Radioanal. Nucl. Chem. 2018, 319, 1–12. [Google Scholar] [CrossRef]
- Millhauser, G.L.; Salpeter, E.E.; Oswald, R.E. Diffusion models of ion-channel gating and the origin of power-law distributions from single-channel recording. Proc. Natl. Acad. Sci. USA 1988, 85, 1503–1507. [Google Scholar] [CrossRef]
- Wijmans, J.; Baker, R. The solution-diffusion model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Yan, C.; Liu, J.; Liu, F.; Wu, J.; Gao, K.; Xue, D. Tube formation in nanoscale materials. Nanoscale Res. Lett. 2008, 3, 473–480. [Google Scholar] [CrossRef]
- Martínez-Balbuena, L.; Hernández-Zapata, E.; Santamaría-Holek, I. Onsager irreversible thermodynamics of the dynamics of transient pores in spherical lipid vesicles. Eur. Biophys. J. 2015, 44, 473–481. [Google Scholar] [CrossRef]
- Wu, R.; Liao, Q.; Zhu, X.; Wang, H. Pore network modeling of cathode catalyst layer of proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2012, 37, 11255–11267. [Google Scholar] [CrossRef]
- Stavarek, P.; Vajglova, Z.; Kristal, J.; Jiricny, V.; Kolena, J. Self-sustained oscillations of temperature and conversion in a packed bed microreactor during 2-methylpropene (isobutene) hydrogenation. Catal. Today 2015, 256, 250–260. [Google Scholar] [CrossRef]
- Adler, P. Porous Media: Geometry and Transports; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Otero, J.A.; Mazarrasa, O.; Villasante, J.; Silva, V.; Prádanos, P.; Calvo, J.I.; Hernández, A. Three independent ways to obtain information on pore size distributions of nanofiltration membranes. J. Membr. Sci. 2008, 309, 17–27. [Google Scholar] [CrossRef]
- Carberry, J.J.; Varma, A. Chemical Reaction and Reactor Engineering; CRC Press: Dover, NY, USA, 2001. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice-Hall International: London, UK, 1999. [Google Scholar]
- Glavatskiy, K.S.; Bhatia, S.K. Effect of pore size on the interfacial resistance of a porous membrane. J. Membr. Sci. 2017, 524, 738–745. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernández Hernández, S.I.; Santamaría-Holek, I. Effectiveness Factor and Mass Transfer Coefficient in Wedge and Funnel Pores Using a Generalized Fick–Jacobs Model. J. Phys. Chem. C 2016, 120, 29153–29161. [Google Scholar] [CrossRef]
- Seetha, S.; Manickam, J.G.; McCutcheon, J.R. Pore structure characterization of asymmetric membranes: Non–destructive characterization of porosity and tortuosity. J. Membr. Sci. 2014, 454, 549–554. [Google Scholar]
- Ledesma-Durán, A.; Hernández, S.I.; Santamaría-Holek, I. Effect of Surface Diffusion on Adsorption–Desorption and Catalytic Kinetics in Irregular Pores. II. Macro-Kinetics. J. Phys. Chem. C 2017, 121, 14557–14565. [Google Scholar] [CrossRef]
- Chandler, M.; Zydney, A. Effects of membrane pore geometry on fouling behavior during yeast cell microfiltration. J. Membr. Sci. 2006, 285, 334–342. [Google Scholar] [CrossRef]
- Kanani, D.M.; Fissell, W.H.; Roy, S.; Dubnisheva, A.; Fleischman, A.; Zydney, A.L. Permeability–selectivity analysis for ultrafiltration: Effect of pore geometry. J. Membr. Sci. 2010, 349, 405–410. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernández-Hernández, S.I.; Santamaría-Holek, I. Generalized Fick–Jacobs Approach for Describing Adsorption–Desorption Kinetics in Irregular Pores under Nonequilibrium Conditions. J. Phys. Chem. C 2016, 120, 7810–7821. [Google Scholar] [CrossRef] [Green Version]
- Zwanzig, R. Diffusion past an entropy barrier. J. Chem. Phys. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Bradley, R.M. Diffusion in a two-dimensional channel with curved midline and varying width: Reduction to an effective one-dimensional description. Phys. Rev. E 2009, 80, 061142. [Google Scholar] [CrossRef]
- Pineda, I.; Alvarez-Ramirez, J.; Dagdug, L. Diffusion in two-dimensional conical varying width channels: Comparison of analytical and numerical results. J. Chem. Phys. 2012, 137, 174103. [Google Scholar] [CrossRef]
- Berezhkovskii, A.; Pustovoit, M.; Bezrukov, S. Diffusion in a tube of varying cross section: Numerical study of reduction to effective one-dimensional description. J. Chem. Phys. 2007, 126, 134706. [Google Scholar] [CrossRef] [PubMed]
- Santamaría-Holek, I.; Grzywna, Z.J.; Miguel Rubi, J. A non-equilibrium thermodynamic model for combined adsorption and diffusion processes in micro-and nanopores. J. Non-Equilib. Thermodyn. 2012, 37, 273–290. [Google Scholar] [CrossRef]
- Santamaría-Holek, I.; Grzywna, Z.; Rubi, J. Entropic effects in diffusion-adsorption processes in micropores. Eur. Phys. J. Spec. Top. 2013, 222, 129–141. [Google Scholar] [CrossRef]
- Rubi, J.; Reguera, D. Thermodynamics and stochastic dynamics of transport in confined media. Chem. Phys. 2010, 375, 518–522. [Google Scholar] [CrossRef]
- Reguera, D.; Rubi, J. Kinetic equations for diffusion in the presence of entropic barriers. Phys. Rev. E 2001, 64, 061106. [Google Scholar] [CrossRef]
- Ledesma-Durán, A.; Hernández, S.; Santamaría-Holek, I. Relation between the porosity and tortuosity of a membrane formed by disconnected irregular pores and the spatial diffusion coefficient of the Fick-Jacobs model. Phys. Rev. E 2017, 95, 052804. [Google Scholar] [CrossRef] [PubMed]
- Ledesma-Durán, A.; Hernández, S.; Santamaría-Holek, I. Effect of Surface Diffusion on Adsorption–Desorption and Catalytic Kinetics in Irregular Pores. I. Local Kinetics. J. Phys. Chem. C 2017, 121, 14544–14556. [Google Scholar] [CrossRef]
- Low, Z.X.; Chua, Y.T.; Ray, B.M.; Mattia, D.; Metcalfe, I.S.; Patterson, D.A. Perspective on 3D printing of separation membranes and comparison to crossmark related unconventional fabrication techniques. J. Membr. Sci. 2017, 523, 596–613. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kärger, J.; Ruthven, D. Diffusion in Zeolites and other Microporous Solids; J. Wiley and Sons Inc.: New York, NY, USA, 1992; p. 341. [Google Scholar]
- Pineda, I.; Dagdug, L. Projection of two-dimensional diffusion in narrow asymmetric channels onto the longitudinal direction. J. Chem. Phys. 2014, 1579, 121–129. [Google Scholar]
- Berezhkovskii, A.; Szabo, A. Time scale separation leads to position–dependent diffusion along a slow coordinate. J. Chem. Phys. 2011, 135, 074108. [Google Scholar] [CrossRef]
- Ho, C.; Qiao, R.; Heng, J.B.; Chatterjee, A.; Timp, R.J.; Aluru, N.R.; Timp, G. Electrolytic transport through a synthetic nanometer-diameter pore. Proc. Natl. Acad. Sci. USA 2005, 102, 10445–10450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mistura, G.; Pozzato, A.; Grenci, G.; Bruschi, L.; Tormen, M. Continuous adsorption in highly ordered porous matrices made by nanolithography. Nat. Commun. 2013, 4, 2966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yameen, B.; Ali, M.; Neumann, R.; Ensinger, W.; Knoll, W.; Azzaroni, O. Single conical nanopores displaying pH-tunable rectifying characteristics. Manipulating ionic transport with zwitterionic polymer brushes. J. Am. Chem. Soc. 2009, 131, 2070–2071. [Google Scholar] [CrossRef] [PubMed]
- Yamauchi, Y.; Nagaura, T.; Ishikawa, A.; Chikyow, T.; Inoue, S. Evolution of standing mesochannels on porous anodic alumina substrates with designed conical holes. J. Am. Chem. Soc. 2008, 130, 10165–10170. [Google Scholar] [CrossRef] [PubMed]
- Siwy, Z.; Heins, E.; Harrell, C.C.; Kohli, P.; Martin, C.R. Conical-nanotube ion-current rectifiers: The role of surface charge. J. Am. Chem. Soc. 2004, 126, 10850–10851. [Google Scholar] [CrossRef]
- Siódmiak, J.; Santamaría-Holek, I.; Gadomski, A. On morphological selection rule of noisy character applied to model (dis) orderly protein formations. J. Chem. Phys. 2010, 132, 05B608. [Google Scholar] [CrossRef]
- Miyabe, K.; Guiochon, G. Measurement of the parameters of the mass transfer kinetics in high performance liquid chromatography. J. Sep. Sci. 2003, 26, 155–173. [Google Scholar] [CrossRef]
- Miyabe, K.; Guiochon, G. Fundamental interpretation of the peak profiles in linear reversed-phase liquid chromatography. Adv. Chromatogr. 2000, 40, 1–113. [Google Scholar]
- Miyabe, K.; Guiochon, G. Surface diffusion in reversed-phase liquid chromatography. J. Chromatogr. A 2010, 1217, 1713–1734. [Google Scholar] [CrossRef]
- Medveď, I.; Černỳ, R. Surface diffusion in porous media: A critical review. Microporous Mesoporous Mater. 2011, 142, 405–422. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Festa, R.; d’Agliano, E.G. Diffusion coefficient for a Brownian particle in a periodic field of force: I. Large friction limit. Phys. A Stat. Mech. Appl. 1978, 90, 229–244. [Google Scholar] [CrossRef]
- Kärger, J.; Kortunov, P.; Vasenkov, S.; Heinke, L.; Shah, D.B.; Rakoczy, R.A.; Traa, Y.; Weitkamp, J. Unprecedented insight into diffusion by monitoring the concentration of guest molecules in nanoporous host materials. Angew. Chem. Int. Edit. 2006, 45, 7846–7849. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Binder, T.; Chmelik, C.; Hibbe, F.; Krautscheid, H.; Krishna, R.; Weitkamp, J. Microimaging of transient guest profiles to monitor mass transfer in nanoporous materials. Nat. Mater. 2014, 13, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Ruthven, D.M.; Theodorou, D.N. Diffusion in Nanoporous Materials; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santamaría-Holek, I.; Hernández, S.I.; García-Alcántara, C.; Ledesma-Durán, A. Review on the Macro-Transport Processes Theory for Irregular Pores able to Perform Catalytic Reactions. Catalysts 2019, 9, 281. https://doi.org/10.3390/catal9030281
Santamaría-Holek I, Hernández SI, García-Alcántara C, Ledesma-Durán A. Review on the Macro-Transport Processes Theory for Irregular Pores able to Perform Catalytic Reactions. Catalysts. 2019; 9(3):281. https://doi.org/10.3390/catal9030281
Chicago/Turabian StyleSantamaría-Holek, Iván, Saúl I. Hernández, Consuelo García-Alcántara, and Aldo Ledesma-Durán. 2019. "Review on the Macro-Transport Processes Theory for Irregular Pores able to Perform Catalytic Reactions" Catalysts 9, no. 3: 281. https://doi.org/10.3390/catal9030281
APA StyleSantamaría-Holek, I., Hernández, S. I., García-Alcántara, C., & Ledesma-Durán, A. (2019). Review on the Macro-Transport Processes Theory for Irregular Pores able to Perform Catalytic Reactions. Catalysts, 9(3), 281. https://doi.org/10.3390/catal9030281