Numerical Simulation of Melting Kinetics of Metal Particles during Tapping with Argon-Bottom Stirring
Abstract
:1. Introduction
2. Description of the Mathematical Model
2.1. Mathematical Model for Fluid Flow
- The metal phase is isothermal. This assumption’s validation is based on the results published by Berg et al. [7], who carried out simulations under isothermal and non-isothermal conditions. The authors reported a slight recirculation at the top of the bath close to the wall, which did not exist in the isothermal simulation. These results indicated that the inertial forces are considerably larger than the buoyancy ones during the tapping operation.
- The impinging jet hits the ladle bottom on its center perpendicularly. Most of the modern plants using the eccentric bottom tapping (EBT) technology observe this condition.
- The additions’ shapes are perfect spheres, which is a reasonable assumption since the shell formed on the surface of a particle rounds up all the possible corners, surface roughness, and irregularities.
- There is no slag phase in the system, which implicitly means that slag carryover does not exist attaining an ideal perfect tapping operation, and the effect of the addition of fluxes is negligible.
- Steel throughput at tapping is constant.
- The steel’s solidus temperature is 1493 °C, under the assumption that it has peritectic chemistry.
- Although argon and air constitute a single gas phase, artificially, they separated using an additional dummy index in the VOF model. This trick is useful to track air–argon interfaces.
- These simulations involve single particles thrown in the steel during the tapping operation. Therefore, there is no interaction with other particles and the particle flow-field does not affect the flow-field of the liquid metal. For a given metal level in the ladle, the residence times and trajectories of sinking particles remain constant.
2.2. Boundary Conditions
2.3. Method of Solution
2.4. Particle Dynamics
2.4.1. Trajectory of Particles
2.4.2. Heat Transfer
3. Results and Discussion
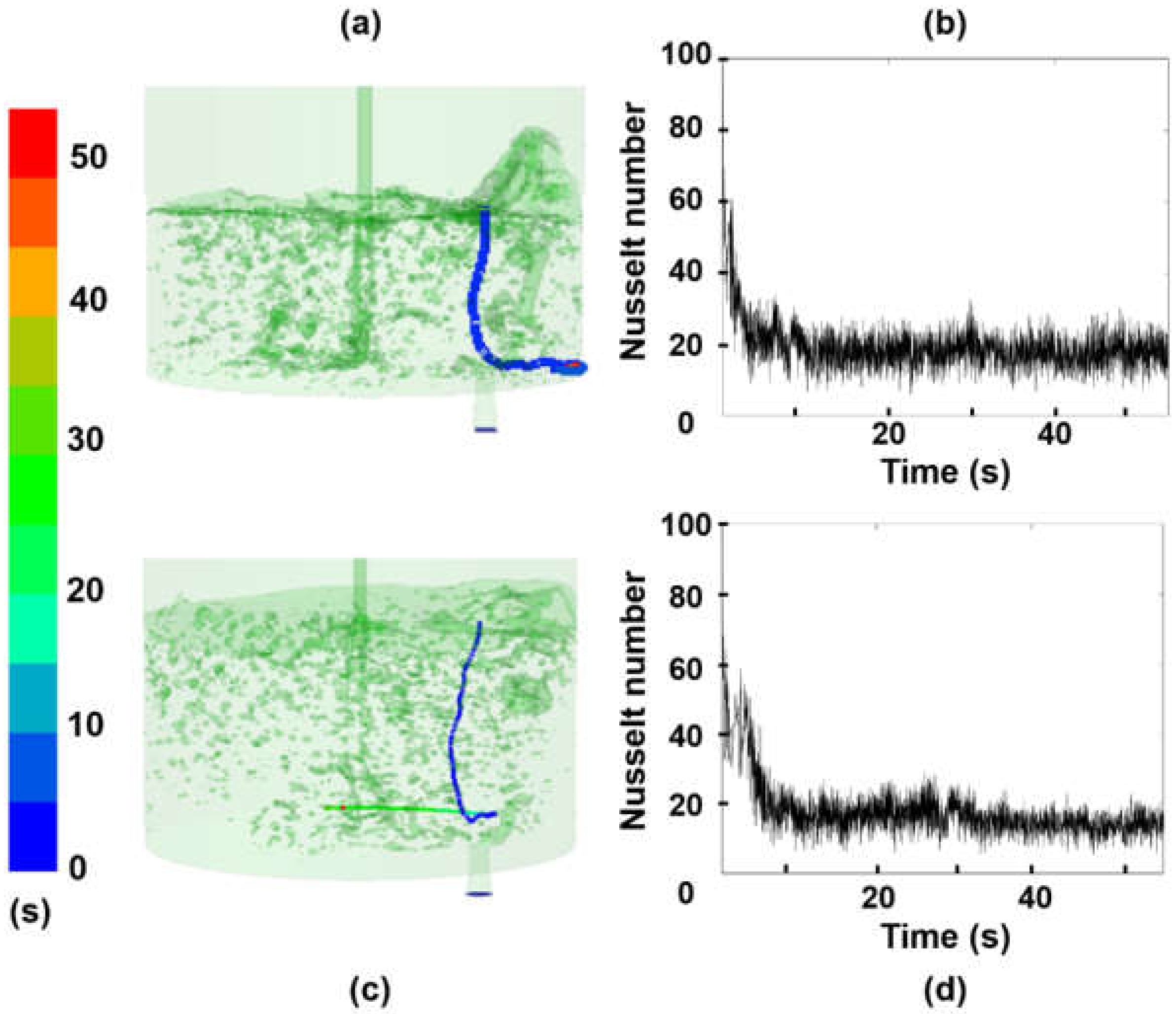
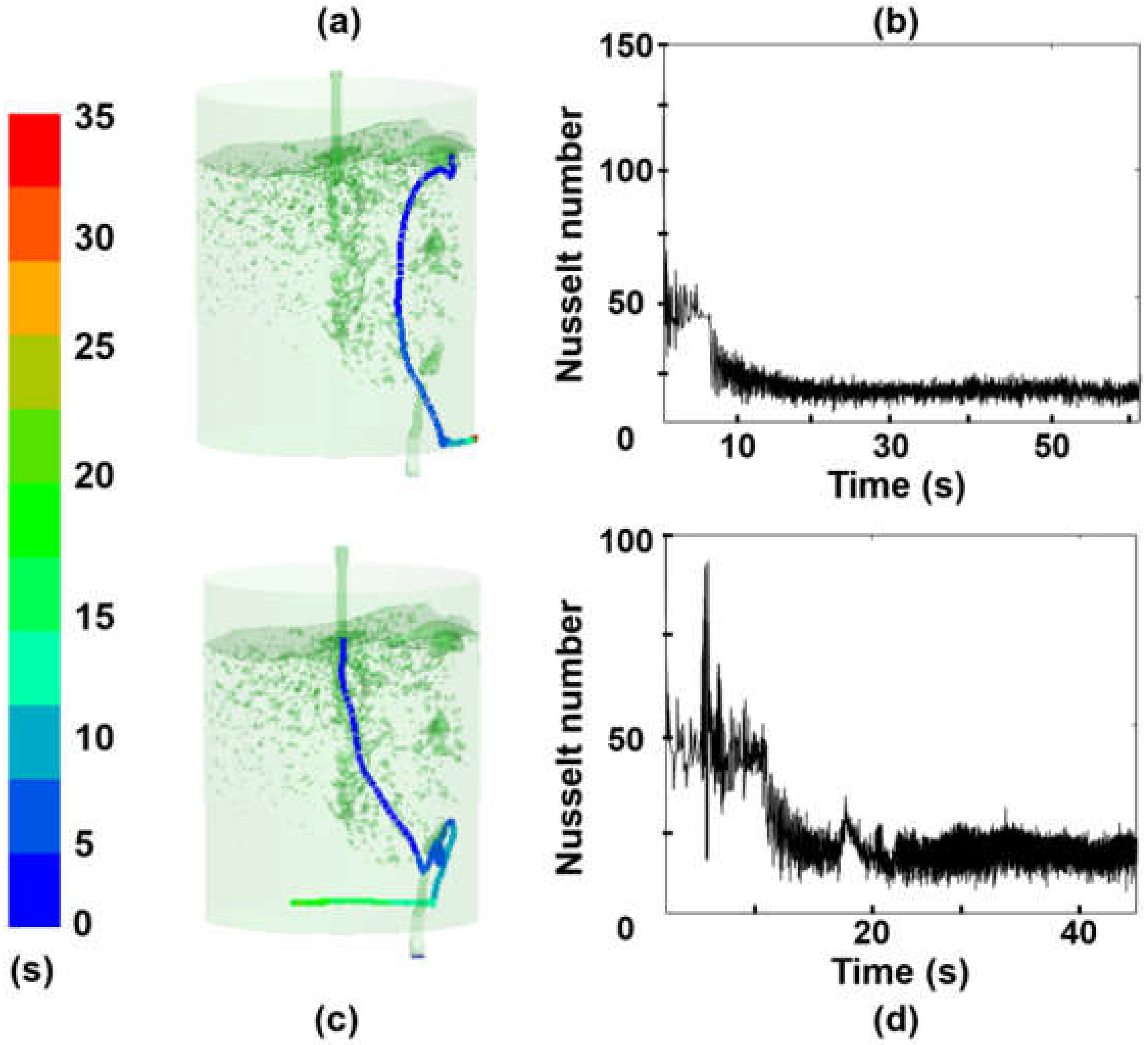
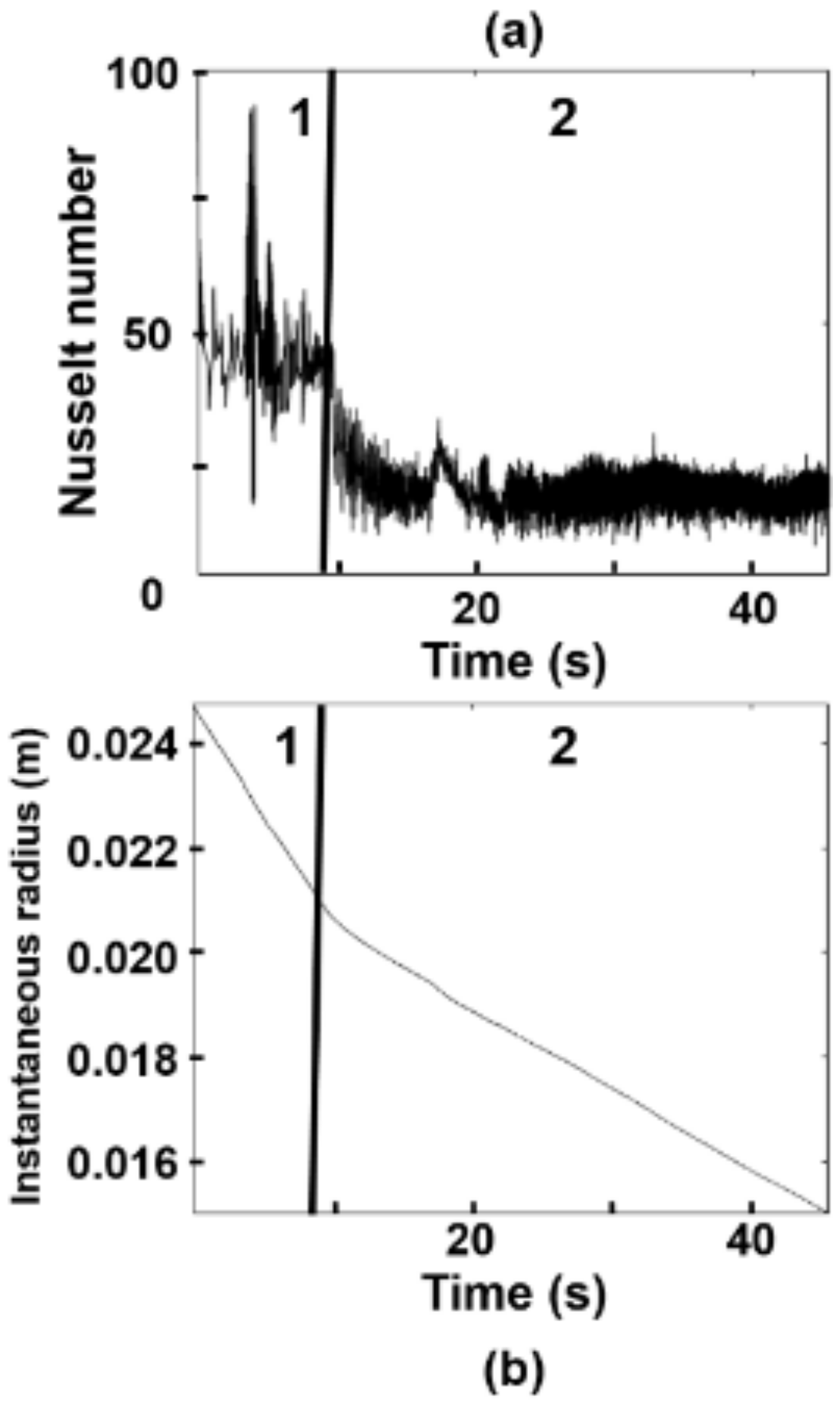
3.1. Effect of Turbulence on the Nusselt Number
3.2. Melting Rates
3.3. Melting Times
3.4. Combined Effects on the Melting Rate
3.5. Practical Implications
4. Conclusions
- The heat transfer coefficient is a function of the time and local coordinates of the particle trajectory. Therefore, the melting rate of particles, for a given superheat, is dependent on the local position of a particle and steel level in the ladle.
- Due to the local turbulence levels, the melting rate of a particle increases when its trajectory crosses through high turbulent fields and decreases when it goes through low turbulence.
- The melting rates of a particle are dependent on the bath level of steel tonnage in the ladle. At low bath levels, the melting rates are higher in the opposite side where the argon plume is due to its deviation driven by the impacting streams of liquid steel in the ladle bottom.
- At high ladle levels, a particle’s melting rates are higher in the side where the argon plume is since it rises straightly, allowing more direct interaction and larger heat fluxes.
- Particles fed on the opposite side can melt fast if they sink through a field of small velocities, and are dragged to the argon bubbling region in the ladle bottom. At higher superheats, particles’ melting times become less dependent on the fluid flow dynamics of liquid steel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-section area of the metallic particle in the bath |
| CP | heat capacity |
| D | diameter |
| g | gravity constant |
| ΔH | enthalpy |
| h | height and heat transfer coefficient hp of the particle |
| curvature radius | |
| thermal conductivity, kinetic energy | |
| m | mass |
| n | normal vector |
| p | pressure |
| q | heat flux and phase q |
| R | particle radius |
| ratio of physical properties like CP, k, α | |
| trajectory of the particle | |
| S | dimensionless shell thickness |
| T | temperature |
| t | time |
| . | averaged velocity of the mixture |
| volume | |
| v | particle velocity |
| Greek Symbols | |
| α | thermal diffusivity |
| δ | thickness of the boundary layer |
| tensor of Levy–Civita | |
| dissipation rate of kinetic energy | |
| Ω | dimensionless number, Equation (16) |
| ωij | vorticity |
| Π | total stress |
| χ | phase indicator |
| µ | viscosity |
| density | |
| τ | stress |
| ratio of thicknesses | |
| Θ | dimensionless temperature |
| Sub-Indexes | |
| B | boundary |
| I | interface |
| L | liquid |
| M | metal |
| m | mean average |
| max | maximum value |
| p | particle |
| q | phase q |
| 0 | initial value of the nickel particle´s radius |
| rms | root mean square |
| i, j, k | are indexes for coordinates. When only one index i used, that means the three directions. |
References
- Carreño-Galindo, V.; Morales, R.D.; Serrano, J.A.; Chavez, J.F. Thermodynamics analysis of steel deoxidation processes during tapping and refining operations. In Proceedings of the 57th Electric Arc Furnace Conference, Iron and Steel Society, Pittsburgh, PA, USA, 14–16 November 1999; pp. 523–534. [Google Scholar]
- Argyropoulos, S.A.; Guthrie, R.I.L. The dissolution of titanium in liquid steel. Metall. Mater. Trans. B 1984, 15, 47–58. [Google Scholar] [CrossRef]
- Pandelaers, L.; Verhaeghe, F.; Blanplain, B.; Wollants, P.; Gardin, P. Interfacial reactions during titanium dissolution in liquid iron: A combined experimental and modeling approach. Metall. Mater. Trans. B 2009, 40, 676–684. [Google Scholar] [CrossRef]
- Guthrie, R.I.L.; Clift, R.; Henein, H. Contacting problems associated with aluminum and ferro-alloy additions in steelmaking-hydrodynamics. Metall. Mater. Trans. B 1975, 6, 321–329. [Google Scholar] [CrossRef]
- Tanaka, M.; Mazumdar, D.; Guthrie, R.I.L. Motions of alloying additions during furnace tapping in steelmaking processing operations. Metall. Mater. Trans. B 1993, 24, 639–648. [Google Scholar] [CrossRef]
- Rodríguez-Ávila, J.; Morales, R.D.; Nájera-Bastida, A. Numerical study of multiphase flow dynamics of plugging jets in liquid steel and trajectories of ferroalloy additions in a ladle during tapping operations. ISIJ Int. 2012, 52, 814–822. [Google Scholar] [CrossRef]
- Berg, H.; Laux, H.; Johanssen, S.T. Flow pattern and alloy dissolution during tapping of steel furnaces. Ironmak. Steelmak. 1999, 26, 127–139. [Google Scholar] [CrossRef]
- Reza Aboutalebi, M.; Vadhati Khaki, J. Heat transfer modelling of the melting of solid particles in an agitated molten metal bath. Can. Metall. Quart. 1998, 37, 305–311. [Google Scholar] [CrossRef]
- Duan, H.; Zhang, L.; Thomas, B.G.; Conejo, A. Fluid flow, dissolution, and mixing phenomena in argon-stirred steel ladles. Metall. Mater. Trans. B 2018, 49, 2722–2743. [Google Scholar] [CrossRef]
- Webber, D.S. Alloy Dissolution in Argon Stirred Steel. Ph.D. Thesis, Metallurgical Engineering, Missouri University of Science and Technology, Rolla, MO, USA, 2011. [Google Scholar]
- Nájera-Bastida, A.; Rodríguez-Ávila, J.; Guarneros-Guarneros, J.; Morales, R.D.; Chattopadhyay, K. Changes of Multiphase Flow Patterns during Steel Tapping with Simultaneous Argon Bottom Stirring in the Ladle. Metals 2020, 10, 1036. [Google Scholar] [CrossRef]
- Water - Physical Properties. Available online: https://www.britannica.com/science/water/Physical-properties (accessed on 10 April 2019).
- Kubaschewski, O.; Alcock, C.B. Metallurgical Thermochemistry, 5th ed.; Oxford-Pergamon: London, UK, 1979; p. 349. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Comp. Physics 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, M. Multiphase Flow with Droplets and Particles, 2nd ed.; CRC Press: New York, NY, USA, 2012; p. 68. [Google Scholar]
- Yeoh, G.H. Computational Techniques for Multiphase-Flows; Butterworth-Heinemann, Oxford: London, UK, 2010; p. 215. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada, CA, USA, 2000; pp. 103–104. [Google Scholar]
- Chung, T.J. Computational Fluid Dynamics; Cambridge University Press: London, UK, 2002; pp. 218–220. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press, Cambridge Press: London, UK, 2000; p. 373. [Google Scholar]
- ANSYS, Inc. Available online: www.ansys.com (accessed on 10 April 2019).
- Ferziger, H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: New York, NY, USA, 2002; p. 72. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley International: Hoboken, NJ, USA, 1960; p. 153. [Google Scholar]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator-splitting. Comp. Physics 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Morsi, A.J.; Alexander, S.A. An investigation of particle trajectories in two-phase flow system. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Zhang, L.; Oeters, F. Melting and Mixing of Alloying Agents in Steel Melts; Verlag Stahleissen GmbH: Dusseldorf, Germany, 2006; p. 1. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops: Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Nordberg, M.; Nordberg, G.F.; Fowler, B.A. Handbook on the Toxicology of Metals; Elsevier-Academic Press: Amsterdam, The Netherlands, 2011; p. 743. [Google Scholar]

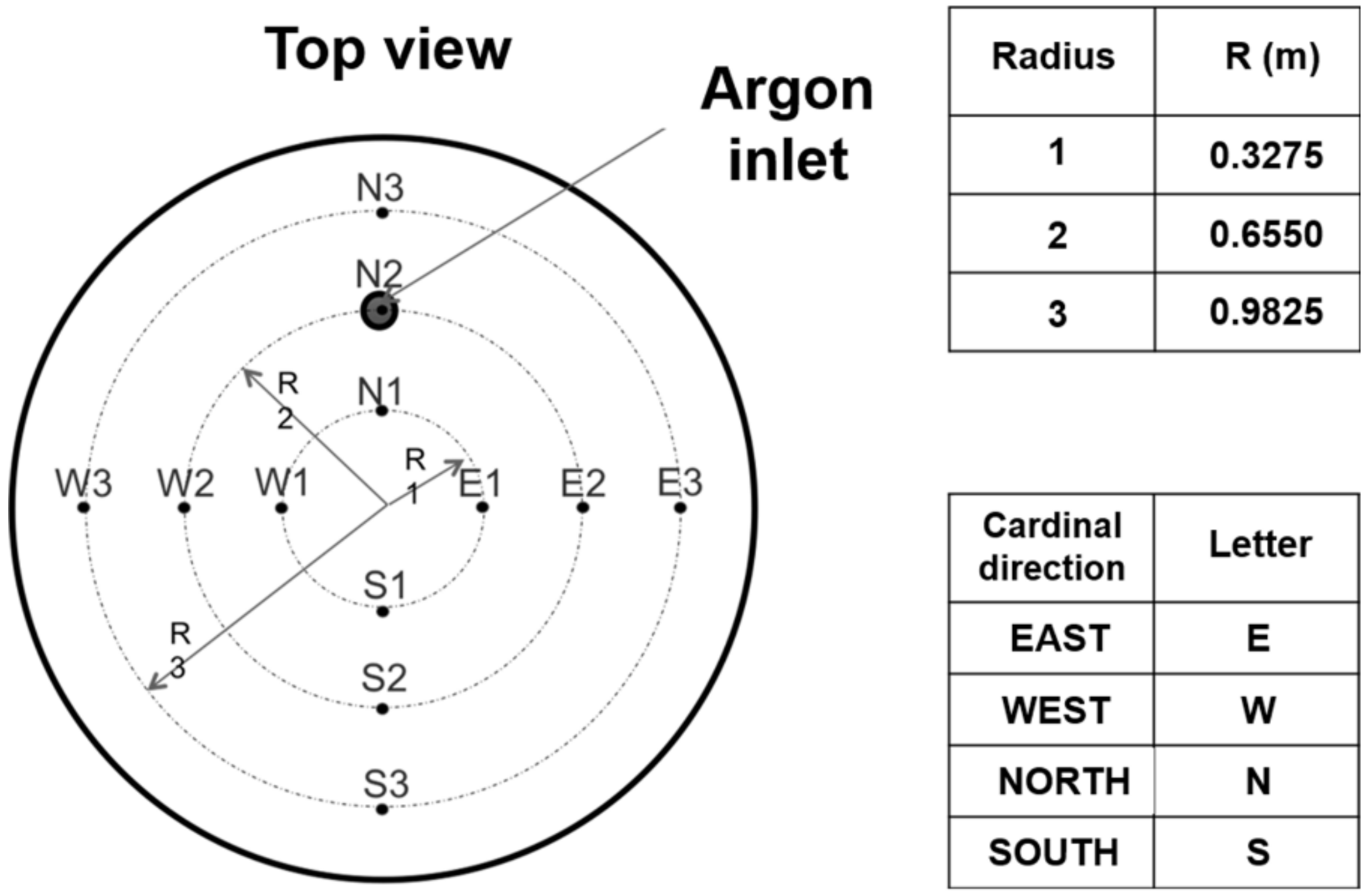







| Item | Description | Observations |
|---|---|---|
| Electric Arc Furnace | AC EAF with a capacity of 100 tons, hot heel of 12–15 tons | Burners, oxygen lances, and EBT system |
| Ladle | Capacity of 80 tons, straight geometry, dolomite lining | Eccentric argon plug, pneumatic stirring |
| EBT | Sleeve diameter is 114 mm, flow rate of argon is 400 L/min | Straight sleeve pointing toward the center of the ladle |
| EBT-Ladle Bottom | The distance between the tip of the EBT sleeve and the ladle bottom is 3.50 m | The length of the EBT is 0.90 m, embedded in the bottom of the EAF |
| Steel Throughput | Between 16 and 23 tons/min, a magnitude of 20 ton/min was assumed | The steel throughput depends on the wear condition of the sleeve |
| Phase | Density kg m−3 | Viscosity Pa-s |
|---|---|---|
| Liquid Steel | 7 100 | 0.006 |
| Argon | 0.458 | 5.7 × 10−5 |
| Air | 0.3289 | 4.36 × 10−5 |
| Fourier | |
| Biot | |
| Phase Transition | |
| Dimensionless Temperature | |
| Dimensionless Radius of the Shell Outside | |
| Dimensionless Radial Coordinate |
| Metal | TS °C | ΔHs J/kg | k W/mK | kg/m3 | CP J/kg K | α m2/s | ||
|---|---|---|---|---|---|---|---|---|
| Fe(l) | 1536 | 277,300 | 40.3 | 7020 | 820 | 6.5 × 10−6 | ||
| Fe(s) | 1536 | 277,300 | 37.7 | 7650 | 820 | 6.4 × 10−6 | 1.00 | 1.00 |
| Cr | 1857 | 371,200 | 60 | 6930 | 972 | 8.9 × 10−6 | 1.49 | 0.93 |
| Mn | 1250 | 266,500 | 50 | 7290 | 800 | 8.6 × 10−6 | 1.24 | 1.08 |
| Ni | 1455 | 292,200 | 85.5 | 8910 | 570 | 17 × 10−6 | 2.12 | 1.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chattopadhyay, K.; Morales-Davila, R.; Nájera-Bastida, A.; Rodríguez-Ávila, J.; Muñiz-Valdés, C.R. Numerical Simulation of Melting Kinetics of Metal Particles during Tapping with Argon-Bottom Stirring. Crystals 2020, 10, 901. https://doi.org/10.3390/cryst10100901
Chattopadhyay K, Morales-Davila R, Nájera-Bastida A, Rodríguez-Ávila J, Muñiz-Valdés CR. Numerical Simulation of Melting Kinetics of Metal Particles during Tapping with Argon-Bottom Stirring. Crystals. 2020; 10(10):901. https://doi.org/10.3390/cryst10100901
Chicago/Turabian StyleChattopadhyay, Kinnor, Rodolfo Morales-Davila, Alfonso Nájera-Bastida, Jafeth Rodríguez-Ávila, and Carlos Rodrigo Muñiz-Valdés. 2020. "Numerical Simulation of Melting Kinetics of Metal Particles during Tapping with Argon-Bottom Stirring" Crystals 10, no. 10: 901. https://doi.org/10.3390/cryst10100901
APA StyleChattopadhyay, K., Morales-Davila, R., Nájera-Bastida, A., Rodríguez-Ávila, J., & Muñiz-Valdés, C. R. (2020). Numerical Simulation of Melting Kinetics of Metal Particles during Tapping with Argon-Bottom Stirring. Crystals, 10(10), 901. https://doi.org/10.3390/cryst10100901







