Mesomorphic, Optical and DFT Aspects of Near to Room-Temperature Calamitic Liquid Crystal
Abstract
:1. Introduction
2. Experimental
2.1. Materials
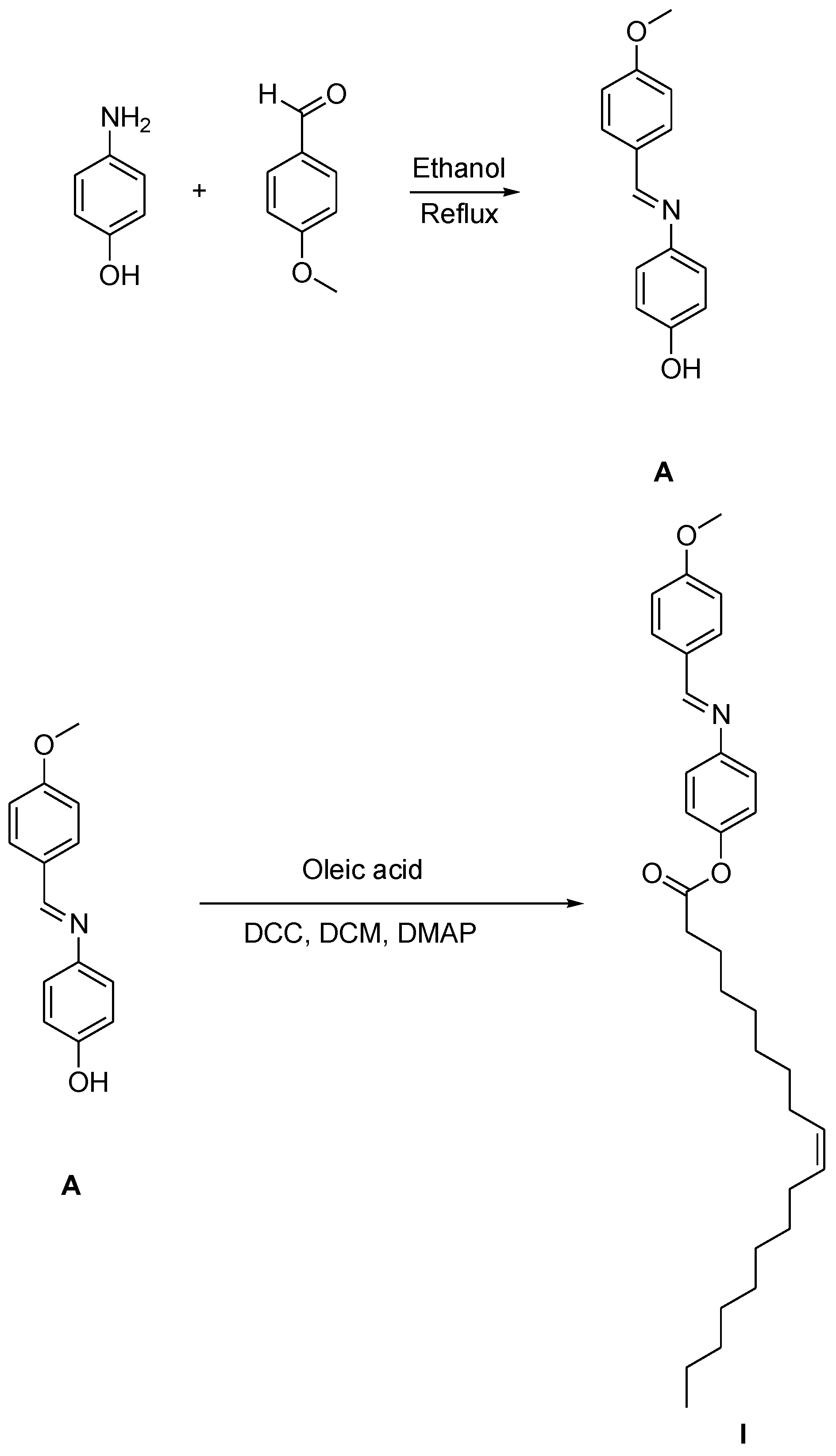
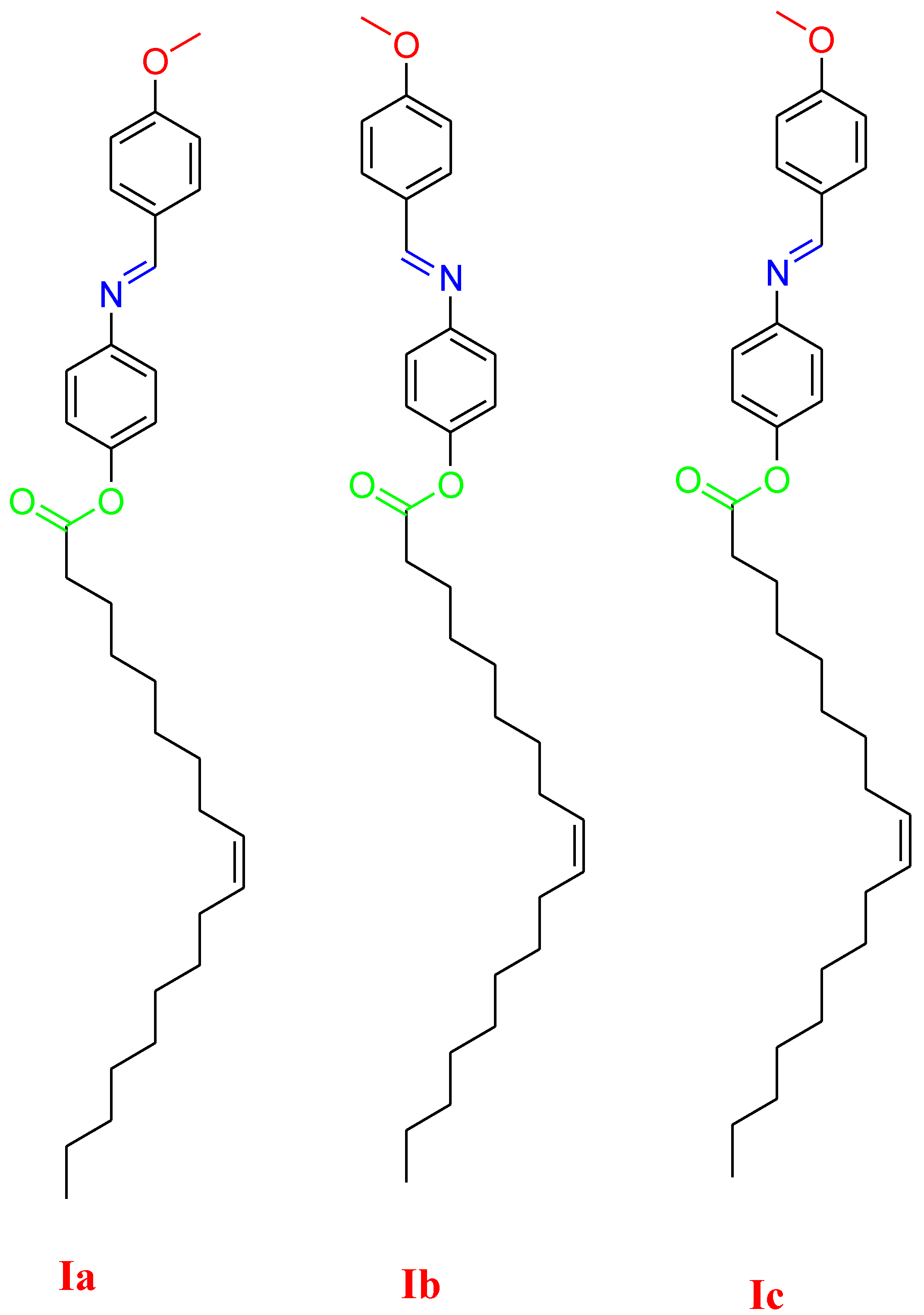
2.2. Synthesis of (4-methoxybenzylideneamino)phenyl oleate, I
2.3. Synthesis
2.3.1. Synthesis of 4-methoxybenzylideneamino)phenol A:
2.3.2. Synthesis of (4-methoxybenzylideneamino)phenyl oleate, I
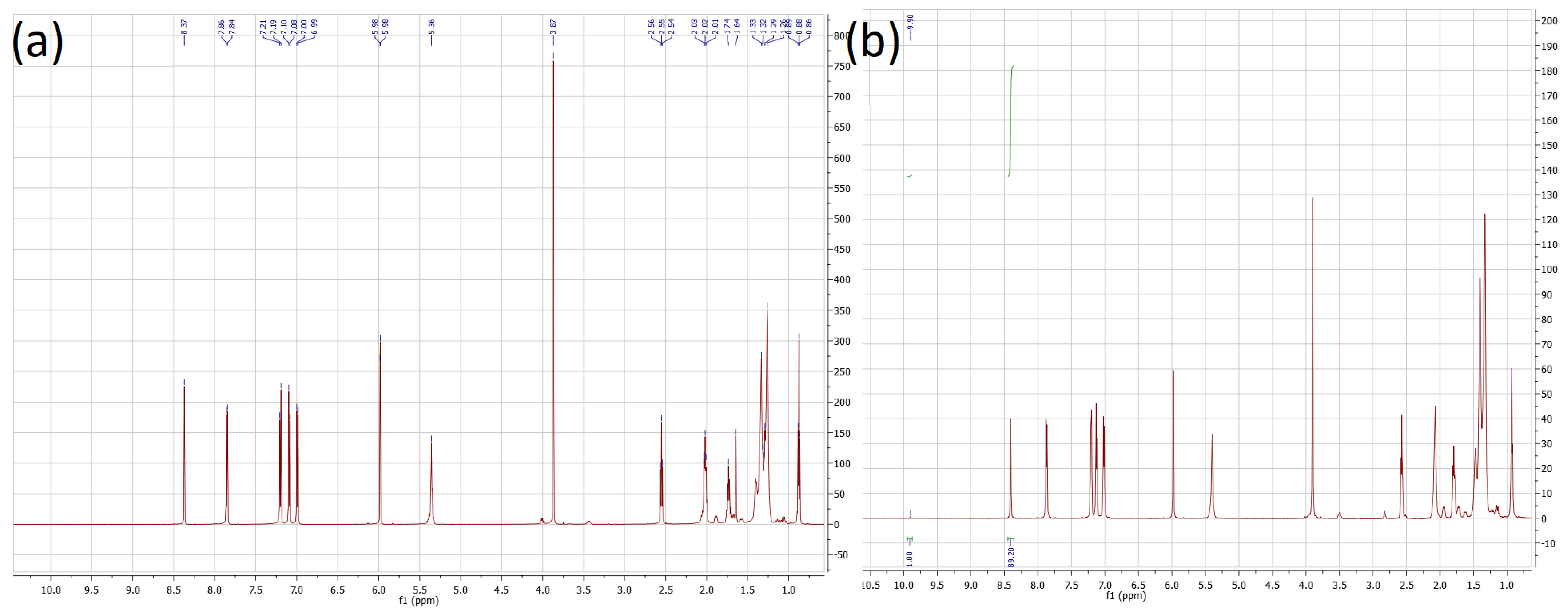
3. Results and Discussion
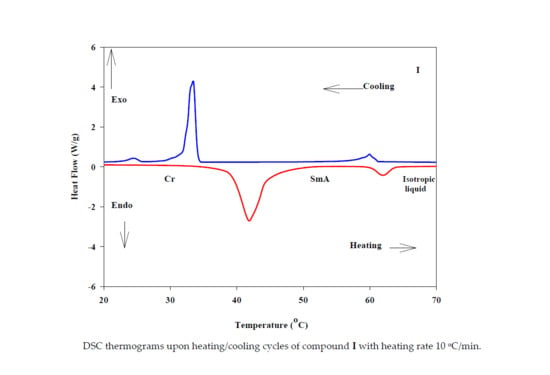
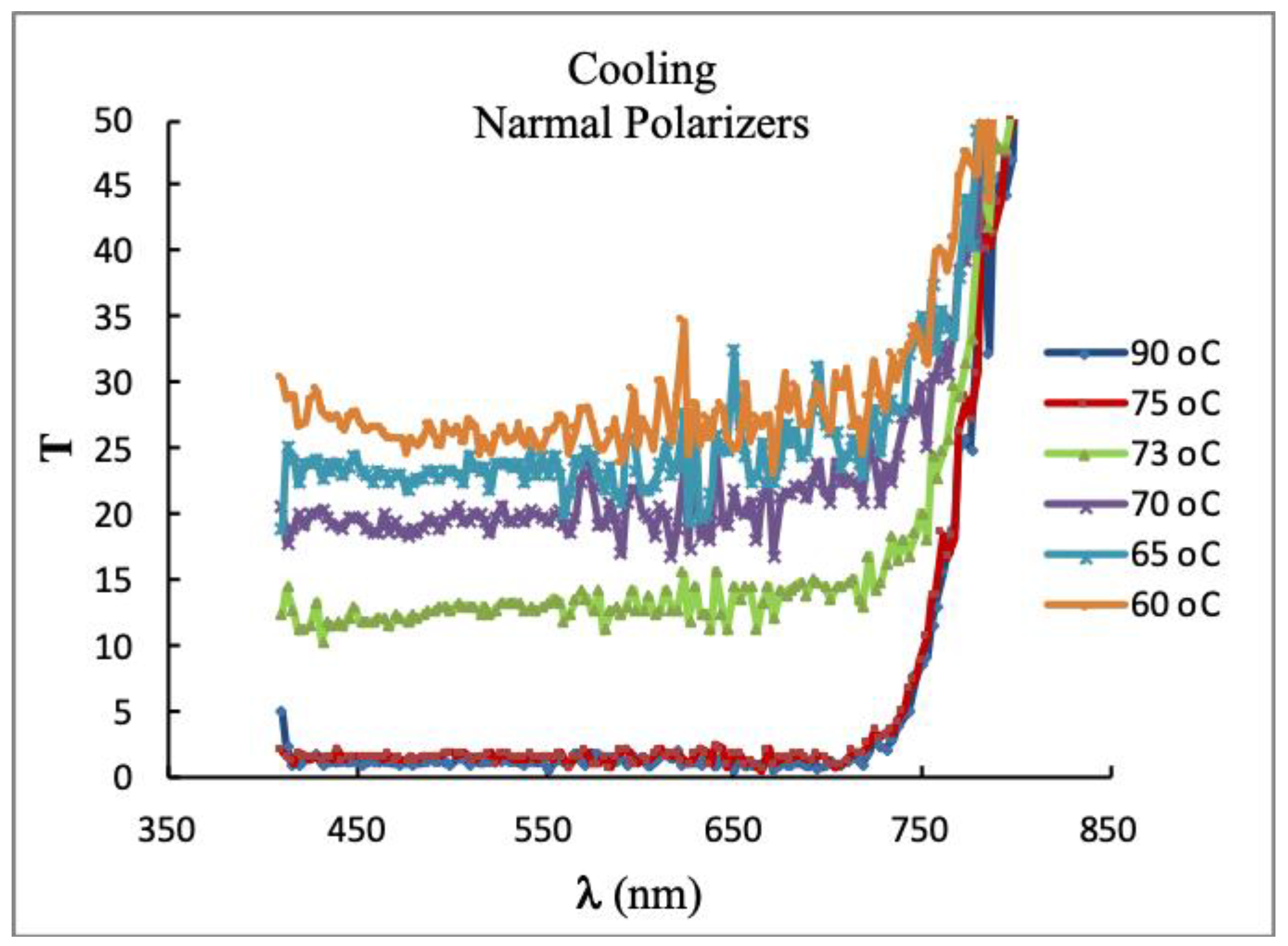
3.1. Mesomorphic Behavior Studies
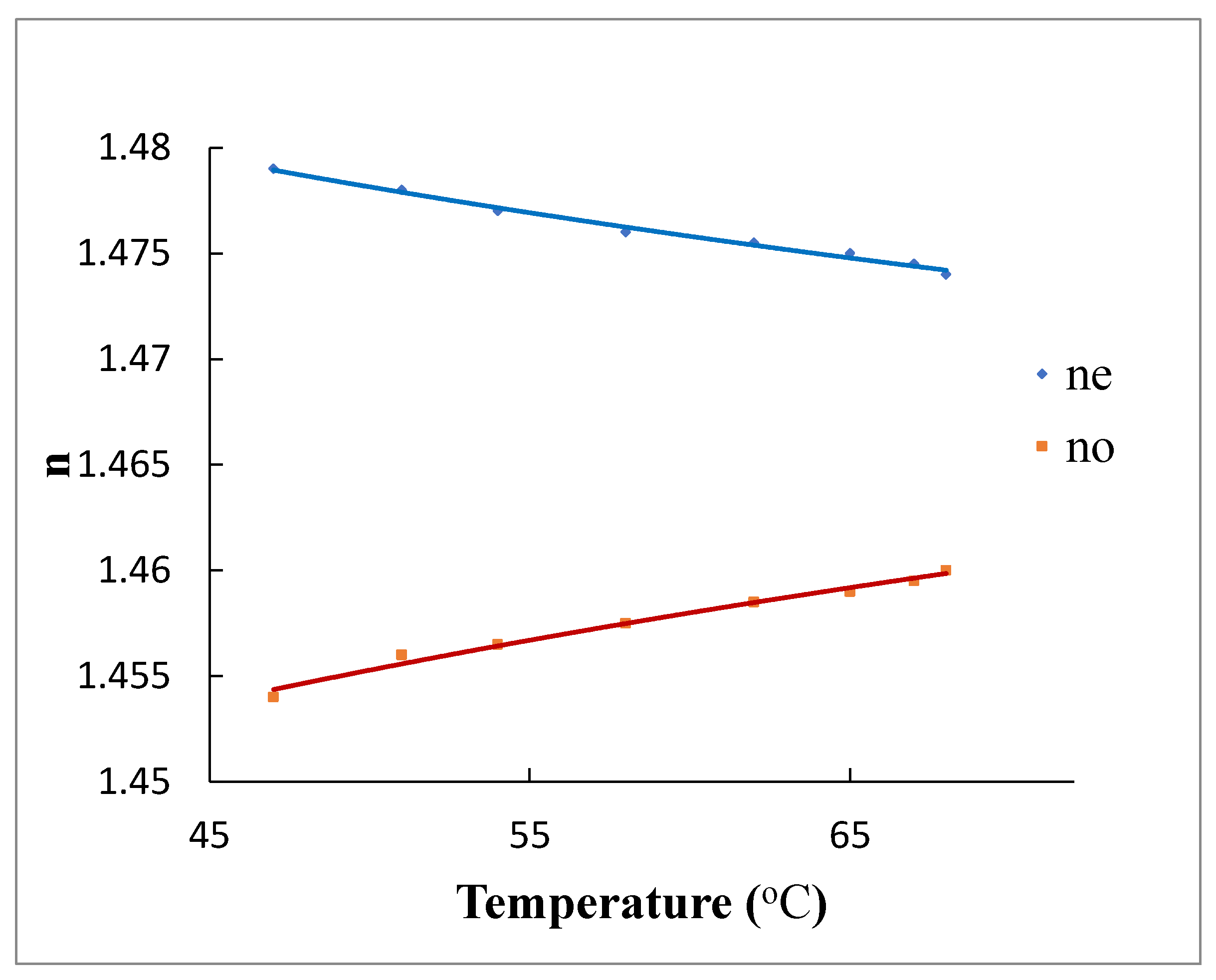
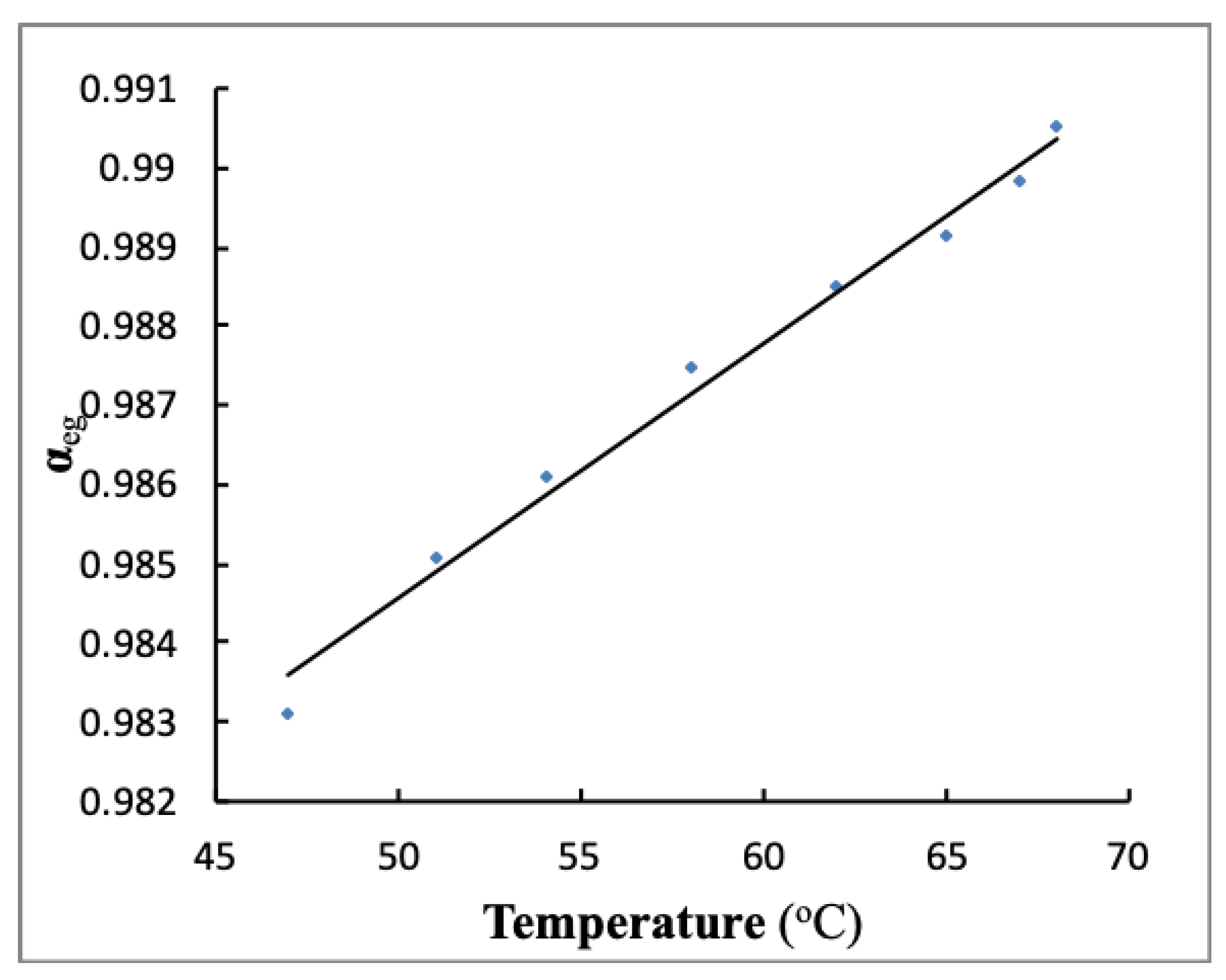
3.2. Measurements of Refractive Index
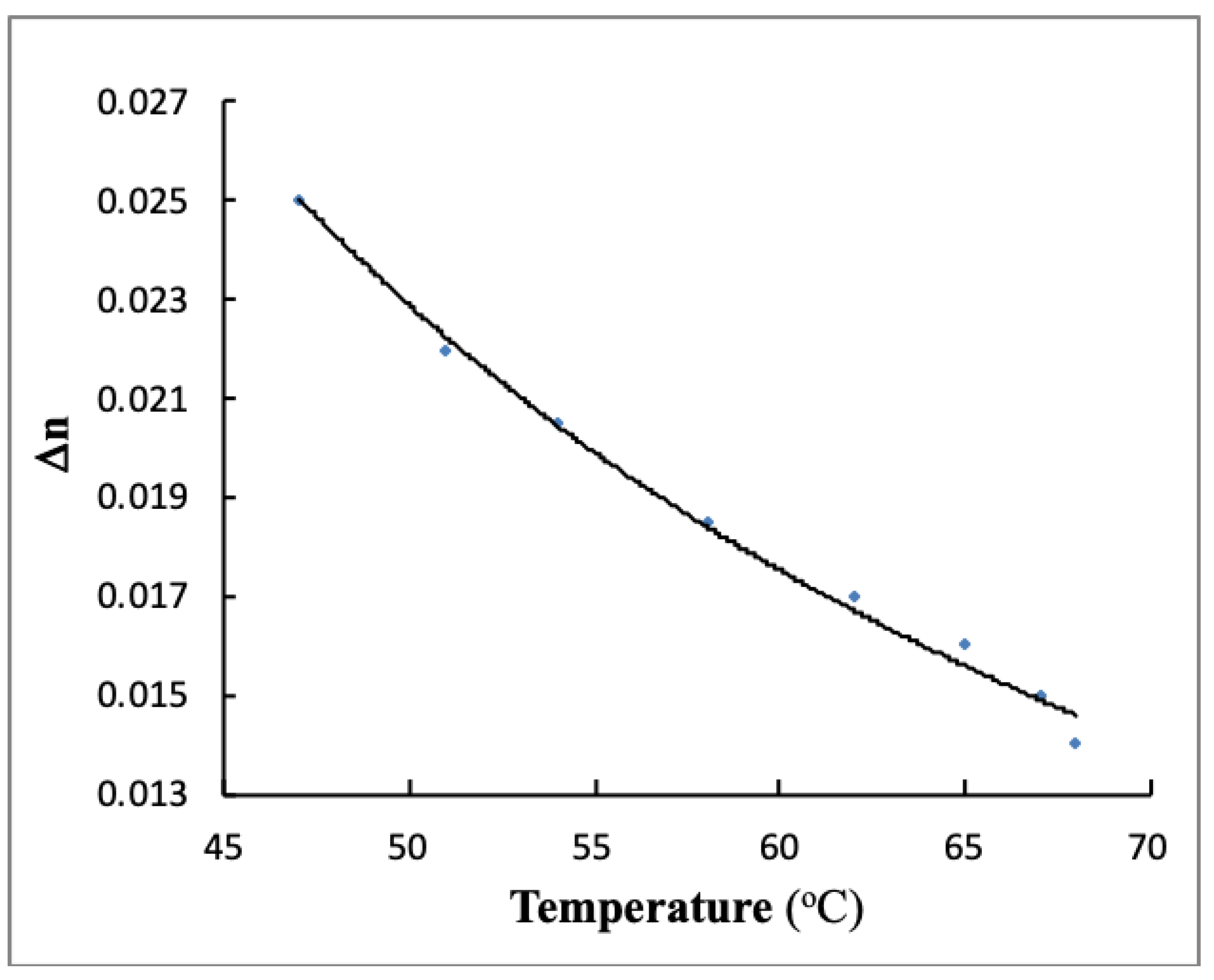
3.3. Measurements for Birefringence
3.3.1. Birefringence Measurement using the Abbe Refractometer
3.3.2. Birefringence Measurement by a Modified Spectrophotometer
3.3.3. Interferometric Method
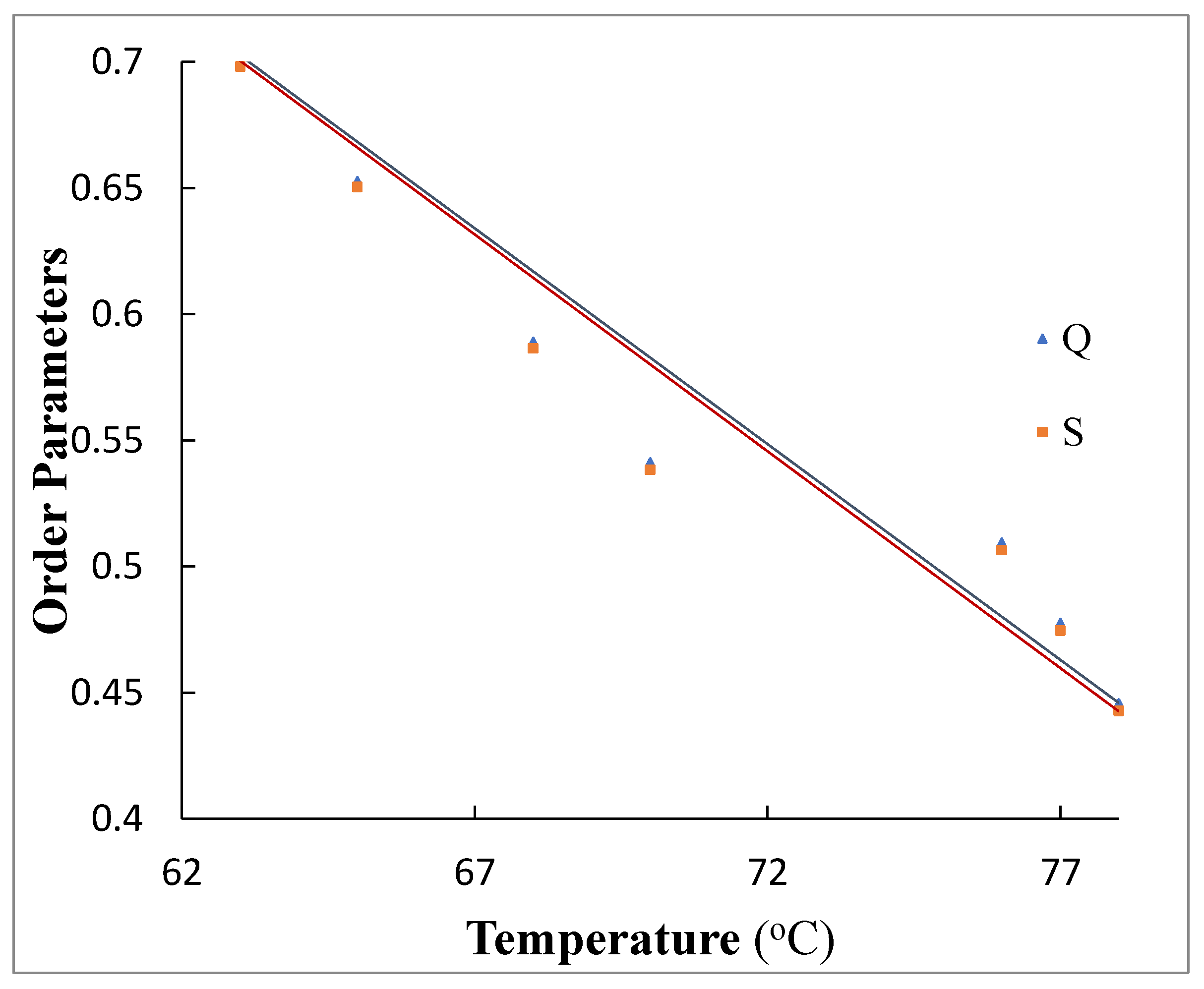
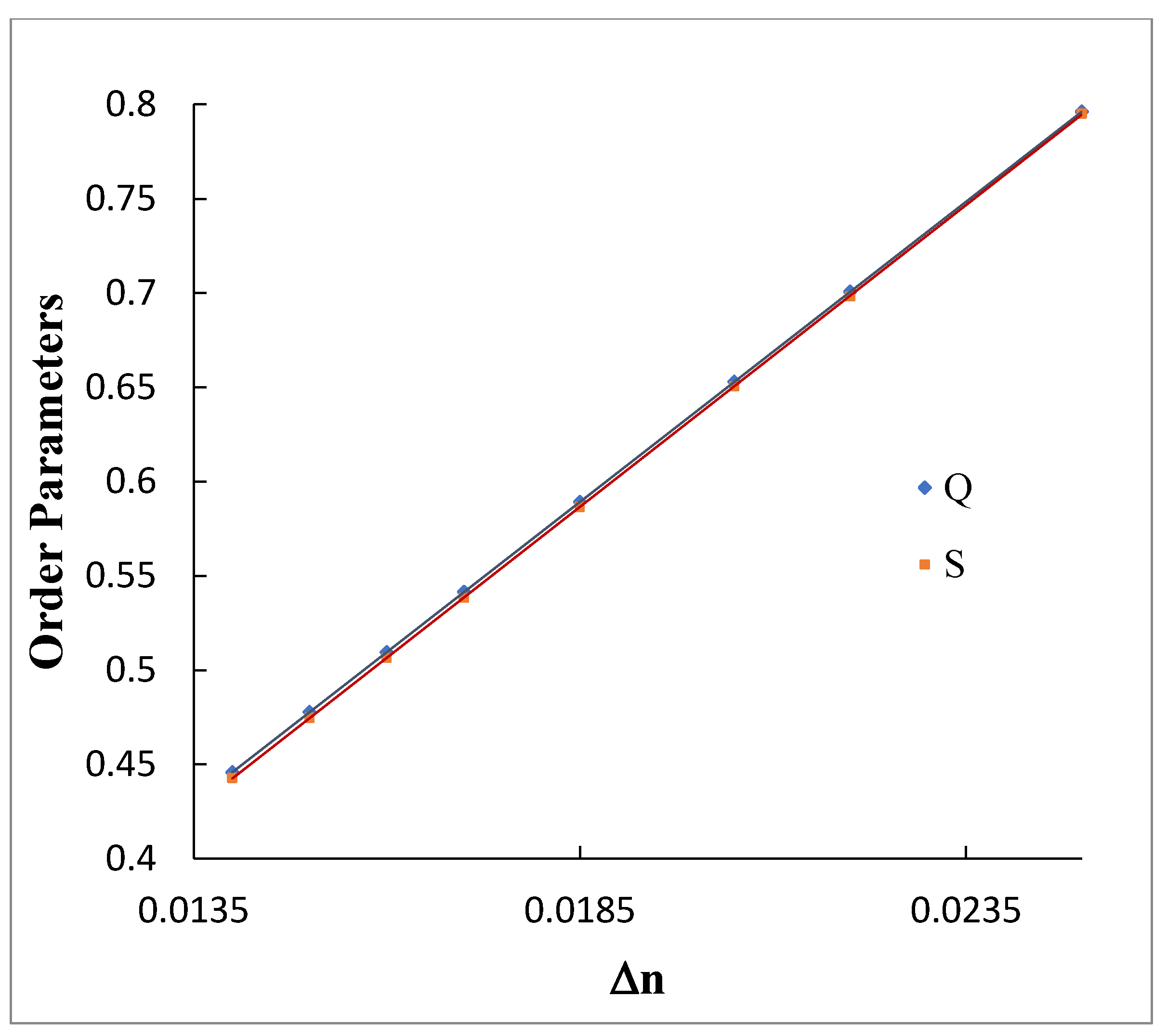
3.4. Order Parameter Measurement
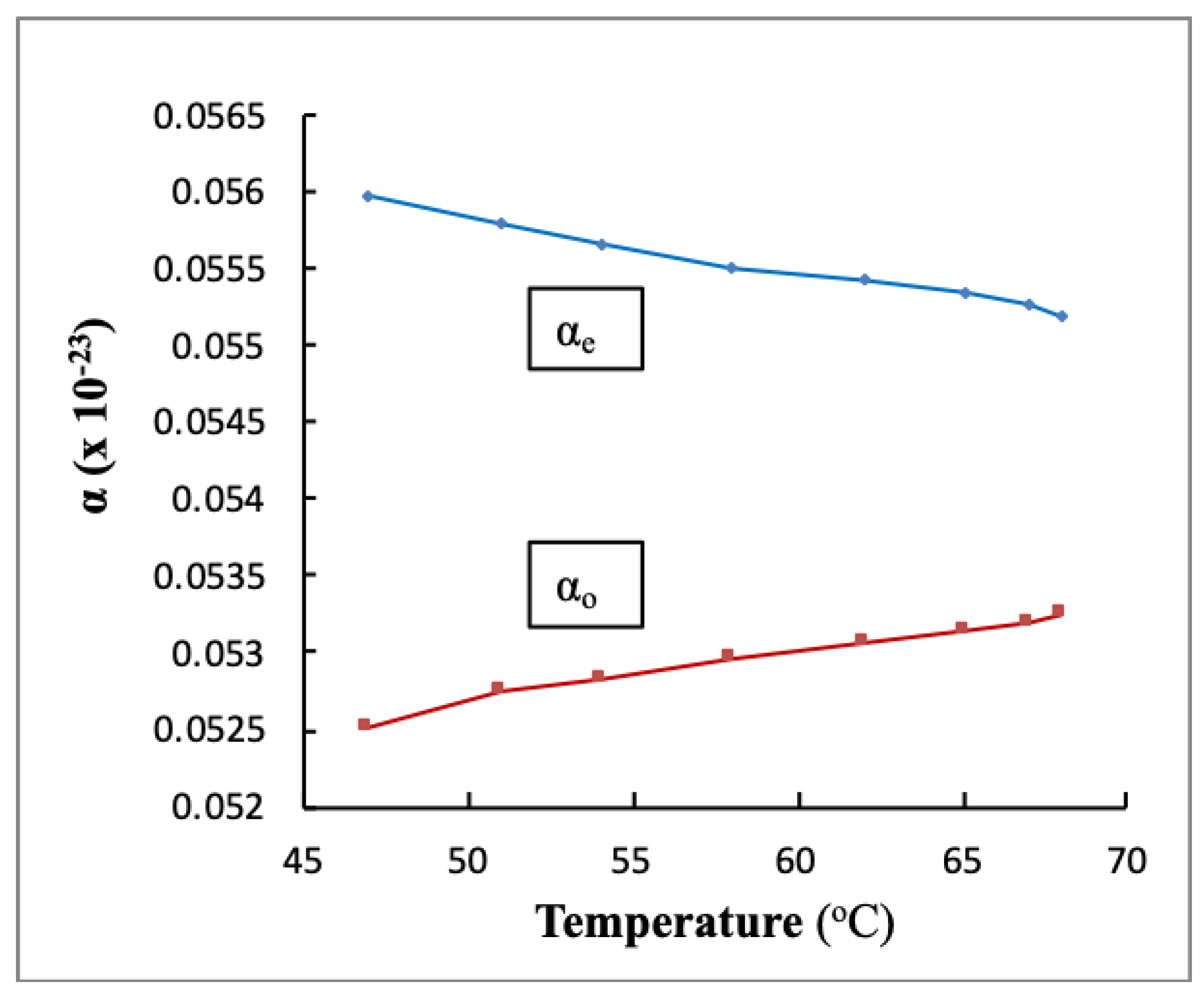
3.5. Molecular Polarizability
3.6. Molecular Modeling (DFT Calculations)
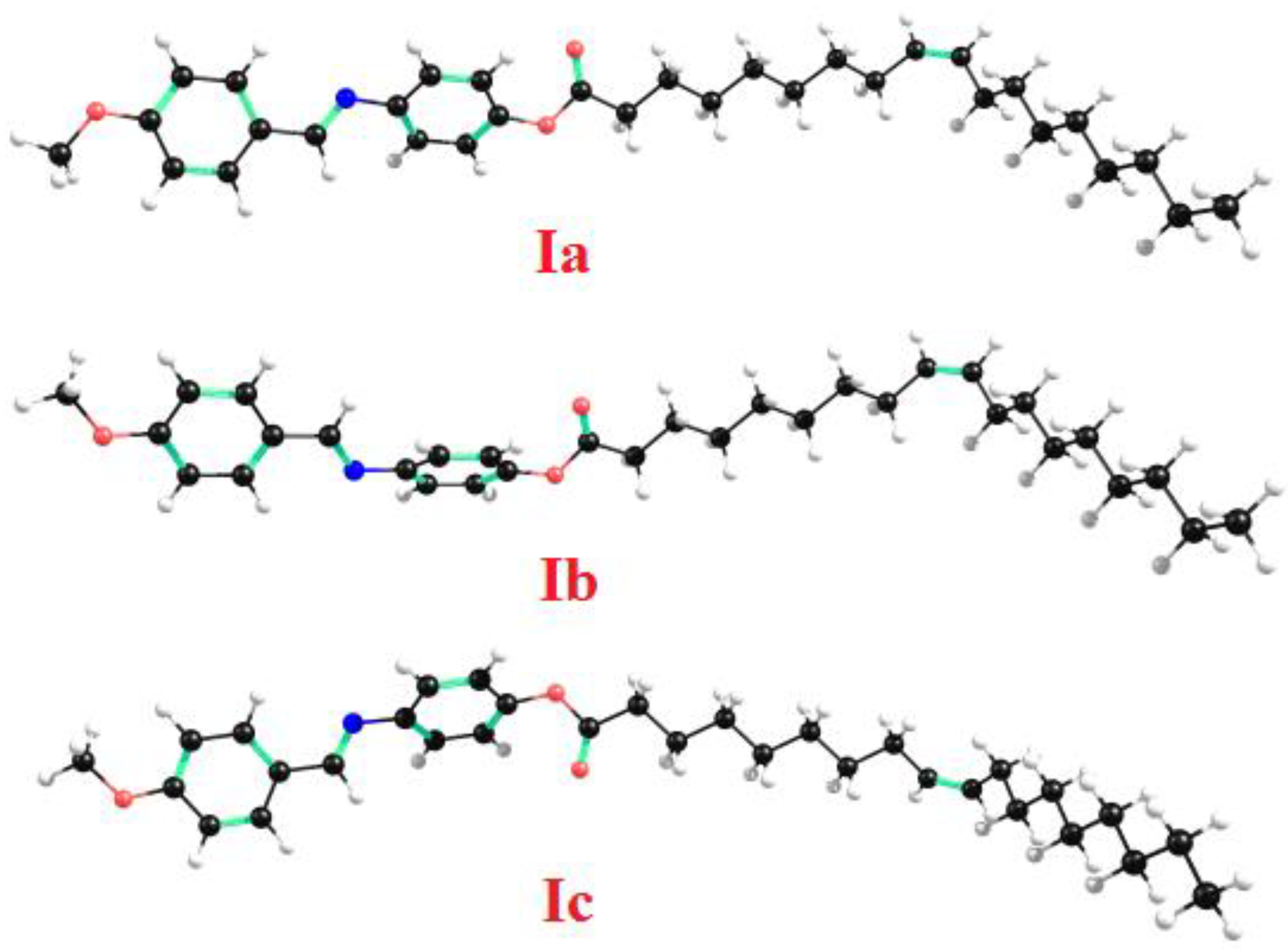
3.6.1. Molecular Geometry
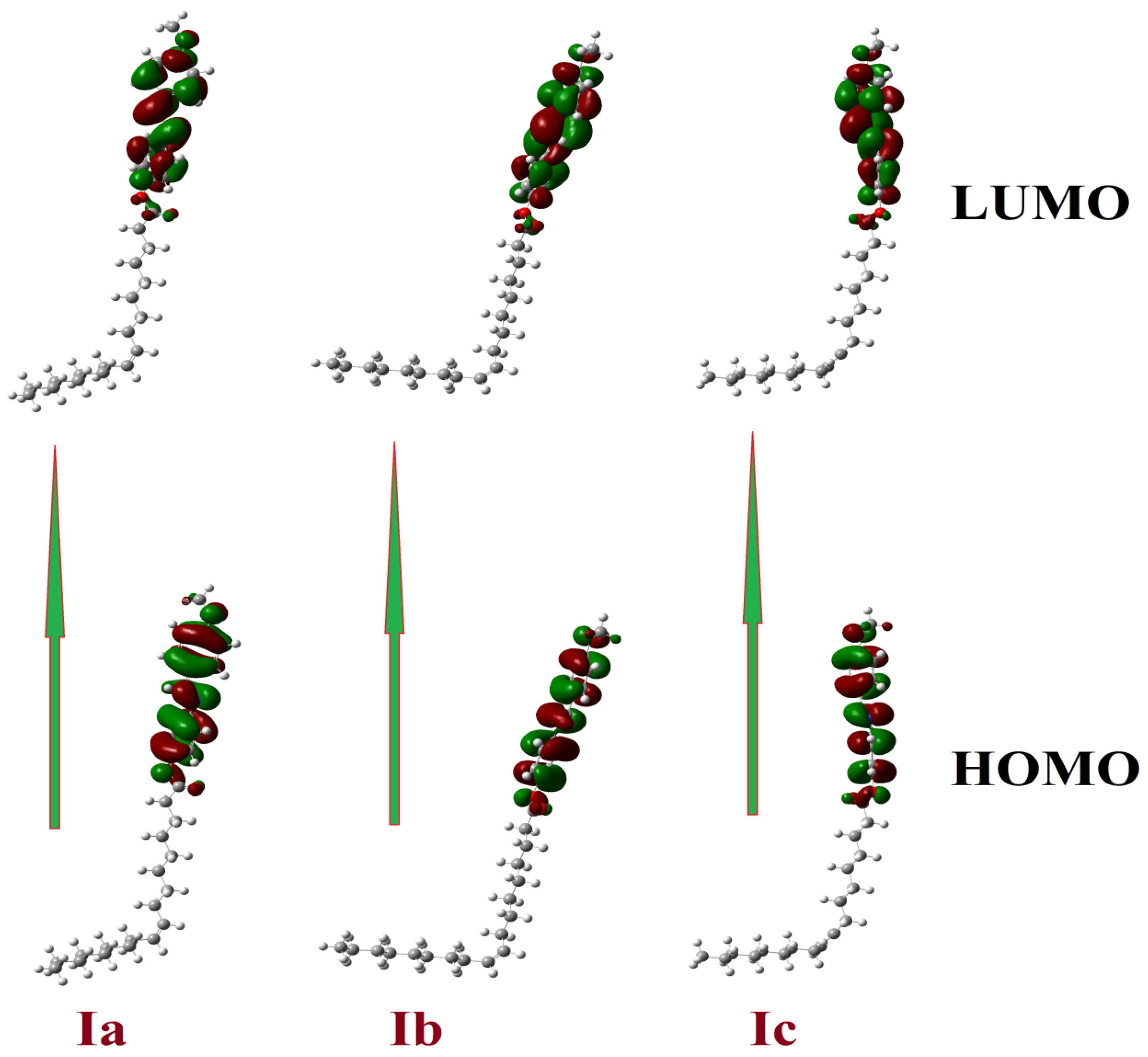
3.6.2. Frontier Molecular Orbitals (FMOs)
3.6.3. MEP Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Seredyuk, M.; Gaspar, A.B.; Ksenofontov, V.; Reiman, S.; Galyametdinov, Y.G.; Haase, W.; Rentschler, E.; Gütlich, P. Room Temperature Operational Thermochromic Liquid Crystals. Chem. Mater. 2006, 18, 2513–2519. [Google Scholar] [CrossRef]
- Hagar, M.; Ahmed, H.A.; Alhaddad, O.A. New azobenzene-based natural fatty acid liquid crystals with low melting point: Synthesis, DFT calculations and binary mixtures. Liq. Cryst. 2019, 46, 2223–2234. [Google Scholar] [CrossRef]
- Pramanik, A.; Das, M.K.; Das, B.; Żurowska, M.; Dąbrowski, R. Electro-optical properties of a new series of fluorinated antiferroelectric orthoconic liquid crystalline esters. Liq. Cryst. 2015, 42, 412–421. [Google Scholar] [CrossRef]
- Heilmeier, G.; Zanoni, L.; Barton, L. Dynamic scattering: A new electrooptic effect in certain classes of nematic liquid crystals. In Proceedings of the Proceedings of the IEEE; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 1968; Volume 56, pp. 1162–1171. [Google Scholar]
- Goodby, J. Ferroelectric Liquid Crystals. Principles, Properties and Applications; Ferroelectricity and related Phenomena Series; Gordon & Breach: London, UK, 1992; Volume 7, p. 496. [Google Scholar] [CrossRef]
- Carlton, R.J.; Hunter, J.T.; Miller, D.S.; Abbasi, R.; Mushenheim, P.C.; Na Tan, L.; Abbott, N.L. Chemical and biological sensing using liquid crystals. Liq. Cryst. Rev. 2013, 1, 29–51. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Cao, R.; Zhang, L.; Yang, X.; Liu, J.; Xu, M.; Shi, Z.; Hu, Z.; Zhong, W.; Xiao, G. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020, 30, 269–271. [Google Scholar] [CrossRef]
- Shvartsman, F.; Krongauz, V. Quasi-liquid crystals. Nat. Cell Biol. 1984, 309, 608–611. [Google Scholar] [CrossRef]
- Aleksandriiskii, V.V.; Novikov, I.V.; Kuvshinova, S.A.; Burmistrov, V.A.; Koifman, O.I. Dielectric, optical and orientational properties of liquid crystalline 4-alkyloxy-4′-cyanoazoxybenzenes and 4-alkyloxy-4′-cyanoazobenzenes. J. Mol. Liq. 2016, 223, 1270–1276. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; International Series of Monographs on Physics; Oxford Science Publication: Oxford, UK, 1993; Volume 83, ISBN 13 978-0198517856. [Google Scholar]
- Kumar, S. Liquid Crystals: Experimental Study of Physical Properties and Phase Transitions. Molecules 2001, 6, 1055–1056. [Google Scholar] [CrossRef] [Green Version]
- Priestly, E. Introduction to Liquid Crystals; Springer Science & Business Media: Princeton, UK, 2012. [Google Scholar]
- Ahmed, H.A.; Khushaim, M.S. Nematic Phase Induced from Symmetrical Supramolecular H-Bonded Systems Based on Flexible Acid Core. Crystals 2020, 10, 801. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Khushaim, M.S. Nematogenic Laterally Substituted Supramolecular H-Bonded Complexes Based on Flexible Core. Crystals 2020, 10, 878. [Google Scholar] [CrossRef]
- Al-Mutabagani, L.A.; Ahmed, H.A.; Hagar, M.; Alshabanah, L.A. Experimental and computational approaches of newly polymorphic supramolecular H-bonded liquid crystal complexes. Front. Chem. 2020, 8, 930. [Google Scholar] [CrossRef]
- Szulc, J.; Stolarz, Z. The Investigation of the Thermal Stability of Liquid Crystals. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1995, 263, 623–633. [Google Scholar] [CrossRef]
- Kelker, H.; Scheurle, B. Eine flüssig-kristalline (nematische) Phase mit besonders niedrigem Erstarrungspunkt. Angew. Chem. 1969, 81, 903–904. [Google Scholar] [CrossRef]
- Gray, G.W.; Vill, V.; Spiess, H.W.; Demus, D.; Goodby, J.W. Physical Properties of Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Raal, J.D. An Analysis of Conductive Heat Losses in a Flow Calorimeter for Heat Capacity Measurement. In Heat Capacities; Chapter 3; Royal Society of Chemistry (RSC): London, UK, 2010; pp. 41–53. [Google Scholar]
- Ogura, I. Low dielectric constant epoxy resins. In Handbook of Low and High Dielectric Constant Materials and Their Applications; Elsevier: Amsterdam, The Netherlands, 1999; Volume 1, pp. 213–240. [Google Scholar] [CrossRef]
- Yildiz, S.; Özbek, H.; Glorieux, C.; Thoen, J. Critical behaviour at the isotropic–nematic and nematic–smectic A phase transitions of 4-butyloxyphenyl 4′-decyloxybenzoate liquid crystal from refractive index data. Liq. Cryst. 2007, 34, 611–620. [Google Scholar] [CrossRef]
- Gramsbergen, E.F.; De Jeu, W.H. First- and second-order smectic-A to nematic phase transitions in p,p?-dialkylazoxybenzenes studied by birefringence. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1988, 84, 1015. [Google Scholar] [CrossRef]
- Nesrullajev, A. Texture transformations and thermo-optical properties of nematic mesogen at nematic–isotropic liquid phase transition. J. Mol. Liq. 2014, 196, 217–222. [Google Scholar] [CrossRef]
- Zaki, A. Optical measurements of mixture thermotropic liquid crystals. Opt. Lasers Eng. 2010, 48, 538–542. [Google Scholar] [CrossRef]
- El-Dessouki, T.A.; Roushdy, M.; Hendawy, N.I.; Naoum, M.M.; Zaki, A.A. Optical Measurements of Thermotropic Liquid Crystals. J. Mod. Phys. 2013, 4, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Zaki, A.A. Optical Measurements and Speckle Photography for Thermotropic Liquid Crystals Mixtures. J. Mod. Phys. 2013, 4, 517–521. [Google Scholar] [CrossRef] [Green Version]
- Yeap, G.-Y.; Hng, T.-C.; Yeap, S.-Y.; Gorecka, E.; Ito, M.M.; Ueno, K.; Okamoto, M.; Mahmood, W.A.K.; Imrie, C.T. Why do non-symmetric dimers intercalate? The synthesis and characterisation of the α-(4-benzylidene-substituted-aniline-4′-oxy)-ω-(2-methylbutyl-4′-(4″-phenyl)benzoateoxy)alkanes. Liq. Cryst. 2009, 36, 1431–1441. [Google Scholar] [CrossRef]
- Yeap, G.-Y.; Lee, H.-C.; Mahmood, W.A.K.; Imrie, C.T.; Takeuchi, D.; Osakada, K. Synthesis, thermal and optical behaviour of non-symmetric liquid crystal dimers α-(4-benzylidene-substituted-aniline-4′-oxy)-ω-[pentyl-4-(4′-phenyl)benzoateoxy]hexane. Phase Transit. 2011, 84, 29–37. [Google Scholar] [CrossRef]
- Yeap, G.-Y.; Osman, F.; Imrie, C.T. Non-symmetric dimers: Effects of varying the mesogenic linking unit and terminal substituent. Liq. Cryst. 2015, 42, 543–554. [Google Scholar] [CrossRef]
- Alnoman, R.; Al-Nazawi, F.K.; Ahmed, H.A.; Hagar, M. Synthesis, Optical, and Geometrical Approaches of New Natural Fatty Acids’ Esters/Schiff Base Liquid Crystals. Molecules 2019, 24, 4293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paterson, D.A.; Crawford, C.A.; Pociecha, D.; Walker, R.; Storey, J.M.; Gorecka, E.; Imrie, C.T. The role of a terminal chain in promoting the twist-bend nematic phase: The synthesis and characterisation of the 1-(4-cyanobiphenyl-4′-yl)-6-(4-alkyloxyanilinebenzylidene-4′-oxy)hexanes. Liq. Cryst. 2018, 45, 2341–2351. [Google Scholar] [CrossRef]
- Bhola, G.N.; Bhoya, U.C. Molecular structural flexibility dependence of mesomorphism through ortho-substituted bromo group. Mol. Cryst. Liq. Cryst. 2016, 630, 188–196. [Google Scholar] [CrossRef]
- Henderson, P.A.; Imrie, C.T. Methylene-linked liquid crystal dimers and the twist-bend nematic phase. Liq. Cryst. 2011, 38, 1407–1414. [Google Scholar] [CrossRef]
- Yeap, G.-Y.; Ha, S.-T.; Lim, P.-L.; Boey, P.-L.; Mahmood, W.A.K.; Ito, M.M.; Sanehisa, S. Synthesis and Mesomorphic properties of Schiff base esters Ortho-hydroxy-para-alkyloxybenzylidene-para-substituted anilines. Mol. Cryst. Liq. Cryst. 2004, 423, 73–84. [Google Scholar] [CrossRef]
- Vertogen, G.; De Jeu, W.H. Thermotropic Liquid Crystals, Fundamentals; Springer Science and Business Media LLC: Princeton, UK, 1988; Volume 45. [Google Scholar]
- Foo, K.-L.; Ha, S.-T.; Yeap, G.Y.; Lee, S.L. Mesomorphic behaviors of a series of heterocyclic thiophene-imine-ester-based liquid crystals. Phase Transit. 2018, 91, 509–520. [Google Scholar] [CrossRef]
- Yagai, S.; Kitamura, A. Recent advances in photoresponsive supramolecular self-assemblies. Chem. Soc. Rev. 2008, 37, 1520–1529. [Google Scholar] [CrossRef]
- Hagar, M.; Ahmed, H.; El-Sayed, T.; Alnoman, R. Mesophase behavior and DFT conformational analysis of new symmetrical diester chalcone liquid crystals. J. Mol. Liq. 2019, 285, 96–105. [Google Scholar] [CrossRef]
- Knapkiewicz, M.; Rachocki, A.; Bielejewski, M.; Sebastião, P.J. NMR studies of molecular ordering and molecular dynamics in a chiral liquid crystal with the Sm C α* phase. Phys. Rev. 2020, 101, 052708. [Google Scholar]
- Roy, M.; Jennings, P.A. Real-time NMR Kinetic Studies Provide Global and Residue-specific Information on the Non-cooperative Unfolding of the β-Trefoil Protein, Interleukin-1β. J. Mol. Biol. 2003, 328, 693–703. [Google Scholar] [CrossRef]
- Hagar, M.; Soliman, S.M.; Ibid, F.; El Ashry, E.S.H. Quinazolin-4-yl-sulfanylacetyl-hydrazone derivatives; Synthesis, molecular structure and electronic properties. J. Mol. Struct. 2013, 1049, 177–188. [Google Scholar] [CrossRef]
- Gordon, M.S.; Sojka, S.A.; Krause, J.G. Carbon-13 NMR of para-substituted hydrazones, phenylhydrazones, oximes, and oxime methyl ethers: Substituent effects on the iminyl carbon. J. Org. Chem. 1984, 49, 97–100. [Google Scholar] [CrossRef]
- Paterson, D.A.; Abberley, J.P.; Harrison, W.T.; Storey, J.M.; Imrie, C.T. Cyanobiphenyl-based liquid crystal dimers and the twist-bend nematic phase. Liq. Cryst. 2017, 44, 1–20. [Google Scholar] [CrossRef]
- Meredith, G.R.; VanDusen, J.; Williams, D.J. Optical and nonlinear optical characterization of molecularly doped thermotropic liquid crystalline polymers. Macromolecules 1982, 15, 1385–1389. [Google Scholar] [CrossRef]
- Iam-Choon, K.; Shin-Tson, W. Optics and Nonlinear Optics of Liquid Crystals; World Scientific: Philadelphia, PA, USA, 1993; Volume 1. [Google Scholar]
- Imrie, C.T.; Karasz, F.E.; Attard, G.S. Comparison of the mesogenic properties of monomeric, dimeric, and side-chain polymeric liquid crystals. Macromolecules 1993, 26, 545–550. [Google Scholar] [CrossRef]
- Donaldson, T.; Staesche, H.; Lu, Z.; Henderson, P.A.; Achard, M.; Imrie, C.T. Symmetric and non-symmetric chiral liquid crystal dimers. Liq. Cryst. 2010, 37, 1097–1110. [Google Scholar] [CrossRef]
- Henderson, P.A.; Niemeyer, O.; Imrie, C.T. Methylene-linked liquid crystal dimers. Liq. Cryst. 2001, 28, 463–472. [Google Scholar] [CrossRef]
- Sastry, S.S.; Rao, B.G.S.; Mallika, K.; Kumari, T.V.; Lakshminarayana, S.; Ha, S.T. Novel method for order parameter of ferroelectric liquid crystals by image analysis. Liq. Cryst. 2013, 40, 384–390. [Google Scholar] [CrossRef]
- Patari, S.; Chakraborty, S.; Nath, A. The optical anisotropy and orientational order parameter of two mesogens having slightly different flexible side chain—A comparative study. Liq. Cryst. 2016, 43, 1017–1027. [Google Scholar] [CrossRef]
- Sastry, S.S.; Kumari, T.V.; Mallika, K.; Rao, B.G.S.; Ha, S.-T.; Lakshminarayana, S. Order parameter studies on EPAP alkanoate mesogens. Liq. Cryst. 2012, 39, 295–301. [Google Scholar] [CrossRef]
- Kumar, A. Determination of orientational order and effective geometry parameter from refractive indices of some nematics. Liq. Cryst. 2013, 40, 503–510. [Google Scholar] [CrossRef]
- Wu, S.-T.; Hsu, C.-S.; Shyu, K.-F. High birefringence and wide nematic range bis-tolane liquid crystals. Appl. Phys. Lett. 1999, 74, 344–346. [Google Scholar] [CrossRef] [Green Version]
- Haller, I. Thermodynamic and static properties of liquid crystals. Prog. Solid State Chem. 1975, 10, 103–118. [Google Scholar] [CrossRef]
- Erkan, S.; Çetinkaya, M.C.; Yildiz, S.; Özbek, H.; Yıldız, S. Critical behavior of a nonpolar smectogen from high-resolution birefringence measurements. Phys. Rev. E 2012, 86, 041705. [Google Scholar] [CrossRef]
- Zaki, A.A.; Ahmed, H.; Hagar, M. Impact of fluorine orientation on the optical properties of difluorophenylazophenyl benzoates liquid crystal. Mater. Chem. Phys. 2018, 216, 316–324. [Google Scholar] [CrossRef]
- Zaki, A.A. Optical measurements of phase transitions in difluorophenylazophenyl benzoate thermotropic liquid crystal with specific orientated fluorine atoms. Phase Transit. 2018, 92, 135–148. [Google Scholar] [CrossRef]
- Uchida, E.; Kawatsuki, N. Photoinduced Orientation in Photoreactive Hydrogen-Bonding Liquid Crystalline Polymers and Liquid Crystal Alignment on the Resultant Films. Macromolecules 2006, 39, 9357–9364. [Google Scholar] [CrossRef]
- Sabirov, L.; Semenov, D. Induced birefringence in the isotropic phase of cholesteric liquid crystals. Opt. Spectrosc. 2006, 101, 299–302. [Google Scholar] [CrossRef]
- Domján, L.; Koppa, P.; Szarvas, G.; Reményi, J. Ternary phase-amplitude modulation with twisted nematic liquid crystal displays for Fourier-plane light homogenization in holographic data storage. Optik 2002, 113, 382–390. [Google Scholar] [CrossRef]
- Tsutsumi, O.; Ikeda, T. Photochemical modulation of alignment of liquid crystals and photonic applications. Curr. Opin. Solid State Mater. Sci. 2002, 6, 563–568. [Google Scholar] [CrossRef]
- Muniandy, S.; Kan, C.; Lim, S.; Radiman, S. Fractal analysis of lyotropic lamellar liquid crystal textures. Phys. A Stat. Mech. Its Appl. 2003, 323, 107–123. [Google Scholar] [CrossRef]
- Pluta, M.; Bisbing, R.E. Advanced Light Microscopy, Vol. 3: Measuring Techniques. Phys. Today 1995, 48, 56. [Google Scholar] [CrossRef]
- Sochacka, M.; Staronski, L.R. Phase-Stepping DIC Technique for Reflecting Surface Evaluation. In Phase Contrast and Differential Interference Contrast Imaging Techniques and Applications; International Society for Optics and Photonics: Scotland, UK, 1994; pp. 222–233. [Google Scholar]
- Born, M.; Wolf, E.; Hecht, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Phys. Today 2000, 53, 77–78. [Google Scholar] [CrossRef] [Green Version]
- Pluta, M. Simplified polanret system for microscopy. Appl. Opt. 1989, 28, 1453. [Google Scholar] [CrossRef]
- Thingujam, K.; Alapati, P.R.; Choudhury, B.; Bhattacharjee, A. Optical studies of a liquid crystalline compound 6O.6. Liq. Cryst. 2013, 40, 810–816. [Google Scholar] [CrossRef]
- Ramakrishna, M.; Rao, N.; Prasad, P.V.D.; Pisipati, V.G.K.M. Orientational Order Parameter in Alkoxy Benzoic Acids—Optical Studies. Mol. Cryst. Liq. Cryst. 2010, 528, 49–63. [Google Scholar] [CrossRef]
- Prasad, P.V.D.; Pisipati, V.G.K.M. Simple, Accurate and Low Cost Optical Techniques for the Measurement of 1. Birefringence in Liquid Crystals and 2. Variation of the Angle of the Small Angled Prism with Temperature. Mol. Cryst. Liq. Cryst. 2009, 511, 102–111. [Google Scholar] [CrossRef]
- Manohar, R.; Shukla, J. Refractive indices, order parameter and principal polarizability of cholesteric liquid crystals and their homogeneous mixtures. J. Phys. Chem. Solids 2004, 65, 1643–1650. [Google Scholar] [CrossRef]
- Vuks, M. Electrical and Optical Properties of Molecules and Condensed Matter; Leningrad Univ. Publ.: Leningrad, Russia, 1984. [Google Scholar]





| Heating Process | TCr-SmA | ΔHCr-SmA | TSmA-I | ΔHSmA-I | ΔSSmA-I/R |
|---|---|---|---|---|---|
| 41.9 | 35.78 | 62 | 2.98 | 1.07 | |
| Cooling Process | TI-SmA | ΔHI-SmA | TSmA-Cr | ΔHSmA-Cr | ΔSI-SmA/R |
| 60 | 2.41 | 33.5 | 31.9 | 0.87 |
| Sample | ∆n (MS) | ∆n (Abbe Refractometer) | ∆n (Interferometric) | ∆no | β |
|---|---|---|---|---|---|
| I | 0.018 ± 0.005 | 0.017 ± 0.005 | 0.022 ± 0.005 | 0.031 ± 0.005 | 0.01 |
| Parameter | Ia | Ib | Ic | |
|---|---|---|---|---|
| Dimensions Å | Width (D) | 33.0 | 32.0 | 32.0 |
| Length (L) | 13.1 | 13.4 | 13.2 | |
| Aspect ratio (L/D) | 2.5 | 2.4 | 2.4 | |
| Twist angle (Degree) | 49.1 | 48.5 | 55.4 | |
| Dipole moment, (Debye) | 3.4804 | 3.9182 | 2.1570 | |
| Polarizability, (Bohr3) | 427.12 | 425.09 | 402.11 | |
| Parameter | Ia | Ib | Ic |
|---|---|---|---|
| Ecorr | 0.706 | 0.706 | 0.710 |
| ZPVE | −1526.629 | −1526.630 | −1526.295 |
| Etot | −1526.589 | −1526.590 | −1526.255 |
| H | −1526.588 | −1526.589 | −1526.254 |
| G | −1526.713 | −1526.714 | −1526.378 |
| ΔE (Kcal/mole) | 0.3 | 0.0 | 209.8 |
| Parameter | Ia | Ia | Ic |
|---|---|---|---|
| ELUMO | −0.05920 | −0.05897 | −0.05128 |
| EHOMO | −0.21328 | −0.21342 | −0.20452 |
| ΔEHOMO-LUMO | 0.154 | 0.154 | 0.153 |
| S Softness | 6.490 | 6.475 | 6.526 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaki, A.A.; Hagar, M.; Alnoman, R.B.; Jaremko, M.; Emwas, A.-H.; Ahmed, H.A. Mesomorphic, Optical and DFT Aspects of Near to Room-Temperature Calamitic Liquid Crystal. Crystals 2020, 10, 1044. https://doi.org/10.3390/cryst10111044
Zaki AA, Hagar M, Alnoman RB, Jaremko M, Emwas A-H, Ahmed HA. Mesomorphic, Optical and DFT Aspects of Near to Room-Temperature Calamitic Liquid Crystal. Crystals. 2020; 10(11):1044. https://doi.org/10.3390/cryst10111044
Chicago/Turabian StyleZaki, Ayman A., Mohamed Hagar, Rua B. Alnoman, Mariusz Jaremko, Abdul-Hamid Emwas, and Hoda A. Ahmed. 2020. "Mesomorphic, Optical and DFT Aspects of Near to Room-Temperature Calamitic Liquid Crystal" Crystals 10, no. 11: 1044. https://doi.org/10.3390/cryst10111044
APA StyleZaki, A. A., Hagar, M., Alnoman, R. B., Jaremko, M., Emwas, A.-H., & Ahmed, H. A. (2020). Mesomorphic, Optical and DFT Aspects of Near to Room-Temperature Calamitic Liquid Crystal. Crystals, 10(11), 1044. https://doi.org/10.3390/cryst10111044