Lithium Niobate Single Crystals and Powders Reviewed—Part II
Abstract
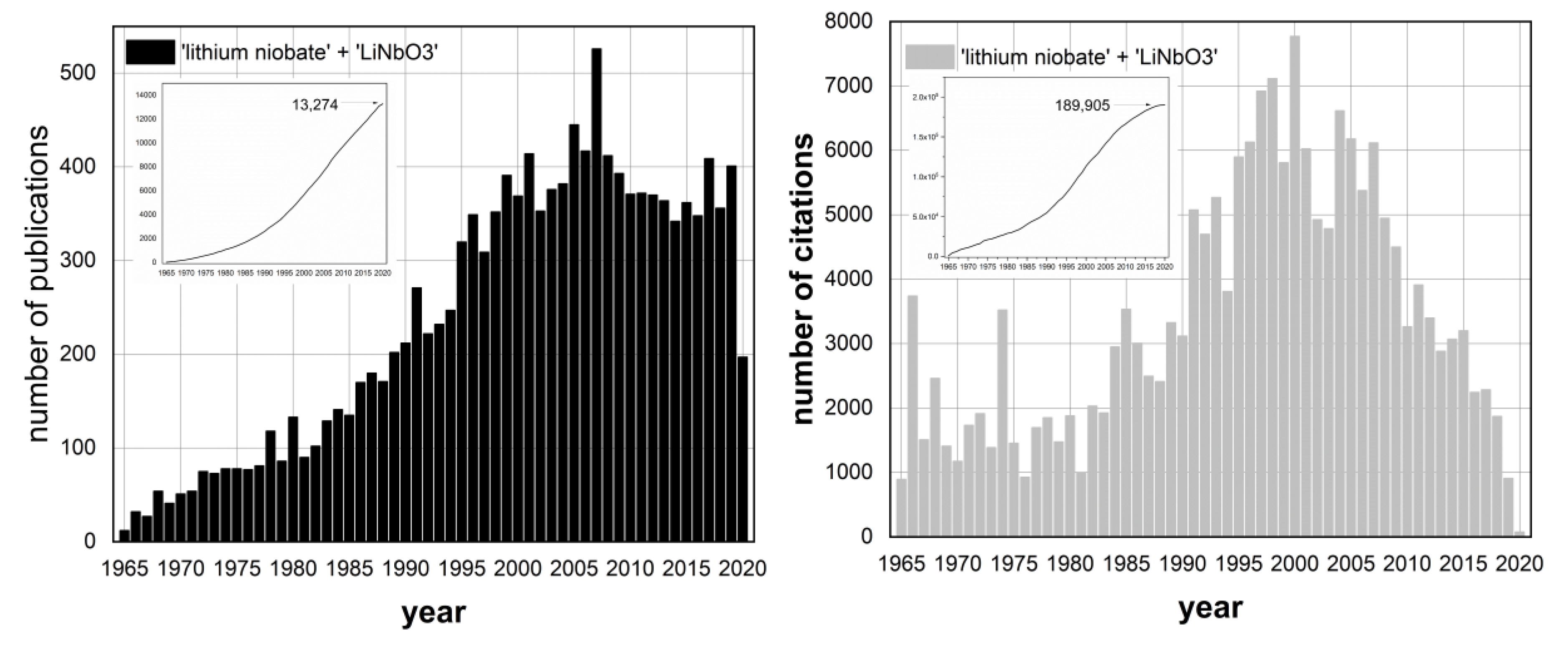
1. Introduction
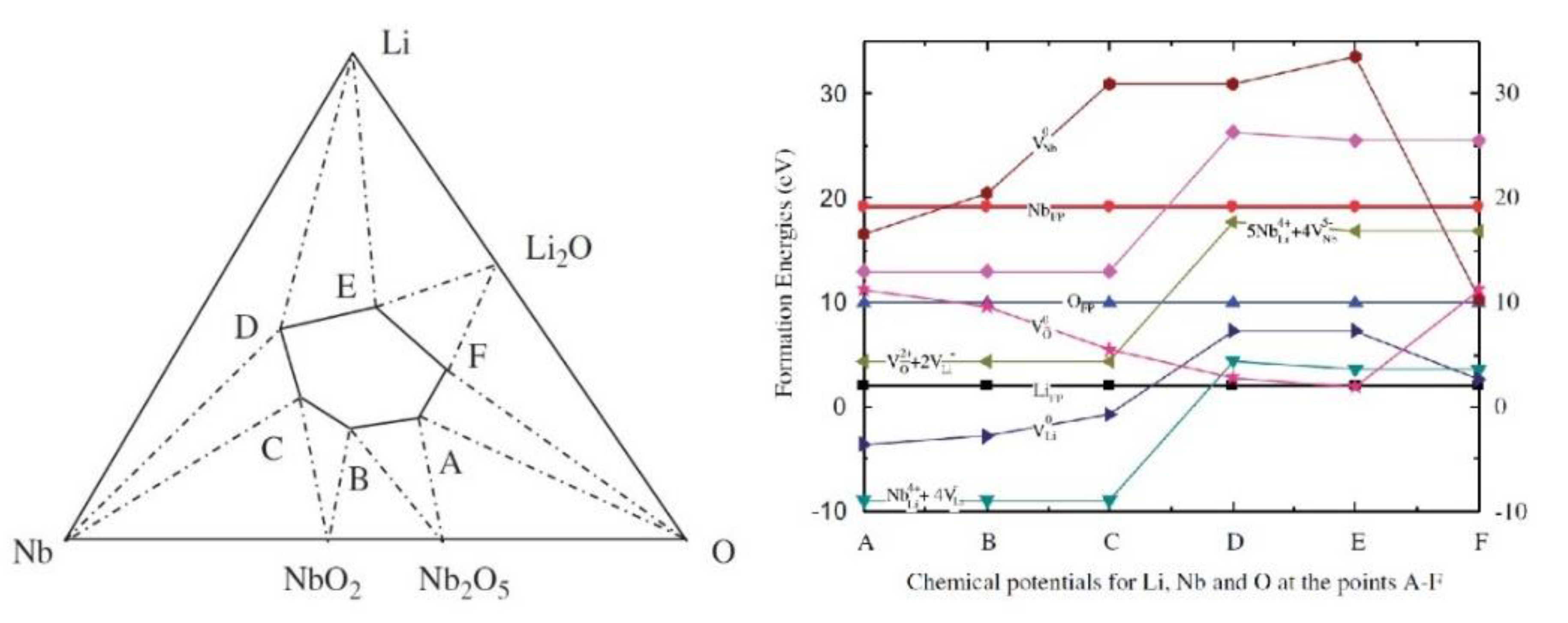
2. Intrinsic Defects
3. Extrinsic Defects
- (1)
- Since 1973, a well-known spectral characteristic of the IR absorption of undoped LN is dichroism. In other words, optical absorption is prominently measured for a given linear polarization state of the incident light, which results in being perpendicular to the polar c-axis of the crystal [127]. It was concluded that the O–H dipole vibration essentially lies in the oxygen plane perpendicular to that axis. On a recent theoretical approach, it has been shown that, in ST crystals, the stretch mode is “tilted weakly out of the oxygen plane by about 4.3°” [50].
- Polarized Raman Spectroscopy of CG LN shows a very low local symmetry of OH− related defect, assigned to point group C1 [128].
- There is a tendency of increasing tilting angle (between the O–H stretch vibration and the oxygen plane) as the valence of the ODRI in doped crystals (above their respective threshold concentration) decreases [94]. As shown in Figure 6 (left side), for Mg2+, the effect is pronounced with an angle of roughly 15°.
- (2)
- For ODRI doping, the threshold concentration is the critical value in mol% describing the amount of incorporated ion into the crystal and “above which the optical damage drastically falls off by more than two orders of magnitude” [10]. It fundamentally depends on the stoichiometry of the crystal and in the valence state of the dopant: as a rule of thumb, less dopant is needed for the obtention of an optical-damage-resistant (ODR) crystal for higher valences (n+ < 5+). Independently of the dopant, it is less than 1 mol% for a near-ST composition. On the other hand, in a congruent crystal, it is roughly (5, 4, 2) mol% for a (di-, tri-, tetra-) valent ODRI [8].
- According to proposed models on the defect structure of LN:Mg, it is usually assumed that the Mg ions compete for Li sites with antisite NbLi ions up to the threshold concentration where all Nb antisites are eliminated [29,132,133]. Hence, regarding ODRI in general, the concentration threshold is also defined as the physical instance in which all NbLi antisites have been replaced by the doping ions, which above the threshold keep replacing regular Li sites and start to replace Nb sites.
- The threshold concentration for Mg can be calculated in mol% units, by use of Equation (1) [132]:x is the same parameter used to describe the chemical composition of undoped LN, the formula (Li2O)50−x(Nb2O5)50+x. Such extension of the x-values to define the [Li]/[Nb] ratio in LN:Mg comes from the lack of a direct method for this purpose, and it assumes that not only this ratio is equal in the melts but also the growing conditions of both crystals, undoped and Mg-doped [8,134]. Precautions must be taken on the ambiguity regarding reported concentration values and their dependence on properties due to the existence of two ways in specifying the impurity content (distinct chemical formulas), as noted by Donnerberg [135].
- LN:Mg has been extensively studied, and similar to undoped LN, there exist various alternatives to determine the dopant concentration (cMg mol%) using linear relationships with a corresponding measured parameter related to a specific experimental technique: IR absorption (OH− vibrational spectroscopy), UV absorption edge, or polarized Raman spectroscopy. The results obtained using these three techniques are consistent for a given crystal; the equations can be consulted in Refs. [8,134,136]. Qualitative results on the effect of cMg on the PR effect presented by the crystals also have been studied through the z-scan method, a standard method often used to assess (quantitatively) third-order optical nonlinearities [137,138].
- (3)
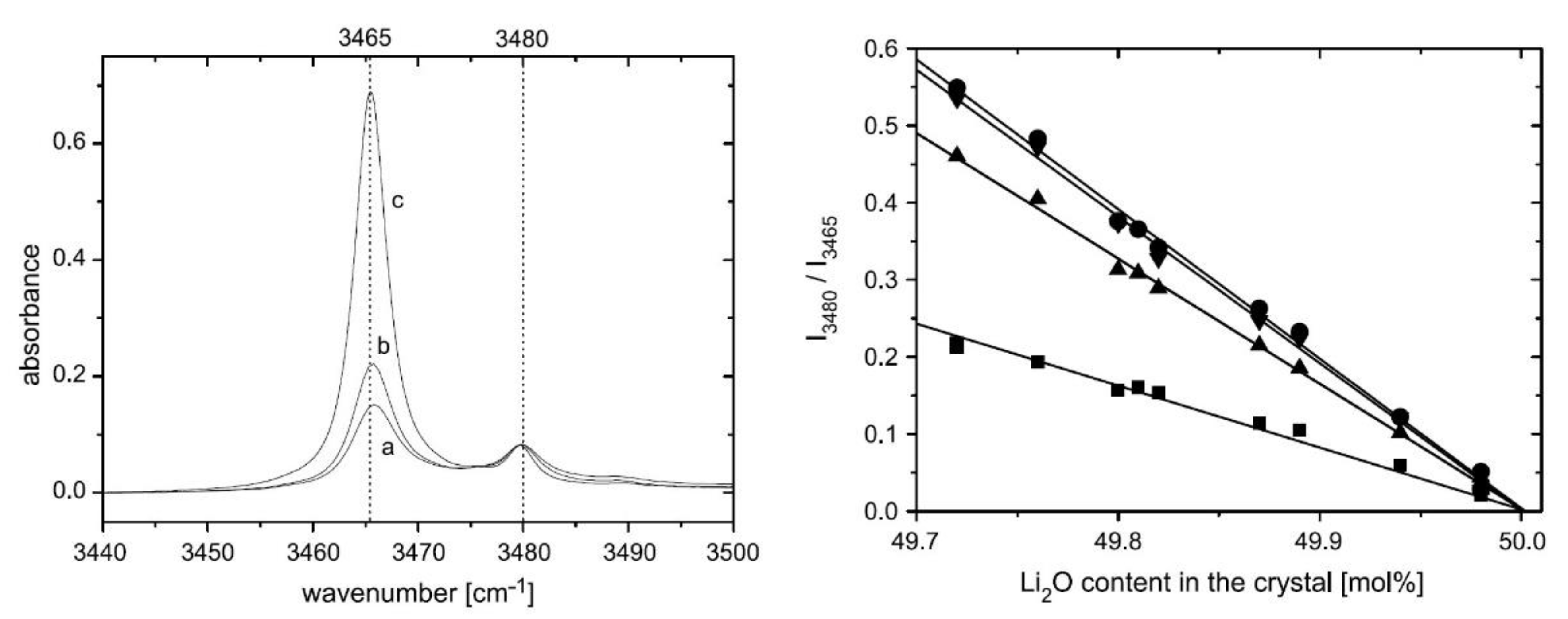
- Regarding other spectral characteristics of the IR absorption, the band components tend to narrow, and the amplitudes of those of higher frequency approach zero as the Li content increases in the crystal (see Figure 5). This tendency culminates at the stoichiometric (ST) point, characterized by a single-mode located at 3465 cm−1 with a Full Width at Half Maximum (FWHM) about equal to 3 cm−1 at room temperature (RT) [93]:
- In doped crystals with ODRI and below the threshold concentration, the IR absorption spectra are essentially the same as undoped crystals: the peak position appears near the 3465 cm−1, and no new OH− bands are detected. In the case of Mg, only the linewidth of the band is affected, decreasing while the doping concentration increases [139].
- Above the threshold, the dopant ions start to occupy regular Nb sites, “opening the way for the formation of –OH− type complexes resulting in new absorption bands in the infrared spectral range” [94]. These bands are well separated from that of the undoped ST crystal (3465 cm−1) and always are of higher frequency, as shown in the center and the right side of Figure 6. Their linewidths are narrower than the OH− of undoped and congruent LN (cLN), for all ODRI doping cases. These characteristics resemble undoped and stoichiometric LN (sLN) so that the existence of different classes of sLN crystals might be postulated. In this regime of concentrations, the intensity ratio between the new and the 3465 cm−1 band increases with the dopant amount [94,140].
- According to a recent investigation (2017), the IR absorption bands of the lanthanide trivalent rare earth Er3+, Nd3+, Yd3+ feature similar characteristics to those of the trivalent ODRI (Sc and In), including the tilting angle out of the oxygen plane, which is around 8° [73]. More recently (2019), similar conclusions have been obtained for transition metal ions Fe3+, Cr3+, and Ti4+ [5].
- Thus, based on these substantial and systematic studies by Kovács et al. [5,73,94], it appears to be that all type of ions follow a generalized trend regarding the substitution mechanisms in doped LN, where the dominant factor is the valence state of the dopant. Even a partial solution to the configuration or distribution of the extrinsic defects (a model of extrinsic defect clusters) is acknowledged locally in the surroundings of a hydroxyl ion. As stated by Kovács et al., “only a small proportion of the incorporated dopants are involved in the type defect complexes while the others are assumed to occupy either Li or Nb sites,” due to significant less concentration of OH− ions compared to that of the dopant [5].
- (4)
- Any given chemical composition, “the bandwidths, peak positions and intensities of different components are almost temperature-independent within the range of liquid-helium temperature to RT. Above RT, the maximum of some bands increase, and those of other bands decrease; the integrated intensity (i.e., the total amount of hydrogen) remains constant up to 200–250 °C” [87]. Conversely, they change slowly with time on a scale of 10 h; an equilibrium state of the OH− vibrational spectra is reached only after some years [141,142]:
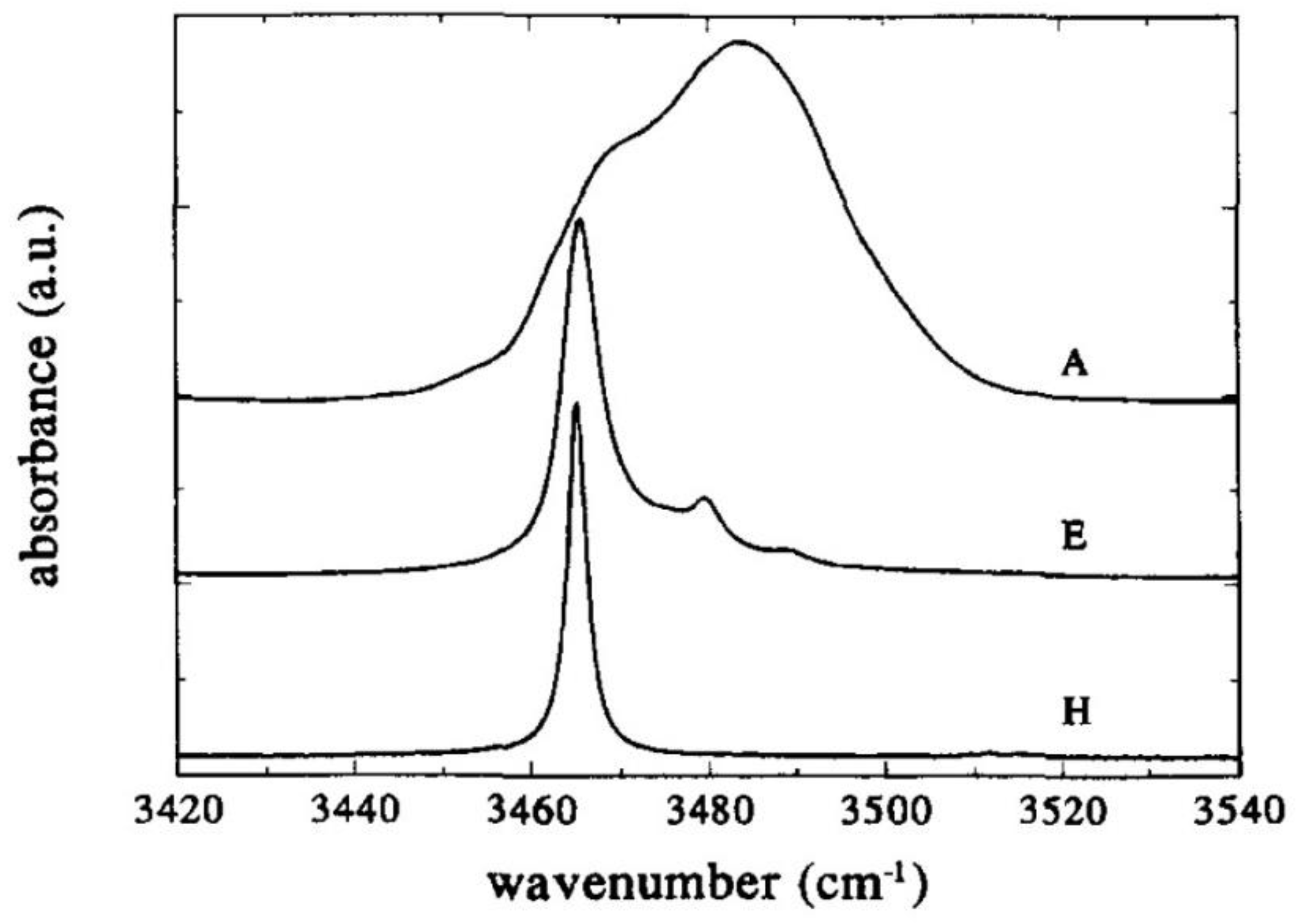
- The time-varying characteristic of the spectra is accounted for by a non-equilibrium distribution of the ocuppancy of the hydroxyl ions over four nonequivalent positions [10,88,143]. Accordingly, the broad OH band should be resolved into at least four overlapping components corresponding to different O–H bonds. In near-ST crystals, up to five distinct Lorentzian components have been resolved (Figure 7): 3466, 3470, 3481, 3490, and 3499 cm−1 [143]. Significantly, with time, the intensities of those in italics increase at the expense of those in bold (slight differences in the numerical assignments scattered throughout the literature), the integrated intensity being essentially unchanged [10].
- The chemical composition of an undoped crystal can be assessed with an absolute accuracy of 0.01 mol%, using the estimation of the Li content cLi in terms of this ratio measured at RT and at a time t after its growth (in units of months) [8]:
- (5)
- Recent advances in OH− Vibrational Spectroscopy have led to a detailed RT study on the dynamics of strongly localized and ultrashort-living lattice distortions in the neighborhood of an O–H dipole. A novel achievement is the reconstruction of the electrostatic potential change in the oxygen plane of LN, based on the local polaronic distortion correlated to a pump-induced (scale of femtoseconds) –3 cm−1 shift of the frequency of the OH− stretch vibration [144].
- This result stands for the first visualization of the important observation made about 15 years earlier (2000–2006, mainly by two German groups) on the antisite being a shallow electron trap, based on transient absorption of LN:Fe crystals induced by ultrashort-pulsed green illumination [145,146,147,148]. By use of λ = 388 nm light with 240 fs pulse duration in undoped CG crystal, Beyer et al. estimated the formation of the small polarons or centers in less than 400 fs [148].
- (6)
- “The basic advantage of choosing higher valence ODR dopants comes from their lower damage threshold concentrations; lower built-in dopant content facilitates the growth of more homogeneous crystals resulting in the high-quality sample for device applications” [8]. Recently, research efforts on LN:Zr4+ have been intensified for various practical reasons, which make it an optimal choice for applications at RT:
- Low doping concentration and high optical-damage resistance: a concentration threshold of 2.0 mol% ZrO2 holds for cLN:Zr [6,149], whereas 0.1 mol% in near- sLN:Zr [140], compared to those of 5 mol% and 0.2 mol% for MgO, respectively [46]. A crystal doped with 2 mol% ZrO2 can withstand a light intensity (λ = 514.5 nm) about 40 times higher (around 20 MW cm−2) than a 6.5 mol% MgO doped crystal [6]. Apropos, only a near- sLN:Mg crystal (1 mol% Mg), competes with the former, withstanding close to 26 MW cm−2 at λ = 488 nm [150]; the obtention of this crystal involves an expensive yet unpractical vapor-transport-equilibria process at 1000 °C for about 120 h. It has recently been demonstrated that near-ST LN:Zr crystals can be illuminated with 80 GW cm−2 of pulsed 10 ns green light without optical breakdown [151].
- Segregation and distribution coefficient: The segregation between solvent and solute and the distribution of dopants between Li and Nb sites influence the incorporation of ODRI into flux-grown LN crystals, the quality (i.e., homogeneity) of the latter per se. Segregation is a severe problem even for the growth of pure or undoped LN crystals since the CG and ST compositions do not coincide. It remains in melt systems for the obtention of ODRI-based compositions, causing the scattering in values of the distribution coefficient (Keff) from unity, except perhaps for the case of Li2O–Nb2O5–ZrO2. Most ODRI are characterized by Keff falling in the range 1.2–1.3 for the low concentration regime [10]. At higher concentrations, they decrease close to 1 for MgO [133] and ZnO [152] in the range 5–6 mol%, and to about 0.9 for In2O3 in the range 1.5–2 mol% [153]. In contrast, Keff ≈ 1 for LN:Zr4+, independently of the concentration range of 1–5 mol% ZrO2 [149]. In addition, “it should be noted that in crystals prepared for device applications, ODR dopant concentrations slightly above the critical threshold are preferred to suppress the formation of unwanted microdomains” [8].
- (7)
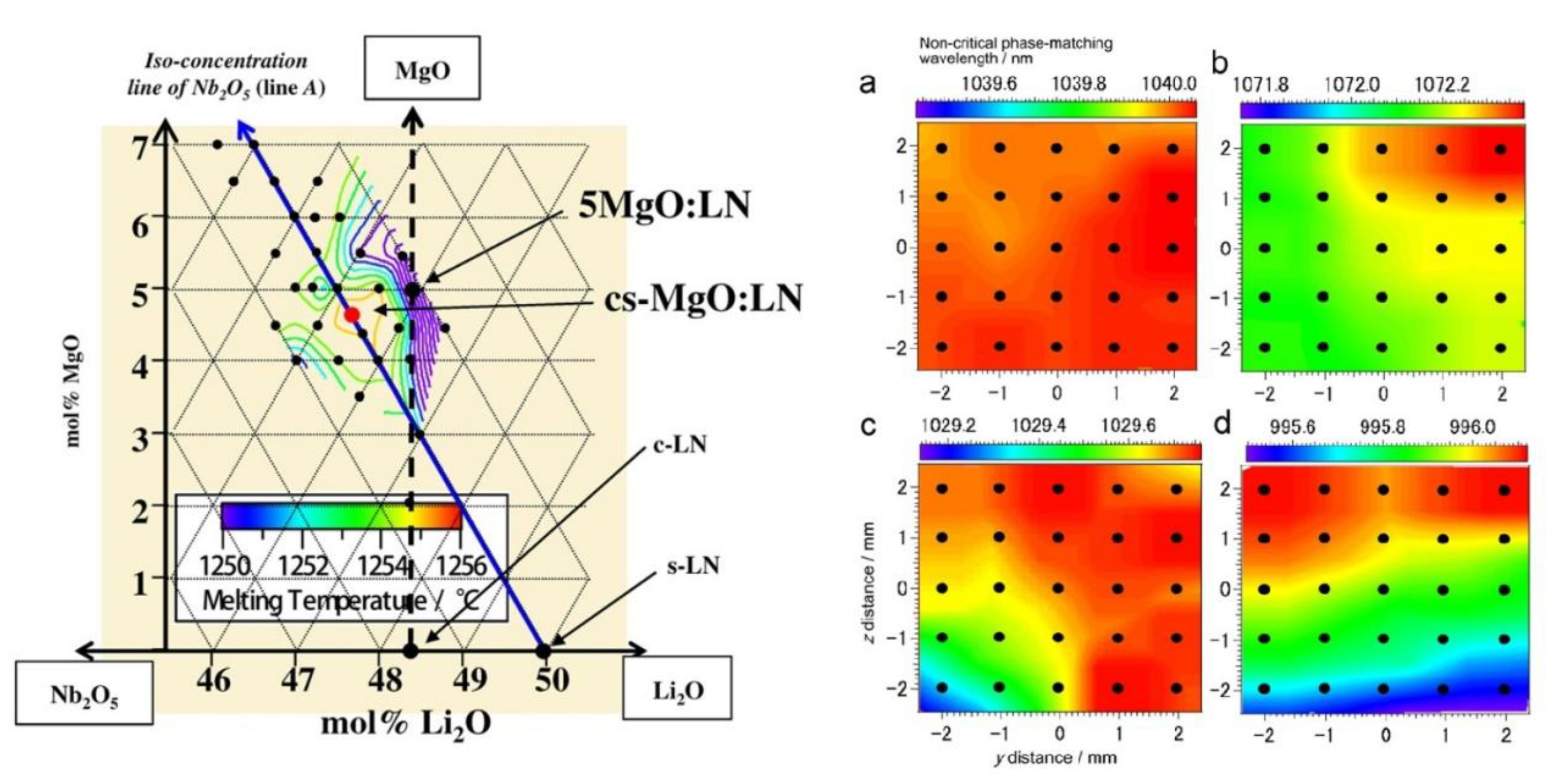
- Recently, a Japanese group reported the novel result of overcoming segregation in the pseudo-ternary system Li2O–Nb2O5–MgO using in melt compositions 45.30:50.00:4.70, respectively [161,162]. As shown in Figure 9 (left side), the CG and ST compositions coincide with the obtained single crystal. For this reason, it has been labeled as ‘cs-MgO:LN’. Because of a higher compositional homogeneity, its optical properties are expected to be superior to those featured by CG, ST, and LN:Mg. Indeed, optical second harmonic generation (SHG) measurements show comparable conversion efficiencies and a more uniform in-plane distribution of the non-critical phase-matching wavelength (right side of Figure 9) [162]. Its ODR, however, has been elsewhere stated to be inferior to that of cLN:Mg—5 mol% [6].
- (8)
- Upon elemental doping with different ions, several defect-related structures and possible charge misfits are compensated by the formation of suitable intrinsic defect complexes. Given the similarity of the octahedral surroundings at the Li and Nb sites, one of the most challenging questions to answer since earlier studies in this field is the dopant-site occupancy, whether a given doped-ion substitutes Li or Nb or both. No consensus exists on these grounds. Depending on the classification of the dopants (ODRI, PR-active, or laser activation, i.e., lanthanides), among other factors, different trends on site occupancy and doping mechanisms (the dynamics) can be stated. As of today, and in general terms, that is in what respects for all kinds of impurity ions and independently of their charge state, a strong statement, say undisputable, is that dopants are “localized dominantly on the Li sites” [10]. It has been qualitatively explained according to the larger dimension of the Li octahedra respect to Nb one [163,164]. According to a recent review by Kang et al. (and references therein), the dopant concentration, ionic radii, and valence states are among the most influential factors [7]. In general:
- The valence state induces priority substitution: a +2 valence dopant substitutes Li+ ions, whereas one with a valence state greater or equal to +5 replaces Nb+5 ions. No explicit priority substitution can be noticed for dopants of valence +3 and +4 [165].
- Longer (smaller or equal) dopant–O bonds than the mean length of the Nb–O bond reflects occupancy at the Li (either Li or Nb) site; a small shift from the regular Li site takes place if the bond is also longer than the mean length of the Li–O bond [163].
- Low (high) doping concentrations occupy Li or (and) Nb sites.
- The doping process has also been shown to influence the site occupancy. Recently, it was found that the OH− vibration spectra are significantly different for two LN:Cr3+ crystals sharing the same dopant concentration (0.5 mol%) but obtained by two distinct growth techniques, thus implying different substitution mechanisms; the IR absorption spectral characteristics of one crystal shows the fingerprint of a heavily doped crystal while those of the other do not [5]. A similar observation has been made for Cu2+ doping [11], although it is not well supported by the bulk of the literature: copper is normally assumed to enter a Li site, irrespective of the charge state [8,115].
- (9)
- The central role of ODRI is to vary the amount of Nb antisites in the crystal. Extensive studies by several experimental methods and model calculations have been motivated by explaining the microscopic origin of the threshold concentrations in ODRI. In other words, the incorporation mechanisms of the dopants and their influence on the threshold values. Among others, a striking result from such is that Mg and Zn at relatively low concentration values may be regarded as controllers of the intrinsic defects NbLi and VLi contents, so their effect is qualitatively analogous a Li enrichment [10].
- Although still being debated, the current most accepted description on the microscopic origin threshold concentrations for ODRI is that its existence is associated with partial incorporation of the dopants onto regular NbNb sites. In contrast, below these critical values, the incorporation mechanism is described by applying a simultaneous substitution of NbLi antisites and regular LiLi sites by the dopants. This framework is constructed upon results reported for Mg2+ [17,132,135,166,167]. The same conclusions were obtained for later detailed structure studies with X-ray and neutron diffraction on LN:Zn [168,169,170]. Of course, this discussion holds for Li-deficient LN-doped crystals (congruent). As the crystal composition is closer to the ST one, less NbLi antisites will be available, so that the incorporation will be split mainly into regular Li and Nb sites. It explains that significantly less dopant content is needed to reach the threshold concentration in near-ST crystals.
- Impurity Zn possesses the largest threshold concentration among ODRI, above 7 mol% [171,172], which is particularly important regarding the reliability of the results obtained by detailed structural studies. The extension of this framework onto the rest of the ODRI seems quite natural; it is also supported by further evidence found for In3+ and Hf4+ [173,174,175]. Based on the study of the structural properties of doped crystals, the available information has been recently updated for In3+ and Zn2+ [60,176], and extended for Zr4+ [177].
- All lanthanide trivalent rare-earth ions were long thought to occupy Li sites only, independently of the [Li]/[Nb] ratio in the crystal [10]. However, based on detailed OH− Vibrational Spectroscopy studies in near-ST LN-doped crystals with Er, Nd, and Yd ions, Kovács et al. have inferred partial occupation at the Nb sites above a critical concentration value, denoted as ‘threshold’ given the similarity of the trends observed in connection to crystals doped with ODRI [94]. Quoting them: “for rare-earth ions, the term ‘threshold’ possibly does not mean a photorefractive damage threshold, but implies the concentration of the dopant above which the rare-earth ions can occupy Nb sites in the lattice” [94]. Still, most of the dopant ions are assumed to enter Li sites; the amount of those entering an Nb site has been estimated to be very small, of the order of the OH− content in the samples (10–100 ppm). The same conclusions were recently obtained for transition metal ions (Fe3+, Cr3+, Ti4+), as discussed in bulletpoint 3 within the present section.
- An intermediate stage of the substitution mechanism has also been suggested, where LiLi substitution alone lies in between the simultaneous occupation of LiLi sites and NbLi antisites, and the partial incorporation of the dopant into regular NbNb sites [178,179,180]. This has led elsewhere to construct the first threshold concept, a lower concentration threshold than the beforehand discussed [10]. Thus, under such a framework, the first threshold would stand for the complete removal of NbLi antisites, whereas the second threshold for the beginning of NbNb site occupancy.
- (10)
- Simultaneous enhancement for both photorefraction (PR) and optical damage (OD) resistance has been reported for MgO and Bi2O3 co-doped LN (LN:Mg, Bi) [181]. This observation conflicts with the mainstream opinion found in literature: for a long time, these terms have been used indistinctly to address the same process: the optically induced inhomogeneities in the refractive indexes. Hence, it had been tacitly conceived that by making a crystal more resistant to OD, it could also hardly be PR enhanced. They had been thought all this time to “be just opposite sides of the same medal” [6]. Inspired from a rather old result, Zhang et al. did experiments involving the coupling of two beams of equal intensity and came to conclude that OD is not the same as PR, but only a form of expression of it [181]:
- Just a year ago, the same group proved this material to efficiently display real-time dynamic holograms with a 30 Hz refresh time when concentrations of 6 mol% Mg and 1 mol% Bi are used [182]. A video of the display of a running leopard is available in the supplementary material of that contribution. Regarding the labeling of co-doped crystals, recall that, in the present contribution, we use the convention of writing first the dopant with higher concentration, after the colon, followed by a comma, and then the dopant of less concentration, so that LN:Mg, Bi, and LN:Bi, Mg stand for two distinct crystals (see Figure 4).
- Doping with more than one ion species, i.e., co-doping, clearly provides some advantages of technological relevance, particularly in the field of photorefraction. The substitution mechanisms in co-doped LN is out of the scope of the present contribution. Nonetheless, it is expected to behave similarly to single yet heavily doping [5]. Further details on this subject can be consulted in Reference [61].
4. Dilute Magnetic Oxides and Ferromagnetism in LiNbO3 Doped with Magnetic 3d Cations
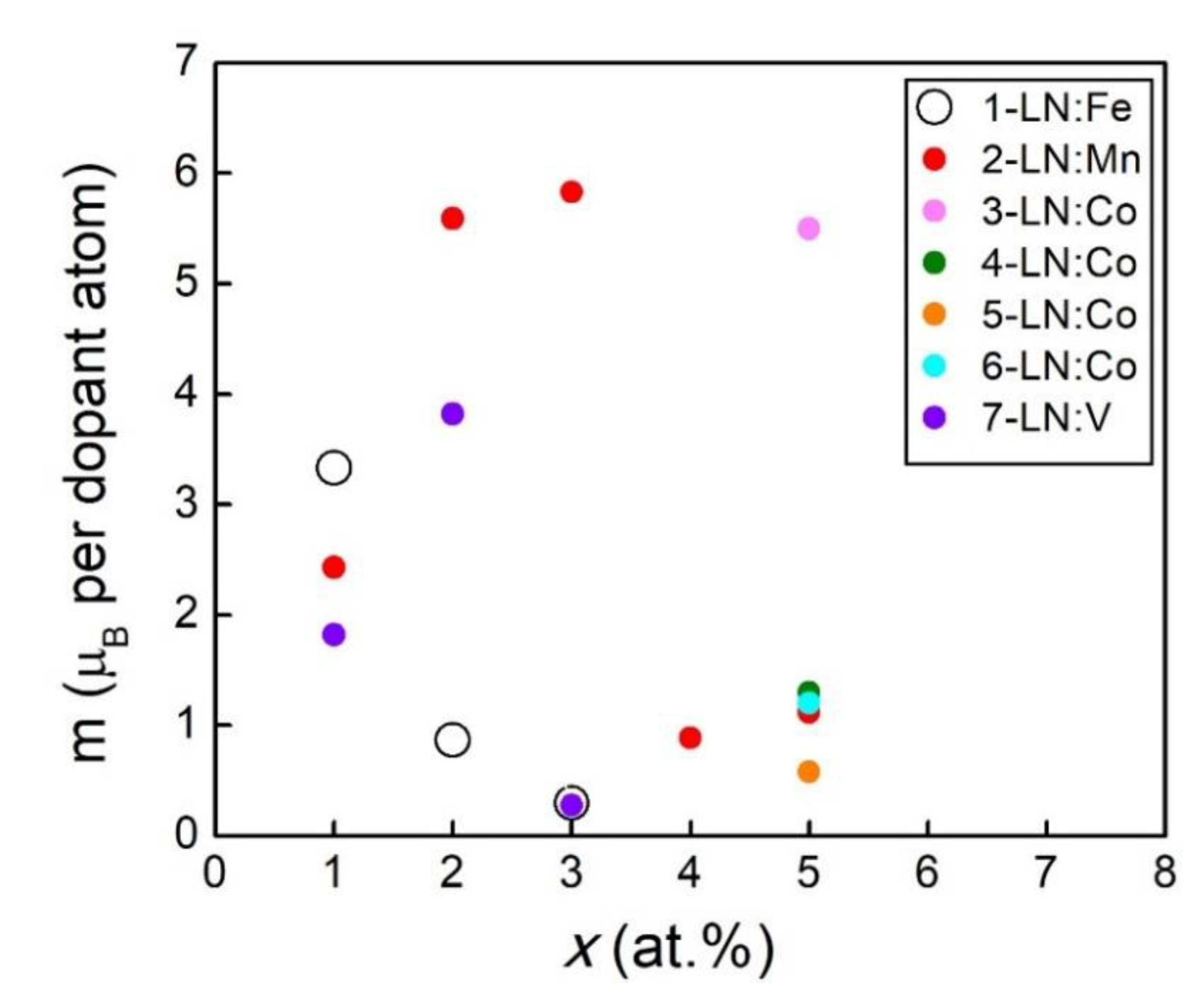
- Based on XANES, EXAFS, and Raman Spectroscopy measurements and ab initio calculations, there is a trend of Fe, Mn, and Co cations to occupy Li sites at low doping concentrations.
- The substitution of Li with Fe and Mn cations modifies the interatomic distances between their closest neighbors, favoring the interaction between the 3d cations and their neighbors.
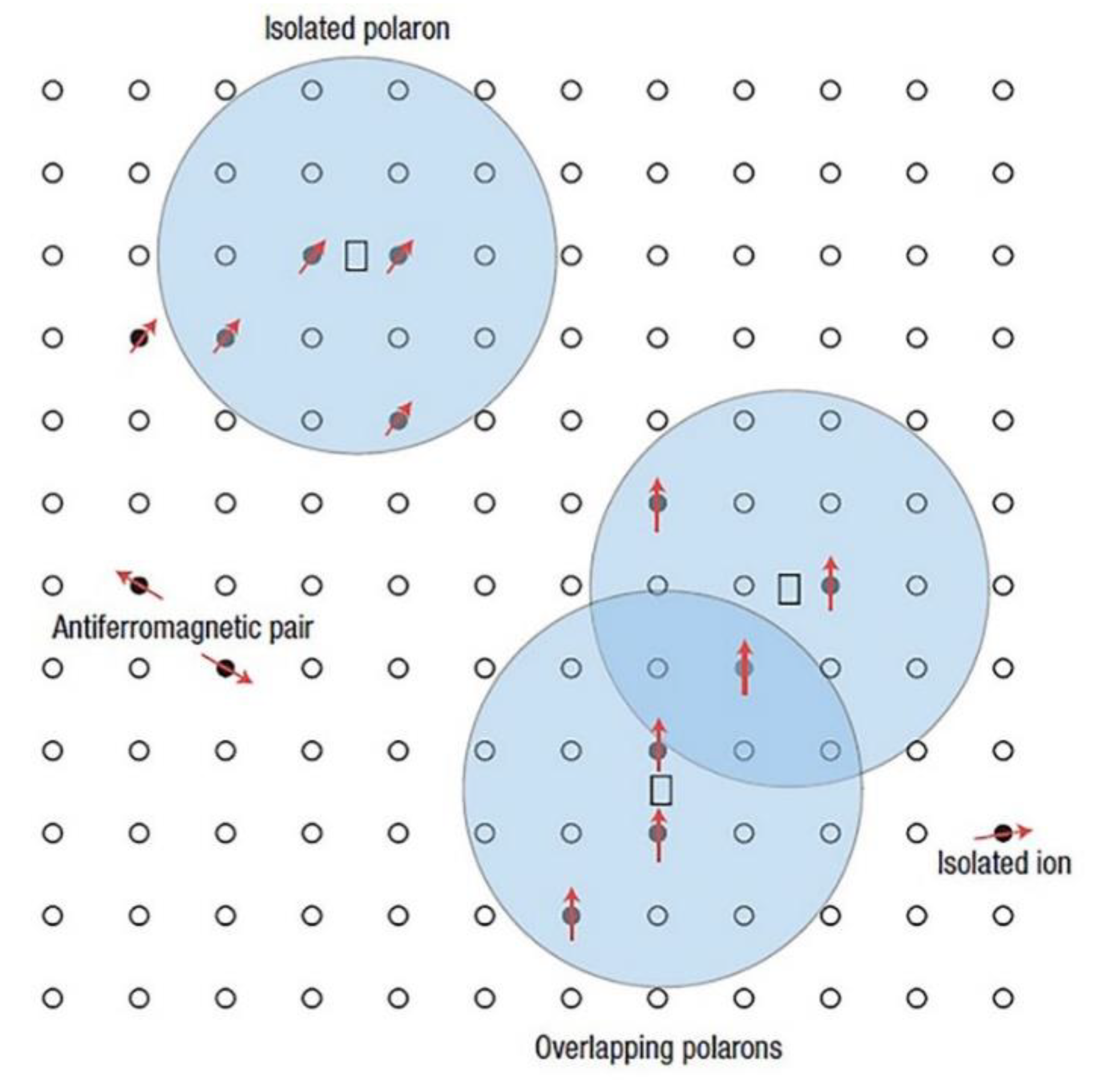
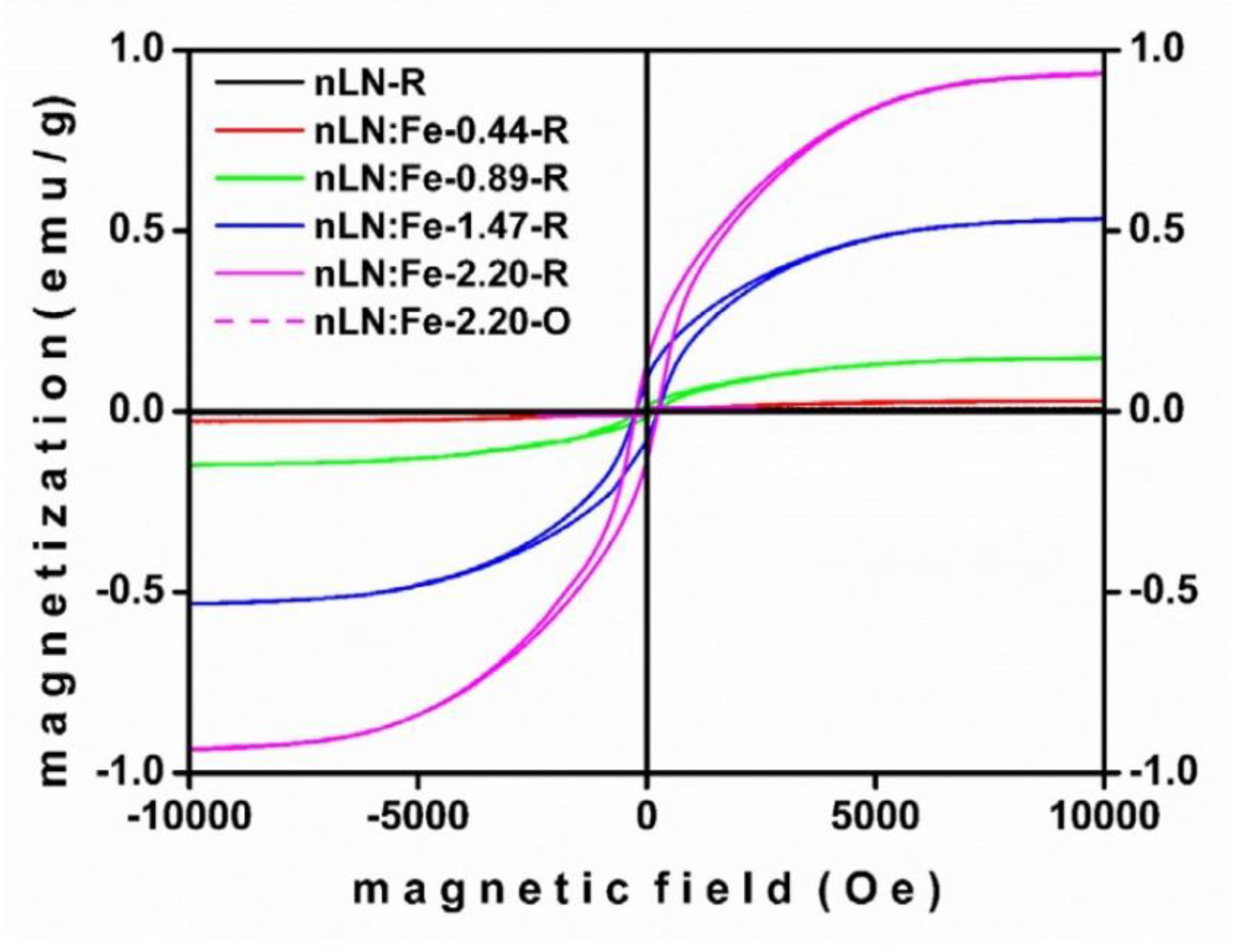
- When LN is doped with a small amount of 3d magnetic cations such as Fe, Mn, and Co, it manifests ferromagnetism at RT. However, in the high-doping concentration regime, the magnetization saturation tends to decrease, mostly due to the destruction of the magnetic coupling around the magnetic 3d cation and sometimes to the formation of secondary magnetic phases.
- The formation of point defects usually addressed as oxygen vacancies after TTRA in either doped or undoped LN serves as a mechanism for ferromagnetism enhancement.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Volk, T.; Wöhlecke, M. Introduction. In Springer Series in Materials Science 115. Lithium Niobate. Defects, Photorefraction and Ferroelectric Switching, 1st ed.; Hull, R., Osgood, R.M., Jr., Parisi, J., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 115, pp. 1–8. [Google Scholar]
- Haertling, G.H. Ferroelectric Ceramics: History and Technology. J. Am. Ceram. Soc. 1999, 82, 797–818. [Google Scholar] [CrossRef]
- Bhalla, A.S.; Guo, R.; Roy, R. The perovskite structure—A review of its role in ceramic science and technology. Mat. Res. Innovat. 2000, 4, 3–26. [Google Scholar] [CrossRef]
- Troiler-McKinstry, S. Impact of ferroelectricity. Am. Cer. Soc. Bull. 2020, 99, 22–23. [Google Scholar]
- Kovács, L.; Kocsor, L.; Tichy-Rács, É.; Lengyel, K.; Béncs, L.; Corradi, G. Hydroxyl ion probing transition metal dopants occupying Nb sites in stoichiometric LiNbO3. Opt. Mater. Express 2019, 9, 4506–4516. [Google Scholar] [CrossRef]
- Kong, Y.; Bo, F.; Wang, W.; Zheng, D.; Liu, H.; Zhang, G.; Rupp, R.; Xu, J. Recent Progress in Lithium Niobate: Optical Damage, Defect Simulation, and On-Chip Devices. Adv. Mater. 2020, 32, 1806453. [Google Scholar] [CrossRef] [PubMed]
- Kang, X.; Liang, L.; Song, W.; Wang, F.; Sang, Y.; Liu, H. Formation mechanism and elimination methods for anti-site defects in LiNbO3/LiTaO3 crystals. CrystEngComm 2016, 18, 8136–8146. [Google Scholar] [CrossRef]
- Lengyel, K.; Péter, Á.; Kovács, L.; Corradi, G.; Pálfalvi, L.; Hebling, J.; Unferdorben, M.; Dravecz, G.; Hajdara, I.; Szaller, Z.; et al. Growth, defect structure, and THz application of stoichiometric lithium niobate. Appl. Phys. Rev. 2015, 2, 040601. [Google Scholar] [CrossRef]
- Vyalikh, A.; Zschornak, M.; Köhler, T.; Nentwich, M.; Weigel, T.; Hanzing, J.; Zaripov, R.; Vavilova, E.; Gemming, S.; Brendler, E.; et al. Analysis of the defect clusters in congruent lithium tantalite. Phys. Rev. Mater. 2018, 2, 013804. [Google Scholar] [CrossRef]
- Volk, T.; Wöhlecke, M. Point defects in LiNbO3. In Springer Series in Materials Science 115. Lithium Niobate. Defects, Photorefraction and Ferroelectric Switching, 1st ed.; Hull, R., Osgood, R.M., Jr., Parisi, J., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 115, pp. 9–50. [Google Scholar]
- Pracka, I.; Bajor, A.L.; Kaczmarek, S.M.; Swirkowickz, M.; Kaczmarek, B.; Kieselewski, J.; Lukasiewicz, T. Growth and Characterization of LiNbO3 Single Crystals Doped with Cu and Fe Ions. Cryst. Res. Technol. 1994, 34, 627–634. [Google Scholar] [CrossRef]
- Fay, H.; Alford, W.J.; Dess, H.M. Dependence of second-harmonic phase-matching temperature in LiNBO3 crystals on melt composition. Appl. Phys. Lett. 1968, 12, 89–92. [Google Scholar] [CrossRef]
- Prokhorov, A.M.; Kuz’minov, Y.S. Physics and Chemistry of Crystalline Lithium Niobate, 1st ed.; Hilger: New York, NY, USA, 1990. [Google Scholar]
- Donnerberg, H.; Tomlinson, S.M.; Catlow, C.R.A.; Schirmer, O.F. Computer-simulation studies of intrinsic defects in LiNbO3 crystals. Phys. Rev. B 1989, 40, 11909–11916. [Google Scholar] [CrossRef] [PubMed]
- Lerner, P.; Legras, C.; Dumas, J.P. Stoechiometrie des monocristaux de metaniobate de lithium. J. Cryst. Growth 1968, 3, 231–235. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Marsh, P. Defect Structure Dependence on Composition in Lithium Niobate. Acta Cryst. 1986, B42, 61–68. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Thiemann, O.; Wöhlecke, M. Defects in LiNbO3—I Experimental aspects. J. Phys. Chem. Solids 1991, 52, 185–200. [Google Scholar] [CrossRef]
- Zotov, N.; Boysen, H.; Frey, F.; Metzger, T.; Born, E. Cation substitution models of congruent LiNbO3 investigated by X-ray and neutron powder diffraction. J. Phys. Chem. Solids 1994, 55, 145–152. [Google Scholar] [CrossRef]
- Wilkinson, A.P.; Cheetham, A.K.; Jarman, R.H. The defect structure of congruently melting lithium niobate. J. Appl. Phys. 1998, 74, 3080–3083. [Google Scholar] [CrossRef]
- DeLeo, G.G.; Dobson, J.L.; Masters, M.F.; Bonjack, L.H. Electronic structure of an oxygen vacancy in lithium niobate. Phys. Rev. B 1988, 37, 8394–8400. [Google Scholar] [CrossRef]
- Peterson, G.E.; Carnevale, A. 93Nb NMR Linewidths in Nonstoichiometric Lithium Niobate. J. Chem. Phys. 1972, 56, 4848–4851. [Google Scholar] [CrossRef]
- Ye, N.; Wang, J.-Y.; Boughton, R.I.; Hong, M.-C. Chapter 20. Functional Crystals. In Modern Inorganic Synthethic Chemistry, 2nd ed.; Xu, R., Xu, Y., Eds.; Elsevier, B. V.: Amsterdam, The Netherlands, 2017; pp. 575–611. [Google Scholar]
- Shannon, R.D.; Prewitt, C.T. Effective Ionic Radii in Oxides and Flourides. Acta Cryst. 1969, B25, 925–946. [Google Scholar] [CrossRef]
- Kim, S.; Gopalan, V.; Kitamura, K.; Furukawa, Y. Domain reversal and nonstoichiometry in lithium tantalate. J. Appl. Phys. 2001, 90, 2949–2963. [Google Scholar] [CrossRef]
- Iyi, N.; Kitamura, K.; Izumi, F.; Yamamoto, J.K.; Hayashi, T.; Asano, H.; Kimura, S. Comparative of defect structures in lithium niobate with different compositions. J. Soild State Chem. 1992, 101, 340–352. [Google Scholar] [CrossRef]
- Zotov, N.; Frey, F.; Boysen, H.; Lehnert, H.; Hornsteiner, A.; Strauss, B.; Sonntag, R.; Mayer, H.M.; Güthoff, F.; Hohlwein, D. X-ray and neutron diffuse scattering in LiNbO3 from 38 to 1200 K. Acta Crystallogr. B 1995, 51, 961–972. [Google Scholar] [CrossRef]
- Blumel, J.; Born, E.; Metzger, T. Solid State NMR study supporting the lithium vacancy defect model in congruent lithium niobate. J. Phys. Chem. Solids 1994, 55, 589–593. [Google Scholar] [CrossRef]
- Yatsenko, A.V.; Ivanova-Maksimova, H.M.; Sergeev, N.A. NMR study of intrinsic defects in congruent LiNbO3. 2. “Overlapping” defects. Phys. B Condens. Matter 1998, 254, 256–259. [Google Scholar] [CrossRef]
- Donnerberg, H.; Tomlinson, S.M.; Catlow, C.R.A. Defects in LiNbO3—II Computer simulation. J. Phys. Chem. Solids 1991, 52, 201–210. [Google Scholar] [CrossRef]
- Safaryan, F.P.; Feigelson, R.S.; Petrosyan, A.M. An approach to the defect structure analysis of lithium niobate single crystals. J. Appl. Phys. 1999, 85, 8079–8082. [Google Scholar] [CrossRef]
- Li, Q.; Wang, B.; Woo, C.H.; Wang, H.; Wang, R. First-principles study on the formation energies of intrinsic defects in LiNbO3. J. Phys. Chem. Solids 2007, 68, 1336–1340. [Google Scholar] [CrossRef]
- Abdi, F.; Fontana, M.D.; Aillerie, M.; Bourson, P. Coexistence of Li and Nb vacancies in the defect structure of pure LiNbO3 and its relationship to optical properties. Appl. Phys. A 2006, 83, 427–434. [Google Scholar] [CrossRef]
- Li, Y.; Sanna, S.; Schmidt, W.G. Modeling intrinsic defects in LiNbO3 within the Slater-Janak transition state model. J. Chem. Phys. 2014, 140, 234113. [Google Scholar] [CrossRef]
- Ivanova, E.M.; Sergeev, N.A.; Yatsenko, A.V. Analysis of Intrinsic Defects in the Lithium Niobate Structure by the NMR 7Li Method. Krist. Crystallogr. Rep. 1998, 43, 303–306. [Google Scholar]
- Yatsenko, A.V.; Ivanova, E.N.; Sergeev, N.A. NMR study of intrinsic defects in congruent LiNbO3. 1. “Unoverlapping” defects. Phys. B Condens. Matter 1997, 240, 254–262. [Google Scholar] [CrossRef]
- Gopalan, V.; Dierolf, V.; Scrymgeour, D.A. Defect-Domain Wall Interactions in Trigonal Ferroelectrics. Annu. Rev. Mater. Res. 2007, 37, 449–489. [Google Scholar] [CrossRef]
- Boysen, H.; Altorfer, F. A Neutron Powder Investigation of the High-Temperature Structure and Phase Transition in LiNbO3. Acta Cryst. 1994, B50, 405–414. [Google Scholar] [CrossRef]
- Lehnert, H.; Boysen, H.; Frey, F.; Hewat, A.; Radaelli, P. A neutron powder investigation of the high-temperature structure and phase transition in stoichiometric LiNbO3. Z. Krist. Cryst. Mater. 1997, 212, 712–719. [Google Scholar] [CrossRef]
- Etschmann, B.; Ishizawa, N.; Streltsov, V.; Oishi, S. A synchrotron X-ray diffraction analysis of near-stoichiometric LiNbO3. Z. Krist. Cryst. Mater. 2001, 216, 455–461. [Google Scholar] [CrossRef]
- Räuber, A. Chemistry and physics of lithium niobate. In Current Topics in Materials Science, 1st ed.; Kaldis, E., Ed.; North-Holland: Amsterdam, The Netherlands, 1978; Volume 1, pp. 481–601. [Google Scholar]
- Araujo, R.M.; Lengyel, K.; Jackson, R.A.; Valerio, M.E.G.; Kovács, L. Computer modelling of intrinsic and substitutional defects in LiNbO3. Phys. Status Solidi A 2007, 4, 1201–1204. [Google Scholar] [CrossRef]
- Araujo, R.M.; Lengyel, K.; Jackson, R.A.; Kovács, L.; Valerio, M.E.G. A computational study of intrinsic and extrinsic defects in LiNbO3. J. Phys. Condens. Matter 2007, 19, 046211. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, D.; Hu, M.; Saeed, S.; Liu, H.; Kong, Y.; Zhang, L.; Xu, J. Effect of Defects on Spontaneous Polarization in Pure and Doped LiNbO3: First-Principles Calculations. Materials 2019, 12, 100. [Google Scholar] [CrossRef]
- Köhler, T.; Mehner, E.; Hanzig, J.; Gärtner, G.; Stöcker, H.; Leisegang, T.; Meyer, D.C. Real structure influencing the hydrogen defect chemistry in congruent LiNbO3 and LiTaO3. J. Solid State Chem. 2016, 244, 108–115. [Google Scholar] [CrossRef]
- Li, Y.; Schmidt, W.G.; Sanna, S. Defect complexes in congruent LiNbO3 and their optical signatures. Phys. Rev. B 2015, 91, 174106. [Google Scholar] [CrossRef]
- Xu, H.; Lee, D.; Sinnott, S.B.; Dierolf, V.; Gopalan, V.; Phillpot, S.R. Structure and diffusion of intrinsic defect complexes in LiNbO3 from density functional theory calculations. J. Phys. Condens. Matter 2010, 22, 135002. [Google Scholar] [CrossRef] [PubMed]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.O. Density functional theory: Its origins, rise to prominence and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef]
- Szalay, V.; Lengyel, K.; Kovács, L.; Timón, V.; Hernández-Laguna, A. Vibrations of H+ (D+) in stoichiometric LiNbO3 single crystal. J. Chem. Phys. 2011, 135, 124501. [Google Scholar] [CrossRef] [PubMed]
- Lengyel, K.; Timón, V.; Hernández-Laguna, A.; Szalay, V.; Kovács, L. Structure of OH− defects in LiNbO3. IOP Conf. Ser. Mater. Sci. Eng. 2010, 15, 012015. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Zhao, X. Doping stability of nonphotorefractive ions in stoichiometric and congruent LiNbO3. Phys. Chem. Chem. Phys. 2018, 20, 17477–17486. [Google Scholar] [CrossRef]
- Volk, T.; Wöhlecke, M. General Introduction to Photorefraction in LiNbO3. In Springer Series in Materials Science 115. Lithium Niobate. Defects, Photorefraction and Ferroelectric Switching, 1st ed.; Hull, R., Osgood, R.M., Jr., Parisi, J., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 115, pp. 51–74. [Google Scholar]
- Ashkin, A.; Boyd, G.D.; Dziedzic, J.M.; Smith, R.G.; Ballman, A.A.; Levinstein, J.J.; Nassau, K. Optically-induced refractive index inhomogeneities in LiNbO3 and LiTaO3. Appl. Phys. Lett. 1966, 9, 72–74. [Google Scholar] [CrossRef]
- Furukawa, Y.; Sato, M.; Nitanda, F.; Ito, K. Growth and characterization of MgO-Doped LiNbO3 for electro-optic devices. J. Cryst. Growth 1990, 99, 832–836. [Google Scholar] [CrossRef]
- Furukawa, Y.; Yokotani, A.; Sasaki, T.; Yoshida, H.; Yoshida, K.; Nitanda, F.; Sato, M. Investigation of bulk laser damage threshold of lithium niobate single crystals by Q-switched pulsed laser. J. Appl. Phys. 1991, 69, 3372–3374. [Google Scholar] [CrossRef]
- Dunn, M.H.; Ebrahimzadeh, M. Parametric Generation of Tunable Light from Continuous-Wave to Femtosecond Pulses. Science 1999, 286, 1513–1517. [Google Scholar] [CrossRef]
- Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Meleki, L. Nonlinear Optics and Crystalline Whispering Gallery Mode Cavities. Phys. Rev. Lett. 2004, 92, 043903. [Google Scholar] [CrossRef] [PubMed]
- Guarino, A.; Poberaj, G.; Rezzonico, D.; Degl’Innocenti, R.; Günter, P. Electro-optically tunable microring resonators in lithium niobate. Nat. Photon. 2007, 1, 407–410. [Google Scholar] [CrossRef]
- Canalias, C.; Pasiskevicius, V. Mirrorles optical parametric oscillator. Nat. Photon. 2007, 1, 459–462. [Google Scholar] [CrossRef]
- Sulyanov, S.; Volk, T. Lattice Parameter of Optical Damage Resistant In-Doped LiNbO3 Crystals. Crystals 2018, 8, 210. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, S.; Xu, J. Recent Advances in the Photorefraction of Doped Lithium Niobate Crystals. Materials 2012, 5, 1954–1971. [Google Scholar] [CrossRef]
- Dhar, L.; Curtis, K.; Fäcke, T. Coming of age. Nat. Poton. 2008, 2, 403–405. [Google Scholar] [CrossRef]
- Haw, M. The light fantastic. Nature 2003, 422, 556–558. [Google Scholar] [CrossRef]
- Staebler, D.L.; Phillips, W. Fe-Doped for Read-Write Applications. Appl. Opt. 1974, 13, 788–794. [Google Scholar] [CrossRef]
- von der Linde, D.; Glass, A.M.; Rodgers, K.F. Multiphoton photorefractive processes for optical storage in LiNbO3. Appl. Phys. Lett. 1974, 25, 155–157. [Google Scholar] [CrossRef]
- Keune, W.; Date, S.K.; Dézsi, I.; Gonser, U. Mösbauser-effect study of Co57 and Fe57 impurities in ferroelectric LiNbO3. J. Appl. Phys. 1975, 46, 3914–3924. [Google Scholar] [CrossRef]
- Falk, M.; Buse, K. Thermoelectric-method for nearly complete oxidation of highly iron-doped lithium niobate crystals. Appl. Phys. B 2005, 81, 853–855. [Google Scholar] [CrossRef]
- Li, S.; Liu, S.; Kong, Y.; Xu, J.; Zhang, G. Enhanced photorefractive properties of LiNbO3:Fe crystals by HfO2 codoping. Appl. Phys. Lett. 2006, 89, 101126. [Google Scholar] [CrossRef]
- Xu, C.; Yang, C.; Zhu, C.; Sun, T.; Wang, R.; Xu, Y. Improved nonvolatile holographic storage properties in Zr:Ru:Fe:LiNbO3 crystal by blue light recording. Mater. Lett. 2012, 67, 320–322. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, S.; Li, W.; Kong, Y.; Chen, S.; Xu, J. Improved ultraviolet photorefractive properties of vanadium-doped lithium niobate crystals. Opt. Lett. 2011, 36, 1779–1781. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, S.; Kong, Y.; Chen, S.; Rupp, R.; Xu, J. Fast photorefractive response of vanadium-doped lithium niobate in the visible region. Opt. Lett. 2012, 37, 1841–1843. [Google Scholar] [CrossRef]
- Tian, T.; Kong, Y.; Liu, S.; Li, W.; Wu, L.; Chen, S.; Xu, J. Photorefraction of molybdenum-doped lithium niobate crystals. Opt. Lett. 2012, 37, 2679–2681. [Google Scholar] [CrossRef] [PubMed]
- Kovács, L.; Kocsor, L.; Szaller, Z.; Hajdara, I.; Dravecz, G.; Lengyel, K.; Corradi, G. Lattice Site of Rare-Earth Ions in Stoichiometric Lithium Niobate Probed by OH− Vibrational Spectroscopy. Crystals 2017, 7, 230. [Google Scholar] [CrossRef]
- García-Solé, J.; Bausá, L.E.; Jaque, D.; Montoya, E.; Murrieta, H.; Jaque, F. Rare earth and transition metal ion centers in LiNbO3. Spectrochim. Acta Part A 1998, 54, 1571–1581. [Google Scholar] [CrossRef]
- Lande, D.; Orlov, S.S.; Akella, A.; Hesselink, L.; Neurgaonkar, R.R. Digital holographic storage system incorporating optical fixing. Opt. Lett. 1997, 22, 1722–1724. [Google Scholar] [CrossRef]
- Lee, M.; Takekawa, S.; Furukawa, Y.; Kitamura, K.; Hatano, H.; Tanaka, S. Nonvolatile two-color holographic recording in Tb-doped LiNbO3. Appl. Phys. Lett. 2000, 76, 1653–1655. [Google Scholar] [CrossRef]
- Kaminow, I.P.; Stulz, L.W. Nd:LiNbO3 laser. IEEE J. Quantum Electron. 1975, 11, 306–308. [Google Scholar] [CrossRef]
- Fan, T.Y.; Cordova-Plaza, A.; Digonnet, M.J.F.; Byer, R.L.; Shaw, H.J. Nd:MgO:LiNbO3 spectroscopy and laser devices. J. Opt. Soc. Am. B 1986, 3, 140–148. [Google Scholar] [CrossRef]
- Yamamoto, J.K.; Sugimoto, A.; Yamagishi, K. Self-frequency doubling in Nd,Sc2O3:LiNbO3 at room temperature. Opt. Lett. 1994, 19, 1311–1313. [Google Scholar] [CrossRef] [PubMed]
- Lhomme, F.; Bourson, P.; Fontana, M.D.; Malovichko, G.; Aillerie, M.; Kokanyan, E. Luminescence of Cr3+ in lithium niobate: Influence of the chromium concentration and crystal composition. J. Phys. Condens. Matter 1998, 10, 1137–1146. [Google Scholar] [CrossRef]
- Qiu, Y. Assesment of tunable laser crystal LiNbO3:Cr3+. J. Phys. Condens. Matter 1993, 5, 2041–2044. [Google Scholar] [CrossRef]
- Babadjanyan, V.G.; Kokanyan, E.P.; Kostanyan, R.B.; Nikogosyan, V.R. Spectral and kinetic properties of LiNbO3:Cr3+ crystals. Opt. Commun. 1990, 78, 247–249. [Google Scholar] [CrossRef]
- Levinstein, H.J.; Ballman, A.A.; Denton, R.T.; Ashkin, A.; Dziedzic, J.M. Reduction of the Susceptibility to Optically Induced Index Inhomogeneities in LiTaO3 and LiNbO3. J. Appl. Phys. 1967, 38, 3101–3102. [Google Scholar] [CrossRef]
- Smith, R.G.; Fraser, D.B.; Denton, R.T.; Rich, T.C. Correlation of Reduction in Optically Induced Refractive-Index Inhomogeneity with OH Content in LiTaO3 and LiNbO3. J. Appl. Phys. 1968, 39, 4600–4602. [Google Scholar] [CrossRef]
- Zhong, G.G.; Jin, J.; Wu, Z.K. Measurements of Optically Induced Refractive-Index Damage of Lithium Niobate Doped with Different Concentrations of Mg. In Proceedings of the 11th International Quantum Electronics Conference, Boston, MA, USA, 23–26 June 1980; Volume 70, p. 631. [Google Scholar]
- Wöhlecke, M.; Kovács, L. OH− ions in Oxide Crystals. Crit. Rev. Solid State Mater. Sci. 2001, 26, 1–86. [Google Scholar] [CrossRef]
- Cabrera, J.M.; Olivares, J.; Carrascosa, M.; Rams, J.; Müller, R.; Diéguez, E. Hydrogen in lithium niobate. Adv. Phys. 1996, 45, 349–392. [Google Scholar] [CrossRef]
- Kovács, L.; Szalay, V.; Capelleti, R. Stoichiomnetry dependence of the OH− absorption band in LiNbO3 crystals. Solid State Commun. 1984, 52, 1029–1031. [Google Scholar] [CrossRef]
- Thomas, D.G.; Lander, J.J. Hydrogen as a Donor in Zinc Oxide. J. Chem. Phys. 1956, 25, 1136–1142. [Google Scholar] [CrossRef]
- Norby, T.; Wideroe, M.; Glöckner, R.; Larring, Y. Hydrogen in oxides. Dalton Trans. 2004, 3012–3018. [Google Scholar] [CrossRef]
- Müller, R.; Arizmendi, L.; Carrascosa, M.; Cabrera, J.M. Determination of H concentration in LiNbO3 by photorefractive fixing. Appl. Phys. Lett. 1992, 60, 3212–3214. [Google Scholar] [CrossRef]
- Rice, C.E. The Structure and Properties of Li1−xHxNbO3. J. Solid State Chem. 1986, 64, 188–199. [Google Scholar] [CrossRef]
- Polgár, K.; Péter, Á.; Kovács, L.; Corradi, G.; Szaller, Z. Growth of stoichiometric LiNbO3 single crystals by top seeded solution growth method. J. Cryst. Growth 1997, 177, 211–216. [Google Scholar] [CrossRef]
- Kovács, L.; Szaller, Z.; Lengyel, K.; Corradi, G. Hydroxyl ions in stoichiometric LiNbO3 crystals doped with optical damage resistant ions. Opt. Mater 2014, 37, 55–58. [Google Scholar] [CrossRef]
- Bäumer, C.; David, C.; Betzler, K.; Hesse, H.; Lengyel, K.; Kovács, L.; Wöhlecke, M. Composition dependence of the OH-stretch-mode spectrum in lithium tantalate. Phys. Stat. Solidi A 2004, 201, R13–R16. [Google Scholar] [CrossRef]
- Bollmann, W.; Gernand, M. On the disorder of LiNbO3 crystals. Phys. Stat. Solidi A 1972, 9, 301–308. [Google Scholar] [CrossRef]
- Bredikhin, S.; Scharner, S.; Klingler, M.; Kveder, V.; Red’kin, B.; Weppner, W. Nonstoichiometry and electrocoloration due to injection of Li+ and O2− ions into lithium niobate crystals. J. Appl. Phys. 2000, 88, 5687–5694. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C.; Schoke, B. Electron small polarons and bipolarons in LiNbO3. J.Phys. Condens. Matter 2009, 21, 123201. [Google Scholar] [CrossRef] [PubMed]
- Imlau, M.; Badorreck, H.; Merschjann, C. Optical nonlinearities of small polarons in lithium niobate. Appl. Phys. Rev. 2015, 2, 040606. [Google Scholar] [CrossRef]
- Clark, M.G.; DiSalvo, F.J.; Glass, A.M.; Peterson, G.E. Electronic structure and optical index damage of iron-doped lithium niobate. J. Chem. Phys. 1973, 59, 6209–6219. [Google Scholar] [CrossRef]
- Eagles, D.M. Optical Absorption in Ionic Crystals Involving Small Polarons. Phys. Rev. 1963, 130, 1381–1400. [Google Scholar] [CrossRef]
- Klinger, M. Quantum theory of non-steady-state conductivity in low mobility solids. Phys. Lett. 1963, 7, 102–104. [Google Scholar] [CrossRef]
- Reik, H.G. Optical properties of small polarons in the infrared. Solid State Commun. 1963, 1, 67–71. [Google Scholar] [CrossRef]
- Reik, H.G.; Heese, D. Frequency dependence of the electrical conductivity of small polarons for high and low temperatures. J. Phys. Chem. Solids 1967, 28, 581–596. [Google Scholar] [CrossRef]
- Austin, I.G.; Mott, N.F. Polarons in crystalline and non-crystalline materials. Adv. Phys. 1969, 18, 41–102. [Google Scholar] [CrossRef]
- Bryksin, V.V.; Voloshin, V.S.; Raitsev, A.V. Sov. Phys. Solid State 1983, 25, 820.
- Emin, D. Optical properties of large and small polarons and bipolarons. Phys. Rev. B 1993, 48, 13691–13702. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Mott, N.F. Bipolarons. Rep. Prog. Phys. 1994, 57, 1197–1288. [Google Scholar] [CrossRef]
- Zylbersztejn, A. Thermally activated trapping in Fe-Doped LiNbO3. Appl. Phys. Lett. 1976, 29, 778–780. [Google Scholar] [CrossRef]
- Schirmer, O.F.; von der Linde, D. Two-photon- and x-ray-induced Nb4+ and O− small polarons in LiNbO3. Appl. Phys. Lett. 1978, 33, 35–38. [Google Scholar] [CrossRef]
- von der Linde, D.; Schirmer, O.F.; Kurz, H. Intrinsic Photorefractive Effect of LiNbO3. Appl. Phys. 1978, 15, 153–156. [Google Scholar] [CrossRef]
- Karaseva, L.G.; Bondarenko, G.P.; Gromov, V.V. Investigation of optical active centres of the irradiated lithium niobate. Radiat. Phys. Chem. 1977, 10, 241–245. [Google Scholar] [CrossRef]
- Bernhardt, H.J. Comparative studies of the LNT coloration of Y3Al5O12, YAlO3, and LiNbO3 crystals. Phys. Status Solidi A 1976, 33, 211–216. [Google Scholar] [CrossRef]
- Schirmer, O.F. Optical Absorption of Small Polarons Bound in Octahedral Symmetry: V− Type Centers in Alkaline Earth Oxides. Z. Physik B 1976, 24, 235–244. [Google Scholar] [CrossRef]
- Arizmendi, L.; Cabrera, J.M.; Agulló-López, F. Defects induced in pure and doped LiNbO3 by irradiation and thermal reduction. J. Phys. C Solid State Phys. 1984, 17, 515–529. [Google Scholar] [CrossRef]
- Ketchum, J.L.; Sweeney, K.L.; Halliburton, L.E. Vacuum Annealing Effects in Lithium Niobate. Phys. Lett. 1983, 94A, 450–453. [Google Scholar] [CrossRef]
- Sweeney, K.L.; Halliburton, L.E. Oxygen vacancies in lithium niobate. Appl. Phys. Lett. 1983, 43, 336–338. [Google Scholar] [CrossRef]
- Smyth, D.M. Defects and transport in LiNbO3. Ferroelectrics 1983, 50, 93–102. [Google Scholar] [CrossRef]
- Jhans, H.; Honig, J.M.; Rao, C.N.R. Optical properties of reduced LiNbO3. J. Phys. C Solid State Phys. 1986, 19, 3649–3658. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Juppe, S.; Koppitz, J. Electron-spin-resonance, optical and photovoltaic studies of reduced undoped LiNbO3. Cryst. Latt. Def. Amorph. Mater. 1987, 16, 353–357. [Google Scholar]
- Koppitz, J.; Schirmer, O.F.; Kuznetsov, A.I. Thermal Dissociation of Bipolarons In Reduced Undoped LiNbO3. Europhys. Lett. 1987, 4, 1055–1059. [Google Scholar] [CrossRef]
- Chakraverty, B.K.; Sienko, M.J.; Bonnerot, J. Low-temperature specific heat and magnetic susceptibility of nonmetallic vanadium bronzes. Phys. Rev. B 1978, 17, 3781–3789. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Salje, E. Conduction bipolarons in low-temperature crystalline WO3−x. J. Phys. C Solid State Phys. 1980, 13, L1067–L1072. [Google Scholar] [CrossRef]
- Dutt, D.A.; Feigl, F.J.; DeLeo, G.G. Optical absorption and electron paramagnetic resonance studies of chemically reduced congruent lithium niobate. J. Phys. Chem. Solids 1990, 51, 407–415. [Google Scholar] [CrossRef]
- Krätzig, E.; Schirmer, O.F. Photorefractive centers in electro-optic crystals. In Photorefractive Materials and Their Applications, I. Topics in Applied Physics; Günter, P., Huignard, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; Volume 61, pp. 131–166. [Google Scholar]
- Tsonev, L. Luminiscent activation of planar optical waveguides in LiNbO3 with rare earth ions Ln3+—A review. Opt. Mater. 2008, 30, 892–899. [Google Scholar] [CrossRef]
- Herrington, J.R.; Dischler, B.; Räuber, A.; Schneider, J. An optical study of the stretching absorption band near 3 microns from OH− defects in LiNbO3. Solid State Commun. 1973, 12, 351–354. [Google Scholar] [CrossRef]
- Klauer, S.; Wöhlecke, M. Incorporation of hydrogen in cubic and uniaxial oxidic crystals deduced from polarized Raman scattering. Phys. Rev. B 1994, 49, 158–181. [Google Scholar] [CrossRef]
- Bryan, D.A.; Gerson, R.; Tomaschke, H.E. Increased optical damage resistance in lithium niobate. Appl. Phys. Lett. 1984, 44, 847–849. [Google Scholar] [CrossRef]
- Bryan, D.A.; Rice, R.R.; Gerson, R.; Tomaschke, H.E.; Sweeney, K.L.; Halliburton, L.E. Magnesium-Doped Lithium Niobate For Higher Optical Power Applications. Opt. Eng. 1985, 24, 241138. [Google Scholar] [CrossRef]
- Sweeney, K.L.; Halliburton, L.E.; Bryan, D.A.; Rice, R.R.; Gerson, R.; Tomaschke, H.E. Point defects in Mg-doped lithium niobate. J. Appl. Phys. 1985, 57, 1036–1044. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Zhang, G. Defect Chemistry Analysis of the Defect Structure in Mg-Doped LiNbO3 Crystals. Phys. Status Solidi A 1996, 156, 285–291. [Google Scholar] [CrossRef]
- Grabmaier, B.C.; Otto, F. Growth and investigation of MgO-doped LiNbO3. J. Cryst. Growth 1986, 79, 682–688. [Google Scholar] [CrossRef]
- Lengyel, K.; Kovács, L.; Péter, Á.; Polgár, K.; Corradi, G. The effect of stoichiometry and Mg doping on the Raman spectra of LiNbO3:Mg crystals. Appl. Phys. B 2007, 87, 317–322. [Google Scholar] [CrossRef]
- Donnerberg, H. Comments on the Defect Chemistry of Magnesium-Doped Lithium Niobate (LiNbO3). J. Solid State Chem. 1996, 123, 208–214. [Google Scholar] [CrossRef]
- Lengyel, K.; Péter, Á.; Polgár, K.; Kovács, L.; Corradi, G. UV and IR absorption studies in LiNbO3:Mg crystals below and above the photorefractive threshold. Phys. Status Solidi C 2005, 2, 171–174. [Google Scholar] [CrossRef]
- Pálfalvi, L.; Hebling, J.; Almási, G.; Péter, A.; Polgár, K.; Lengyel, K.; Szipöcs, R. Nonlinear refraction and absorption of Mg doped stoichiometric and congruent LiNbO3. J. Appl. Phys. 2004, 95, 902–908. [Google Scholar] [CrossRef]
- Pálfalvi, L.; Almási, G.; Hebling, J.; Péter, Á.; Polgár, K. Measurement of laser-induced refractive index changes of Mg-doped congruent and stoichiometric LiNbO3. Appl. Phys. Lett. 2002, 80, 2245–2247. [Google Scholar] [CrossRef]
- Polgár, K.; Kovács, L.; Földvári, I.; Cravero, I. Spectroscopic and electrical conductivity investigation of Mg doped LiNbO3 single crystals. Solid State Commun. 1986, 59, 375–379. [Google Scholar] [CrossRef]
- Kovács, L.; Szaller, Z.; Lengyel, K.; Péter, Á.; Hajdara, I.; Mandula, G.; Pálfvalvi, L.; Hebling, J. Photorefractive damage resistance threshold in stoichiometric LiNbO3:Zr crystals. Opt. Lett. 2013, 38, 2861–2864. [Google Scholar] [CrossRef]
- Kovács, L.; Polgár, K.; Capelletti, R. IR absorption study of OH− in pure and Mg-doped LiNbO3 single crystals. Cryst. Latt. Def. Amorph. Mater. 1987, 15, 115–121. [Google Scholar]
- Dravecz, G.; Kovács, L. Determination of the crystal composition from OH− vibrational spectrum in lithium niobate. Appl. Phys. B 2007, 88, 305–307. [Google Scholar] [CrossRef]
- Kovács, L.; Wöhlecke, M.; Jovanovic, A.; Polgár, K.; Kapphan, S. Infrared absorption study of the OH vibrational band in LiNbO3 crystals. J. Phys. Chem. Solids 1991, 52, 797–803. [Google Scholar] [CrossRef]
- Freytag, F.; Corradi, G.; Imlau, M. Atomic insight to lattice distortions caused by carrier self-trapping in oxide materials. Sci. Rep. 2016, 6, 36929. [Google Scholar] [CrossRef] [PubMed]
- Berben, D.; Buse, K.; Wevering, S.; Herth, P.; Imlau, M.; Woike, T. Lifetime of small polarons in iron-doped lithium-niobate crystals. J. App. Phys. 2000, 87, 1034–1041. [Google Scholar] [CrossRef]
- Herth, P.; Schaniel, D.; Woike, T.; Graznow, T.; Imlau, M.; Krätzig, E. Polarons generated by laser pulses in doped LiNbO3. Phys. Rev. B 2005, 71, 125128. [Google Scholar] [CrossRef]
- Herth, P.; Graznow, T.; Schaniel, D.; Woike, T.; Imlau, M.; Krätzig, E. Evidence for Light-Induced Hole Polarons in LiNbO3. Phys. Rev. Lett. 2005, 95, 067404. [Google Scholar] [CrossRef]
- Beyer, O.; Maxein, D.; Woike, T.; Buse, K. Generation of small bound polarons in lithium niobate crystals on the subpicosecond time scale. Appl. Phys. B 2006, 83, 527–530. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, S.; Zhao, Y.; Liu, H.; Chen, S.; Xu, J. High optical damage resistant crystal: Zirconium-oxide-doped lithium niobate. Appl. Phys. Lett. 2007, 91, 081908. [Google Scholar]
- Chen, S.; Liu, H.; Kong, Y.; Huang, Z.; Xu, J.; Zhang, G. The resistance against optical damage of near-stoichiometric LiNbO3:Mg crystals prepared by vapor transport equilibration. Opt. Mater. 2007, 29, 885–888. [Google Scholar]
- Liu, H.; Liang, Q.; Zhu, M.; Li, W.; Liu, S.; Zhang, L.; Chen, S.; Kong, Y.; Xu, J. An excellent crystal for high resistance against optical damage in visible-UV range: Near-stoichiometric zirconium-doped lithium niobate. Opt. Exp. 2011, 19, 1743–1748. [Google Scholar]
- Schlarb, U.; Wöhlecke, M.; Gather, B.; Reichert, A.; Betzler, K.; Volk, T.; Rubinina, N. Refractive indices of Zn-doped lithium niobate. Opt. Mater. 1995, 4, 791–795. [Google Scholar]
- Schlarb, U.; Matzas, B.; Reichert, A.; Betzler, K.; Wöhlecke, M.; Gather, B.; Volk, T. Refractive indices of Zn/In-co-doped lithium niobate. Ferroelectrics 1996, 185, 269–272. [Google Scholar]
- Liu, F.; Kong, Y.; Li, W.; Liu, H.; Liu, S.; Chen, S.; Zhang, X.; Rupp, R.; Xu, J. High resistance against ultraviolet photorefraction in zirconium-doped lithium niobate crystals. Opt. Lett. 2010, 35, 10–12. [Google Scholar] [PubMed]
- Xu, J.; Zhang, G.; Li, F.; Zhang, X.; Sun, Q.; Liu, S.; Song, F.; Kong, Y.; Chen, X.; Qiao, H.; et al. Enhancement of ultraviolet photorefraction in highly magnesium-doped lithium niobate crystals. Opt. Lett. 2000, 25, 129–131. [Google Scholar]
- Qiao, H.; Xu, J.; Zhang, G.; Zhang, X.; Sun, Q.; Zhang, G. Ultraviolet photorefractive features in doped lithium niobate crystals. Phys. Rev. B 2004, 70, 094101. [Google Scholar]
- Razzari, L.; Minzioni, P.; Cristiani, I.; Degiorgio, V.; Kokanyan, E.P. Photorefractivity of Hafnium-doped congruent lithium–niobate crystals. Appl. Phys. Lett. 2005, 86, 131914. [Google Scholar]
- Li, S.; Liu, S.; Kong, Y.; Deng, D.; Gao, G.; Li, Y.; Gao, H.; Zhang, L.; Hang, Z.; Chen, S.; et al. The optical damage resistance and absorption spectra of LiNbO3:Hf crystals. J. Phys. Condens. Matter 2006, 18, 3527–3534. [Google Scholar]
- Minzioni, P.; Cristiani, I.; Degiorgio, V.; Kokanyan, E.P. Strongly sublinear growth of the photorefractive effect for increasing pump intensities in doped lithium-niobate crystals. J. Appl. Phys. 2007, 101, 116105. [Google Scholar]
- Minzioni, P.; Cristiani, I.; Yu, J.; Parravicini, J.; Kokanyan, E.P.; Degiorgio, V. Linear and nonlinear optical properties of Hafnium-doped lithium-niobate crystals. Opt. Express 2007, 15, 14171–14176. [Google Scholar] [CrossRef]
- Kimura, H.; Uda, S. Conversion of non-stoichiometry of LiNbO3 to constitutional stoichiometry by impurity doping. J. Cryst. Growth 2009, 311, 4094–4101. [Google Scholar] [CrossRef]
- Kimura, H.; Taniuchi, T.; Iida, S.; Uda, S. Bulk crystal growth of congurent MgO-Doped LiNbO3 crystal with stoichiometric structure and its second-harmonic-generation properties. J. Cryst. Growth 2010, 312, 3425–3427. [Google Scholar]
- Rebouta, L.; Smulders, P.J.M.; Boerma, D.O.; Agúllo-López, F.; da Silva, M.F.; Soares, J.C. Ion-beam channeling yields of host and impurity atoms in LiNbO3: Computer simulations. Phys. Rev. B 1993, 48, 3600–3610. [Google Scholar]
- Kling, A.; Soares, J.C.; da Silva, M.F. Channeling Investigations of Oxide Materials for Optoelectronic Applications. In Insulating Materials for Optoelectronics: New Developments; Agúllo-López, F., Ed.; World Scientific: Singapore, 1995; pp. 175–200. [Google Scholar]
- Xue, D.; He, X. Dopant occupancy and structural stability of doped lithium niobate crystals. Phys. Rev B 2006, 73, 064113. [Google Scholar] [CrossRef]
- Donnerberg, H.; Tomlinson, S.M.; Catlow, C.R.A.; Schirmer, O.F. Computer-simulation studies of extrinsic defects in LiNbO3 crystals. Phys. Rev. B 1991, 44, 4877–4883. [Google Scholar]
- Feng, X.; Wang, D.; Zhang, J. NMR Spectra of Mg Nuclei in Mg-Doped LiNbO3 Crystals. Phys. Stat. Solidi B 1990, 157, K127–K130. [Google Scholar]
- Chernaya, T.S.; Maksimov, B.A.; Volk, T.R.; Rubinina, N.M.; Simonov, V.I. Zn atoms in lithium niobate and mechanism of their insertion into crystals. JETP Lett. 2000, 73, 103–106. [Google Scholar]
- Volk, T.; Maximov, B.; Chernaya, T.; Rubinina, N.; Wöhlecke, M.; Simonov, V. Photorefractive properties of LiNbO3:Zn crystals related to the defect structure. Appl. Phys. B 2001, 72, 647–652. [Google Scholar]
- Sulyanov, S.; Maximov, B.; Volk, T.; Boysen, H.; Schneider, J.; Rubininca, N.; Hansen, T. Neutron and X-ray study of stoichiometric and doped LiNbO3:Zn0.08. Appl. Phys. A 2001, 74, s1031–s1033. [Google Scholar]
- Volk, T.R.; Rubinina, N.M.; Pryalkin, V.I.; Krasnikov, V.V.; Volkov, V.V. Optical and non-linear optical investigations in LiNbO3:Mg and LiNbO3:Zn. Ferroelectrics 1990, 109, 345–350. [Google Scholar]
- Volk, T.R.; Pryalkin, V.I.; Rubinina, N.M. Optical-damage-resistant LiNbO3:Zn crystal. Opt. Lett. 1990, 15, 996–998. [Google Scholar] [PubMed]
- Volk, T.; Maximov, B.; Sulyanov, S.; Rubinina, N.; Wöhlecke, M. Relation of the photorefraction and optical-damage resistance to the intrinsic defect structure in LiNbO3 crystals. Opt. Mater. 2003, 23, 229–233. [Google Scholar] [CrossRef]
- Marques, J.G.; Kling, A.; Soares, J.C.; Rebouta, L.; da Silva, M.F.; Diéguez, E.; Agulló-López, F. Lattice site location of Hf in LiNbO3: Influence of dopant concentration and crystal stoichiometry. Nuclr. Instr. Meth. B 1998, 136–138, 431–435. [Google Scholar] [CrossRef]
- Marques, J.G.; Kling, A.; Rebouta, L.; da Silva, M.F.; Melo, A.A.; Soares, J.C.; Serrano, M.D.; Diéguez, E.; Agulló-López, F. Lattice Location of Hf in Near-Stoichiometric LiNbO3: RBS/Channeling and PAC Studies. Mater. Sci. Forum 1997, 248–249, 395–398. [Google Scholar]
- Chia, C.-T.; Lee, C.-C.; Chang, P.-J.; Hu, M.-L.; Hu, L.-J. Substitution mechanism of ZnO-doped lithium niobate crystal determined by powder x-ray diffraction and coercive field. Appl. Phys. Lett. 2005, 86, 182901. [Google Scholar] [CrossRef]
- Argiolas, N.; Bazzan, M.; Ciampolillo, M.V.; Pozzobon, P.; Sada, C.; Saoner, L.; Zaltron, A.M.; Bacci, L.; Minzioni, P.; Nava, G.; et al. Structural and optical properties of zirconium doped lithium niobate crystals. J. Appl. Phys. 2010, 108, 093508. [Google Scholar] [CrossRef]
- Iyi, N.; Kitamura, K.; Yajima, Y.; Kimura, S.; Furukawa, Y.; Sato, M. Defect Structure Modelo f MgO-Doped LiNbO3. J. Solid State Chem. 1995, 118, 148–152. [Google Scholar]
- Hammoum, R.; Fontana, M.D.; Gilliot, M.; Bourson, P.; Kokanyan, E.P. Site spectroscopy of Hf doping in Hf-doped LiNbO3 crystals. Solid State Comm. 2009, 149, 1967–1970. [Google Scholar]
- Kokanyan, N.; Chapron, D.; Kokanyan, E.; Fontana, M.D. Zr doping on lithium niobate crystals: Raman spectroscopy and chemometrics. J. Appl. Phys. 2017, 121, 095103. [Google Scholar] [CrossRef]
- Zheng, D.; Kong, Y.; Liu, S.; Chen, M.; Chen, S.; Zhang, L.; Rupp, R.; Xu, J. The simultaneous enhancement of photorefraction and optical damage resistance in MgO and Bi2O3 co-doped LiNbO3 crystals. Sci. Rep. 2016, 6, 20308. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Wang, W.; Wang, S.; Qu, D.; Liu, H.; Kong, Y.; Liu, S.; Chen, S.; Rupp, R.; Xu, J. Real-time dynamic holographic display realized by bismuth and magnesium co-doped lithium niobate. Appl. Phys. Lett. 2019, 114, 241903. [Google Scholar] [CrossRef]
- Bader, S.D. Colloquium: Opportunities in nanomagnetism. Rev. Mod. Phys. 2006, 78, 1–15. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; IEEE/Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Spaldin, N.A. Magnetic Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Coey, J.M.D.; Venkatesan, M.; Fitzgerald, C.B. Donor impurity band exchange in dilute ferromagnetic oxides. Nat. Mater. 2005, 4, 173–179. [Google Scholar] [CrossRef]
- Villalobos-Mendoza, S.D.; Holguín-Momaca, J.T.; Elizalde-Galindo, J.T.; Carrillo-Flores, D.M.; Olive-Méndez, S.F.; Farías-Mancilla, J.R. Iron-Doped Lithium Tantalate Thin Films Deposited by Magnetron Sputtering: A Study of Iron Role in the Structure and the Derived Magnetic Properties. Crystals 2020, 10, 50. [Google Scholar] [CrossRef]
- Song, Y.-J.; Zhang, Q.-H.; Shen, X.; Ni, X.-D.; Yao, Y.; Yu, R.-C. Room-Temperature Magnetism Realized by Doping Fe into Ferroelectric LiTaO3. Chin. Phys. Lett. 2014, 31, 017501. [Google Scholar] [CrossRef]
- Verma, K.C.; Gupta, V.; Kaur, J.; Kotnala, R.K. Raman spectra, photoluminescence, magnetism and magnetoelectric coupling in pure and Fe doped BaTiO3 nanostructures. J. Alloy. Compnd. 2013, 578, 5–11. [Google Scholar] [CrossRef]
- Zeng, F.; Sheng, P.; Tang, G.S.; Pan, F.; Yan, W.S.; Hu, F.C.; Zou, Y.; Huang, Y.Y.; Jiang, Z.; Guo, D. Electronic structure and magnetism of Fe-doped LiNbO3. Mater. Chem. Phys. 2012, 136, 783–788. [Google Scholar] [CrossRef]
- Yao, D.; Zhou, X.; Ge, S. Raman scattering and room temperature ferromagnetism in Co-doped SrTiO3 particles. Appl. Surf. Sci. 2011, 257, 9233–9236. [Google Scholar] [CrossRef]
- Chen, C.; Zeng, F.; Li, J.H.; Sheng, P.; Luo, J.T.; Yang, Y.C.; Pan, F.; Zou, Y.; Huang, Y.Y.; Jiang, Z. Strong d–d electron interaction inducing ferromagnetism in Mn-doped LiNbO3. Thin Film Solids 2011, 520, 764–768. [Google Scholar] [CrossRef]
- Coey, J.M.D. Dilute Magnetic Oxides. Curr. Opin. Solid State Mater. Sci. 2006, 10, 83–92. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Mlack, J.T.; Venkatesan, M.; Stamenov, P. Magnetization Process in Dilute Magnetic Oxides. IEEE Trans. Magn. 2010, 46, 2501–2503. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
- Edwards, D.M.; Katsnelson, M.I. High-temperature ferromagnetism of sp electrons in narrow impurity bands: Application to CaB6. J. Phys. Condens. Matter 2006, 18, 7209–7225. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Wongsaprom, K.; Alaria, J.; Venkatesan, M. Charge-transfer ferromagnetism in oxide nanoparticles. J. Phys. D Appl. Phys. 2008, 41, 134012. [Google Scholar] [CrossRef]
- Song, C.; Zeng, F.; Shen, Y.X.; Geng, K.W.; Xie, Y.N.; Wu, Z.Y.; Pan, F. Local Co structure and ferromagnetism in ion-implanted Co-doped LiNbO3. Phys. Rev. B 2006, 73, 172412. [Google Scholar] [CrossRef]
- Vitova, T.; Hormes, J.; Falk, M.; Buse, K. Site-selective investigation of site symmetry and site occupation of iron in Fe-doped lithium niobate crystals. J. Appl. Phys. 2009, 105, 013524. [Google Scholar] [CrossRef]
- Olimov, K.; Falk, M.; Buse, K.; Woike, T.; Hormes, J.; Modrow, H. X-ray absorption near edge spectroscopy investigations of valency and lattice occupation site of Fe in highly iron-doped lithium niobate crystals. J. Phys. Condes. Matter 2006, 18, 5135–5146. [Google Scholar] [CrossRef]
- Bush, T.S.; Catlow, C.R.A.; Chadwick, A.V.; Cole, M.; Geatches, R.M.; Greaves, G.N.; Tomlinson, S.M. Studies of cation dopant sites in metal oxides by EXAFS and computer-simulation techniques. J. Mater. Chem. 1992, 2, 309–316. [Google Scholar] [CrossRef]
- Ye, J.; Sun, X.; Wu, Z.; Liu, J.; An, Y. Evidence of the oxygen vacancies-induced room temperature ferromagnetism in multiferroic Co-doped LiNbO3 films. J. Alloy. Compnd. 2018, 768, 750–755. [Google Scholar] [CrossRef]
- Sheng, P.; Zeng, F.; Tang, G.S.; Pan, F.; Yan, W.S.; Hu, F.C. Structure and ferromagnetism in vanadium-doped LiNbO3. J. Appl. Phys. 2012, 112, 033913. [Google Scholar] [CrossRef]
- Song, C.; Wang, C.; Liu, X.; Zeng, F.; Pan, F. Room Temperature Ferromagnetism in Cobalt-Doped LiNbO3 Single Crystalline Films. Cryst. Growth Des. 2009, 9, 1235–1239. [Google Scholar] [CrossRef]
- Song, C.; Wang, C.Z.; Yang, Y.C.; Liu, X.J.; Zeng, F.; Pan, F. Room temperature ferromagnetism and ferroelectricity in cobalt-doped LiNbO3 film. Appl. Phys. Lett. 2008, 92, 262901. [Google Scholar] [CrossRef]
- Yang, D.-S.; Sung, N.; Yeom, T.H. Local Structure of Fe-Doped LiNbO3 Crystal Measured by X-ray Absorption Fine Structure. J. Phys. Soc. Jpn. 2009, 78, 114605. [Google Scholar] [CrossRef]
- Bu, D.; Fu, Y.; Sun, N.; Li, C.; Li, Y.; An, Y.; Liu, J. Effect of Cu doping on room temperature ferromagnetic behavior of Mn doped LiNbO3 films. J. Cryst. Growth 2016, 453, 198–202. [Google Scholar] [CrossRef]
- Fierro-Ruíz, C.D.; Sánchez-Dena, O.; Cabral-Larquier, E.M.; Elizalde-Galindo, J.T.; Farías, R. Structural and Magnetic Behavior of Oxidized and Reduced Fe Doped LiNbO3 Powders. Crystals 2018, 8, 108. [Google Scholar] [CrossRef]
- Díaz-Moreno, C.A.; Farías-Mancilla, R.; Matutes-Aquino, J.A.; Elizalde-Galindo, J.; Espinosa-Magaña, F.; Hernández-González, J.; Hurtado-Macías, A. Magnetic behavior in LiNbO3 nanocrystallites caused by oxygen vacancies. J. Magn. Magn. Mater. 2014, 356, 82–86. [Google Scholar] [CrossRef]
- Díaz-Moreno, C.; Farias, R.; Hurtado-Macias, A.; Elizalde-Galindo, J.; Hernandez-Paz, J. Multiferroic response of nanocrystalline lithium niobate. J. Appl. Phys. 2012, 111, 07D907. [Google Scholar] [CrossRef]
- Ishii, M.; Ohta, D.; Uehara, M.; Kimishima, Y. Ferromagnetism of Nano-LiNbO3 with Vacancies. Trans. Mat. Res. Soc. Jpn. 2012, 37, 443–446. [Google Scholar] [CrossRef][Green Version]
- Cao, E.; Zhang, Y.; Qin, H.; Zhang, L.; Hu, J. Vacancy-induced magnetism in ferroelectric LiNbO3 and LiTaO3. Phys. B Condens. Matter 2013, 410, 68–73. [Google Scholar] [CrossRef]
- Yan, T.; Ye, N.; Xu, L.; Sang, Y.; Chen, Y.; Song, W.; Long, X.; Wang, J.; Liu, H. Ferromagnetism in chemically reduced LiNbO3 and LiTaO3 crystals. J. Phys. D Appl. Phys. 2016, 49, 195005. [Google Scholar] [CrossRef]
- Kocsor, L.; Péter, L.; Corradi, G.; Kis, Z.; Gubicza, J.; Kovács, L. Mechanochemical Reactions of Lithium Niobate Induced by High-Energy Ball-Milling. Crystals 2019, 9, 334. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Reddy, J.M.; Bernstein, J.L. Ferroelectric Lithium Niobate—3. Single crystal X-ray diffraction study at 24 °C. J. Phys. Chem. Solids 1966, 27, 971–1012. [Google Scholar]
- Abrahams, S.C.; Reddy, J.M.; Bernstein, J.L. Ferroelectric Lithium Tantalate—1. Single crystal X-ray diffraction study at 24 °C. J. Phys. Chem. Solids 1967, 28, 1685–1692. [Google Scholar] [CrossRef]
- Huband, S.; Keeble, D.S.; Zhang, N.; Glazer, A.M.; Bartasyte, A.; Thomas, P.A. Crystallographic and optical study of LiNb1−xTaxO3. Acta Cryst. 2017, B73, 498–506. [Google Scholar] [CrossRef] [PubMed]
- Sidorov, N.V.; Serebryakov, Y.A. Investigation of structural peculiarities of impure lithium niobate crystals by Raman spectroscopy. Vib. Spectrosc. 1994, 6, 215–223. [Google Scholar] [CrossRef]
- Bäumer, C.; David, C.; Tunyagi, A.; Betzler, K.; Hesse, H.; Krätzig, E.; Wöhlecke, M. Composition dependene of the ultraviolet absorption edge in lithium tantalite. J. Appl. Phys. 2003, 93, 3102–3104. [Google Scholar] [CrossRef]
- Kovács, L.; Ruschhaupt, G.; Polgár, K.; Corradi, G.; Wöhlecke, M. Composition dependence of the ultraviolet absorption edge in lithium niobate. Appl. Phys. Lett. 1997, 70, 2801–2803. [Google Scholar] [CrossRef]
- Young, S.-L.; Kao, M.-C.; Chen, H.-Z. The properties of tantalum modified lithium niobate thin films prepared by a diol-based sol-gel process. Eur. Phys. J. Appl. Phys. 2006, 36, 5–10. [Google Scholar] [CrossRef]
- Kao, M.C.; Chen, H.Z.; Yang, S.L.; Chen, Y.C.; Hsieh, P.T.; Yu, C.C. Pyroelectric Ta-modified LiNbO3 thin films and devices for thermal infrared detection. Thin Film Solids 2008, 516, 5518–5522. [Google Scholar] [CrossRef]
- Irzaman; Sitompul, H.; Masitoh; Misbakhusshudur, M.; Mursyidah. Optical and structural properties of lanthanum doped lithium niobate thin films. Ferroelectrics 2016, 502, 9–18. [Google Scholar] [CrossRef]
- Thierfelder, C.; Sanna, S.; Schindlmayr, A.; Schmidt, W.G. Do we know the band gap of lithium niobate? Phys. Status Solidi C 2010, 7, 362–365. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Dena, O.; Villalobos-Mendoza, S.D.; Farías, R.; Fierro-Ruiz, C.D. Lithium Niobate Single Crystals and Powders Reviewed—Part II. Crystals 2020, 10, 990. https://doi.org/10.3390/cryst10110990
Sánchez-Dena O, Villalobos-Mendoza SD, Farías R, Fierro-Ruiz CD. Lithium Niobate Single Crystals and Powders Reviewed—Part II. Crystals. 2020; 10(11):990. https://doi.org/10.3390/cryst10110990
Chicago/Turabian StyleSánchez-Dena, Oswaldo, Sergio David Villalobos-Mendoza, Rurik Farías, and Cesar David Fierro-Ruiz. 2020. "Lithium Niobate Single Crystals and Powders Reviewed—Part II" Crystals 10, no. 11: 990. https://doi.org/10.3390/cryst10110990
APA StyleSánchez-Dena, O., Villalobos-Mendoza, S. D., Farías, R., & Fierro-Ruiz, C. D. (2020). Lithium Niobate Single Crystals and Powders Reviewed—Part II. Crystals, 10(11), 990. https://doi.org/10.3390/cryst10110990






