Cyclic Automated Model Building (CAB) Applied to Nucleic Acids
Abstract
1. Introduction
2. CAB Algorithm for Locating Ligand Heavy Atoms
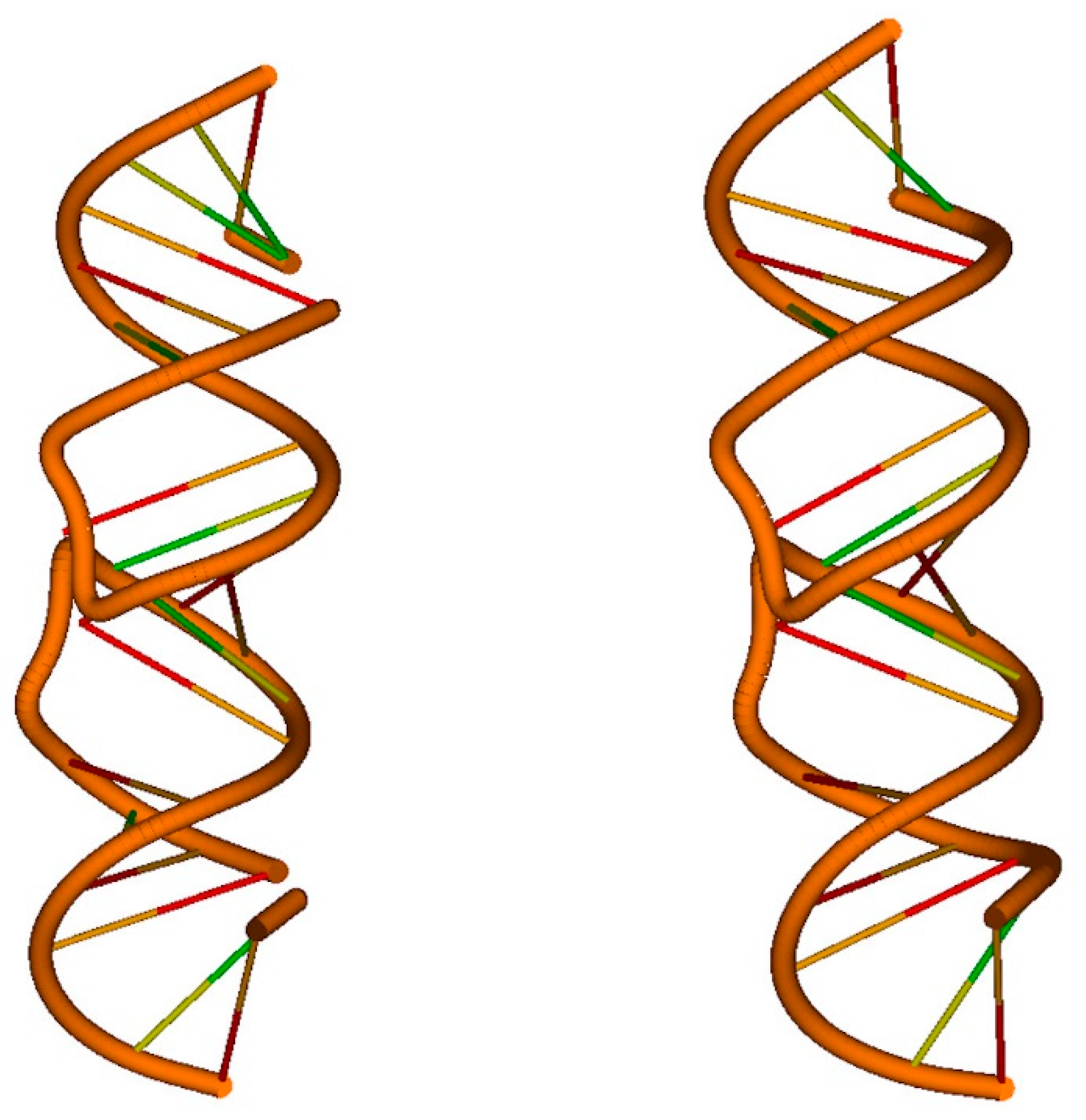
3. The Recursive Algorithm
4. Applications
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMB | automated model building. |
| MR | molecular replacement. |
| R | crystallographic residual between observed and calculated structure factor amplitudes (for all of the experimental data). |
| Rf | cross validation R-value for the free data set [63]. |
| MA | ratio “number of residues with P atoms within 0.6Å distance from the published positions/number of residues in the asymmetric unit”, according to the published sequence. It is an indication of the accuracy of the model. |
| MAM ratio | “number of non-hydrogen atoms within 0.6Å distance from published positions/number of non-hydrogen atoms in the asymmetric unit”. |
References
- Cowtan, K.D. The Buccaneer software for automated model building. Tracing protein chains. Acta Cryst. 2006, D62, 1002–1011. [Google Scholar] [CrossRef]
- Langer, G.; Cohen, S.X.; Lamzin, V.S.; Perrakis, A. Automated macromolecular model building for X-ray crystallography using ARP/wARP version 7. Nat. Protoc. 2008, 3, 1171–1179. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Grosse-Kunstleve, R.W.; Afonine, P.V.; Moriarty, N.W.; Zwart, P.H.; Hung, L.-W.; Read, R.J.; Adams, P.D. Iterative model building, structure refinement and density modification with the PHENIX AutoBuild wizard. Acta Cryst. 2008, D64, 61–69. [Google Scholar] [CrossRef]
- Wang, X.; Kapral, G.; Murray, L.; Richardson, D.; Richardson, J.; Snoeying, J. RNABC: Forward kinematics to reduce all-atom steric clashes in RNA backbone. J. Math. Biol. 2008, 56, 253–278. [Google Scholar] [CrossRef][Green Version]
- Yamashita, K.; Zhou, Y.; Tanaka, I.; Yao, M. New model-fitting and model-completion programs for automated iterative nucleic acid refinement. Acta Cryst. 2013, D69, 1171–1179. [Google Scholar] [CrossRef]
- Keating, K.S.; Pyle, A.M. RCrane: Semi-automated RNA model building. Acta Cryst. 2012, D68, 985–995. [Google Scholar] [CrossRef]
- Keating, K.S.; Pyle, A.M. Semi-automated model building for RNA crystallography using a directed rotameric approach. Proc. Natl. Acad. Sci. USA 2010, 107, 8177–8182. [Google Scholar] [CrossRef]
- Murray, L.J.; Arendall, W.B.; Richardson, D.C.; Richardson, J.S. RNA backbone is rotameric. Proc. Natl. Acad. Sci. USA 2003, 100, 13904–13909. [Google Scholar] [CrossRef]
- Hattne, J.; Lamzin, V.S. Pattern-recognition-based detection of planar objects in three-dimensional electron-density maps. Acta Cryst. 2008, D64, 834–842. [Google Scholar] [CrossRef]
- Cowtan, K. Automated nucleic acid chain tracing in real time. IUCR J. 2014, 1, 387–392. [Google Scholar] [CrossRef]
- Murshudov, G.N.; Vagin, A.A.; Lebedev, A.; Wilson, K.S.; Dodson, E.J. Efficient anisotropic refinement of macromolecular structures using FFT. Acta Cryst. 1999, D55, 247–255. [Google Scholar] [CrossRef]
- Afonine, P.V.; Grosse-Kunstleve, R.W.; Echols, N.; Headd, J.J.; Moriarty, N.W.; Mustyakimov, M.; Terwilliger, T.C.; Urzhumtsev, A.; Zwart, P.H.; Adams, P.D. Towards automated crystallographic structure refinement with phenix.refine. Towards automated crystallographic structure refinement with phenix.refine. Acta Cryst. 2012, D68, 352–367. [Google Scholar] [CrossRef]
- Burla, M.C.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Polidori, G. CAB: A cyclic automatic model building procedure. Acta Cryst. 2018, D74, 1096–1104. [Google Scholar] [CrossRef]
- Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Mazzone, A.; Siliqi, D. Molecular replacement: The probabilistic approach of the program REMO09 and its applications. Acta Cryst. 2009, A65, 512–527. [Google Scholar] [CrossRef]
- Burla, M.C.; Cascarano, G.L.; Giacovazzo, C.; Polidori, G. Synergy among phase-refinement techniques in macromolecular crystallography. Acta Cryst. 2017, D73, 877–888. [Google Scholar] [CrossRef]
- Cowtan, K. Fast Fourier feature recognition. Acta Cryst. 2001, D57, 1435–1444. [Google Scholar] [CrossRef]
- Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; De Caro, L.; Giacovazzo, C.; Siliqi, D. Phasing at resolution higher than the experimental resolution. Acta Cryst. 2005, D61, 556–565. [Google Scholar] [CrossRef]
- Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; De Caro, L.; Giacovazzo, C.; Siliqi, D. Ab initio phasing at resolution higher than experimental resolution. Acta Cryst. 2005, D61, 1080–1087. [Google Scholar] [CrossRef]
- Giacovazzo, C.; Siliqi, D. Improving Direct Methods phases by Heavy-Atom information and Solvent Flattening. Acta Cryst. 1997, D53, 789–798. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Giacovazzo, C.; Polidori, G. The difference electron density: A probabilistic reformulation. Acta Cryst. 2010, A66, 347–361. [Google Scholar] [CrossRef]
- Burla, M.C.; Giacovazzo, C.; Polidori, G. From a random to the correct structure: The VLD algorithm. J. Appl. Cryst. 2010, 43, 825–836. [Google Scholar] [CrossRef]
- Giacovazzo, C. Solution of the phase problem at non-atomic resolution by the Phantom Derivative method. Acta Cryst. 2015, D71, 483–512. [Google Scholar] [CrossRef] [PubMed]
- Giacovazzo, C. From direct-space discrepancy functions to crystallographic least squares. Acta Cryst. 2015, D71, 36–45. [Google Scholar] [CrossRef]
- Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C. Phase improvement via the Phantom Derivative technique: Ancils that are related to the target structure. Acta Cryst. 2016, A72, 551–557. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; Cuocci, C.; Giacovazzo, C.; Mallamo, M.; Mazzone, A.; Polidori, G. Crystal structure determination and refinement via SIR2014. J. Appl. Cryst. 2015, 48, 306–309. [Google Scholar] [CrossRef]
- Burla, M.C.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Polidori, G. How far are we from automatic crystal structure solution via molecular-replacement techniques? Acta Cryst. 2020, D76, 9–18. [Google Scholar] [CrossRef]
- Campbell, N.H.; Parkinson, G.N.; Reszka, A.P.; Neidle, S. Structural basis of DNA quadruplex recognition by an acridine drug. J. Am. Chem. Soc. 2008, 130, 6722–6724. [Google Scholar] [CrossRef]
- Millonig, H.; Pous, J.; Gouyette, C.; Subirana, J.A.; Campos, J.L. The interaction of manganese ions with DNA. J. Inorg. Biochem. 2009, 103, 876–880. [Google Scholar] [CrossRef]
- Juan, E.C.M.; Shimizu, S.; Ma, X.; Kurose, T.; Haraguchi, T.; Zhang, F.; Tsunoda, M.; Ohkubo, A.; Sekine, M.; Shibata, T.; et al. Insights into the DNA stabilizing contributions of a bicyclic cytosine analogue: Crystal structures of DNA duplexes containing 7,8-dihydropyrido [2,3-d]pyrimidin-2-one. Nucleic Acids Res. 2010, 38, 6737–6745. [Google Scholar] [CrossRef]
- Carter, M.; Ho, P.S. Assaying the energies of biological halogen bonds. Cryst. Growth Des. 2011, 11, 5087–5095. [Google Scholar] [CrossRef]
- Carter, M.; Voth, A.R.; Scholfield, M.R.; Rummel, B.; Sowers, L.C.; Ho, P.S. Enthalpy-entropy compensation in biomolecular halogen bonds measured in DNA junctions. Biochemistry 2013, 52, 4891–4903. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.P. The Effects of Disubstitution on the Binding of Ruthenium Complexes to DNA. Ph.D. Thesis, University of Reading, Reading, UK, 2014. [Google Scholar]
- Rohner, M.; Medina-Molner, A.; Spingler, B. N,N,O and N,O,N meridional cis coordination of two guanines to copper(II) by d(CGCGCG)2. Inorg. Chem. 2016, 55, 6130–6140. [Google Scholar] [CrossRef] [PubMed]
- Russo Krauss, I.; Ramaswamy, S.; Neidle, S.; Haider, S.; Parkinson, G.N. Structural insights into the quadruplex-duplex 3′ interface formed from a telomeric repeat: A potential molecular target. J. Am. Chem. Soc. 2016, 138, 1226–1233. [Google Scholar] [CrossRef] [PubMed]
- Ahmad Sobri, A.F.; Brady, R.L. Non-natural DNA pair Z (6-amino-5-nitro-2[1H] pyridone heterocycle)-guanosine. 2016; Unpublished work. [Google Scholar]
- Sbirkova, H.I.; Schivachev, B.L. Crystal structure of a DNA sequence d(CGTGAATTCACG) at 130K. Bulg. Chem. Commun. 2016, 48, 589–593. [Google Scholar]
- Reichenbach, L.F.; Sobri, A.A.; Zaccai, N.R.; Agnew, C.R.J.; Burton, N.; Eperon, L.P.; de Ornellas, S.; Eperon, I.C.; Brady, R.L.; Burley, G.A. Structural basis of the mispairing of an artificially expanded genetic information system. Chemistry 2016, 1, 946–958. [Google Scholar] [CrossRef][Green Version]
- Hardwick, J.S.; Ptchelkine, D.; El-Sagheer, A.H.; Tear, I.; Singleton, D.; Phillips, S.E.V.; Lane, A.N.; Brown, T. 5-Formylcytosine does not change the global structure of DNA. Nat. Struct. Mol. Biol. 2017, 24, 544–552. [Google Scholar] [CrossRef]
- Sbirkova, H.I.; Schivachev, B.L. The effect of berenil and cacodylate on the crystal structure of d(CGTGAATTCACG). 2017; Unpublished work. [Google Scholar]
- Sbirkova-Dimitrova, H.I.; Shivachev, B.L. Crystal structure of the DNA sequence d(CGTGAATTCACG)2 with DAPI. Acta Cryst. 2017, 73, 500–504. [Google Scholar] [CrossRef]
- Cruse, W.; Saludjian, P.; Neuman, A.; Prange, T. Destabilizing effect of a fluorouracil extra base in a hybrid RNA duplex compared with bromo and chloro analogues. Acta Cryst. 2001, D57, 1609–1613. [Google Scholar] [CrossRef]
- Gherghe, C.M.; Krahn, J.M.; Weeks, K.M. Crystal structures, reactivity and inferred acylation transition states for 2′-amine substituted RNA. J. Am. Chem. Soc. 2005, 127, 13622–13628. [Google Scholar] [CrossRef]
- Haeberli, P.; Berger, I.; Pallan, P.S.; Egli, M. Syntheses of 4′-thioribonucleosides and thermodynamic stability and crystal structure of RNA oligomers with incorporated 4′-thiocytosine. Nucleic Acids Res. 2005, 33, 3965–3975. [Google Scholar] [CrossRef][Green Version]
- Ennifar, E.; Paillart, J.C.; Bodlenner, A.; Walter, P.; Weibel, J.-M.; Aubertin, A.-M.; Pale, P.; Dumas, P.; Marquet, R. Targeting the dimerization initiation site of HIV-1 RNA with aminoglycosides: From crystal to cell. Nucleic Acids Res. 2006, 34, 2328–2339. [Google Scholar] [CrossRef]
- Zhao, Q.; Han, Q.; Kissinger, C.R.; Hermann, T.; Thompson, P.A. Structure of hepatitis C virus IRES subdomain IIa. Acta Cryst. 2008, D64, 436–443. [Google Scholar] [CrossRef]
- Thore, S.; Frick, C.; Ban, N. Structural basis of thiamine pyrophosphate analogues binding to the eukaryotic riboswitch. J. Am. Chem. Soc. 2008, 130, 8116–8117. [Google Scholar] [CrossRef]
- Pitt, J.N.; Ferre-D’Amare, A.R. Structure-guided engineering of the regioselectivity of RNA ligase ribozymes. J. Am. Chem. Soc. 2009, 131, 3532–3540. [Google Scholar] [CrossRef]
- Ren, A.; Rajashankar, K.R.; Patel, D.J. Fluoride ion encapsulation by Mg2+ ions and phosphates in a fluoride riboswitch. Nature 2012, 486, 85–89. [Google Scholar] [CrossRef]
- Vorobiev, S.M.; Ma, L.-C.; Montelione, G.T. Crystal structure of the 16-mer double stranded RNA. 2016; Unpublished work. [Google Scholar]
- Monestier, A.; Aleksandrov, A.; Coureux, P.D.; Panvert, M.; Mechulam, Y.; Schmitt, E. The structure of an E. coli tRNAf(Met) A1-U72 variant shows an unusual conformation of the A1-U72 base pair. RNA 2017, 23, 673–682. [Google Scholar] [CrossRef]
- Huang, L.; Wang, J.; Wilson, T.J.; Lilley, D.M.J. Structure of the guanidine III riboswitch. Cell Chem. Biol. 2017, 24, 1407–1415. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Z. DNA 8mer containing two 2SeT modifications. 2016; Unpublished work. [Google Scholar]
- Zhang, W.; Tam, C.P.; Zhou, L.; Oh, S.S.; Wang, J.; Szostak, J.W. Structural Rationale for the Enhanced Catalysis of Nonenzymatic RNA Primer Extension by a Downstream Oligonucleotide. J. Am. Chem. Soc. 2018, 140, 2829–2840. [Google Scholar] [CrossRef]
- Emsley, P.; Lohkamp, B.; Scott, W.G.; Cowtan, K. Features and development of Coot. Acta Cryst. 2010, D66, 486–501. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E.I.I.I.; Darden, T.; Gohlke, H.; Luo, R.; Merz KMJr Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Chou, F.C.; Sripakdeevong, P.; Dibrov, S.M.; Hermann, T.; Das, R. Correcting pervasive errors in RNA crystallography through enumerative structure prediction. Nat. Methods 2013, 10, 74–76. [Google Scholar] [CrossRef]
- Das, R.; Karanicolas, J.; Baker, D. Atomic accuracy in predicting and designing noncanonical RNA structure. Nat. Methods 2010, 7, 291–294. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Chou, F.-C.; Das, R. Modeling Complex RNA Tertiary Folds with Rosetta. Methods Enzymol. 2015, 553, 35–64. [Google Scholar] [CrossRef]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.W.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. Rosetta3: An Object-Oriented Software Suite for the Simulation and Design of Macromolecules. Methods Enzymol. 2011, 487, 545–574. [Google Scholar] [CrossRef]
- Pavelcik, F.; Schneider, B. Building of RNA and DNA double helices into electron density. Acta Cryst. 2008, D64, 620–626. [Google Scholar] [CrossRef]
- Pavelcik, F. Application of constrained real-space refinement of flexible molecular fragments to automatic model building of RNA structures. J. Appl. Cryst. 2012, 45, 309–315. [Google Scholar] [CrossRef]
- Lu, X.L.; Olson, W.K. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003, 31, 5108–5121. [Google Scholar] [CrossRef]
- Brünger, A.T. Free R value: A novel statistical quantity for assessing the accuracy of crystal structures. Nature 1992, 355, 472–475. [Google Scholar] [CrossRef]


| PDB | SG | RES | nN | Model | Ligand(s) |
|---|---|---|---|---|---|
| 3ce5 [27] | I 4 | 2.50 | 2·12 | 1k8p | 2·K + BRA |
| 3eil [28] | P 32 | 2.60 | 6·12 | 3·463d | 7·Mn |
| 3n4o [29] | P 21 21 21 | 2.90 | 2·12 | 1dnh | 2·B7C + HT |
| 3tok [30] | C 2 | 1.74 | 10 + 10 | 2org | Na |
| 4gsg [31] | C 2 | 2.00 | 2·(10 + 10) | 2·2org | UCL |
| 4ms5 [32] | P 43 21 2 | 2.23 | 1·10 | 3qrn | Ba + RKF |
| 4xqz [33] | P 21 | 2.15 | 8·6 | 2·5ihd | 6·Cu + 4·Ca + 7·Cl + MES + MOH |
| 5dwx [34] | P 4 21 2 | 2.71 | 24 + 8 | 1kf1 | K |
| 5i4s [35] | R 3 | 2.46 | 2·12 | 476d | 8·Ca + 2·1W5 |
| 5ihd [33] | P 21 | 1.57 | 4·6 | 2·2dcg | 4·Cu + 2·Ca + 2·2OP + SIN |
| 5ju4 [36] | P 21 21 21 | 2.00 | 2·12 | 1d29 | Mg + Cl |
| 5lj4 [37] | R 3 | 2.17 | 2·12 | 463d | 4·Ca + 2·1W5 + 2·1WA |
| 5mvt [38] | P 31 2 1 | 1.89 | 2·12 | 5mvl | 3·Co |
| 5nt5 [39] | P 21 21 21 | 2.30 | 2·12 | 1d29 | Na + CAC |
| 5t4w [40] | P 21 21 21 | 2.30 | 2·12 | 5jua | DAP |
| 1iha [41] | C 2 | 1.60 | 2·9 | 165d | 2·Cl + 2·BRU + 2·RHD |
| 1z7f [42] | P 31 2 1 | 2.10 | 3·16 | 1yrm | 2·Sr |
| 2a0p [43] | R 3 2 | 1.95 | 2·8 | 259d | S4C |
| 2fd0 [44] | C 2 2 21 | 1.80 | 2·23 | 2fcy | K + Cl + 5BU + LIV |
| 2pn4 [45] | P 21 21 21 | 2.32 | 2·(24 + 20) | 2·2pn3 | 10·Sr + 4·5BU |
| 3d2v [46] | P 21 21 2 | 2.00 | 2·77 | 2cky | 10·Mg + 2·PYI |
| 3fs0 [47] | P 31 | 2.30 | 10 + 11 | ½·3ftm | 3·Mg |
| 4enc [48] | P 21 21 2 | 2.27 | 52 | 4enb | 5·Mg + K + F |
| 5kvj [49] | R 3 | 2.26 | 16 + 16 | 2·3nd3 | ARG |
| 5l4o [50] | P 32 1 2 | 2.80 | 77 | 3cw5 | Na + PSU + OMC + 4SU + 5MU + H2U |
| 5nz6 [51] | P 32 1 2 | 2.94 | 41 | ½·5nwq | 2·CBV + GAI |
| 5tgp [52] | P 61 | 1.60 | 2·8 | 2·1dns | 4·US3 |
| 5uz6 [53] | C 2 | 2.10 | 3·(25 + 8) | 3·5ux3 | 8OS + LCC |
| 6az4 [53] | P 41 21 2 | 2.98 | 32 + 9 | 4fnj | GP3 |
| Ligand Information | |||||
| Code | Formula | Code | Formula | Code | Formula |
| 1W5 | C10 H14 N3 O9 P | BRU | C9 H12 Br N2 O8 P | MES | C6 H13 N O4 S |
| 1WA | C10 H16 N5 O7 P | CAC | C2 H6 As O2 | MOH | C H4 O |
| 2OP | C3 H6 O3 | CBV | C9 H13 Br N3 O8 P | OMC | C10 H16 N3 O8 P |
| 4SU | C9 H13 N2 O8 P S | DAP | C16 H15 N5 | PSU | C9 H13 N2 O9 P |
| 5BU | C9 H12 Br N2 O9 P | GAI | C H5 N3 | PYI | C14 H21 N4 O7 P2 |
| 5MU | C10 H15 N2 O9 P | GP3 | C20 H27 N10 O18 P3 | RHD | Rh3 H18 N6 |
| 8OS | C14 H18 N7 O7 P | H2U | C9 H15 N2 O9 P | RKF | C38 H20 F2 N13 Ru |
| ARG | C6 H15 N4 O2 | HT | C25 H24 N6 O | S4C | C9 H14 N3 O7 P S |
| B7C | C12 H16 N3 O7 P | LCC | C11 H16 N3 O8 P | SIN | C4 H6 O4 |
| BRA | C35 H43 N7 O2 | LIV | C29 H55 N5 O18 | UCL | C9 H12 Cl N2 O8 P |
| US3 | C10 H15 N2 O7 P Se | ||||
| PDB | <|Δϕr|>° | Rr | Rf | RN | RfN | MAN | MAMN | RC | RfC | MAC | MAMC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3ce5 | 50 | 41 | 43 | 54 | 59 | 36 | 16 | 52 | 53 | 41 | 18 |
| 3eil | 46 | 31 | 36 | 47 | 50 | 59 | 43 | 36 | 38 | 82 | 76 |
| 3n4o | 33 | 23 | 26 | 44 | 45 | 55 | 36 | 23 | 26 | 91 | 69 |
| 3tok | 49 | 35 | 35 | 57 | 58 | 44 | 15 | 52 | 56 | 72 | 24 |
| 4gsg | 53 | 34 | 38 | 45 | 45 | 17 | 9 | 42 | 46 | 44 | 17 |
| 4ms5 | 59 | 46 | 64 | 56 | 57 | 0 | 4 | 37 | 41 | 78 | 57 |
| 4xqz | 48 | 32 | 35 | 58 | 58 | 30 | 22 | 27 | 30 | 80 | 94 |
| 5dwx | 58 | 41 | 44 | 57 | 58 | 18 | 5 | 48 | 59 | 32 | 25 |
| 5i4s | 35 | 25 | 29 | 36 | 37 | 59 | 49 | 35 | 34 | 82 | 51 |
| 5ihd | 39 | 34 | 36 | 51 | 52 | 50 | 39 | 25 | 29 | 100 | 92 |
| 5ju4 | 26 | 26 | 28 | 37 | 37 | 95 | 83 | 26 | 28 | 100 | 100 |
| 5lj4 | 29 | 25 | 29 | 44 | 48 | 86 | 58 | 41 | 45 | 82 | 58 |
| 5mvt | 28 | 29 | 28 | 38 | 37 | 82 | 79 | 31 | 31 | 95 | 92 |
| 5nt5 | 24 | 27 | 28 | 46 | 47 | 86 | 64 | 27 | 28 | 100 | 99 |
| 5t4w | 25 | 25 | 29 | 43 | 42 | 86 | 64 | 25 | 29 | 100 | 96 |
| 1iha | 41 | 34 | 35 | 36 | 37 | 94 | 77 | 23 | 25 | 88 | 81 |
| 1z7f | 34 | 32 | 34 | 42 | 43 | 69 | 71 | 30 | 30 | 100 | 100 |
| 2a0p | 31 | 27 | 35 | 32 | 39 | 100 | 93 | 27 | 35 | 100 | 99 |
| 2fd0 | 33 | 32 | 36 | 37 | 38 | 89 | 78 | 32 | 36 | 95 | 85 |
| 2pn4 | 40 | 34 | 40 | 41 | 48 | 87 | 68 | 36 | 41 | 86 | 74 |
| 3d2v | 57 | 47 | 51 | 49 | 51 | 34 | 29 | 49 | 50 | 32 | 30 |
| 3fs0 | 63 | 42 | 47 | 40 | 41 | 68 | 51 | 29 | 33 | 89 | 86 |
| 4enc | 28 | 25 | 28 | 36 | 39 | 83 | 74 | 25 | 28 | 98 | 95 |
| 5kvj | 49 | 31 | 39 | 37 | 46 | 94 | 55 | 32 | 41 | 94 | 63 |
| 5l4o | 40 | 31 | 36 | 35 | 39 | 74 | 51 | 34 | 39 | 74 | 53 |
| 5nz6 | 45 | 23 | 23 | 39 | 43 | 75 | 44 | 31 | 32 | 90 | 53 |
| 5tgp | 26 | 28 | 29 | 51 | 51 | 43 | 40 | 27 | 27 | 100 | 100 |
| 5uz6 | 34 | 34 | 36 | 30 | 33 | 99 | 88 | 30 | 33 | 99 | 88 |
| 6az4 | 51 | 36 | 40 | 28 | 30 | 87 | 63 | 28 | 30 | 87 | 63 |
| With | Without | |||
|---|---|---|---|---|
| PDB | MAC | MAMC | MAC | MAMC |
| 3n4o | 91 | 69 | 77 | 38 |
| 4xqz | 80 | 94 | 43 | 30 |
| 5ihd | 100 | 92 | 70 | 47 |
| 5ju4 | 100 | 100 | 95 | 83 |
| 5nt5 | 100 | 99 | 100 | 87 |
| 5t4w | 100 | 96 | 91 | 64 |
| 1iha | 88 | 81 | 81 | 77 |
| 2a0p | 100 | 99 | 100 | 99 |
| 2fd0 | 95 | 85 | 95 | 81 |
| 4enc | 98 | 95 | 83 | 78 |
| 5tgp | 100 | 100 | 100 | 75 |
| ARP/wARP | PHENIX.AUTOBUILD | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PDB | <|Δϕr|>° | RA | RfA | MAA | MAMA | RP | RfP | MAP | MAMP |
| 3ce5 | 50 | 53 | 56 | 23 | 11 | 45 | 47 | 50 | 40 |
| 3eil | 46 | 48 | 56 | 26 | 15 | 43 | 47 | 73 | 53 |
| 3n4o | 33 | 33 | 52 | 64 | 25 | 33 | 37 | 82 | 57 |
| 3tok | 49 | 52 | 53 | 28 | 10 | 45 | 47 | 94 | 34 |
| 4gsg | 53 | 37 | 43 | 44 | 16 | 38 | 38 | 39 | 17 |
| 4ms5 | 59 | 0 | 0 | 0 | 0 | 48 | 53 | 44 | 29 |
| 4xqz | 48 | 53 | 54 | 13 | 5 | 57 | 60 | 10 | 11 |
| 5dwx | 58 | 40 | 47 | 36 | 10 | 49 | 53 | 27 | 27 |
| 5i4s | 35 | 34 | 44 | 50 | 20 | 36 | 39 | 50 | 49 |
| 5ihd | 39 | 51 | 51 | 10 | 5 | 52 | 56 | 25 | 19 |
| 5ju4 | 26 | 49 | 58 | 59 | 14 | 35 | 33 | 100 | 84 |
| 5lj4 | 29 | 41 | 52 | 55 | 25 | 40 | 41 | 68 | 65 |
| 5mvt | 28 | 45 | 51 | 50 | 22 | 46 | 44 | 91 | 60 |
| 5nt5 | 24 | 35 | 48 | 91 | 43 | 35 | 38 | 100 | 84 |
| 5t4w | 25 | 31 | 45 | 91 | 49 | 31 | 33 | 95 | 83 |
| 1iha | 41 | 41 | 41 | 75 | 51 | 36 | 33 | 81 | 64 |
| 1z7f | 34 | 40 | 46 | 69 | 32 | 35 | 36 | 91 | 82 |
| 2a0p | 31 | 39 | 53 | 86 | 40 | 31 | 37 | 93 | 93 |
| 2fd0 | 33 | 45 | 52 | 73 | 30 | 37 | 36 | 95 | 80 |
| 2pn4 | 40 | 47 | 55 | 32 | 13 | 42 | 48 | 57 | 52 |
| 3d2v | 57 | 56 | 57 | 6 | 3 | 47 | 48 | 26 | 23 |
| 3fs0 | 63 | 0 | 0 | 0 | 0 | 29 | 34 | 74 | 69 |
| 4enc | 28 | 33 | 46 | 79 | 34 | 40 | 41 | 71 | 67 |
| 5kvj | 49 | 39 | 55 | 59 | 20 | 35 | 40 | 84 | 63 |
| 5l4o | 40 | 44 | 53 | 46 | 16 | 45 | 50 | 54 | 49 |
| 5nz6 | 45 | 34 | 38 | 53 | 29 | 35 | 37 | 78 | 56 |
| 5tgp | 26 | 45 | 51 | 86 | 45 | 34 | 33 | 100 | 89 |
| 5uz6 | 34 | 34 | 40 | 91 | 53 | 33 | 33 | 91 | 82 |
| 6az4 | 51 | 42 | 46 | 38 | 15 | 39 | 40 | 67 | 53 |
| SUB1 | SUB2 | SUB3 | SUB4 |
|---|---|---|---|
| NAUTILUS [10] | RCRANE [6] in COOT [54] | NAFIT, NABUILD in LAFIRE [5] | AMBER [55] |
| ARP/wARP [9] | ERRASER [56] | FARFAR [57,58] | |
| PHENIX.AUTOB [3] | ROSETTA [59] | ||
| NUT/DHL/RSR [60,61] | 3DNA [62] | ||
| CAB |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burla, M.C.; Carrozzini, B.; Cascarano, G.L.; Giacovazzo, C.; Polidori, G. Cyclic Automated Model Building (CAB) Applied to Nucleic Acids. Crystals 2020, 10, 280. https://doi.org/10.3390/cryst10040280
Burla MC, Carrozzini B, Cascarano GL, Giacovazzo C, Polidori G. Cyclic Automated Model Building (CAB) Applied to Nucleic Acids. Crystals. 2020; 10(4):280. https://doi.org/10.3390/cryst10040280
Chicago/Turabian StyleBurla, Maria Cristina, Benedetta Carrozzini, Giovanni Luca Cascarano, Carmelo Giacovazzo, and Giampiero Polidori. 2020. "Cyclic Automated Model Building (CAB) Applied to Nucleic Acids" Crystals 10, no. 4: 280. https://doi.org/10.3390/cryst10040280
APA StyleBurla, M. C., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., & Polidori, G. (2020). Cyclic Automated Model Building (CAB) Applied to Nucleic Acids. Crystals, 10(4), 280. https://doi.org/10.3390/cryst10040280







