Abstract
The analysis of line broadening in X-ray and neutron diffraction patterns using profile functions constructed on the basis of well-established physical principles and TEM observations of lattice defects has proven to be a powerful tool for characterizing microstructures in crystalline materials. These principles are applied in the convolutional multiple-whole-profile (CMWP) procedure to determine dislocation densities, crystallite size, stacking fault and twin boundary densities, and intergranular strains. The different lattice defect contributions to line broadening are separated by considering the hkl dependence of strain anisotropy, planar defect broadening and peak shifts, and the defect dependent profile shapes. The Levenberg–Marquardt (LM) peak fitting procedure can be used successfully to determine crystal defect types and densities as long as the diffraction patterns are relatively simple. However, in more complicated cases like hexagonal materials or multiple-phase patterns, using the LM procedure alone may cause uncertainties. Here, we extended the CMWP procedure by including a Monte Carlo statistical method where the LM and a Monte Carlo algorithm were combined in an alternating manner. The updated CMWP procedure eliminated uncertainties and provided global optimized parameters of the microstructure in good correlation with electron microscopy methods.
1. Introduction
Line profile analysis (LPA) of X-ray and neutron diffraction patterns has proven to be a powerful method for quantitative and qualitative characterization of lattice defects in crystalline materials [1,2,3,4,5,6,7]. Formally, there are two different approaches for treating diffraction line broadening. The top-down approach uses closed-form profile functions, like Gaussian, Lorentzian, pseudo-Voight, or Pearson-VII, for fitting peak profiles [8,9,10,11]. Since these profile functions are of ad hoc mathematical character, it is difficult to establish a sound correlation between specific lattice defects and the parameters of these functions. The bottom-up approach is based on physical profiles developed by using the physical properties of specific lattice defects [2,3,4,5,6,12,13,14,15]. Size profile calculation is based on optical principles [16] and the concept of column lengths [17,18]. Size distribution is taken into account, assuming log-normal size distribution [6,12,19]. Strain broadening is described by the Krivoglaz–Wilkens theory of diffractions in dislocated crystals [2,3,20,21]. The Krivoglaz–Wilkens theory has been extended to heterogeneous dislocation distributions [4,22,23,24], to small dislocation loops in irradiated crystals [25], and to infinitesimal dislocation dipoles in strongly deformed crystals [26]. Line broadening caused by planar defects has been treated theoretically [27,28,29] and modeled numerically for twinning and staking faults [30,31,32]. Broadening related to elastic intergranular strains is modeled by taking into account the elastic anisotropy of the materials [25,33,34].
The Levenberg–Marquardt optimization procedure has been used successfully in innumerable cases, cf. [5,6,7,19,25,26,27,28,29,30,31,32,33,34,35] to determine crystal defect types and densities. In the present work, we developed a more robust procedure where the Levenberg–Marquardt and the Monte Carlo methods are applied consecutively to provide the global optimum values of the physical parameters characterizing microstructures. In a previous short letter-type report [15], the basics of the method were outlined briefly. Here, we provide a detailed and more elaborate description of the procedure and show its power by analyzing the depth dependence of the dislocation density, the planar defect density, and the grain size in a Zr matrix and in ZrH precipitates in a hydrated Zr specimen.
2. Fundamental Principles of the Convolutional Multiple-Whole-Profile (CMWP) Optimization Procedure
The convolutional multiple-whole-profile (CMWP) optimization method is based on physically modeled profile functions of different microstructure elements [12,13,14,15]. The two fundamental microstructure elements are size and strain [1]. In diffraction patterns they combine as convolution, and in a particular hkl diffraction peak they are
where and are the size and strain profiles. The variable s is
where ghkl is the fundamental reciprocal lattice vector of the hkl reflection and K is an arbitrary reciprocal space vector. Diffraction peaks are three-dimensional in reciprocal space [35]. In powder diffraction experiments, the intensity distributions are integrated along the surface perpendicular to the diffraction vector, ghkl, and Equations (1) and (2) reduce to one dimension in the radial direction.
where s = 2(sinθ − sinθB)/λ, θ and θB are the diffraction angle and the exact Bragg angle of the hkl peak, λ is the wavelength of radiation and * indicates convolution. The equivalent of Equation (1) in Fourier space is
where L is the Fourier variable. If planar defects, intergranular strains, and instrumental effects become substantial, the above equation is extended:
where , , and are the Fourier transforms of the profile functions of planar defects, intergranular strains, and instrumental effects. The Fourier transforms , , , and are modeled using physical properties of these lattice defects [15,25,30,31,32,33,34], whereas is determined by using measured patterns of defect-free standard materials. The latter can be determined by measuring the patterns of standard specimens, e.g., of Si, CeO2, diamond, or LaB6 standards. The diffraction pattern is calculated from the inverse Fourier transforms of Ahkl(L):
where and are the exact Bragg position and the intensity of the hkl reflection. The least-squares optimization is made by minimizing the weighted sum of squared residuals (WSSR):
where BG(2θi) is the background intensity at 2θi and wi are weights applied to the ith measured data.
s = K − ghkl
The size profile is calculated by taking into account the shape and size distribution of coherently scattering domains [17]. Assuming log-normal size distribution, the Fourier transform of size profiles can be written as [12,19]
where L is the Fourier variable, m and σ are the median and variance of the log-normal size distribution density function, and erfc is the complementary error function. Equation (8) is valid for spherical crystallites. The CMWP procedure yields the option to evaluate elliptical flat of long crystallites using the ellipticity parameter e which is the ratio of the long and short axis of rotational ellipsoids. With m and σ, the arithmetic-, area-, and volume-weighted mean crystallite diameters can be calculated [36].
where k = 0.5, 2.5, and 3.5 for arithmetic-, area-, and volume-weighted means, respectively, and j stands for these averages.
<x>j = m exp(kσ2)
The Fourier coefficients of the strain profile are [1]
where is the mean square strain (mss). Krivoglaz showed that strain broadening can only be caused by one-dimensional linear defects [20,21], and calculated for dislocations at small L values:
where ρ, C, and b are the density, the contrast, and the Burgers vector of dislocations, and D is the size of the crystal. This expression is logarithmically singular with increasing crystal size and is only valid for small L values. Wilkens [2,3] corrected the expression by replacing the crystal size with the effective outer cut-off radius of dislocations, Re, and calculated in the entire L range:
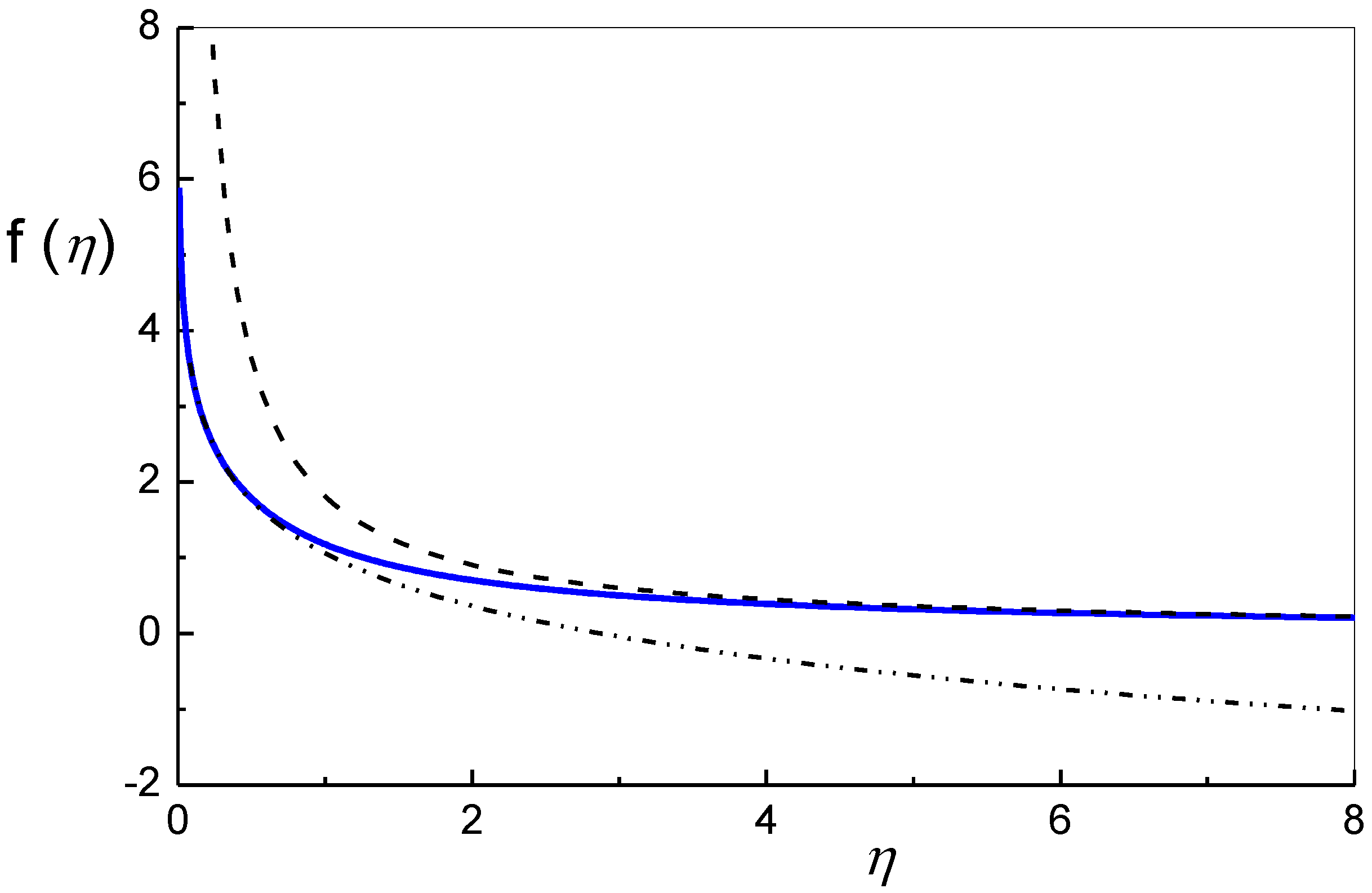
where η=L/Re. The f(η) function is logarithmic at small L values and hyperbolic at large L values. The explicit form of f(η) is given in Equations (A6) to (A8) in Reference [2] and is shown in Figure 1. The figure shows f(η) as a solid blue line, and the logarithmic and hyperbolic components are shown as dash-dot-dot and dashed lines, respectively.
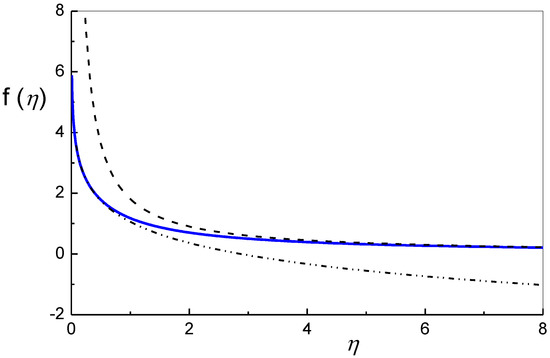
Figure 1.
The Wilkens function [2] (blue curve). The dot-dot-dash line is the logarithmic part, as in the Krivoglaz approximation [21]. The dash curve is the hyperbolic part. (Copyright by courtesy of Ribárik [12].)
The profile functions of faulted and twinned crystals consist of several sub-profiles [1]. Typical sub-profiles of the 311 reflection of copper containing 4% intrinsic stacking faults are shown in Figure 2 [30]. The number, positions and breadths of sub-profiles depend on the hkl indices of the fundamental Bragg peaks [1,27,28,29,30,31,32]. In the CMWP procedure, the shifts and breadths of the sub-profiles are parameterized as a function of the density of specific planar faults or twin boundaries [30,31]. The fractions of the sub-profiles are based on the multiplicities within the hkl reflection. The shifts and breadths of the sub-profiles are given by fifth-order polynomials of the planar fault density. The coefficients of the polynomials, along with the fractions of sub-profiles, are listed in the materials’ specific parameter tables. CMWP uses these tables to evaluate the density of planar defects. The parameter tables are free to edit by users. Based on theoretical considerations, it was shown that the sub-profiles are the sum of a symmetrical and an anti-symmetrical Lorentzian function [30,31]. The theoretical derivations were verified by numerical simulations using the DIFFaX software [32]. The anti-symmetrical component of the profile function is produced by interference between two overlapping sub-reflections in reciprocal space. One of these sub-reflections corresponds to the parent, whereas the other corresponds to the twin crystal. The symmetrical and the anti-symmetrical parts of the sub-reflections are correlated with each other and can be characterized by a breadth and an anti-symmetry parameter [27]. These two values are also parameterized as a function of stacking fault and twin density, and are included in the parameter tables freely available through the web [30,31].
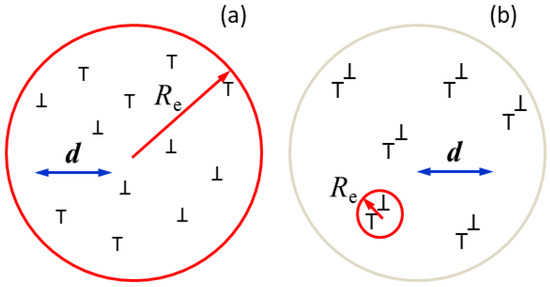
Figure 2.
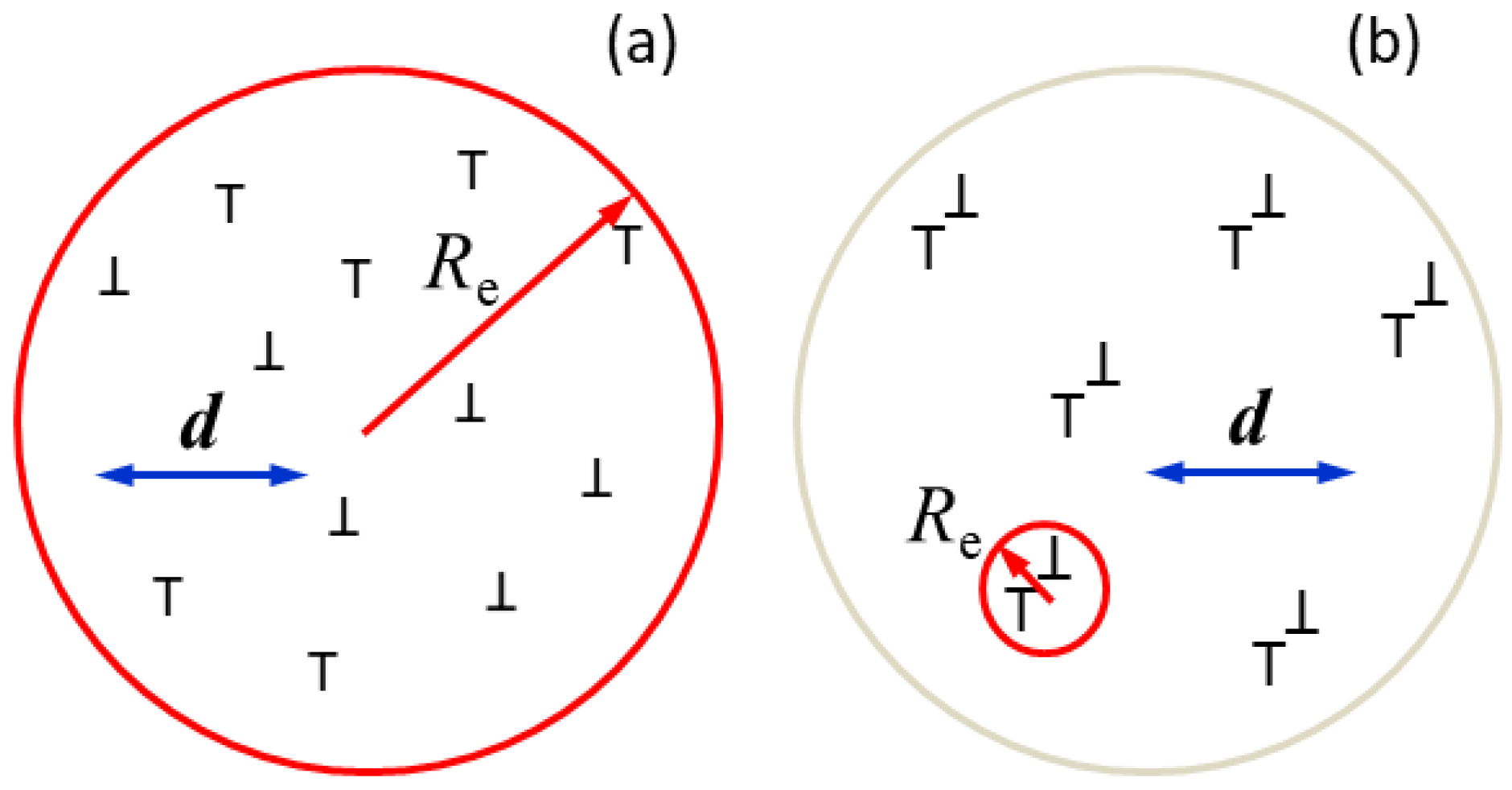
An intuitive schematic interpretation of the dislocation dipole character parameter, M=Re (a) Random dislocation distribution, where M ⟩⟩ 1. (b) Dislocations arranged in strong dipole configuration where M ⟨⟨ 1. The size of the regions of the material in (a) (red circle) and (b) (gray circle) and the number of plus and minus dislocations (up and down Ts) in the two regions are the same. The red arrows are for Re and the blue double arrows are for the average dislocation distance.
2.1. Physical and Secondary Parameters in the CMWP Procedure
The aim of the CMWP procedure is the qualitative and quantitative characterization of microstructures in crystalline materials. The crystallographic structure of the different components in the materials is assumed to be known. In this sense, CMWP is different, but complementary to Rietveld methods. The parameters used in the optimization procedure are divided into two groups of (i) physical and (ii) secondary ones. Physical parameters include the size distribution parameters, m and σ, the dislocation parameters, ρ and M, the planar defect densities, α or β for stacking faults of twin boundaries, and the elastic intergranular strain, εIGS. The peak positions and peak intensities are also fitted during the optimization procedure; however, these parameters are only used to improve the match between the measured and calculated diffraction patterns.
2.1.1. The Density and the Arrangement Parameter of Dislocations
Krivoglaz and coworkers [20,21] showed that the Fourier transform of the strain profile is a logarithmic function of K as long as D/L is larger than unity, where D is a number of length dimensions. In References [20,21] D was suggested to be the grain size. The problem with this definition of D is the same as in the elastic stored energy of dislocations, which becomes logarithmically singular if the upper integration limit is set to be the crystal size. In the case of elastic stored energy, this problem is solved by setting the upper integration limit by the average distance of dislocations [37,38]. Wilkens realized the correlation between the elastic stored energy of dislocations and strain broadening of diffraction peaks, and replaced D in the Krivoglaz formula with the effective outer cut-off radius of dislocations, Re [2,3,39]. Wilkens introduced the concept of “restrictedly random” dislocation distributions and calculated the strain function, f(η), in the entire L range [3]. The concept assumes that the equal number of plus and minus straight parallel screw dislocations are randomly distributed within cylinders of Re radii, where the cylinders cover the whole crystal. Since the value of Re depends on the actual dislocation density, Wilkens introduced the dimensionless parameter M = Re to describe the dislocation arrangements [3]. The value of M is large when the dislocations are uncorrelated and arranged randomly and the related strain fields are of long-range character. In contrast, M is small when opposite-sign dislocations are in strong correlation close to each other and the related strain fields, due to screening, are of short-range character. An intuitive schematic illustration is shown in in Figure 2, where 12 dislocations are randomly distributed in Figure 2a and in a strong dipole configuration in Figure 2b. In the case of random distribution, the strain fields reach out much further than the average dislocation distance, ddisloc, (the red circle is Re and the blue double arrow the average dislocation distance), whereas in the case of strong dipole configuration, the strain fields are strongly screened and Re becomes shorter than ddisloc. The M value is in direct correlation with the average dislocation distance:
Random or strong correlated dislocation arrangements can be called weak or strong dipole characters. In the first case, M is larger than unity, M1, whereas in the second case, it is close to unity or even smaller: M ≤ 1. Due to the reciprocity of length scales in crystal and reciprocal space,
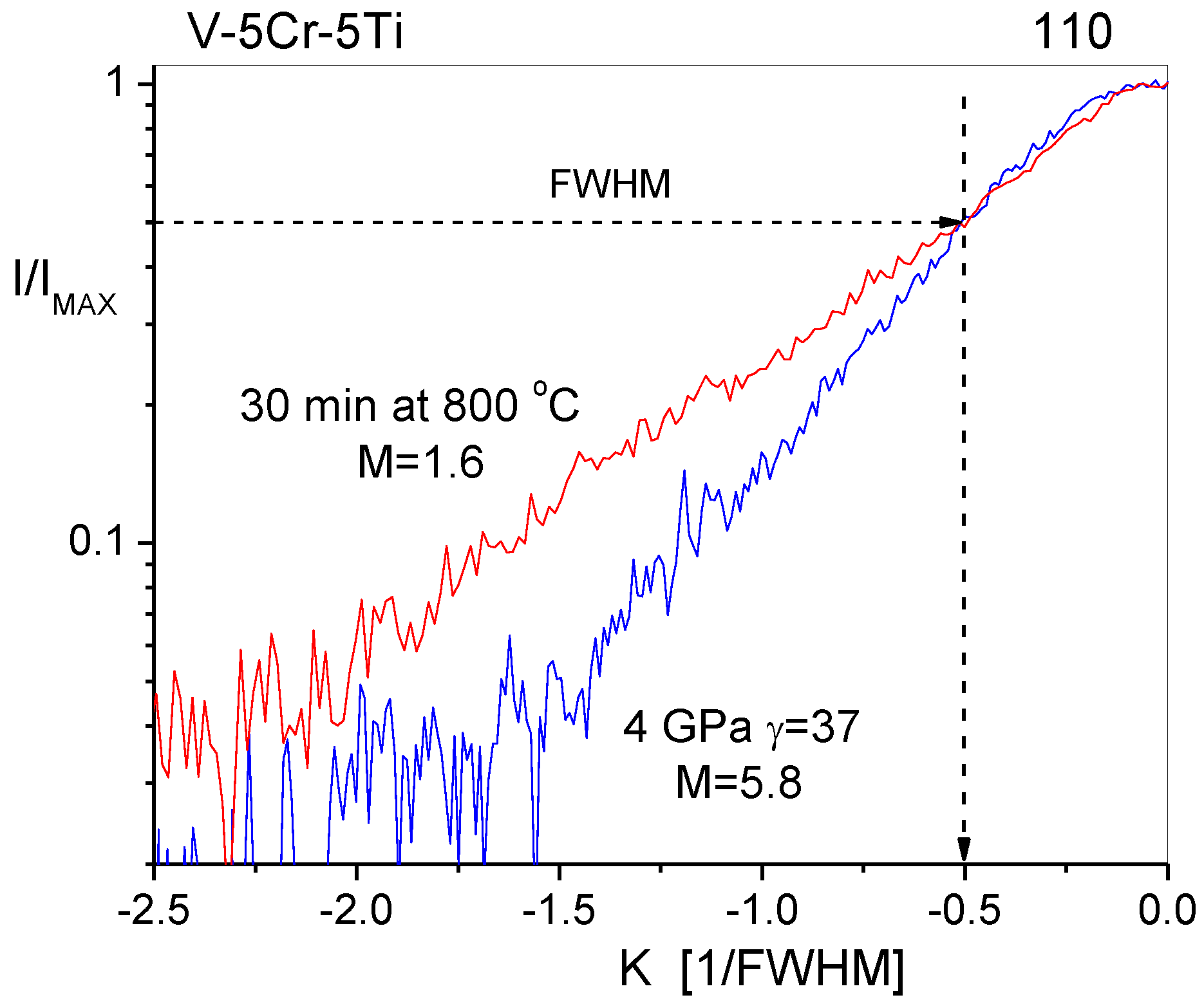
When the strain fields are of long- or short-range character, the tail regions of diffraction peaks decay faster or slower. Figure 3 shows the intensity distributions of the {110} reflections of a V-5Cr-5Ti [40] alloy deformed by high-pressure torsion at 4 GPa pressure to the shear strain of γ = 37 (blue curve) and after.
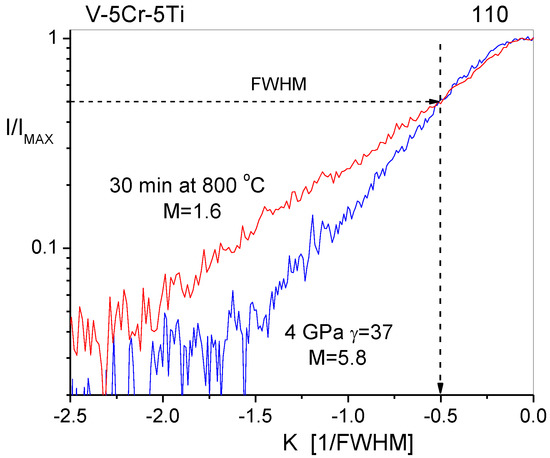
Figure 3.
Intensity distributions of the {110} reflections of a V-5Cr-5Ti alloy deformed by high-pressure torsion at 4 GPa pressure to the shear strain of γ = 37 (red curve) and after heating to 800 °C (blue curve) with logarithmic intensity scale normalized to the maximum intensities and the FWHM. More details about material processing and the heat treatments can be found in Reference [40].
Heating to 800 °C (red curve) with a logarithmic intensity scale normalized to the maximum and the FWHM. The dislocation density did not decrease after heat treatment at 800 °C for 30 min, but the dislocations rearranged into narrow dipole configurations [40]. This rearrangement of dislocations is a kind of recovery process before recrystallization, when the dislocations annihilate and their density drops to low values. In the as-deformed state (blue curve), the tail of the peak decays much faster than in the heat-treated (red curve) recovery state. In the recovery state, the plus–minus dislocations form close pairs of dipoles for which the efficiently screened strain fields are of short-range character. The change of the M parameter from 5.8 to 1.6 is the quantitative measure of rearrangement of the dislocation distribution during the recovery process. When the strain fields are of long-range character, i.e. M1, the profile tails will be short and the profiles will have a bell-shaped character. Meanwhile, when the strain fields are of short-range character, the profile tails will be long and the profiles will be more of Lorentzian character. This is one of the reasons why attributing Gaussian or Lorentzian components in a pseudo-Voight profile function to strain or size broadening is physically incorrect.
2.1.2. The Contrast Factor of Dislocations
The mean square strain is proportional to the contrast, C, of dislocations. In X-ray or neutron diffraction, the contrast has the same physical meaning and origin as in TEM. It depends on the relative orientation between the Burgers and line vectors, b and l, the particular diffraction vector, g, and the elastic constants of the crystal, cijkl: C = C(b,l,g,cijkl) [2,3,19]. In a polycrystal, or if all possible Burgers vectors are randomly populated, C can be averaged either over the permutations of the hkl indices or all possible Burgers vectors [41,42]. In the case of cubic and hexagonal crystals, the average contrast factors, , can be written as [5,43,44]
where h00 and hk.0 are the average contrast factors for of the h00 and hk.0 type reflections, H2 = (h2k2 + h2l2 + k2l2)/(h2 + k2 + l2)2, and x = (2/3)(l/ga)2 (a is the basal lattice constant of the hexagonal crystal). In the CMWP code, Equation (15) is included in a more direct manner as Equation (15a) [12]:
where = {[h2 + k2 + (h + k)2]/l2}/[h2 + k2 + (h + k)2 + (3/2)(a/c)2l2], = l4/[h2 + k2 + (h + k)2 + (3/2)(a/c)2l2], a1 = q1 and a2 = q2 + q1/[(2/3)(c/a)2]. The mss in Equation (12) consists of ρ, C, and b in the product. Therefore, only ρ and the hkl dependent q or q1 and q2 can be determined independently via the CMWP procedure. The scaling factors h00 and hk.0 can only be refined after the q or q1 and q2 values have been determined. The same is true for the Burgers vector values of <a>, <c>, and <c+a> slip modes in hcp materials [15,45]. The effect of changing dislocation density on the elastic constants and the h00 and hk.0 scaling constants was investigated in References [46,47]. In Reference [47], it was shown that the effects could change the absolute values of dislocation densities up to 40%.
2.1.3. Determination of Slip Modes in hcp Crystals
Once the a1 and a2 parameters are determined, the true dislocation densities, ρtrue, and the <a>, <c>, and <c + a> slip mode fractions in hcp materials can be determined [15,45]. A simpler and more straightforward method than in References [15,45] is briefly described here. The mss can be written as the sum of the partial mss values, , related to the different slip modes:
where i stands for the different slip modes. We can assume that the strain function f(η) is global for all hk.l peaks:
where ρ* and are the dislocation density and the contrast factor values given by the CMWP procedure. Here, = *hk.0 (1 + a1 + a2), where *hk.0 is the input value of the scaling factor and q1* and q2* are the contrast factor parameters given by the CMWP procedure. The fractions, ξ⟨a⟩, ξ⟨c⟩ and ξ⟨c+a⟩ of the partial mss values are
where = 1. The partial dislocation densities will be
Since Equations (5) must hold for all hk.l values, ξi can be obtained using the least-squares method.
The CMWP procedure allows the evaluation of diffraction patterns consisting of more than one phase. In such cases, the number of physical parameters increases. In the simplest case of a cubic single-phase material with a spherical crystallite shape and no planar defects, the number of physical parameters will be five: ρ, M, and q for the strain profile and m and σ for the size profile. In an hcp specimen, containing two different phases, the number of physical parameters becomes twelve: ρ, M, m, σ, and q1, q2, and ρ1, M1, m1, σ1, and , , where the upper index ’1’ is for the second phase. (Note that the major phase is not labeled.) Since line profile analysis evaluates only the shape and broadening of diffraction peaks, the peak positions and maxima are treated in CMWP as secondary parameters. The peak shifts caused by faulting or twinning are taken into account by the shifts of the sub-profiles included in the parameter files for planar defects [30,31].
2.2. Algorithms Used for Solving Equation (7)
Equation (7) requires a non-linear problem with correlations between the different parameters to be solved. The possibilities are (a) nonlinear least-squares algorithms [48], (b) direct search methods [49], and (c) statistical methods [50]. The most frequently used nonlinear least-squares algorithms are the Newton method, the steepest descent or conjugate gradient method, and the LM [51,52] procedure. The nonlinear least-squares algorithms find the local minimum of the WSSR in the parameter space, which does not necessarily coincide with the global minimum of the WSSR. Statistical methods [37,39] can be used to find the global minimum of the WSSR in the parameter space. In order to find the global minimum in the CMWP procedure, we applied a special MC statistical algorithm and the LM nonlinear least-squares algorithm in a multiple successive process. The MC method only optimizes the physical parameters. Based on physical considerations, each parameter is restricted between a minimum and maximum value which cannot be bypassed; however, these can be edited by the user. In consecutive iterations, the new parameter values are searched in the proximity of the previous ones:
where i is the parameter index and n is the current iteration number. is defined as
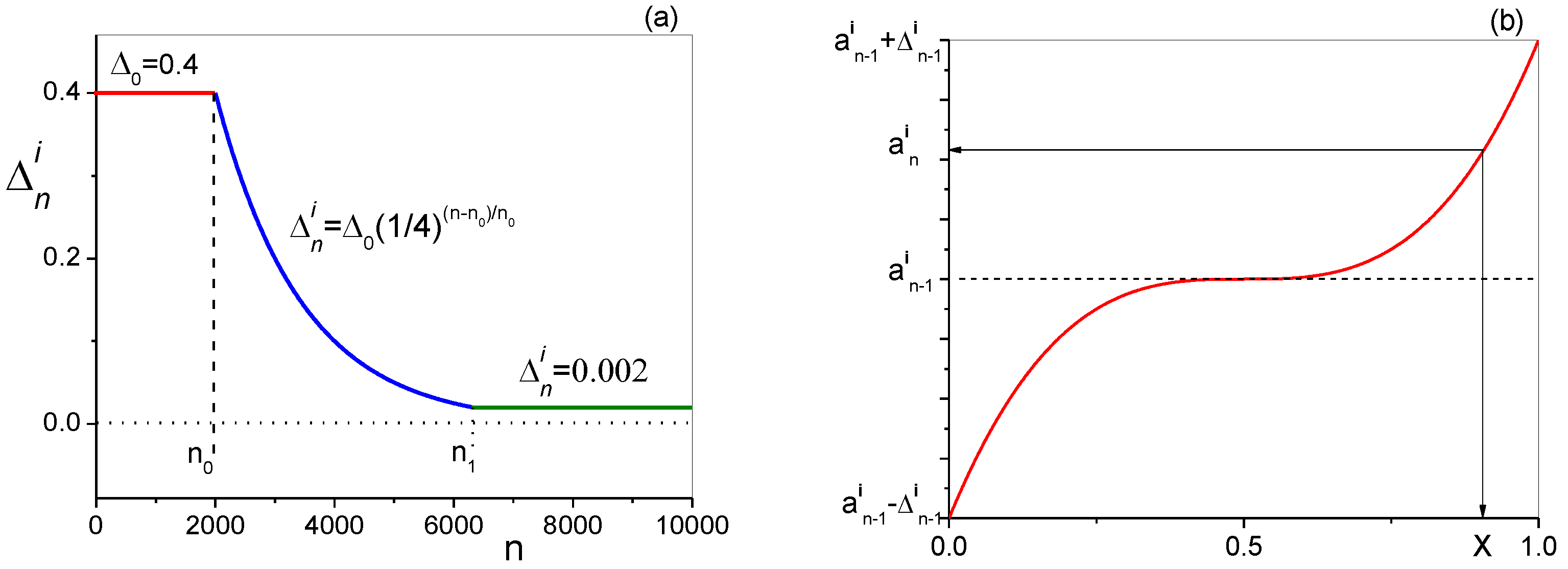
The value of is the same during the first n0 iterations. During further iterations, decreases exponentially to . Once reaches , when n reaches n1, the values remain constant. For example, if = 50, the value of is reached after about 4000 iterations, as shown in Figure 4. In the special MC algorithm developed for CMWP, we applied a bias towards the prevailing parameter values in the consecutive iterations. The consecutive parameter values follow a cubic probability function vs. generated by a random number generator:
where . The star in indicates that this consecutive value has not yet been accepted as a better value than . The biased cubic probability function is shown schematically in Figure 4b.
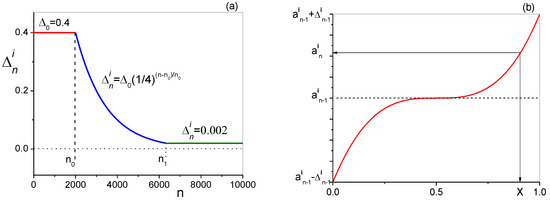
Figure 4.
(a) Half-breadth of the parameter interval, , as a function of the number of iterations, n. Up to the first no steps (horizontal red line), stays constant. Between the steps no and n1, decays exponentially (blue line). Beyond n1, stays constant (horizontal green line). (b) Schematic drawing of the parameter values vs. the random generated number, , in the biased cubic probability function used in the special MC algorithm.
Due to the biased probability function, the parameter space is sampled on a finer scale around preceding values. However, as Figure 4b shows, there is also a good chance of sampling remote regions of the parameter space. The condition for accepting the new parameters, is
The errors of the parameter values are determined in terms of p% fractions of the WSSR [53]. If a particular WSSR value is larger than the best value, WSSRbest, found until the actual iteration, but within a certain p% fraction of WSSRbest, i.e.,
then the parameter values corresponding to this WSSR value are stored in an array. At the end of the fitting procedure, the largest and the smallest of each parameter value in the array will be considered as the plus-minus absolute errors of the respective parameters with the given p% number. The relative errors are calculated and listed accordingly. The convergence criteria of the special MC procedure are that (i) the number of steps reaches a user-defined value and (ii) that the 1 + p% statistics reaches at least Np, where Np is an editable minimum number of MC iterations in which the WSSR was not larger than the last WSSR value. The systematic testing of the combined LM + MC algorithm showed that n0 = 2000, p = 3.5% and Np = 100 gave excellent pattern fittings and good physical parameter values even if the diffraction patterns were complicated. Our experience showed that the MC procedure outlined above is ideally suited in the case of line profile analysis. In agreement with the copyright conditions of CMWP, the source code of this MC is accessible in the software package, which is free to use for academia purposes.
WSSR > WSSRbest AND WSSR < (1 + p%)·WSSRbest,
2.3. Organization of the Combined LM and MC Algorithms
The total number of parameters can become quite large when more than ten diffraction peaks and more than one phase comprise the diffraction pattern. In such cases, the LM procedure can get frustrated and the optimization procedure can get stuck. This problem is overcome by sectioning the LM procedure. One full cycle of the optimization procedure consists of the following sections: (1) MC optimization, (2) LM optimization of only the peak positions, (3) LM optimization of only the peak heights, (4) LM optimization of only the physical parameters, (5) LM optimization of all parameters including the physical parameters, the peak positions, and peak heights, and (6) readjustment of the BG. The cycle of six steps is repeated until convergence is reached.
2.4. Systematic Comparison of the Performance of the LM and MC Procedures
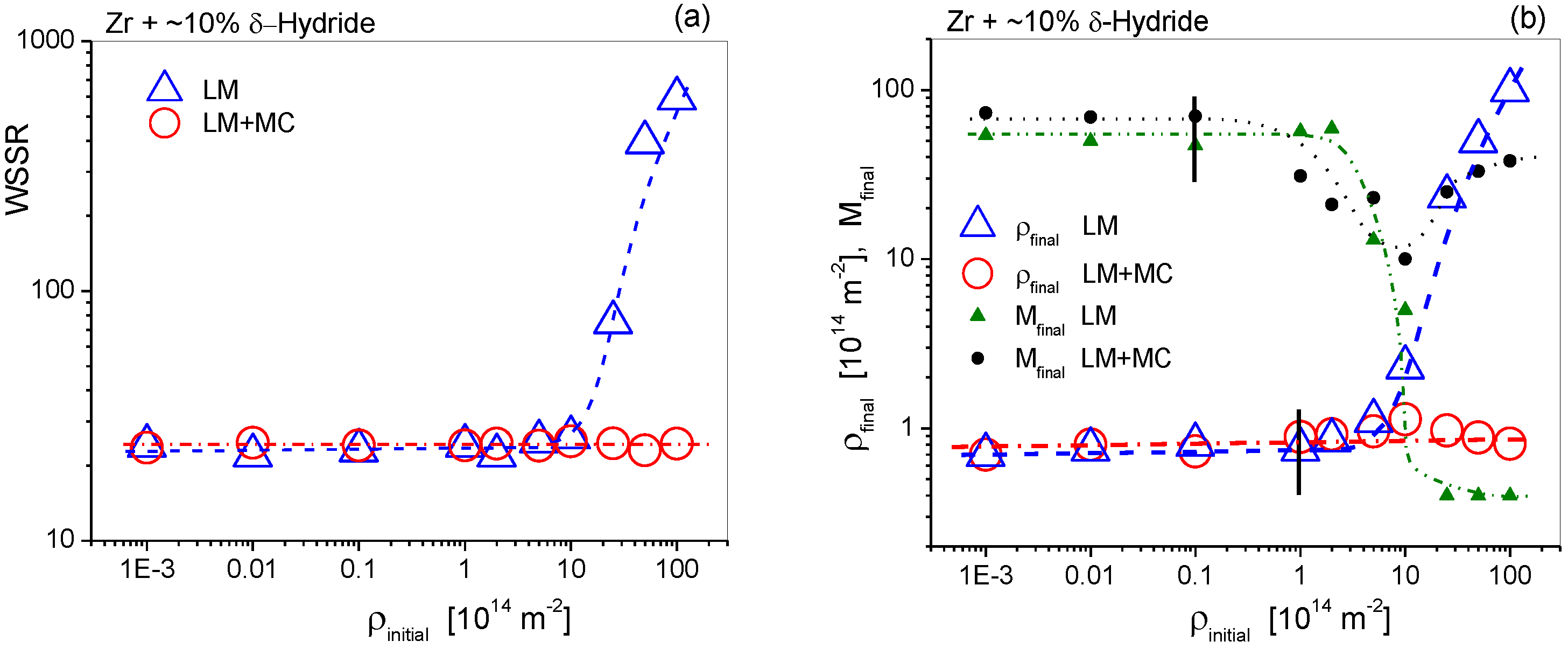
Though the LM optimization procedure is a well-established and widely used analytical method, in nonlinear problems, the parameter space can have more than a single minimum and LM can get stuck in one which is not the absolute minimum. The implementation of the MC procedure combined with LM aimed to find the global minimum in the parameter space. A systematic analysis was carried out to check the performance of both the LM procedure alone and the combined alternative with LM plus MC. The most critical parameters were the dislocation density concomitant with the dipole character number, i.e., ρ and M. One of the Zircaloy-4 X-ray diffraction patterns containing about 10% δ-hydride, discussed in detail in the next paragraph, was evaluated by varying the starting values of ρ over 5 orders of magnitude, from 10−3 × 1014 m−2 to 100 × 1014 m−2. The results are shown in Figure 5. CMWP is governed by optimizing the parameters for obtaining the smallest weighted sum of squared residuals (WSSR). The WSSR values are shown in Figure 5a vs. the starting values of ρ when LM alone (open blue triangles) and LM combined with MC (open red circles) were applied. The figure shows that LM alone could not find the minimum of WSSR, especially when the initial ρ values were larger than the optimum, which was about 0.9(± 0.1) × 1014 m−2. The combined application of LM + MC always found the optimum WSSR whatever the initial values of ρ were. The dislocation density and the dipole character number, ρ and M, are shown vs. the initial ρ values in Figure 5b. The figure shows that both ρ and M varied up to about two orders of magnitude when only LM was applied: 0.7 ≤ ρ≤ 100×1014 m−2, 0.4 ≤ M ≤ 60. With the combination of LM + MC, the optima of both ρ and M were found within reasonable error margins: 0.7 ≤ ρ ≤ 1.13 × 1014 m−2, 10 ≤ M ≤ 60. The relatively large variation of M does not mean that it could not be determined. Whenever the value of M is of the order of 10 or larger, it only means that the dipole character of dislocations is very weak. Or, in other words, the dislocation arrangement is “random” [2,3].
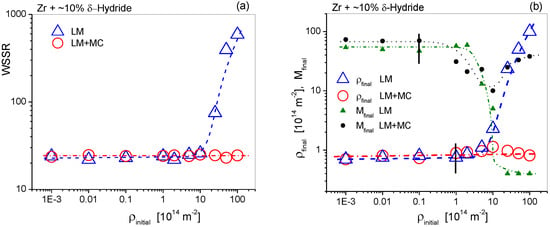
Figure 5.
Systematic investigation of the LM and MC optimization procedures. (a) The WSSR vs. the initial value of the dislocation density, , when LM alone (open blue triangles) and the LM and MC (open red circles) optimization procedures were used. (b) The final dislocation density and dipole character parameter values, and , vs. the initial, values, and , in logarithmic scales, calculated using either the LM alone (open blue triangles and green triangles) or the LM and MC optimization procedures (open red circles and black dots). The vertical black lines indicate error bars. All curves in the two figures are only to guide the eye.
2.5. Extension of CMWP for Handling Satellites or Diffuse Scattering
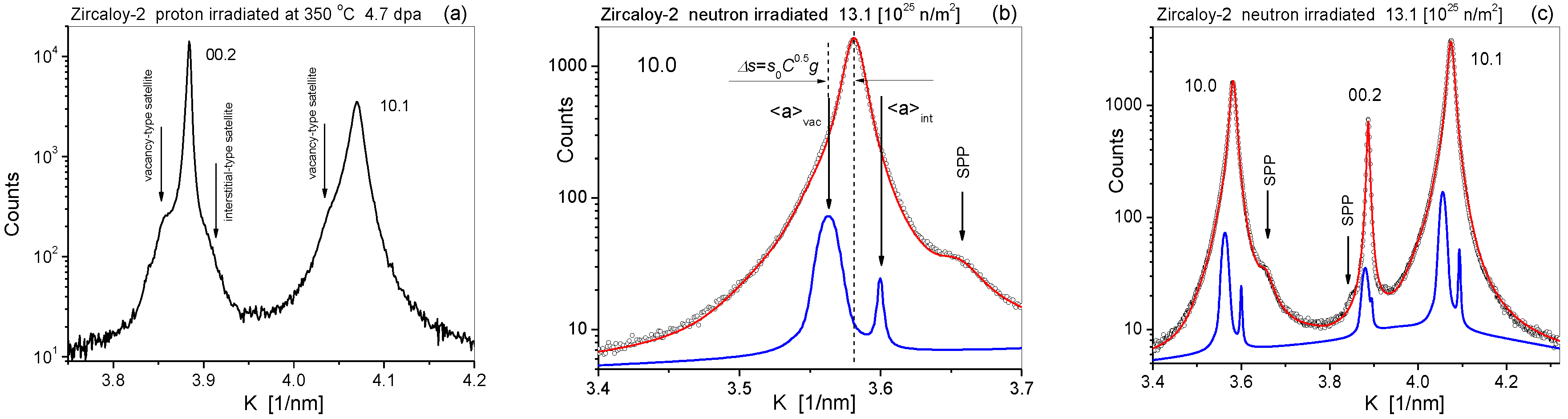
Guinier–Preston (GP) zones [54,55], small dislocation loops [56,57], or diffuse scattering of solute atoms [58] can produce satellites or diffuse scattering peaks around or below the fundamental Bragg peaks. Typical satellites in the lower intensity ranges of diffraction peaks of a proton-irradiated Zircaloy-2 specimen are shown in Figure 6a. The vertical arrows point to the satellite peaks produced either by vacancy- (on the left side of the peaks) or interstitial-type dislocation loops (on the right side of the 00.2 reflection). The interstitial-type satellite on the 10.1 peak cannot be seen because it is blending in with the broader main peak. The strain profile given by Equations (10)–(12) relies strongly on the tail regions of Bragg peaks. Satellites or diffuse scattering peaks, not related directly to the strain profiles, may distort the physical parameter values defining the true strain profiles and the true strain parameters. The option to handle satellites or diffuse scattering peaks is also implemented in the CMWP procedure [25]. Irradiation-induced dislocation loops evolve from knocked out vacancies and interstitials in irradiated materials [56,57,59,60,61,62]. Larson and Young [61] and Mason et al. [62] showed that irradiation-induced dislocation loops have a very wide size distribution, ranging from a few tenths to a few hundred nanometers. The strain fields of small dislocation loops overlap and strengthen each other inside the loop regions. As a consequence, within the strained regions of the small vacancy- or small interstitial-type loops, the lattice constants increase or decrease relative to the matrix lattice constants, respectively [61,63]. The strained regions around small loops produce satellite peaks around the fundamental Bragg reflections in proton-, neutron-, or ion-irradiated materials [25,57,62]. Based on the theoretical description of satellites and diffuse scattering of point defect clusters and small dislocation loops [61,63,64], we developed a procedure to handle satellites in the CMWP procedure [25]. Taking into account the small size and wide size distribution of the strained volumes of small loops, the satellite profiles, , were modeled as size profiles according to Equation (8), where Δs is the shift of the satellite peaks relative to the main hkl reflection. In References [64,65,66], it was shown that although the strained volumes are coherent with the matrix, the intensities scattered by the strained volumes are incoherent; therefore, the intensities of the main and the satellite peaks are additive. The satellite intensities are usually a few percent of the intensities of the main peaks; therefore, the optimization of the main diffraction pattern and the satellite peaks can be done in separate steps. The two steps can be repeated subsequently until the procedure converges. Figure 6b,c shows zoomed parts of the measured (open circles) and CMWP-calculated (red lines) diffraction patterns of a Zircaloy-2 specimen neutron irradiated to the fluence of 13.1 × 1025 n/m2 at about 300(± 25) °C [58,67]. The satellites are shown as blue lines. The shift of satellites is , where s0 is a global shift parameter for the entire pattern and Δs scales for the different reflections, with the average contrast factor of <a>-type dislocation loops [25]. The intensities of the satellites were adjusted to the heights of the related main peaks. Although the procedure was conceived for treating satellites produced by irradiation-induced dislocation loops, it is a general option in the CMWP procedure which can be used to handle diffuse scattering satellites of any kind around fundamental Bragg peaks.
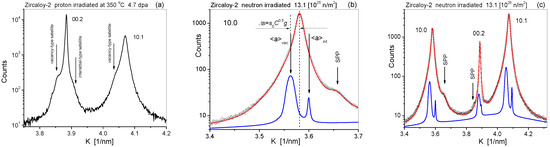
Figure 6.
(a) Typical satellites in the lower intensity ranges of diffraction peaks in a proton irradiated Zircaloy-2 specimen. The vertical arrows point to the satellite peaks produced either by vacancy- (on the left side of the peaks) or interstitial-type dislocation loops (on the right side of the 00.2 reflection). The interstitial-type satellite peak is blending in with the broader 10.1 Bragg peak. (b) Measured (open circles) and CMWP-calculated (red line) zoomed part of the diffraction pattern of a Zircaloy-2 cladding material specimen [58] neutron irradiated to 13.1 × 1025 n/m2. The blue line shows the satellite peak related to vacancy- and interstitial-type dislocation loops. (c) The same as in (a) for the first three Zr peaks. The alloy contains second-phase particles (SPPs) of different precipitates, as indicated in the (b) and (c) figures.
2.6. Stabilizing the Fluctuations of the Physical Parameters When the Effective Outer Cut-Off Radius, Re, Approaches the Lower Limit of Continuum Theory
The actual value of the effective outer cut-off radius of dislocations, Re, as it was shown in Equation (12), depends on both the dislocation density and the dipole character of the dislocation arrangement.
A systematic investigation of the f(η) function revealed that when M drops into the range around or below unity along with large dislocation densities in the range of 1016 × m−2, the effective outer cut-off radius, Re, can reach small values of a few nm, approaching the lower limit of the continuum approach [66,67]. The dislocation density in neutron- [57] or proton-irradiated [68,69] Zr alloys can reach a few times 1016⋅m-2 while the M value is M ≤ 1. In these diffraction patterns, the profiles broaden mainly in the tail regions of the profiles, while the FWHM change much less. The diffraction profiles of the 10.3 Bragg reflections of Zircaloy-2 proton irradiated to 2.3 dpa at 280, 350, and 450 °C are shown in Figure 8a in Reference [68]. The figure shows that the tails are short when irradiation is at a high temperature, whereas they are very long when the irradiation is at a low temperature. TEM images of the same specimens are shown in Figure 3 in Reference [68]. Figure 3a in Reference [68] shows that at low temperatures, small dislocation loops form with very high density, whereas at high-temperature irradiation (see Figure 3c in Reference [68]) only a few large dislocation loops are present. When ρ is in the range of 1016⋅m-2 and M is around unity or smaller, Re can approach the lower limit of the continuum approach. During the optimization procedure, M can become uncertain in the sense that Re can approach extremely small, and ρ extremely large values. In order to avoid this kind of uncertainty, we introduced a lower limit, Rc, for Re by replacing η = L/Re with η = L/(Re + Rc).
where Rc is in the range of the lower limit of the length scale of the continuum approach [68,69].
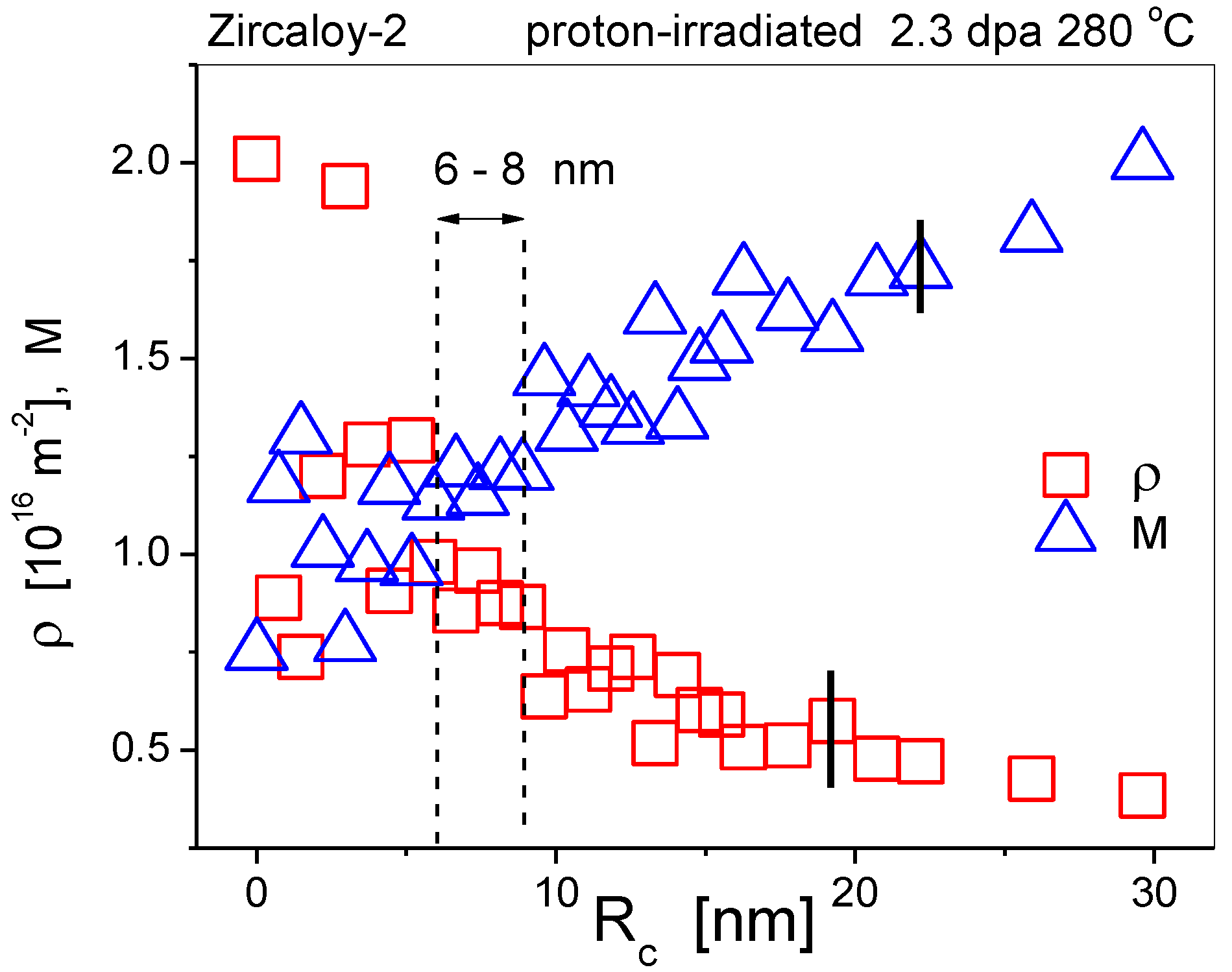
A systematic investigation of the effect of Rc on the physical parameters is shown in Figure 7. We carried out this analysis on the diffraction pattern of a Zircaloy-2 specimen proton-irradiated to 2.3 dpa at 280 °C, in which the dislocation density was very large and the M parameter about unity [68]. The figure shows ρ and M vs. Rc in the range of 0 < Rc < 30 nm. With Rc decreasing to about Rc ≅ 8 nm, M decreased, whereas ρ increased. Below Rc ≅ 8 nm, there was a range of Rc between about 6 ≤ Rc ≤ 8 nm in which both ρ and M were stable around ρ ≅ 9 × 1015 m−2 and M ≅ 0.75. The introduction of Rc in the range of about 6 to 8 nm stabilized the physical parameters, especially the values of ρ and M. When Re is significantly larger than Rc, then its value has no effect on the physical parameters.
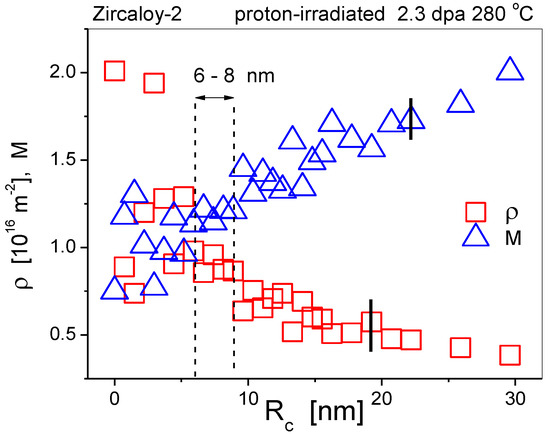
Figure 7.
Systematic analysis of the effect of value of Rc in the CMWP procedure. The dislocation density, ρ, and the dipole character parameter, M, vs. Rc in the range of 0≤ Rc ≤30. The vertical black lines indicate the error margin.
Neutron diffraction patterns are usually measured in time of flight (TOF) mode. In TOF patterns, the intensities are given vs. d = 1/K. The software also works in I(K) representation. The TOF patterns have to be converted to I(1/K) = I(d*) representation (where d* = 1/d), which is a very simple task.
3. Dislocation Density and Crystallite Size in Zr Matrix and Zr Hydrides in a Hydrated Zircaloy-4 Sheet Material
The performance of the CMWP procedure with the combination of the MC and the LM optimization methods was shown by the evaluation of the dislocation structure in a hydrated Zircaloy-4 specimen. The dislocation and stacking fault densities and the subgrain size were determined within the two coexisting Zr and ZrH phases. The spatial distribution of the volume fraction of ZrH in a hydrated Zircaloy-4 specimen was investigated using high-resolution scanning synchrotron experiments in References [70,71]. The diffraction patterns were re-evaluated using the CMWP procedure described in Section 2.3.
3.1. Experiment
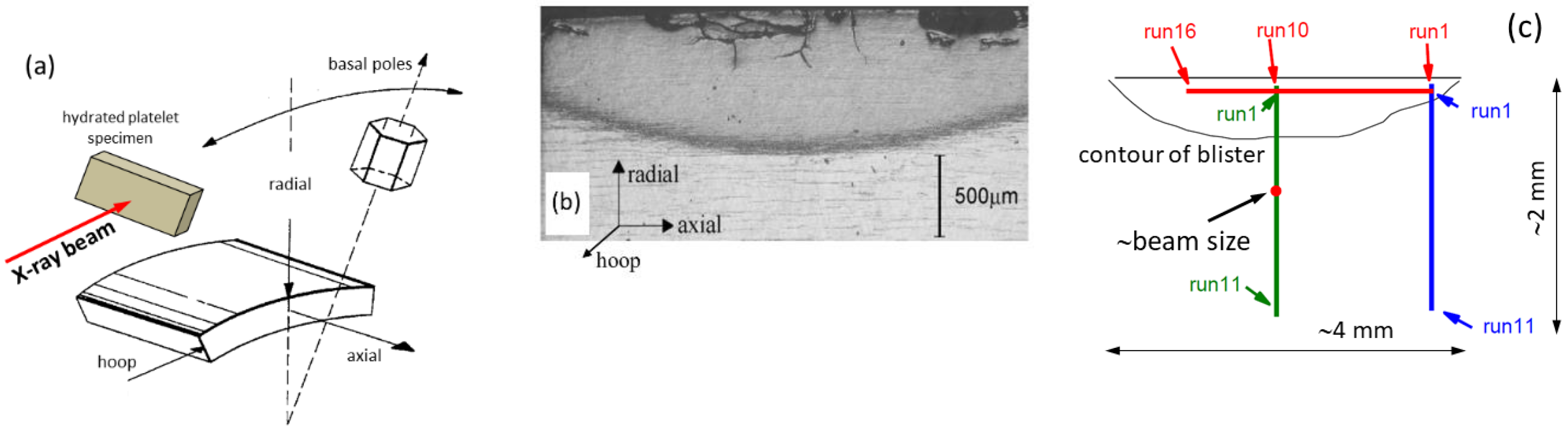
A hydride blister was grown on a Zircaloy-4 alloy platelet sectioned from a CANDU pressure tube. The alloy composition was Zr-1.49%Sn-0.2%Fe-0.11%Cr-2.5%Nb, all in wt %. [71]. For the hydration procedure, see References [70,72]. The schematic configuration of the hydrated platelet within the pressure tube, along with an optical micrograph of the hydrated blister, is shown in Figure 8a,b. High-angular-resolution X-ray microdiffraction was carried out at the 1-ID beamline at the Advanced Photon Source synchrotron at the Argonne National Laboratory [71]. The schematic positions of the X-ray diffraction experiments on the hydrated platelet are shown in Figure 8c. X-ray diffraction scans were taken along three linear traces, one horizontal (red line) and two vertical (center green line and right blues line), with 16 and two times 11 positions, respectively. The beam size on the specimen was 300 × 300 μm2, illustrated approximately by the small red dot in the center vertical line in Figure 8c.
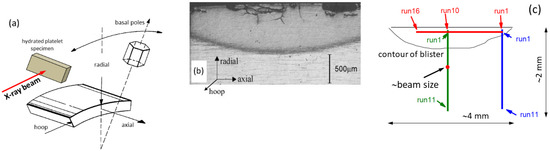
Figure 8.
(a) Schematic configuration of the hydrated platelet sectioned from a CANDU pressure tube. The conventional coordinate system with the residual stress directions, radial, axial, and hoop strain/stress directions, along with the typical basal pole directions in the textured Zr tube material, is also indicated. (b) Optical micrograph of the hydrated Zircaloy-4 platelet. The darker region is the hydrated blister. (c) Schematic drawing of the X-ray diffraction positions along the hydrated platelet.
The diffraction patterns were recorded in a solid-state detector of 200 μm pixel size with 2048 × 2048 pixels at a distance of 1.948 m from the sample. In order to obtain more reflections, the detector was shifted so that the beam hit the lower left corner of the detector, as shown in Figure 2a in Reference [71]. The Debye–Scherrer rings of the reflections were integrated along azimuth sections of arcs in ±2.5 degrees.
3.2. Results
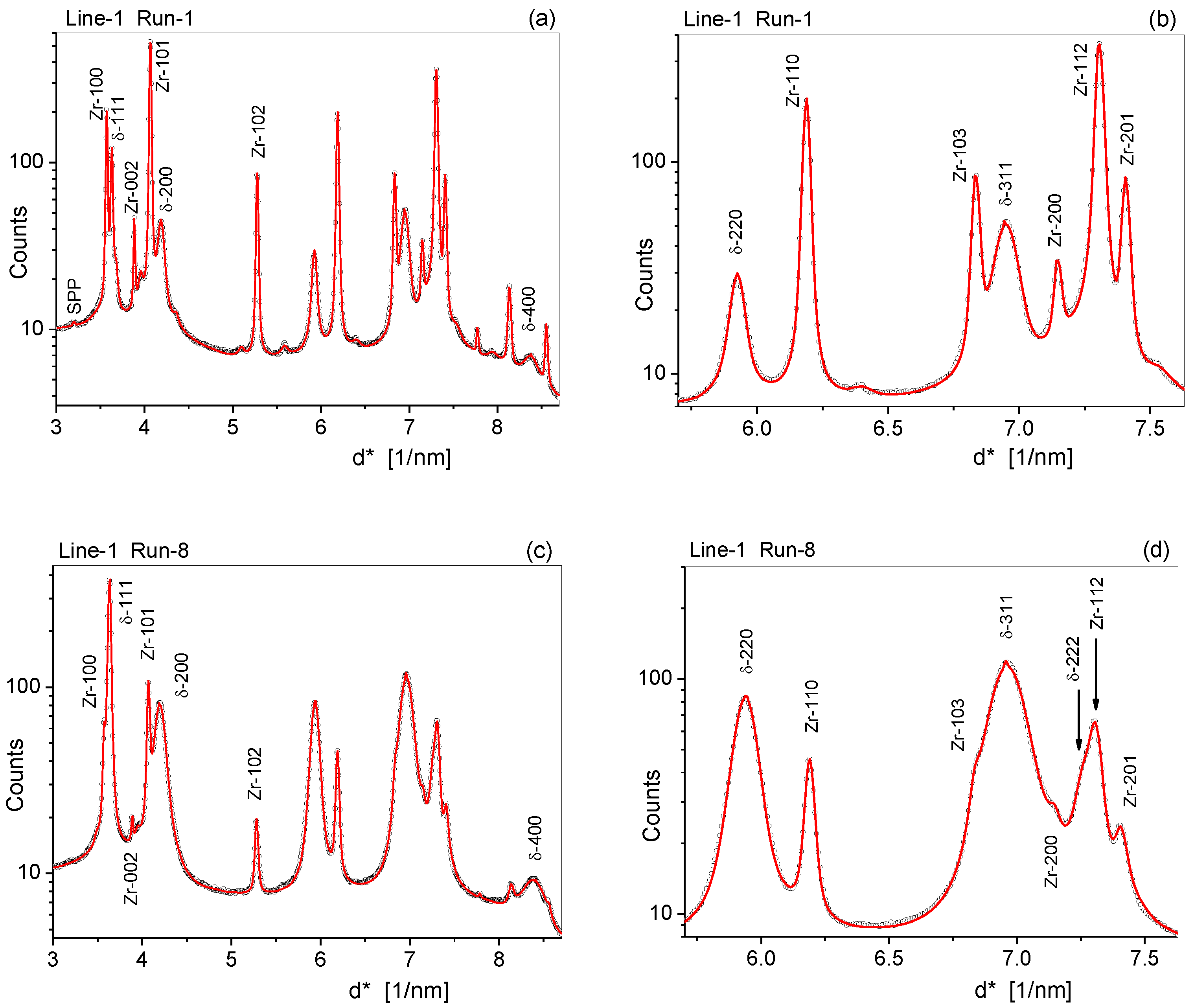
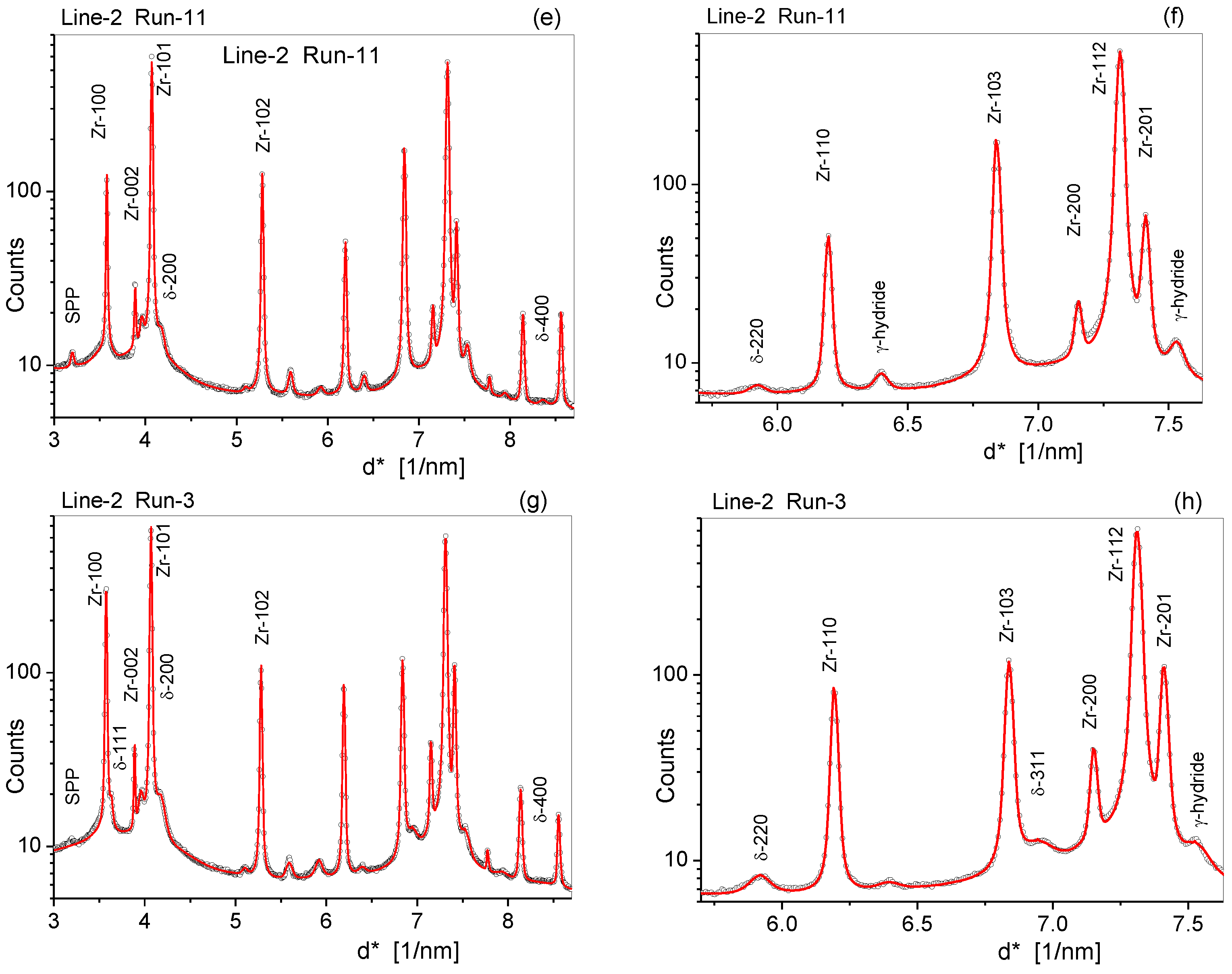
The diffraction patterns were evaluated for the dislocation density, the subgrain size, the dislocation arrangement parameter, and the stacking fault density, ρ, <x>area, M, and β in the fcc δ−ZrH and in the Zr matrix phases. Typical measured (open circles) and fitted (red solid lines) diffraction patterns corresponding to four different positions along the scanning lines are shown in Figure 9. In order to show the different reflections of very different relative heights, the intensities are in logarithmic scale. The patterns in Figure 9a,c,e,g show the entire measured range for the positions Line-1 Run-1, Line-1 Run-8, Line-2 Run-3, and Line-3 Run-11, respectively. Figure 9b,d,f,h shows zoomed ranges from 5.5 to 7.5 degrees, showing the detailed structure of the patterns where relatively large number of diffraction peaks were in complicated sequences and overlapped.
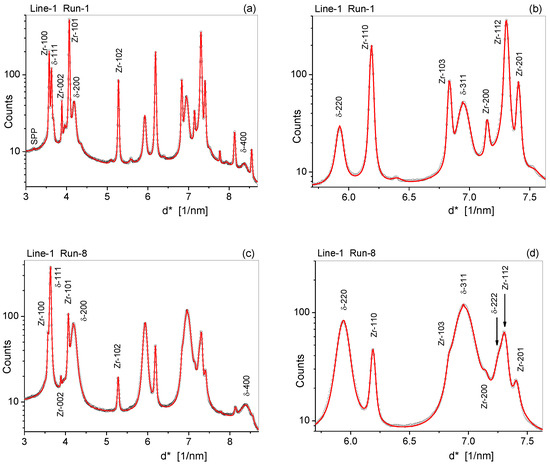
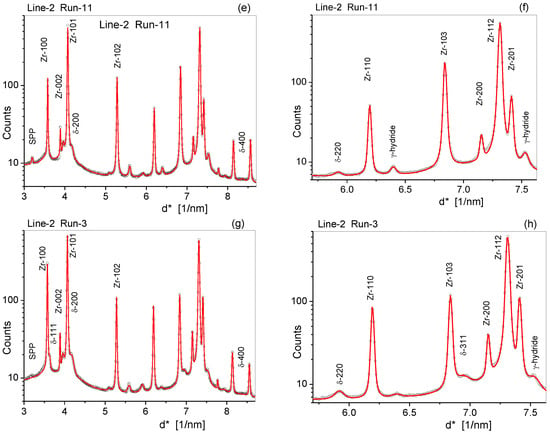
Figure 9.
Measured (open circles) and CMWP-calculated (red lines) diffraction patterns (a,c,e,g) in the entire, and (b,d,f,h) in a zoomed angular range at four different depths in the ZrH blister. (a,b) are along Line-1 Run-1 at the top right edge, (c,d) are along Line-1 Run-8 at the center, (e,f) are along Line-2 Run-11 at the lower center edge, and (g,h) are along Line-3 Run-3 at the right middle edge of the blister, respectively.
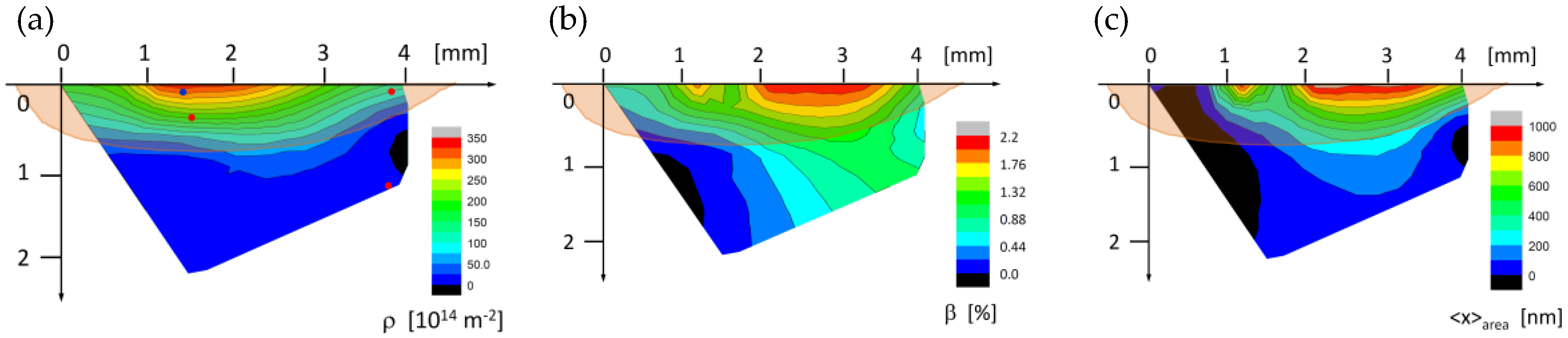
In the Line-1 Run-1 position (in Figure 9c, the top right edge position of the blister), the Zr peaks were much stronger than the δ-ZrH peaks. This ratio was reversed in the Line-1 Run-8 pattern, where the δ-hydride peaks were much stronger than the Zr peaks (in Figure 9c, the center top position of the blister). The Line-2 Run-11 position was at a distance of about 1.8 mm from the outer edge of the blister, but the δ-hydride peaks were still clearly visible. Although the Line-3 Run-3 position, at the outer edge of the blister, was a very different position compared to Line-2 Run-11, the two patterns indicated very similar ratios of the volume fractions between ZrH and Zr, and similar dislocation and subgrain structures. The lateral and depth profiles of the dislocation density, ρ, the stacking fault density, β and the area average mean crystallite size, <x>area, in the δ-ZrH are shown as a function of position in Figure 10. The light brown shade in the figures indicates the blister. The blue and the three red dots in Figure 10a show the approximate positions of the four diffraction patterns in Figure 9. The dislocation density in the Zr matrix varied between 1(± 0.15) × and 11(± 1.5) × 1014 m−2, whereas in the ZrH phase, it varied between about 10(± 2) × and 350(± 50) × 1014 m−2.
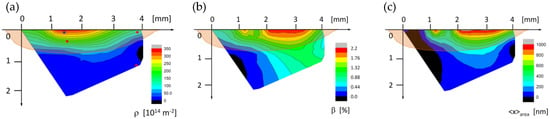
Figure 10.
(a) The dislocation density, ρ, (b) the stacking fault density, β, and (c) the area average mean crystallite size, <x>area, in δ-ZrH as a function of lateral and depth positions in the ZrH blister.
The experimental error of the stacking fault density in the δ-hydride was about ± 20%. The volume fraction of the δ-hydride was determined in Reference [71]. It was shown to vary from about 80% in the center region of the blister to a few percent at a distance of about 2 mm from the edge of it. For details, see Figure 2 in Reference [71]. The results showed that the dislocation density and the volume fraction were in close correlation with each other in the ZrH phase. At the largest volume fractions of ZrH, the dislocation densities reached extremely large values. The dislocation density in the Zr matrix was also correlated with the volume fraction of the ZrH phase. ZrH is well-known to exert large intergranular strains on the surrounding Zr matrix [73]. These strains induce large dislocation densities in both phases and cause cracking of the Zr phase, as shown in Figure 2a in Reference [71].
4. Conclusions
The CMWP line profile analysis procedure was extended by implementing a special MC method in combination with the LM algorithm to provide the global optima for dislocation densities, dislocation arrangement or dipole character parameters, planar defect densities, subgrain size, and intergranular strains in polycrystalline or single-crystal materials. The procedure has the capacity to evaluate multiphase materials where the microstructures of the different component phases are determined at the same time. Taking into account the possible large number of optimization parameters, a sectioning was introduced where the physical, peak position, and peak height values are optimized in a cycle of six subsequent steps. The six-step cycle is repeated until convergence is reached.
Profile shape plays a decisive role in determining dislocation densities from the strain profile. The dislocation arrangement or dipole character parameter is one of the more sensitive parameters in the strain profile. The Krivoglaz–Wilkens strain function was modified in order to protect it from becoming unstable in cases when a large dislocation density is accompanied by a very strong dipole character. In such cases, the effective outer cut-off radius approaches the length limit of continuum theory. An editable hard limit was introduced into the Krivoglaz–Wilkens strain function in order to prevent the effective outer cut-off radius becoming smaller than the lower length limit of continuum theory.
We developed a procedure to handle the satellite peaks appearing on the flanks of the major Bragg peaks in polycrystalline materials. Such satellites are produced by e.g., neutron- or proton-irradiated Zr alloys [58,70] or by GP zones in supersaturated solid solutions [55,56,59].
The implementation of the MC procedure and the six-step cycle procedure was tested by evaluating the coexisting hcp Zr and fcc δ-ZrH phases in a hydrated blister on a Zircaloy-4 specimen. The two-dimensional lateral and depth profiles of the dislocation densities, the stacking fault densities, and the subgrain size were determined by evaluating position-sensitive high-resolution synchrotron X-ray diffraction patterns. The results were in good correlation with the mechanical and electron microscopy analysis done on the same specimen.
Author Contributions
Conceptualization, T.U. and G.R.; methodology, G.R. and T.U., and B.J.; software, R.G. and J.B.; formal analysis, G.R., T.U., and B.J.; investigation, G.R., T.U., and B.J.; resources, T.U.; data curation, G.R., T.U., and B.J.; writing—original draft preparation, G.R. and T.U., writing—review and editing, G.R. and T.U., review and interpretation, G.R. and T.U., supervision, T.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by EPSRC programme grant MIDAS (EP/S01702X/1) https://gow.epsrc.ukri.org/NGBOViewGrant.aspx?GrantRef=EP/S01702X/1. This research was partially funded by ELTE Institutional Excellence Program (1783e3/2018/FEKUTSRAT) supported by the Hungarian Ministry of Human Capacities, https://ttk.elte.hu/content/kivalosagi-programok.t.2544?m=269.
Acknowledgments
T. Ungár acknowledges support from EPSRC programme grant MIDAS (EP/S01702X/1). G.R. gratefully acknowledges the support of the ELTE Institutional Excellence Program (1783e3/2018/FEKUTSRAT) supported by the Hungarian Ministry of Human Capacities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Warren, B.E. X-ray studies of deformed metals. Prog. Metal. Phys. 1959, 8, 147–202. [Google Scholar] [CrossRef]
- Wilkens, M. Theoretical aspects of kinematical X-ray diffraction profiles from crystals containing dislocation distributions. In NBS Fundamental Aspects of Dislocation Theory; Simmons, J.A., deWit, R., Bullough, R., Eds.; Spec. Publ. 317, II.: Washington, DC, USA, 1970; pp. 1195–1221. [Google Scholar]
- Wilkens, M. The Determination of Density and Distribution of Dislocations in Deformed Single Crystals from Broadened X-Ray Diffraction Profiles. Phys. Stat. Sol. 1970, 2, 359–370. [Google Scholar] [CrossRef]
- Groma, I. X-ray line broadening due to an inhomogeneous dislocation distribution. Phys. Rev. B 1998, 57, 7535–7542. [Google Scholar] [CrossRef]
- Ungár, T.; Dragomir, I.; Révész, Á.; Borbély, A. The contrast factors of dislocations in cubic crystals: The dislocation model of strain anisotropy in practice. J. Appl. Cryst. 1999, 32, 992–1002. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M. Whole powder pattern modelling. Acta Cryst. 2002, 58, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Mittemeijer, E.J.; Scardi, P. (Eds.) Diffraction Analysis of the Microstructure of Materials; Springer: Berlin, Heidelberg, 2004. [Google Scholar]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Cryst. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Langford, J.I. A rapid method for analysing the breadths of diffraction and spectral lines using the Voigt function. J. Appl. Cryst. 1978, 11, 10–14. [Google Scholar] [CrossRef]
- Langford, J.I.; Delhez, R.; de Keijser, T.H.; Mittemeijer, E.J. Profile analysis for microcrystalline properties by the Fourier and other methods. Profile analysis for microcrystalline properties by the Fourier and other methods. Aust. J. Phys. 1988, 41, 173–187. [Google Scholar] [CrossRef]
- Balzar, D. Profile fitting of X-ray diffraction lines and Fourier analysis of broadening. J. Appl. Cryst. 1992, 25, 559–570. [Google Scholar] [CrossRef]
- Ribárik, G. Modeling of Diffraction Patterns based on Microstructural Properties. Ph.D. Dissertation, Eötvös University Budapest, Budapest, Hungary, 2008. [Google Scholar]
- Ribárik, G.; Ungár, T. Characterization of the microstructure in random and textured polycrystals and single crystals by diffraction line profile analysis. Mater. Sci. Eng. 2010, 528, 112–121. [Google Scholar] [CrossRef]
- Ungár, T.; Balogh, L.; Ribárik, G. Defect-Related Physical-Profile-Based X-Ray and Neutron Line Profile Analysis. Met. Mater. Transact. 2010, 41, 1202–1209. [Google Scholar]
- Ribárik, G.; Jóni, B.; Ungár, T. Global optimum of microstructure parameters in the CMWP line-profile analysis method by combining Marquardt-Levenberg and Monte-Carlo procedures. J. Mater. Sci. Technol. 2018, 35, 1508–1514. [Google Scholar] [CrossRef]
- James, R.W. The Optical Principles of the Diffraction of X-ray; Bell, G. and Sons Ltd., CERN Document Server: London, UK, 1965. [Google Scholar]
- Bertaut, E.F. Raies de Debye–Scherrer et repartition des dimensions des domaines de Bragg dans les poudres polycristallines. Acta Crystallogr. 1950, 3, 14–18. [Google Scholar] [CrossRef]
- Langford, J.I.; Louër, D.; Scardi, P. Effect of a crystallite size distribution on X-ray diffraction line profiles and whole-powder-pattern fitting. J. Appl. Crystallogr. 2000, 33, 964–974. [Google Scholar] [CrossRef]
- Ungár, T.; Gubicza, J.; Ribárik, G.; Borbély, A. Crystallite size distribution and dislocation structure determined by diffraction profile analysis: Principles and practical application to cubic and hexagonal crystals. J. Appl. Cryst. 2001, 34, 298–310. [Google Scholar] [CrossRef]
- Krivoglaz, M.A.; Ryaboshapka, K.P. Theory of X-ray Scattering by Crystals Containing Dislocations, Randomly Distributed Dislocation Loops. Phys. Met. Metall. 1963, 16, 1–13. [Google Scholar]
- Krivoglaz, M.A. Theory of X-ray and Thermal Neutron Scattering by Real Crystals; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Groma, I.; Ungár, T.; Wilkens, M. Asymmetric X-ray Line Broadening of Plastically Deformed Crystals. I. Theory. J. Appl. Cryst. 1988, 21, 47–53. [Google Scholar] [CrossRef]
- Ungár, T.; Groma, I.; Wilkens, M. Asymmetric X-ray Line Broadening of Plastically Deformed Crystals. II. Evaluation Procedure and Application to [001]-Cu Crystals. J. Appl. Cryst. 1989, 22, 26–34. [Google Scholar]
- Borbély, A.; Groma, I. Variance method for the evaluation of particle size and dislocation density from x-ray Bragg peaks. Appl. Phys. Lett. 2001, 79, 1772–1774. [Google Scholar]
- Ungár, T.; Ribárik, G.; Topping, M.; Jones, R.M.A.; Xu, X.D.; Hulse, R.; Harte, H.; Tichy, G.; Race, C.P.; Frankel, P.; et al. Characterizing Dislocation Loops in Irradiated Zr alloys by X-ray Line Profile Analysis of Diffraction Patterns with Satellites. submitted to J. Appl. Cryst 2020. [Google Scholar]
- Groma, I.; Monnet, G.J. Analysis of asymmetric broadening of X-ray diffraction peak profiles caused by randomly distributed polarized dislocation dipoles and dislocation walls. J. Appl. Cryst. 2002, 35, 589–593. [Google Scholar] [CrossRef]
- Velterop, L.; Delhez, R.; de Keijser, T.H.; Mittemeijer, E.J.; Reefman, D. X-ray diffraction analysis of stacking and twin faults in f.c.c. metals: A revision and allowance for texture and non-uniform fault probabilities. J. Appl. Cryst. 2000, 33, 296–306. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Penton-Madrigal, A.; Lora-Serrano, R.; Martinez-Garcia, J. Direct determination of microstructural parameters from the X-ray diffraction profile of a crystal with stacking faults. J. Appl. Cryst. 2001, 34, 730–736. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Leoni, M.; Scardi, P.; Aragon-Fernandez, B.; Fuess, H. On the powder diffraction pattern of crystals with stacking faults. Philos. Mag. 2003, 83, 4045–4057. [Google Scholar] [CrossRef]
- Balogh, L.; Ribárik, G.; Ungár, T. Stacking faults and twin boundaries in fcc crystals determined by x-ray diffraction profile analysis. J. Appl. Phys. 2006, 100, 023512. [Google Scholar] [CrossRef]
- Balogh, L.; Tichy, G.; Ungár, T. Twinning on pyramidal planes in hexagonal close packed crystals determined along with other defects by X-ray line profile analysis. J. Appl. Cryst. 2009, 42, 580–591. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Newsam, J.M.; Deem, M.W. A general recursion method for calculating diffracted intensities from crystals containing planar faults. Proc. Roy. Soc. London 1991, 433, 499–520. [Google Scholar]
- Leineweber, A. Anisotropic diffraction-line broadening due to microstrain distribution: Parametrization opportunities. J. Appl. Cryst. 2006, 39, 509–518. [Google Scholar] [CrossRef]
- Leineweber, A. Anisotropic microstrain broadening in cementite, Fe3C, caused by thermal microstress: Comparison between prediction and results from diffraction-line profile analysis. J. Appl. Cryst. 2012, 45, 944–949. [Google Scholar] [CrossRef]
- Zilahi, G.; Ungár, T.; Tichy, G. A common theory of line broadening and rocking curves. J. Appl. Cryst. 2015, 48, 418–430. [Google Scholar] [CrossRef]
- Hinds, W.C. Aerosol Technology: Properties, Behavior and Measurement of Airborne Particles; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Nabarro, F.R.N. Mathematical theory of stationary dislocations. Adv. Phys. 1952, 1, 269–394. [Google Scholar] [CrossRef]
- Kocks, U.F.; Scattergood, R.O. Elastic Interactions Between Dislocations in a Finite Body. Acta Metall. 1969, 17, 1161–1168. [Google Scholar] [CrossRef]
- Wilkens, M. Das Mittlere Spannungquadrat <σ2> Begrentzt Regellos Verteilter Vesetzungen in einem Zylinderförmigen Körper. Acta Metall. 1969, 17, 1155–1159. [Google Scholar] [CrossRef]
- Fan, Z.; Jóni, B.; Ribárik, G.; Ódor, É.; Fogarassy, Z.; Ungár, T. The microstructure and strength of a V-5Cr-5Ti alloy processed by high pressure torsion. Mater. Sci. Eng. 2019, 758, 139–146. [Google Scholar] [CrossRef]
- Borbély, A.; Dragomir-Cernatescu, I.; Ribárik, G.; Ungár, T. Computer program ANIZC for the calculation of diffraction contrast factors of dislocations in elastically anisotropic cubic, hexagonal and trigonal crystals. J. Appl. Cryst. 2003, 36, 160–162. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Leoni, M.; Scardi, P. A general approach for determining the diffraction contrast factorof straight line dislocations. Acta Cryst. 2009, 56A, 109–119. [Google Scholar] [CrossRef]
- Ungár, T.; Tichy, G. The effect of dislocation contrast on X-ray line profiles in untextured polycrystals. Phys. Stat. Sol. 1999, 171, 425–434. [Google Scholar] [CrossRef]
- Dragomir, I.; Ungár, T. Contrast factors of dislocations in the hexagonal crystal system. J. Appl. Cryst. 2002, 35, 556–564. [Google Scholar] [CrossRef]
- Ungár, T.; Castelnau, O.; Ribárik, G.; Drakopoulos, M.; Béchade, J.L.; Chauveau, T.; Snigirev, A.; Snigireva, I.; Schroer, C.; Bacroix, B. Grain to grain slip activity in plastically deformed Zr determined by X-ray micro-diffraction line profile analysis. Acta Mater. 2007, 55, 1117–1127. [Google Scholar] [CrossRef]
- Mujica, N.; Cerda, M.T.; Espinoza, R.; Lisoni, J.; Lund, F. Ultrasound as a probe of dislocation density in aluminum. Cond. Mat. Mtrl. Sci. 2012, 60, 5828–5837. [Google Scholar] [CrossRef]
- Dai, X.; Jiang, F.-L.; Liu, J.; Wu, L.-Y.; Fu, D.-F.; Teng, J.; Zhang, H. Insights into the strain anisotropy models for refined diffraction line profile analysis in cubic metals. Transact. Nonferr. Met. Soc. China 2020. (in the press). [Google Scholar]
- Strutz, T. Data Fitting and Uncertainty (A Practical Introduction to Weighted Least Squares and Beyond), 2nd ed.; Springer Vieweg: New York, NY, USA, 2016. [Google Scholar]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by Direct Search: New Perspectives on Some Classical and Modern Methods. SIAM Rev. Soc. Industr. Appl. Mathcs. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-1-4757-4145-2. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Quart. Appl. Mathcs. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM Rev. Soc. Industr. Appl. Mathcs. 1963, 2, 431–441. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D.; Kozanis, S. An algorithm to construct Monte Carlo confidence intervals for an arbitrary function of probability distribution parameters. Comput. Stat. 2013, 28, 1501–1527. [Google Scholar] [CrossRef]
- Müller, P.P.; Schönfeld, B.; Kostorz, G.; Bührer, W. Guinier-Preston I Zones in Al-1.75 at.% Cu Single Crystals. Acta Met. 1989, 37, 2125–2132. [Google Scholar] [CrossRef]
- Ungár, T.; Dubey, P.A.; Kostorz, G. Distortion scattering due to guinier-preston zones in Al-3 at%Ag. Acta Metall. Mater. 1990, 38, 2583–2586. [Google Scholar] [CrossRef]
- Larson, B.C. X-ray diffuse scattering near Bragg reflections for the study of clustered defects in crystalline materials. In Diffuse Scattering and the Fundamental Properties of Materials; Barabash, R.I., Ice, G.E., Turchi, P.E.A., Eds.; Momentum Press: New York, NY, USA, 2009; pp. 139–160. [Google Scholar]
- Seymour, T.; Frankel, P.; Balogh, L.; Ungár, T.; Thompson, S.P.; Jädernäs, D.; Romero, J.; Hallstadius, L.; Daymond, M.R.; Ribárik, G.; et al. Evolution of dislocation structure in neutron irradiated Zircaloy-2 studied by synchrotron x-ray diffraction peak profile analysis. Acta Mater. 2007, 126, 102–113. [Google Scholar] [CrossRef]
- Schönfeld, B.; Kostorz, G. Elastic diffuse scattering of alloys: Status and perspectives. In Diffuse Scattering and the Fundamental Properties of Materials; Barabash, R.I., Ice, G.E., Turchi, P.E.A., Eds.; Momentum Press: New York, NY, USA, 2009; pp. 119–137. [Google Scholar]
- Carpenter, G.J.C.; Zee, R.H.; Rogerson, A. Irradiation Growth of Zirconium Single Crystals. J. Nucl. Mater. 1988, 159, 86–100. [Google Scholar] [CrossRef]
- Onimus, F.; Bechade, J.L. Radiation Effects in Zirconium Alloys. Compr. Nucl. Mater. 2012, 4, 246–273. [Google Scholar]
- Larson, B.C.; Young, F.W., Jr. X-ray diffuse scattering study of irradiation induced dislocation loops in copper. Phys. Stat. Sol. 1987, 104, 273–286. [Google Scholar] [CrossRef]
- Mason, D.R.; Yi, X.; Kirk, M.A.; Dudarev, S.L. Direct observation of size scaling and elastic interaction between nano-scale defects in collision cascades. J. Phys. Cond. Matter. 2014, 110, 375701. [Google Scholar] [CrossRef] [PubMed]
- Dederichs, P.H. Diffuse scattering from defect clusters near Bragg reflections. Phys. Rev. B 1971, 4, 1041–1050. [Google Scholar] [CrossRef]
- Ehrhart, P.; Averback, R.S. Diffuse X-ray scattering studies of neutron- and electron-irradiated Ni, Cu and dilute alloys. Phil. Mag. 1989, 60, 283–306. [Google Scholar] [CrossRef]
- Valizadeh, S.; Ledergerber, G.; Abolhassan, S.; Jädernäs, D.; Dahlbäck, M.; Mader, E.V.; Zhou, G.; Wright, J.; Hallstadius, L. Effects of Secondary Phase Particle Dissolution on the In-Reactor Performance of BWR Cladding. J. ASTM Internat. 2011, 8, 103025. [Google Scholar] [CrossRef]
- Wagner, G.J.; Liu, W.K. Coupling of atomistic and continuum simulations using a bridging scale decomposition. J. Comput. Phys. 2003, 190, 249–274. [Google Scholar] [CrossRef]
- Seif, D.; Po, G.; Mrovec, M.; Lazar, M.; Elsässer, C.; Gumbsch, P. Atomistically enabled nonsingular anisotropic elastic representation of near-core dislocation stress fields in α-iron. Phy. Rev. B 2015, 91, 184102. [Google Scholar] [CrossRef]
- Topping, M.; Harte, A.; Ungár, T.; Race, C.P.; Dumbill, S.; Frankel, P.; Preuss, M. The effect of irradiation temperature on damage structures in proton-irradiated zirconium alloys. J. Nucl. Mater. 2019, 514, 358–367. [Google Scholar] [CrossRef]
- Jones, R.M.A. The Effect of Niobium on the Microstructural Evolution of Zirconium Alloys during Proton Irradiation. Ph.D. Dissertatio, The University of Manchester, Manchester, UK, 2019. [Google Scholar]
- Vicente-Alvarez, M.A.; Santisteban, J.R.; Domizzi, G.; Almer, J. Phase and texture analysis of a hydride blister in a Zr–2.5%Nb tube by synchrotron X-ray diffraction. Acta Mater. 2011, 59, 2210–2220. [Google Scholar] [CrossRef]
- Vicente-Alvarez, M.A.; Santisteban, J.R.; Vizcaíno, P.; Ribárik, G.; Ungár, T. Quantification of dislocations densities in zirconium hydride by X-ray line profile analysis. Acta Mater. 2016, 117, 1–12. [Google Scholar] [CrossRef]
- Domizzi, G.; Enrique, R.A.; Ovejero-Garcia, J.; Buscaglia, G.C. Blister growth in zirconium alloys: Experimentation and modeling. J. Nucl. Mater. 1996, 229, 36–47. [Google Scholar] [CrossRef]
- Qin, W.; Szpunar, J.A.; Kozinsk, J. Hydride-induced degradation of zirconium alloys: A criterion for complete ductile-to-brittle transition and its dependence on microstructure. Proc. Roy. Soc. 2015, 471, 20150192. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).