Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances
Abstract
:1. Acoustic Metamaterials: A Brief Overview
2. Recent Applications of Acoustic Metamaterials for Sound Attenuation and Ventilation
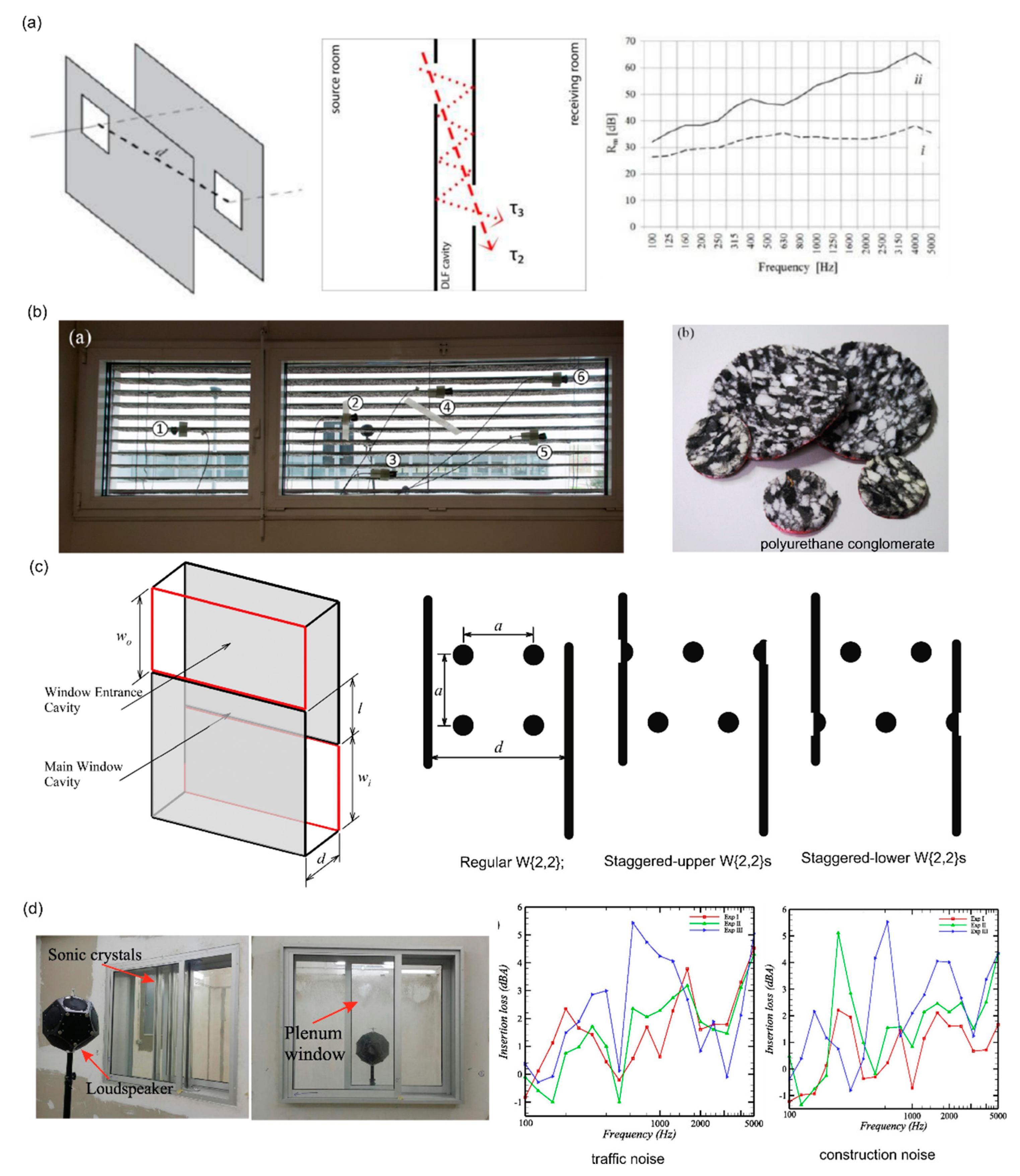
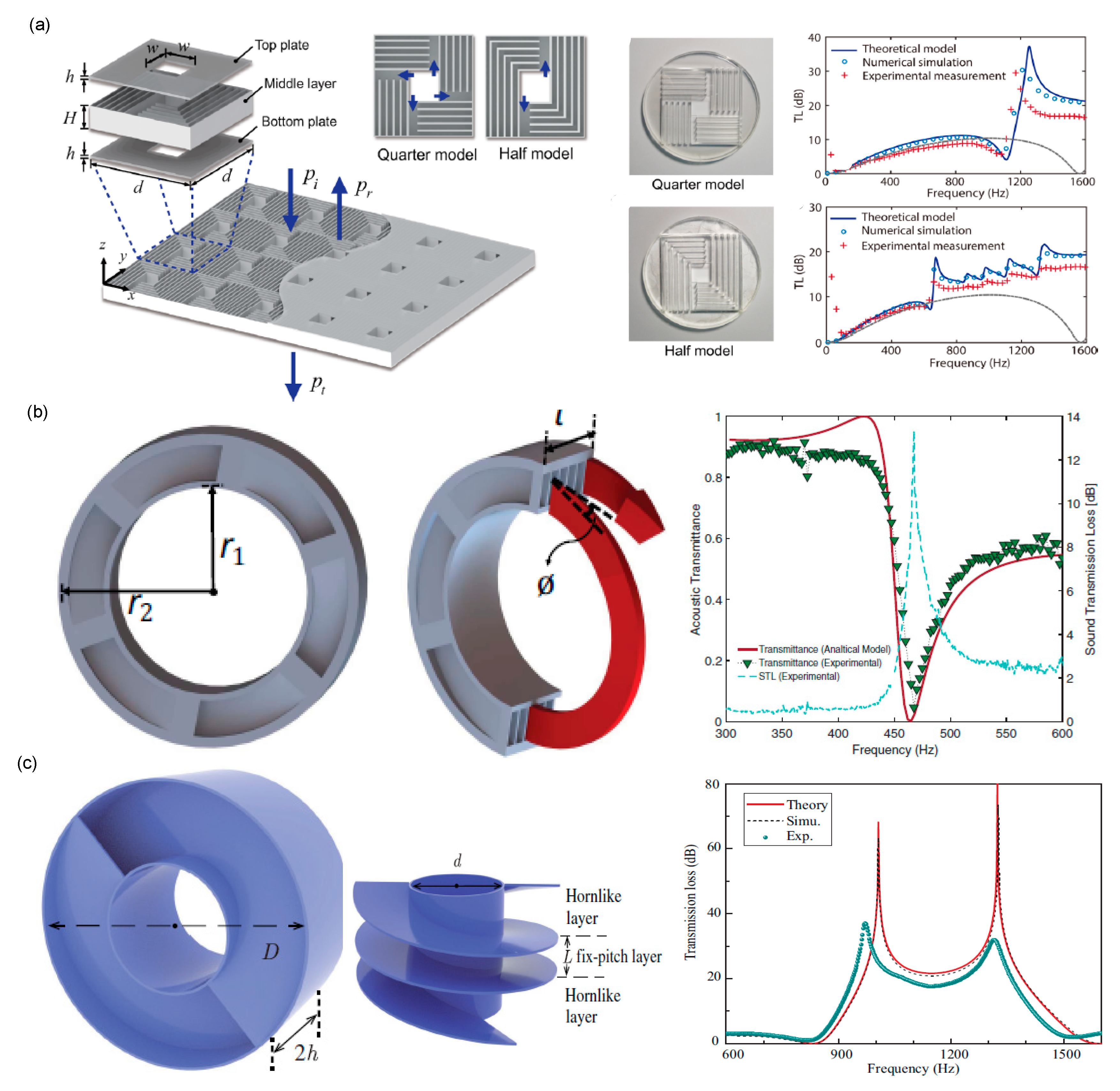
2.1. Acoustic Façade Systems
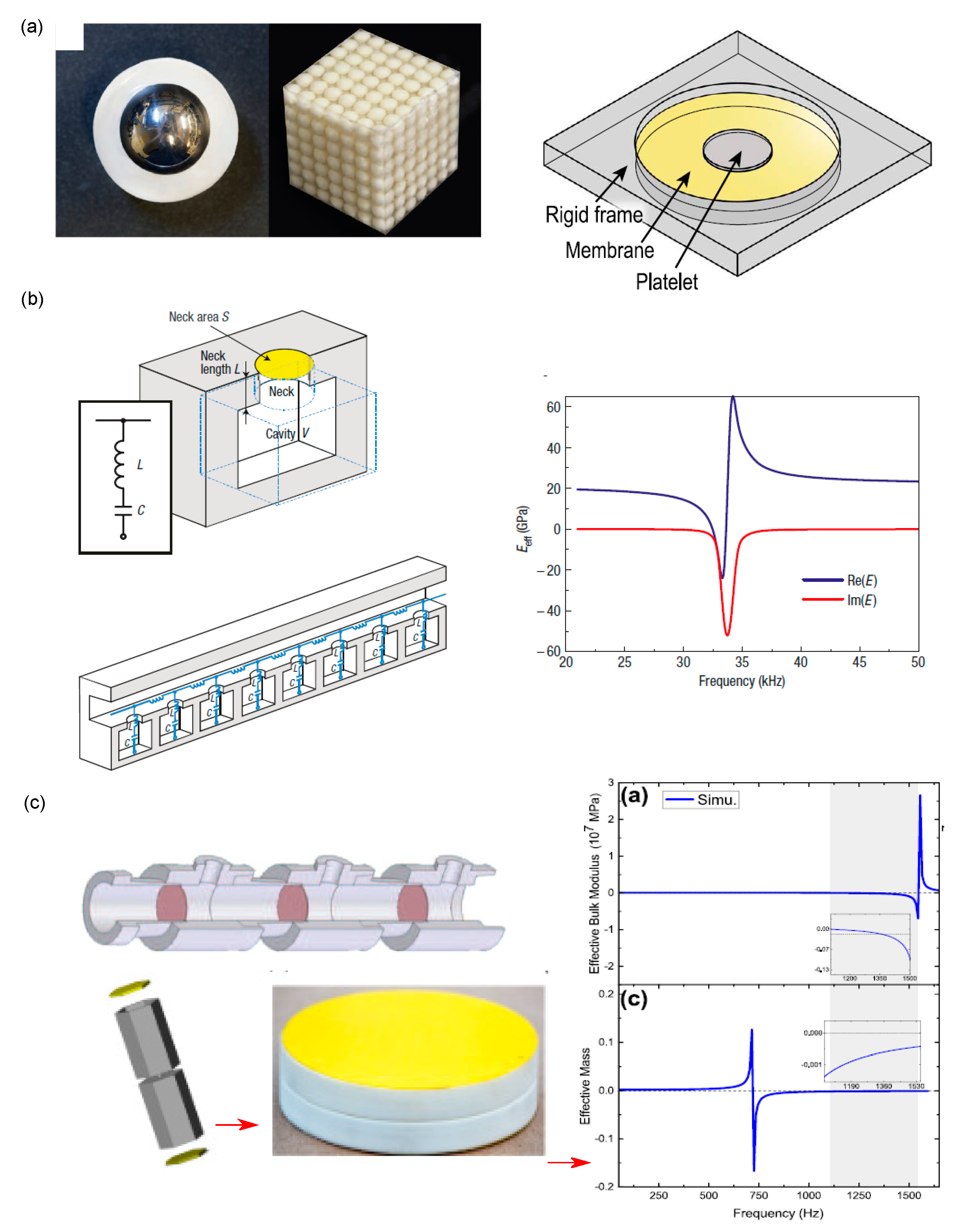
2.2. Helmholtz Resonators
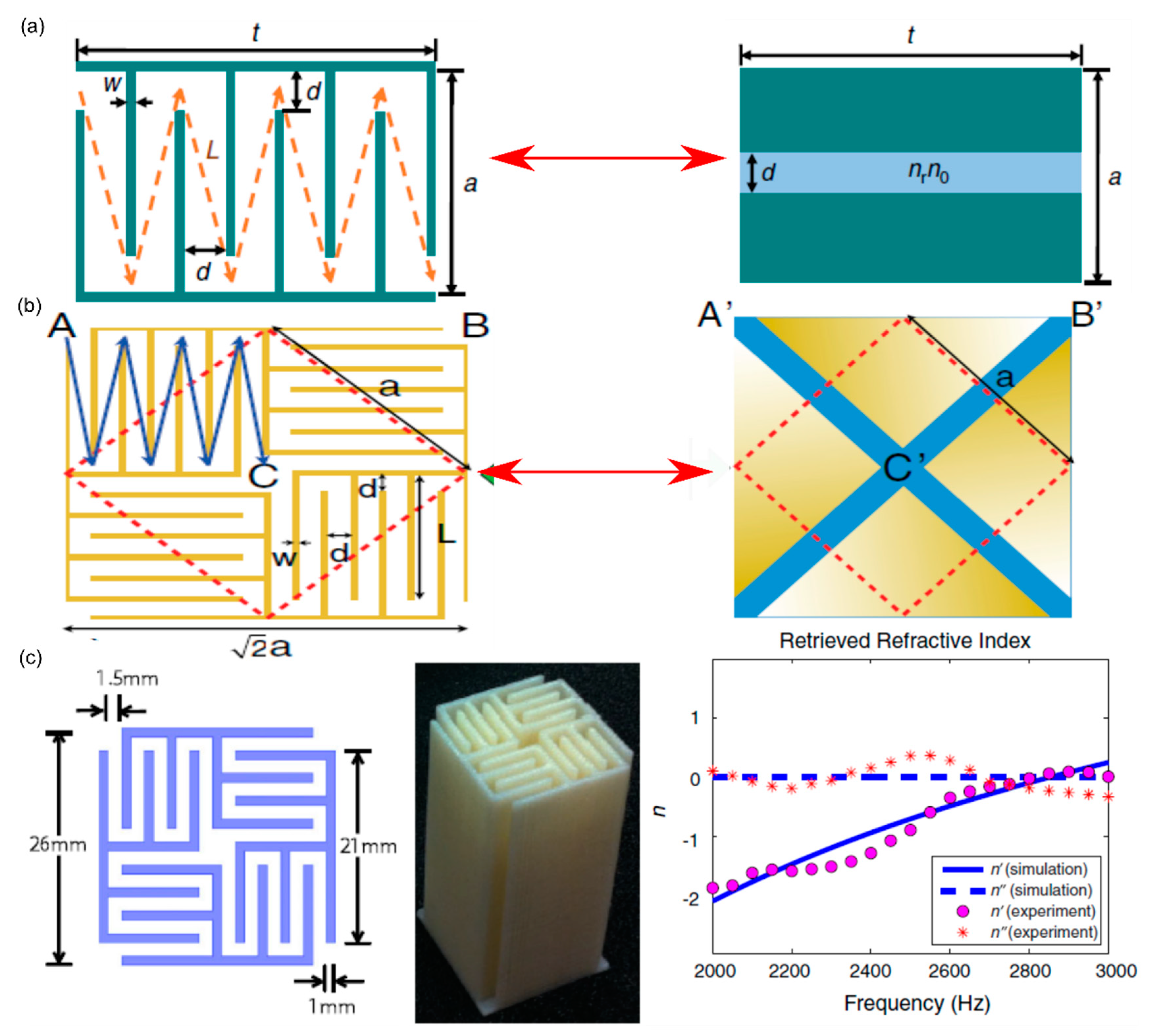
2.3. Noise Attenuation Through Coiling-Up-Space
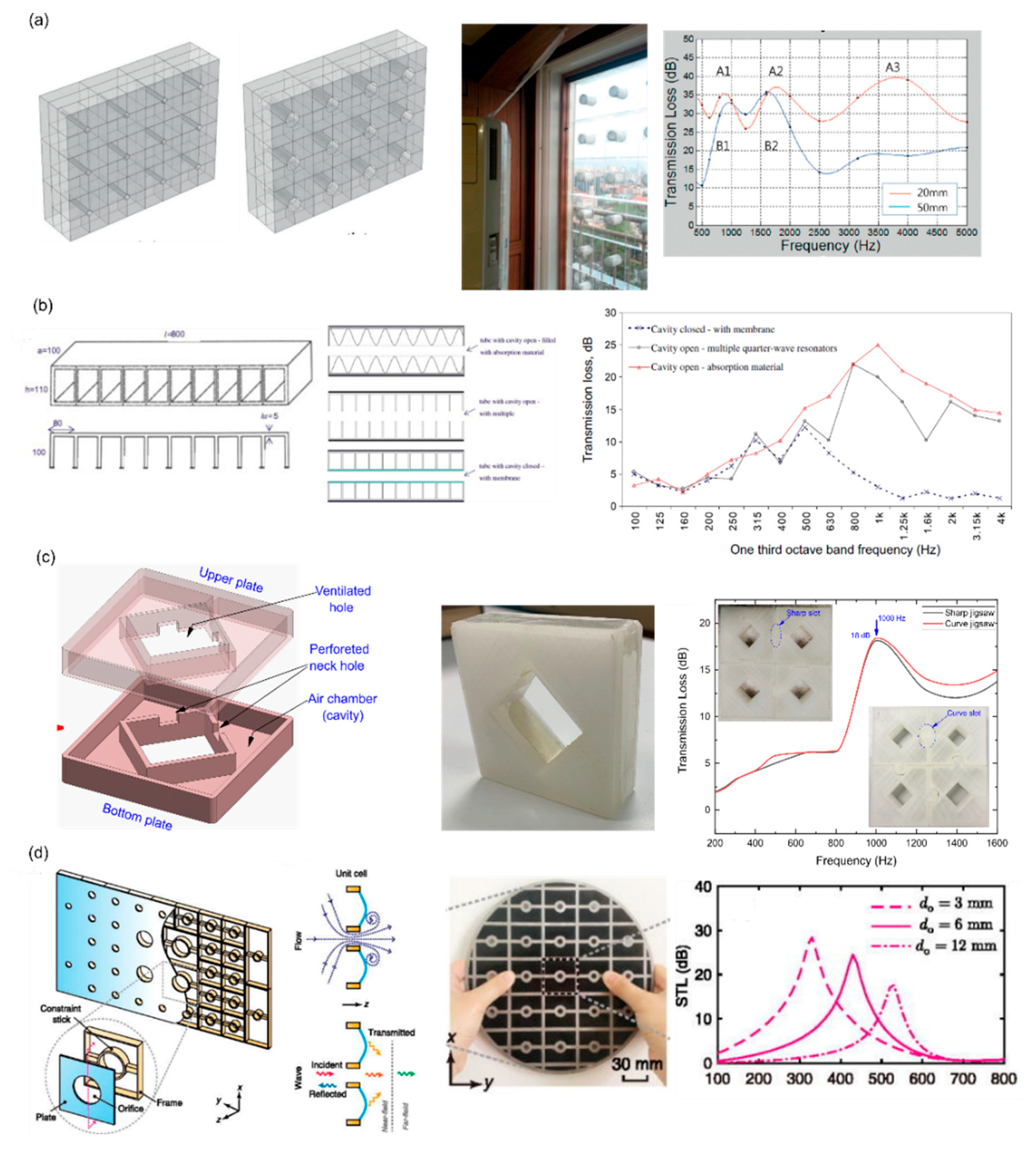
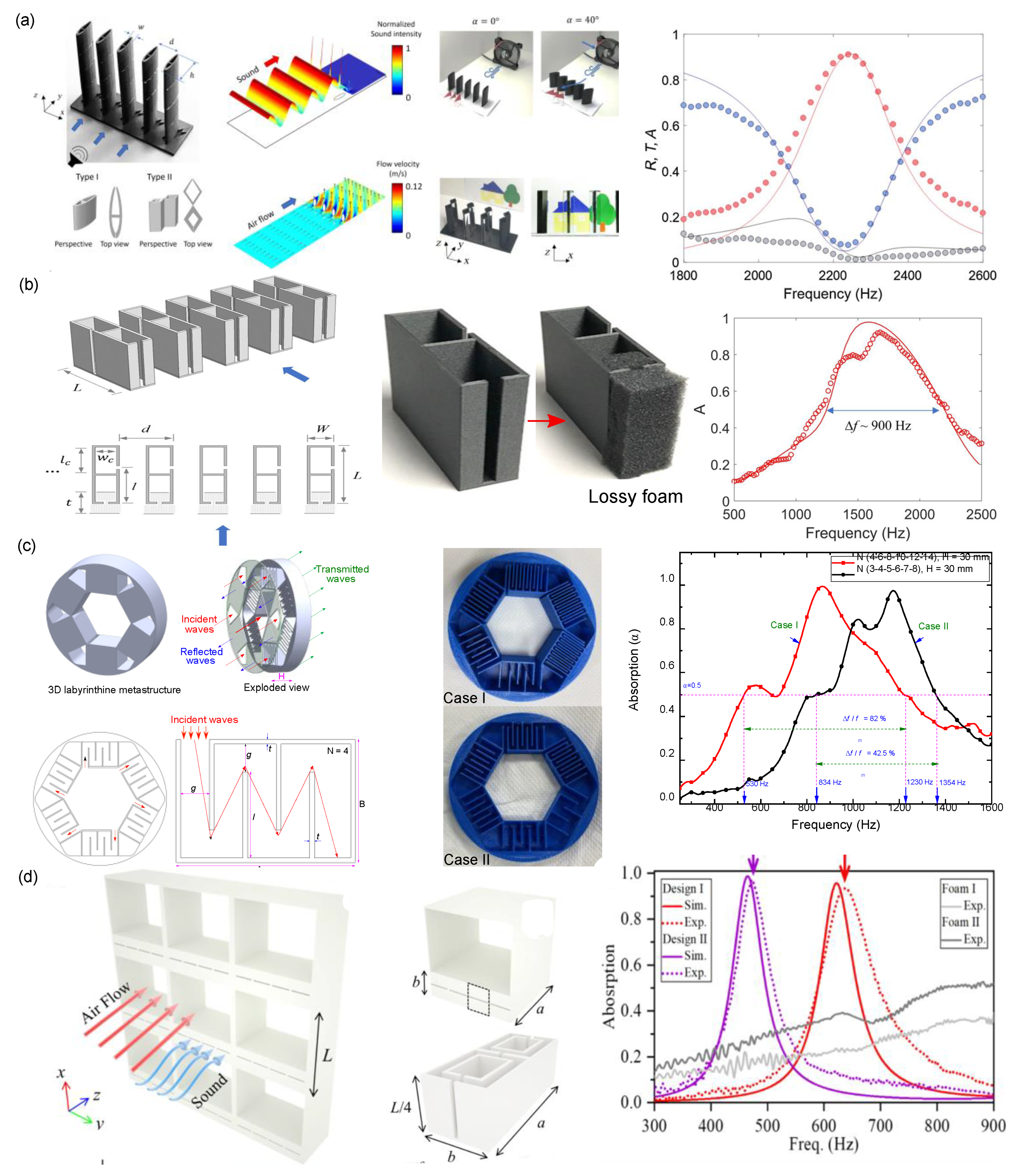
2.4. Acoustic Metacage
2.5. Acoustic Meta-Absorbers
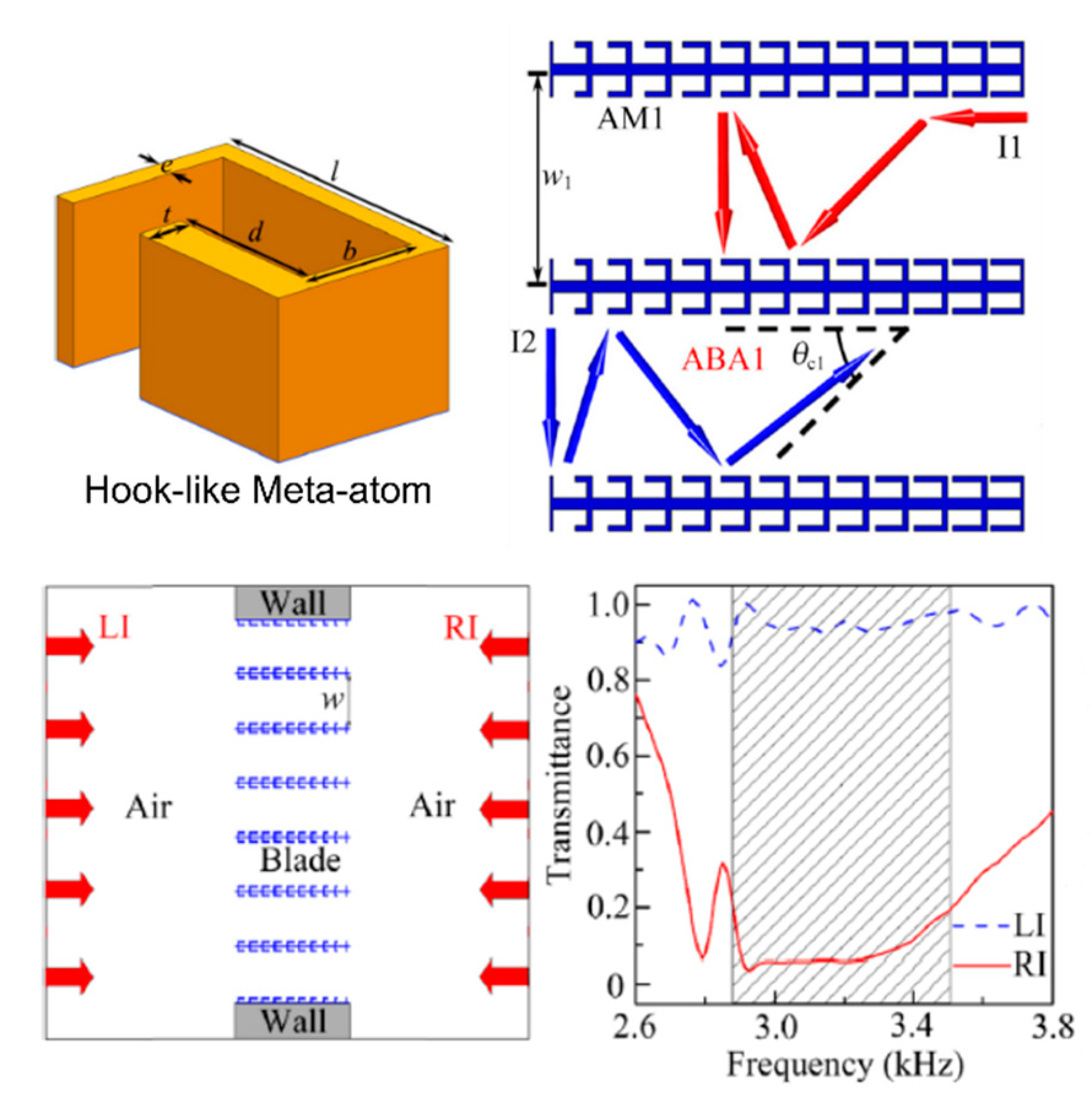
2.6. Omnidirectional/Unidirectional Sound Insulators
3. Outlook
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of and μ. Sov. Phys. Uspekhi 1968, 10, 509. [Google Scholar] [CrossRef]
- Walser, R.M. Metamaterials: An introduction. In Introduction to Complex Mediums for Optics and Electromagnetics; 2003; Volume 1, pp. 295–316. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.; Stewart, W.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76, 4773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engheta, N. An idea for thin subwavelength cavity resonators using metamaterials with negative permittivity and permeability. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Ziolkowski, R.W. Design, fabrication, and testing of double negative metamaterials. IEEE Trans. Antennas Propag. 2003, 51, 1516–1529. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Linden, S.; Wegener, M. Negative refractive index at optical wavelengths. Science 2007, 315, 47–49. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Weber, L.; Gomez-Agustina, L. Investigation into the application of an acoustic metamaterial for sound attenuation with air-flow. ICSV22 Proc. Florence Italy Pap. 2015, 0508105747633. [Google Scholar]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ge, H.; Yang, M.; Ma, C.; Lu, M.-H.; Chen, Y.-F.; Fang, N.; Sheng, P. Breaking the barriers: Advances in acoustic functional materials. Natl. Sci. Rev. 2017, 5, 159–182. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H.P. The present and future role of acoustic metamaterials for architectural and urban noise mitigations. Acoustics 2019, 1, 590–607. [Google Scholar] [CrossRef] [Green Version]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yablonovitch, E.; Gmitter, T.; Leung, K.-M. Photonic band structure: The face-centered-cubic case employing nonspherical atoms. Phys. Rev. Lett. 1991, 67, 2295. [Google Scholar] [CrossRef]
- Cubukcu, E.; Aydin, K.; Ozbay, E.; Foteinopoulou, S.; Soukoulis, C.M. Negative refraction by photonic crystals. Nature 2003, 423, 604–605. [Google Scholar] [CrossRef]
- Reed, E.J.; Soljačić, M.; Joannopoulos, J.D. Reversed doppler effect in photonic crystals. Phys. Rev. Lett. 2003, 91, 133901. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Lin, X.; Kaminer, I.; Gao, F.; Yang, Z.; Joannopoulos, J.D.; Soljačić, M.; Zhang, B. Superlight inverse Doppler effect. Nat. Phys. 2018, 14, 1001–1005. [Google Scholar] [CrossRef] [Green Version]
- Xi, S.; Chen, H.; Jiang, T.; Ran, L.; Huangfu, J.; Wu, B.-I.; Kong, J.A.; Chen, M. Experimental verification of reversed Cherenkov radiation in left-handed metamaterial. Phys. Rev. Lett. 2009, 103, 194801. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Easo, S.; Shen, Y.; Chen, H.; Zhang, B.; Joannopoulos, J.D.; Soljačić, M.; Kaminer, I. Controlling cherenkov angles with resonance transition radiation. Nat. Phys. 2018, 14, 816–821. [Google Scholar] [CrossRef]
- Luo, C.; Johnson, S.G.; Joannopoulos, J.; Pendry, J. Subwavelength imaging in photonic crystals. Phys. Rev. B 2003, 68, 045115. [Google Scholar] [CrossRef] [Green Version]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Psarobas, I.E. Phononic crystals–sonic band-gap materials. Z. Krist.-Cryst. Mater. 2005, 220, IV. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.-H.; Feng, L.; Chen, Y.-F. Phononic crystals and acoustic metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Bloch, F. Elektron im periodischen Potential, Bändermodell des Festkörpers, Z. Phys 1928, 52, 555. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976; Volume 8. [Google Scholar]
- Ruzzene, M.; Scarpa, F. Directional and band-gap behavior of periodic auxetic lattices. Phys. Status Solidi (b) 2005, 242, 665–680. [Google Scholar] [CrossRef]
- Gorishnyy, T.; Maldovan, M.; Ullal, C.; Thomas, E. Sound ideas. Phys. World 2005, 18, 24. [Google Scholar] [CrossRef]
- Deymier, P.A. Acoustic Metamaterials and Phononic Crystals; Springer Science & Business Media: Berlin, Germany, 2013; Volume 173. [Google Scholar]
- Khelif, A.; Adibi, A. Phononic Crystals; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Sigalas, M.; Economou, E.N. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- De Espinosa, F.M.; Jimenez, E.; Torres, M. Ultrasonic band gap in a periodic two-dimensional composite. Phys. Rev. Lett. 1998, 80, 1208. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.V.; Caballero, D.; Mártinez-Sala, R.; Rubio, C.; Sánchez-Dehesa, J.; Meseguer, F.; Llinares, J.; Gálvez, F. Sound attenuation by a two-dimensional array of rigid cylinders. Phys. Rev. Lett. 1998, 80, 5325. [Google Scholar] [CrossRef] [Green Version]
- Fok, L.; Ambati, M.; Zhang, X. Acoustic metamaterials. MRS Bull. 2008, 33, 931–934. [Google Scholar] [CrossRef]
- Fokin, V.; Ambati, M.; Sun, C.; Zhang, X. Method for retrieving effective properties of locally resonant acoustic metamaterials. Phys. Rev. B 2007, 76, 144302. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Sun, C. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 2009, 11, 013003. [Google Scholar] [CrossRef]
- Lee, S.H.; Wright, O.B. Origin of negative density and modulus in acoustic metamaterials. Phys. Rev. B 2016, 93, 024302. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.; Sheng, P. Membrane-type acoustic metamaterial with negative dynamic mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Acoustic metamaterial with negative density. Phys. Lett. A 2009, 373, 4464–4469. [Google Scholar] [CrossRef]
- Chen, J.-S.; Chien, I.-T. Dynamic behavior of a metamaterial beam with embedded membrane-mass structures. J. Appl. Mech. 2017, 84, 121007. [Google Scholar] [CrossRef]
- Yang, M.; Li, Y.; Meng, C.; Fu, C.; Mei, J.; Yang, Z.; Sheng, P. Sound absorption by subwavelength membrane structures: A geometric perspective. Comptes Rendus Mécanique 2015, 343, 635–644. [Google Scholar] [CrossRef] [Green Version]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chan, C. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with simultaneously negative bulk modulus and mass density. Phys. Rev. Lett. 2007, 99, 093904. [Google Scholar] [CrossRef] [PubMed]
- Burov, V.; Dmitriev, K.; Sergeev, S. Acoustic double-negative media. Acoust. Phys. 2009, 55, 298–310. [Google Scholar] [CrossRef]
- Fok, L.; Zhang, X. Negative acoustic index metamaterial. Phys. Rev. B 2011, 83, 214304. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Park, C.M.; Seo, Y.M.; Wang, Z.G.; Kim, C.K. Composite acoustic medium with simultaneously negative density and modulus. Phys. Rev. Lett. 2010, 104, 054301. [Google Scholar] [CrossRef]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled membranes with doubly negative mass density and bulk modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef]
- Chen, H.; Zeng, H.; Ding, C.; Luo, C.; Zhao, X. Double-negative acoustic metamaterial based on hollow steel tube meta-atom. J. Appl. Phys. 2013, 113, 104902. [Google Scholar] [CrossRef] [Green Version]
- Brunet, T.; Merlin, A.; Mascaro, B.; Zimny, K.; Leng, J.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O. Soft 3D acoustic metamaterial with negative index. Nat. Mater. 2015, 14, 384. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, C.; Yuan, B.; Wu, D.; Wei, Q.; Liu, X. Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial mie resonances. Nat. Mater. 2015, 14, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Alu, A.; Silveirinha, M.G.; Salandrino, A.; Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 2007, 75, 155410. [Google Scholar] [CrossRef] [Green Version]
- Fleury, R.; Alù, A. Extraordinary sound transmission through density-near-zero ultranarrow channels. Phys. Rev. Lett. 2013, 111, 055501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Li, J. Total reflection and cloaking by zero index metamaterials loaded with rectangular dielectric defects. Appl. Phys. Lett. 2013, 102, 183105. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liang, B.; Tao, X.; Zhu, X.-F.; Zou, X.-Y.; Cheng, J.-C. Acoustic focusing by coiling up space. Appl. Phys. Lett. 2012, 101, 233508. [Google Scholar] [CrossRef]
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar helmholtz resonators. Appl. Phys. Lett. 2014, 105, 121901. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Gao, F.; Shi, X.; Lin, X.; Gao, Z.; Chong, Y.; Zhang, B. Topological acoustics. Phys. Rev. Lett. 2015, 114, 114301. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheng, Q.; Huang, B.; Dong, H.Y.; Cui, T.J. Broadband fractal acoustic metamaterials for low-frequency sound attenuation. Appl. Phys. Lett. 2016, 109, 131901. [Google Scholar] [CrossRef]
- Liu, J.; Li, L.; Xia, B.; Man, X. Fractal labyrinthine acoustic metamaterial in planar lattices. Int. J. Solids Struct. 2018, 132, 20–30. [Google Scholar] [CrossRef]
- Man, X.; Luo, Z.; Liu, J.; Xia, B. Hilbert fractal acoustic metamaterials with negative mass density and bulk modulus on subwavelength scale. Mater. Des. 2019, 180, 107911. [Google Scholar] [CrossRef]
- Man, X.-F.; Xia, B.-Z.; Luo, Z.; Liu, J. 3D Hilbert fractal acoustic metamaterials: Low-frequency and multi-band sound insulation. J. Phys. D Appl. Phys. 2019, 52, 195302. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, G.; Xia, D. Maze-like acoustic metamaterial for low-frequency broadband noise suppression. Appl. Phys. Express 2020, 13, 027002. [Google Scholar]
- Zhu, X.; Li, K.; Zhang, P.; Zhu, J.; Zhang, J.; Tian, C.; Liu, S. Implementation of dispersion-free slow acoustic wave propagation and phase engineering with helical-structured metamaterials. Nat. Commun. 2016, 7, 11731. [Google Scholar] [CrossRef] [PubMed]
- Esfahlani, H.; Lissek, H.; Mosig, J.R. Generation of acoustic helical wavefronts using metasurfaces. Phys. Rev. B 2017, 95, 024312. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Jiang, X.; Li, R.-Q.; Liang, B.; Zou, X.-Y.; Yin, L.-L.; Cheng, J.-C. Experimental realization of full control of reflected waves with subwavelength acoustic metasurfaces. Phys. Rev. Appl. 2014, 2, 064002. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, H.; Yang, H.; Wang, Y.; Yin, J.; Wen, J. Theoretical requirements and inverse design for broadband perfect absorption of low-frequency waterborne sound by ultrathin metasurface. Sci. Rep. 2019, 9, 1181. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Li, J. Extreme acoustic metamaterial by coiling up space. Phys. Rev. Lett. 2012, 108, 114301. [Google Scholar] [CrossRef]
- Liu, C.; Luo, J.; Lai, Y. Acoustic metamaterials with broadband and wide-angle impedance matching. Phys. Rev. Mater. 2018, 2, 045201. [Google Scholar] [CrossRef]
- Chen, C.; Du, Z.; Hu, G.; Yang, J. A low-frequency sound absorbing material with subwavelength thickness. Appl. Phys. Lett. 2017, 110, 221903. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Assouar, B.M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via spiral metasurfaces with embedded apertures. Appl. Phys. Lett. 2018, 113, 233501. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X. Three-dimensional single-port labyrinthine acoustic metamaterial: Perfect absorption with large bandwidth and tunability. Phys. Rev. Appl. 2016, 6, 064025. [Google Scholar] [CrossRef] [Green Version]
- Long, H.; Shao, C.; Liu, C.; Cheng, Y.; Liu, X. Broadband near-perfect absorption of low-frequency sound by subwavelength metasurface. Appl. Phys. Lett. 2019, 115, 103503. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, Y.; Guo, X.; Shen, Y.; Zhang, D. Low-frequency anechoic metasurface based on coiled channel of gradient cross-section. Appl. Phys. Lett. 2019, 114, 083501. [Google Scholar] [CrossRef]
- Kumar, S.; Bhushan, P.; Prakash, O.; Bhattacharya, S. Double negative acoustic metastructure for attenuation of acoustic emissions. Appl. Phys. Lett. 2018, 112, 101905. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Holt, R.G.; Anderson, S.; Zhang, X. Horn-like space-coiling metamaterials toward simultaneous phase and amplitude modulation. Nat. Commun. 2018, 9, 1349. [Google Scholar] [CrossRef]
- Xie, Y.; Popa, B.-I.; Zigoneanu, L.; Cummer, S.A. Measurement of a broadband negative index with space-coiling acoustic metamaterials. Phys. Rev. Lett. 2013, 110, 175501. [Google Scholar] [CrossRef]
- Corbusier, L. Towards a New Architecture; Courier Corporation: New York, NY, USA, 2013. [Google Scholar]
- Bajraktari, E.; Lechleitner, J.; Mahdavi, A. The sound insulation of double facades with openings for natural ventilation. Build. Acoust. 2015, 22, 163–176. [Google Scholar] [CrossRef]
- Zuccherini Martello, N.; Fausti, P.; Santoni, A.; Secchi, S. The use of sound absorbing shading systems for the attenuation of noise on building facades. An experimental investigation. Buildings 2015, 5, 1346–1360. [Google Scholar] [CrossRef]
- Tong, Y.; Tang, S. Plenum window insertion loss in the presence of a line source—A scale model study. J. Acoust. Soc. Am. 2013, 133, 1458–1467. [Google Scholar] [CrossRef]
- Tong, Y.; Tang, S.; Kang, J.; Fung, A.; Yeung, M. Full scale field study of sound transmission across plenum windows. Appl. Acoust. 2015, 89, 244–253. [Google Scholar] [CrossRef]
- Tang, S. Reduction of sound transmission across plenum windows by incorporating an array of rigid cylinders. J. Sound Vib. 2018, 415, 25–40. [Google Scholar] [CrossRef]
- Li, X.; Tong, Y.; Tang, S.; Lau, K. Empirical prediction of traffic noise transmission loss across plenum windows. Appl. Acoust. 2019, 151, 45–54. [Google Scholar] [CrossRef]
- Lee, H.M.; Wang, Z.; Lim, K.M.; Xie, J.; Lee, H.P. Novel plenum window with sonic crystals for indoor noise control. Appl. Acoust. 2020, 167, 107390. [Google Scholar]
- Kim, S.-H.; Lee, S.-H. Air transparent soundproof window. AIP Adv. 2014, 4, 117123. [Google Scholar] [CrossRef]
- Wang, Z.; Hui, C.; Ng, C. The acoustic performance of ventilated window with quarter-wave resonators and membrane absorber. Appl. Acoust. 2014, 78, 1–6. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Cheng, L.; Cui, F. On the sound insulation of acoustic metasurface using a sub-structuring approach. J. Sound Vib. 2017, 401, 190–203. [Google Scholar] [CrossRef]
- Jung, J.W.; Kim, J.E.; Lee, J.W. Acoustic metamaterial panel for both fluid passage and broadband soundproofing in the audible frequency range. Appl. Phys. Lett. 2018, 112, 041903. [Google Scholar] [CrossRef]
- Kumar, S.; Xiang, T.B.; Lee, H.P. Ventilated acoustic metamaterial window panels for simultaneous noise shielding and air circulation. Appl. Acoust. 2020, 159, 107088. [Google Scholar] [CrossRef]
- Wang, X.; Luo, X.; Yang, B.; Huang, Z. Ultrathin and durable open metamaterials for simultaneous ventilation and sound reduction. Appl. Phys. Lett. 2019, 115, 171902. [Google Scholar] [CrossRef]
- Yang, J.; Lee, J.S.; Lee, H.R.; Kang, Y.J.; Kim, Y.Y. Slow-wave metamaterial open panels for efficient reduction of low-frequency sound transmission. Appl. Phys. Lett. 2018, 112, 091901. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Zhu, Y.-F.; Liang, B.; Yang, J.; Yang, J.; Cheng, J.-C. Omnidirectional ventilated acoustic barrier. Appl. Phys. Lett. 2017, 111, 203502. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Lu, Z.; Liu, T.; Cheng, L.; Zhu, J.; Cui, F. Sound transmission through a periodic acoustic metamaterial grating. J. Sound Vib. 2019, 449, 140–156. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Anderson, S.; Zhang, X. Ultra-open acoustic metamaterial silencer based on Fano-like interference. Phys. Rev. B 2019, 99, 024302. [Google Scholar] [CrossRef]
- Sun, M.; Fang, X.; Mao, D.; Wang, X.; Li, Y. Broadband Acoustic Ventilation Barriers. Phys. Rev. Appl. 2020, 13, 044028. [Google Scholar] [CrossRef]
- Shen, C.; Xie, Y.; Li, J.; Cummer, S.A.; Jing, Y. Acoustic metacages for sound shielding with steady air flow. J. Appl. Phys. 2018, 123, 124501. [Google Scholar] [CrossRef]
- Melnikov, A.; Maeder, M.; Friedrich, N.; Pozhanka, Y.; Wollmann, A.; Scheffler, M.; Oberst, S.; Powell, D.; Marburg, S. Acoustic metamaterial capsule for reduction of stage machinery noise. J. Acoust. Soc. Am. 2020, 147, 1491–1503. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Sheng, P. Sound absorption structures: From porous media to acoustic metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Lee, T.; Nomura, T.; Dede, E.M.; Iizuka, H. Ultrasparse acoustic absorbers enabling fluid flow and visible-light controls. Phys. Rev. Appl. 2019, 11, 024022. [Google Scholar] [CrossRef]
- Lee, T.; Nomura, T.; Iizuka, H. Damped resonance for broadband acoustic absorption in one-port and two-port systems. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Li, L.-J.; Zheng, B.; Zhong, L.-M.; Yang, J.; Liang, B.; Cheng, J.-C. Broadband compact acoustic absorber with high-efficiency ventilation performance. Appl. Phys. Lett. 2018, 113, 103501. [Google Scholar] [CrossRef]
- Wu, X.; Au-Yeung, K.Y.; Li, X.; Roberts, R.C.; Tian, J.; Hu, C.; Huang, Y.; Wang, S.; Yang, Z.; Wen, W. High-efficiency ventilated metamaterial absorber at low frequency. Appl. Phys. Lett. 2018, 112, 103505. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Lee, H.P. Labyrinthine acoustic metastructures enabling broadband sound absorption and ventilation. Appl. Phys. Lett. 2020, 116, 134103. [Google Scholar] [CrossRef]
- Xiang, X.; Wu, X.; Li, X.; Wu, P.; He, H.; Mu, Q.; Wang, S.; Huang, Y.; Wen, W. Ultra-open ventilated metamaterial absorbers for sound-silencing applications in environment with free air flows. Extrem. Mech. Lett. 2020, 100786. [Google Scholar] [CrossRef]
- Ge, Y.; Sun, H.-X.; Yuan, S.-Q.; Lai, Y. Broadband unidirectional and omnidirectional bidirectional acoustic insulation through an open window structure with a metasurface of ultrathin hooklike meta-atoms. Appl. Phys. Lett. 2018, 112, 243502. [Google Scholar] [CrossRef]
- Ge, Y.; Sun, H.-X.; Yuan, S.-Q.; Lai, Y. Switchable omnidirectional acoustic insulation through open window structures with ultrathin metasurfaces. Phys. Rev. Mater. 2019, 3, 065203. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Chapman, C.D.; Saitou, K.; Jakiela, M.J. Genetic algorithms as an approach to configuration and topology design. J. Mech. Des. 1994, 116, 1005–1012. [Google Scholar] [CrossRef] [Green Version]
- Jakiela, M.J.; Chapman, C.; Duda, J.; Adewuya, A.; Saitou, K. Continuum structural topology design with genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 339–356. [Google Scholar] [CrossRef]
- Goldenberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Kumar, S.; Dubey, A.K.; Pandey, A.K. Computer-aided genetic algorithm based multi-objective optimization of laser trepan drilling. Int. J. Precis. Eng. Manuf. 2013, 14, 1119–1125. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Huber, S.D. Topological mechanics. Nat. Phys. 2016, 12, 621–623. [Google Scholar] [CrossRef]
- Hawley, S.H.; Chatziiannou, V.; Morrison, A. Synthesis of musical instrument sounds: Physics-based modeling or machine learning? Phys. Today 2020, 16, 20–28. [Google Scholar] [CrossRef]
- Li, D.; Zigoneanu, L.; Popa, B.-I.; Cummer, S.A. Design of an acoustic metamaterial lens using genetic algorithms. J. Acoust. Soc. Am. 2012, 132, 2823–2833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, L.; Yamamoto, T.; Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization of an acoustic metamaterial with negative bulk modulus using local resonance. Finite Elem. Anal. Des. 2013, 72, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Souslov, A.; Van Zuiden, B.C.; Bartolo, D.; Vitelli, V. Topological sound in active-liquid metamaterials. Nat. Phys. 2017, 13, 1091–1094. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z. Topological optimization of phononic crystal thin plate by a genetic algorithm. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bacigalupo, A.; Gnecco, G.; Lepidi, M.; Gambarotta, L. Machine-learning techniques for the optimal design of acoustic metamaterials. J. Optim. Theory Appl. 2019, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Zhang, Z. Bandgap design of three-phase phononic crystal by topological optimization. Wave Motion 2020, 93, 102496. [Google Scholar] [CrossRef]
- Jung, J.; Goo, S.; Kook, J. Design of a local resonator using topology optimization to tailor bandgaps in plate structures. Mater. Des. 2020, 108627. [Google Scholar] [CrossRef]
- Dong, H.-W.; Zhao, S.-D.; Wang, Y.-S.; Cheng, L.; Zhang, C. Robust 2D/3D multi-polar acoustic metamaterials with broadband double negativity. J. Mech. Phys. Solids 2020, 137, 103889. [Google Scholar] [CrossRef] [Green Version]
- Weiner, M.; Ni, X.; Li, M.; Alù, A.; Khanikaev, A.B. Demonstration of a third-order hierarchy of topological states in a three-dimensional acoustic metamaterial. Sci. Adv. 2020, 6, eaay4166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wojciechowski, K. Constant thermodynamic tension monte carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Beg, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Kolken, H.M.; Zadpoor, A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Liu, Z.; Matsuhisa, N.; Qi, D.; Leow, W.R.; Yang, H.; Yu, J.; Chen, G.; Liu, Y.; Wan, C. Auxetic mechanical metamaterials to enhance sensitivity of stretchable strain sensors. Adv. Mater. 2018, 30, 1706589. [Google Scholar] [CrossRef]
- Li, J.; Slesarenko, V.; Rudykh, S. Auxetic multiphase soft composite material design through instabilities with application for acoustic metamaterials. Soft Matter 2018, 14, 6171–6180. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H.P. Recent Advances in Active Acoustic Metamaterials. Int. J. Appl. Mech. 2019, 11, 1950081. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Kumar, S.; Lee, H.P. Thermal tuning of negative effective mass density in a two-dimensional acoustic metamaterial with hexagonal lattice. J. Appl. Phys. 2019, 126, 155102. [Google Scholar] [CrossRef]
- Kumar, S.; Bhushan, P.; Pandey, M.; Bhattacharya, S. Additive manufacturing as an emerging technology for fabrication of microelectromechanical systems (MEMS). J. Micromanuf. 2019, 2, 175–197. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Lee, H.P. Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances. Crystals 2020, 10, 686. https://doi.org/10.3390/cryst10080686
Kumar S, Lee HP. Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances. Crystals. 2020; 10(8):686. https://doi.org/10.3390/cryst10080686
Chicago/Turabian StyleKumar, Sanjay, and Heow Pueh Lee. 2020. "Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances" Crystals 10, no. 8: 686. https://doi.org/10.3390/cryst10080686
APA StyleKumar, S., & Lee, H. P. (2020). Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances. Crystals, 10(8), 686. https://doi.org/10.3390/cryst10080686





