Polarization Splitter-Rotator Based on Multimode Waveguide Grating
Abstract
:1. Introduction
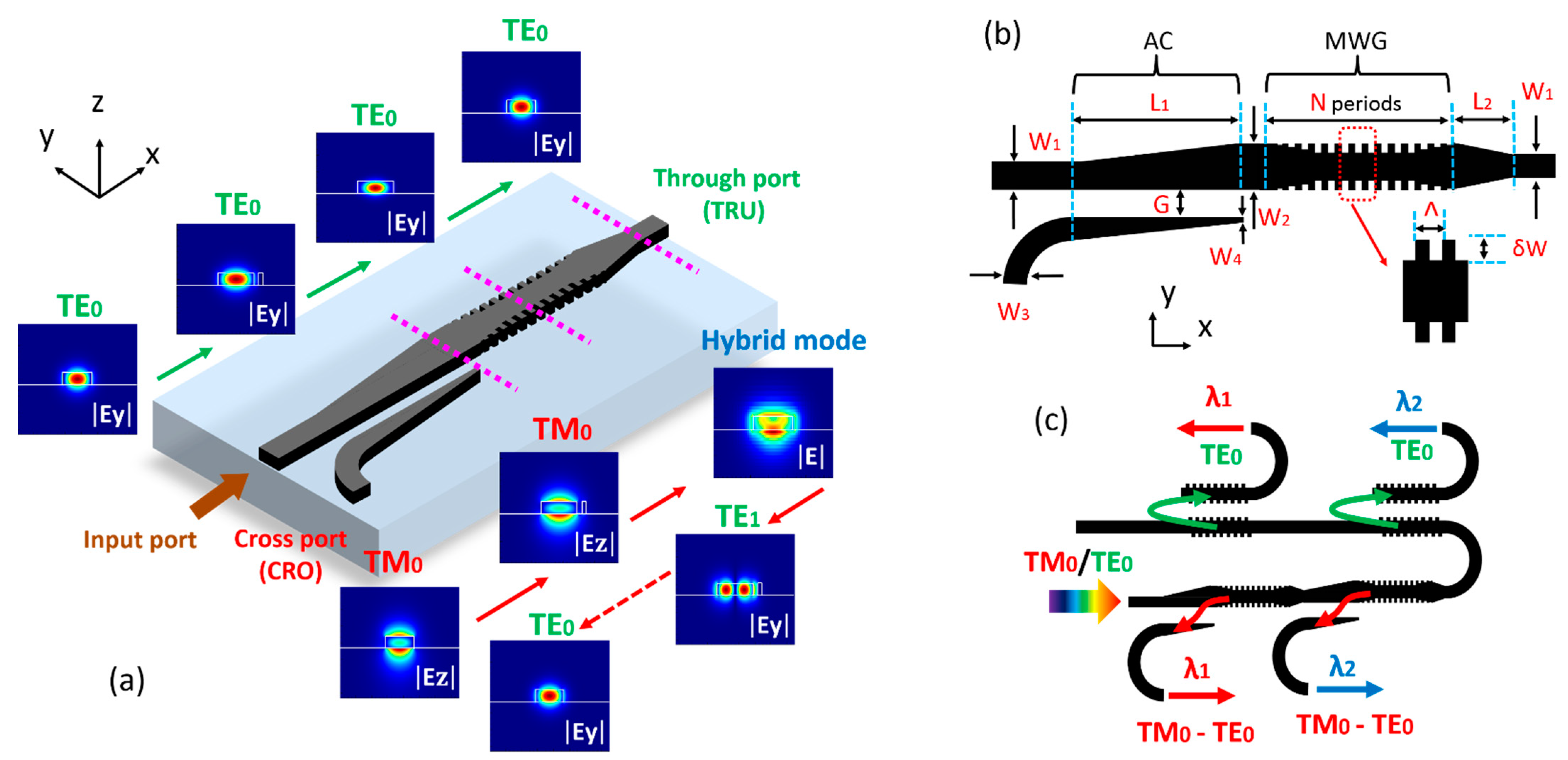
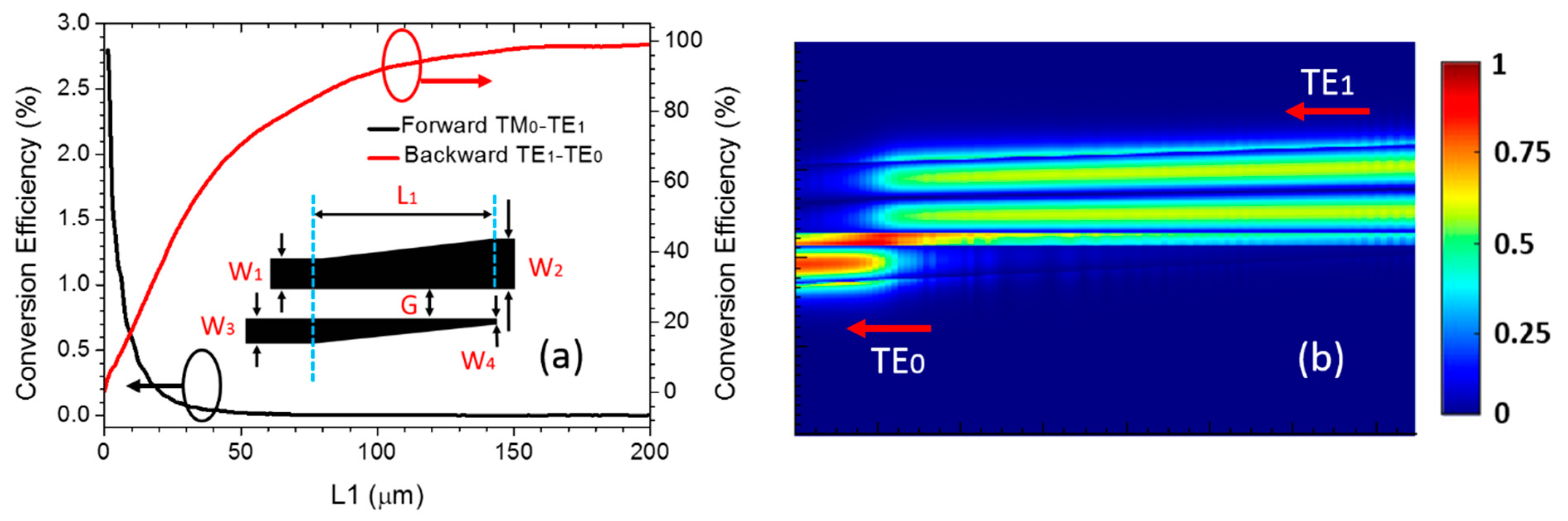
2. Device Structure and Working Principle
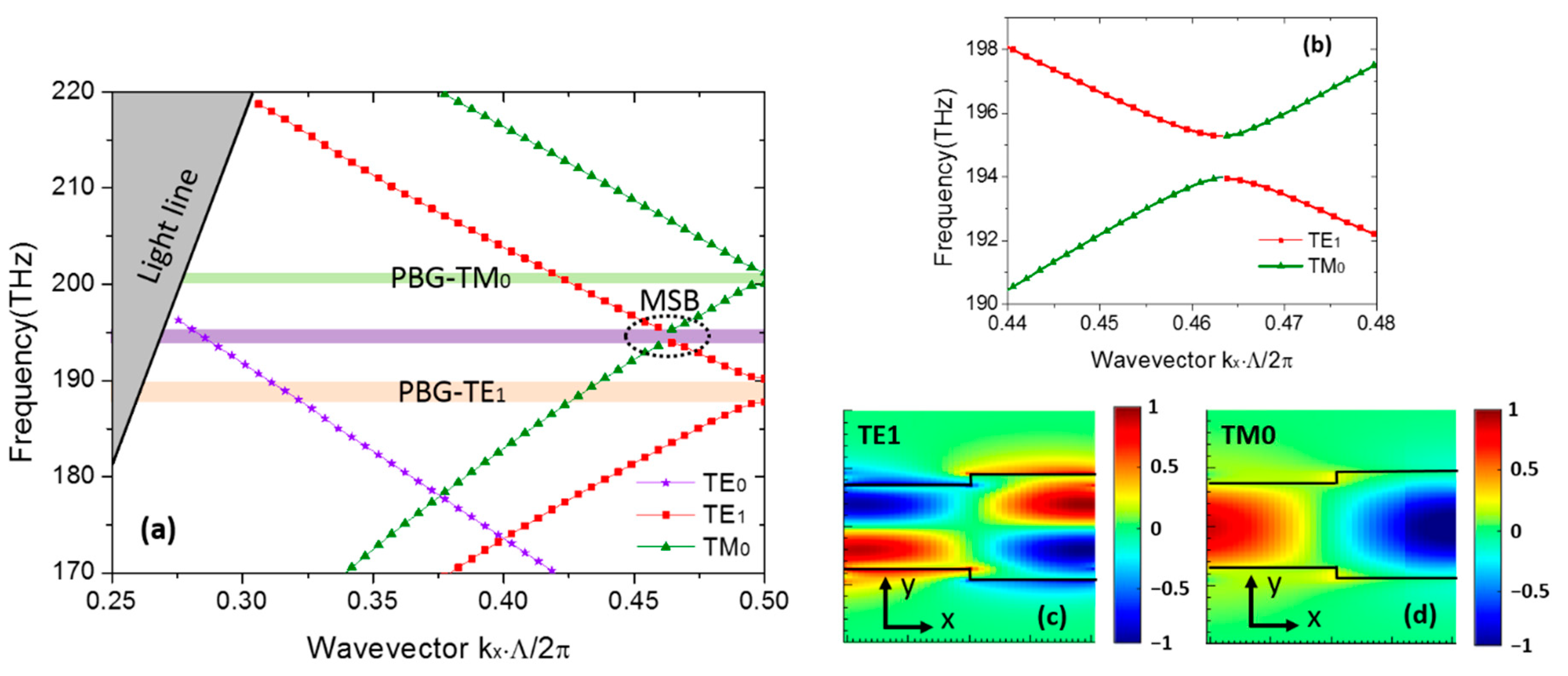
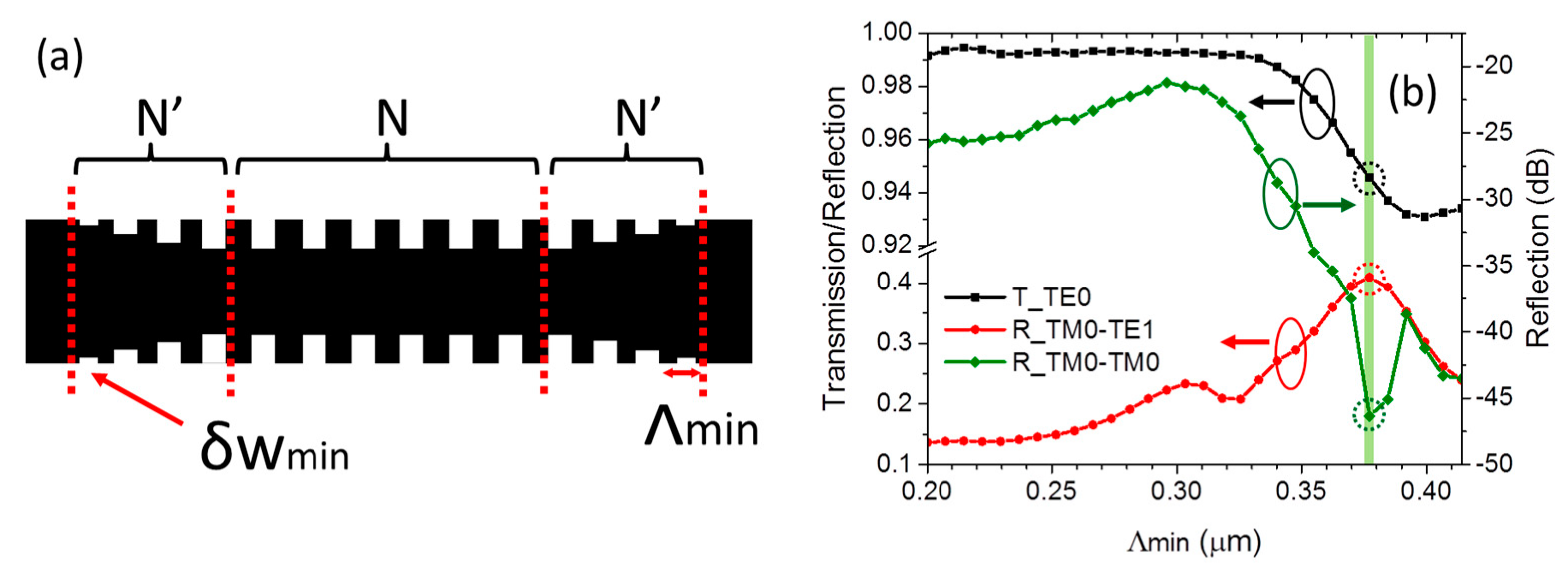
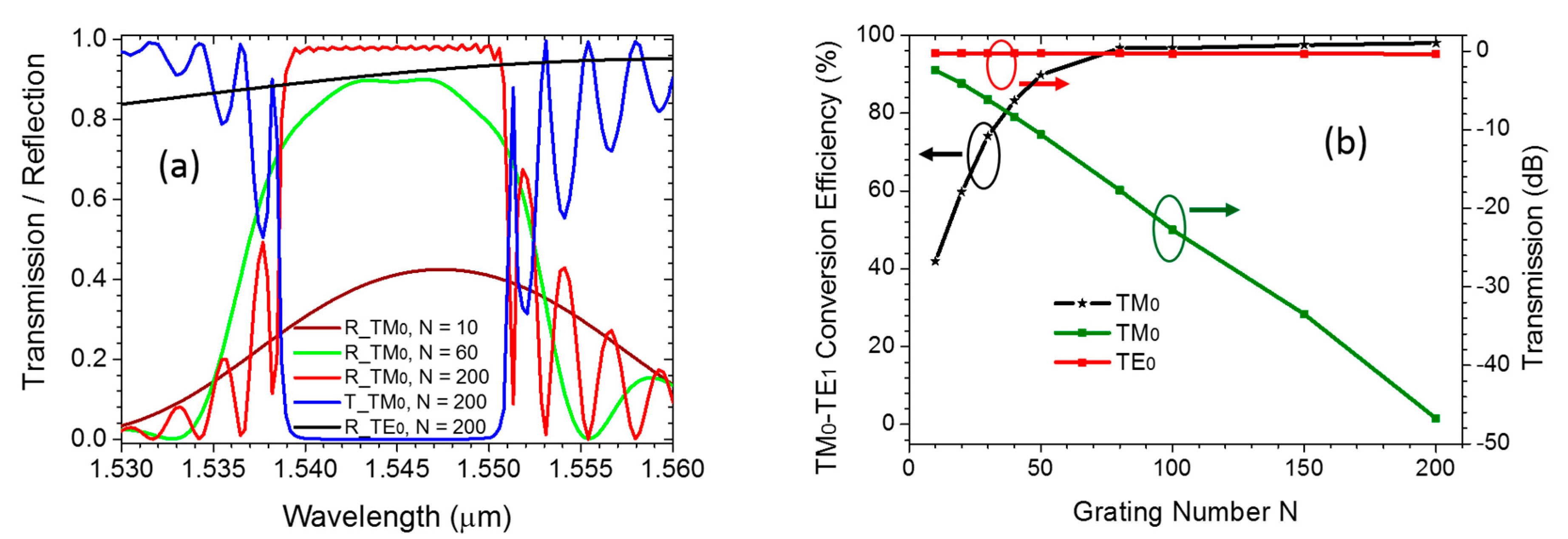
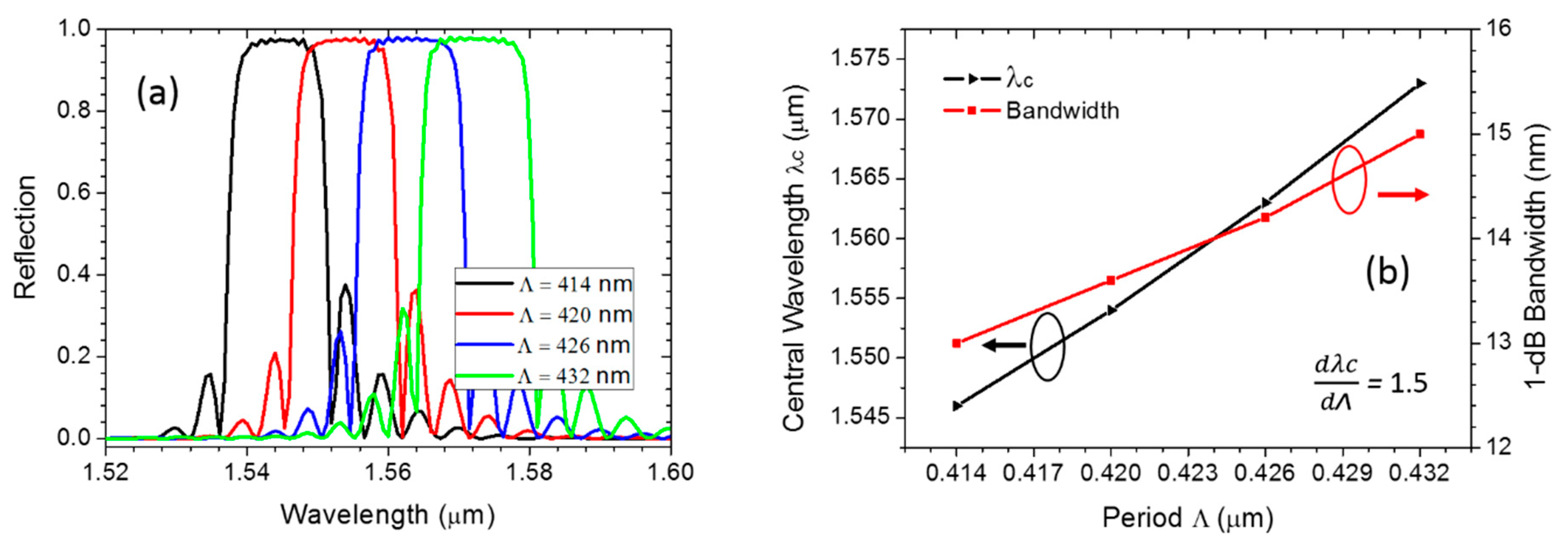
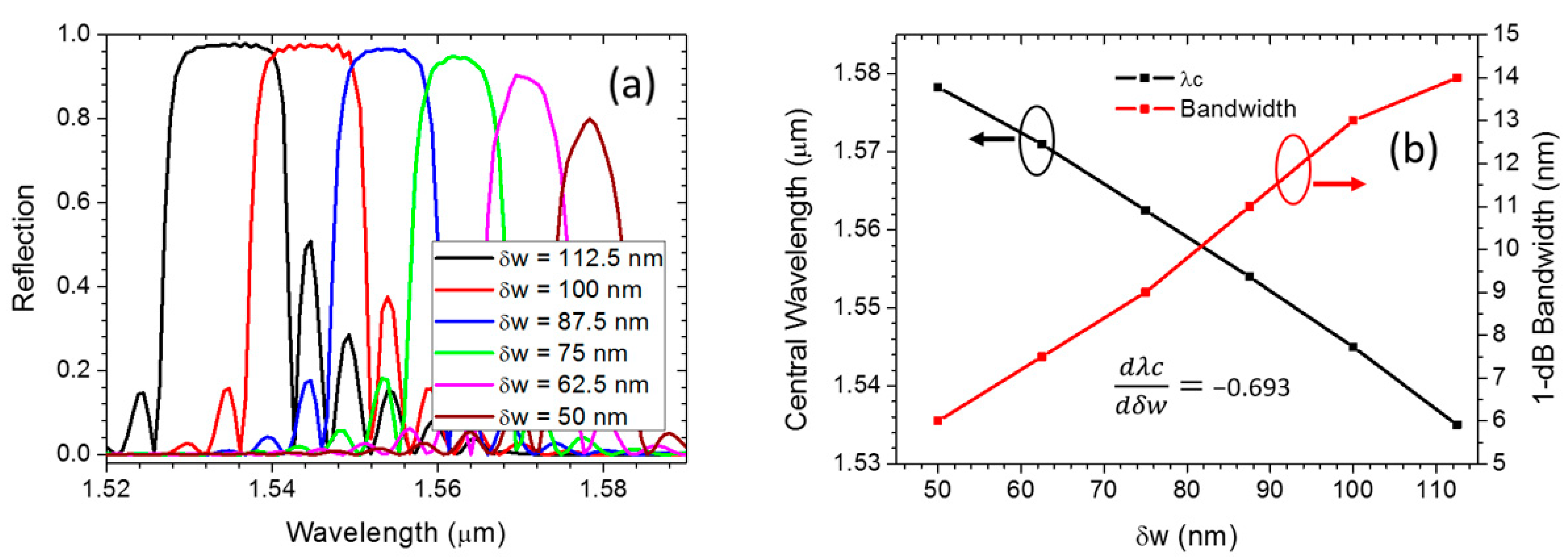
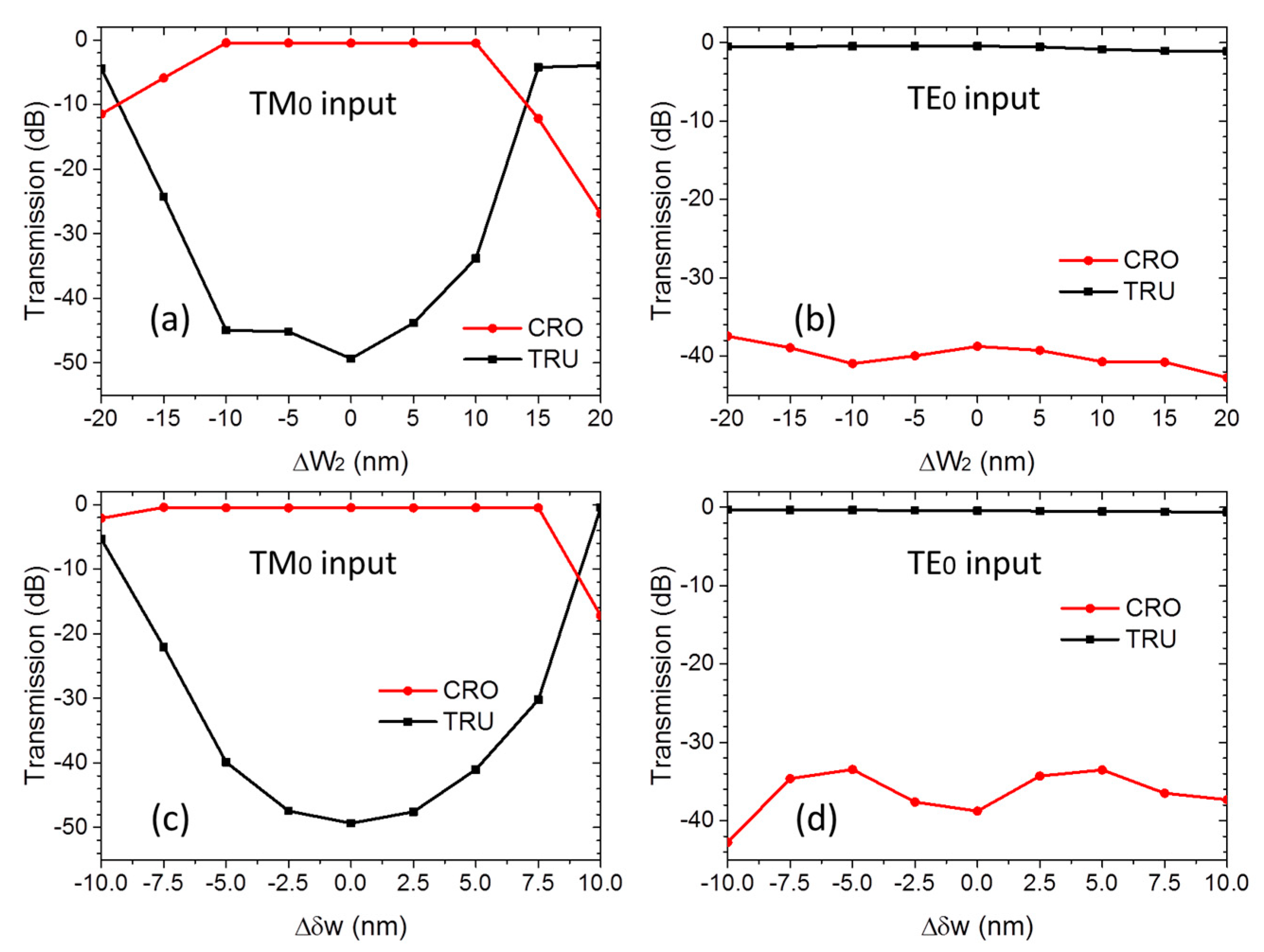
3. Device Performance and Analysis
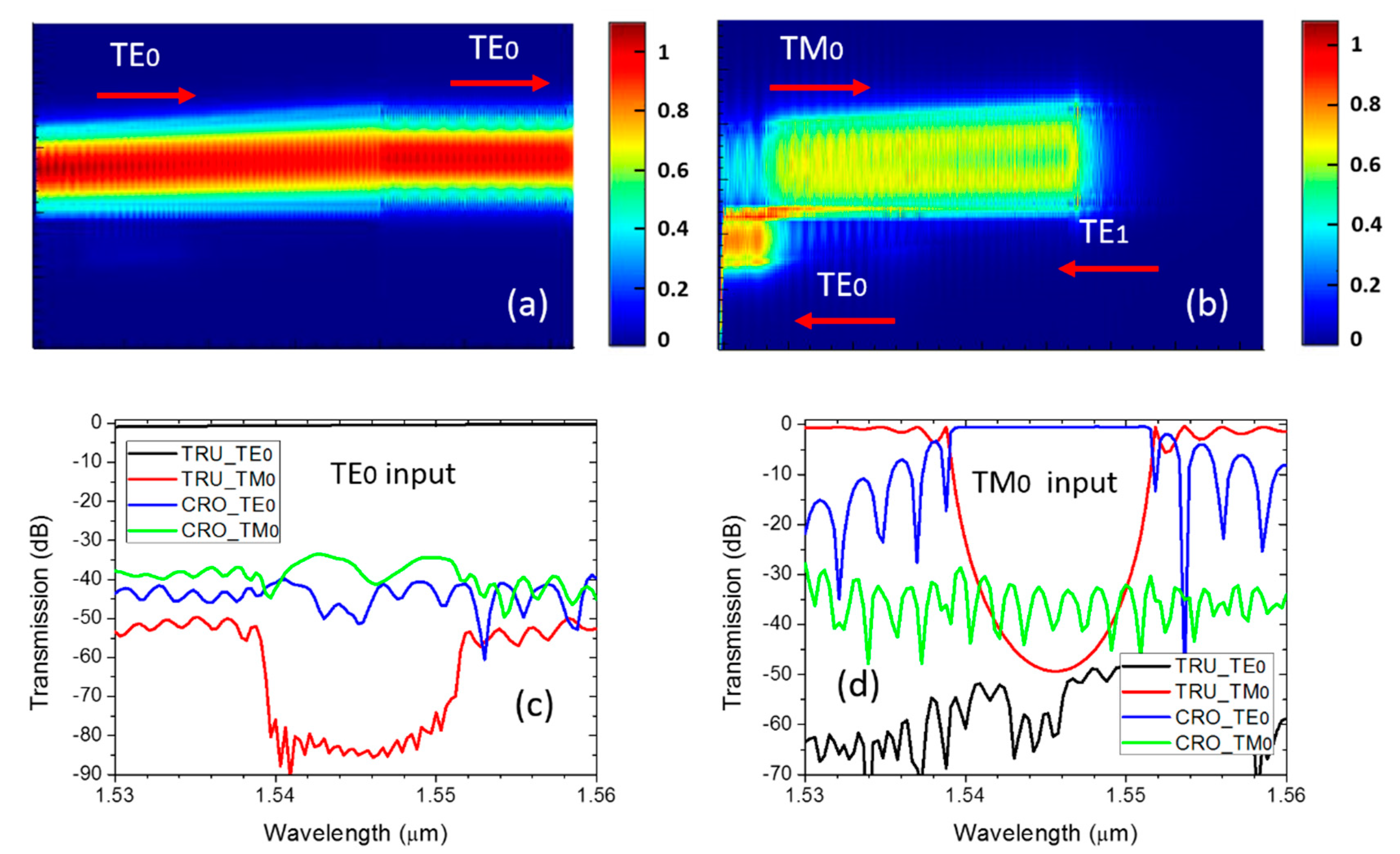
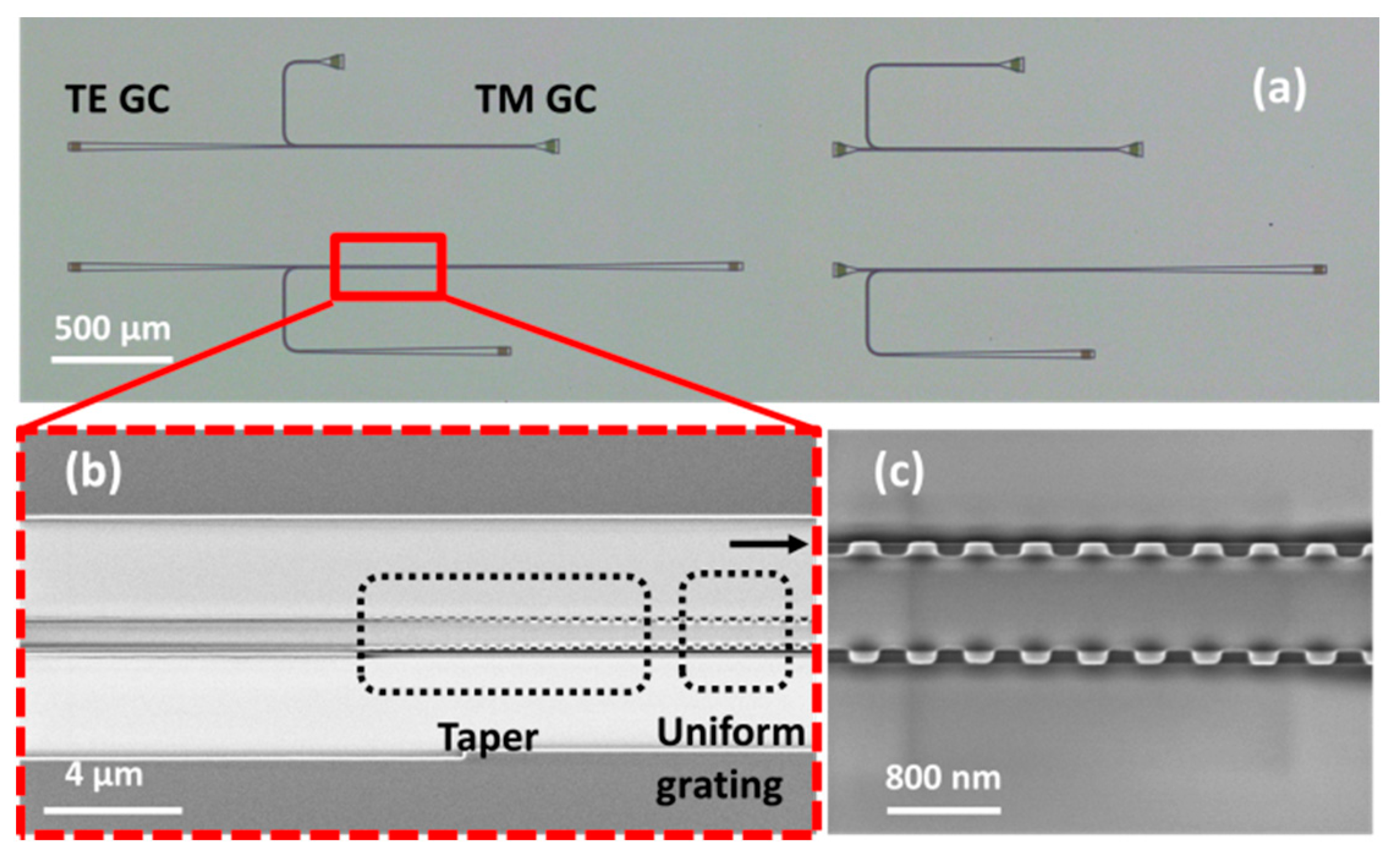
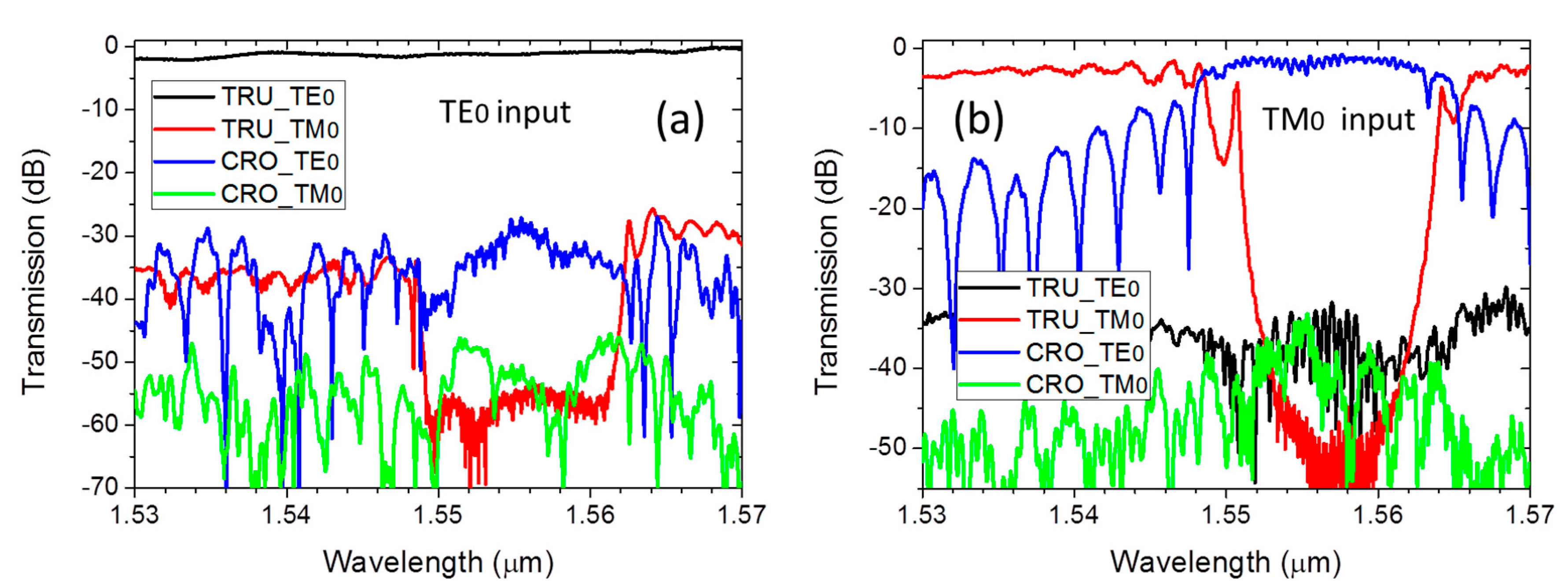
4. Fabrication and Measurement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, D.; Bowers, J.E. Novel concept for ultracompact polarization splitter-rotator based on silicon nanowires. Opt. Exp. 2011, 19, 10940–10949. [Google Scholar] [CrossRef] [Green Version]
- Dai, D.; Liu, L.; Gao, S.; Xu, D.X.; He, S. Polarization management for silicon photonic integrated circuits. Laser Photonics Rev. 2013, 7, 303–328. [Google Scholar] [CrossRef]
- Doerr, C.; Chen, L.; Vermeulen, D.; Nielsen, T.; Azemati, S.; Stulz, S.; McBrien, G.; Xu, X.-M.; Mikkelsen, B.; Givehchi, M. Single-chip silicon photonics 100-Gb/s coherent transceiver. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014; p. Th5C.1. [Google Scholar]
- Sacher, W.D.; Barwicz, T.; Taylor, B.J.F.; Poon, J.K.S. Polarization rotator-splitters in standard active silicon photonics platforms. Opt. Exp. 2014, 22, 3777–3786. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, M.; Yun, H.; Lu, Z.; Wang, X.; Jaeger, N.A.; Chrostowski, L. Ultra-compact sub-wavelength grating polarization splitter-rotator for silicon-on-insulator platform. IEEE Photon. J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Keyvaninia, S.; Boerma, H.; Wössner, M.; Ganzer, F.; Runge, P.; Schell, M. Highly efficient passive InP polarization rotator-splitter. Opt. Exp. 2019, 27, 25872–25881. [Google Scholar] [CrossRef] [PubMed]
- Chung, C.-J.; Midkiff, J.; Yoo, K.M.; Rostamian, A.; Guo, J.; Chen, R.T.; Chakravarty, S. InP-based polarization rotator-splitter for mid-infrared photonic integration circuits. AIP Adv. 2019, 9, 015303. [Google Scholar] [CrossRef]
- Dai, X.; Lu, Q.; Guo, W. Fabrication-Tolerant Polarization Rotator-Splitter based on Silicon Nitride Platform. In Proceedings of the Optical Fiber Communication Conference, Washington, DC, USA, 6–11 June 2021; p. Th1A.31. [Google Scholar]
- Chen, Z.; Pan, Y.; Liu, X.; Lin, H.; Zhong, X.; Cai, X. Single-step Etching Polarization Splitter-rotator based on Lithium Niobate Ridge Waveguide. In Proceedings of the Asia Communications and Photonics Conference, Chengdu, China, 2–5 November 2019; p. M4A.285. [Google Scholar]
- Zhang, L.; Yang, S.; Zhang, G.; Fu, X.; Yang, L. Broadband 2 × 2 Polarization Splitter-Rotator Based on an Adiabatic Asymmetric Directional Coupler on the Lithium-Niobate-on-Insulator. In Proceedings of the Asia Communications and Photonics Conference, Beijing, China, 24–27 October 2020; p. M4A.176. [Google Scholar]
- Tu, X.; Li, M.; Xing, J.; Fu, H.; Geng, D. Compact PSR based on an asymmetric bi-level lateral taper in an adiabatic directional coupler. J. Light. Technol. 2016, 34, 985–991. [Google Scholar] [CrossRef]
- Wang, J.; Qi, M.; Xuan, Y.; Huang, H.; Li, Y.; Li, M.; Chen, X.; Jia, Q.; Sheng, Z.; Wu, A. Proposal for fabrication-tolerant SOI polarization splitter-rotator based on cascaded MMI couplers and an assisted bi-level taper. Opt. Exp. 2014, 22, 27869–27879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bai, B.; Liu, L.; Zhou, Z. Ultracompact, high extinction ratio polarization beam splitter-rotator based on hybrid plasmonic-dielectric directional coupling. Opt. Lett. 2017, 42, 4752–4755. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Doerr, C.R.; Chen, Y.-K. Compact polarization rotator on silicon for polarization-diversified circuits. Opt. Lett. 2011, 36, 469–471. [Google Scholar] [CrossRef]
- Guan, H.; Novack, A.; Streshinsky, M.; Shi, R.; Fang, Q.; Lim, A.E.-J.; Lo, G.-Q.; Baehr-Jones, T.; Hochberg, M. CMOS-compatible highly efficient polarization splitter and rotator based on a double-etched directional coupler. Opt. Exp. 2014, 22, 2489–2496. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Wu, H. Realization of a compact polarization splitter-rotator on silicon. Opt. Lett. 2016, 41, 2346–2349. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Li, Z.; Dai, D. Ultra-broadband polarization splitter-rotator based on the mode evolution in a dual-core adiabatic taper. J. Light. Technol. 2017, 35, 2227–2233. [Google Scholar] [CrossRef]
- Liu, L.; Ding, Y.; Yvind, K.; Hvam, J.M. Silicon-on-insulator polarization splitting and rotating device for polarization diversity circuits. Opt. Exp. 2011, 19, 12646–12651. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Liu, L.; Peucheret, C.; Ou, H. Fabrication tolerant polarization splitter and rotator based on a tapered directional coupler. Opt. Exp. 2012, 20, 20021–20027. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.; Huang, Y.; Lo, G.-Q.; Lee, C.; Yu, C. Compact highly-efficient polarization splitter and rotator based on 90° bends. Opt. Exp. 2016, 24, 14506–14512. [Google Scholar] [CrossRef] [Green Version]
- Zafar, H.; Pereira, M.F.; Kennedy, K.L.; Anjum, D.H. Fabrication-tolerant and CMOS-compatible polarization splitter and rotator based on a compact bent-tapered directional coupler. AIP Adv. 2020, 10, 125214. [Google Scholar] [CrossRef]
- Xu, H.; Shi, Y. Ultra-broadband silicon polarization splitter-rotator based on the multi-mode waveguide. Opt. Exp. 2017, 25, 18485–18491. [Google Scholar] [CrossRef]
- Jeong, S.-H.; Onawa, Y.; Shimura, D.; Okayama, H.; Aoki, T.; Yaegashi, H.; Horikawa, T.; Nakamura, T. Polarization diversified 16λ demultiplexer based on silicon wire delayed interferometers and arrayed waveguide gratings. J. Light. Technol. 2020, 38, 2680–2687. [Google Scholar] [CrossRef]
- Onawa, Y.; Okayama, H.; Shimura, D.; Takahashi, H.; Yaegashi, H.; Sasaki, H. Polarisation insensitive wavelength de-multiplexer using arrayed waveguide grating and polarisation rotator/splitter. Electron. Lett. 2019, 55, 475–476. [Google Scholar] [CrossRef]
- Chen, S.; Fu, X.; Wang, J.; Shi, Y.; He, S.; Dai, D. Compact dense wavelength-division (de) multiplexer utilizing a bidirectional arrayed-waveguide grating integrated with a Mach–Zehnder interferometer. J. Light. Technol. 2015, 33, 2279–2285. [Google Scholar] [CrossRef]
- Olivier, S.; Rattier, M.; Benisty, H.; Weisbuch, C.; Smith, C.; De La Rue, R.; Krauss, T.; Oesterle, U.; Houdré, R. Mini-stopbands of a one-dimensional system: The channel waveguide in a two-dimensional photonic crystal. Phys. Rev. B 2001, 63, 113311. [Google Scholar] [CrossRef]
- Olivier, S.; Benisty, H.; Weisbuch, C.; Smith, C.J.; Krauss, T.F.; Houdré, R. Coupled-mode theory and propagation losses in photonic crystal waveguides. Opt. Exp. 2003, 11, 1490–1496. [Google Scholar] [CrossRef]
- Cao, T.; Cryan, M.J.; Ivanov, P.S.; Ho, D.; Ren, B.; Craddock, I.J.; Rorison, J.M.; Railton, C.J. Modeling of chirped pulse propagation through a mini-stop band in a two-dimensional photonic crystal waveguide. J. Opt. Soc. Am. B 2007, 24, 1575–1583. [Google Scholar] [CrossRef]
- Benisty, H.; Cambournac, C.; Van Laere, F.; Van Thourhout, D. Photonic-crystal demultiplexer with improved crosstalk by second-order cavity filtering. J. Light. Technol. 2010, 28, 1201–1208. [Google Scholar] [CrossRef]
- Shahid, N.; Amin, M.; Naureen, S.; Swillo, M.; Anand, S. Junction-type photonic crystal waveguides for notch-and pass-band filtering. Opt. Exp. 2011, 19, 21074–21080. [Google Scholar] [CrossRef] [PubMed]
- Ayre, M.; Cambournac, C.; Khayam, O.; Benisty, H.; Stomeo, T.; Krauss, T. Photonic crystal waveguides for coarse-selectivity devices. Photonics Nanostruct. 2008, 6, 19–25. [Google Scholar] [CrossRef]
- Moore, S.; O’Faolain, L.; White, T.; Krauss, T. Photonic crystal laser with mode selective mirrors. Opt. Exp. 2008, 16, 1365–1370. [Google Scholar] [CrossRef]
- Qiu, H.; Jiang, J.; Yu, P.; Yang, J.; Yu, H.; Jiang, X. Broad bandwidth and large fabrication tolerance polarization beam splitter based on multimode anti-symmetric Bragg sidewall gratings. Opt. Lett. 2017, 42, 3912–3915. [Google Scholar] [CrossRef]
- Huang, Q.; Jie, K.; Liu, Q.; Huang, Y.; Wang, Y.; Xia, J. Ultra-compact, broadband tunable optical bandstop filters based on a multimode one-dimensional photonic crystal waveguide. Opt. Exp. 2016, 24, 20542–20553. [Google Scholar] [CrossRef]
- Shi, W.; Yun, H.; Lin, C.; Greenberg, M.; Wang, X.; Wang, Y.; Fard, S.T.; Flueckiger, J.; Jaeger, N.A.; Chrostowski, L. Ultra-compact, flat-top demultiplexer using anti-reflection contra-directional couplers for CWDM networks on silicon. Opt. Exp. 2013, 21, 6733–6738. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Shi, Y. Flat-Top CWDM (De) multiplexers Based on Contra-directional Couplers with Subwavelength Gratings. IEEE Photon. Technol. Lett. 2019, 31, 2003–2006. [Google Scholar] [CrossRef]
- Chen, L.; Doerr, C.R.; Chen, Y.-k. Polarization-diversified DWDM receiver on silicon free of polarization-dependent wavelength shift. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012; pp. 1–3. [Google Scholar]
- Corzine, S.W.; Evans, P.; Fisher, M.; Gheorma, J.; Kato, M.; Dominic, V.; Samra, P.; Nilsson, A.; Rahn, J.; Lyubomirsky, I. Large-scale InP transmitter PICs for PM-DQPSK fiber transmission systems. IEEE Photon. Technol. Lett. 2010, 22, 1015–1017. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Flueckiger, J.; Bojko, R.; Liu, A.; Reid, A.; Pond, J.; Jaeger, N.A.; Chrostowski, L. Precise control of the coupling coefficient through destructive interference in silicon waveguide Bragg gratings. Opt. Lett. 2014, 39, 5519–5522. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Qiu, H.; Wang, G.; Li, Y.; Dai, T.; Mu, D.; Yu, H.; Yang, J.; Jiang, X. Silicon lateral-apodized add–drop filter for on-chip optical interconnection. Appl. Opt. 2017, 56, 8425–8429. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Chrostowski, L. Spectral Design of Silicon Integrated Bragg Gratings: A Tutorial. J. Light. Technol. 2020, 39, 712–729. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Wang, Y.; Liu, W.; Xie, H.; Yao, Y.; Song, Q.; Zhang, X.; Yu, Y.; Xu, K. Subwavelength polarization splitter–rotator with ultra-compact footprint. Opt. Lett. 2019, 44, 4495–4498. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Ge, R.; Luo, H.; Wu, M.; Zhou, L.; Aryal, M.; Li, W.; Yuan, J.; Xu, J.; Lan, Q.; et al. Polarization Splitter-Rotator Based on Multimode Waveguide Grating. Crystals 2021, 11, 1170. https://doi.org/10.3390/cryst11101170
Luo Y, Ge R, Luo H, Wu M, Zhou L, Aryal M, Li W, Yuan J, Xu J, Lan Q, et al. Polarization Splitter-Rotator Based on Multimode Waveguide Grating. Crystals. 2021; 11(10):1170. https://doi.org/10.3390/cryst11101170
Chicago/Turabian StyleLuo, Yannong, Renyou Ge, Haozhi Luo, Meiyan Wu, Lidan Zhou, Makunda Aryal, Wenwei Li, Jianhui Yuan, Jian Xu, Quanxue Lan, and et al. 2021. "Polarization Splitter-Rotator Based on Multimode Waveguide Grating" Crystals 11, no. 10: 1170. https://doi.org/10.3390/cryst11101170
APA StyleLuo, Y., Ge, R., Luo, H., Wu, M., Zhou, L., Aryal, M., Li, W., Yuan, J., Xu, J., Lan, Q., Li, Y., & Cai, X. (2021). Polarization Splitter-Rotator Based on Multimode Waveguide Grating. Crystals, 11(10), 1170. https://doi.org/10.3390/cryst11101170




